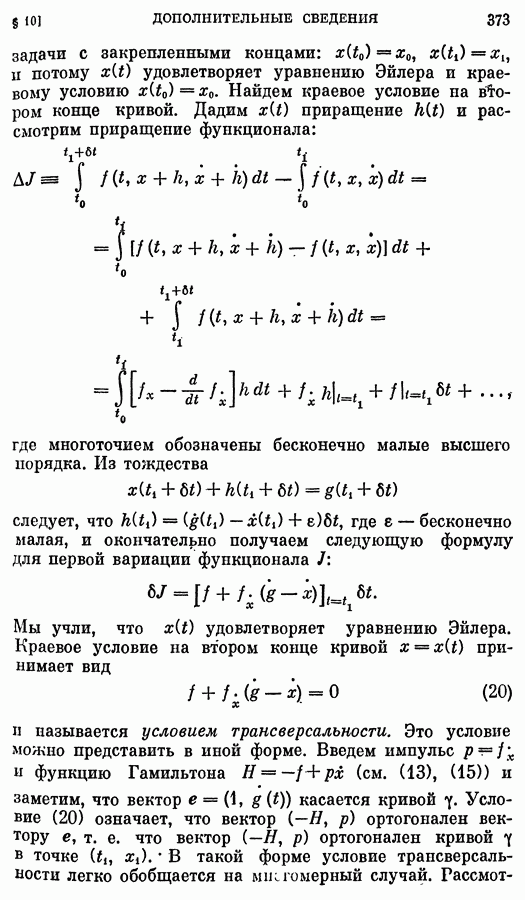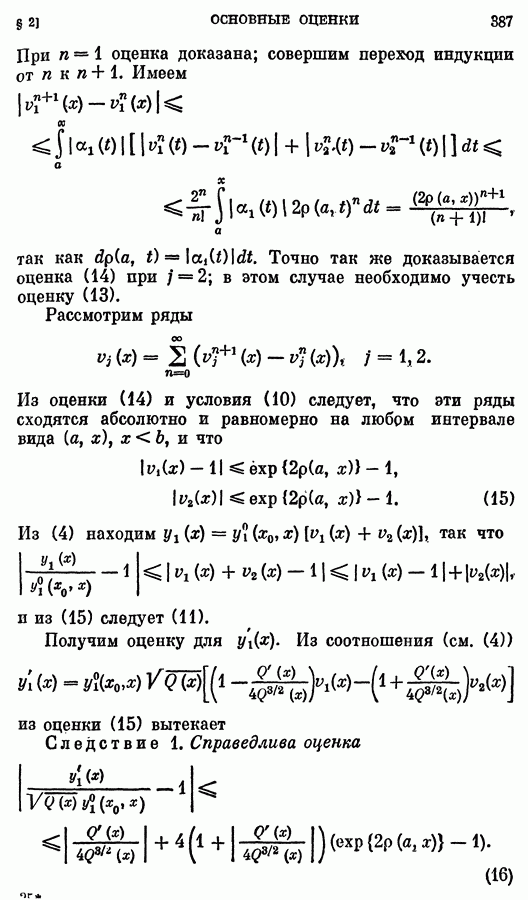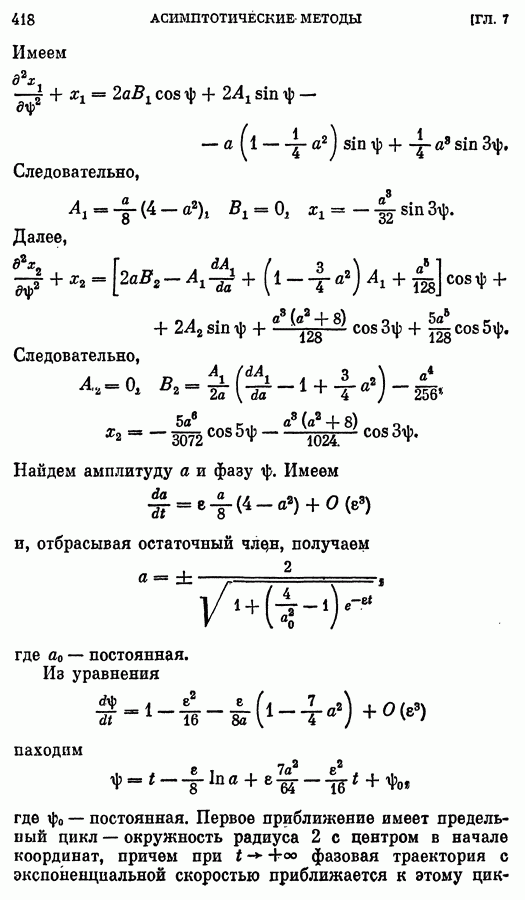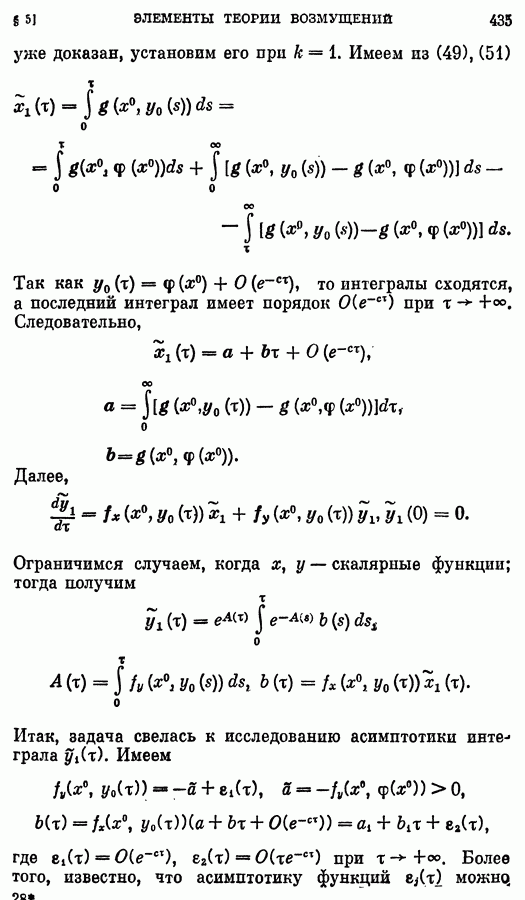| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Лемма Адамара
Для дифференцируемой функции  одной переменной справедлива формула конечных приращений Лагранжа:
одной переменной справедлива формула конечных приращений Лагранжа:

где точка  лежит в интервале
лежит в интервале  Докажем многомерный аналог этой формулы.
Докажем многомерный аналог этой формулы.
Область  в пространстве
в пространстве  называется выпуклой, если вместе с любыми двумя точками у эта область содержит отрезок, их соединяющий. Примеры выпуклых областей в трехмерном пространстве: параллелепипед, шар, эллипсоид. Пусть
называется выпуклой, если вместе с любыми двумя точками у эта область содержит отрезок, их соединяющий. Примеры выпуклых областей в трехмерном пространстве: параллелепипед, шар, эллипсоид. Пусть 
Лемма 1. Пусть функция  непрерывно дифференцируема в выпуклой области
непрерывно дифференцируема в выпуклой области  Если точки
Если точки  то
то

где точка  лежит на отрезке, соединяющем точки х, у.
лежит на отрезке, соединяющем точки х, у.
Доказательство. Так как область  выпукла, то она содержит отрезок
выпукла, то она содержит отрезок  , соединяющий точки х, у. Всякая точка этого отрезка имеет вид
, соединяющий точки х, у. Всякая точка этого отрезка имеет вид  и на этом отрезке функция
и на этом отрезке функция  есть функция от одной переменной
есть функция от одной переменной  По формуле конечных приращений Лагранжа
По формуле конечных приращений Лагранжа

Так как 

то из (3) следует (2), где 
Ввиду важности этой леммы для последующего приведем другую формулировку и другое доказательство.
Лемма 2. Если условия леммы 1 выполнены, то

где функции  непрерывны по совокупности переменных при
непрерывны по совокупности переменных при 
Доказательство. Имеем, пспользуя (4),

где функции  равны
равны

Из этой формулы следует непрерывность функций 
Лемма 3. Пусть вектор-функция  непрерывно дифференцируема в замкнутой ограниченной выпуклой области
непрерывно дифференцируема в замкнутой ограниченной выпуклой области  Тогда для любых точек
Тогда для любых точек

где обозначено

Доказательство. Применяя формулу (2) к компоненте  получаем
получаем

так как  Из полученной оценки и определения нормы вектора (§ 2, пример 3) следует лемма.
Из полученной оценки и определения нормы вектора (§ 2, пример 3) следует лемма.
Аналогом формулы конечных приращений Лагранжа для вектор-функций (в условиях леммы 3) служит формула

которая следует из (1). Здесь  есть
есть  -матрица
-матрица
с элементами

точки 1 лежат на отрезке, соединяющем точки х, у. Матрица-функция  непрерывна при
непрерывна при 
Рассмотрим функцию  , где
, где 
Лемма Ада мара. Пусть  — область в пространстве
— область в пространстве  выпуклая по переменным х, функция
выпуклая по переменным х, функция  имеет в области
имеет в области  непрерывные производные до порядка
непрерывные производные до порядка
1 включительно. Тогда существуют функции  имеющие непрерывные производные по
имеющие непрерывные производные по  до порядка
до порядка  включительно, такие, что
включительно, такие, что

Доказательство следует из (5), (6); в данном случае

где  — производная
— производная  по переменной
по переменной 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
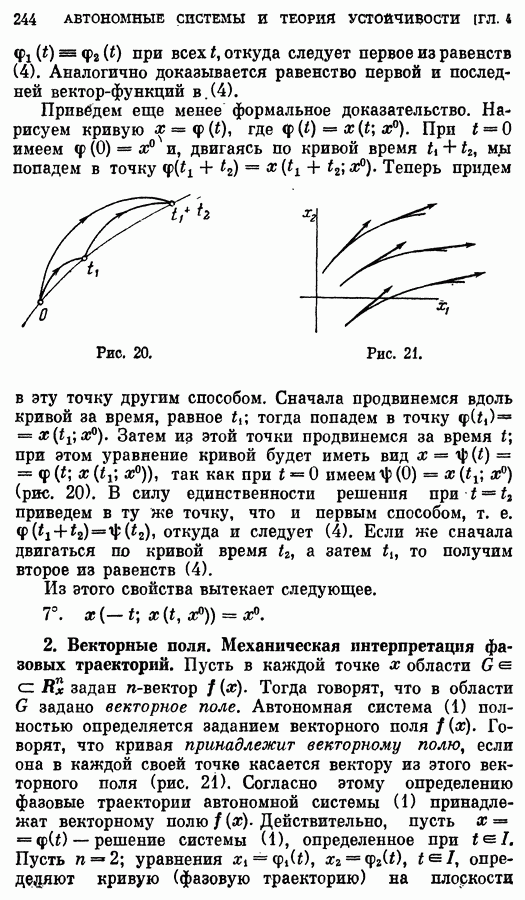
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
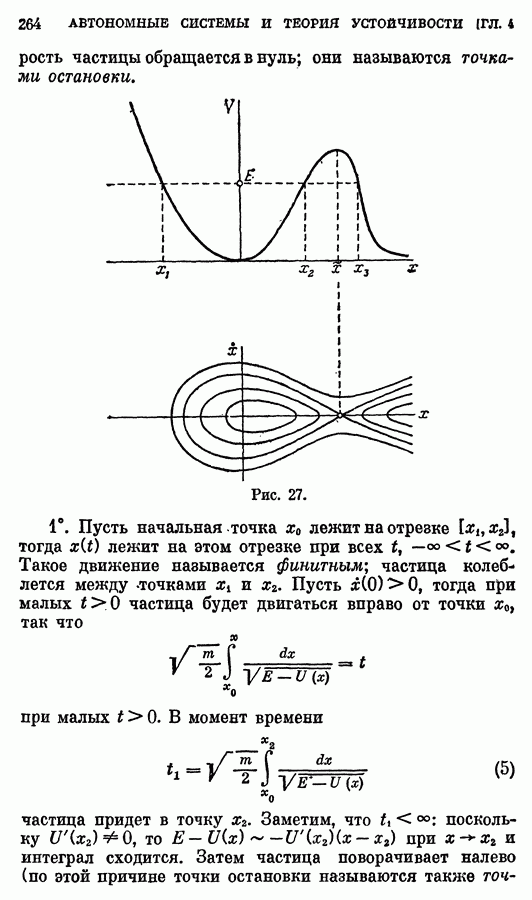
- § 5. Одномерное движение частицы в потенциальном поле
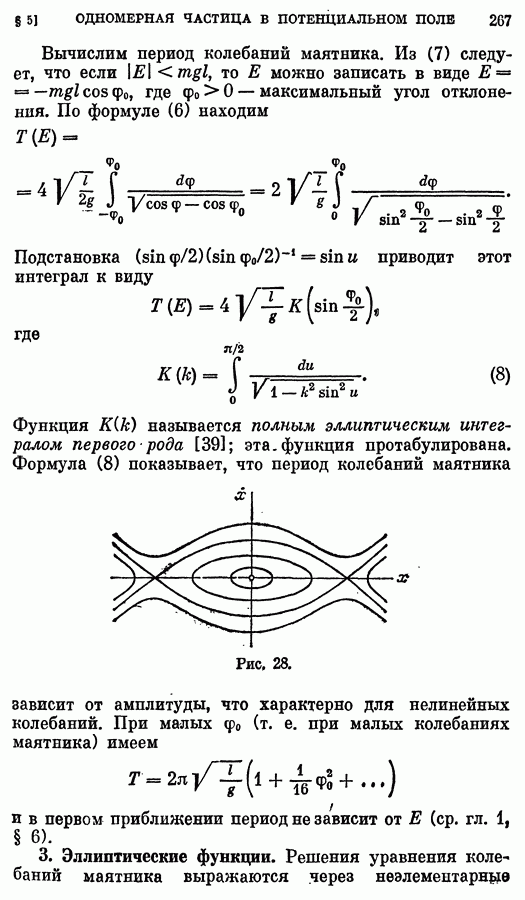
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
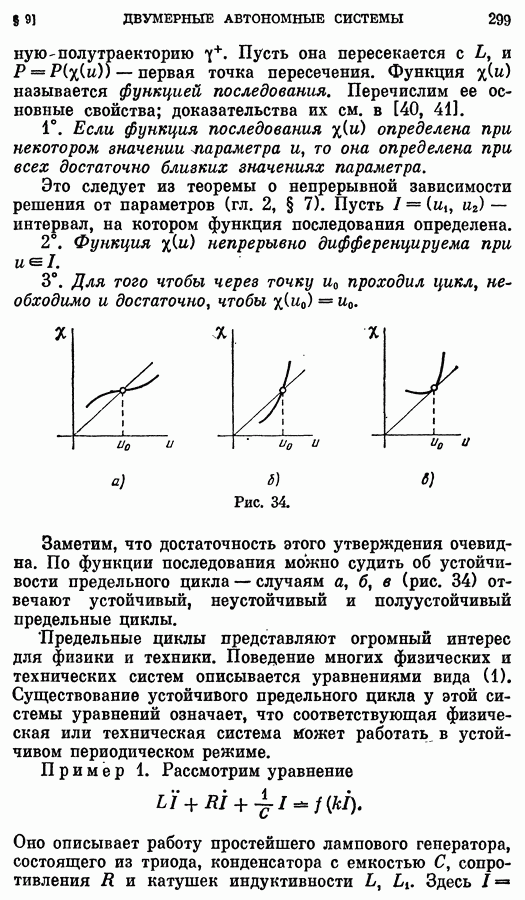
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ