| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Линейные уравнения с правой частью — квазимногочленом
Частное решение неоднородного линейного дифференциального уравнения вида

где  — многочлен степени
— многочлен степени  может быть найдено элементарно.
может быть найдено элементарно.
Лемма 1. Если  — дифференциальный оператор с постоянными коэффициентами, то справедлива формула сдвига:
— дифференциальный оператор с постоянными коэффициентами, то справедлива формула сдвига:

Доказательство. По формуле Лейбница имеем

Следовательно,

Теорема. 1°. Нерезонансный случай. Пусть  не является корнем характеристического уравнения.
не является корнем характеристического уравнения.
Тогда уравнение (1) имеет частное решение вида

где  — многочлен степени
— многочлен степени  .
.
2°. Резонансный случай. Пусть — корень характеристического уравнения, кратности к. Тогда уравнение (1) имеет частное решение вида

где  — многочлен степени т.
— многочлен степени т.
Доказательство. Сделаем замену

и применим формулу сдвига (2). Тогда для  получим уравнение
получим уравнение

Многочлен  равен
равен  и так как
и так как  , то
, то  . По условию,
. По условию,

Будем искать  в виде
в виде

где  — неизвестные коэффициенты (метод неопределенных коэффициентов). Подставляя
— неизвестные коэффициенты (метод неопределенных коэффициентов). Подставляя  в уравнение (6), получаем
в уравнение (6), получаем

Приравняем коэффициенты при степенях  тогда получим уравнения
тогда получим уравнения

Так как  , то из этой системы последовательно находятся коэффициенты
, то из этой системы последовательно находятся коэффициенты  . Из формул (7), (5) следует формула (3).
. Из формул (7), (5) следует формула (3).
В случае 2° характеристическое уравнение  имеет корень
имеет корень  кратности к, так как
кратности к, так как  Поэтому
Поэтому

Введем новую неизвестную функцию  тогда для
тогда для  получим уравнение
получим уравнение

Поскольку  то для этого уравнения имеет место случай 1°, и оно имеет частное решение вида
то для этого уравнения имеет место случай 1°, и оно имеет частное решение вида

Интегрируя, получаем

Интегрируя от 0 до а: еще  раз, получаем
раз, получаем  где
где  — многочлен степени
— многочлен степени  . Из этой формулы и (5) следует (4).
. Из этой формулы и (5) следует (4).
Рассмотрим уравнение

Пусть коэффициенты уравнения  число
число  и коэффициенты многочлена
и коэффициенты многочлена  вещественны. Найдем вещественное частное решение уравнения (8). Заметим, что если число
вещественны. Найдем вещественное частное решение уравнения (8). Заметим, что если число  не является корнем характеристического уравнения или является корнем кратности к, то тем же свойством обладает комплексно сопряженное число
не является корнем характеристического уравнения или является корнем кратности к, то тем же свойством обладает комплексно сопряженное число  Уравнение (8) имеет вещественное частное решение вида
Уравнение (8) имеет вещественное частное решение вида

если  не является корнем характеристического уравнения, и вида
не является корнем характеристического уравнения, и вида

если  — корень характеристического уравнения кратности k. Здесь
— корень характеристического уравнения кратности k. Здесь  — многочлен степени
— многочлен степени  с вещественными коэффициентами.
с вещественными коэффициентами.
Пример 1. Рассмотрим уравнение Ньютона

Здесь  вещественно. Удобнее вместо уравнения (9) решать уравнение
вещественно. Удобнее вместо уравнения (9) решать уравнение

Вещественная часть решения  удовлетворяет уравнению (9).
удовлетворяет уравнению (9).
1°. Пусть  тогда частное решение ищем в виде
тогда частное решение ищем в виде  Подставляя в (9), находим
Подставляя в (9), находим  , так что всякое решение уравнения (9) имеет вид
, так что всякое решение уравнения (9) имеет вид

а всякое вещественное решение уравнения (9) имеет вид

2°. Пусть  тогда частное решение ищем в виде
тогда частное решение ищем в виде  (так как кратность к корня
(так как кратность к корня  уравнения
уравнения  Всякое решение уравнения (9) имеет вид
Всякое решение уравнения (9) имеет вид

а всякое вещественное решение уравнения (9) имеет вид

Приведем физическую интерпретацию формул (11), (12). Однородное уравнение (9) (при  описывает свободные колебания материальной точки, частоты
описывает свободные колебания материальной точки, частоты  (§ 6). Уравнение (9) описывает колебания материальной точки под действием внешней периодической силы, с частотой со.
(§ 6). Уравнение (9) описывает колебания материальной точки под действием внешней периодической силы, с частотой со.
Если со  то все решения уравнения (9) ограничены при
то все решения уравнения (9) ограничены при  как видно из формулы (11).
как видно из формулы (11).
Если же  то любое решение уравнения (9) неограничено при
то любое решение уравнения (9) неограничено при  из-за наличия слагаемого
из-за наличия слагаемого  (см. (12)), т. е. колебания точки становятся о неограниченными. Это явление называется резонансом — совпадают собственная частота колебаний
(см. (12)), т. е. колебания точки становятся о неограниченными. Это явление называется резонансом — совпадают собственная частота колебаний  и частота колебаний внешней силы со. Типичным примером резонансного явления служат обычные качели, если подталкивать их «в такт».
и частота колебаний внешней силы со. Типичным примером резонансного явления служат обычные качели, если подталкивать их «в такт».
3°. Вернемся к случаю со  и пусть правая часть в (9) равна
и пусть правая часть в (9) равна  Тогда
Тогда

где  вещественные постоянные; пусть
вещественные постоянные; пусть 
А. Если частоты  соизмеримы, т. е. их отношение есть рациональное число, то
соизмеримы, т. е. их отношение есть рациональное число, то  — периодическая функция. Действительно,
— периодическая функция. Действительно,  где
где  — целые числа; можно считать, что они положительны и взаимно просты. Тогда период колебаний равен
— целые числа; можно считать, что они положительны и взаимно просты. Тогда период колебаний равен

Б. Если частоты  несоизмеримы, т. е. их отношение есть иррациональное число, то
несоизмеримы, т. е. их отношение есть иррациональное число, то  — непериодическая функция. Допустим противное, и пусть
— непериодическая функция. Допустим противное, и пусть  — период функции
— период функции  Из тождества
Из тождества  находим:
находим:

Выберем  так, чтобы
так, чтобы  где к — целое число, тогда первое слагаемое в (14) обратится в нуль, и мы получим соотношение
где к — целое число, тогда первое слагаемое в (14) обратится в нуль, и мы получим соотношение

Если равен нулю первый сомножитель, то  где
где  — целое число. Это значение Т есть период второго слагаемого из (13), следовательно, Т — период первого слагаемого. Все периоды первого слагаемого из (13) имеют вид
— целое число. Это значение Т есть период второго слагаемого из (13), следовательно, Т — период первого слагаемого. Все периоды первого слагаемого из (13) имеют вид  где
где  целое число. Поэтому
целое число. Поэтому  при некотором целом
при некотором целом  так что отношение
так что отношение  — рациональное число. Это противоречит несоизмеримости частот
— рациональное число. Это противоречит несоизмеримости частот 
Пусть второй сомножитель из (15) равен нулю, тогда

где  — целое число. Полагая
— целое число. Полагая  и вычитая первое тождество из второго, получаем
и вычитая первое тождество из второго, получаем  где
где  — целое число. Поэтому отношение
— целое число. Поэтому отношение  — рациональное число, что противоречит предположению о их несоизмеримости. Итак,
— рациональное число, что противоречит предположению о их несоизмеримости. Итак,  — непериодическая функция.
— непериодическая функция.
Покажем, что

где  числовая прямая. Пусть
числовая прямая. Пусть  для простоты. Положим
для простоты. Положим  где к — целое число, тогда первое слагаемое в (13) будет равно
где к — целое число, тогда первое слагаемое в (13) будет равно  Покажем, что второе слагаемое может принимать при
Покажем, что второе слагаемое может принимать при  значения, сколь угодно близкие к
значения, сколь угодно близкие к  Аргумент косинуса равен
Аргумент косинуса равен

число  не зависит от k. Нам понадобится
не зависит от k. Нам понадобится
Лемма 2. Пусть а — иррациональное число. Тогда для любого числа  и для любого
и для любого  найдется такое целое число
найдется такое целое число  что
что

Здесь  — целая часть числа х (если
— целая часть числа х (если  , где
, где  — целое число,
— целое число,  то
то  ).
).
Доказательство. Пусть С — окружность длины  - фиксированная точка. Будем откладывать от точки А о дуги длин
- фиксированная точка. Будем откладывать от точки А о дуги длин  против часовой стрелки; тогда получим множество точек
против часовой стрелки; тогда получим множество точек  на окружности. Длина дуги, соединяющей точки
на окружности. Длина дуги, соединяющей точки  (дуга
(дуга  ориентирована против часовой стрелки), равна
ориентирована против часовой стрелки), равна  Все точки множества М различны. Действительно, если
Все точки множества М различны. Действительно, если  при
при  то
то

откуда следует, что  — рациональное число. Фиксируем число
— рациональное число. Фиксируем число  и малое число
и малое число  Отложим от точки А о дуги длины
Отложим от точки А о дуги длины  и пусть А — дуга с этими концами. Покажем, что А содержит точки множества
и пусть А — дуга с этими концами. Покажем, что А содержит точки множества  Выберем такое
Выберем такое  что
что  Точки
Точки  разбивают окружность на
разбивают окружность на  дуг. Длина
дуг. Длина  хотя бы одной из них меньше
хотя бы одной из них меньше  т. е. меньше длины дуги А. Пусть это будет дуга
т. е. меньше длины дуги А. Пусть это будет дуга  для определенности. Рассмотрим точки
для определенности. Рассмотрим точки  Расстояние между точками
Расстояние между точками  равно
равно  и потому хотя бы одна из этих точек
и потому хотя бы одна из этих точек  будет лежать внутри дуги А. Расстояние от этой точки до середины дуги А меньше
будет лежать внутри дуги А. Расстояние от этой точки до середины дуги А меньше 
так что

Замечание 1. Из леммы 2 следует, что последовательность  при иррациональном а всюду плотна на отрезке [0, 1], т. е. в любой сколь угодно малой окрестности любой точки
при иррациональном а всюду плотна на отрезке [0, 1], т. е. в любой сколь угодно малой окрестности любой точки  лежат точки этой последовательности. Более того, последовательность равномерно распределена на отрезке
лежат точки этой последовательности. Более того, последовательность равномерно распределена на отрезке  Это означает следующее: пусть
Это означает следующее: пусть  — любой отрезок, содержащийся в
— любой отрезок, содержащийся в  — его длина и
— его длина и  — число точек последовательности, которые лежат на
— число точек последовательности, которые лежат на  и номера которых не превосходят
и номера которых не превосходят  Тогда
Тогда

Докажем, что  может принимать значения сколь угодно близкие к единице; тем самым первое из соотношений (16) будет доказано. Представим
может принимать значения сколь угодно близкие к единице; тем самым первое из соотношений (16) будет доказано. Представим  в виде
в виде  где
где  — целое число,
— целое число,  и выберем к в соответствии с (18). Тогда
и выберем к в соответствии с (18). Тогда

где  так что
так что

и это значение может быть сколь угодно близким к единице. Аналогично доказывается утверждение (16) относительно нижней грани.
Замечание 2. Функция  (см. (13)) с несоизмеримыми
(см. (13)) с несоизмеримыми  является почти периодической. Это означает, что для всякого
является почти периодической. Это означает, что для всякого  существует
существует  такое, что в каждом интервале длины
такое, что в каждом интервале длины  найдется число Т такое, что
найдется число Т такое, что

Это число называется  -почти периодом. Почти периодическая функция повторяет свои значения, но, в отлпчпе от периодической функции, с ошибкой.
-почти периодом. Почти периодическая функция повторяет свои значения, но, в отлпчпе от периодической функции, с ошибкой.
Аналогичные утверждения справедливы и для суммы нескольких гармонических колебаний:

Пусть частоты  рационально независимы,
рационально независимы,
т. е. не существует целых чисел  не равных нулю одновременно и таких, что
не равных нулю одновременно и таких, что

Для двух частот  их рациональная независимость эквивалентна несоизмеримости. В этом случае функция
их рациональная независимость эквивалентна несоизмеримости. В этом случае функция  — непериодическая, но почти периодическая.
— непериодическая, но почти периодическая.
Пример 2. Рассмотрим функцию (13) в случае, когда  и частоты
и частоты  близки, т. е.
близки, т. е.  , где
, где  Функцию
Функцию  можно представить в виде
можно представить в виде

«Амплитуда»  есть медленно меняющаяся функция, периодическая, с периодом
есть медленно меняющаяся функция, периодическая, с периодом  Если
Если  то
то  меняется в пределах от
меняется в пределах от  до
до 

Рис. 6.
Множитель  есть быстро меняющаяся функция; график функции
есть быстро меняющаяся функция; график функции  см. на рис. 6; здесь
см. на рис. 6; здесь  Такая картина называется биениями; график функции
Такая картина называется биениями; график функции  называется огибающей. Этот физический термин
называется огибающей. Этот физический термин  совпадает с математическим понятием огибающей (гл. 2, § 11).
совпадает с математическим понятием огибающей (гл. 2, § 11).
Можно рассматривать функцию  например, как сумму звуковых полей двух излучателей с близкими частотами;
например, как сумму звуковых полей двух излучателей с близкими частотами;  — это значение звукового давления в фиксированной точке пространства в момент времени
— это значение звукового давления в фиксированной точке пространства в момент времени  Если частоты
Если частоты  высокие, то человеческое ухо не сможет услышать каждое из колебаний в отдельности, но услышит их огибающую — звук поочередно усиливается и ослабляется, т. е. человек услышит биения,
высокие, то человеческое ухо не сможет услышать каждое из колебаний в отдельности, но услышит их огибающую — звук поочередно усиливается и ослабляется, т. е. человек услышит биения,
Пример 3. Рассмотрим уравнение

где  Все решения однородного уравнения экспоненциально затухают при
Все решения однородного уравнения экспоненциально затухают при  Но мы имеем дело с нёрезонанснйм случаем, так что уравнение (20) имеет частное решение вида
Но мы имеем дело с нёрезонанснйм случаем, так что уравнение (20) имеет частное решение вида

Поэтому всякое решение уравнения (18) при больших  имеет вид
имеет вид

т. e. очень близко к периодической функции. В уравнении (20) член  отвечает «трению» (§ 6), которое стремится уменьшить колебания. Правая часть
отвечает «трению» (§ 6), которое стремится уменьшить колебания. Правая часть  есть периодическая сила, которая стремится раскачать колебания. Взаимодействие между трением и внешней силой приводит к установлению колебаний, близких к периодическим. Аналогичные примеры будут рассмотрены в гл. 3, § 12.
есть периодическая сила, которая стремится раскачать колебания. Взаимодействие между трением и внешней силой приводит к установлению колебаний, близких к периодическим. Аналогичные примеры будут рассмотрены в гл. 3, § 12.
Пример. Найдем все вещественные решения уравнения

где  — вещественные постоянные. Корня характеристического уравнения
— вещественные постоянные. Корня характеристического уравнения  равны
равны

так что всякое вещественное решение  однородного уравнения имеет вид
однородного уравнения имеет вид

Здесь  — произвольные вещественные постоянные. Всякое вещественное решение неоднородного уравнения имеет вид
— произвольные вещественные постоянные. Всякое вещественное решение неоднородного уравнения имеет вид

где  частные решения уравнений
частные решения уравнений

Так как  корень характеристического уравнения кратности 1, то решение
корень характеристического уравнения кратности 1, то решение  ищем в виде
ищем в виде  Подставим
Подставим  в уравнение. При вычислении производной у воспользуемся формулой Лейбница:
в уравнение. При вычислении производной у воспользуемся формулой Лейбница:

Отсюда находим  Так как
Так как  не является корнем характеристического уравнения, то решение
не является корнем характеристического уравнения, то решение  возьмем в виде
возьмем в виде  и из уравнения находим
и из уравнения находим  . Найдем
. Найдем  так как
так как  — корень характеристического уравнения кратности 1, то
— корень характеристического уравнения кратности 1, то  . Подставим
. Подставим  в уравнение, используя формулу Лейбница
в уравнение, используя формулу Лейбница

Отсюда находим  Так как
Так как  — не корень характеристического уравнения, то возьмем
— не корень характеристического уравнения, то возьмем  в виде
в виде  и из уравнения найдем
и из уравнения найдем  Итак, все вещественные решения данного уравнения имеют вид
Итак, все вещественные решения данного уравнения имеют вид

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
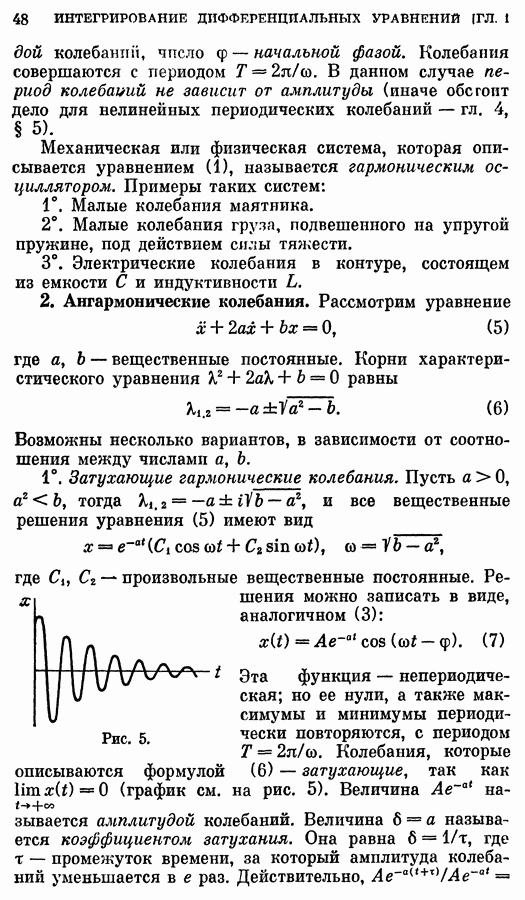
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
- § 5. Одномерное движение частицы в потенциальном поле
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ