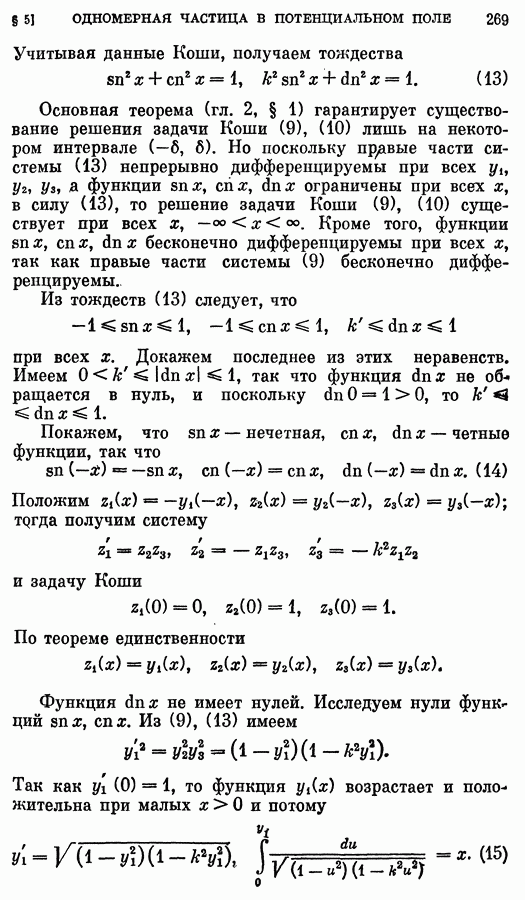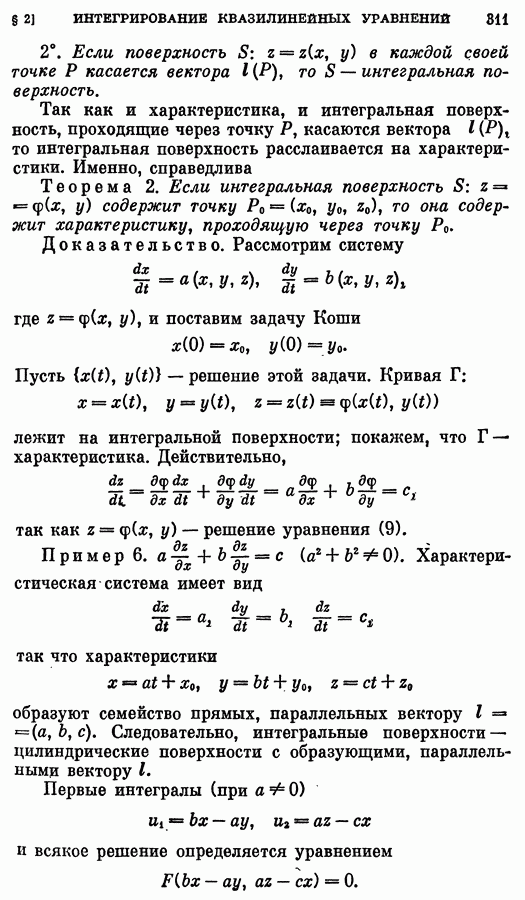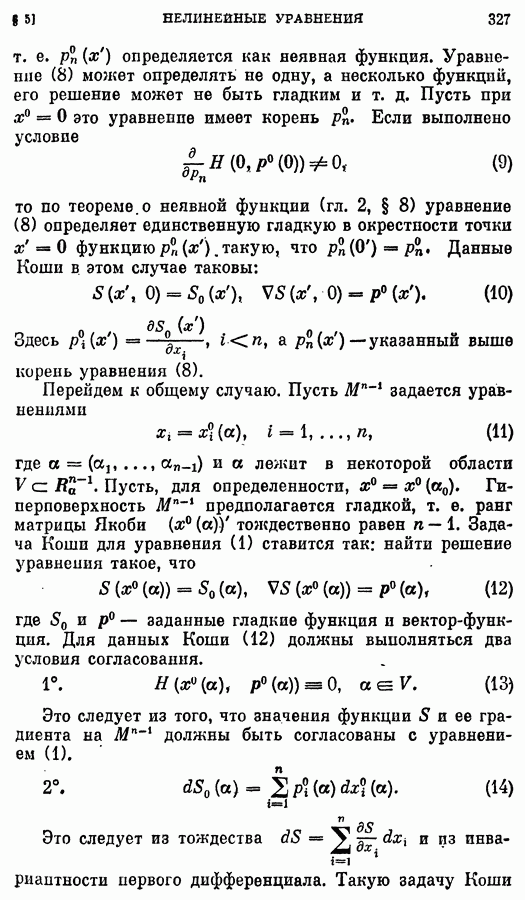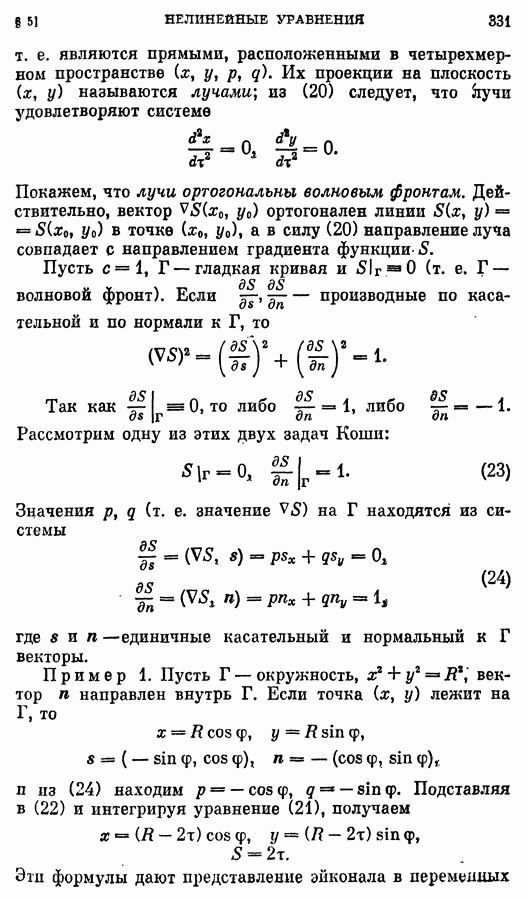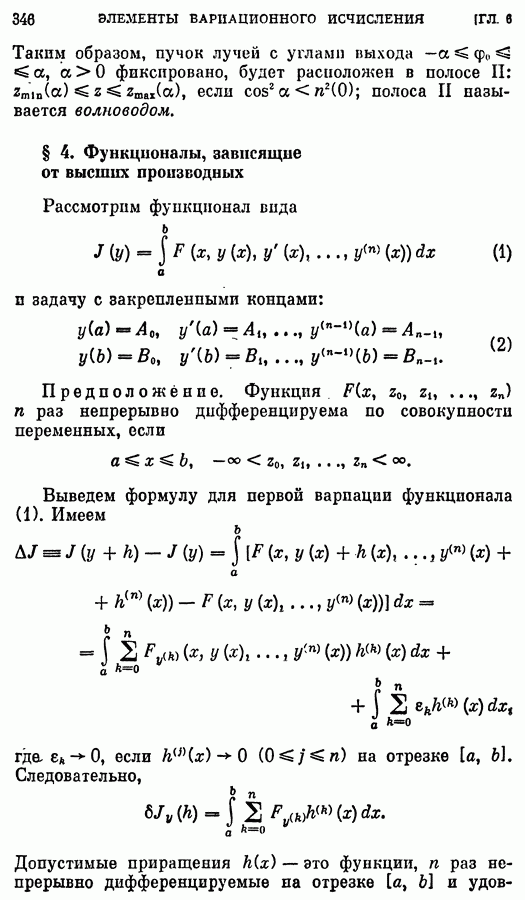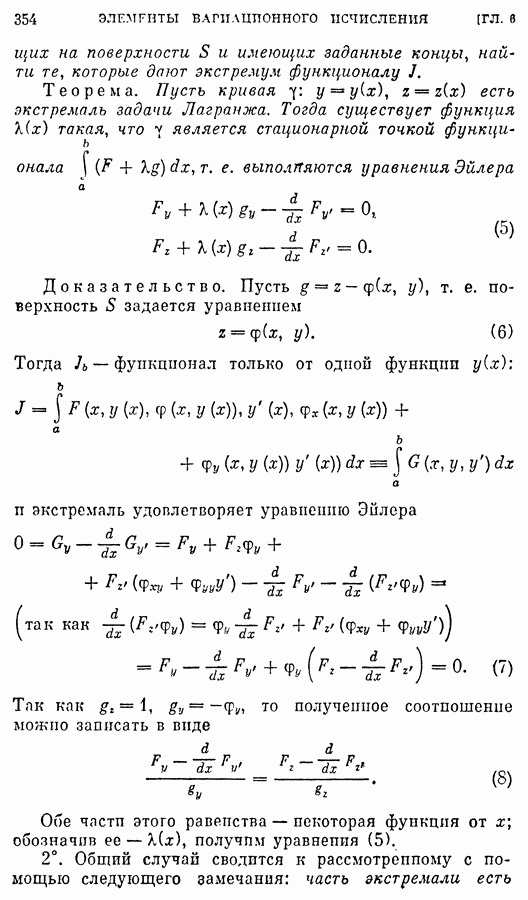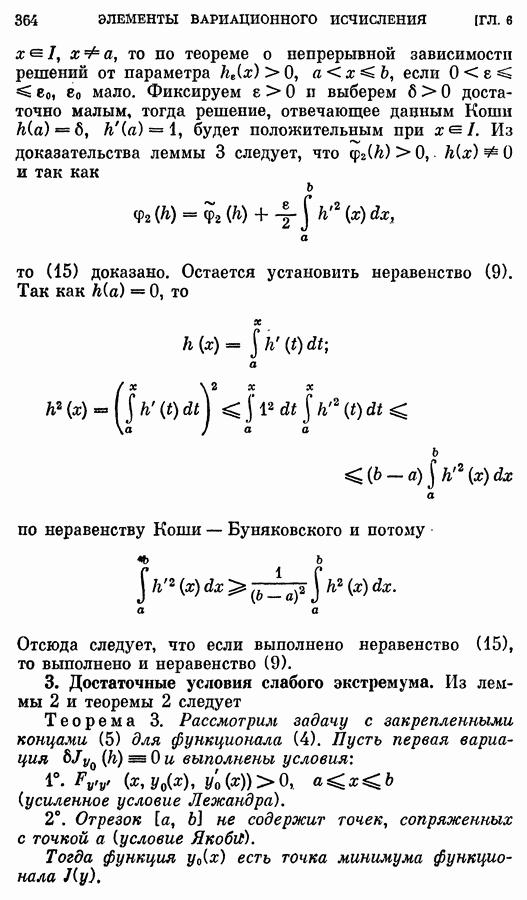| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Принцип суперпозиции.
Будем предполагать, что функции  непрерывны, функции
непрерывны, функции
 раз непрерывно дифференцируемы на некотором интервале
раз непрерывно дифференцируемы на некотором интервале  Всюду в дальнейшем
Всюду в дальнейшем 
Лемма 1. Если  — постоянные, то
— постоянные, то

Это свойство называется линейностью оператора  Доказательство. Так как
Доказательство. Так как  — постоянные, то
— постоянные, то

Умножая обе части на  и суммируя полученные выражения при к
и суммируя полученные выражения при к  получаем (5).
получаем (5).
Теорема 1. 1°. Принцип суперпозиции. Если  — решения однородного уравнения
— решения однородного уравнения  то их линейная комбинация
то их линейная комбинация

при любых постоянных  является решением однородного уравнения.
является решением однородного уравнения.
2°. Если  решения неоднородного уравнения (2), то их разность
решения неоднородного уравнения (2), то их разность

есть решение однородного уравнения (4).
Доказательство. 1°. Применяя лемму 1, получаем

2°. По условию,

так что, в силу линейности оператора 

Свойство 2° можно сформулировать иначе.
3°. Всякое решение неоднородного уравнения (1) есть сумма частного (т. е. фиксированного) решения неоднородного уравнения и некоторого решения однородного уравнения.
Действительно, пусть  — фиксированное (частное) решение уравнения (1),
— фиксированное (частное) решение уравнения (1),  — произвольное решение этого уравнения. Тогда
— произвольное решение этого уравнения. Тогда

где  — решение однородного уравнения, в силу 2°.
— решение однородного уравнения, в силу 2°.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
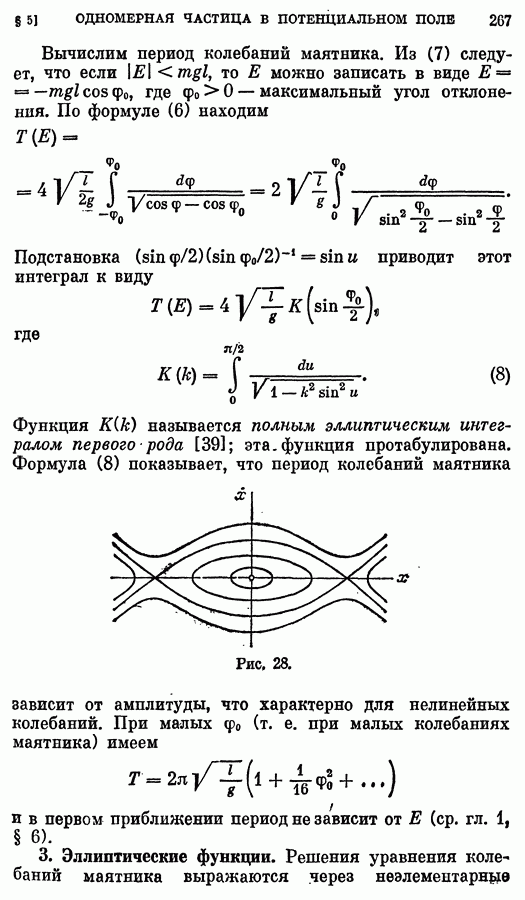
- § 5. Одномерное движение частицы в потенциальном поле
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
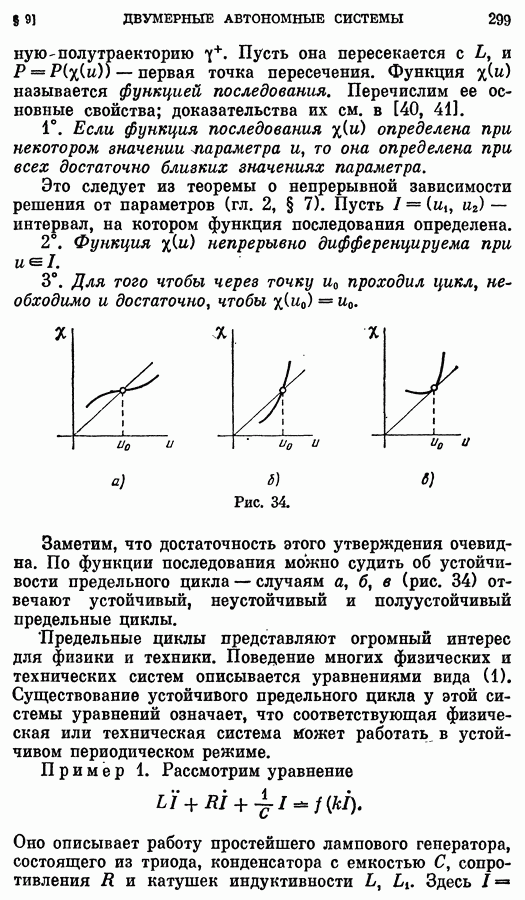
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
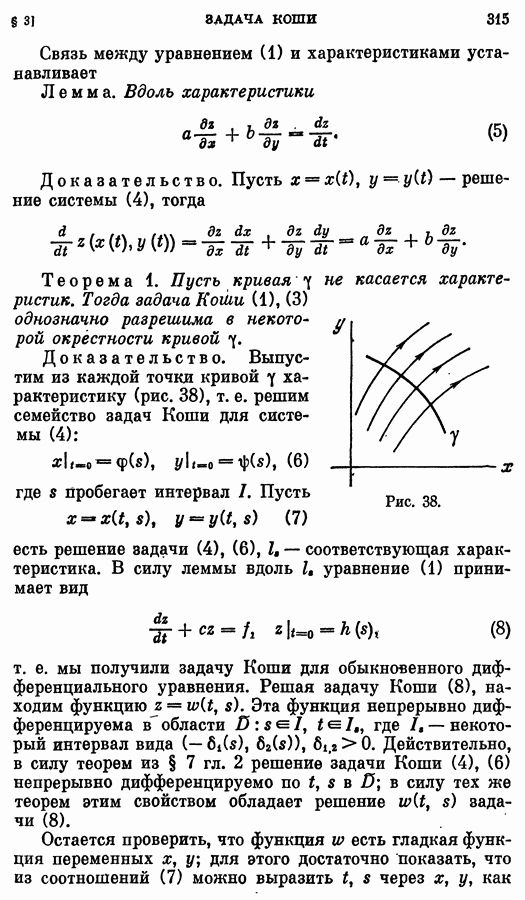
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
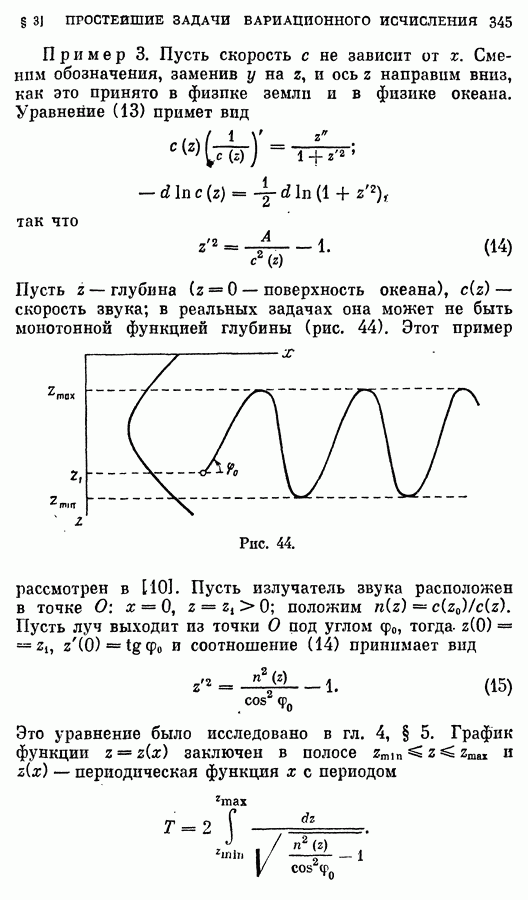
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ