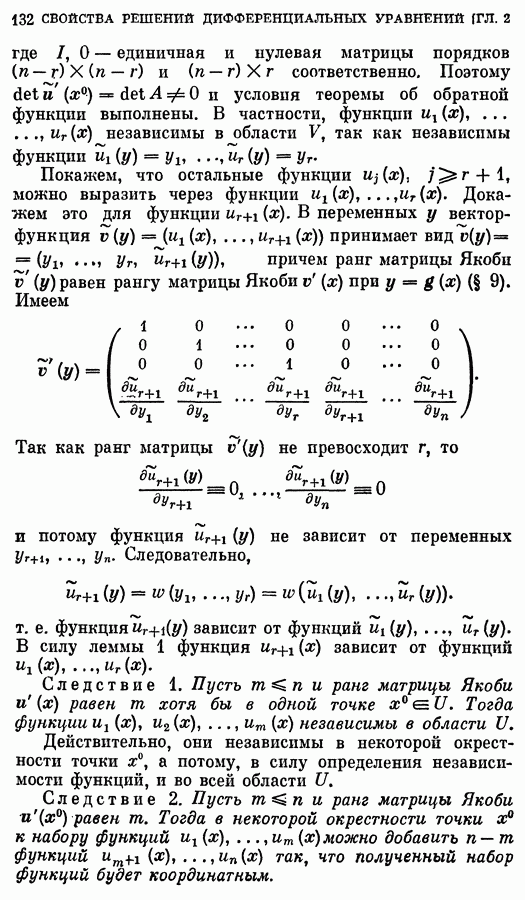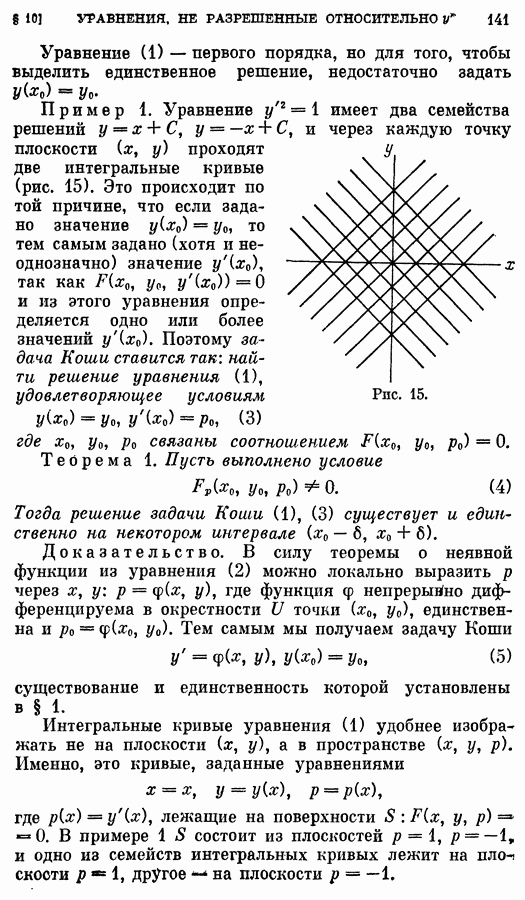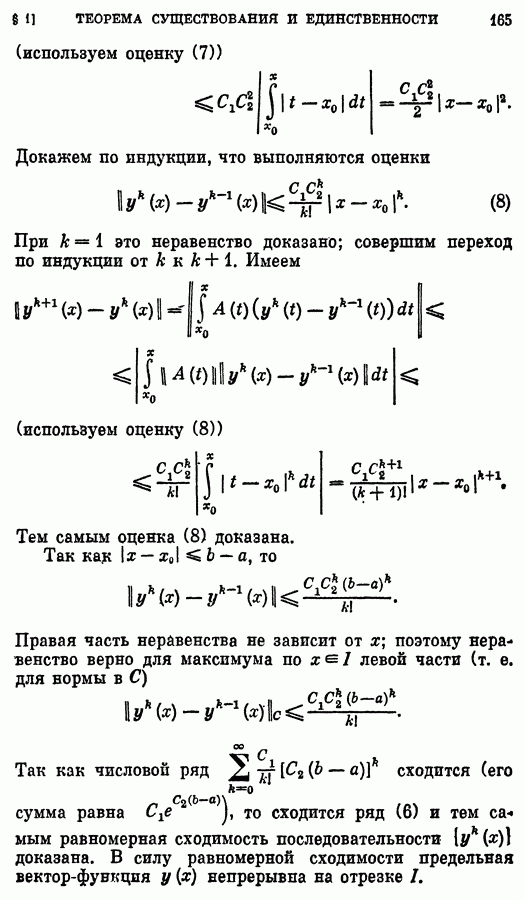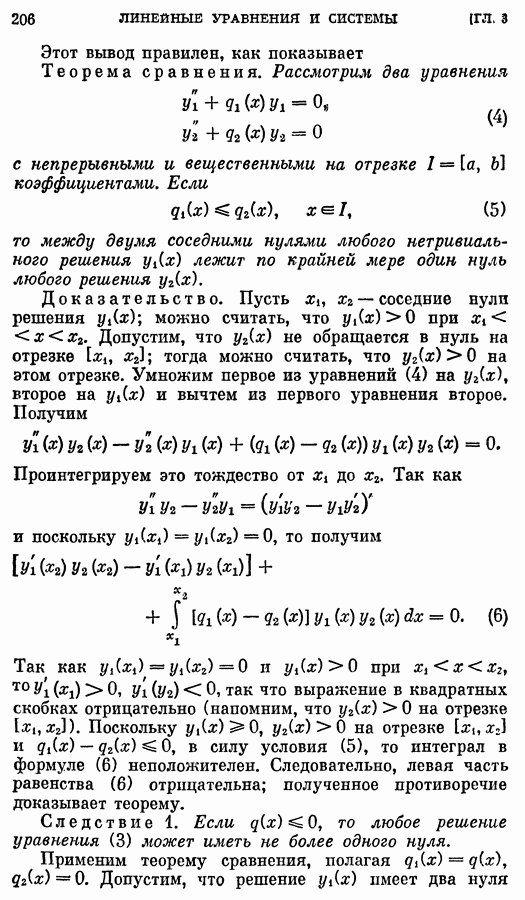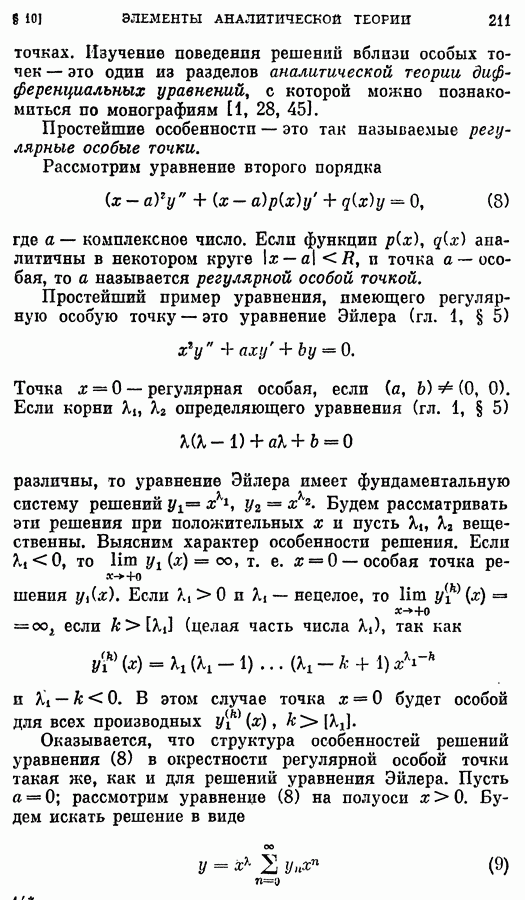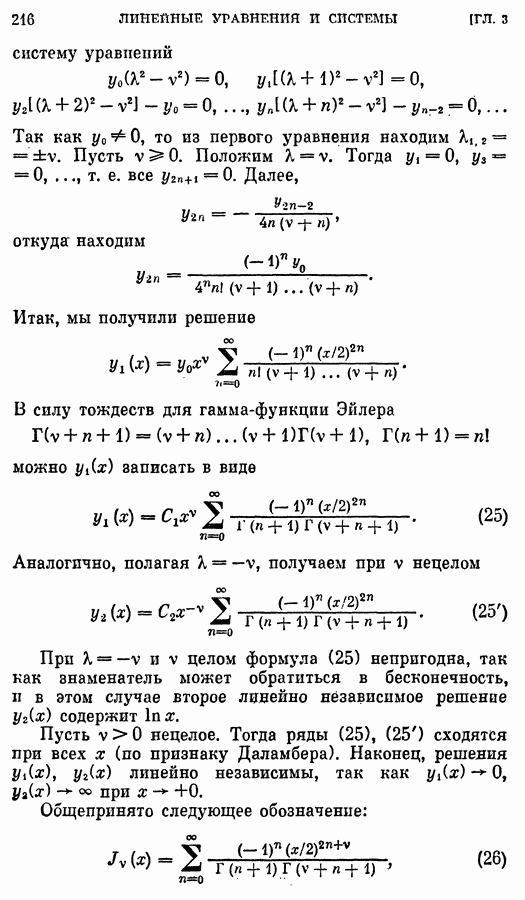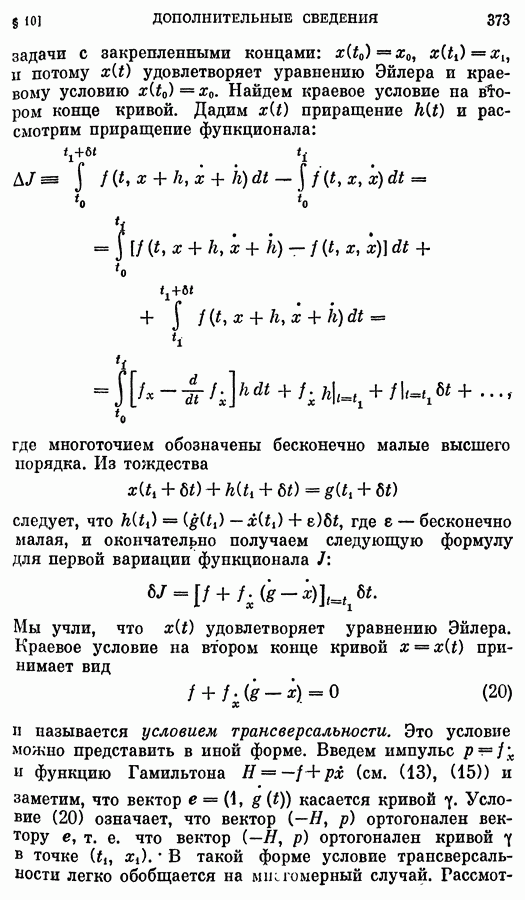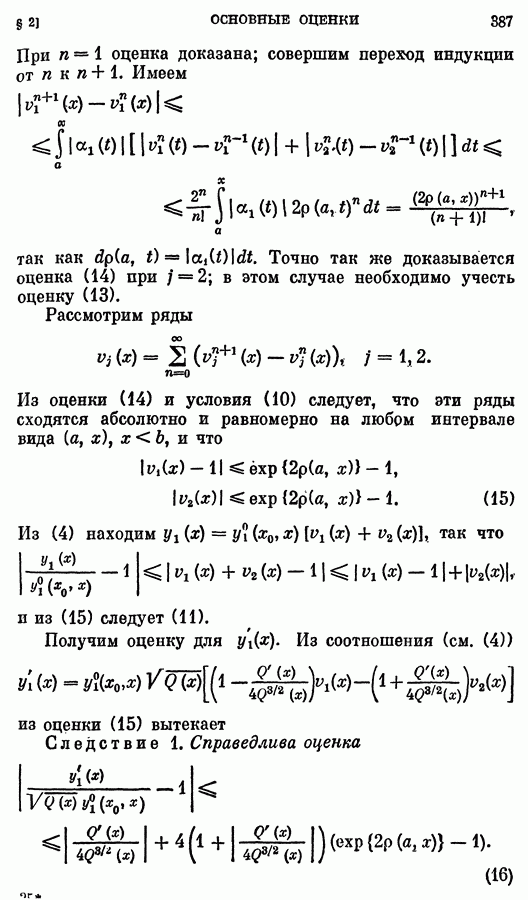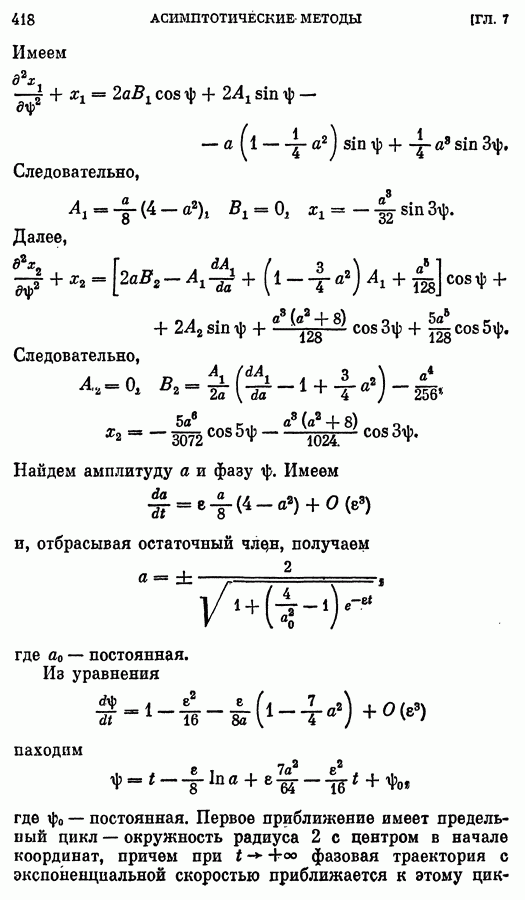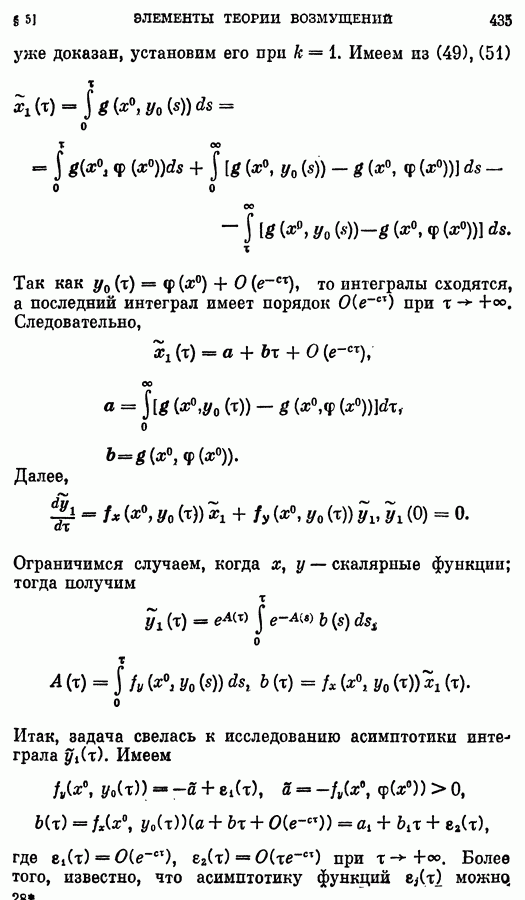| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Интегрирование уравнений вида (1).
Одним из наиболее мощных методов интегрирования является метод введения параметра или, как его еще называют, интегрирование посредством дифференцирования. Суть метода состоит в следующем.
1. Вводится новая переменная (параметр)  по формуле
по формуле

При этом переменные  рассматриваются как функции от
рассматриваются как функции от 
2. Полученное уравнение  дифференцируется по х или по у.
дифференцируется по х или по у.
Поясним замену переменной (11). Пусть функция  дважды непрерывно дифференцируема на интервале
дважды непрерывно дифференцируема на интервале  и строго выпукла кверху или книзу, так что
и строго выпукла кверху или книзу, так что  при
при  Тогда производная
Тогда производная  строго монотонна на интервале
строго монотонна на интервале  и из уравнения
и из уравнения  переменная х определяется однозначно:
переменная х определяется однозначно:  значения
значения  лежат в интервале
лежат в интервале  Далее,
Далее,  так что кривая
так что кривая  задана параметрически:
задана параметрически:

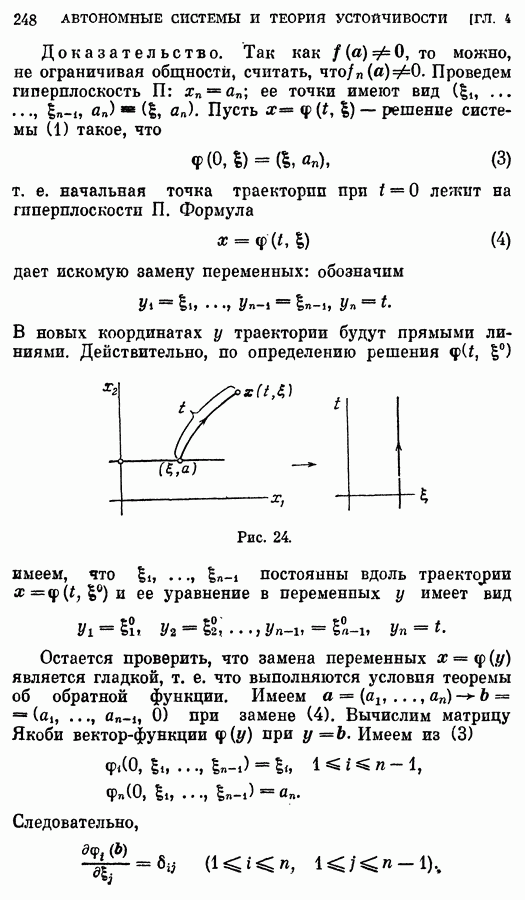
Замена переменной  имеет простой геометрический смысл. Пусть выполнены сформулированные выше условия; тогда кривая Г:
имеет простой геометрический смысл. Пусть выполнены сформулированные выше условия; тогда кривая Г:  строго выпукла (кверху или книзу). Величина
строго выпукла (кверху или книзу). Величина  есть тангенс угла наклона касательной к кривой Г в точке
есть тангенс угла наклона касательной к кривой Г в точке  Из строгой выпуклости кривой Г следует, что наклоны касательных в различных точках кривой Г различны. Поэтому задание углового коэффициента касательной
Из строгой выпуклости кривой Г следует, что наклоны касательных в различных точках кривой Г различны. Поэтому задание углового коэффициента касательной  однозначно определяет при
однозначно определяет при  точку кривой Г.
точку кривой Г.
Приведем основные типы интегрируемых уравнений вида (1).
 Уравнения, не содержащие х или у. Пусть уравнение (1) не содержит х:
Уравнения, не содержащие х или у. Пусть уравнение (1) не содержит х:

Если можно выразить у через  то мы получаем уравнение с разделяющимися переменными. Допустим, что можно выразить у через
то мы получаем уравнение с разделяющимися переменными. Допустим, что можно выразить у через  так что уравнение принимает вид
так что уравнение принимает вид

Положим  тогда
тогда  Дифференцируя это соотношение по х:
Дифференцируя это соотношение по х:

окончательно получаем параметрическое представление интегральной кривой 

Допустим, что уравнение кривой  задано в параметрической форме
задано в параметрической форме

Дифференцируя первое из этих соотношений по  имеем
имеем 

и мы получим параметрическое представление интегральной кривой

Пусть уравнение (1) не содержит переменной у:

и из уравнения  можно выразить х через
можно выразить х через 

Так как  то семейство решений имеет вид
то семейство решений имеет вид

Если кривая  задана параметрически:
задана параметрически:

то, продифференцировав первое из уравнений по  получим
получим

откуда найдем параметрическое представление интегральных кривых

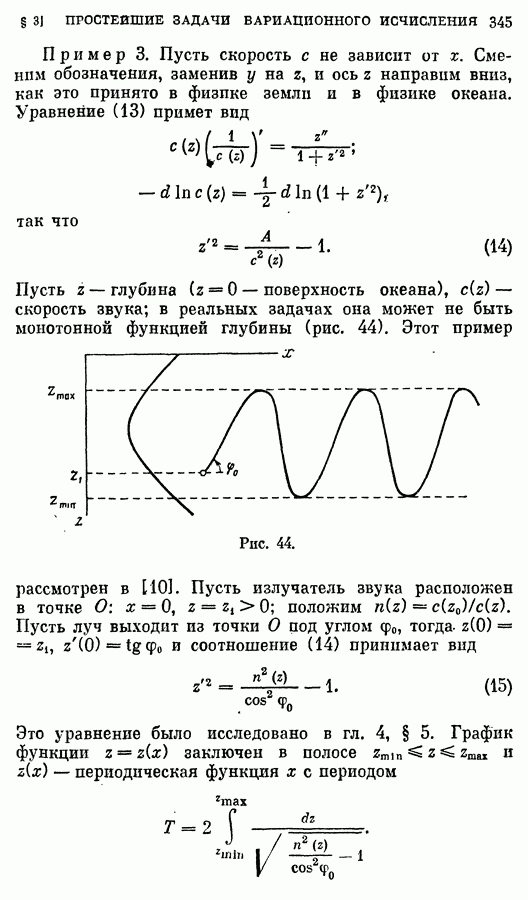
Пример 7. Решим уравнение

где  — постоянная. Полагая
— постоянная. Полагая  получаем
получаем

Возьмем знак плюс в этом равенстве и продифференцируем по х:

откуда находим, что либо  либо
либо

Интегральные кривые задаются уравнениями

Возводя эти равенства в квадрат и складывая, получаем уравнение

которое определяет семейство окружностей радиуса а с центрами, расположенными на оси х. Выбор знака минус в формуле для у приводит к этому же уравнению.
Если  то мы получаем два решения
то мы получаем два решения  , которые касаются данного семейства окружностей. Следовательно, решения
, которые касаются данного семейства окружностей. Следовательно, решения  — особые.
— особые.
Пример 8. Решим уравнение

Кривая  задается параметрически уравнениями
задается параметрически уравнениями

Дифференцируя первое уравнение по  получаем
получаем

откуда находим

2°. Однородные уравнения. Пусть  — однородная функция степени
— однородная функция степени  отпосительпо у:
отпосительпо у:

Тогда уравнение (1) можно записать в виде

Если  выражается через
выражается через  то мы получаем однородное уравнение (гл. 1, § 2). Пусть
то мы получаем однородное уравнение (гл. 1, § 2). Пусть  выражается через
выражается через 

Дифференцируя это уравнение по х, получаем

Выбирая  в качестве независимого переменного, получаем уравнение относительно х с разделяющимися переменными
в качестве независимого переменного, получаем уравнение относительно х с разделяющимися переменными

так что решения имеют вид

Пример 9. Решим уравнение

Имеем

Дифференцируя по у, получаем

Исключая  из соотношений
из соотношений

получаем семейство решений

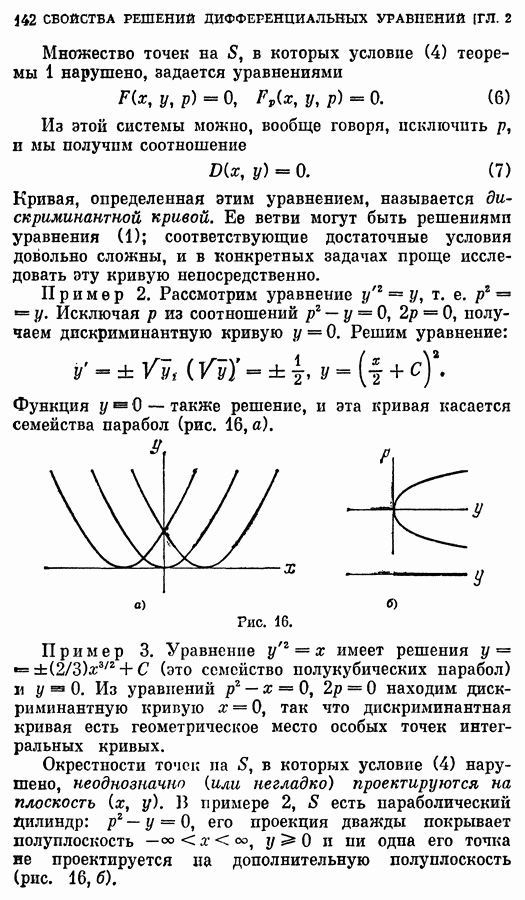
Выясним, есть ли в данном случае особые решения. Найдем дискриминантную кривую, исключив  из
из
уравнений

Из второго уравнения находим  и подставляя в первое, получаем
и подставляя в первое, получаем  Следовательно, данное уравнение не имеет особых решений.
Следовательно, данное уравнение не имеет особых решений.
3°. Уравнение Лагранжа. Если функция  линейна по переменным
линейна по переменным  то уравнение (1) приводится к виду
то уравнение (1) приводится к виду

и называется уравнением Лагранжа.
Дифференцируя уравнение по  , получаем
, получаем

так что

Это уравнение — линейное неоднородное. Найдя из этого уравнения  и подставив в исходное, получим С); тем самым получено параметрическое представление семейства решений. Кроме того, если
и подставив в исходное, получим С); тем самым получено параметрическое представление семейства решений. Кроме того, если

то имеется решение

и соответствующая интегральная кривая есть прямая.
Случай  является исключительным и будет рассмотрен ниже.
является исключительным и будет рассмотрен ниже.
Пример 10. Решим уравнение

Дифференцируя по х тождество  получаем
получаем

Итак, имеется семейство решений

Кроме того, возможен случай  которому отвечает решение
которому отвечает решение  Выясним, имеются ли в дапном случав
Выясним, имеются ли в дапном случав
особые решения. Найдем дискриминантную кривую, исключив  из уравнений
из уравнений

так что  Эта функция не является решением, так что особых решений нет.
Эта функция не является решением, так что особых решений нет.
Исследуем интегральные кривые. Пусть кривая задана параметрически:  где
где  — гладкие функции. Точка на кривой может быть особой только тогда, когда
— гладкие функции. Точка на кривой может быть особой только тогда, когда  (в противном случае в этой точке имеется ненулевой касательный вектор
(в противном случае в этой точке имеется ненулевой касательный вектор  к кривой). В данном случае критические значения
к кривой). В данном случае критические значения  определяются из системы
определяются из системы

откуда находим  Все эти точки расположены на параболе
Все эти точки расположены на параболе

так как при  имеем
имеем

Эта парабола — дискриминантная кривая. Исключительным является значение  если
если  , то
, то  при
при  а при
а при  значения
значения  конечны. При
конечны. При  интегральная кривая — парабола В:
интегральная кривая — парабола В:

Можно не сомневаться в том, что именно эти две выделенные кривые во многом определяют структуру семейства интегральных кривых.
Покажем, что все интегральные кривые лежат в области  под параболой А. Действительно,
под параболой А. Действительно,  так что
так что

Так как величина  вещественна, то
вещественна, то 
Исследуем поведение интегральной кривой вблизи точки  Положим
Положим  тогда при малых
тогда при малых 
получим

Следовательно, локально кривая состоит из двух ветвей — одна при  вторая при
вторая при  с общей касательной, так как
с общей касательной, так как  при
при  и потому
и потому  есть точка возврата. В данном примере дискриминантная кривая
есть точка возврата. В данном примере дискриминантная кривая  есть мпожество особых точек интегральных кривых.
есть мпожество особых точек интегральных кривых.
Уравнение (14) определяет две кривые, при значениях параметра  Функции
Функции  имеют следующее асимптотическое поведение при
имеют следующее асимптотическое поведение при  и при
и при 

Все интегральные кривые бесконечные, оба конца кривой уходят на бесконечность (т. е.  вдоль кривой). Имеются следующие типы интегральных кривых.
вдоль кривой). Имеются следующие типы интегральных кривых.
1.  . Кривая лежит в квадранте
. Кривая лежит в квадранте  (под параболой
(под параболой  и имеет точку возврата
и имеет точку возврата  Вблизи этой точки имеются две ветви кривой, одна из которых лежит выше другой. Верхняя ветвь асимптотически приближается к правой ветви
Вблизи этой точки имеются две ветви кривой, одна из которых лежит выше другой. Верхняя ветвь асимптотически приближается к правой ветви  параболы
параболы  нижняя — к верхней
нижняя — к верхней  ветви параболы
ветви параболы 
Интегральная кривая не имеет особых точек и потому является гладкой, В силу (15) имеем

Поэтому один конец кривой асимптотически приближается к левой  ветви параболы
ветви параболы  второй — к нижней
второй — к нижней  ветви параболы
ветви параболы 
Интегральная кривая не имеет особых точек и потому является гладкой. В силу (15) имеем

Поэтому один конец кривой асимптотически приближается к нижней  ветви параболы
ветви параболы  второй — к правой
второй — к правой  ветви параболы
ветви параболы 
Интегральная кривая имеет точку возврата  и лежит в квадранте
и лежит в квадранте  Одна из ее ветвей асимптотически приближается к левой
Одна из ее ветвей асимптотически приближается к левой  ветви параболы
ветви параболы  другая — к нижней
другая — к нижней  ветви параболы
ветви параболы 
Выше мы употребили не вполне определенный термин «кривая асимптотически приближается к другой кривой». В данном контексте смысл этого термина совершенно четкий. Именно, парабола  параметрически задается уравнениями
параметрически задается уравнениями  Из сравнения этой формулы с уравнениями (14) следует, что
Из сравнения этой формулы с уравнениями (14) следует, что

так что ветвь интегральной кривой неограниченно сближается с правой ветвью параболы при  То же самое справедливо для парабол
То же самое справедливо для парабол 
В этом примере можно найти уравнение семейства интегральных кривых в виде  если в уравнение
если в уравнение  подставить найденное выше выражение
подставить найденное выше выражение  через х, у. Тогда уравнение примет вид
через х, у. Тогда уравнение примет вид

Если избавиться от корня  , то получится уравнение шестой степени относительно
, то получится уравнение шестой степени относительно 

Но, разумеется, значительно проще исследовать параметрические уравнения (14), чем последнее уравнение.
Пример 11. Решим уравнение

Этот поучительный пример приведен в [46]. Имеем

Одно решение отвечает значению  так что
так что  остальные решения имеют вид
остальные решения имеют вид

так что интегральные кривые — полукубические параболы 
Интегральная кривая имеет точку возврата  . Найдем дискриминантную кривую. Исключая
. Найдем дискриминантную кривую. Исключая  из
из

исходного уравнения и уравнения  , получаем, что дискриминантная кривая состоит из двух прямых;
, получаем, что дискриминантная кривая состоит из двух прямых; 
Прямая  есть геометрическое место точек возврата и не является решением. Прямая
есть геометрическое место точек возврата и не является решением. Прямая  решение и в каждой точке касается одной из интегральных кривых. Действительно, полагая
решение и в каждой точке касается одной из интегральных кривых. Действительно, полагая  в уравнении интегральной кривой, получаем
в уравнении интегральной кривой, получаем

Следовательно, решение  особое.
особое.
4е. Уравнение Клеро. Это уравнение (12) при 

Полагая  и дифференцируя соотношение
и дифференцируя соотношение  по
по  получаем
получаем

В случае  имеем семейство прямых
имеем семейство прямых

В случае  получаем интегральпую кривую
получаем интегральпую кривую

которая, вообще говоря, является особым решением.
Пусть функция  дважды непрерывно дифференцируема на интервале
дважды непрерывно дифференцируема на интервале  Для определенности будем считать, что
Для определенности будем считать, что  Тогда функция
Тогда функция  строго монотонно возрастает при
строго монотонно возрастает при  из уравнения
из уравнения  можно однозначно выразить
можно однозначно выразить  через х как гладкую функцию:
через х как гладкую функцию:  Функция
Функция  также будет гладкой, в силу (18). Прямая, заданная уравнением (17), касается интегральной кривой
также будет гладкой, в силу (18). Прямая, заданная уравнением (17), касается интегральной кривой  в точке
в точке

Следовательно, определенная уравнением (18) интегральная кривая есть огибающая семейства решений  потому является особым решением.
потому является особым решением.
Пример 12. Решим уравнение

Имеется семейство прямых

и особое решение

Возведем каждое из этих уравнений в степень 2/3 и сложим, тогда получим уравнение

Эта кривая называется астроидой.
Уравнение Клеро возникает в таких геометрических задачах, в которых ищется плоская кривая по каким-либо свойствам ее касательных, не зависящих от положения точки касания. Если  — уравнение искомой кривой, то уравнение касательной есть
— уравнение искомой кривой, то уравнение касательной есть  что приводит к соотношению между функциями
что приводит к соотношению между функциями  и
и  т. е. к уравнению Клеро.
т. е. к уравнению Клеро.
Пример 13. Найти такую кривую, что произведение расстояний от двух заданных точек  до любой касательной к кривой есть величина постоянная.
до любой касательной к кривой есть величина постоянная.
Направим ось  вдоль отрезка
вдоль отрезка  начало координат поместим в середину отрезка; тогда
начало координат поместим в середину отрезка; тогда 
Расстояния от точек  до касательной (ее уравнение написано выше) в точке
до касательной (ее уравнение написано выше) в точке  равны
равны  так что
так что

где  — заданное произведение расстояний от точек
— заданное произведение расстояний от точек  до касательной. Получаем два уравнения Клеро
до касательной. Получаем два уравнения Клеро

решения которых имеют вид

Исключая параметр  получаем особое решение — эллипс
получаем особое решение — эллипс

которое и дает нетривиальное решение задачи. Случай, когда у — линейная функция, малоинтересен, так как касательные к прямой совпадают с ней самой.
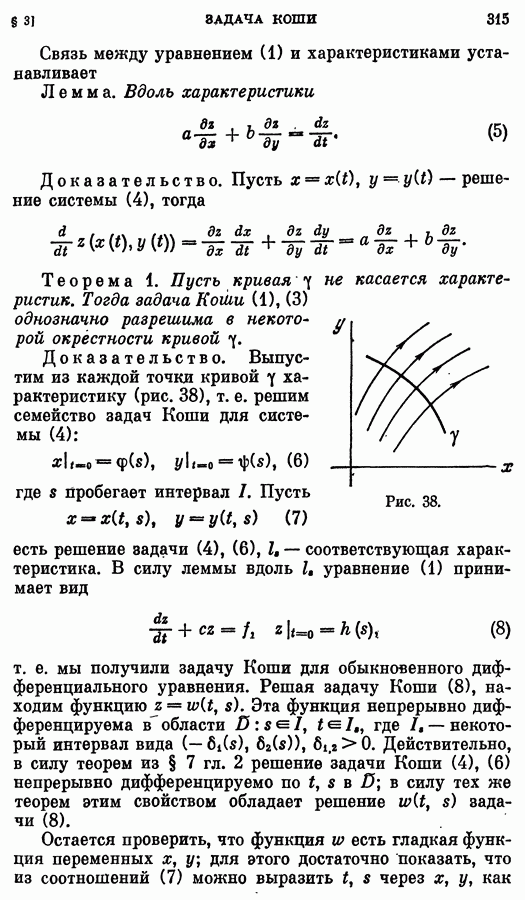
Структура семейства интегральных кривых уравнения (1) вблизи точки  достаточно проста и описывается теоремой 1, если эта точка не лежит на дискриминантной кривой. Уравнение Клеро (точнее, его решения) описывает структуру семейства решений уравнения (1) вблизи дискриминантной кривой в простейших (и в то же время основных) случаях. Пусть
достаточно проста и описывается теоремой 1, если эта точка не лежит на дискриминантной кривой. Уравнение Клеро (точнее, его решения) описывает структуру семейства решений уравнения (1) вблизи дискриминантной кривой в простейших (и в то же время основных) случаях. Пусть

так что точка  лежит на дискриминантной кривой. Будем предполагать, что
лежит на дискриминантной кривой. Будем предполагать, что  — гладкая поверхность (она задается уравнением
— гладкая поверхность (она задается уравнением  Достаточное условие для этого таково (§ 9, теорема 3):
Достаточное условие для этого таково (§ 9, теорема 3):  если
если  Без ограничения общности можно считать, что
Без ограничения общности можно считать, что

и пусть  Исследуем поверхность
Исследуем поверхность  вблизи этой точки. Разлагая функцию
вблизи этой точки. Разлагая функцию  до степеням
до степеням
 получаем
получаем

где многоточием обозначены члены третьего и более высокого порядка малости, а значения всех частных производных берутся в начале координат. Упростим уравнение, отбрасывая члены третьего и высших порядков малости, а также слагаемые, содержащие  малые по сравнению с у; тогда получим уравнение
малые по сравнению с у; тогда получим уравнение

Заменой переменных

можно убрать слагаемые, содержащие  Тогда получим уравнение
Тогда получим уравнение

Предположим, что

Ясно, что это случай «общего положения». Тогда, делая замену  получаем (тильды над переменными опущены) уравнение Клеро
получаем (тильды над переменными опущены) уравнение Клеро

Это уравнение получено при следующих предположениях: в точке 

Выше были приведены нестрогие соображения, но можно строго доказать, что если условия (19) выполнены, то с помощью гладкой обратимой замены переменных можно привести уравнение  к виду
к виду

в малой окрестности точки 
5°. Преобразование Лежандра. Пусть на интервале  задана гладкая фуйкция
задана гладкая фуйкция  Введем
Введем
новую переменную X и новую функцию У по формулам

Это и есть преобразование Лежандра — отображение пар

Если функция  дважды непрерывно дифференцируема и
дважды непрерывно дифференцируема и  при
при  то, как было показано в п. 3, соответствие между
то, как было показано в п. 3, соответствие между  взаимно однозначно и
взаимно однозначно и  — гладкая функция X.
— гладкая функция X.
Найдем обратное преобразование. Положим  тогда
тогда

так что  Далее,
Далее,  и обратное преобразование дается формулами:
и обратное преобразование дается формулами:

Поэтому с помощью преобразования Лежандра можно перевести любое из уравнений

в другое. Если одно из этих уравнений интегрируется, то интегрируется и другое.
Пример 14. Решим уравнение

Сделаем преобразование Лежандра

тогда получим уравнение

так как  Это уравнение однородно, и его решения имеют вид
Это уравнение однородно, и его решения имеют вид

Дифференцируя по  получаем
получаем

Следовательно, решения исходного уравнения имеют вид

откуда находим

Здесь С — произвольная постоянная, так как исходное уравнение имеет решение  .
.
Преобразование Лежандра имеет следующую геометрическую интерпретацию. Пусть Г:  строго выпуклая гладкая кривая. Она задается как множество точек
строго выпуклая гладкая кривая. Она задается как множество точек  на плоскости. Проведем все касательные к кривой Г; тогда Г — огибающая семейства этих прямых. Итак, имеются два способа задания кривой на плоскости.
на плоскости. Проведем все касательные к кривой Г; тогда Г — огибающая семейства этих прямых. Итак, имеются два способа задания кривой на плоскости.
1. Кривая задается как множество точек на плоскости.
2. Кривая задается как огибающая семейства прямых. Преобразование Лежандра — это переход от одного способа задания кривой к другому. Действительно, уравнение касательной к Г в точке  имеет вид
имеет вид

так что пара чисел  однозначно определяет точку
однозначно определяет точку  Сравнивая с формулой (20), видим, что эта пара есть
Сравнивая с формулой (20), видим, что эта пара есть  , т. е. преобразование Лежандра пары
, т. е. преобразование Лежандра пары 
6°. Задача о траекториях. Пусть имеется семейство кривых на плоскости, зависящих от параметра С. Требуется построить кривые (они называются траекториями), которые пересекают каждую кривую данного семейства под заданным углом а. При  траектории называются ортогональными, при а
траектории называются ортогональными, при а  — изогональными. Если, например, кривые семейства — силовые линии некоторого силового поля, то ортогональные траектории
— изогональными. Если, например, кривые семейства — силовые линии некоторого силового поля, то ортогональные траектории  эквипотенциальные линии.
эквипотенциальные линии.
Эту задачу удобно решать, если семейство кривых задано уравнением вида (1). Пусть семейство кривых задано уравнением (8)

Покажем, как получить для этого семейства уравнение вида (1). Продифференцируем тождество (8) по  считается функцией от
считается функцией от  тогда получим
тогда получим

Исключив С из соотношений  получим соотношение
получим соотношение  т. е. уравнение вида (1). Оно называется дифференциальным уравнением семейства, Пусть
т. е. уравнение вида (1). Оно называется дифференциальным уравнением семейства, Пусть  угол наклона касательной в некоторой точке к кривой семейства и к траектории соответственно. Тогда
угол наклона касательной в некоторой точке к кривой семейства и к траектории соответственно. Тогда

Заменив в уравнении семейства  велпчпну
велпчпну  на
на  получим дифференциальное уравнение семейства изогональных траекторий
получим дифференциальное уравнение семейства изогональных траекторий

Уравнение семейства ортогональных траекторий имеет вид

Пример 15. Найдем ортогональные траектории семейства парабол

Исключая С из системы

получаем дифференциальное уравнение семейства  и затем уравнение ортогональных траекторий
и затем уравнение ортогональных траекторий

Следовательно, ортогональными траекториями являются эллипсы

Пример 16. Найдем ортогональные траектории семейства

Его дифференциальное уравнение есть  , уравнение ортогональных траекторий есть
, уравнение ортогональных траекторий есть

так что ортогональные траектории — кривые

При  это семейство эллипсов, при
это семейство эллипсов, при  семейство гипербол. В частности, при
семейство гипербол. В частности, при  получаем ортогональные семейства равнобочных гипербол
получаем ортогональные семейства равнобочных гипербол

Пример 17. Рассмотрим конфокальное семейство кривых второго порядка

где  Фокусы этих кривых расположены в точках
Фокусы этих кривых расположены в точках  Исключая С из данного уравнения и уравнения
Исключая С из данного уравнения и уравнения

находим дифференциальное уравнение семейства

Если заменить  на
на  то это уравнение не изменится. Следовательно, данное семейство софокусных кривых второго порядка образует ортогональную систему.
то это уравнение не изменится. Следовательно, данное семейство софокусных кривых второго порядка образует ортогональную систему.
Пусть  тогда семейство существует при
тогда семейство существует при  Если
Если  , то кривые являются софокусными гиперболами, ортогональное семейство — софокусные эллипсы. Если —
, то кривые являются софокусными гиперболами, ортогональное семейство — софокусные эллипсы. Если —  то кривые семейства — эллипсы, ортогональные кривые — гиперболы. При значениях
то кривые семейства — эллипсы, ортогональные кривые — гиперболы. При значениях  кривые второго порядка вырождаются.
кривые второго порядка вырождаются.
Пр им  Найдем изогональные траектории семейства прямых
Найдем изогональные траектории семейства прямых  Дифференциальные уравнения семейства есть
Дифференциальные уравнения семейства есть  уравнение траекторий есть
уравнение траекторий есть

Переходя к полярным координатам  получаем
получаем

Здесь  — произвольная постоянная. Изогональные траектории — логарифмические спирали
— произвольная постоянная. Изогональные траектории — логарифмические спирали  орто тональные траектории — окружности
орто тональные траектории — окружности  ,
,
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
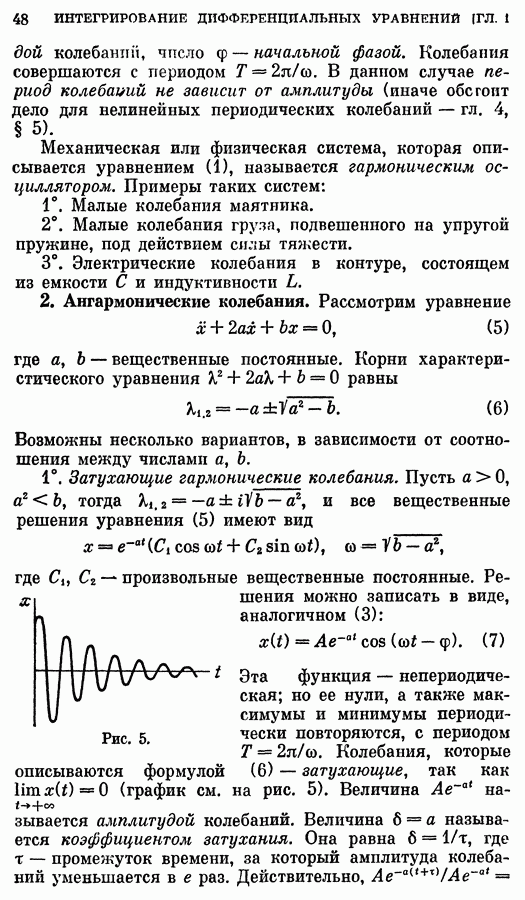
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
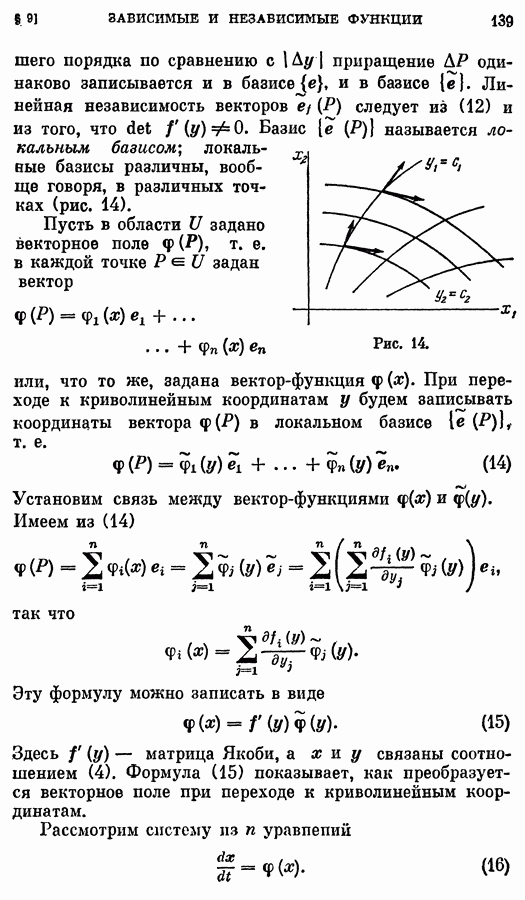
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
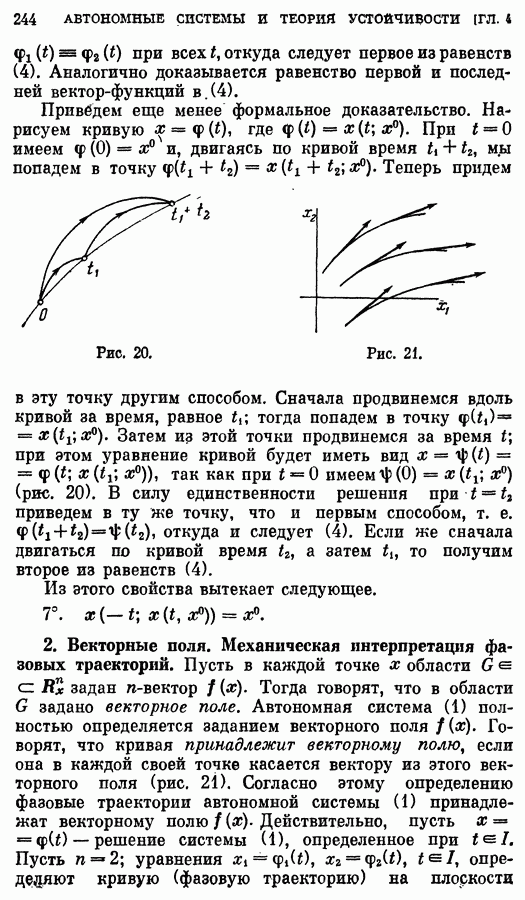
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
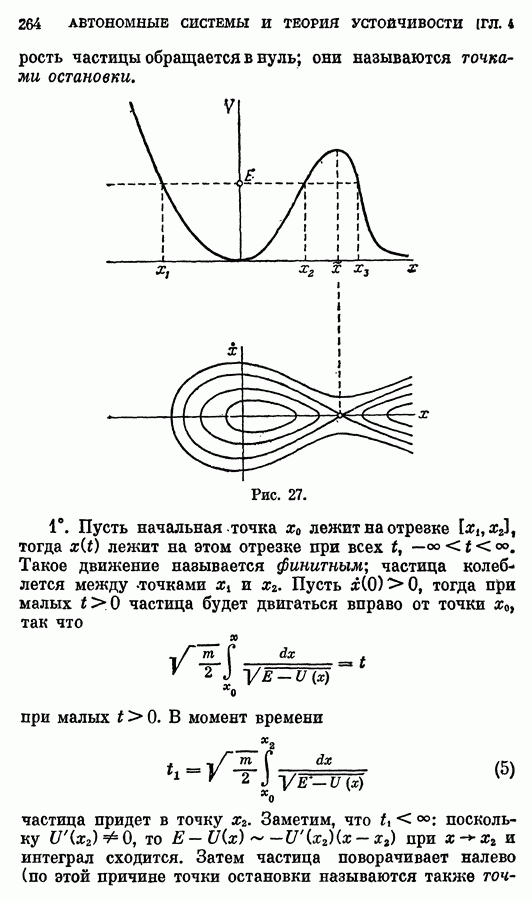
- § 5. Одномерное движение частицы в потенциальном поле
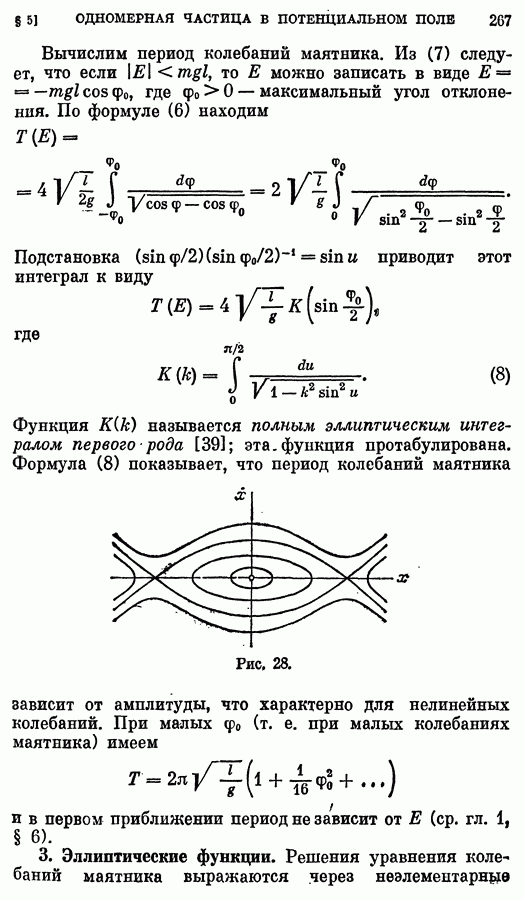
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
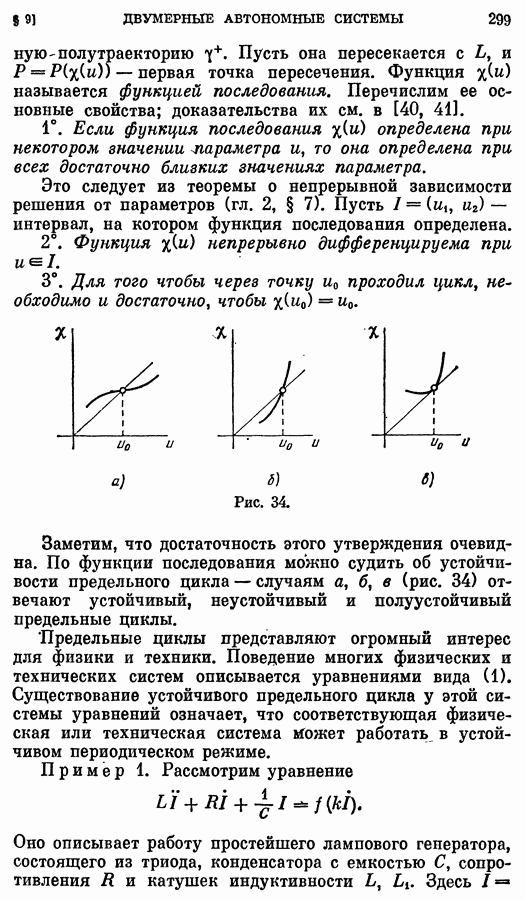
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
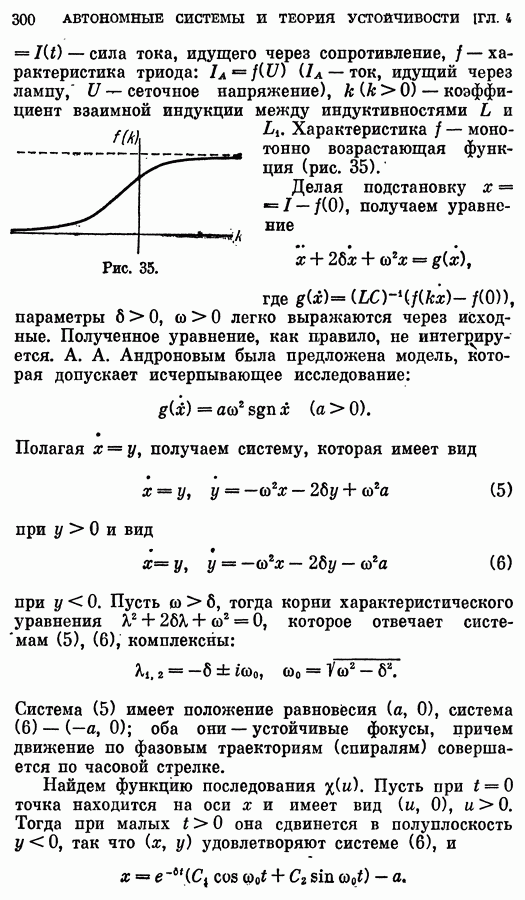
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ