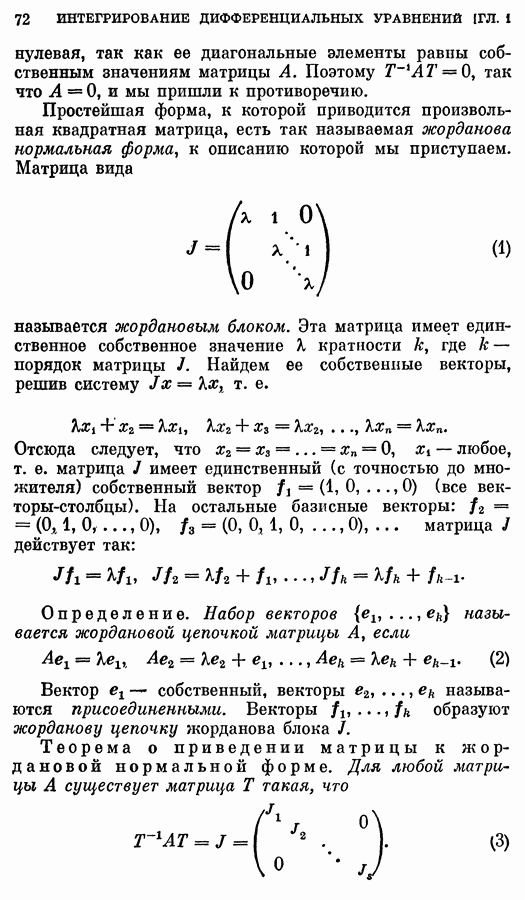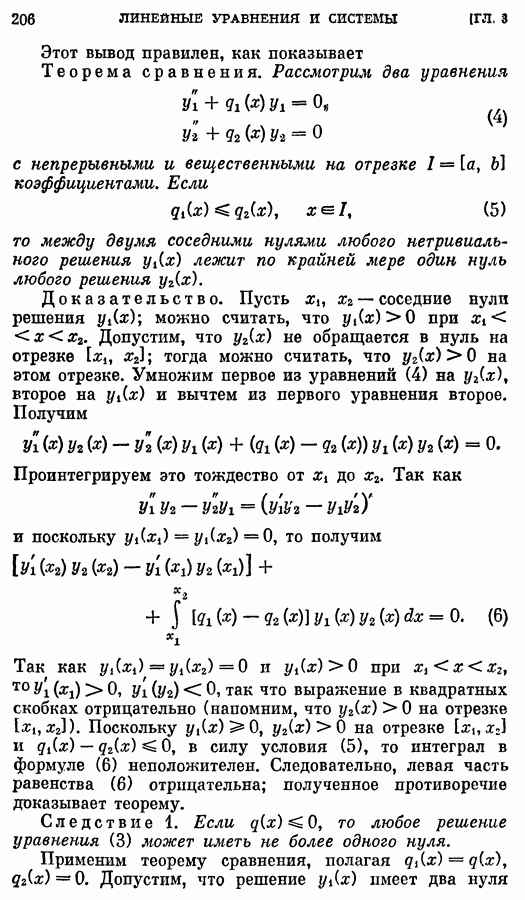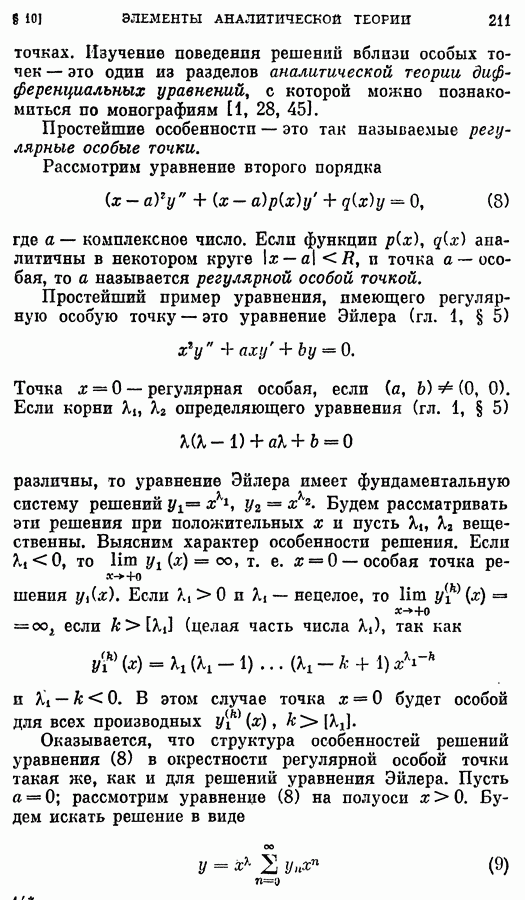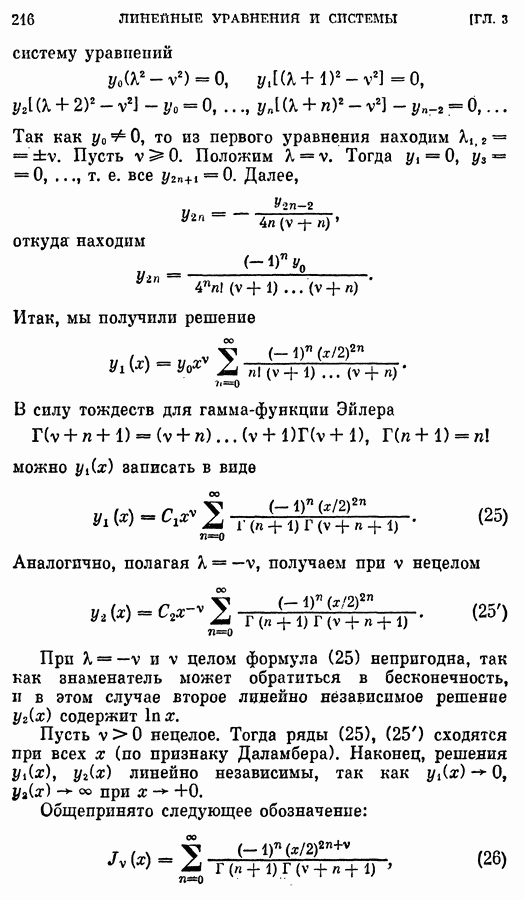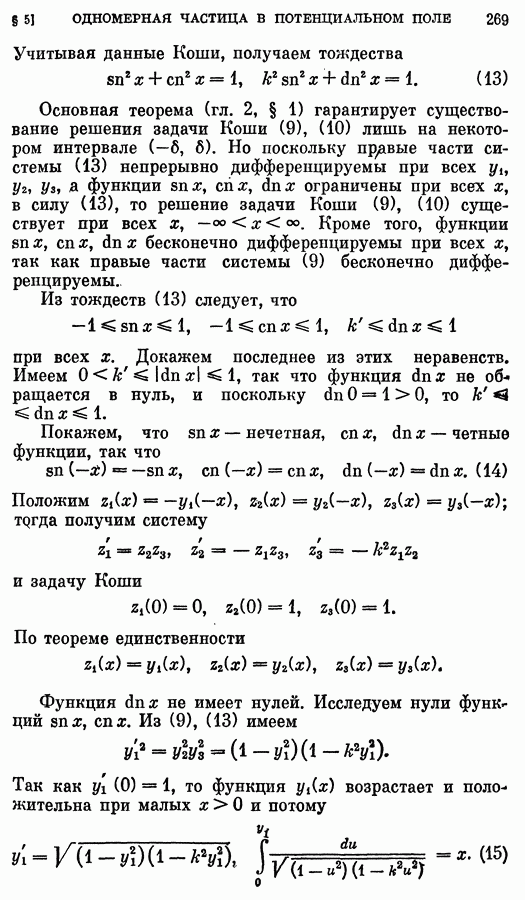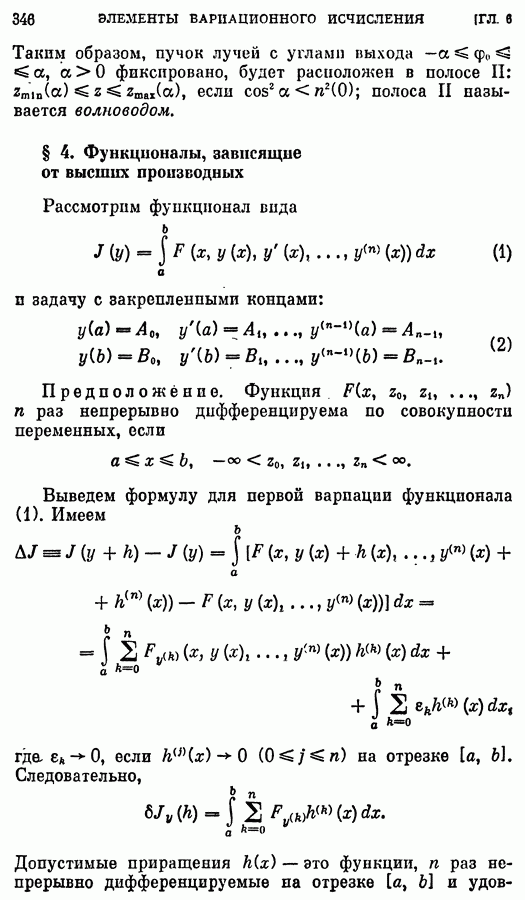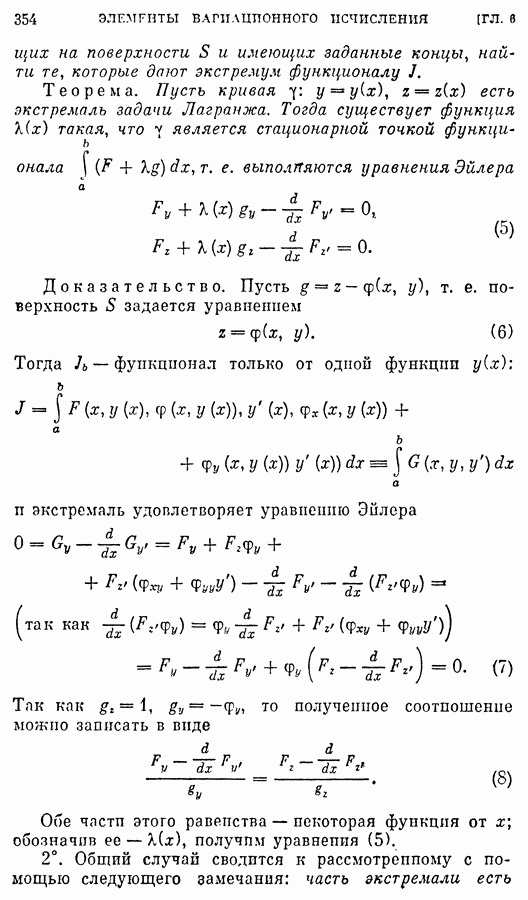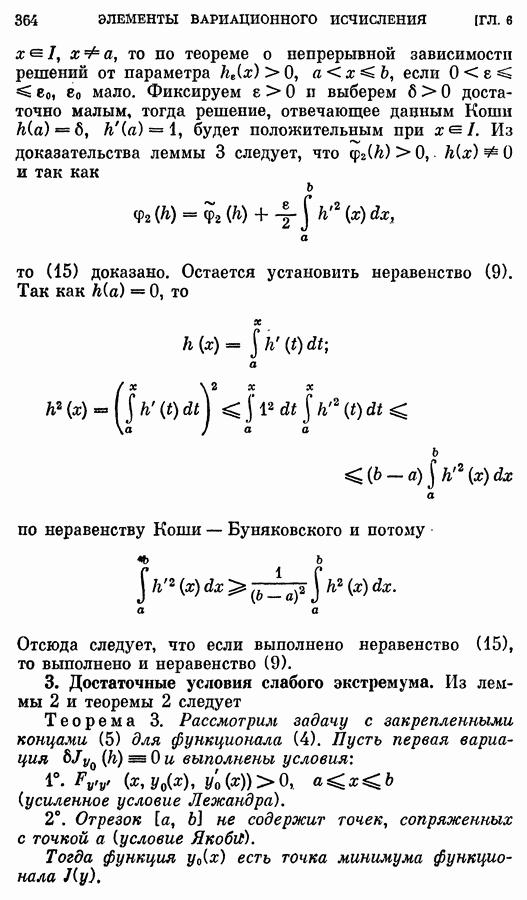| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
1. Жорданова нормальная форма матрицы.
В § 8 были найдены все решения однородной линейной системы с постоянными коэффициентами в случае, когда матрица системы А имела различные собственные значения. Такие матрицы приводятся к диагональному виду, и этот факт сыграл основную роль при интегрировании системы. Если же матрица А имеет кратное собственное значение, то ее не всегда можно привести к диагональному виду. Пример. Матрицу

нельзя привести к диагональному виду (ее собственные значения равны  . Действительно, допустим противное; тогда существует
. Действительно, допустим противное; тогда существует  -матрица Т такая, что
-матрица Т такая, что  диагональная матрица. Матрица
диагональная матрица. Матрица 
нулевая, так как ее диагональные элементы равны собственным значениям матрицы А. Поэтому  так что
так что  и мы пришли к противоречию.
и мы пришли к противоречию.
Простейшая форма, к которой приводится произвольная квадратная матрица, есть так называемая жорданова нормальная форма, к описанию которой мы приступаем. Матрица вида

называется жордановым блоком. Эта матрица имеет единственное собственное значение X кратности  , где k — порядок матрицы
, где k — порядок матрицы  Найдем ее собственные векторы, решив систему
Найдем ее собственные векторы, решив систему  т. е.
т. е.

Отсюда следует, что  — любое, т. е. матрица
— любое, т. е. матрица  имеет единственный (с точностью до множителя) собственный вектор
имеет единственный (с точностью до множителя) собственный вектор  (все векторы-столбцы). На остальные базисные векторы:
(все векторы-столбцы). На остальные базисные векторы:  матрица
матрица  действует так:
действует так:

Определение. Набор векторов  называется жордановой цепочкой матрицы А, если
называется жордановой цепочкой матрицы А, если

Вектор  — собственный, векторы
— собственный, векторы  называются присоединенными. Векторы
называются присоединенными. Векторы  образуют жорданову цепочку жорданова блока
образуют жорданову цепочку жорданова блока 
Теорема о приведении матрицы к жордановой нормальной форме. Для любой матрицы А существует матрица Т такая, что

Здесь  жордановьг блоки порядков
жордановьг блоки порядков 

и  собственные значения матрицы
собственные значения матрицы 
Матрица, стоящая в правой части равенства (3), называется нормальной жордановой формой матрицы А. Жордановы блоки выстроены вдоль главной диагонали.
Нормальная жорданова форма матрицы А определяется единственным образом, с точностью до перестановки жордановых блоков.
Доказательство см. в [40, 41]. Приведем другую формулировку этой теоремы.
Теорема. Пусть А — произвольная квадратная матрица порядка  Тогда существует базис, состоящий из жордановых цепочек
Тогда существует базис, состоящий из жордановых цепочек

Эти цепочки отвечают собственным значениям  матрицы А; действие матрицы А на векторы цепочки описывается формулой (2).
матрицы А; действие матрицы А на векторы цепочки описывается формулой (2).
Возникает естественный вопрос. Дана матрица А; как найти ее жорданову нормальную форму? Например, если дана матрица порядка  и известно, что она имеет единственное (собственное) значение X кратности 3, то ее жорданова нормальная форма может иметь один из трех видов:
и известно, что она имеет единственное (собственное) значение X кратности 3, то ее жорданова нормальная форма может иметь один из трех видов:

Какой же именно? Ответ на этот вопрос известен: читатель может найти его в [40].
В гл. 4 нам понадобится следующий результат.
Теорема о приведении матрицы к почти диагональному виду. Всякую  -матрицу А можно привести к почти диагональному виду, т. е. существует матрица Т такая, что
-матрицу А можно привести к почти диагональному виду, т. е. существует матрица Т такая, что

Здесь А — диагональная матрица, элементами которой являются (все) собственные значения матрицы  , а для элементов
, а для элементов  матрицы Вв имеет место оценка I где
матрицы Вв имеет место оценка I где  может быть выбрано сколь угодно малым. Доказательство. Выберем матрицу Р такую, что
может быть выбрано сколь угодно малым. Доказательство. Выберем матрицу Р такую, что

где  — нормальная жорданова форма матрицы А. Рассмотрим жорданов блок
— нормальная жорданова форма матрицы А. Рассмотрим жорданов блок

Пусть

где  — порядок матрицы
— порядок матрицы  Тогда
Тогда

Положим  тогда
тогда

Рассмотрим матрицу

Тогда, по правилу умножения блочных матриц,

где  — диагональная матрица с элементами
— диагональная матрица с элементами  , а
, а

 или
или  . В качестве Т возьмем матрицу
. В качестве Т возьмем матрицу  Тогда
Тогда

Теорема доказана.
2. Интегрирование системы. Рассмотрим систему из  уравнений:
уравнений:

где А — постоянная матрица. Эта система полностью интегрируется. Рассмотрим вначале систему из к уравнений

где  — жорданов блок вида (1). В покомпонентной
— жорданов блок вида (1). В покомпонентной
записи эта система имеет вид 

Решим эту систему «снизу вверх». Имеем  Далее,
Далее,  что, в силу теоремы 1, § 4,
что, в силу теоремы 1, § 4,

Аналогично получаем

Следовательно, всякое решение системы (6) дается формулой

где  — произвольные постоянные, а решения имеют вид
— произвольные постоянные, а решения имеют вид

Все решения системы (5) строятся следующим образом.
1°. По каждой жордановой цепочке  матрицы А строится набор решений
матрицы А строится набор решений  по формуле (7).
по формуле (7).
2°. Решение системы (5) есть линейная комбинация всех построенных решений с произвольными постоянными коэффициентами.
Наметим доказательство этого факта. После подстановки  где матрица Т приводит матрицу А к жордановой нормальной форме, система (5) принимает вид
где матрица Т приводит матрицу А к жордановой нормальной форме, система (5) принимает вид

Эта система распадается на  отдельных подсистем
отдельных подсистем

где  есть вектор-столбец высоты
есть вектор-столбец высоты  а каждая из этих подсистем интегрируется так же, как и система (6). Пример. Рассмотрим систему
а каждая из этих подсистем интегрируется так же, как и система (6). Пример. Рассмотрим систему

Собственные значения матрицы А этой системы равны  Собственный вектор определяется из системы
Собственный вектор определяется из системы  т. е.
т. е.

откуда следует, что  и собственный вектор только один (с точностью до множителя):
и собственный вектор только один (с точностью до множителя):  . Поэтому имеется присоединенный вектор
. Поэтому имеется присоединенный вектор  который определяется из системы
который определяется из системы  Для компонент
Для компонент  вектора
вектора  получаем систему
получаем систему

и вектор  можно взять в виде
можно взять в виде  . По формуле (7) строим решения
. По формуле (7) строим решения

и всякое решение системы имеет вид

или, в покомпонентной записи,

Здесь  — произвольные постоянные.
— произвольные постоянные.
Сделаем еще несколько замечаний о системах вида (5), в случае кратных сооственных значении матрицы А.
Пусть  все различные собственные значения кратностей
все различные собственные значения кратностей  Всякое решение системы (5) имеет вид
Всякое решение системы (5) имеет вид

Здесь  есть вектор-функция, компоненты которой — многочлены от х степени не выше чем
есть вектор-функция, компоненты которой — многочлены от х степени не выше чем  Это следует из того, что длина жордановой цепочки, отвечающей собственному значению не может быть больше чем
Это следует из того, что длина жордановой цепочки, отвечающей собственному значению не может быть больше чем  (а может быть только короче, так одному и тому же собственному значению может отвечать несколько жордановых цепочек). Как видно из формулы (7), соответствующие решения имеют вид
(а может быть только короче, так одному и тому же собственному значению может отвечать несколько жордановых цепочек). Как видно из формулы (7), соответствующие решения имеют вид  где компоненты вектор-функции
где компоненты вектор-функции  — многочлены степени не выше, чем длина жордановой цепочки минус единица.
— многочлены степени не выше, чем длина жордановой цепочки минус единица.
Случай кратных корней значительно сложнее случая простых корней, но, по счастью, кратные корни — исключения, а не правило. Поясним это на примере  -матрицы А с вещественными элементами. Ее характеристическое уравнение имеет вид
-матрицы А с вещественными элементами. Ее характеристическое уравнение имеет вид

где  — вещественные постоянные. На плоскости параметров
— вещественные постоянные. На плоскости параметров  каждому такому уравнению отвечает точка, а уравнениям, корни которых совпадают, отвечает парабола
каждому такому уравнению отвечает точка, а уравнениям, корни которых совпадают, отвечает парабола  Ясно, что точку
Ясно, что точку  можно сдвинуть с параболы за счет сколь угодно малого изменения чисел
можно сдвинуть с параболы за счет сколь угодно малого изменения чисел  (или что то же, за счет сколь угодно малого изменения элементов матрицы А). Полученная матрица уже будет иметь простые собственные значения.
(или что то же, за счет сколь угодно малого изменения элементов матрицы А). Полученная матрица уже будет иметь простые собственные значения.
С точки зрения вычислительной, приведение матрицы к жордановой нормальной форме есть неустойчивая операция. Действительно, на ЭВМ можно найти собственные значения только с вполне определенной точностью. Поэтому можно утверждать с уверенностью лишь то, что два собственных значения различны, если у них не совпадают некоторые десятичные знаки. Проверить же, что они равны, нельзя, и потому очень близкие собственные значения воспринимаются ЭВМ как равные. В силу этого, в случаях, когда имеются очень близкие (возможно, равные) собственные значения, матрицу приводят не к жордановой нормальной форме, а к какой-либо иной (например, к треугольной).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
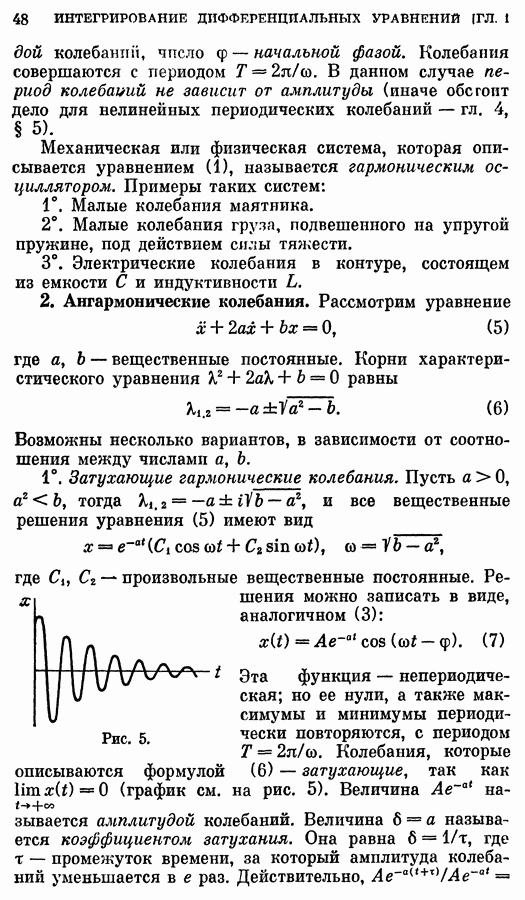
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
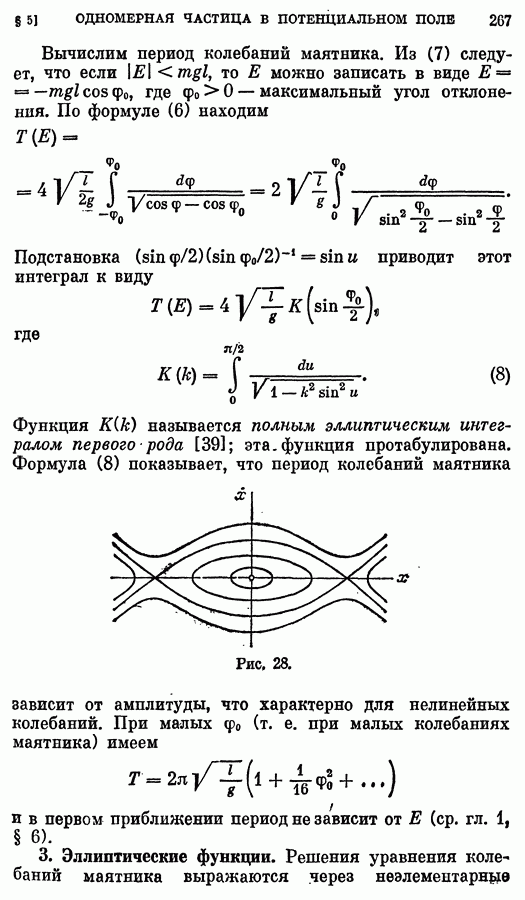
- § 5. Одномерное движение частицы в потенциальном поле
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
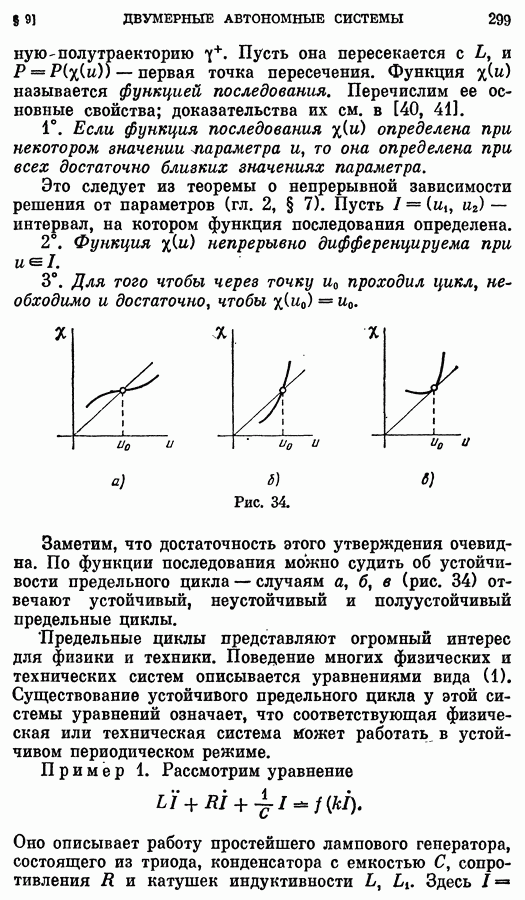
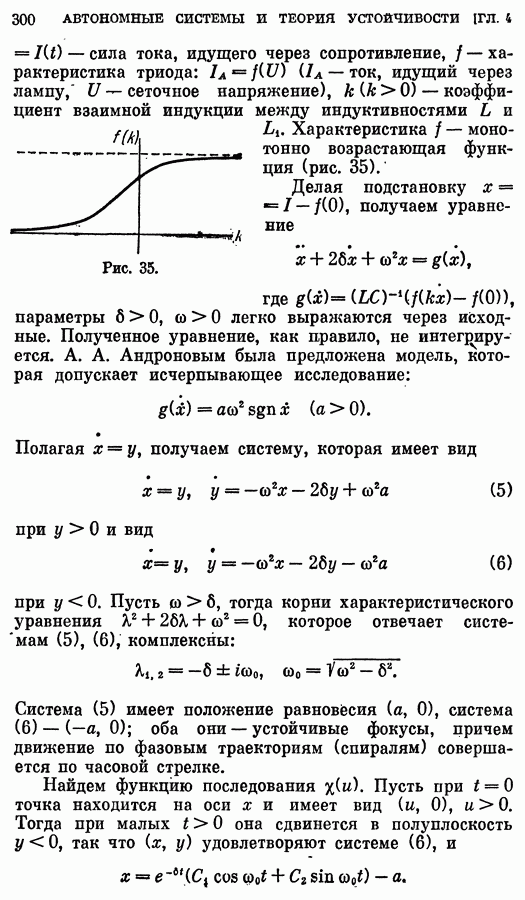
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
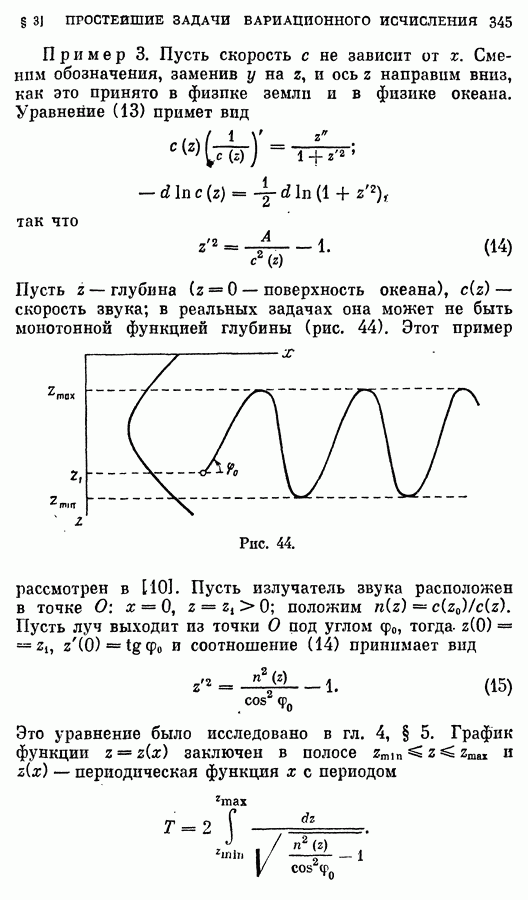
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ