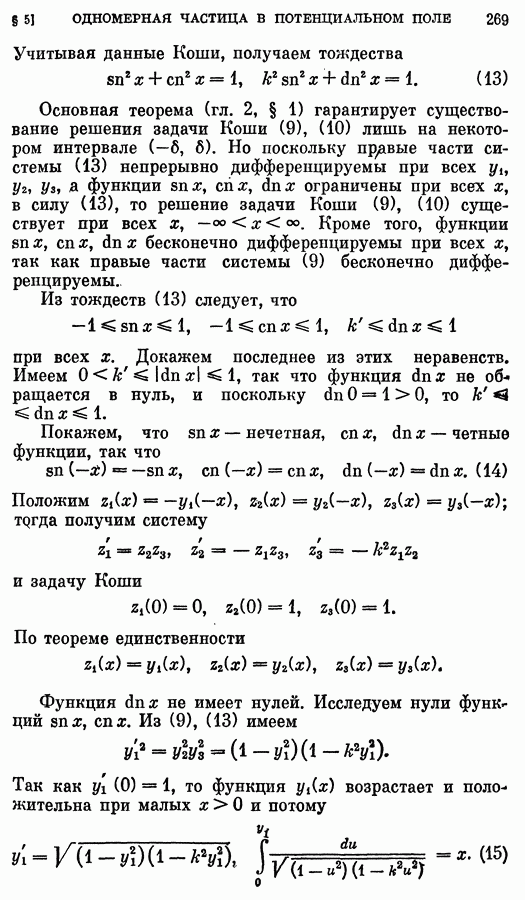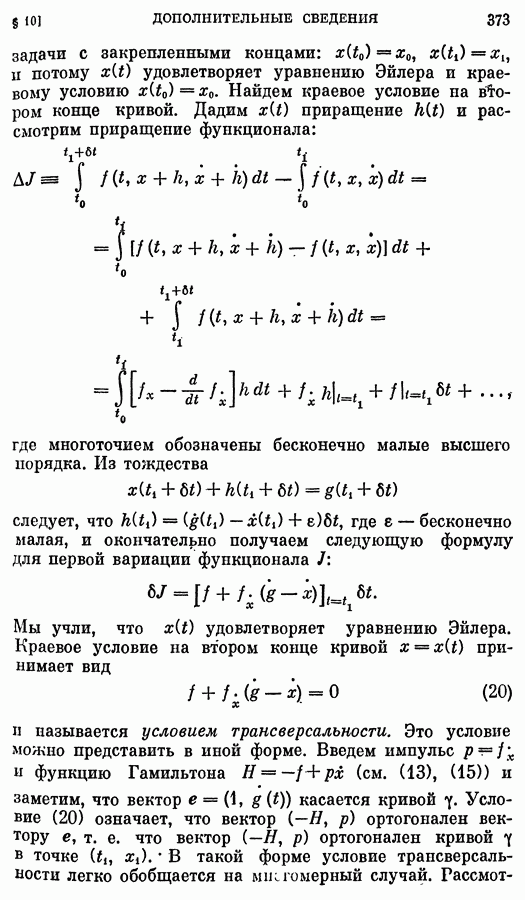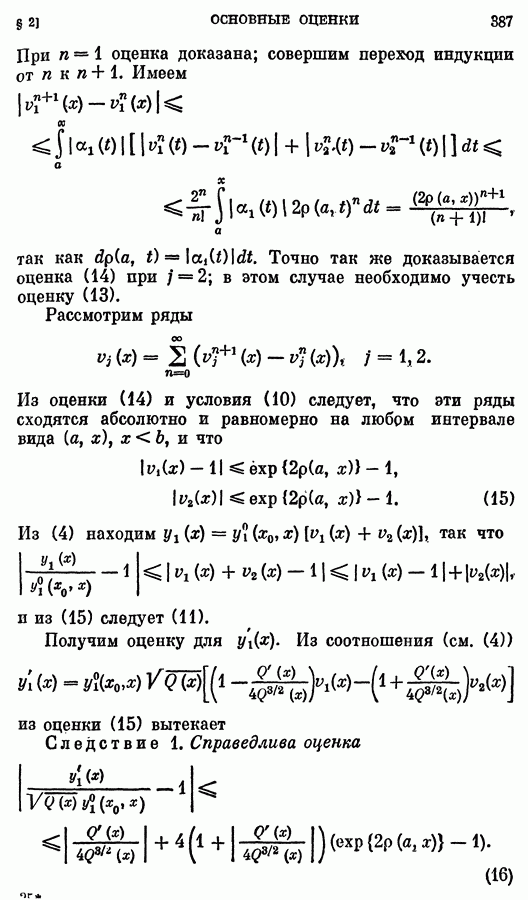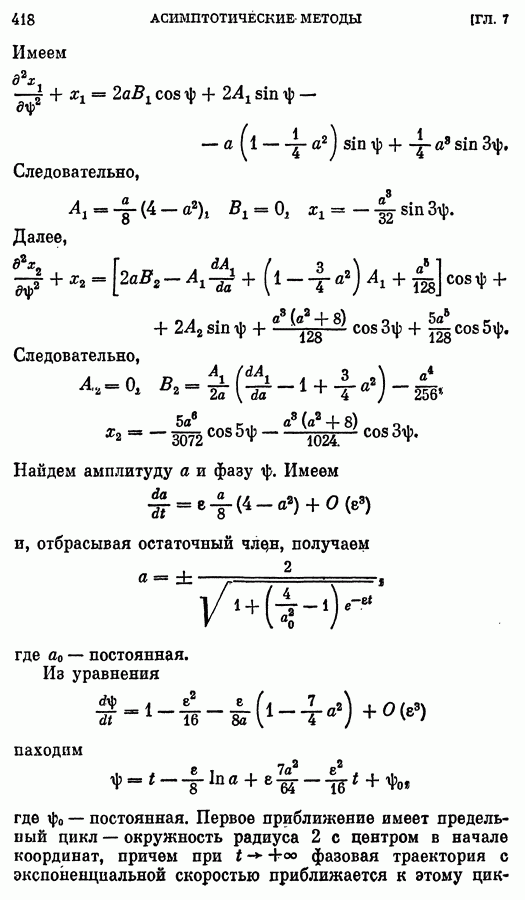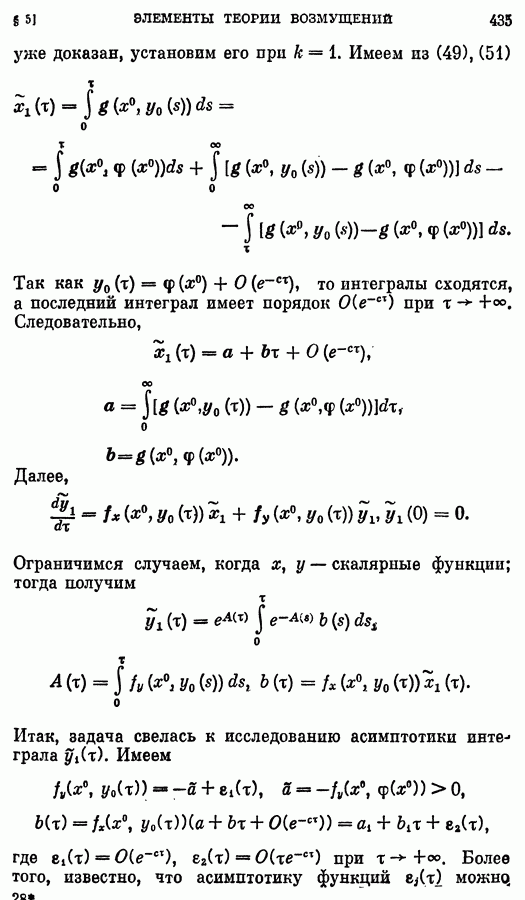| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. Устойчивость. Функция Ляпунова
1. Устойчивость положения равновесия.
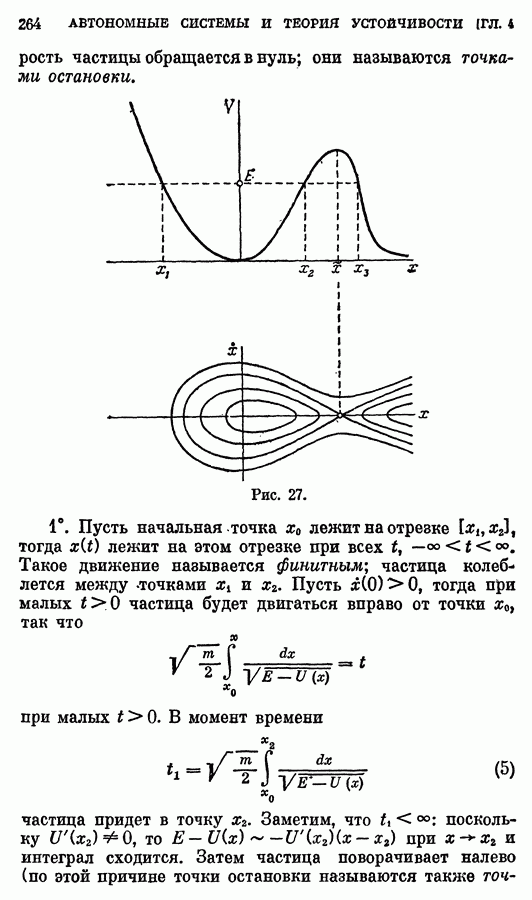
Слово «устойчивость» настолько выразительно, что правильные интуитивные представления об устойчивости имеются у всех Рассмотрим металлический шарик, который катается  горке (рис. 27). Имеются ровно две точки покоя (положения равновесия): дно впадины
горке (рис. 27). Имеются ровно две точки покоя (положения равновесия): дно впадины  и вершиш горки
и вершиш горки  Ясно, что первое из них устойчиво, а второе — нет. Действительно, если слегка подтолкнуть
Ясно, что первое из них устойчиво, а второе — нет. Действительно, если слегка подтолкнуть  сместить шарик с вершины, то он либо будет колебаться во впадине, либо укатится на бесконечность. Если же шарику, находящемуся в точке 1, сообщить малую начальную скорость и слегка его сместить, то он будет
сместить шарик с вершины, то он либо будет колебаться во впадине, либо укатится на бесконечность. Если же шарику, находящемуся в точке 1, сообщить малую начальную скорость и слегка его сместить, то он будет
совершать малые колебания вблизи этого положения равновесия.
Но таких наглядных представлений об устойчивости совершенно недостаточно, чтобы решить мало-мальски серьезную задачу об устойчивости реальной физической или технической системы. Теория устойчивости создавалась многими математиками, механиками, физиками. Фундаментальные результаты в теории устойчивости принадлежат знаменитому русскому математику А. М. Ляпунову.
Рассмотрим автономную систему из  уравнений
уравнений

Обозначим  решение этой системы с начальными данными
решение этой системы с начальными данными

Определение 1. Положение равновесия а называется устойчивым по Ляпунову, если:
1°. Существует  такое, что если
такое, что если  то решение
то решение  существует при 0
существует при 0
2°. Для всякого  существует
существует  такое, что если
такое, что если  то
то

при  .
.
Это означает, что если в начальный момент времени точка находится достаточно близко к положению равновесия (т. е. величина  мала), то и во все последующие моменты времени, двигаясь по траектории, точка будет оставаться вблизи положения равновесия.
мала), то и во все последующие моменты времени, двигаясь по траектории, точка будет оставаться вблизи положения равновесия.
Определение 2. Положение равновесия а называется асимптотически устойчивым, если оно устойчиво по Ляпунову и если

при достаточно малых 
Это означает, что если точку немного сдвинуть из положения равновесия, то она с ростом времени будет стремиться вернуться в положение равновесия.
В примере с шариком положение равновесия 1 будет устойчивым по Ляпунову, если трение отсутствует. Если
имеется трение, то колебания шарика сбудут уменьшаться с ростом времени, т. е. положение равновесия будет асимптотически устойчивым.
Следует подчеркнуть, что мы рассматриваем устойчивость положения равновесия по отношению к малым возмущениям. Устойчивость по отношению к возмущениям, которые не являются малыми — это значительно более сложная задача.
В гл. 1, § 9 были исследованы фазовые траектории двумерной автономной системы  где
где  и А есть
и А есть  -матрица. Начало координат
-матрица. Начало координат  есть положение равновесия, и его устойчивость в этом примере легко исследуется:
есть положение равновесия, и его устойчивость в этом примере легко исследуется:
1. Устойчивый узел, устойчивый фокус — асимптотически устойчивые положения равновесия (рис. 7, 10).
2. Центр — устойчивое по Ляпунову, но не асимптотически устойчивое положение равновесия (рис. 9).
3. Седло (рис. 8), неустойчивый узел, неустойчивый фокус — неустойчивые положения равновесия!
2. Функция Ляпунова. Пусть  функция
функция  непрерывно дифференцируема в окрестности
непрерывно дифференцируема в окрестности  точки
точки  Эта функция называется положительно определенной (в области
Эта функция называется положительно определенной (в области  если
если

Если же выполнены условия

то функция  называется отрицателъно определенной.
называется отрицателъно определенной.

Рис. 29.
Пример 1. Функция

положительно определена в любой окрестности точки 
При  уравнение
уравнение  определяет параболоид вращения (рис. 29), который касается плоскости
определяет параболоид вращения (рис. 29), который касается плоскости  в начале координат, а его остальные точки лежат выше этой плоскости. Линии уровня фуцкции V — это окружности
в начале координат, а его остальные точки лежат выше этой плоскости. Линии уровня фуцкции V — это окружности  которые стягиваются в точку при
которые стягиваются в точку при  Справедлива
Справедлива
Теорема [7]. Пусть функция  положительно определена в окрестности
положительно определена в окрестности  точки а. Тогда множества уровня
точки а. Тогда множества уровня  лежащие в
лежащие в  замкнутые гиперповерхности, окружающие точку а, если
замкнутые гиперповерхности, окружающие точку а, если  достаточно мало.
достаточно мало.
Пример 2. Рассмотрим квадратичную форму

Здесь  эти числа вещественны, так что
эти числа вещественны, так что  вещественная симметрическая матрица. Квадратичная форма называется положительно определенной,
вещественная симметрическая матрица. Квадратичная форма называется положительно определенной, 

Положительно определенная квадратичная форма есть положительно определенная функция в любой окрестности точки 
Этот пример существенно используется в последующем, и мы исследуем его более тщательно.
Лемма. Если А — вещественная симметрическая  -матрица, то для любого
-матрица, то для любого  справедливо неравенство
справедливо неравенство

Здесь а — наименьшее,  — наибольшее собственное значение матрицы А.
— наибольшее собственное значение матрицы А.
Доказательство. Из линейной алгебры известно [8, 20], что матрицу А можно привести к диагональному виду с помощью ортогонального преобразования, т. е. существует ортогональная матрица Т такая, что  где
где  — диагональная матрица с диагональными элементами
— диагональная матрица с диагональными элементами  Сделаем подстановку
Сделаем подстановку  тогда
тогда

(так как  )
)

так что а  Ортогональное преобразование сохраняет длину вектора;
Ортогональное преобразование сохраняет длину вектора;  , и (4) доказано.
, и (4) доказано.
Определение 3. Положительно определенная в окрестности  точки а функция
точки а функция  называется функцией Ляпунова (системы (1)), если
называется функцией Ляпунова (системы (1)), если

Здесь  — производная в силу системы (1).
— производная в силу системы (1).
Теорема Ляпунова об устойчивости. Если в некоторой окрестности  положения равновесия а существует функция Ляпунова
положения равновесия а существует функция Ляпунова  то это положение равновесия устойчиво по Ляпунову.
то это положение равновесия устойчиво по Ляпунову.
Наметим идею доказательства при  пусть
пусть  Линии уровня
Линии уровня  — замкнутые кривые при малых
— замкнутые кривые при малых  Эти кривые стягиваются в точку
Эти кривые стягиваются в точку  при
при  и при малых
и при малых  линия уровня
линия уровня  лежит внутри линии уровня
лежит внутри линии уровня  если
если  (Читателю, который найдет ошибку в этом утверждении, рекомендуем перейти к чтению строгого доказательства.) Выпустим фазовую траекторию у в момент времени
(Читателю, который найдет ошибку в этом утверждении, рекомендуем перейти к чтению строгого доказательства.) Выпустим фазовую траекторию у в момент времени  из точки
из точки  Так как
Так как  то
то  вдоль траектории
вдоль траектории  лемма), т. е.
лемма), т. е.  лежит внутри линии уровня
лежит внутри линии уровня  при всех
при всех  (рис. 30). Поэтому точка не может сильно отклониться от положения равновесия.
(рис. 30). Поэтому точка не может сильно отклониться от положения равновесия.

Рис. 30.

Рис. 31.
Чем меньше  тем меньше область
тем меньше область  она стягивается в точку при
она стягивается в точку при  что и показывает устойчивость положения равновесия.
что и показывает устойчивость положения равновесия.
Доказательство. Пусть  выберем
выберем  такое, что шар
такое, что шар  лежит в окрестности
лежит в окрестности  точки
точки
 Пусть
Пусть  — граница шара — сфера
— граница шара — сфера  Так как
Так как  — замкнутое ограниченное множество, функция
— замкнутое ограниченное множество, функция  непрерывна и
непрерывна и  на
на  Рассмотрим шар
Рассмотрим шар  содержащийся в
содержащийся в  Так как
Так как  то
то  можно выбрать настолько малым, чтобы выполнялось неравенство
можно выбрать настолько малым, чтобы выполнялось неравенство  при
при  в силу непрерывности функции
в силу непрерывности функции 
Покажем, что если  то
то  при
при  Тем самым теорема будет доказана. Так как
Тем самым теорема будет доказана. Так как  в области
в области  то
то  при
при  вдоль фазовой траектории
вдоль фазовой траектории  Следовательно, траектория, которая начинается в шаре
Следовательно, траектория, которая начинается в шаре  не может пересечь границы шара
не может пересечь границы шара  на
на  на траектории.
на траектории.
Теорема Ляпунова об асимптотической устойчивости. Пусть в некоторой окрестности  положения равновесия а существует функция Ляпунова
положения равновесия а существует функция Ляпунова  такая, что функция
такая, что функция  отрицательно определена в
отрицательно определена в  Тогда положение равновесия а асимптотически устойчиво.
Тогда положение равновесия а асимптотически устойчиво.
Доказательство. Выберем шары  так же, как и в предыдущем доказательстве. Если
так же, как и в предыдущем доказательстве. Если  то
то  при
при  Рассмотрим функцию и)
Рассмотрим функцию и)  Так как
Так как  то функция
то функция  не возрастает (§ 4, лемма), и существует предел
не возрастает (§ 4, лемма), и существует предел  При этом
При этом  , поскольку
, поскольку 
Если  то
то  так как
так как  при
при  этом случае теорема доказана. Допустим, что
этом случае теорема доказана. Допустим, что  и приведем это предположение к противоречию. В этом случае
и приведем это предположение к противоречию. В этом случае  при всех
при всех  и существует
и существует  такое, что
такое, что  а при
а при  В противном случае на траектории у имелись бы точки, сколь угодно близкие к точке
В противном случае на траектории у имелись бы точки, сколь угодно близкие к точке  а потому функция
а потому функция  на у принимала бы сколь угодно малые значения. В шаровом слое
на у принимала бы сколь угодно малые значения. В шаровом слое  функция
функция  строго отрицательна, по условию теоремы. В силу непрерывности
строго отрицательна, по условию теоремы. В силу непрерывности  в этом слое, а стало быть, и на траектории у. Следовательно,
в этом слое, а стало быть, и на траектории у. Следовательно,

Интегрируя, получаем  и правая часть этого неравенства отрицательна при
и правая часть этого неравенства отрицательна при  Это противоречит предположению:
Это противоречит предположению: 
Пусть  — окрестность положения равновесия
— окрестность положения равновесия  — область, которая содержится в
— область, которая содержится в  и имеет а своей граничной точкой (рис. 32).
и имеет а своей граничной точкой (рис. 32).

Рис. 32.
Теорема Четаева, о неустойчивости. Пусть функция  непрерывно дифференцируема в области
непрерывно дифференцируема в области 

 в тех граничных точках области
в тех граничных точках области  которые лежат внутри области
которые лежат внутри области  Тогда положение равновесия а неустойчиво.
Тогда положение равновесия а неустойчиво.
Доказательство. Пусть точка  — фазовая траектория, выходящая из точки
— фазовая траектория, выходящая из точки  ее уравнение имеет вид
ее уравнение имеет вид  Покажем, что траектория
Покажем, что траектория  не может пересечь ту часть границы области
не может пересечь ту часть границы области  которая лежит внутри
которая лежит внутри  Рассмотрим функцию
Рассмотрим функцию  вдоль
вдоль  Так как
Так как  пока у содержится в
пока у содержится в  то
то  пока у содержится в
пока у содержится в  и траектория не может пересечь ту часть границы области
и траектория не может пересечь ту часть границы области  на которой
на которой  Следовательно, траектория у должна покинуть
Следовательно, траектория у должна покинуть  Так как.
Так как.  содержит точки, сколь угодно близкие к точке а, то это положение равновесия неустойчиво.
содержит точки, сколь угодно близкие к точке а, то это положение равновесия неустойчиво.
Рассмотрим примеры.
Теорема 1. Пусть система (1) имеет первый интеграл  положительно определенный в окрестности положения равновесия а. Тогда положение равновесия а устойчиво по Ляпунову.
положительно определенный в окрестности положения равновесия а. Тогда положение равновесия а устойчиво по Ляпунову.
Действительно,  и потому все условия теоремы Ляпунова об устойчйвости выполнены.
и потому все условия теоремы Ляпунова об устойчйвости выполнены.
Пример 3. Рассмотрим материальную точку массы  которая движется в потенциальном поле сил с потенциальной энергией
которая движется в потенциальном поле сил с потенциальной энергией  Движение частицы описывается системой уравнений
Движение частицы описывается системой уравнений

Эта система эквивалентна системе уравнений первого порядка

и имеет первый интеграл (§ 4)

Положения равновесия определяются из уравнений  т. е. имеют вид
т. е. имеют вид  где
где  — стационарная точка потенциальной энергии.
— стационарная точка потенциальной энергии.
Пусть  — изолированная точка минимума потенциальной энергии
— изолированная точка минимума потенциальной энергии  , тогда положение равновесия
, тогда положение равновесия  устойчиво по Ляпунову. Это утверждение было высказано Лагранжем и впоследствии доказано Дирихле.
устойчиво по Ляпунову. Это утверждение было высказано Лагранжем и впоследствии доказано Дирихле.
Так как потенциальная энергия определяется с точностью до постоянного слагаемого, то можно считать, что  Функция
Функция  обращается в нуль (в малой окрестности точки
обращается в нуль (в малой окрестности точки  только при
только при  так как
так как  при
при  и теорема Дирихле следует из теоремы 1.
и теорема Дирихле следует из теоремы 1.
Теорема 2. Пусть  — положение равновесия системы (1) и существует функция Ляпунова
— положение равновесия системы (1) и существует функция Ляпунова  такая, что
такая, что

в некоторой окрестности  точки
точки  где
где  — положительные постоянные. Тогда существует положительная постоянная С такая, что
— положительные постоянные. Тогда существует положительная постоянная С такая, что

если точка  достаточно близка к точке
достаточно близка к точке 
Доказательство. Положим  тогда
тогда  или
или  Интегрируя это неравенство от 0 до
Интегрируя это неравенство от 0 до  , получаем
, получаем  Учитывая второе из неравенств (6), получаем
Учитывая второе из неравенств (6), получаем

откуда следует (7).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
- § 5. Одномерное движение частицы в потенциальном поле
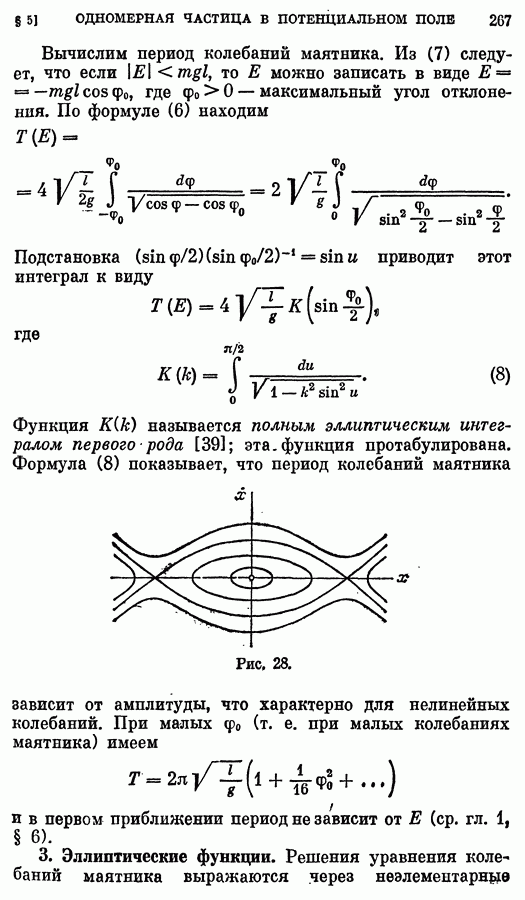
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
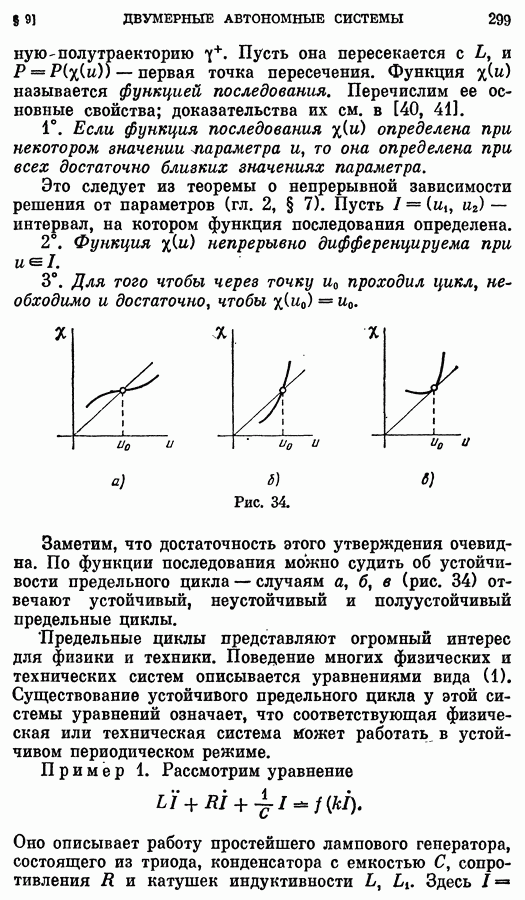
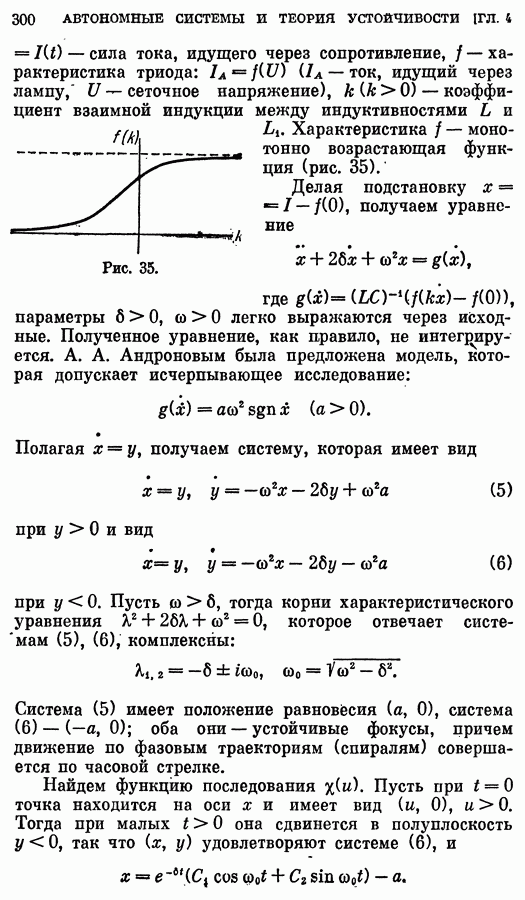
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ