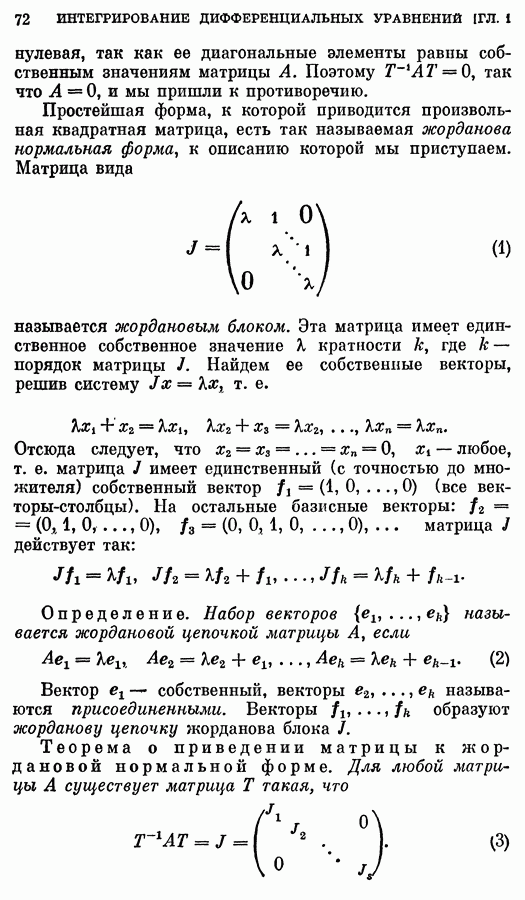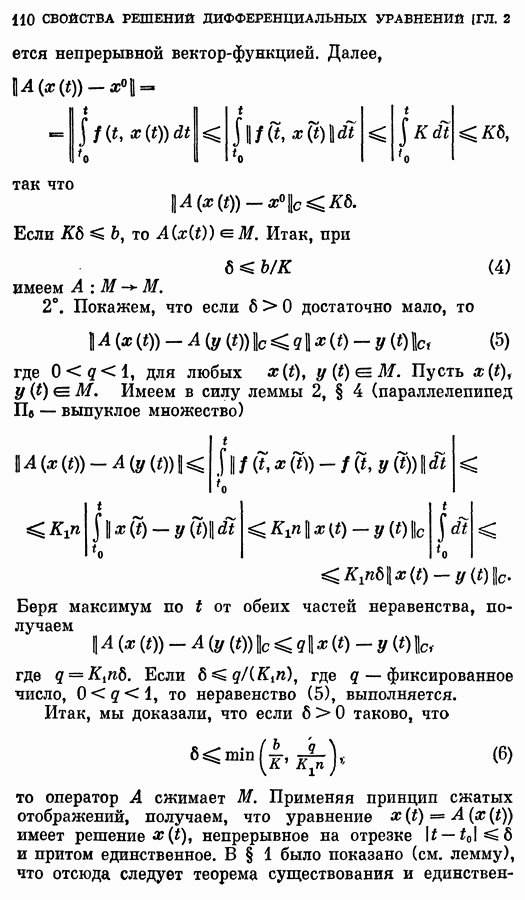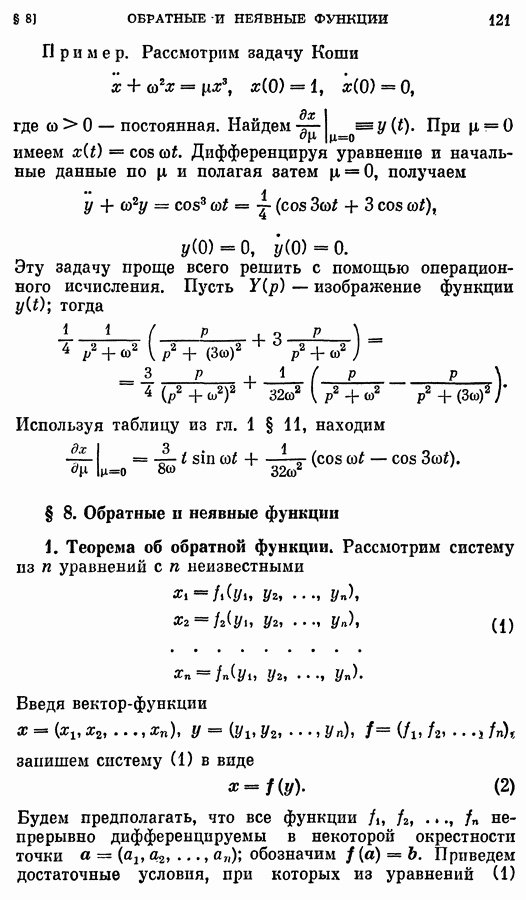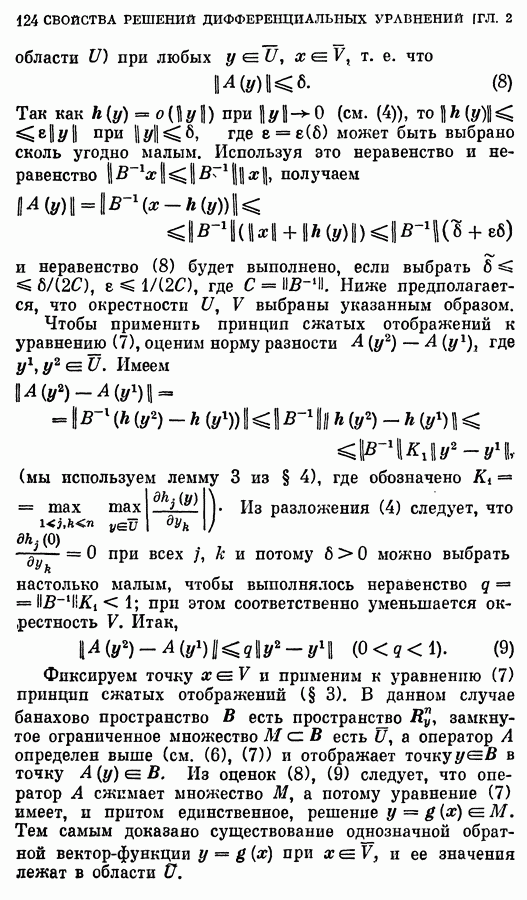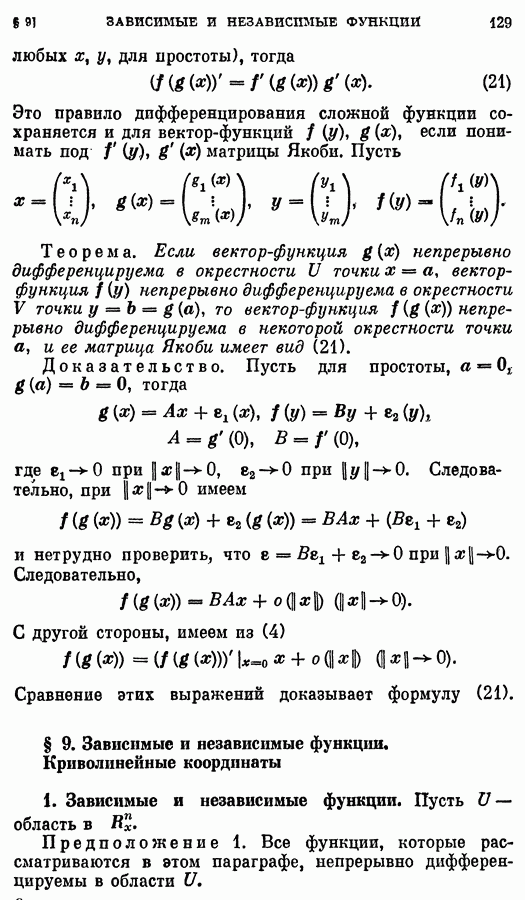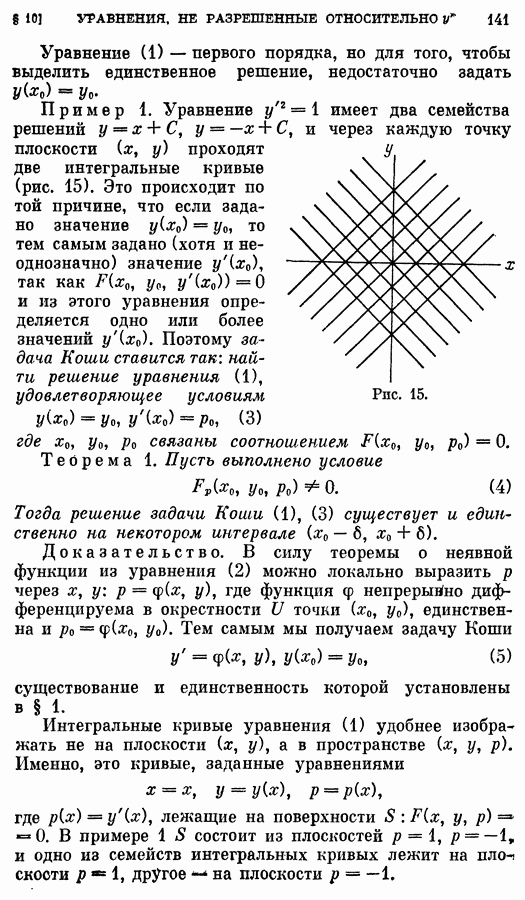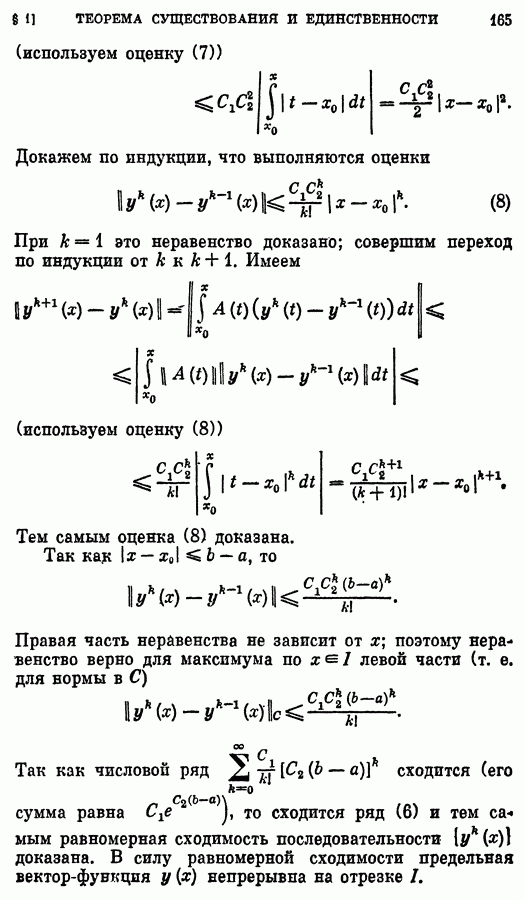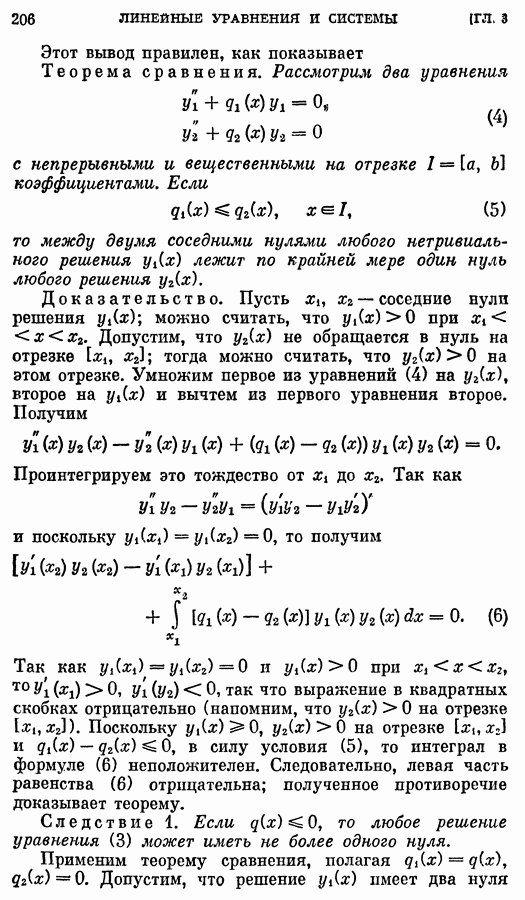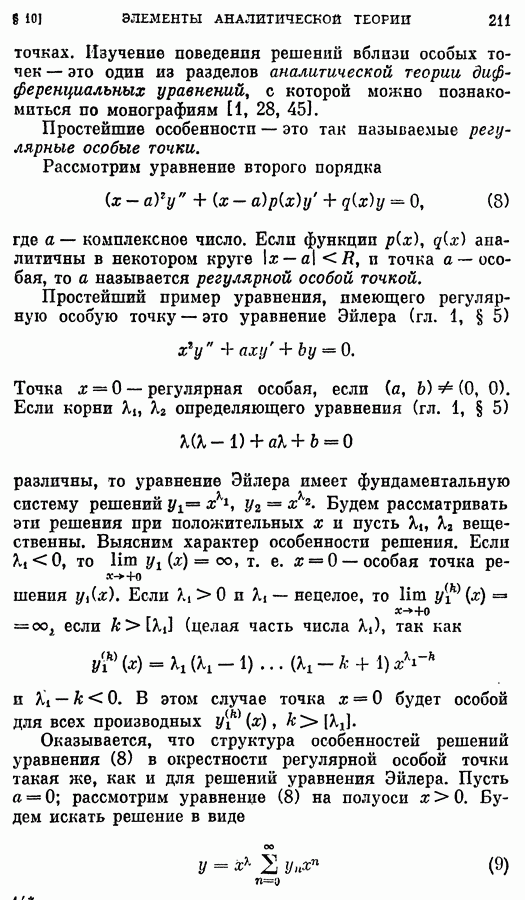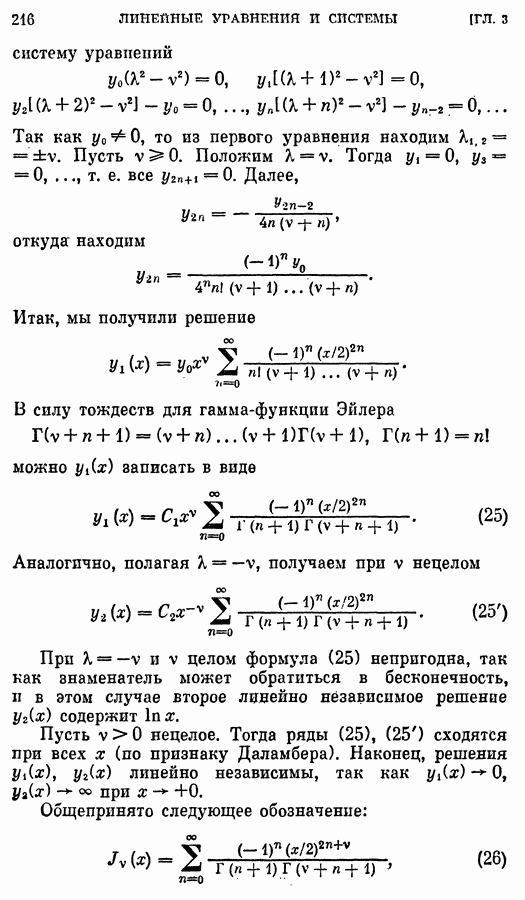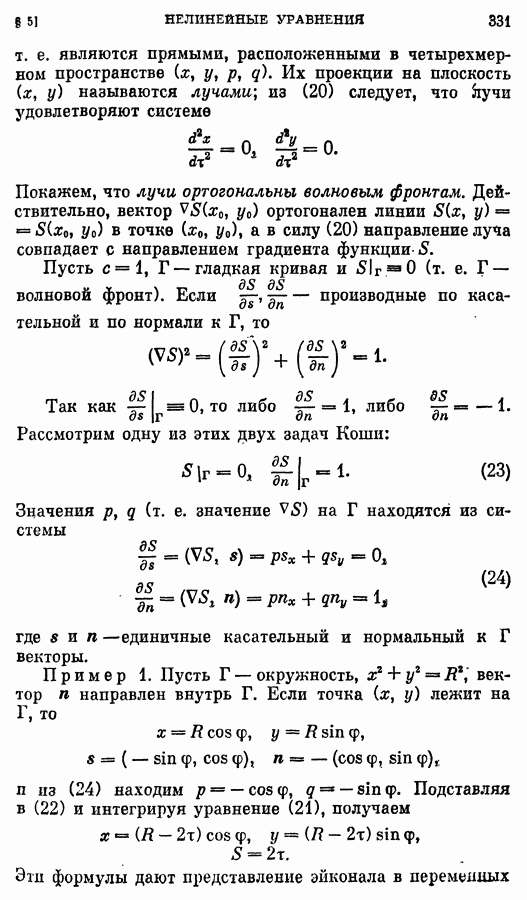| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
§ 1. Основная теорема
1. Формулировка.
В этой главе независимое переменное есть  (оно играет роль времени), неизвестные функции обозначаются
(оно играет роль времени), неизвестные функции обозначаются  Все функции и вектор-функции принимают вещественные значения. Рассмотрим систему дифференциальных уравнений:
Все функции и вектор-функции принимают вещественные значения. Рассмотрим систему дифференциальных уравнений:

Мы будем использовать векторные обозначения. Введем вектор-функции

Тогда система запишется в виде

Это общий вид системы первого порядка в нормальной форме т. е. разрешенной относительно 
Задачей Коши (или задачей с начальными данными) называется следующая задача: найти решение  системы (1) такое, что
системы (1) такое, что

где  заданное число,
заданное число,  — заданный вектор. Решением системы (1) называется вектор-функция
— заданный вектор. Решением системы (1) называется вектор-функция  которая определена и непрерывно дифференцируема на некотором интервале
которая определена и непрерывно дифференцируема на некотором интервале  и удовлетворяет системе.
и удовлетворяет системе.
Пусть  — решение системы (1), определенное при
— решение системы (1), определенное при  Интегральной кривой системы (1) называется кривая
Интегральной кривой системы (1) называется кривая  -мерном пространстве
-мерном пространстве  с координатами
с координатами  Геометрическая интерпретация задачи Коши такова: требуется найти интегральную кривую системы (1), проходящую через заданную точку
Геометрическая интерпретация задачи Коши такова: требуется найти интегральную кривую системы (1), проходящую через заданную точку 
Вектор  касается интегральной кривой
касается интегральной кривой  в точке
в точке  . В силу (1) этот вектор равен вектору
. В силу (1) этот вектор равен вектору  . Пусть вектор-функция
. Пусть вектор-функция  определена в области
определена в области  Построив в каждой точке
Построив в каждой точке  вектор
вектор  , получим в области
, получим в области  векторное поле. Интегральные кривые системы (1) принадлежат этому полю, т. е. касаются векторов этого поля в каждой точке, и обратно, всякая непрерывно дифференцируемая кривая
векторное поле. Интегральные кривые системы (1) принадлежат этому полю, т. е. касаются векторов этого поля в каждой точке, и обратно, всякая непрерывно дифференцируемая кривая  принадлежащая данному векторному полю, является интегральной кривой системы (1). Такова геометрическая интерпретация системы (1).
принадлежащая данному векторному полю, является интегральной кривой системы (1). Такова геометрическая интерпретация системы (1).
Сформулируем основную теорему теории обыкновенных дифференциальных уравнений.
Теорема существования и единственности. Пусть  — область в пространстве
— область в пространстве  (с координатами
(с координатами  ), вектор-функция
), вектор-функция  и ее производные —7 определены и непрерывны в области
и ее производные —7 определены и непрерывны в области  Рассмотрим задачу Коши (1), (2), где
Рассмотрим задачу Коши (1), (2), где  Тогда
Тогда
1°. Решение задачи Коши существует на некотором интервале 
2°. Решение задачи Коши единственно, т. е. если имеется два решения  задачи (1), (2), то
задачи (1), (2), то  в некоторой окрестности точки
в некоторой окрестности точки 
Геометрическая интерпретация основной теоремы такова: в условиях теоремы через каждую точку области  проходит интегральная кривая, и притом только одна.
проходит интегральная кривая, и притом только одна.
Для доказательства этой теоремы сведем систему дифференциальных уравнений (1) к системе интегральных уравнений.
Лемма 1. Задача Коши (1), (2) эквивалентна системе интегральных уравнений

Именно: 1) всякое решение задачи (1), (2) удовлетворяет уравнению (3); 2) всякое непрерывное на некотором интервале  решение уравнения (3) является решением задачи (1), (2).
решение уравнения (3) является решением задачи (1), (2).
Доказательство. Пусть  — решение задачи Коши (1), (2), определенное на интервале
— решение задачи Коши (1), (2), определенное на интервале  , и пусть
, и пусть  лежит на этом интервале. Интегрируя обе части (1) от
лежит на этом интервале. Интегрируя обе части (1) от  до
до  и учитывая (2), получаем (3).
и учитывая (2), получаем (3).
Пусть  — непрерывное на интервале I решение уравнения (3). Тогда
— непрерывное на интервале I решение уравнения (3). Тогда  так что (2) выполнено. Далее, так как вектор-функции
так что (2) выполнено. Далее, так как вектор-функции  непрерывны, то вектор-функция
непрерывны, то вектор-функция  непрерывна при
непрерывна при  и потому вектор-функция
и потому вектор-функция  дифференцируема при
дифференцируема при  Следовательно, вектор-функция
Следовательно, вектор-функция  дифференцируема при
дифференцируема при  Дифференцируя обе части равенства (3), получаем, что
Дифференцируя обе части равенства (3), получаем, что  удовлетворяет системе (1). Уравнение (3) запишем в операторной форме:
удовлетворяет системе (1). Уравнение (3) запишем в операторной форме:

Здесь А — оператор

Сформулируем определение оператора.
Пусть каждой функции  из некоторого множества функций М поставлена в соответствие некоторая функция
из некоторого множества функций М поставлена в соответствие некоторая функция  Тогда мы говорим, что задан оператор А, переводящий функцию
Тогда мы говорим, что задан оператор А, переводящий функцию  в функцию
в функцию 
Будем записывать это в виде  или
или  (читается: А переводит
(читается: А переводит 
Это определение дословно переносится на тот случай, когда  — вектор-функции.
— вектор-функции.
Приведем примеры операторов.
1. Оператор умножения на функцию:

Здесь  — заданная непрерывная на отрезке
— заданная непрерывная на отрезке  функция.
функция.
2. Оператор дифференцирования:

3. Оператор интегрирования:

В примерах 1, 3 функция  непрерывна, а в примере 2 — дифференцируема на отрезке
непрерывна, а в примере 2 — дифференцируема на отрезке  .
.
4. Оператор  действующий по формуле (5). Здесь
действующий по формуле (5). Здесь  — непрерывная на некотором интервале I вектор-функция такая, что все точки
— непрерывная на некотором интервале I вектор-функция такая, что все точки  при
при  лежат в области определения вектор-функции
лежат в области определения вектор-функции 
Как и в случае обычных функций, вводятся понятия: область определения и область значений оператора.
Понятие оператора является естественным обобщением понятия функции. Именно,
функция: число число,
оператор: функция функцию, вектор-функция  вектор-функцию.
вектор-функцию.
Оба эти понятия — частный случай понятия «отображение», напомним его.
Пусть даны два произвольных множества X, Y. Мы скажем, что задано отображение множества X в множество У, если каждому элементу  поставлен в соответствие некоторый элемент
поставлен в соответствие некоторый элемент  . Для функции X и Y — множества чисел, для оператора X и Y — множества функция (или вектор-фупкций).
. Для функции X и Y — множества чисел, для оператора X и Y — множества функция (или вектор-фупкций).
Доказательство основной теоремы будет проведено в § 5 с помощью принципа сжатых отображений, что потребует введения ряда новых понятий и дополнительных фактов из анализа (§§ 2—4). Здесь мы ограничимся случаем одного уравнения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
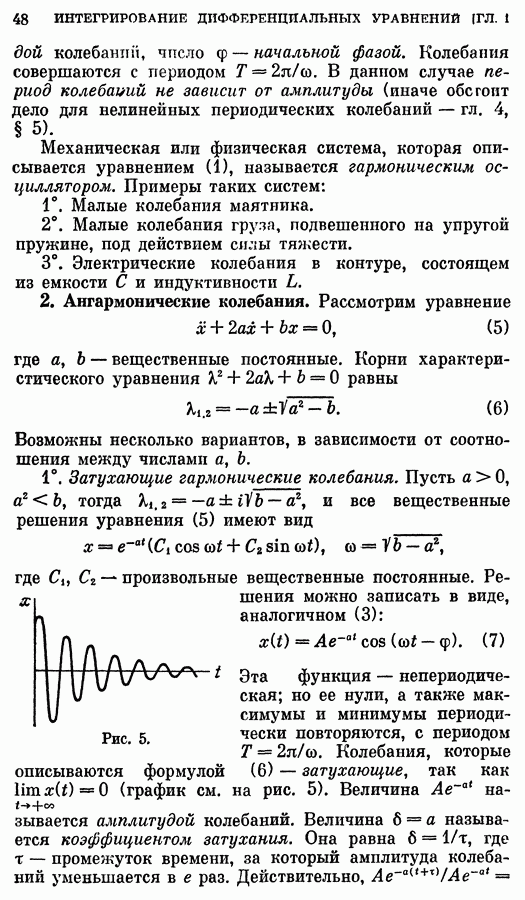
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
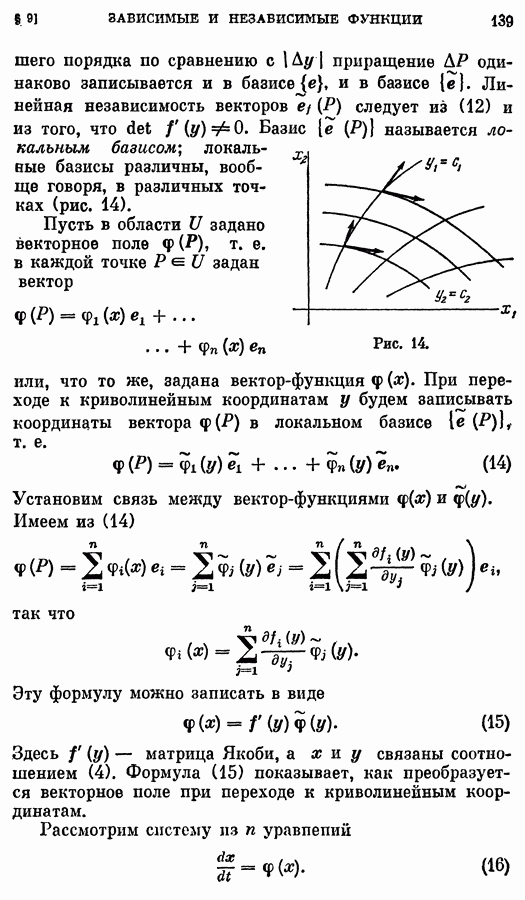
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
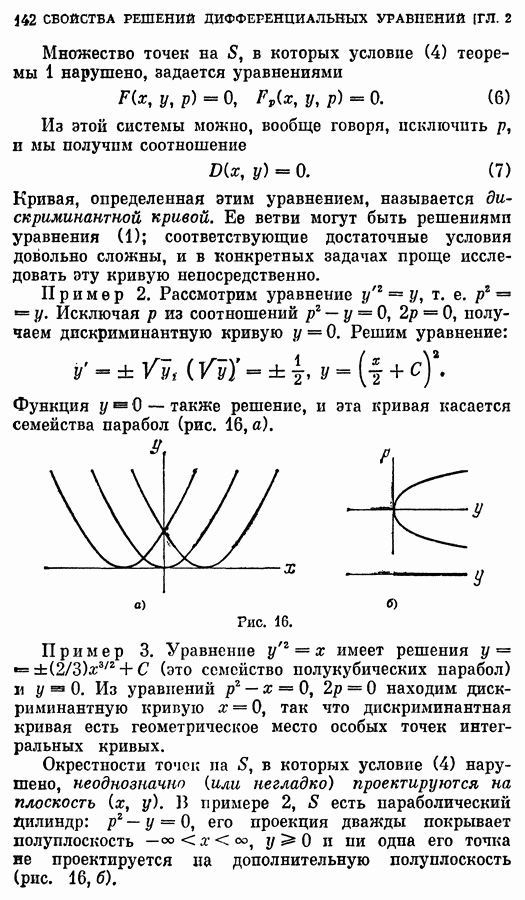
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
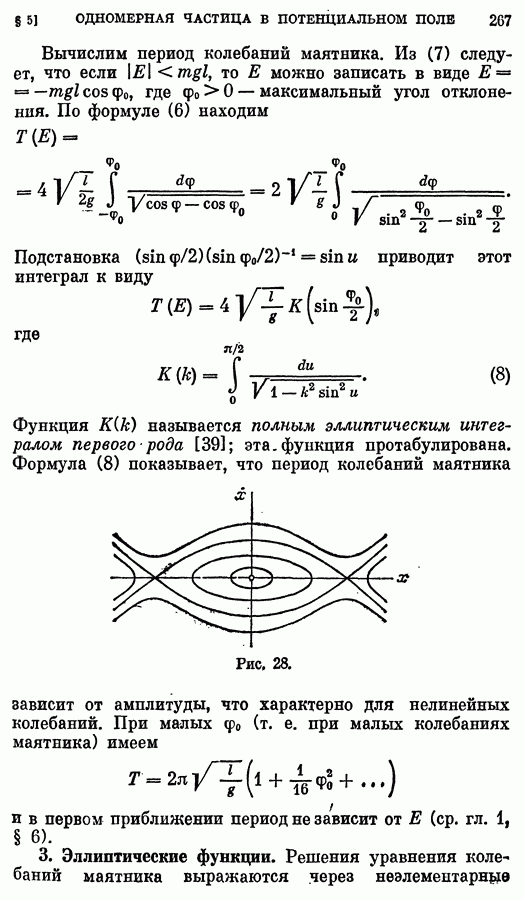
- § 5. Одномерное движение частицы в потенциальном поле
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
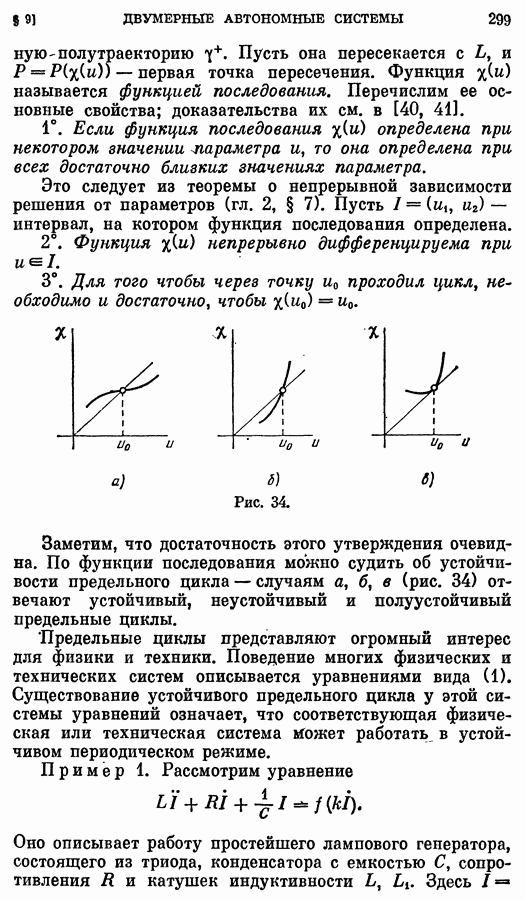
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
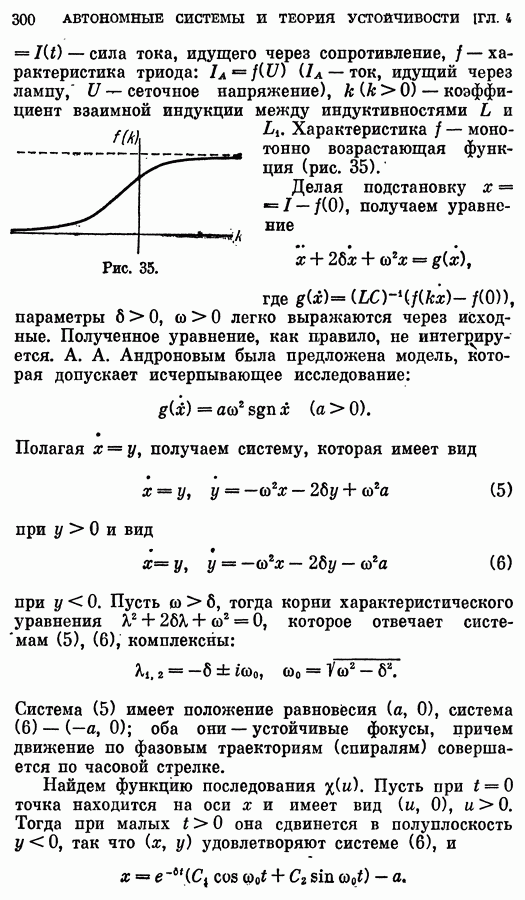
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
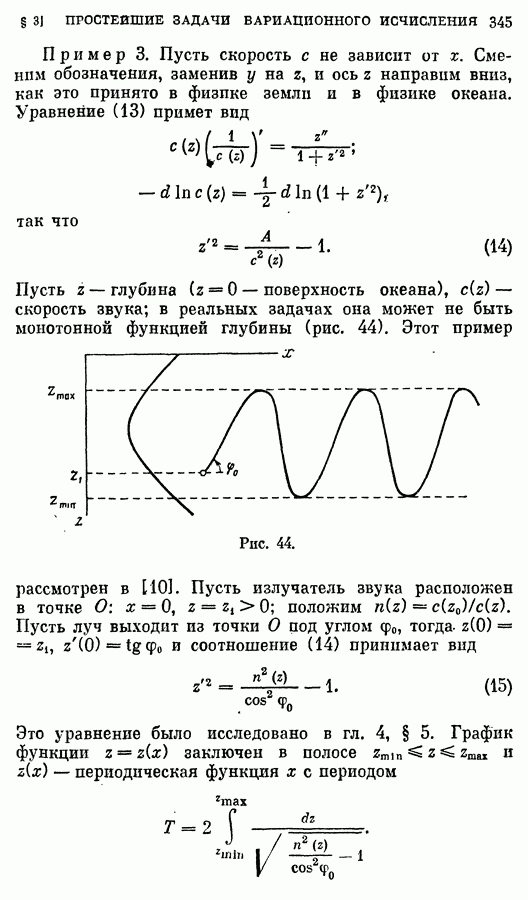
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ