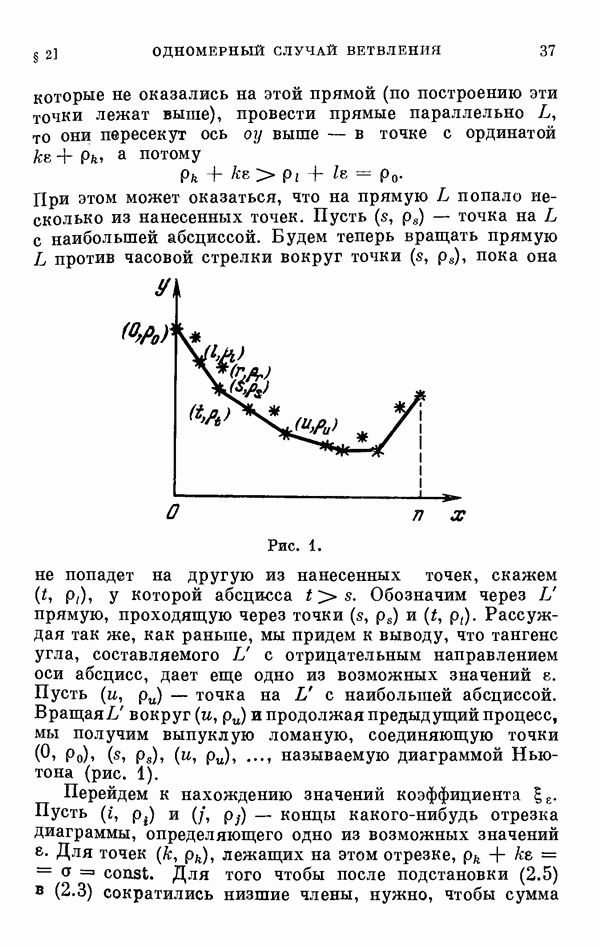
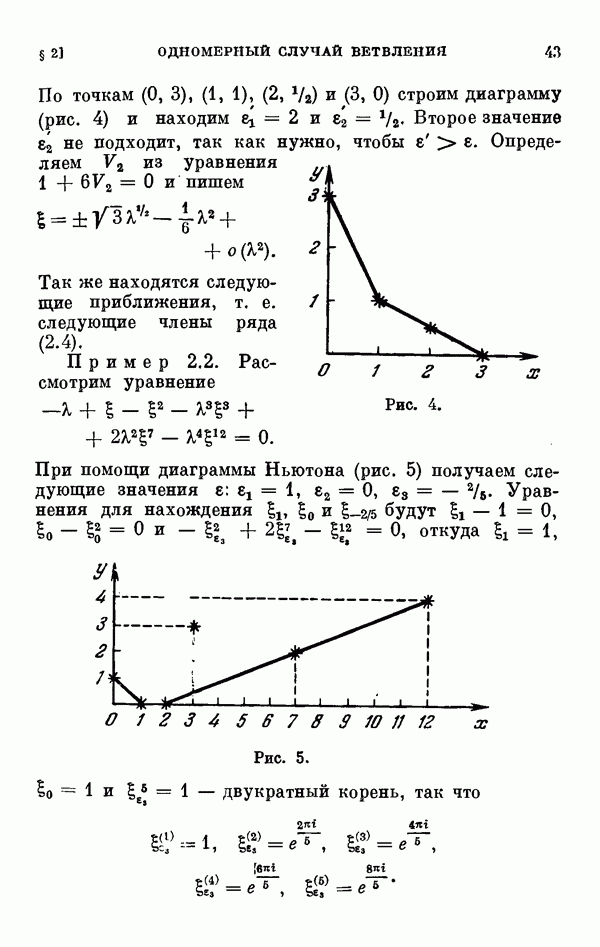
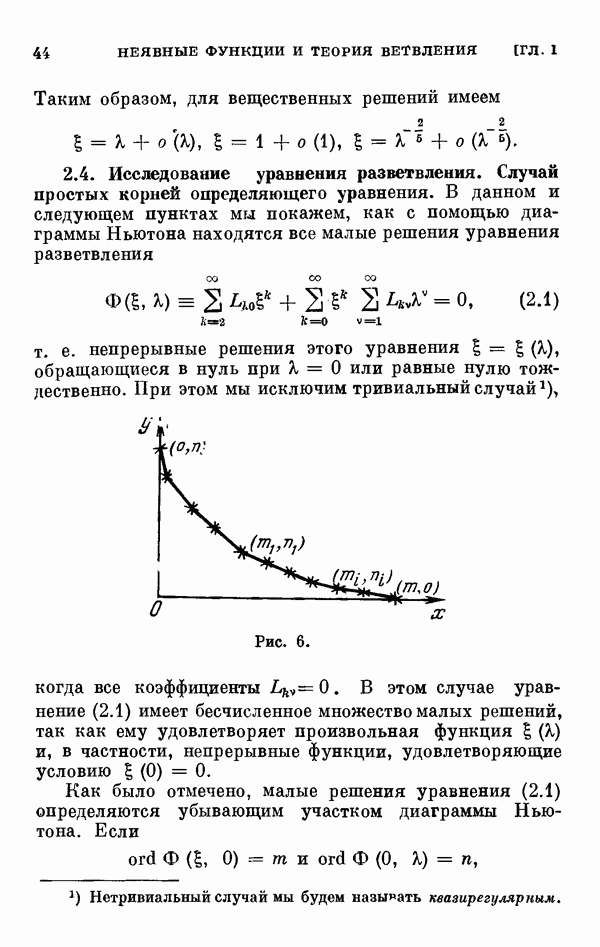
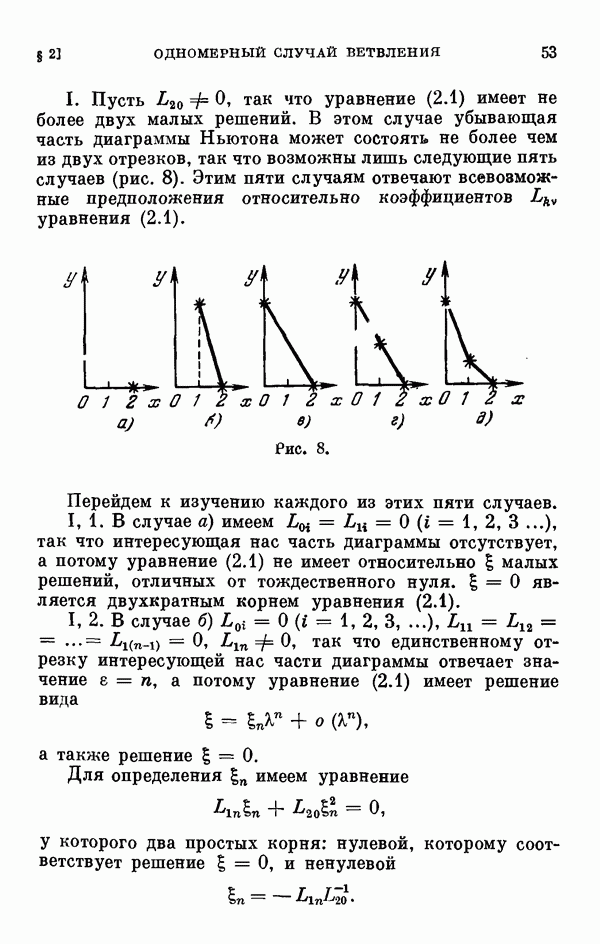
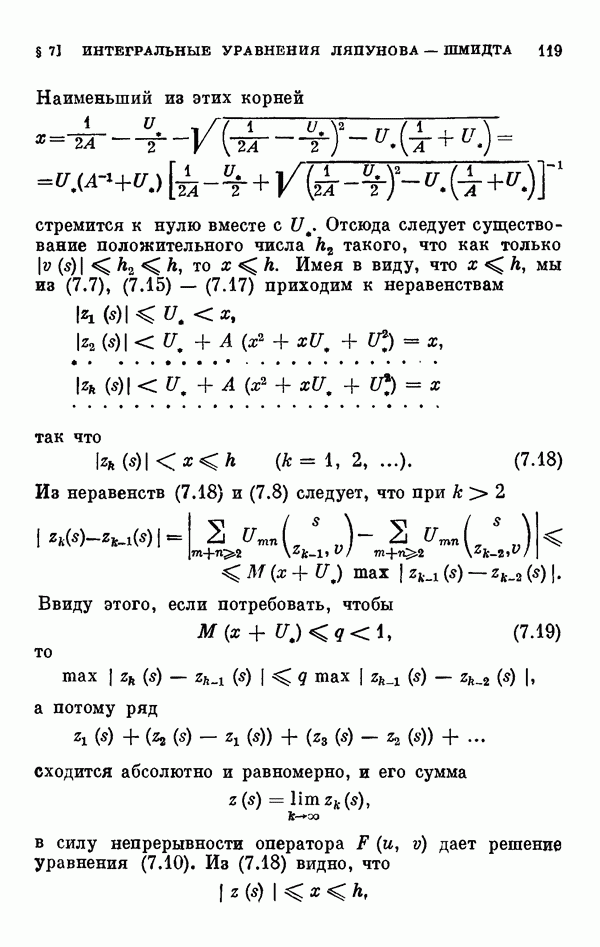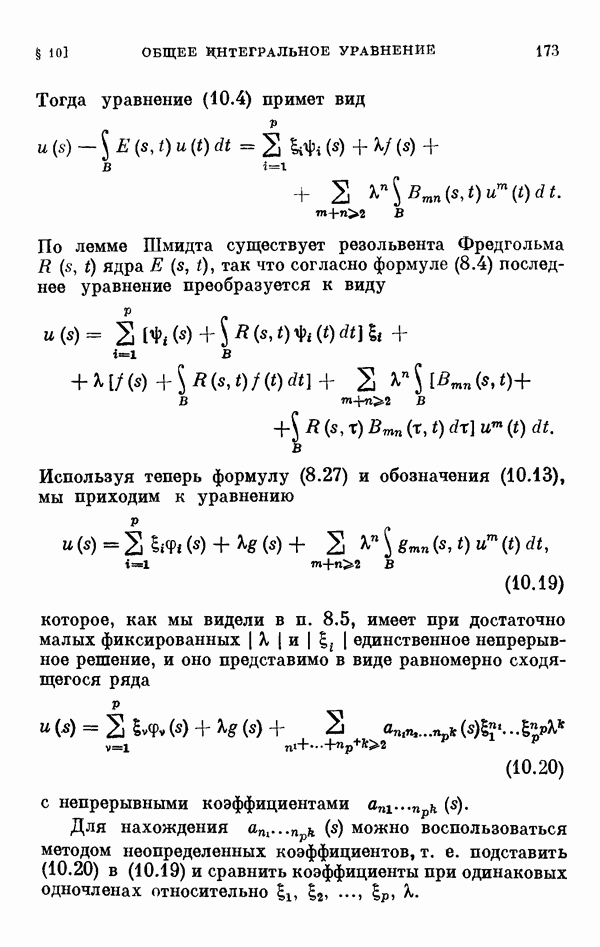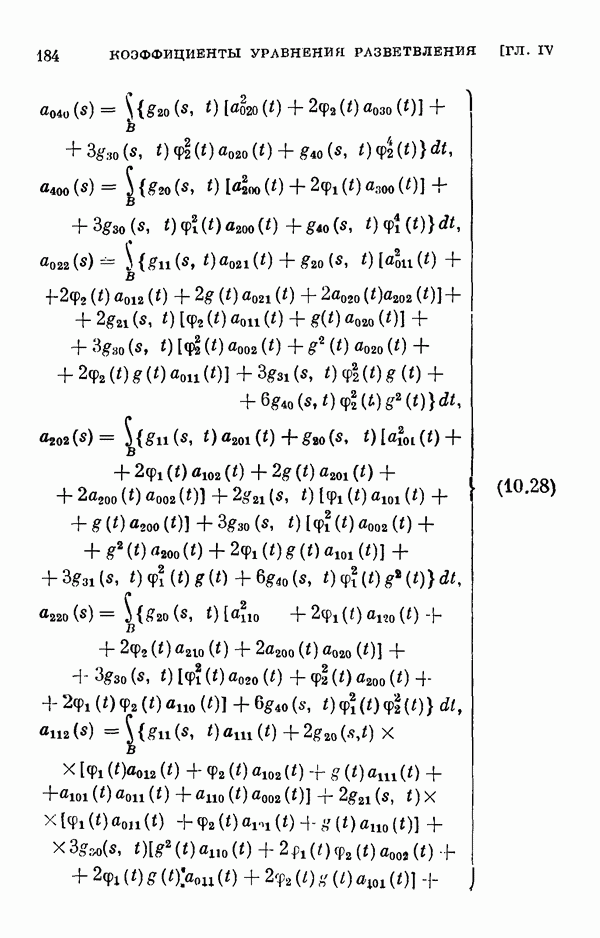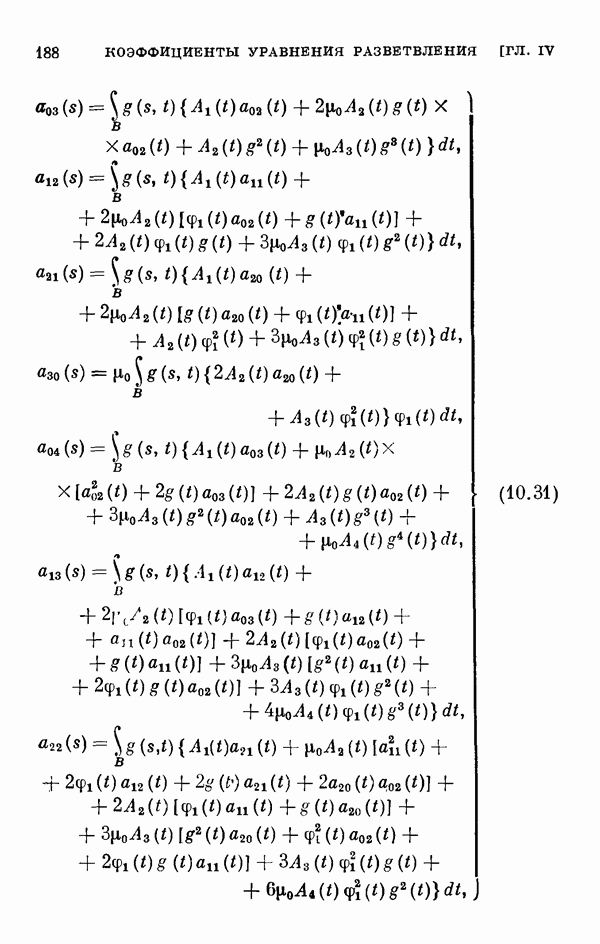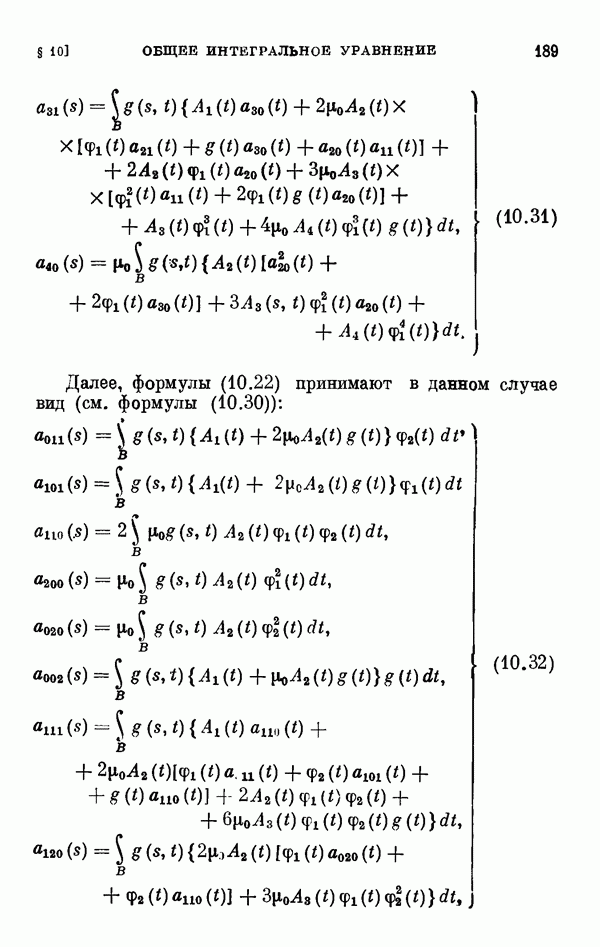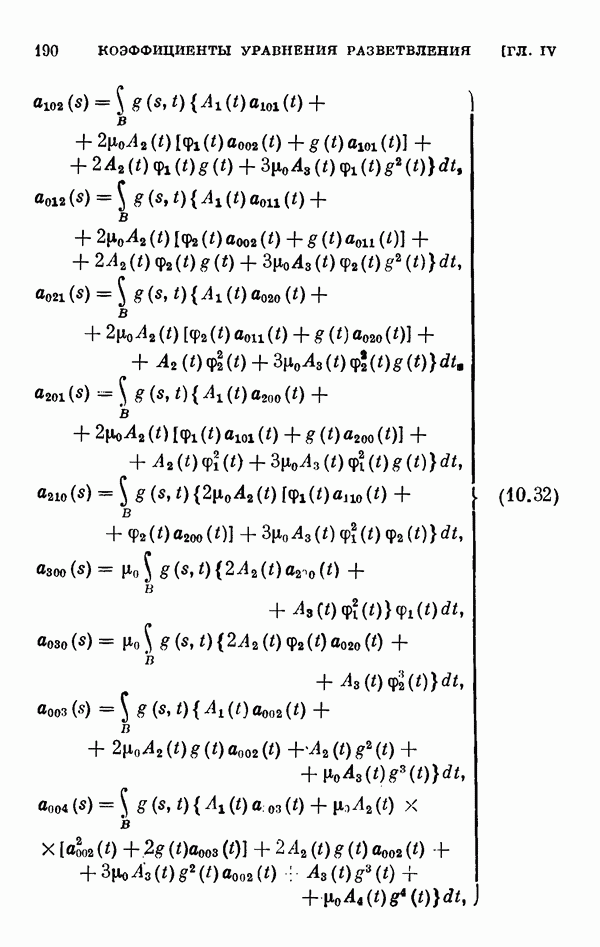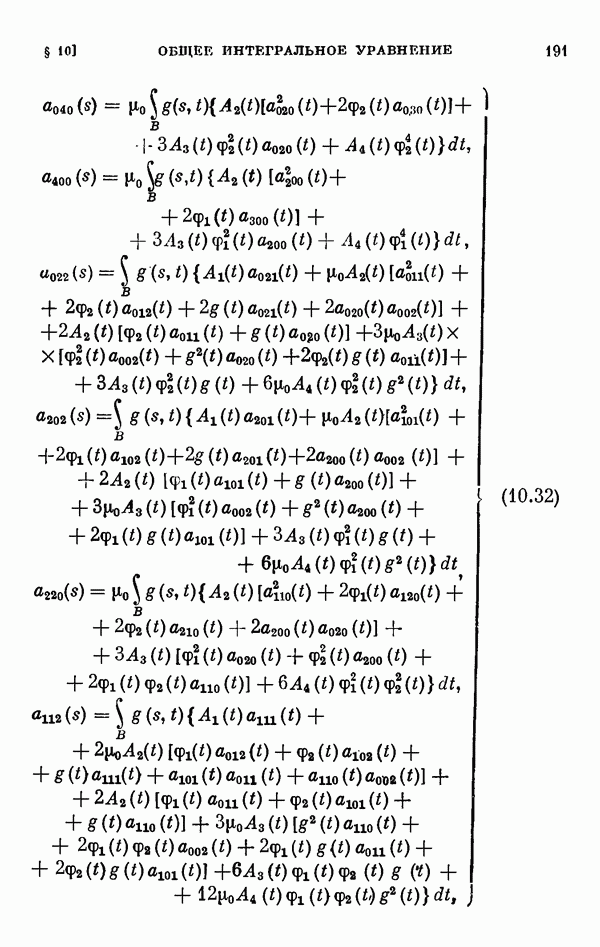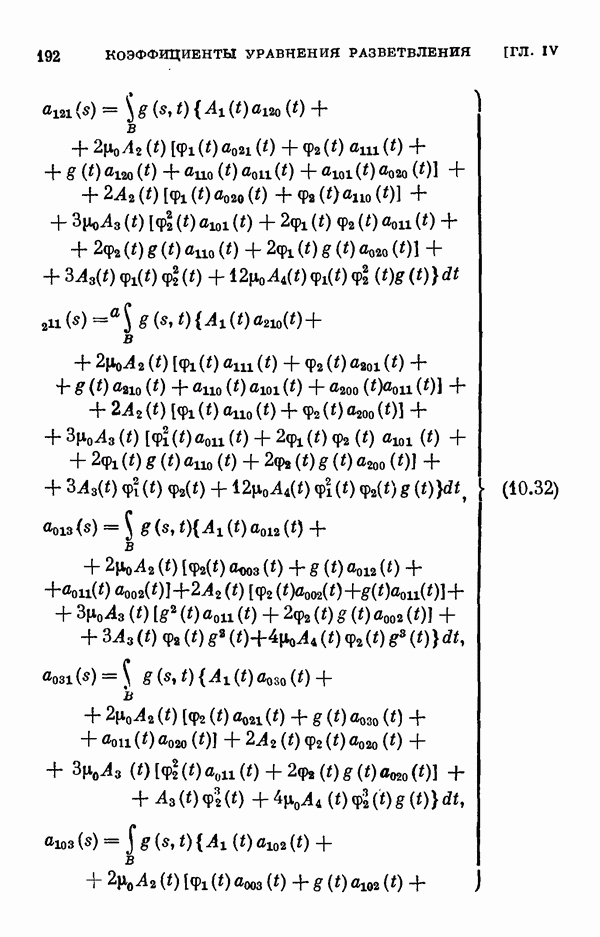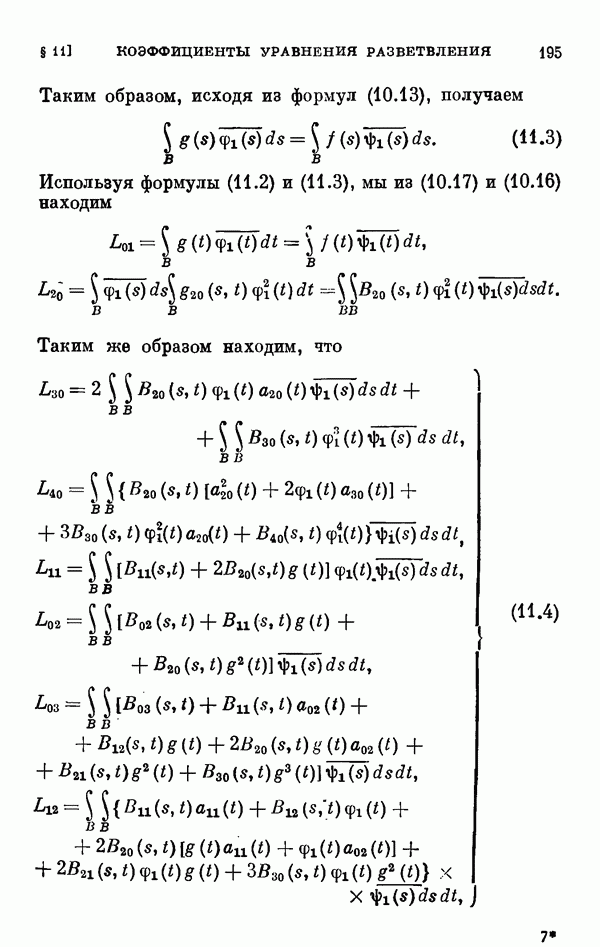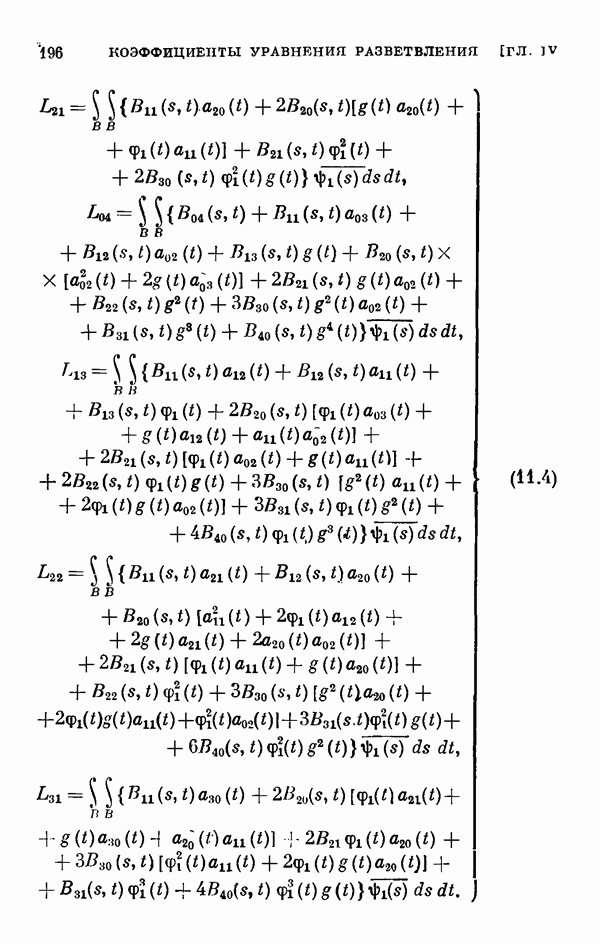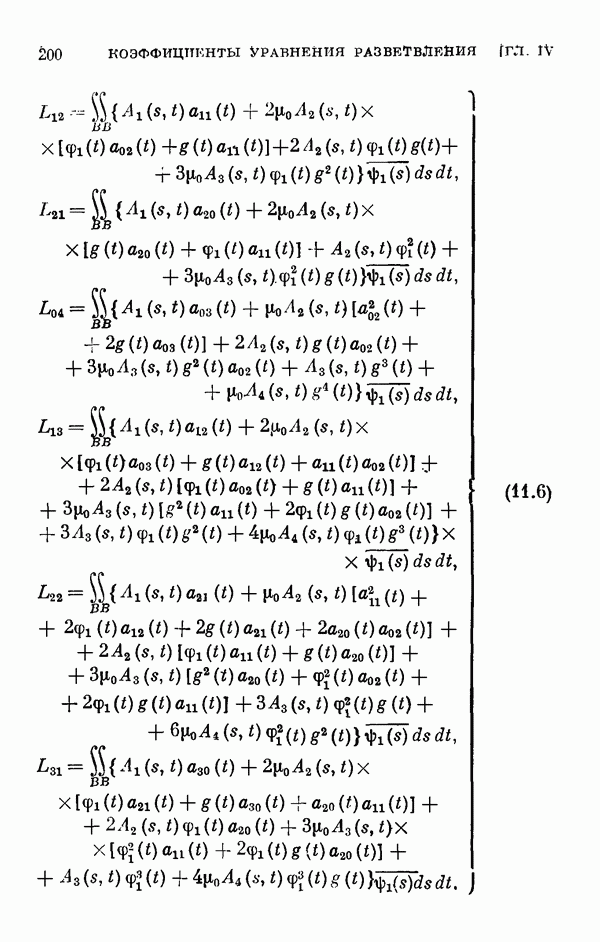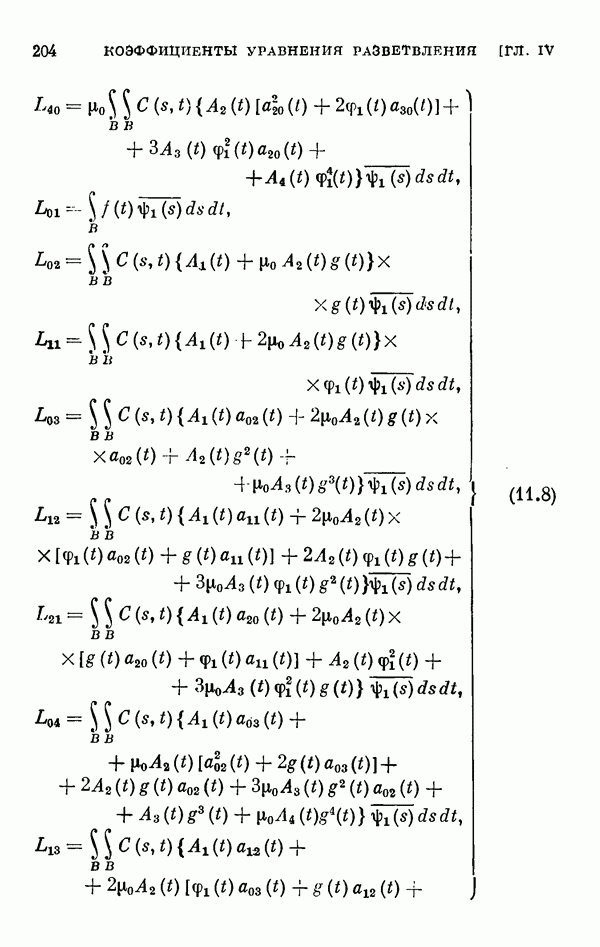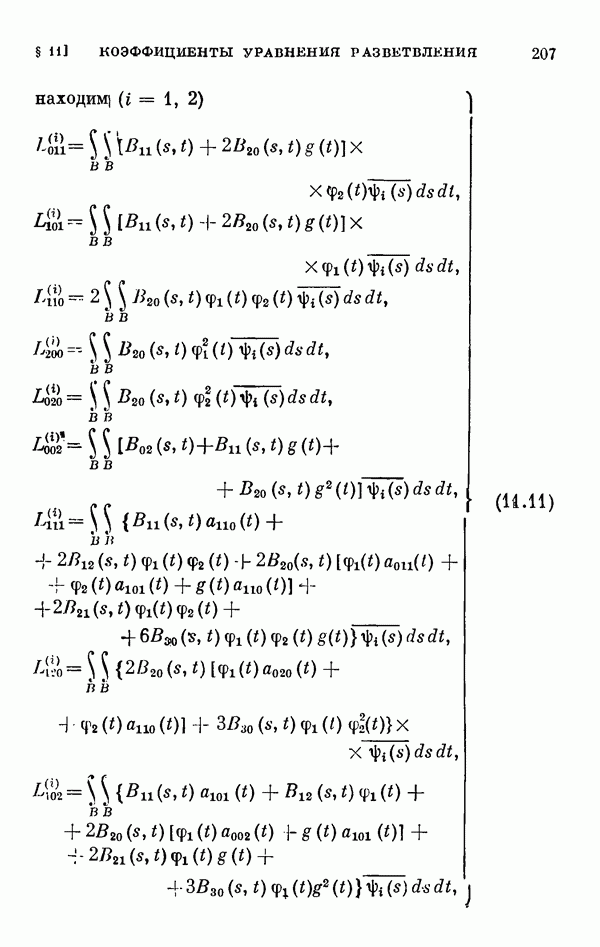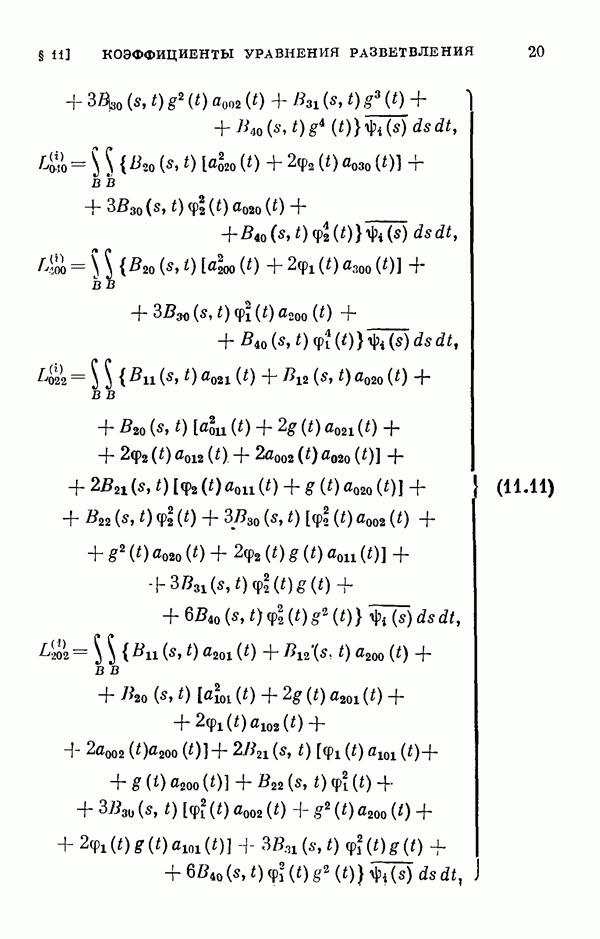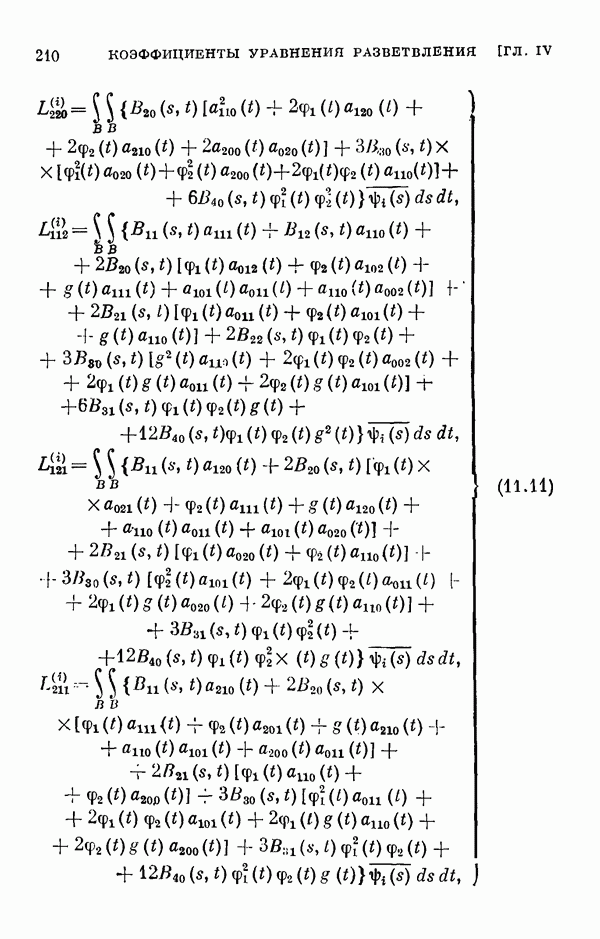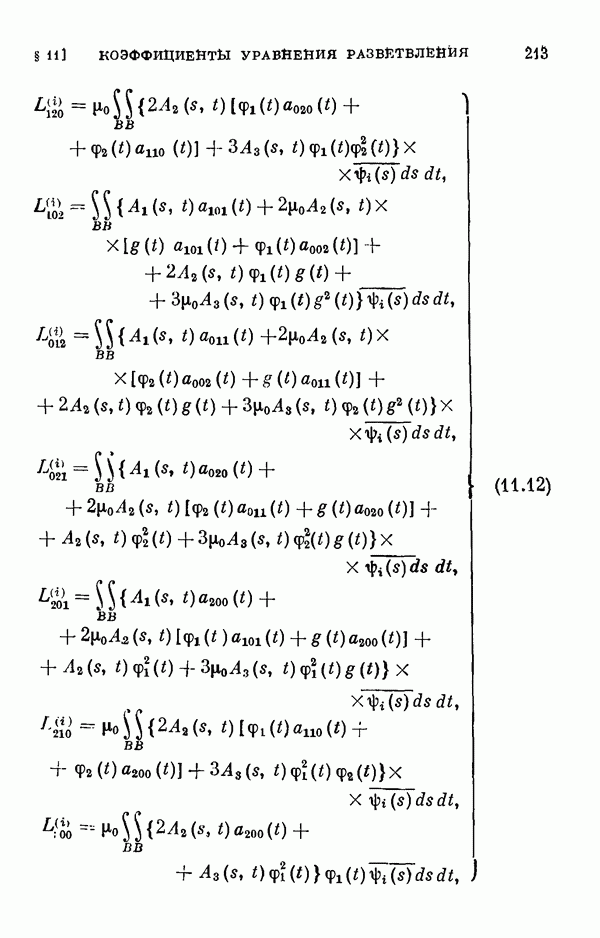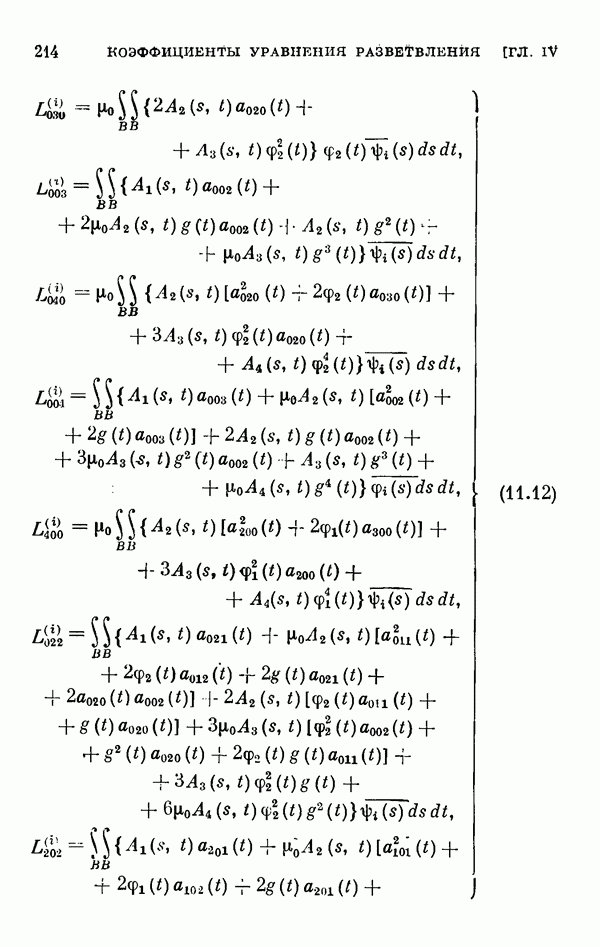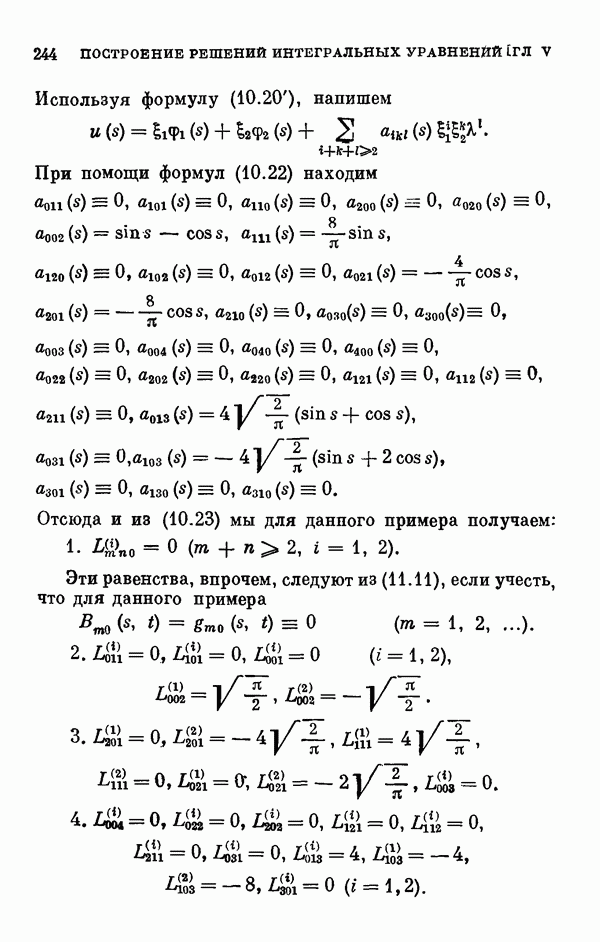| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
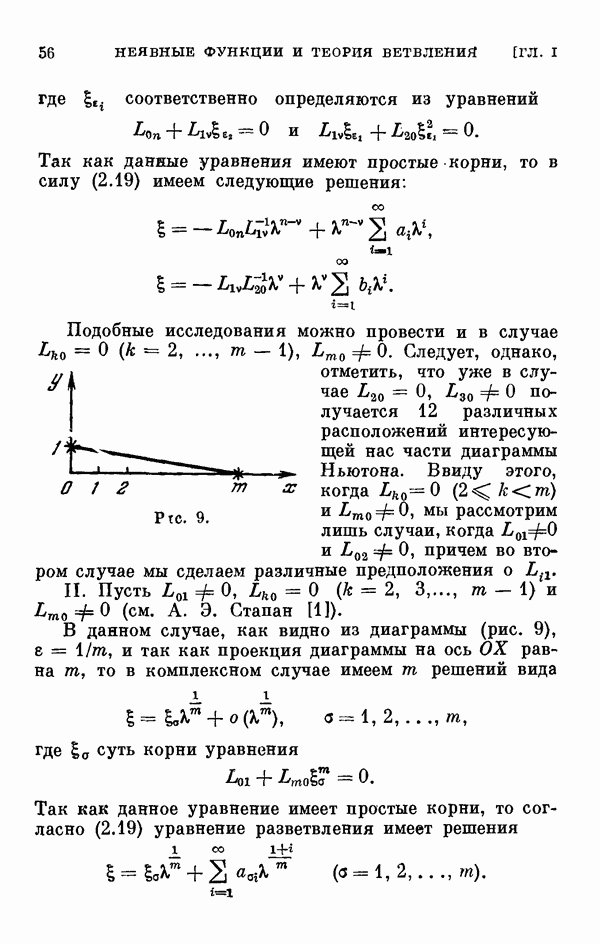
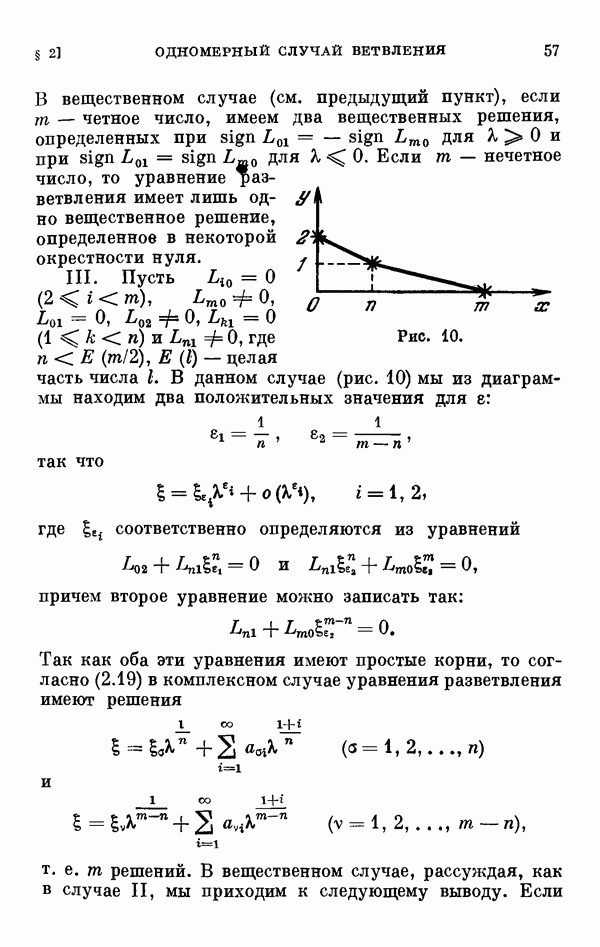
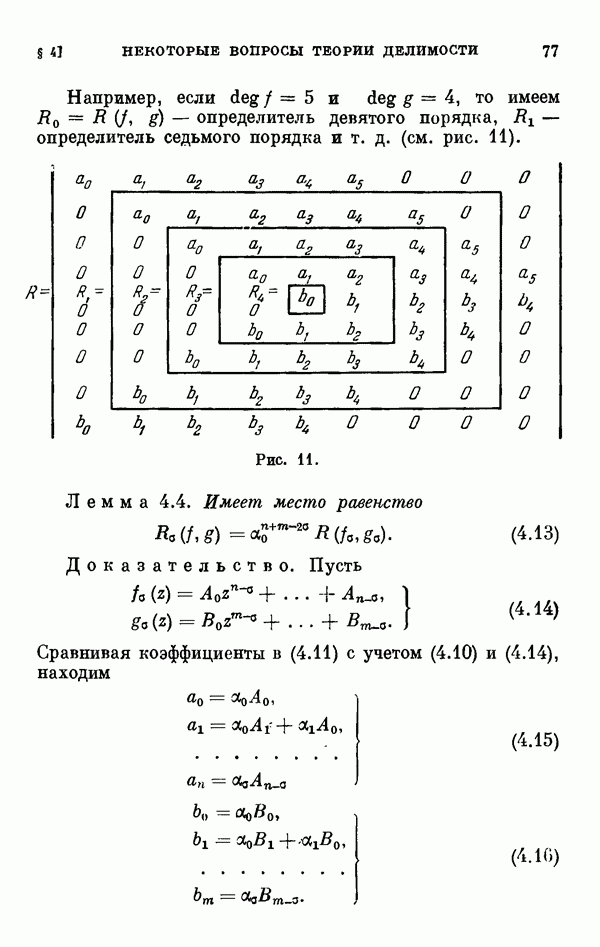
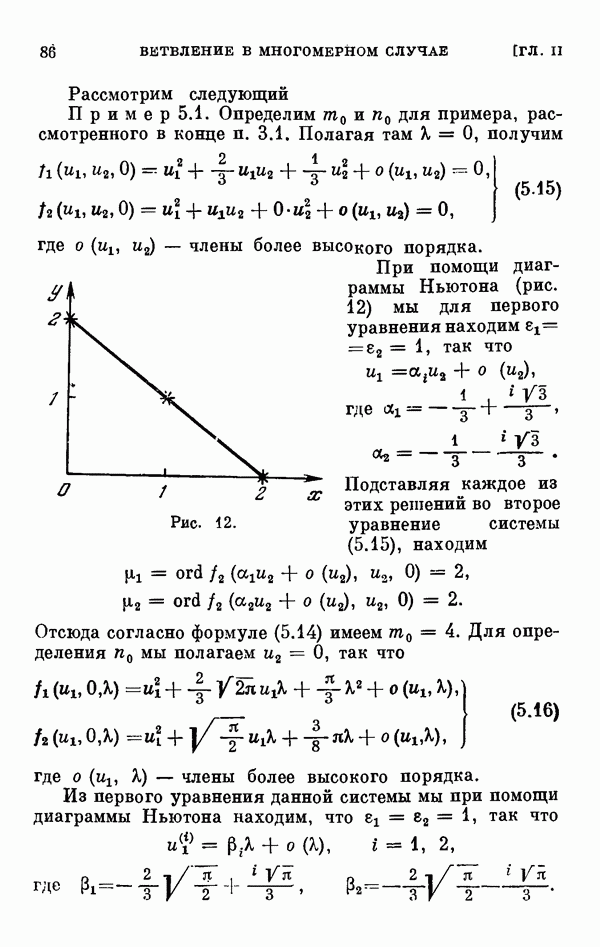
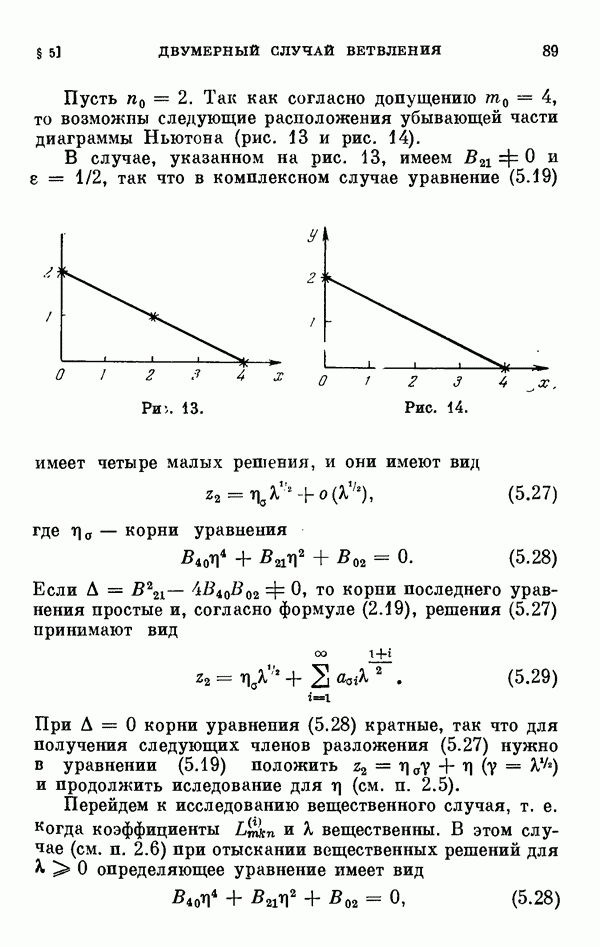
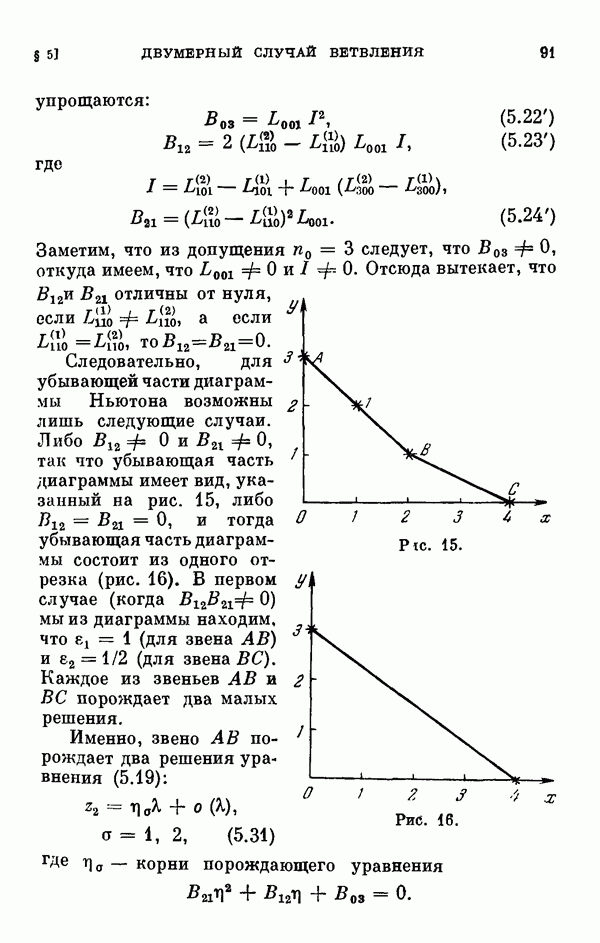
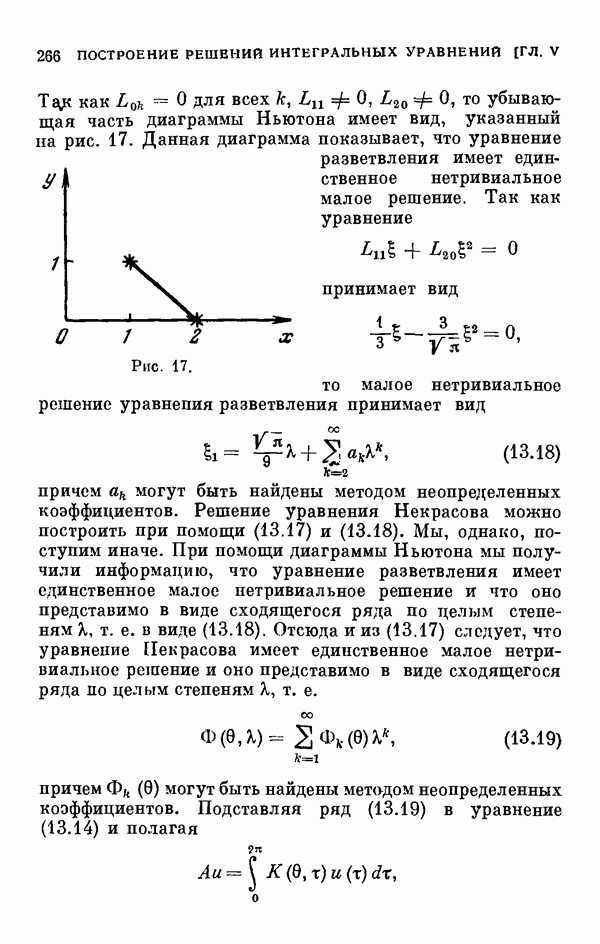
2.5. Случай кратных корней определяющего уравнения.
Пусть  — кратный корень определяющего уравнения (2.18), так что
— кратный корень определяющего уравнения (2.18), так что  и теорема 1.2 неприменима. В этом случае соответствующие ряды (2.4) имеют одинаковые первые члены, а потому для определения следующих членов разложения (2.4) нужно будет последовательно пользоваться представлениями вида (2.5). Для того чтобы иметь дело с целыми показателями, мы преобразуем уравнение (2.1) не при помощи (2.5), а следующей подстановкой:
и теорема 1.2 неприменима. В этом случае соответствующие ряды (2.4) имеют одинаковые первые члены, а потому для определения следующих членов разложения (2.4) нужно будет последовательно пользоваться представлениями вида (2.5). Для того чтобы иметь дело с целыми показателями, мы преобразуем уравнение (2.1) не при помощи (2.5), а следующей подстановкой:

и при помощи диаграммы Ньютона определим разложение  в окрестности точки
в окрестности точки  как это было сделано в
как это было сделано в  при определении V.
при определении V.
Повторяя рассуждения предыдущего пункта, получим

При этом согласно замечанию  кратности корней
кратности корней  соответствующих определяющих уравнений не возрастают. Ввиду этого либо при некотором
соответствующих определяющих уравнений не возрастают. Ввиду этого либо при некотором  окажется, что — простой корень соответствующего определяющего уравнения, либо
окажется, что — простой корень соответствующего определяющего уравнения, либо  будут корнями одной и той же кратности
будут корнями одной и той же кратности  соответствующих определяющих уравнений, а
соответствующих определяющих уравнений, а  будут корнями соответствующих уравнений, кратности которых не меньше
будут корнями соответствующих уравнений, кратности которых не меньше 
В первом случае мы из (2.20) получим

а во втором случае  будет
будет  -кратным малым решением как уравнения (2.1), так и уравнения (2.14). В данном случае мы представим левую часть уравнения (2.14), т. е. отмеченный многочлен
-кратным малым решением как уравнения (2.1), так и уравнения (2.14). В данном случае мы представим левую часть уравнения (2.14), т. е. отмеченный многочлен  в виде произведения степеней неприводимых отмеченных многочленов (см. определение 3.2 и теорему 3.2).
в виде произведения степеней неприводимых отмеченных многочленов (см. определение 3.2 и теорему 3.2).
Именно, напишем, что

где  — неприводимые отмеченные многочлены.
— неприводимые отмеченные многочлены.
Рассмотрим теперь все те многочлены  , которые входят в правую часть равенства (2.22) с одинаковыми степенями. Пусть, например,
, которые входят в правую часть равенства (2.22) с одинаковыми степенями. Пусть, например,  Положим тогда
Положим тогда

Разумеется,  принимает какие-то значения из ряда натуральных чисел. При помощи многочленов
принимает какие-то значения из ряда натуральных чисел. При помощи многочленов  равенство (2.22) принимает вид
равенство (2.22) принимает вид

Эту запись нужно понимать так, что если среди чисел  нет числа
нет числа  то
то  т. е. в правой части (2.23) нет тогда сомножителя
т. е. в правой части (2.23) нет тогда сомножителя  . Равенство (2.23) показывает, что если
. Равенство (2.23) показывает, что если  является
является  -кратным решением уравнения
-кратным решением уравнения  то
то  — простое решение уравнения
— простое решение уравнения

Применяя к данному уравнению (2.23) предыдущие рассуждения, мы при помощи диаграммы Ньютона получим для  представление в виде сходящегося ряда (2.21).
представление в виде сходящегося ряда (2.21).
Таким образом, и в случае кратных корней определяющего уравнения нами доказаны утверждения 2.2 и 2.3.
Отметим еще, что многочлены, входящие в равенство (2.22), а значит и многочлены  , входящие в равенство (2.23), могут быть найдены при помощи алгоритма, изложенного в § 4.
, входящие в равенство (2.23), могут быть найдены при помощи алгоритма, изложенного в § 4.
Замечание 2.2. Отметим, что рассуждения, содержащиеся в данном и предыдущем пунктах, приводят
к другому доказательству утверждения теоремы 2.1 для уравнения (2.1).
Пусть  — корень уравнения (2.18), кратность которого
— корень уравнения (2.18), кратность которого  , так что первый член разложения (2.4) будет
, так что первый член разложения (2.4) будет  и (2.5) примет вид
и (2.5) примет вид

Учитывая замену  получим
получим

и, полагая  будем иметь
будем иметь

Подставляя данное выражение  в (2.17), точнее, в выражение для
в (2.17), точнее, в выражение для  получим
получим

или

Применяя к данному уравнению диаграмму Ньютона, получим

Отсюда и из предыдущего имеем

так что

Продолжая данный процесс, мы и получим разложение по возрастающим степеням К (ибо  ).
).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ГЛАВА I. Системы неявных функций и классическая теория ветвления
- § 1. Задача о неявных функциях
- 1.2. Общее исследование задачи о неявных функциях.
- 1.3. Аналитический случай.
- § 2. Одномерный сличай ветвления и диаграмма Ньютона
- 2.2. О свойствах решений.
- 2.3. Примеры.
- 2.4. Исследование уравнения разветвления. Случай простых корней определяющего уравнения.
- 2.5. Случай кратных корней определяющего уравнения.
- 2.6. О вещественных решениях.
- 2.7. Некоторые частные случаи расположения диаграммы Ньютона.
- ГЛАВА II. Исследование уравнения разветвления в многомерном случае
- 3.2. Приведение к нормальному виду.
- § 4. Некоторые вопросы теории делимости
- 4.2. Общий делитель и аналог алгоритма Евклида.
- 4.3. Примитивный ОНД.
- 4.4. Применение к отмеченным многочленам.
- § 5. Двумерный случай ветвления
- 5.2. Указатели двумерного случая ветвления.
- 5.3. Частные случаи.
- § 6. Многомерный случай ветвления
- 6.2. Малые решения уравнения разветвления и метод исключения неизвестных.
- 6.3. Квазирегулярный случай ветвления.
- 6.4. Вырожденный случай ветвления.
- 6.5. Об изолированности нулевого решения.
- ГЛАВА III. Уравнение разветвления для нелинейных интегральных и интегро-дифференциальных уравнений
- § 7. Интегральные уравнения Ляпунова — Шмидта
- 7.2. Интегро-степенные ряды от многих функциональных аргументов.
- 7.3. Интегро-степенные ряды от интегро-степенных рядов.
- 7.4. Сжатость оператора Ляпунова—Шмидта.
- 7.5. Простейшее уравнение.
- 7.6. Последовательные приближения Лихтенштейна.
- 7.7. Применение метода мажорант.
- 7.8. Простейшее уравнение в случае равномерной сходимости.
- § 8. Общее интегральное уравнение Ляпунова—Шмидта
- 8.2. Регулярный случай при наличии многих аргументов.
- 8.3. Лемма Шмидта.
- 8.4. Одномерный случай ветвления.
- 8.5. Многомерный случай ветвления.
- 8.6. Возможные обобщения.
- § 9. Системы уравнений Ляпунова—Шмидта и некоторые интегро-дифференциальные уравнения
- 9.2. Регулярный случай.
- 9.3. Случай ветвления.
- 9.4. Некоторые нелинейные интегро-дифференциальные уравнения первого порядка.
- 9.5. Другие виды интегро-дифференциальных уравнений.
- 9.6. Другой способ построения уравнения разветвления
- ГЛАВА IV. Общее интегральное уравнение и коэффициенты уравнения разветвления
- 10.2. Регулярный случай.
- 10.3. Одномерный случай ветвления.
- 10.4. Многомерный случай ветвления.
- 10.5 Частный случай.
- 10.6. Уравнение Гаммерштейна.
- § 11. Коэффициенты уравнения разветвления
- 11.2. Коэффициенты одиомерного уравнения разветвления нелинейного интегрального уравнения Гаммерштейна.
- 11.3. Коэффициенты двумерного уравнения разветвления общего нелинейного интегрального уравнения.
- 11.4. Коэффициенты двумерного уравнения разветвления для частных случаев.
- 11.5. Некоторые свойства коэффициентов уравнения разветвления.
- ГЛАВА V. Описание и построение решений нелинейных интегральных уравнений
- § 12. Описание решений нелинейных интегральных уравнений
- 12.2. Описание решении в одномерном случае ветвления.
- 12.3. О точках бифуркации в одномерном случае ветвления.
- 12.4. Описание решений в двумерном случае ветвления.
- 12.5. Описание решений в многомерном случае ветвления.
- 12.6. О ветвлении изолированного решения.
- 12.7. Точки бифуркации в многомерном случае ветвления.
- § 13. Построение решений нелинейных интегральных уравнений
- 13.3. Двумерный случай ветвления.
- 13.4. Уравнение Некрасова.
- 13.5. Уравнение разветвления для уравнения Некрасова.
- § 14. Особые решения нелинейных интегральных уравнений
- 14.2. Сведение к малым решениям.
- 14.3. Особые решения в регулярном случае.
- 14.4. Исследование вспомогательного уравнения.
- 14.5. Ветвление решений основного уравнения.
- 14.6 Особые решения в пространствах Лебега.
- ГЛАВА VI. Ветвление периодических решений дифференциальных уравнений
- § 15. Периодические решения неавтономных систем
- 15.2. Метод Пуанкаре.
- 15.3. Условия периодичности и уравненне разветвления.
- 15.4. Описание решений в регулярном случае.
- 15.5. Описание решений в одномерном случае ветвления.
- 15.6. Описание решений в многомерном случае ветвления.
- § 16. Периодические решения квазилинейных систем
- 16.2. Условия периодичности.
- 16.3. Вывод уравнения разветвления.
- 16.4. Описание решений и дополнительные замечания.
- § 17. Периодические решения автономных систем
- 17.2. Уравнение разветвления.
- 17.3. Основные выводы.
- 17.4. Метод неопределенных коэффициентов.
- 17.5. Автономные системы с одной степенью свободы.
- § 18. Примеры
- 18.1. Неавтономные системы с одной степенью свободы.
- 18.2 Автономные системы с одной степенью свободы.
- § 19. Другие задачи о периодических решениях
- 19.1. Особые периодические решения неавтономных систем.
- 19.2. Ветвление периодических решений в банаховых пространствах
- § 20. Об устойчивости периодических решений, зависящих от малого параметра
- 20.2. Устойчивость решений задачи Пуанкаре.
- ГЛАВА VII. Нелинейные уравнения в банаховых пространствах
- § 21. Некоторые вопросы теории линейных операторов в банаховых пространствах
- 21.2. Специальные разложения пространств в прямые суммы подпространств.
- 21.3. Сужение оператора и обобщенная лемма Шмидта.
- 21.4 Связь с сопряженным оператором.
- 21.5. Неограниченные фредгольмовские операторы.
- § 22. Степенные операторы, ряды Тейлора, теоремы о неявных операторах
- 22.2 Степенные ряды. Ряды Тейлора.
- 22.3 Теоремы о неявных операторах.
- § 23. Уравнение разветвления Ляпунова — Шмидта
- 23.2. Вывод уравнения разветвления с помощью сужения оператора B.
- 23.3. Вывод уравнения разветвления с помощью леммы Шмидта.
- 23.4. Основная теорема об уравнении разветвления.
- 23.5. Уравление разветвления в аналитическом случае.
- 23.6. Уравнение разветвления для неограниченных операторов.
- § 24. Исследование одномерного случая ветвления
- 24.2. Вырожденный случай.
- 24.3. Квазирегулярный случай (задача А).
- 24.4. Задача Б (невырожденный случай).
- 24.5 Вещественный случай.
- 24.6. О ветвлении решений уравнений о достаточно гладкими операторами.
- 24.7 Случай функционального параметра. Ряды по однородным операторам.
- 24.8. Случай двух числовых параметров.
- § 25. Многомерный случай ветвления
- 25.2. Коэффициенты двумерного уравнения разветвления.
- 25.3. Двумерный случай ветвления.
- 25.4 Общий случай.
- 25.5. О ветвлении изолированного решения.
- 25.6. О точках бифуркации.
- ГЛАВА VIII. Ветвление решений нелинейных уравнений в сингулярном случае
- 26.2. Разложение пространств в прямые суммы подпространств.
- 26.3. Теорема Аткинсона.
- 23.4. О нетеровских неограниченных операторах.
- § 27. Теоремы о ветвлении решений
- 27.2. Случай n > 0, m = 0.
- 27.3. Случай n = 0, m > 0.
- 27.4. Основной случай. Уравнение разветвления.
- 27.5. О ветвлении решений уравнения с неограниченным оператором.
- § 28. Ветвление решений нелинейных сингулярных интегральных уравнений.
- 28.2. Нелинейные сингулярные интегральные уравнения с ядром типа Коши в пространствах Гёльдера.
- 28.3. Аналитический случай.
- 28.4. Нелинейные сингулярные интегральные уравнения с ядром Гильберта в пространствах Лебега.
- § 29. Ветвление решений краевых задач для нелинейных эллиптических уравнений
- 29.2. Краевые задачи на плоскости для эллиптических систем k-го порядка в пространстве Гёльдера.
- 29.3. Краевые задачи для эллиптических уравнений в пространстве суммируемых функций.
- ГЛАВА IX. Некоторые задачи теории вовмущений
- § 30. Жордановы цепочки и наборы фредгольмовских операторов
- 30.2. А-жордановы цепочки и наборы при n > 1.
- 30.3. Условия полноты А-жорданова набора.
- 30.4. Пример.
- § 31. Возмущение линейного уравнения малым линейным слагаемым
- 31.2. Случай n > 1.
- 31.3. Метод неопределенных коэффициентов.
- § 32. Ветвление собственных значений и собственных элементов фредгольмовских операторов
- 32.2. Уравнение разветвления в аналитическом случае.
- 32.3. Вырожденный и невырожденный случаи.
- 32.4. Одномерный случай.
- 32.5. Метод неопределенных коэффициентов.
- 32.6. Многомерный случай.
- 32.7. Некоторые обобщения.
- § 33. Особые решения нелинейных уравнений
- 33.2. Задача о возмущении линейного уравнения малым нелинейным слагаемым.
- 33.3. Понятие обобщенной жордановой цепочки.
- 33.4. Свойства некоторых многочленов.
- 33.5 Основной случай задачи о возмущении.
- 33.6. Случаи возмущения второго порядка.
- 33.7. Решения порядка …
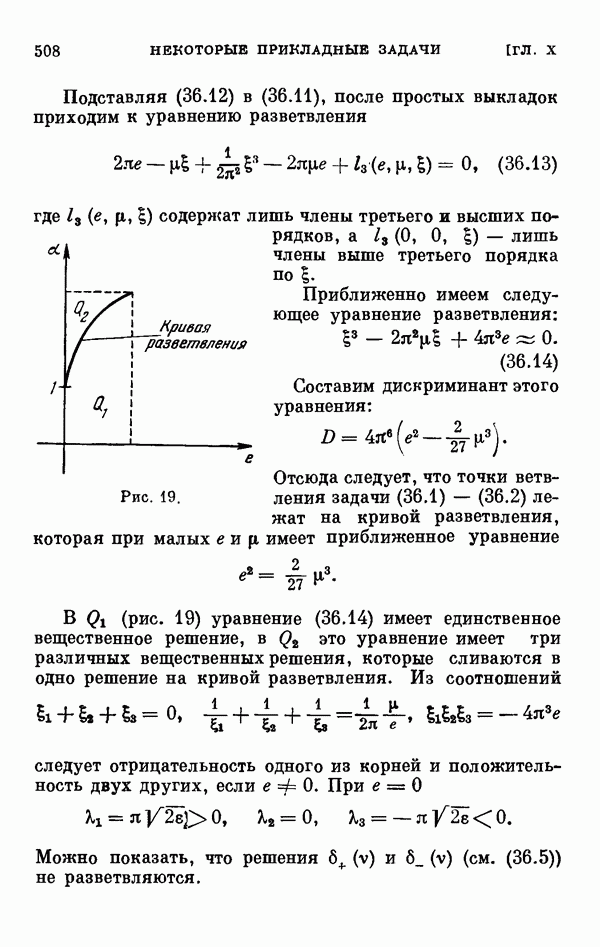
- ГЛАВА X. Некоторые прикладные задачи
- § 34. О малых изгибах прямолинейного стержня под действием постоянной нагрузки
- § 35. К теории малых прогибов гибких пластин
- 35.2. Случай круглой пластины.
- 35.3. Исследование уравнения разветвления.
- 35.4. Круглая пластина с нулевой внешней нагрузкой.
- § 36. О колебаниях спутника в плоскости эллиптической орбиты
- § 37. Об одном виде установившихся волн
- 37.2. Сведение к системе.
- 37.3. Регулярный случай.
- 37.4. Случай ветвления.
- Литература