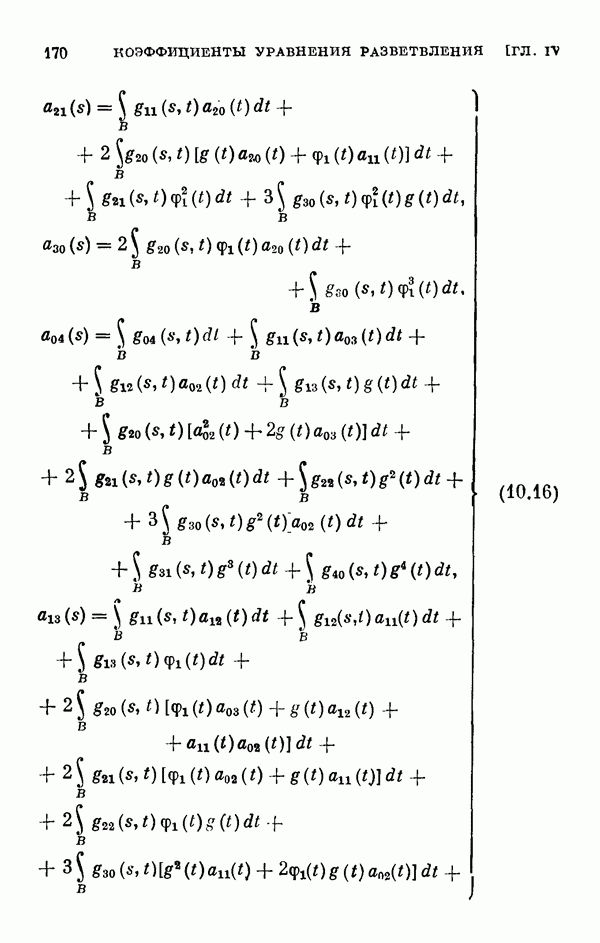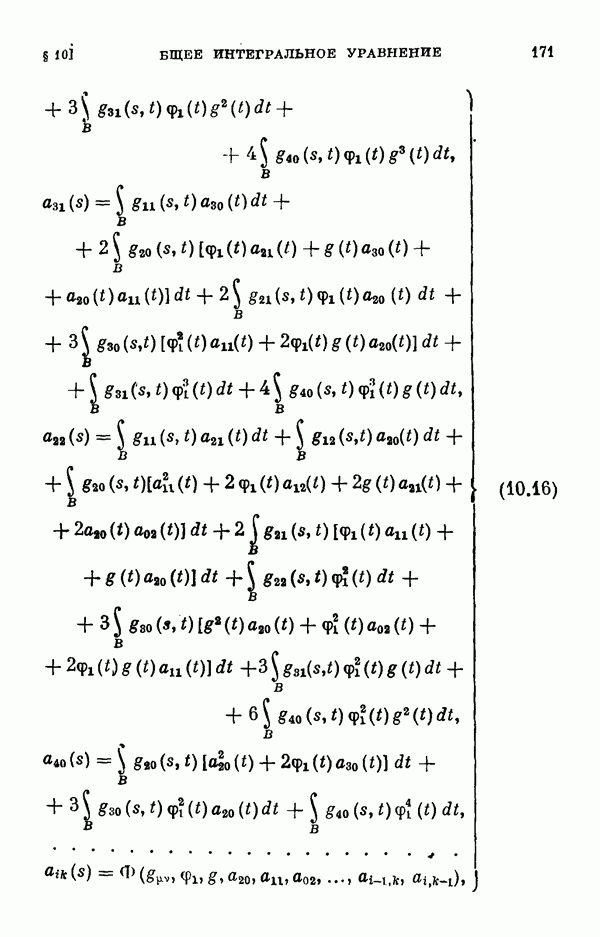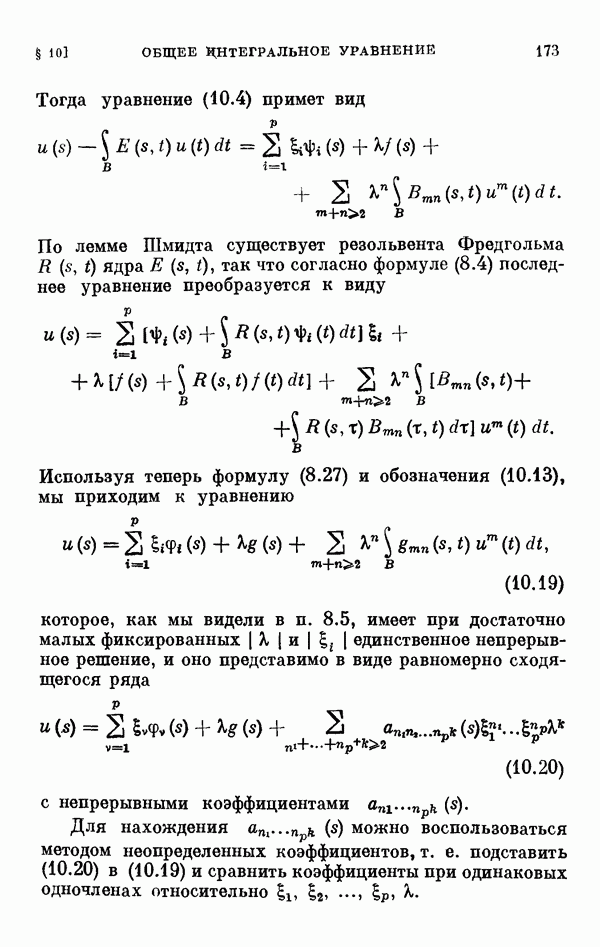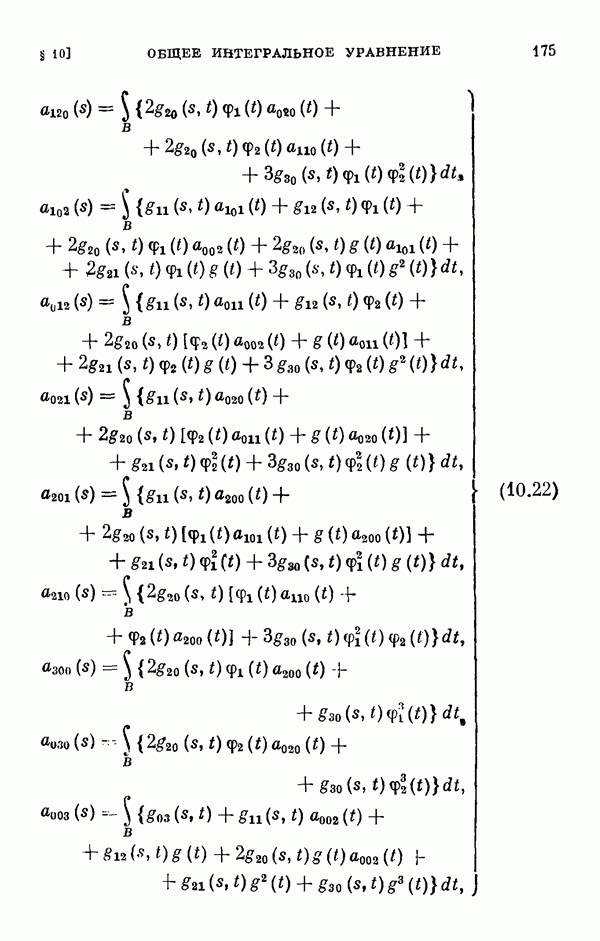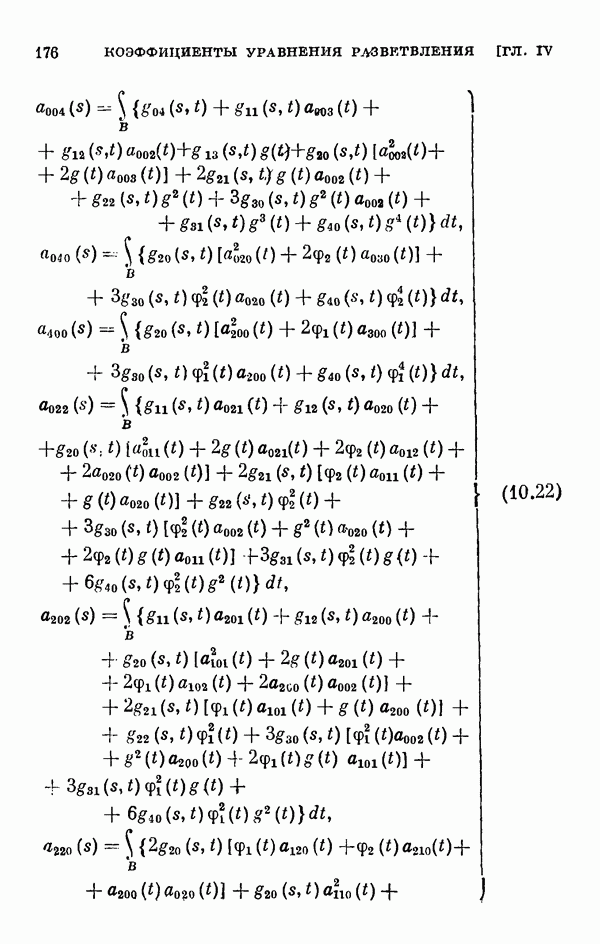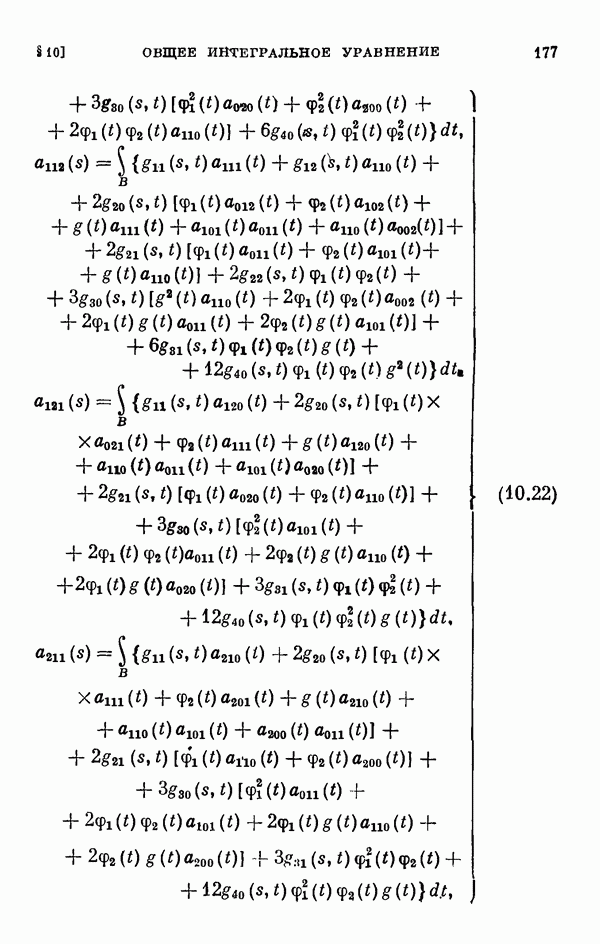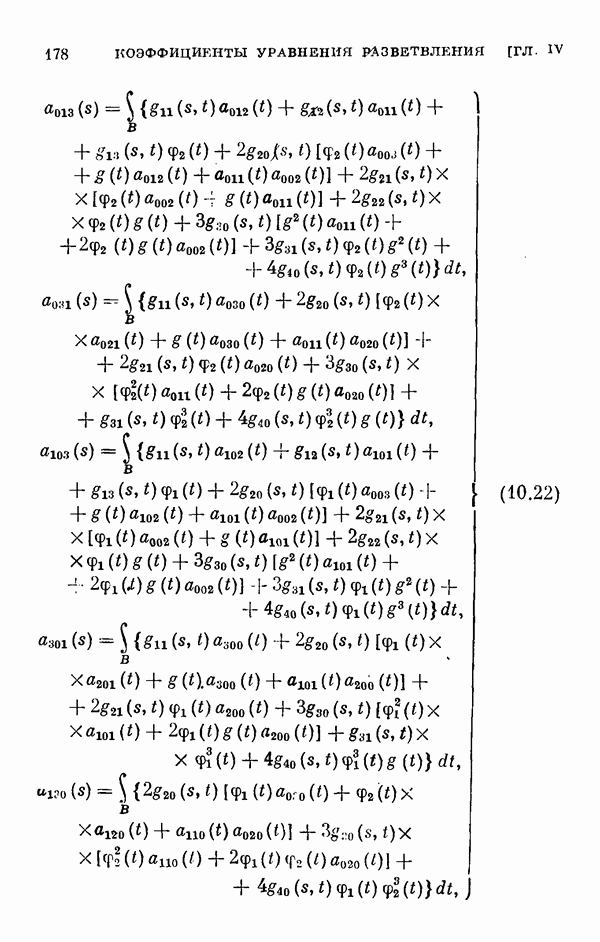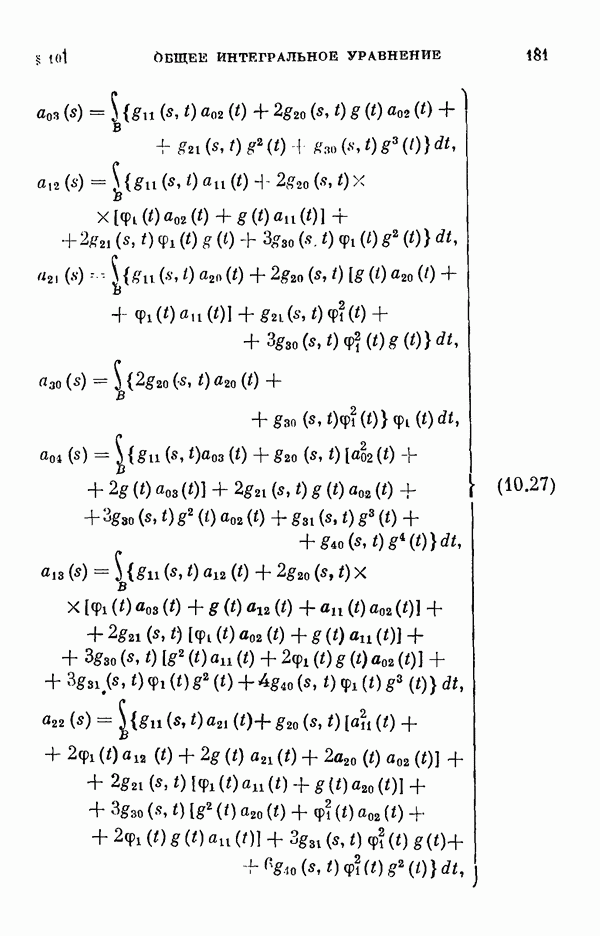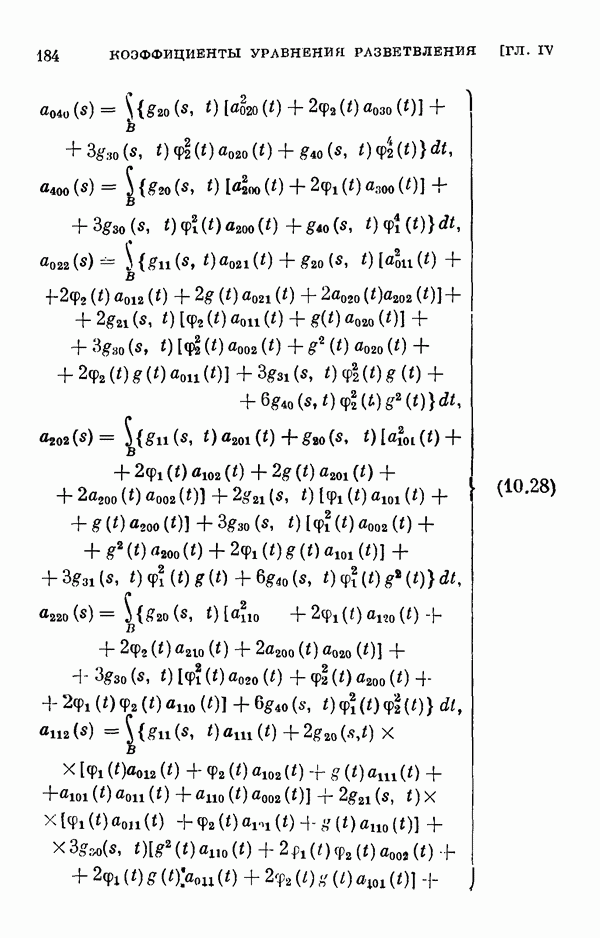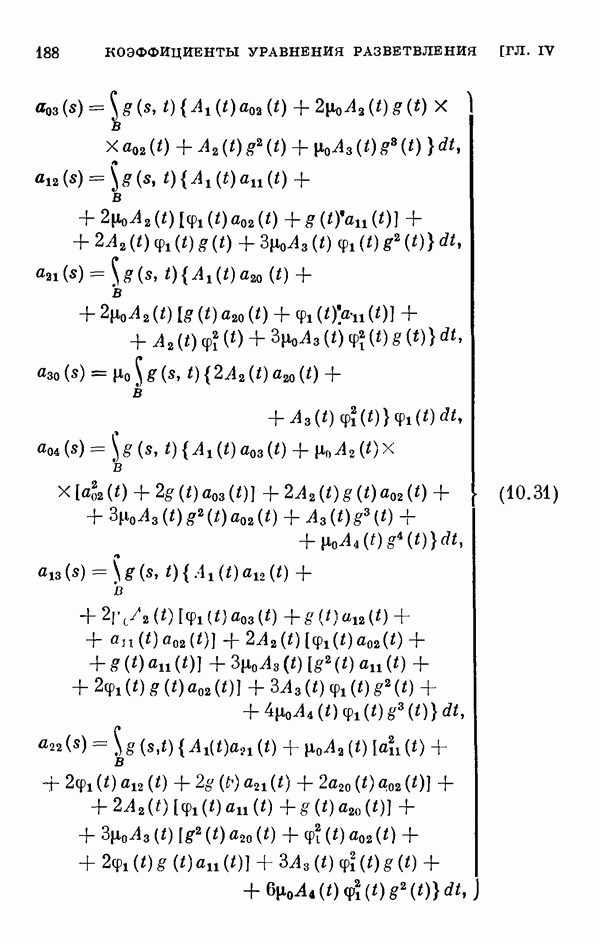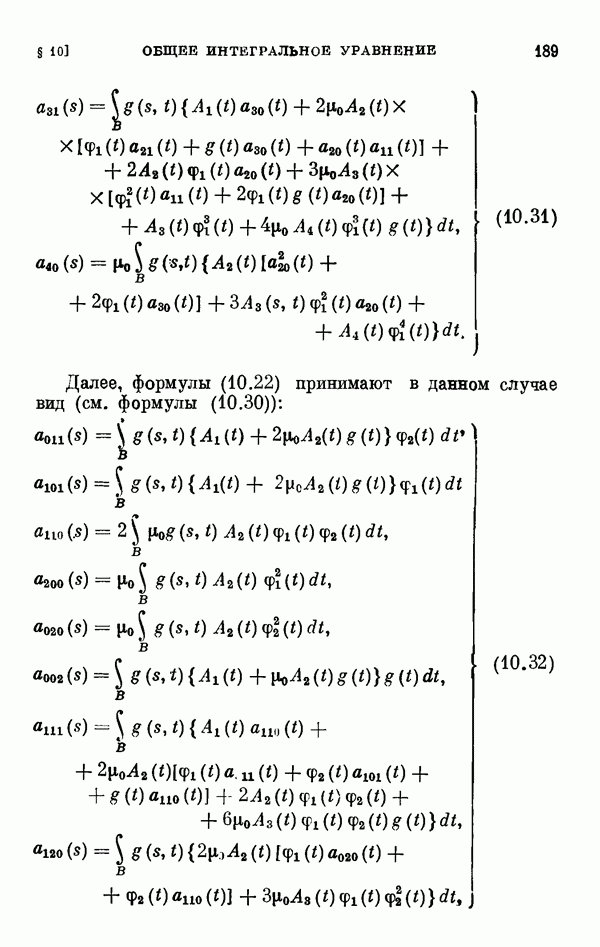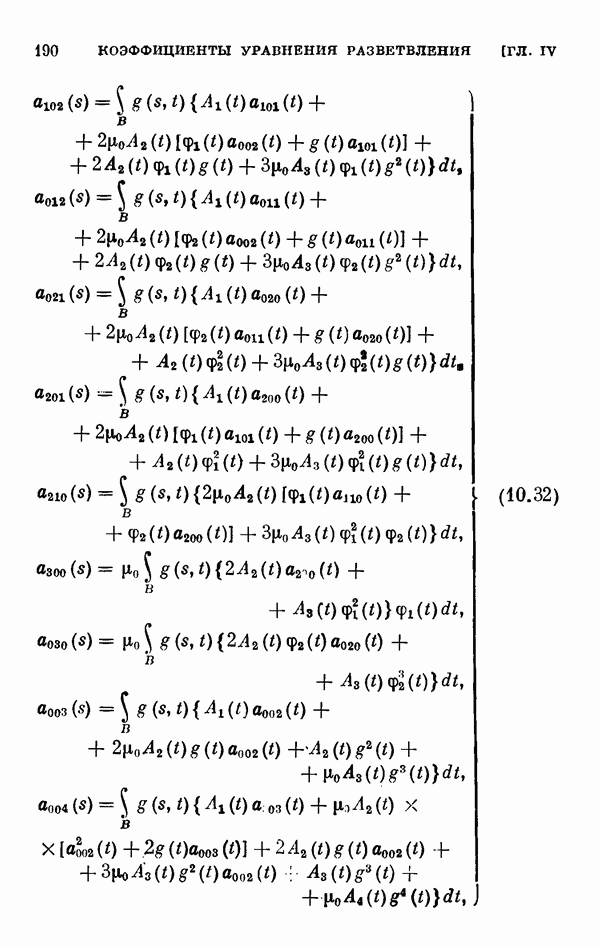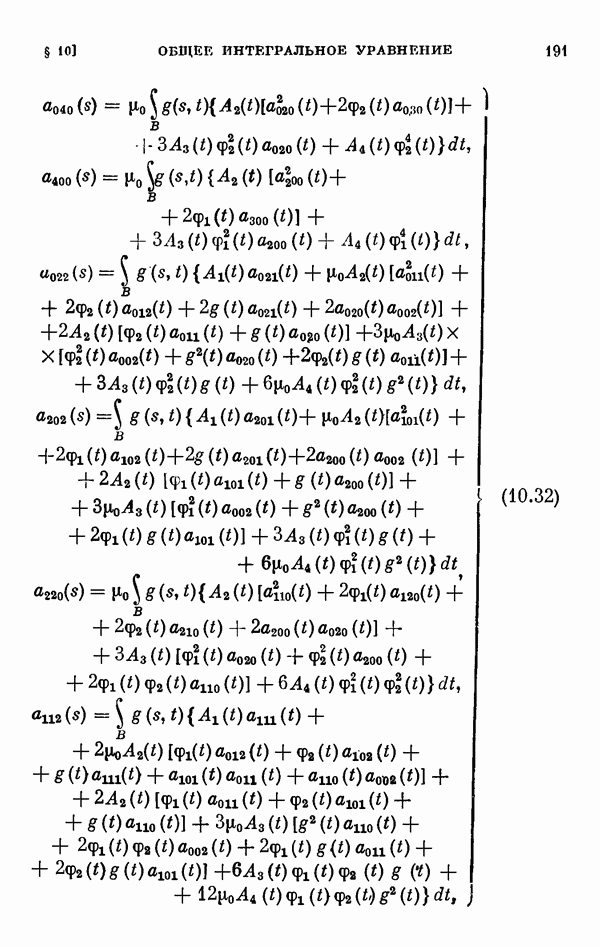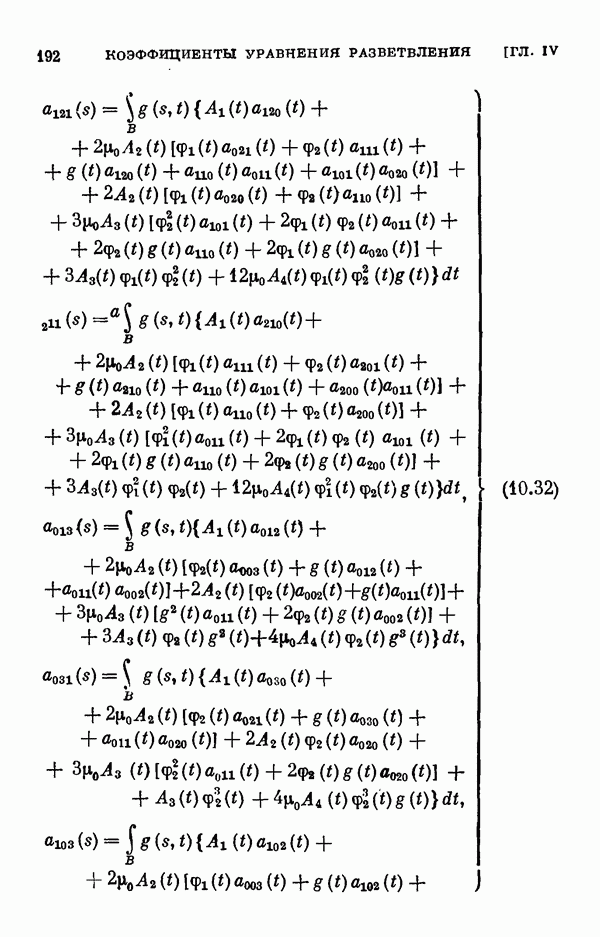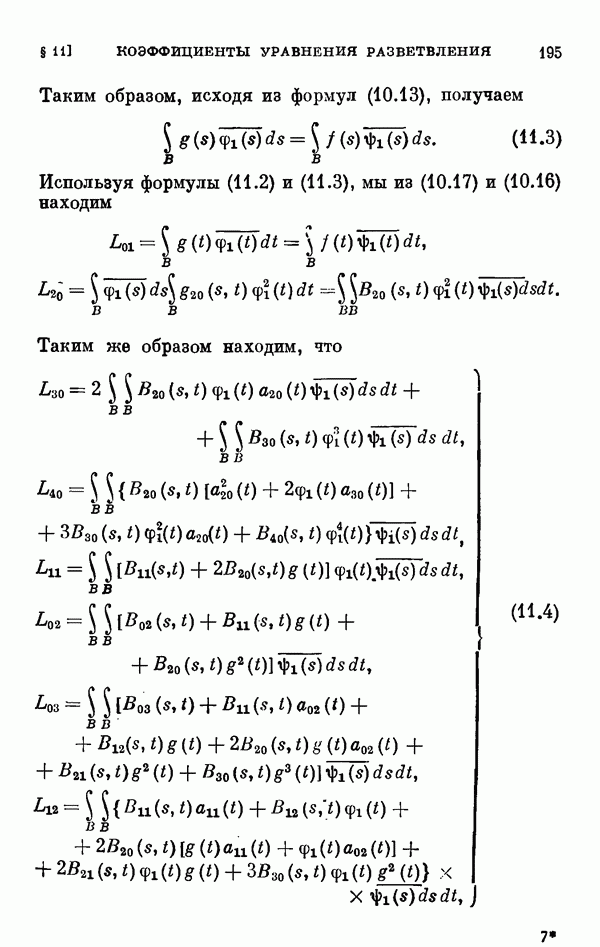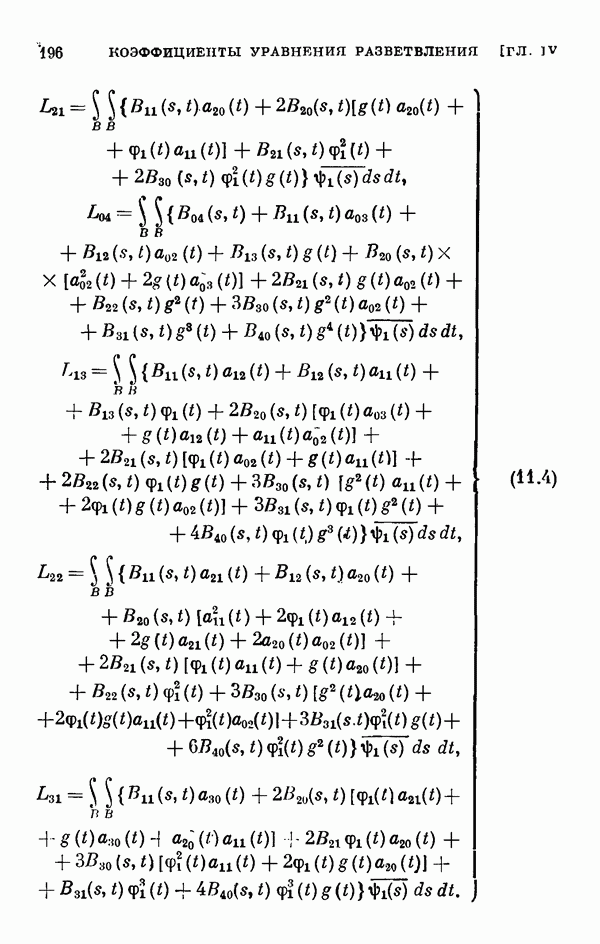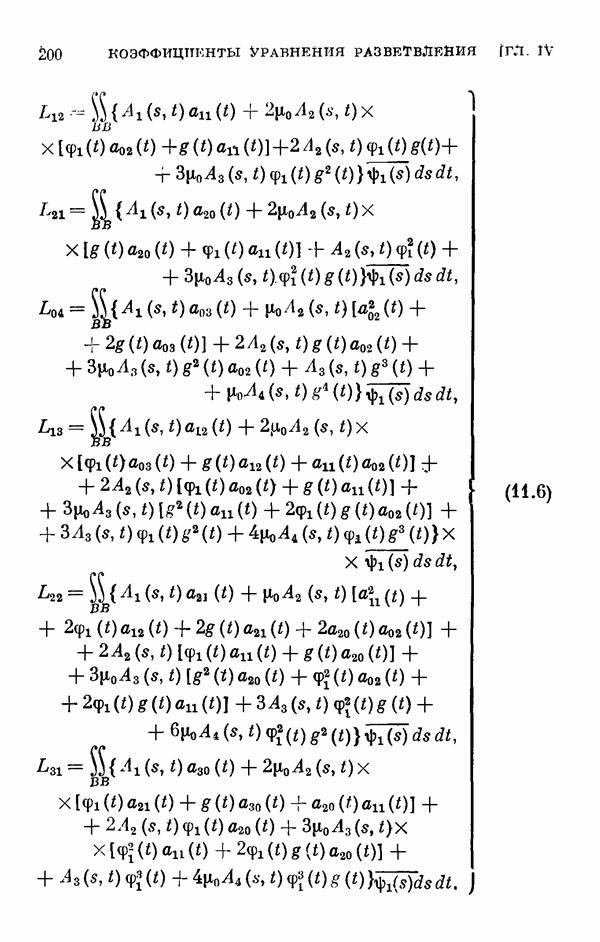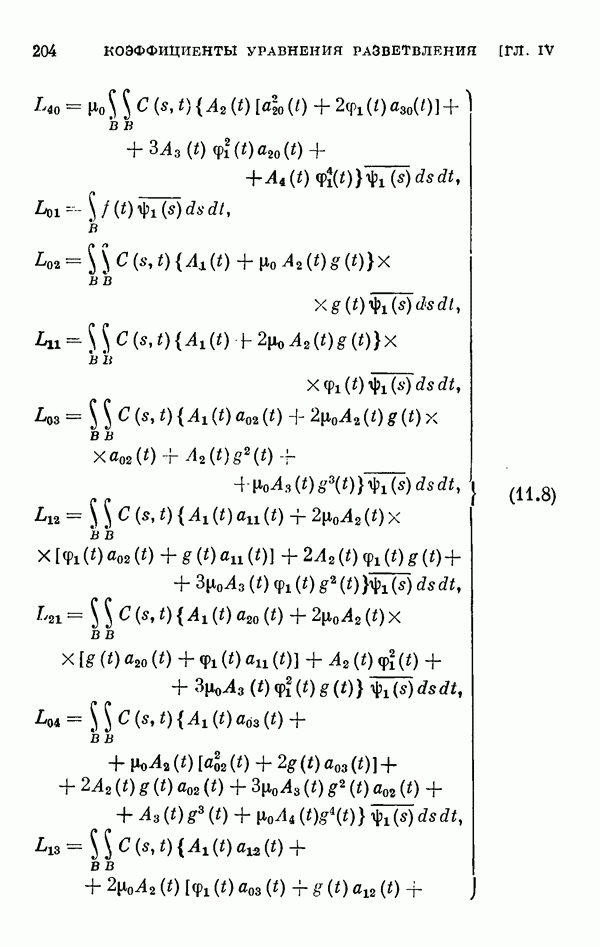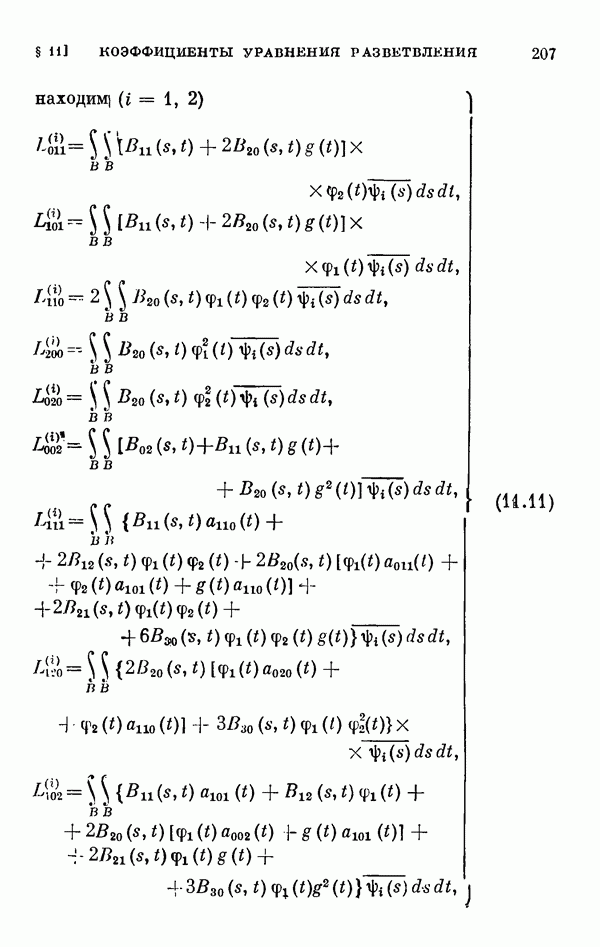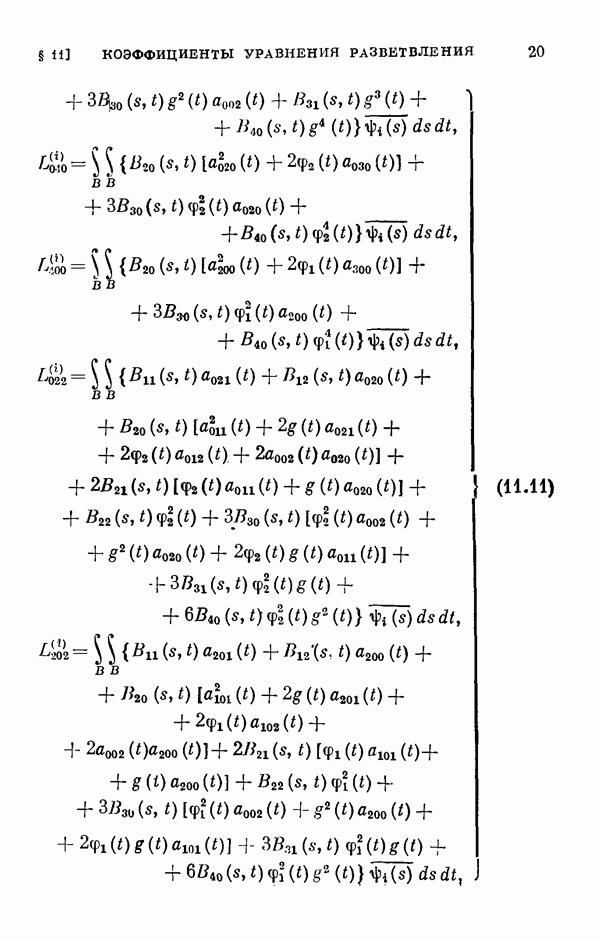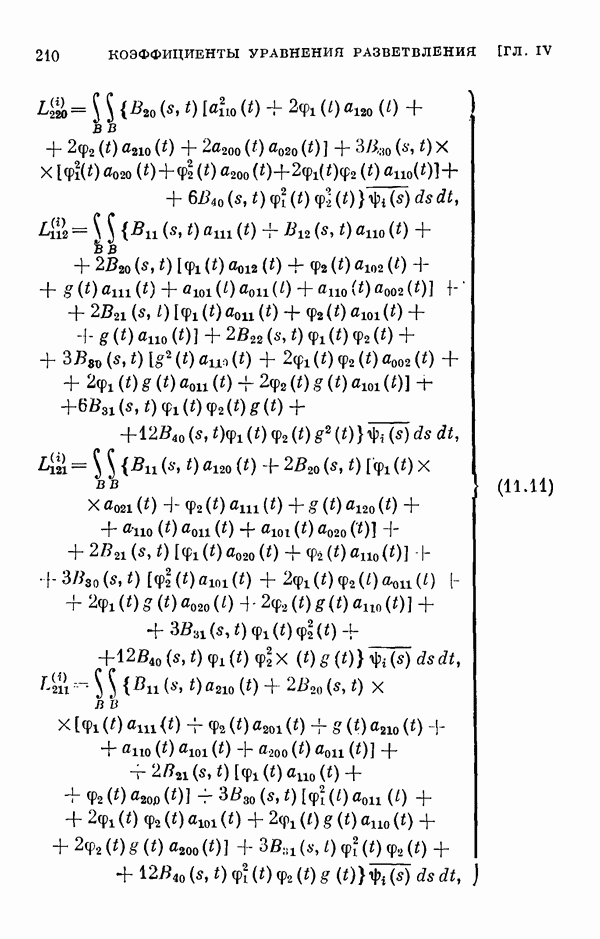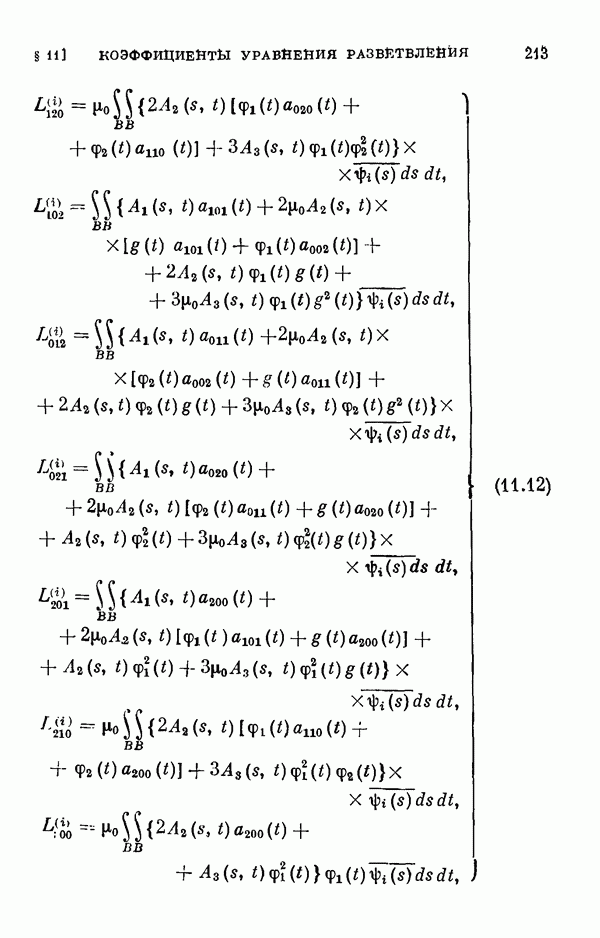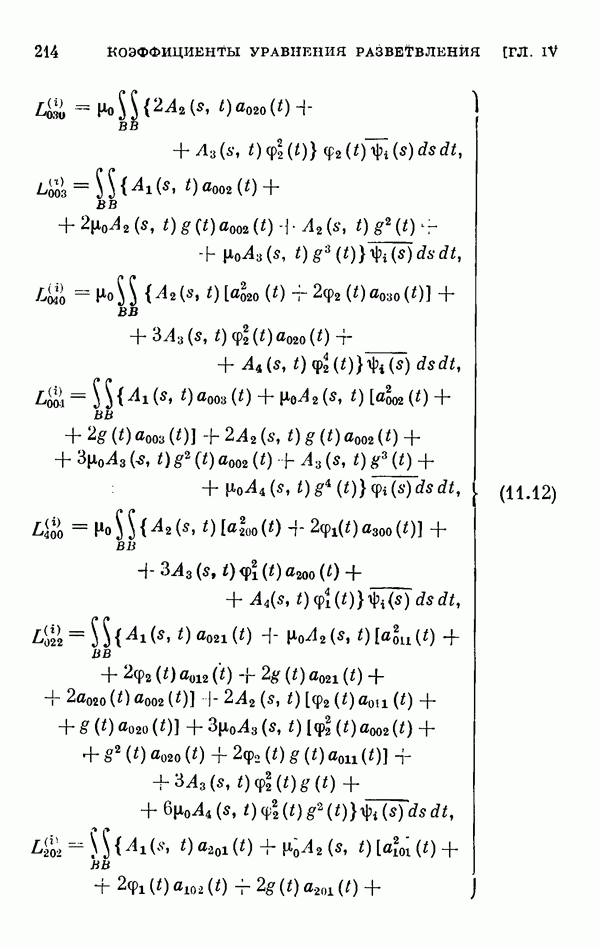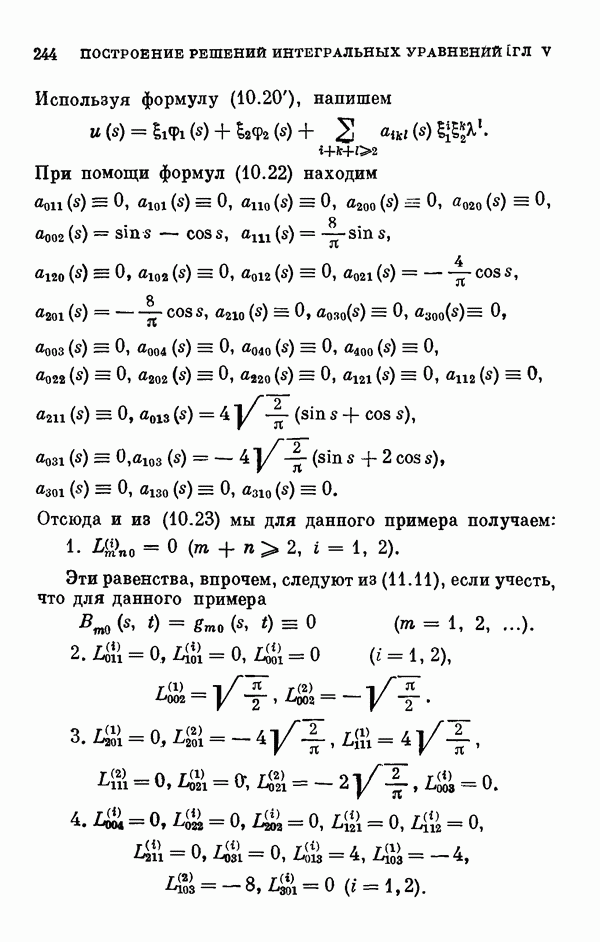Введение

В начале нашего столетия были опубликованы работы А. М. Ляпунова [1] и Э. Шмидта [1], заложившие основы теории ветвления решений функциональных уравнений.

В этих работах было показано, что задача о ветвлении решений нелинейных интегральных уравнений с аналитическими операторами может быть сведена к аналогичной задаче для систем неявных аналитических функций.

Хотя исследования Ляпунова возникли в связи с известной проблемой о фигурах равновесия вращающейся жидкости, они (а также исследования Шмидта) нашли применения в других областях и, в частности, в теории нелинейных колебаний.

За последнее время под влиянием различных задач механики и физики теория ветвления интенсивно развивалась, и это привело к решению ряда ее проблем и, в частности,— одной из трудных ее частей — о ветвлении решений нелинейных уравнений с аналитическими операторами в многомерном случае.

Настоящая книга и посвящена исследованию различных задач о ветвлении решений нелинейных уравнений с аналитическими операторами.

Математически задача о ветвлении решений уравнения может быть сформулирована следующим образом.

Пусть — нелинейный оператор, заданный на прямой сумме (топологическом произведении) линейных топологических пространств Е и со значениями в линейном пространстве Пусть, далее, известно, что при уравнение

имеет решение Возникает вопрос о решениях уравнения

ответвляющихся от (уточнения см. ниже) при значениях параметра (функционального или числового), близкого в некотором смысле к Путем сдвига

и замены

задача сводится к нахождению решений уравнения

ответвляющихся от нулевого (ибо при значениях у, близких к нулю пространства

Такие задачи возникли давно. К ним, в частности, относится классическая задача о неявных функциях, когда частная производная или якобиан обращается в нуль в соответствующей точке.

Как известно, Ньютон ([1], стр. 33—44) рассмотрел задачу об отыскании всех решений уравнения

стремящихся к при если разлагается в ряд по целым положительным степеням: Решение уравнения (0.2) он искал в виде ряда

где — возрастающая последовательность циональных чисел. Для нахождения возможных значений Ньютон воспользовался геометрическим приемом, получившим название диаграммы Ньютона.

Дальнейшие исследования, в которых приняли участие Лагранж, Пюизе [1] и другие (см. статью Н. Г. Чеботарева [1], в которой освещена история вопроса), показали, что дробные степени, входящие В каждый ряд вида (0.3), имеют конечный общий знаменатель и что эти ряды сходятся вблизи точки

Аналогичная задача возникает при изучении систем неявных функций. Пусть — вещественные или комплексные переменные и — соответственно вещественные или

коммлекснозначные функции, аналитические в начале координат и удовлетворяющие условиям

Положим

Тогда система

если положить вектор примет вид

где А — вектор с координатами и вектор-функция удовлетворяет условию: при — какая-нибудь норма конечномерного пространства).

Если матрица В обратима, то по известной теореме о неявных функциях в некоторой окрестности точки уравнение (0.4) имеет единственное решение стремящееся к нулю при и это решение является аналитической функцией от х.

Однако если В — вырожденная матрица, то возможно явление ветвления, т. е. уравнение (0.4) может иметь в классе непрерывных функций более одного решения, каждое из которых удовлетворяет условию Говорят тогда, что решения (ветви) выходят из точки или что является точкой ветвления решений уравнения (0.4).

В вещественном случае, т. е. когда вещественны, возможны и такие явления ветвления, когда уравнение (0.4) имеет одно число решений при и другое число решений при

Таким образом, если В — вырожденная матрица, то возникает задача о нахождении числа всех непрерывных решений уравнения (0.4), удовлетворяющих условию вида каждого решения и о построении этих решений.

Подобные задачи возникают и в теории интегральных и дифференциальных уравнений. Приведем два примера.

Пусть заданные непрерывные функции в единичном квадрате заданная непрерывная функция на неизвестная функция, непрерывная на и К — числовой параметр. Рассмотрим нелинейное интегральное уравнение

где

Если 1 не является собственным значением оператора А, то оператор имеет ограниченный обратный Применяя к обеим частям равенства (0.5) оператор мы получим уравнение , эквивалентное уравнению (0.5), причем при достаточно малых оператор будет сжимающим относительно и Ввиду этого уравнение (0.5) имеет при достаточно малых единственное решение непрерывно зависящее от параметра К и обращающееся в нуль при

Если 1 — собственное значение оператора А, то оператор В необратим, и тогда возможно явление ветвления, как и в классической задаче о неявных функциях. Здесь, в случае ветвления, каждая ветвь их представляет собою семейство функций, непрерывно зависящее от параметра К и стремящееся к нулю при При этом функция при каждом фиксированном К непрерывна по и удовлетворяет уравнению (0.5).

К явлению ветвления здесь можно отнести и такие случаи, когда в некоторой окрестности точки (точки функционального пространства) уравнение (0.5) не имеет решений.

Рассмотрим еще задачу Пуанкаре о периодических решениях системы

где представляют собою -мерные векторы, X — числовой параметр. Предполагается, что и — аналитические функции по х и X, непрерывные по совокупности аргументов и -периодические по

Пусть при система (0.6) имеет -периодическое решение Ставится задача о нахождении при достаточно малых всех непрерывных и -периодических решений системы (0.6), удовлетворяющих условию Оказывается (см. гл. VI), что если некоторая матрица В обратима, то данная задача имеет единственное решение, а если В — вырожденная матрица, то возможно явление ветвления, как и в классической задаче о неявных функциях.

Эти и другие примеры приводят к постановке следующей абстрактной задачи

Пусть Е и — линейные топологические пространства (в частности, банаховы пространства), X — числовой параметр, — аналитический оператор в точке со значениями в пространстве удовлетворяющий условию Рассмотрим уравнение которое в силу аналитичности (см., например, Хилле и Филлипс [1], гл. 26) принимает вид

где — линейный оператор из Е в — элемент из — частные производные Фреше от в точке порядка по порядка к по X. Так же, как в предыдущих примерах, ставится задача об отыскании всех решений уравнения (0.7), непрерывно зависящих от параметра X и стремящихся к нулю при

Оказывается, что если оператор В обратим, то при достаточно малых уравнение (0.7) имеет единственное решение, непрерывно зависящее от X и стремящемся к нулю при причем это решение представимо в виде сходящегося ряда

Если оператор В необратим, то возможно явление ветвления.

В случае ветвления уравнение (0.7) может иметь при достаточно малых бесконечное или конечное число решений х (X), непрерывно зависящих от К и удовлетворяющих условию Когда число решений конечное, каждое из них представимо в виде

где — натуральное число (свое для каждого решения).

Для решения этой задачи нужно выяснить, сколько решений она имеет, каков вид каждого решения, и указать пути их построения.

Перейдем к освещению основных методов, применяемых в теории ветвления.

Нами было отмечено, что если оператор В обратим, то уравнение (0.7) имеет единственное решение непрерывно зависящее от К и удовлетворяющее условию причем оно представимо в виде (0.8). Для построения этого решения можно воспользоваться методом неопределенных коэффициентов. Именно, подставляя (0.8) в обе части равенства (0.7) и сравнивая коэффициенты при одинаковых степенях К, мы для определения неизвестных получим рекуррентную систему. Эта рекуррентная система разрешима и имеет единственное решение, ибо уравнение (0.7) имеет единственное решение вида (0.8).

Укажем, что таким способом отыскания решений пользовался еще Лагранж в работах [1, 2], послуживших началом метода малого параметра.

Метод построения решений в виде рядов по малому параметру широко применяется в задачах механики и физики (например, методы Пуанкаре и Ляпунова в теории нелинейных колебаний, работы Н. Н. Боголюбова и его учеников по теоретической физике). Однако когда оператор В необратим, то применение этого метода без дополнительной информации о решениях изучаемой задачи может привести (и приводит иногда) к почти неопределимым трудностям по следующим причинам.

Во-первых, в этом случае решения уравнения (0,7), обращающиеся в нуль при могут быть представимы как по целым, так и по дробным степеням К. Ввиду этого, если искать решение уравнения (0.7) в виде ряда (0.9), т. е. по степеням без предварительной информации об то рекуррентная система, получающаяся для определения неизвестных коэффициентов может оказаться неразрешимой. При этом может случиться, что первое неразрешимое уравнение рекуррентной системы имеет очень большой номер.

Во-вторых, когда оператор В необратим, уравнение (0.7) может иметь решения, зависящие от одного или более произвольных параметров. В данном случае ряды вида (0.8) и (0.9) могут расходиться при любом но формально удовлетворять уравнению (0.7). По этой причине до последнего времени не было общих теорем о сходимости рядов вида (0.9), представляющих решения уравнения (0.7), а в каждой отдельной задаче для доказательства сходимости таких рядов строились мажоранты.

В данной книге будет выделен широкий класс уравнений вида (0.7), названный ниже квазирегуляриым, для которого все решения, непрерывно зависящие от параметра К и обращающиеся в нуль при представимы при достаточно малых в виде сходящихся рядов (0.8) и (0.9). При этом будет указан прием для нахождения всех дробных степеней, входящих в (0.9).

Будет также доказано, что для этого класса метод неопределенных коэффициентов (с учетом предварительной информации о виде дробных степеней) приводит к разрешимой рекуррентной системе, причем ряды, получающиеся этим методом, сходятся при достаточно малых Таким образом, если уравнение вида (0.7) принадлежит к квазирегулярному классу, то всякое его решение вида (0.8) или (0.9), полученное методом неопределенных коэффициентов, является сходящимся при достаточно малых

Отметим еще, что если уравнение вида (0.7) не принадлежит к упомянутому классу, то оно имеет бесчисленное множество решений вида (0.8) и (0.9), сходящихся при достаточно малых бесчисленное множество решений вида (0.8) и (0.9), расходящихся при всяком и

бесчисленное множество решений, не представимых в виде рядов.

Выделение квазирегулярного класса и доказательство перечисленных утверждений используют метод Ляпунова и Шмидта и недавние исследования, связанные с развитием этого метода. А. М. Ляпунов [1—3] и Э. Шмидт [1] рассмотрели нелинейные интегральные уравнения вида (0.7) в предположении, что область значений линейного оператора В замкнута и что подпространства нулей операторов имеют одинаковые конечные размерности

При выполнении этих условий их метод исследования заключается в том, что задача об отыскании всех решений уравнения (0.7), непрерывно зависящих от X и обращающихся в нуль при сводится к аналогичной задаче в конечномерном пространстве следующим образом.

Доказывается, что формула

в которой являются непрерывными решениями системы

удовлетворяющими условию дает все решения задачи Именно, устанавливается взаимно однозначное соответствие между множеством всех решений задачи и множеством всех непрерывных решений системы (0.11), удовлетворяющих условию Такие решения системы (0.11) называются малыми. В силу этого соответствия и формулы (0.10) задача сводится к определению всех малых решений системы (0.11), называемой уравнением разветвления для задачи Исходя из

формулы (0.10), мы путем исследования уравнения разветвления (0.11) получаем информацию о числе и виде всех решений задачи (4). Эта информация, когда решения имеют вид (0.8) или (0.9), используется при нахождении этих решений методом неопределенных коэффициентов.

Таким образом, при решении различных задач теории ветвления метод Ляпунова и Шмидта сочетается с методом неопределенных коэффициентов.

Книга состоит из десяти глав.

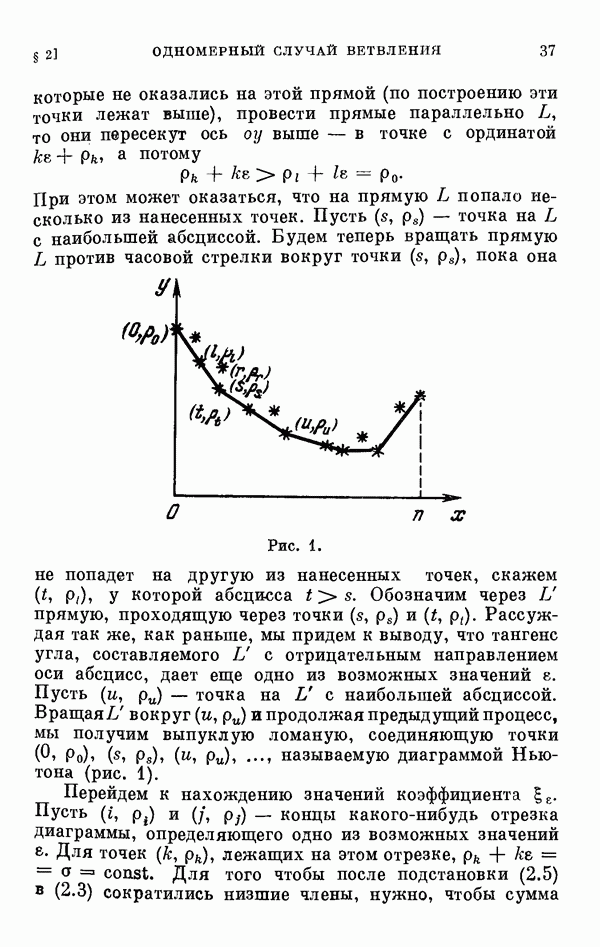
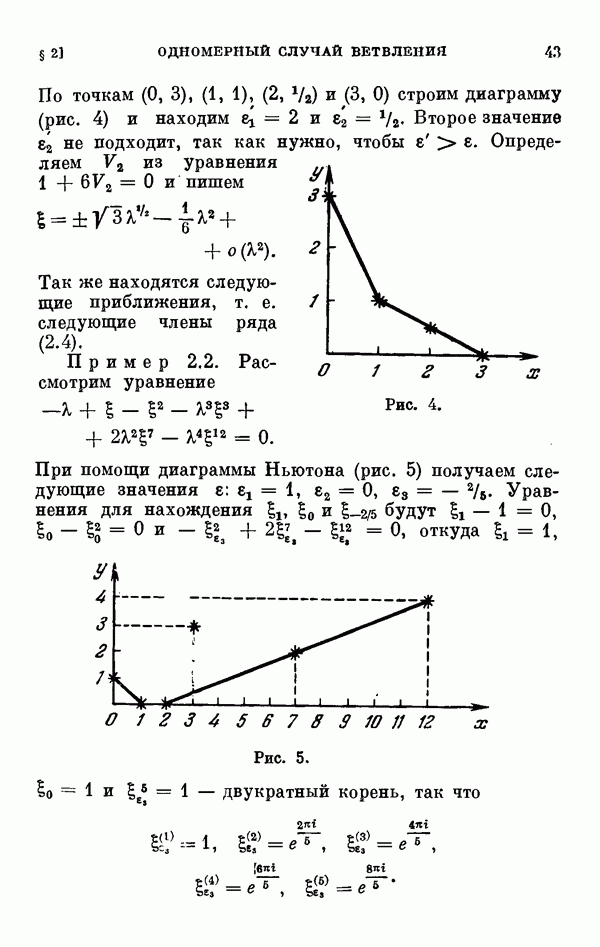
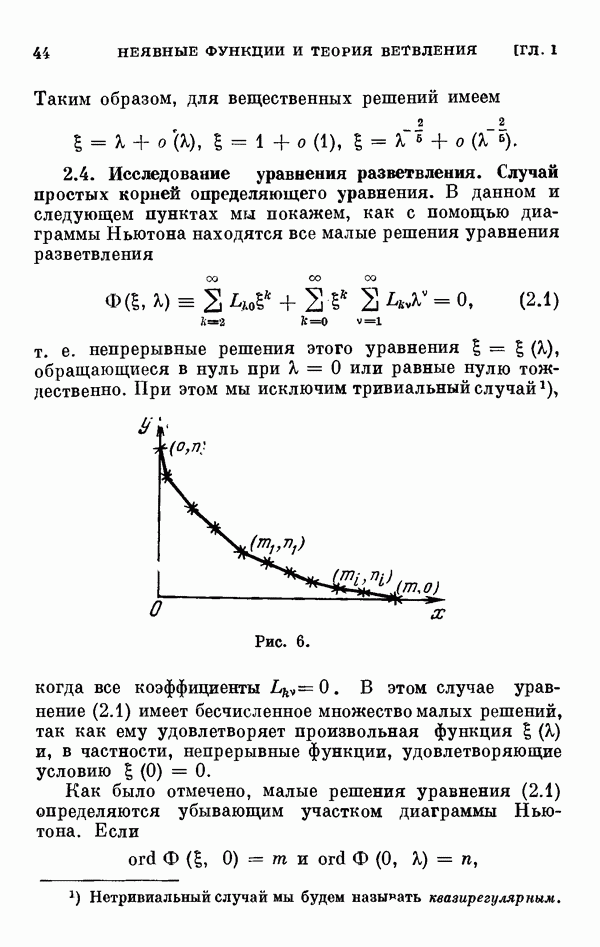
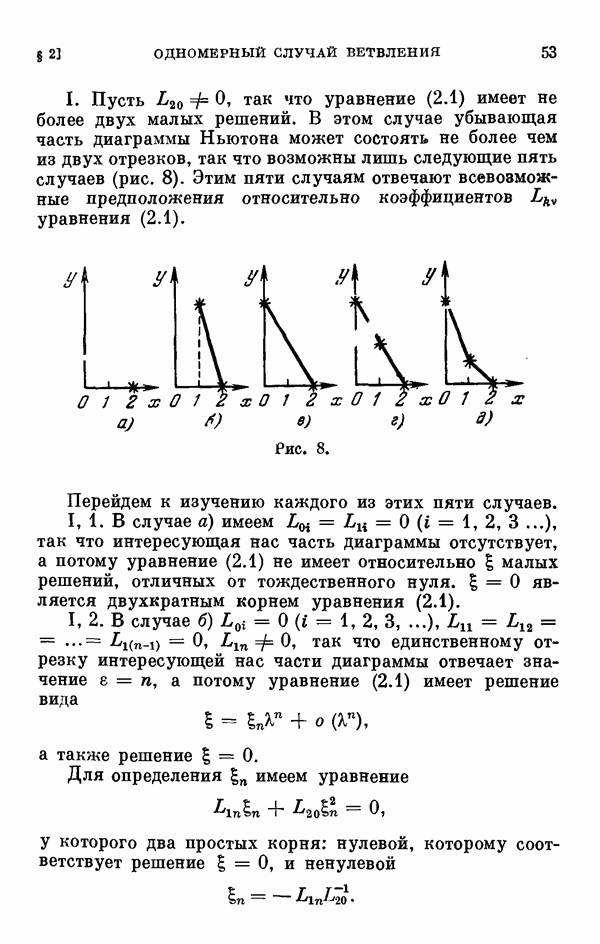
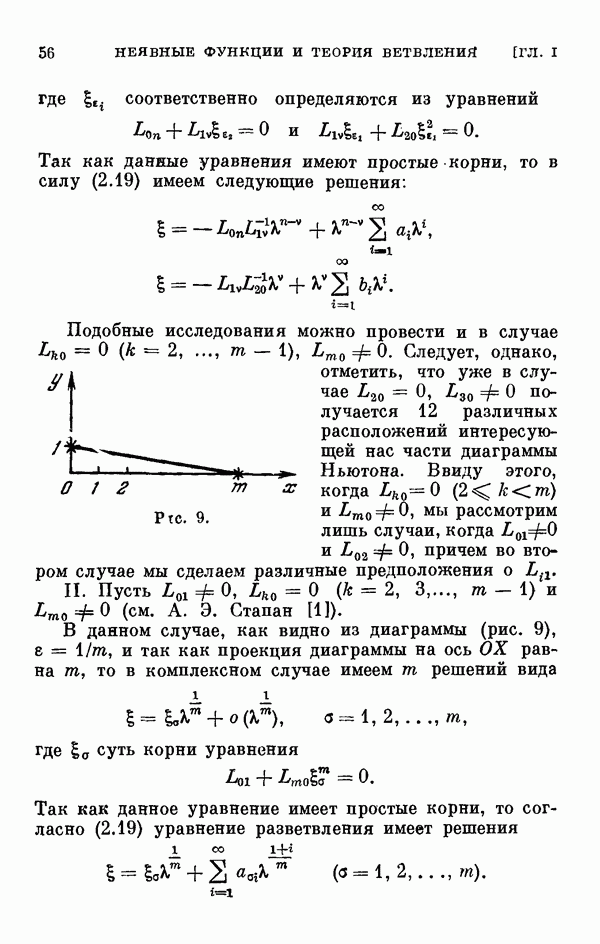
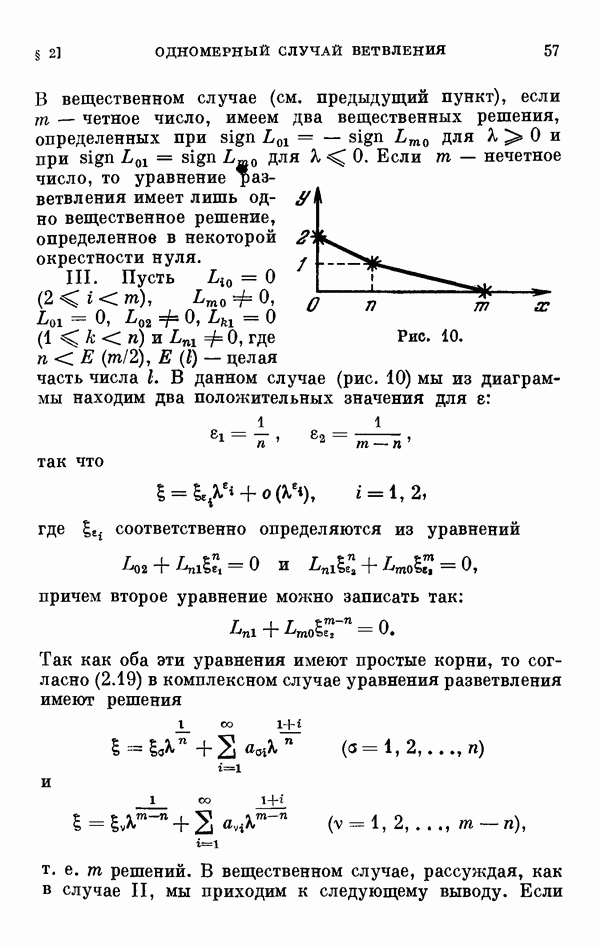
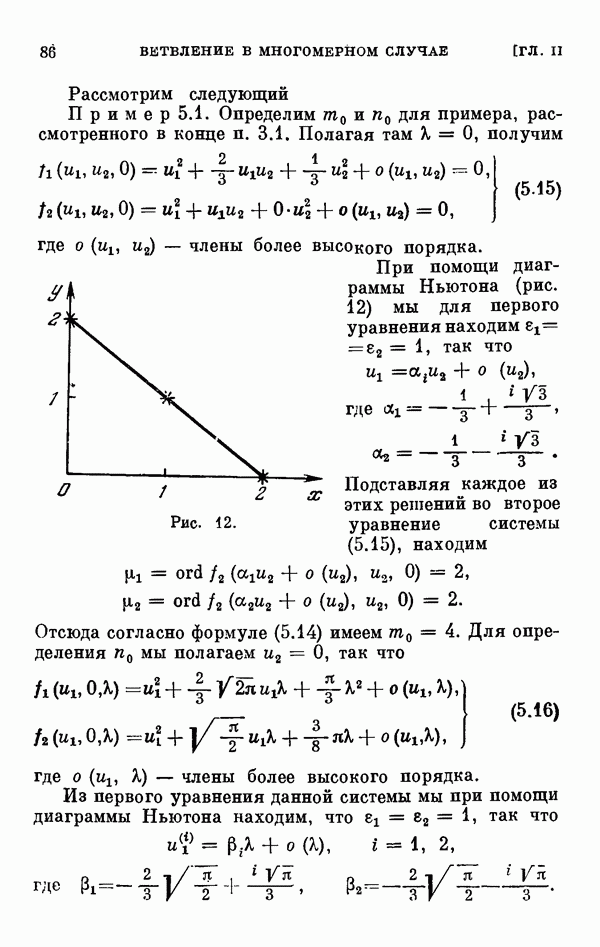
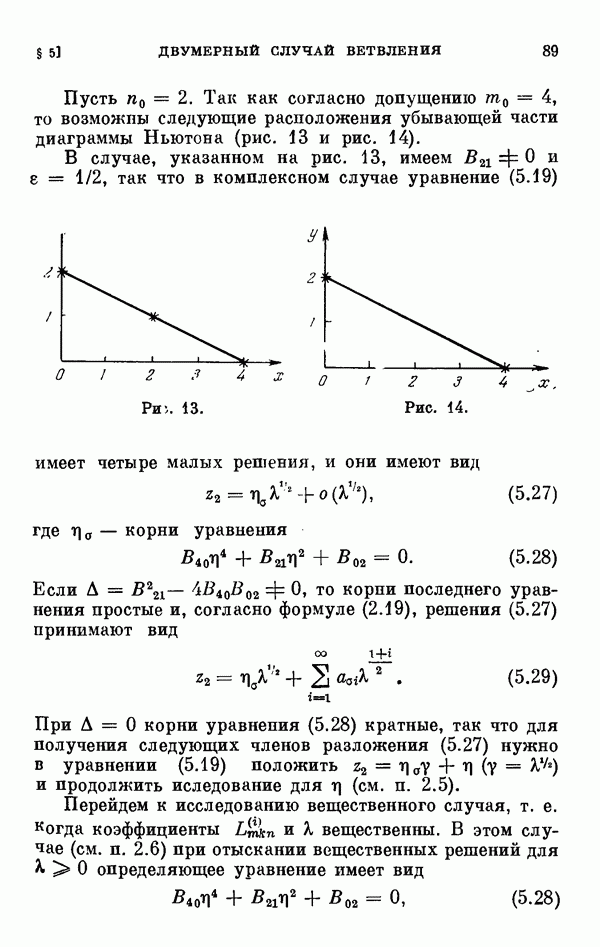
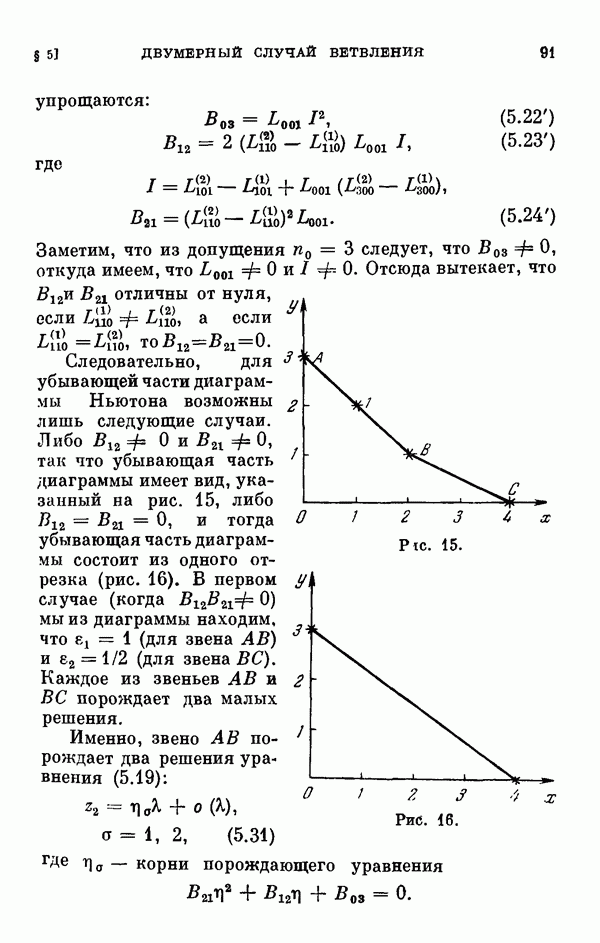
Главы I и II служат основой всей книги. Они начинаются с изучения задачи о неявных функциях, когда матрица Якоби в соответствующей точке является вырожденной. Показано, в частности, что если дефект матрицы В, входящей в уравнение (0.4), равен то задача об отыскании всех непрерывных решений уравнения (0.4), стремящихся к нулю при сводится к нахождению всех малых решений уравнения разветвления (0.11). В связи с этим §§ 2—6 глав I и II посвящены исследованию уравнения разветвления, играющего важную роль во всех других главах книги. Исследование уравнения разветвления начинается с одномерного случая, т. е. когда одномерном случае исследование ведется при помощи диаграммы Ньютона. Дается описание диаграммы Ньютона, обоснование метода исследования при помощи этой диаграммы, а затем на конкретных примерах иллюстрируется, как этот метод приводит к описанию и построению всех малых решений уравнения разветвления.

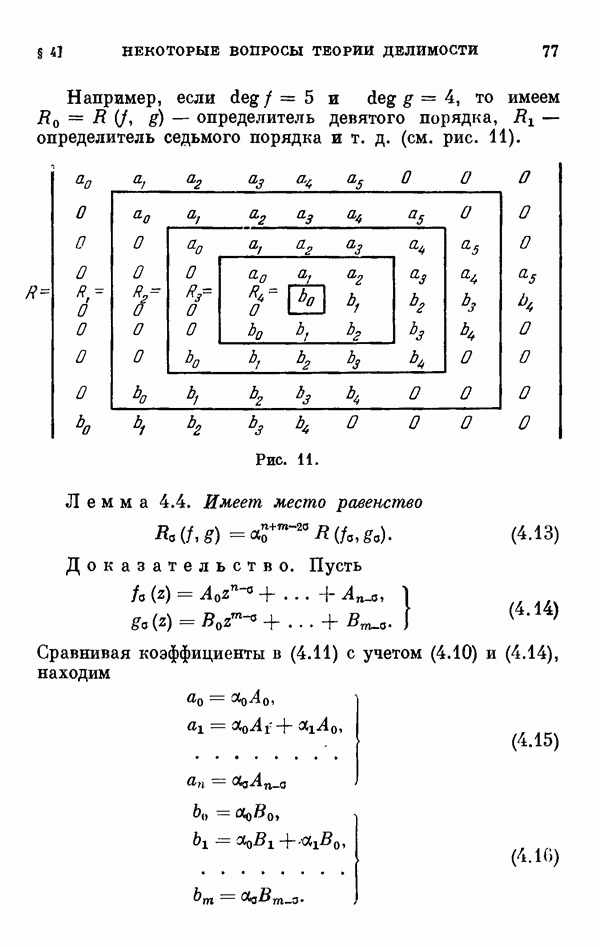
В §§ 3 и 4 рассматриваются некоторые вопросы алгебры и теории функций многих комплексных переменных, нужные для исследования уравнения разветвления в общем виде. При этом наиболее важным является вопрос о делимости в специальном кнльце псевдомногочленов, который используется как в § 5, так и в § 6 при изложении некоторого видоизменения кронекеровского метода исключения. В §§ 5 и 6 устанавливаются предложения, при помощи которых в последнее время удалось развить наиболее трудную часть теории ветвления. Эти предложения существенно используются в других главах.

В главах III и IV излагается теория ветвления решении нелинейных интегральных и интегро-дифференциальных уравнений и освещаются основные факты этой

теории. В § 7 вводятся интегро-степенные ряды и оператор Ляпунова — Шмидта, изучаются их свойства, а затем применяются различные методы исследования простейшего нелинейного интегрального уравнения.

В § 8 исследуется общее нелинейное интегральное уравнение Ляпунова — Шмидта. Сначала изучается регулярный случай, а затем при помощи леммы Шмидта — и случай ветвления. Выводится уравнение разветвления как в одномерном случае ветвления, так и в многомерном случае ветвления.

В § 9 рассматриваются системы уравнений Ляпунова — Шмидта, нелинейные интегро-дифференциальные уравнения с интегро-степенными рядами, другие виды интегро-дифференциальных уравнений и выводятся соответствующие уравнения разветвления.

В § 10 изучаются общее интегральное уравнение и интегральное уравнение Гаммерштейна с аналитическими правыми частями в предположении, что при некотором значении параметра они имеют решения, и ставится для них задача о ветвлении. Путем сдвига эти уравнения приводятся соответственно к следующим видам:

и

для которых задача о ветвлении в точке изучается в основном в пространстве комплекснозначных функций, непрерывных на ограниченном замкнутом множестве В конечномерного евклидова пространства.

Для этих уравнений выводятся уравнения разветвления, вычисляются коэффициенты рядов, представляющих решения этих уравнений, обращающиеся в нуль при а в § 11 вычисляются коэффициенты соответствующих уравнений разветвления для одномерного и двумерного случаев ветвления.

В главе V излагаются методы, приводящие к описанию и построению решений уравнений, рассмотренных в § 10, и изучается задача об особых решениях нелинейных интегральных уравнений.

В § 12 путем исследования уравнения разветвления дается описание малых решений нелинейных интегральных уравнений в одномерном, двумерном и многомерном случаях ветвления. Дается описание ветвей в случае бифуркации и исследуется вопрос о ветвлении изолированного решения. В § 13 показано, как строить решения путем сочетания методов теории ветвления с методом неопределенных коэффициентов. В качестве примеров рассмотрены краевая задача для квазилинейных дифференциальных уравнений эллиптического типа и задача Некрасова о волнах установившегося вида.

В § 14 дается описание особых решений нелинейных интегральных уравнений и указывается, как их строить. При этом используются те же методы, что и в предыдущих двух параграфах.

Глава VI посвящена изучению задачи Пуанкаре о периодических решениях. Этой задачей занимались многие авторы (см., например, Л. Чезари [1]), которые в своих исследованиях ограничились рассмотрением отдельных частных случаев. Оказывается, что методы теории ветвления дают подход для решения задачи Пуанкаре в общей постановке. Это и показано в данной главе.

В §§ 15 и 16 исследуются уравнения, которые в векторной записи имеют соответственно вид ранее приведенного уравнения (0.6) и

После постановки задачи и освещения метода Пуанкаре приводятся некоторые вспомогательные предложения и выводятся соответствующие уравнения разветвления. Исследование уравнения разветвления приводит к выводам о числе решений рассматриваемой задачи и о виде каждого решения.

Аналогичное исследование проводится в § 17 для автономных систем дифференциальных уравнений. Как всегда, изучение задачи Пуанкаре для автономных систем

связано с преодолением дополнительных трудностей, так как и период отыскиваемых ветвей неизвестен. В § 18 показано, как строятся решения изучаемой задачи для автономных и неавтономных систем.

В § 19 показано, что задача об особых периодических решениях некоторого вида сводится к задаче Пуанкаре, изученной в § 16. В этом параграфе изучается также задача Пуанкаре в банаховых пространствах.

В последнем параграфе данной главы изучается вопрос об устойчивости периодических решений задачи Пуанкаре. Этот вопрос представляет большой интерес как для теории, так и для ее приложений. Оказывается, что и в вопросе об устойчивости периодических решений, зависящих от малого параметра, методы теории ветвления позволяют изучить задачу в более общей постановке и приводят к новым важным фактам.

В предыдущих главах были рассмотрены алгебраические, интегральные, интегро-дифференциальные уравнения, а также задача о периодических решениях. Однако круг задач, в которых применяется теория ветвления, все время расширяется. Поэтому имеет смысл дать изложение общей абстрактной теории, которая охватывала бы возможно широкие классы задач.

В главе VII такая теория строится для уравнений в банаховых пространствах с линейной фредгольмовской частью. § 21 содержит вспомогательные сведения из теории нормально разрешимых ограниченных линейных операторов в банаховых пространствах.

Если фредгольмовский оператор В необратим, то для изучения уравнения можно поступить двояко: либо рассмотреть сужение оператора В, имеющее обратный оператор либо построить обратимый оператор В, действующий во всем пространстве (обобщенная лемма Шмидта). В этом же параграфе приводится известная теорема С. М. Никольского и устанавливается связь с сопряженным оператором В.

В § 22 приведены известные факты нелинейного функционального анализа, относящиеся к теории аналитических операторов. Излагаются теоремы о неявных операторах в аналитическом и неаналитическом случаях.

Рассмотрен и случай неограниченных операторов. Основное содержание главы составляют §§ 23—25, в которых дается решение основной задачи теории ветвления в аналитическом случае, а также получен ряд других результатов.

В § 23 показано, что задача отыскания малых решений уравнения где оператор Ф достаточно гладкий, а — оператор фредгольмовский, с числом нулей эквивалентна задаче отыскания малых решений некоторой алгебраической системы числовых уравнений с неизвестными и параметром у. Эта система, называемая уравнением разветвления, имеет, вообще говоря, неединственное решение. Уравнение разветвления выведено как с помощью оператора В, так и с помощью обобщенной леммы Шмидта. При этом получены две эквивалентные формы уравнения разветвления, каждая из них имеет свои преимущества при рассмотрении конкретных вопросов.

В 24 и 25 в основном изучается уравнение вида (0.7), когда число нулей оператора В равно Уравнение разветвления имеет вид (0.11). Вычисляются его первые коэффициенты при а затем путем применения соответствующих результатов глав I, II устанавливаются различные предложения о числе и виде решений уравнения (0.7).

В главе VIII рассмотрен более общий случай, когда линейная часть В оператора Ф является нетеровской.

В § 26 рассмотрены вспомогательные вопросы линейной теории. § 27 содержит теоремы о ветвлении решений.

Пусть — число нулей оператора число нулей оператора В. Если то, как и выше, задача отыскания малых решений уравнения (0.7) сводится к уравнению разветвления, которое представляет собою систему числовых уравнений с числовыми неизвестными и параметром и может быть исследовано методами §§ 5 и 6.

Если то уравнение (0.7) перегружено и, оказывается, может иметь не более одного решения. Рассмотрен и случай когда уравнение (0.7) недогружено и имеет семейство решений, зависящих от свободных параметров.

В § 28 ноказана применимость полученных результатов к сингулярным нелинейным интегральным уравнениям с ядром типа Коши в пространствах Гёльдера и к сингулярным нелинейным интегральным уравнениям с ядром типа Гильберта в пространствах Лебега.

В последние годы различными авторами установлена нетеровость (или фредгольмовость) различных операторов, порожденных эллиптическими краевыми задачами для дифференциальных и интегро-дифференциальных уравнений. Каждый такой результат позволяет применить абстрактную схему глав VII и VIII к соответствующему классу нелинейных задач. При этом получается большое разнообразие как методов, так и результатов в зависимости от того, какой класс задач и в каких пространствах рассматривается. В § 29 рассмотрено три класса краевых задач для нелинейных эллиптических уравнений, достаточно полно на наш взгляд иллюстрирующих имеющиеся возможности.

К теории ветвления тесно примыкает большая группа задач теории возмущений. Некоторые из этих задач приводятся в главе IX.

В § 30 изложены в основном известные результаты о жордановых цепочках и наборах фредгольмовских операторов, близкие к исследованиям М. В. Келдыша, А. С. Маркуса и других. В § 31 изучается задача о возмущении линейного уравнения малым линейным слагаемым. Этой задаче посвящены работы многих авторов. Наиболее полно ее рассмотрели М. И. Вишик и Л. А. Люстерник. Оказывается, что методы теории ветвления позволяют уточнить некоторые известные факты.

§ 32 содержит решение задачи о собственных значениях и собственных элементах линейных операторов. Этой задаче посвящена обширная литература. Хороший обзор относящихся сюда работ имеется в книге Данфорда и Шварца. Наш подход отличается от общепринятого лишь систематическим применением методов теории ветвления, развитых для нелинейных задач. Это позволяет не только довольно просто получить известные результаты, но и в ряде случаев установить новые. Некоторые утверждения § 32 являются уточнениями или обобщениями результатов М. И. Вишика и Л. А. Люстерника.

В § 33 рассмотрена задача, являющаяся обобщением на нелинейный случай задачи, рассмотренной в § 31.

Понятие жордановой цепочки переносится на нелинейный случай. Это позволяет в сочетании с методами главы VII исследовать все решения задачи с заданным порядком роста как ограниченные, так и особые. Близкая задача изучалась в § 14.

Заметим, что аппарат, развитый в § 33, нашел применение и в других нелинейных задачах, например в задаче об «уединенной волне».

В последней X главе книги приводятся некоторые конкретные прикладные задачи, решение которых получается методами теории ветвления.