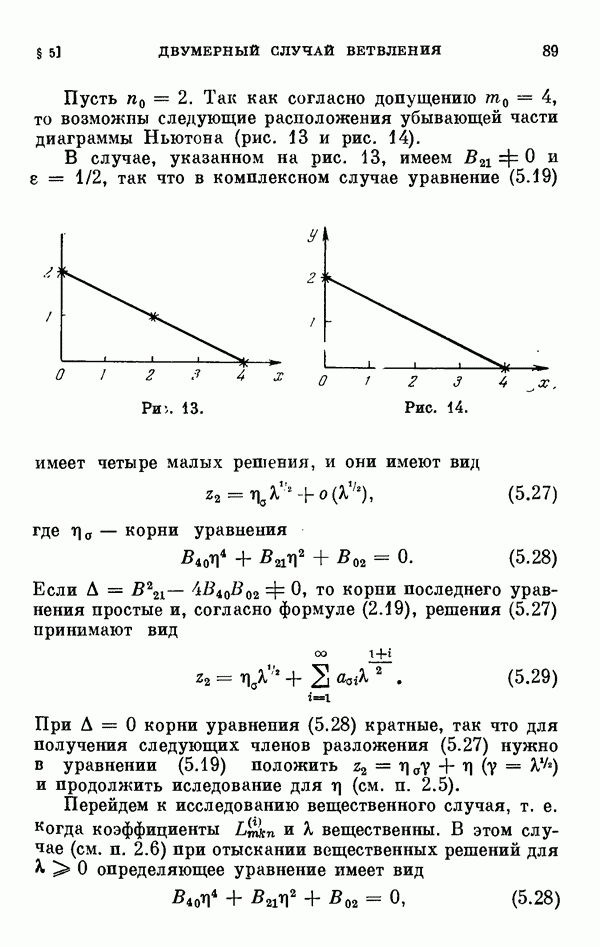
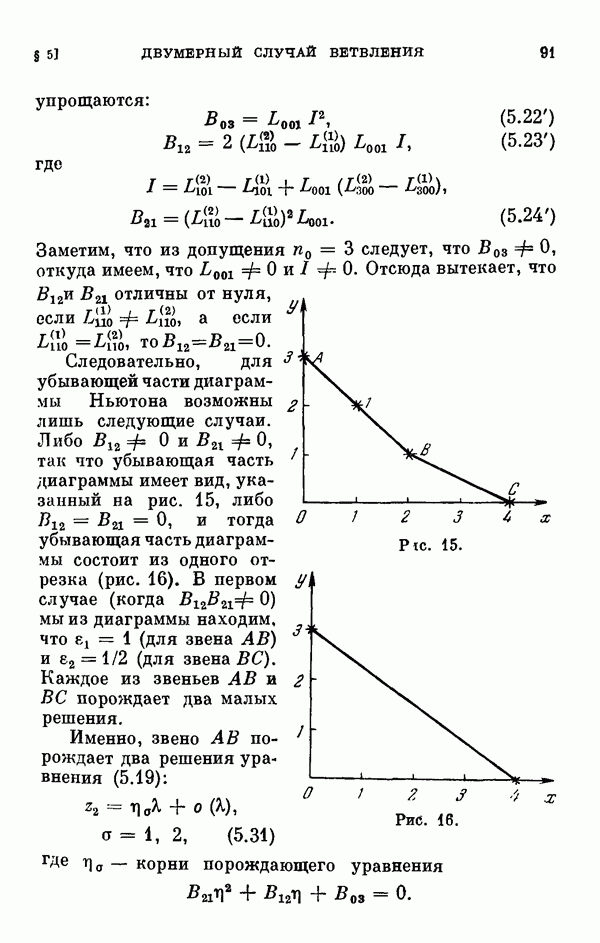
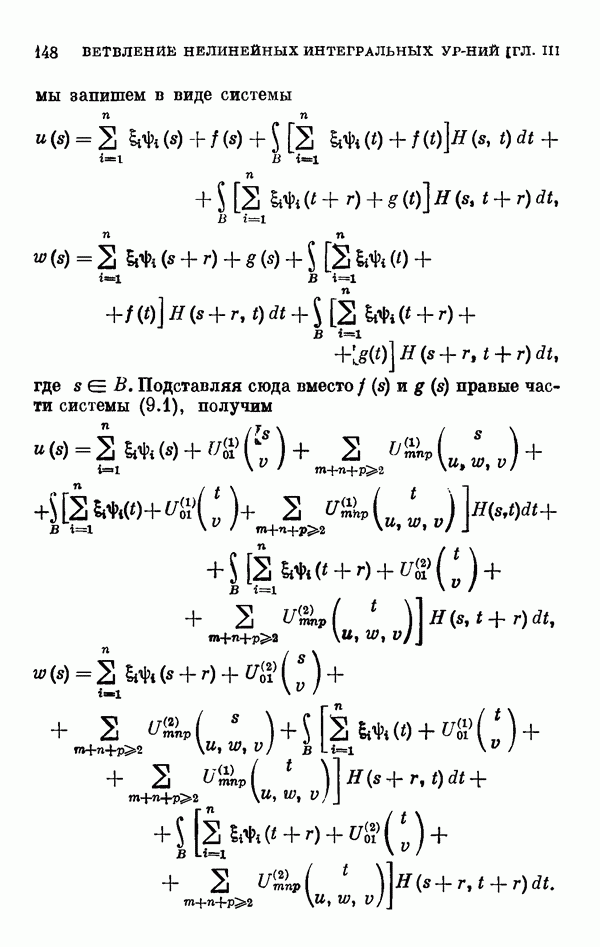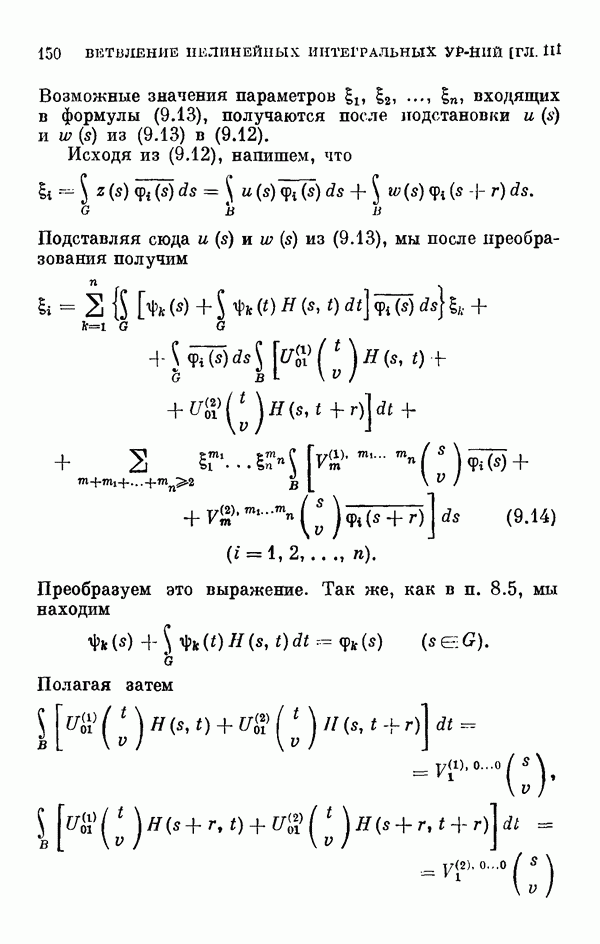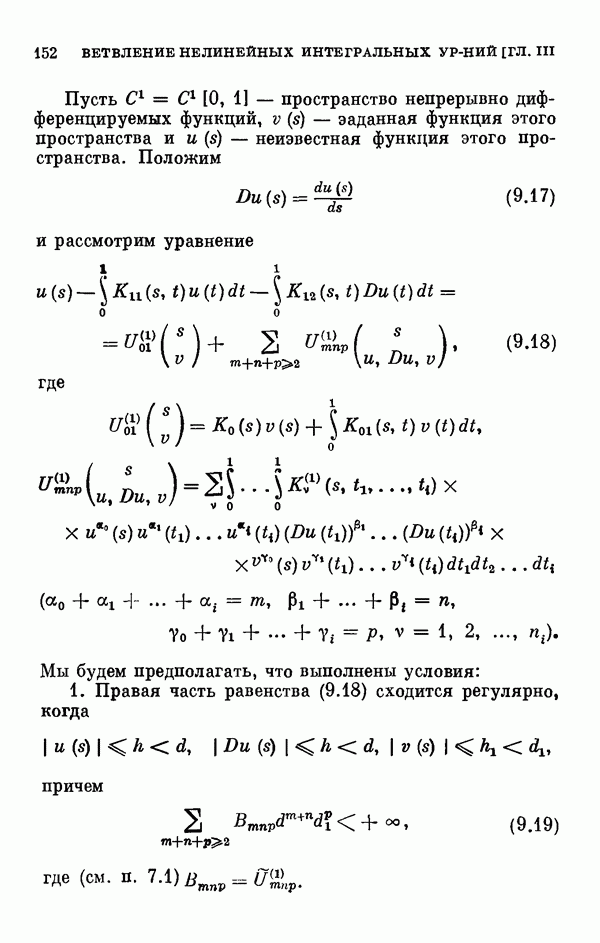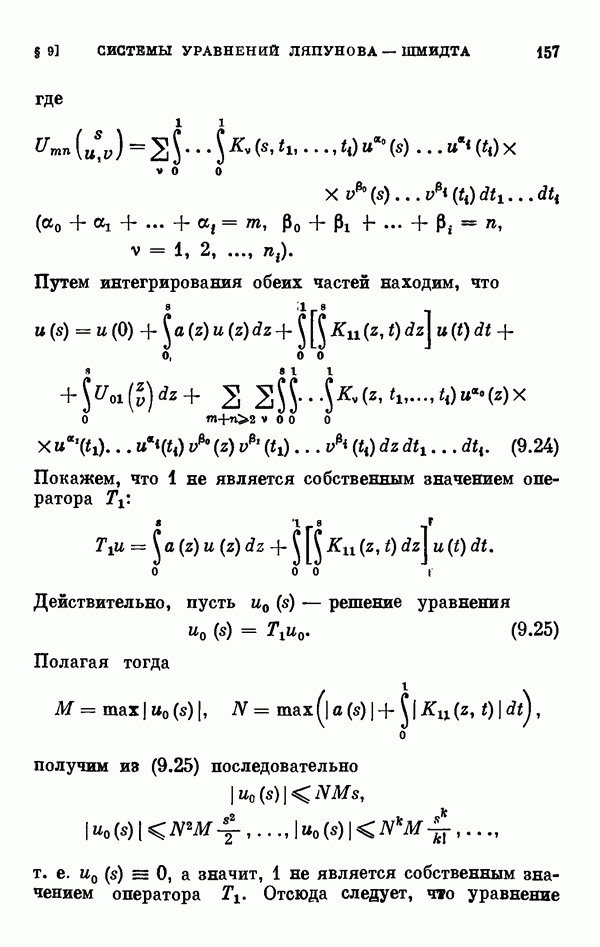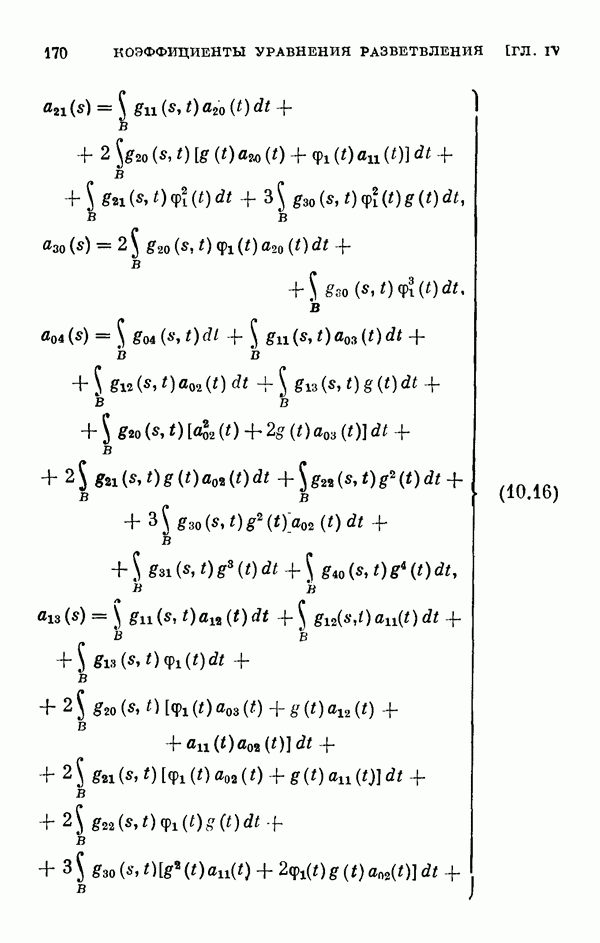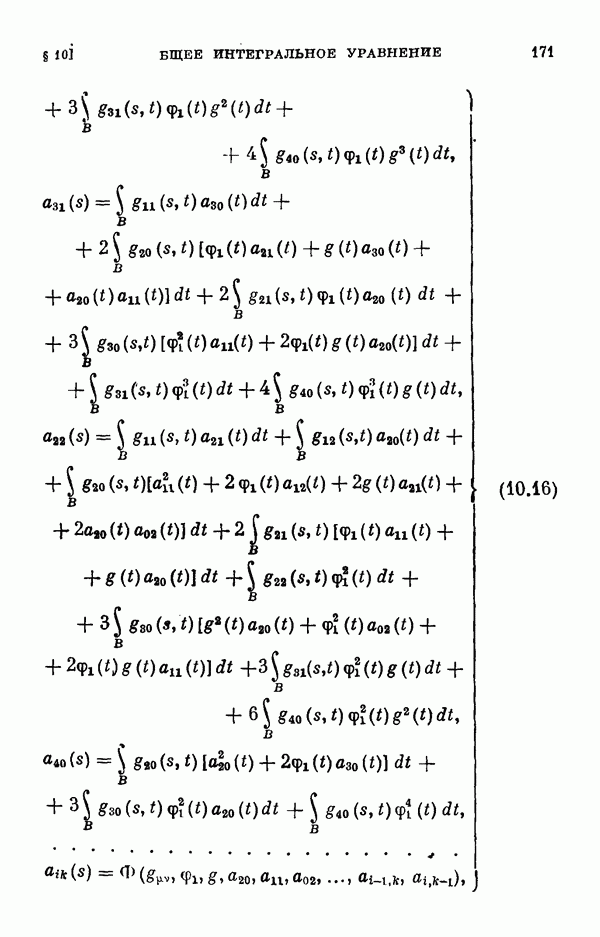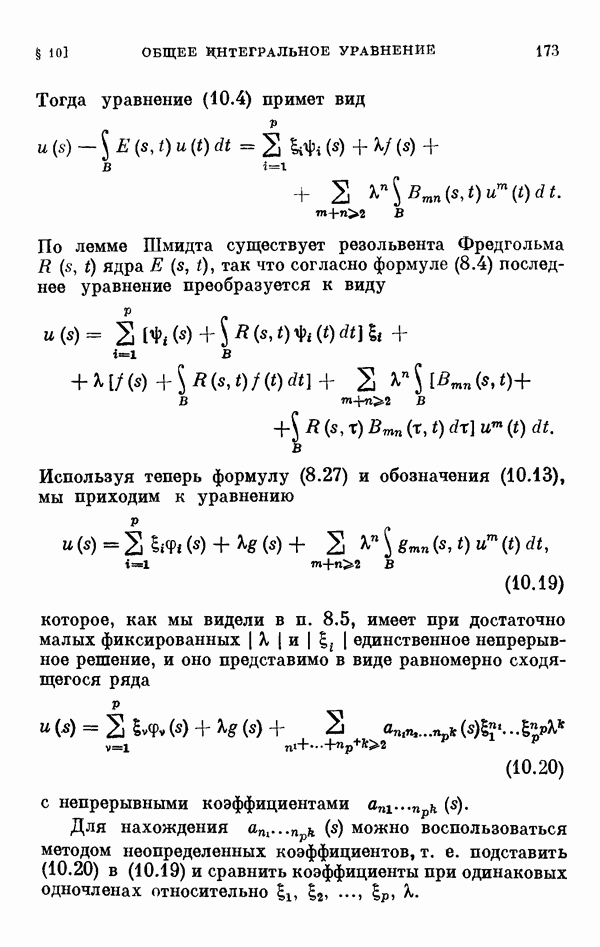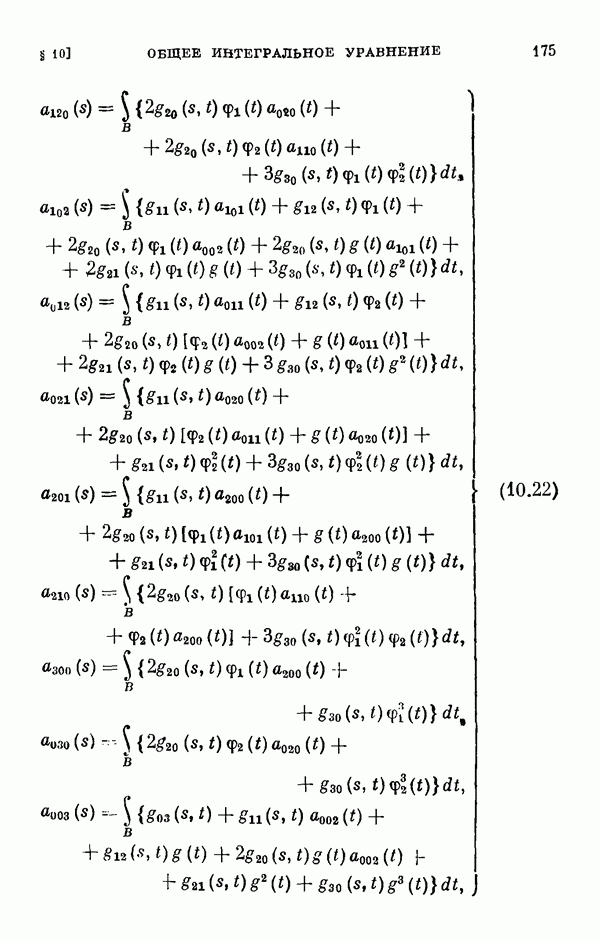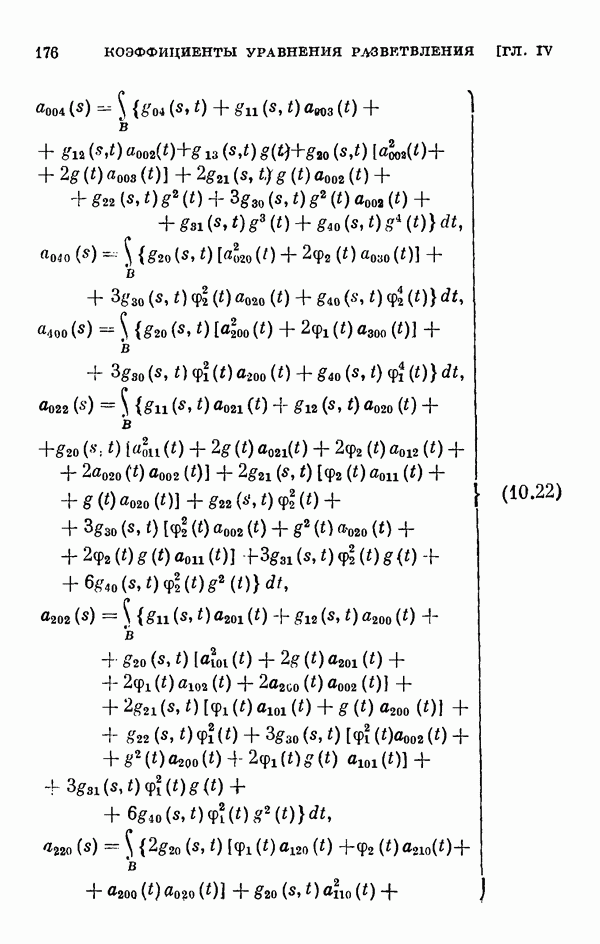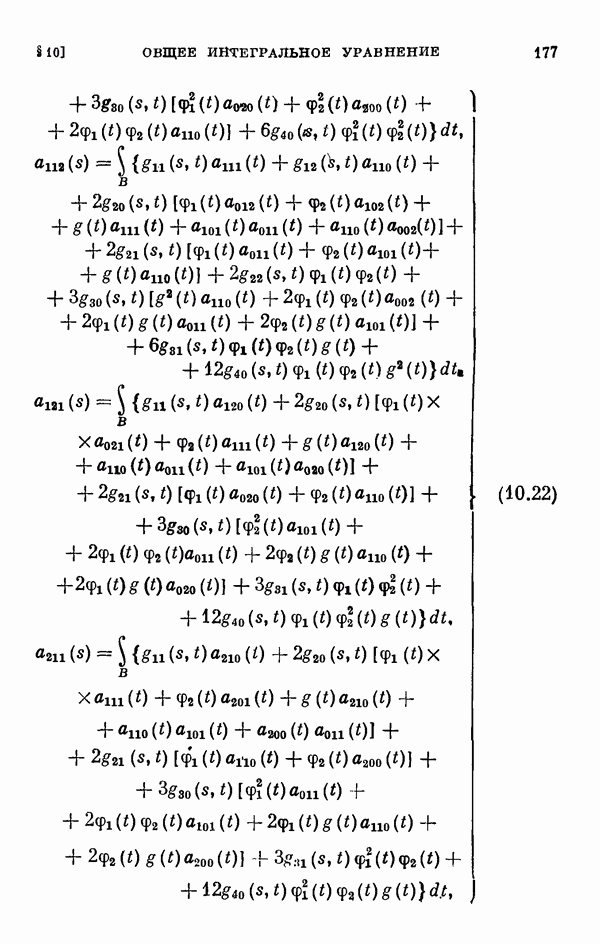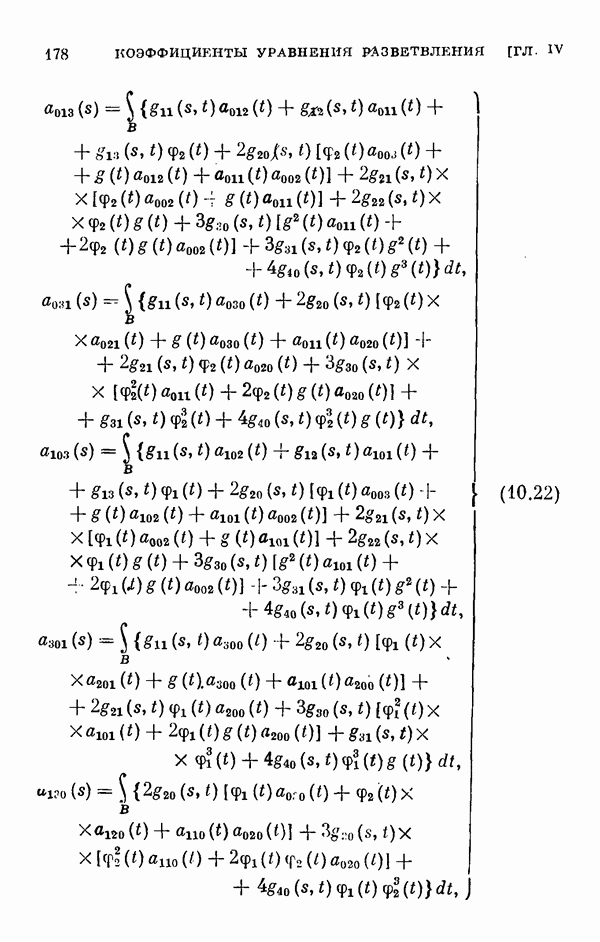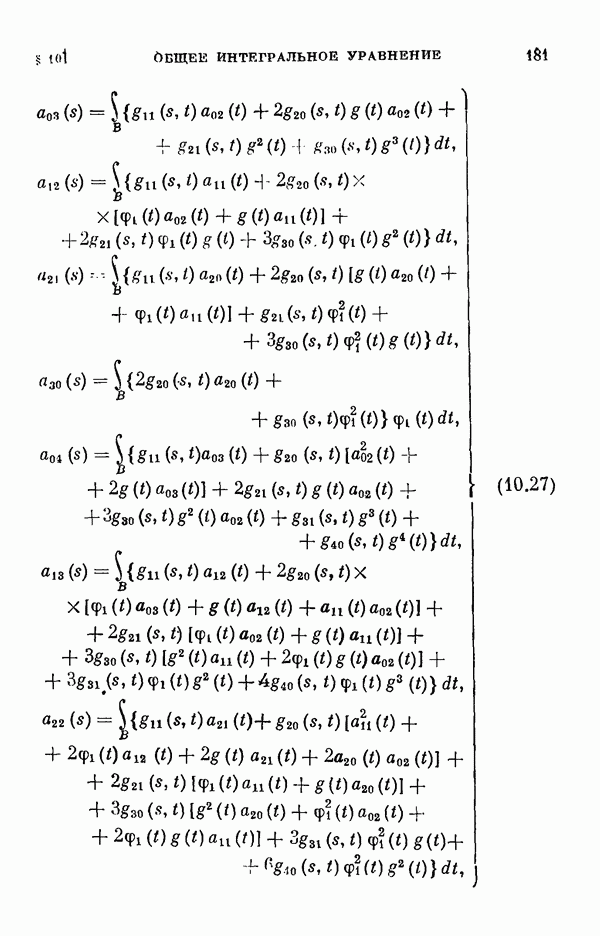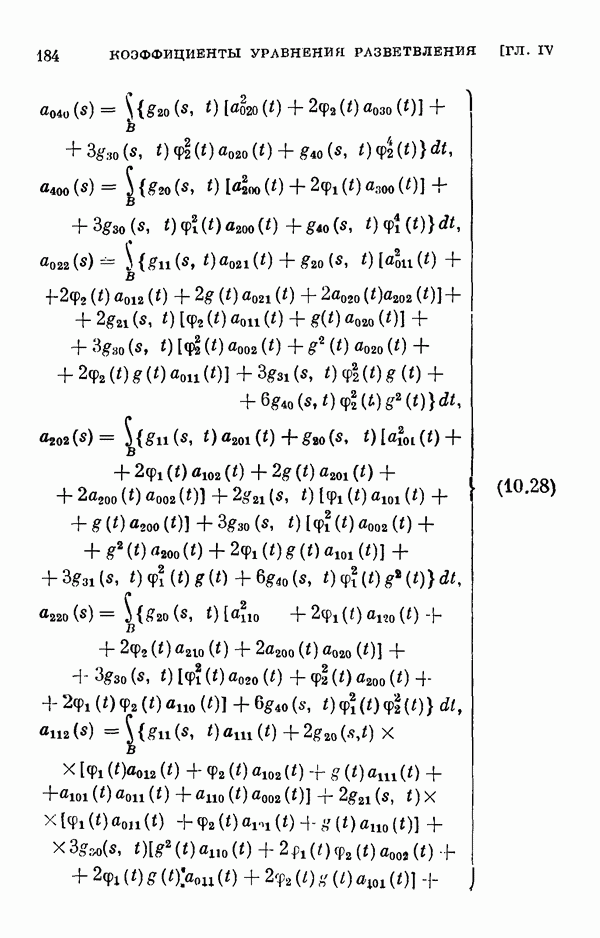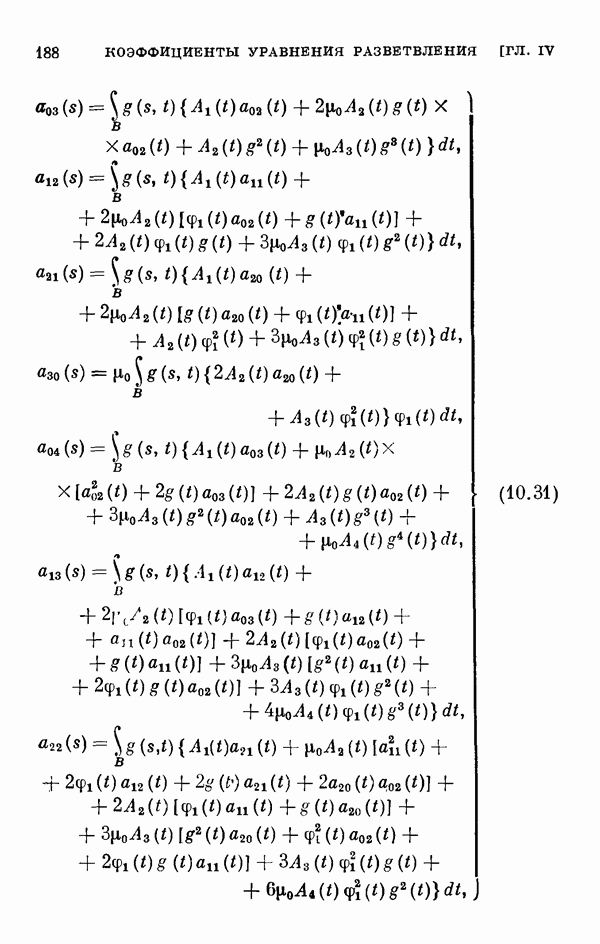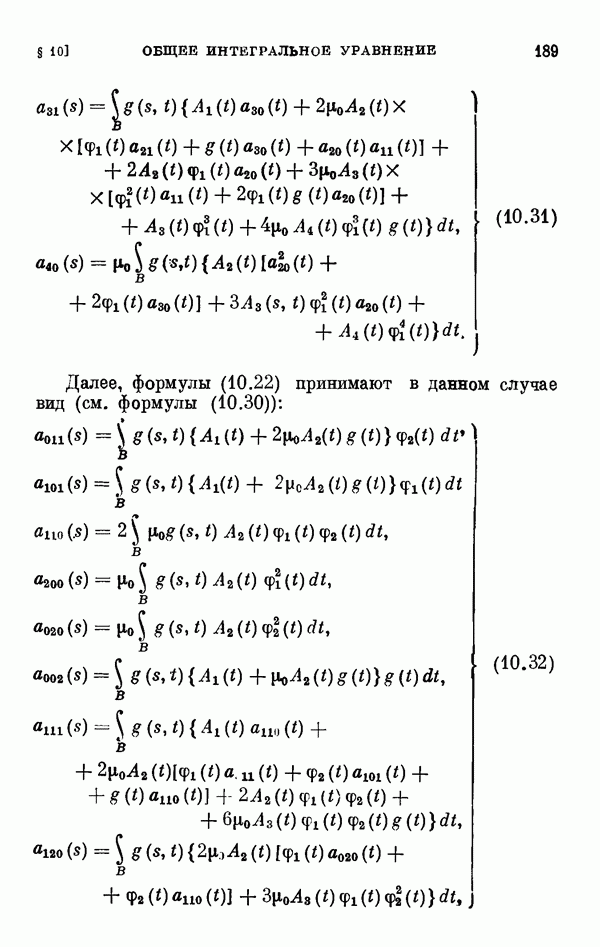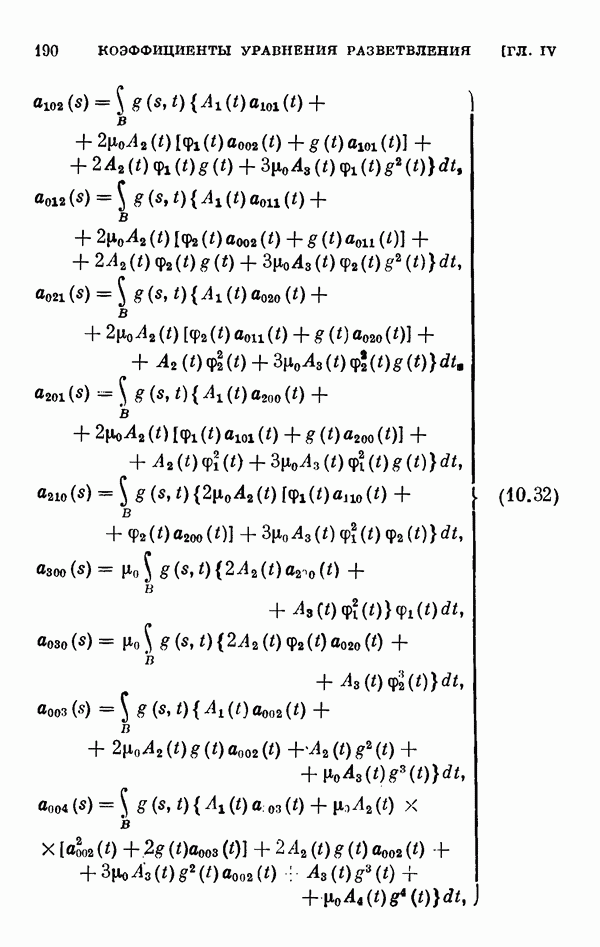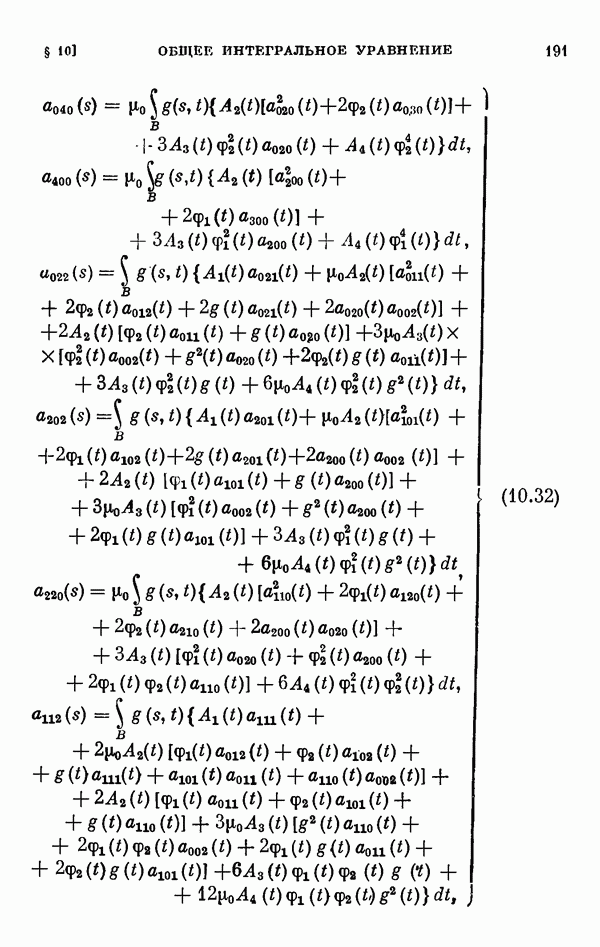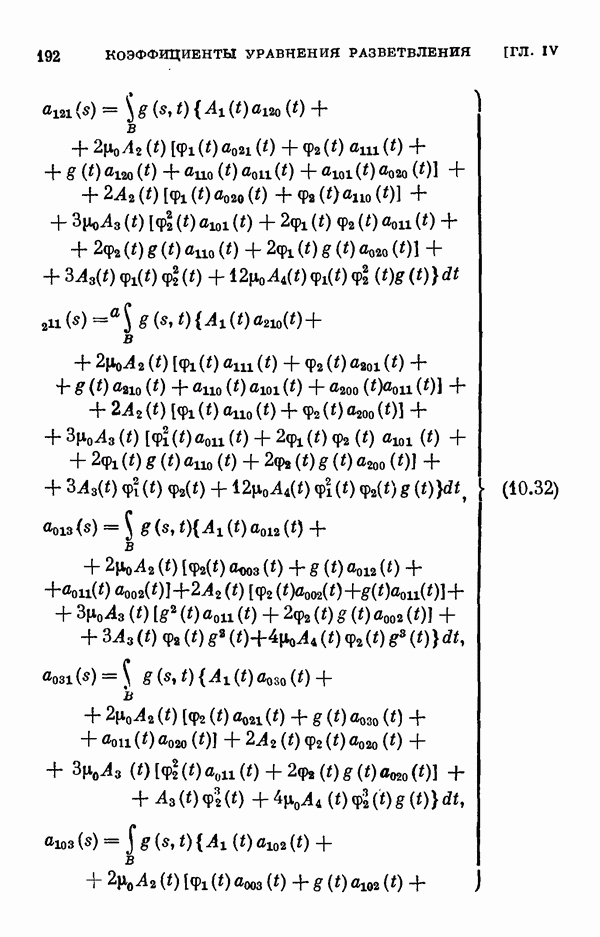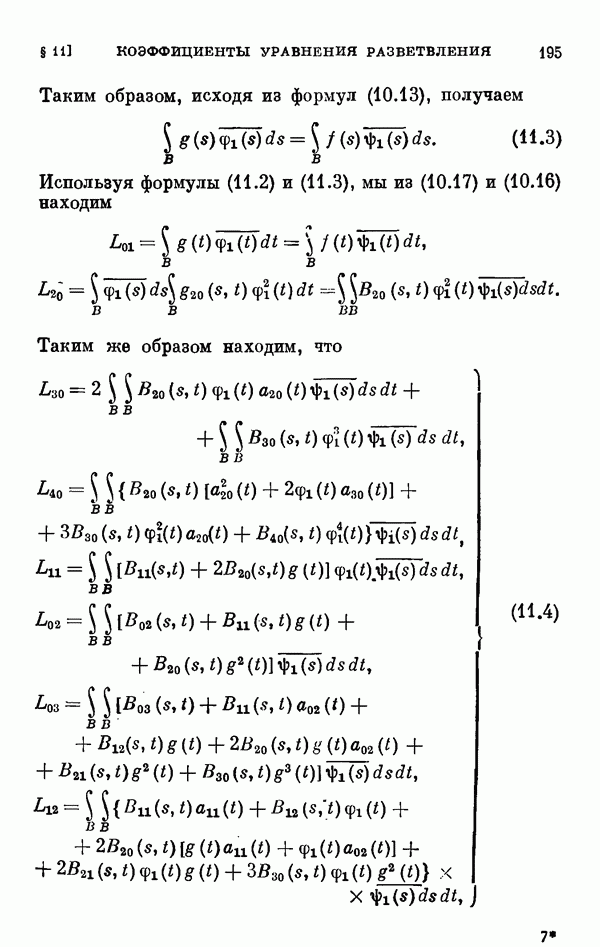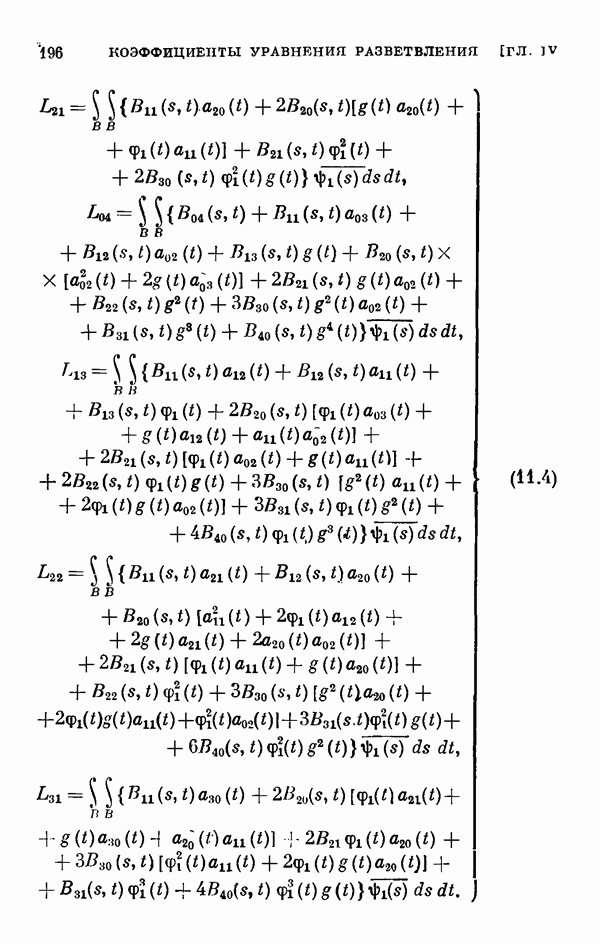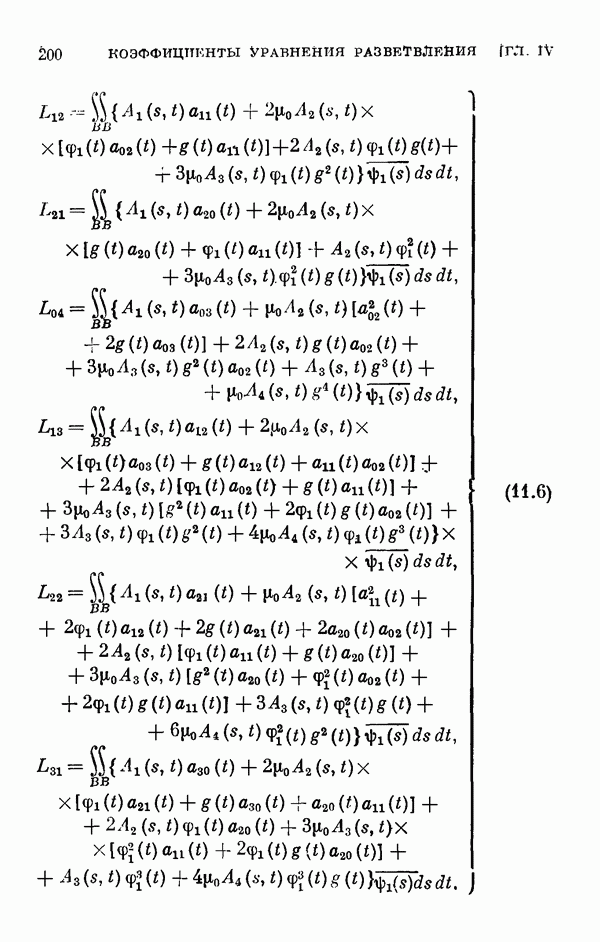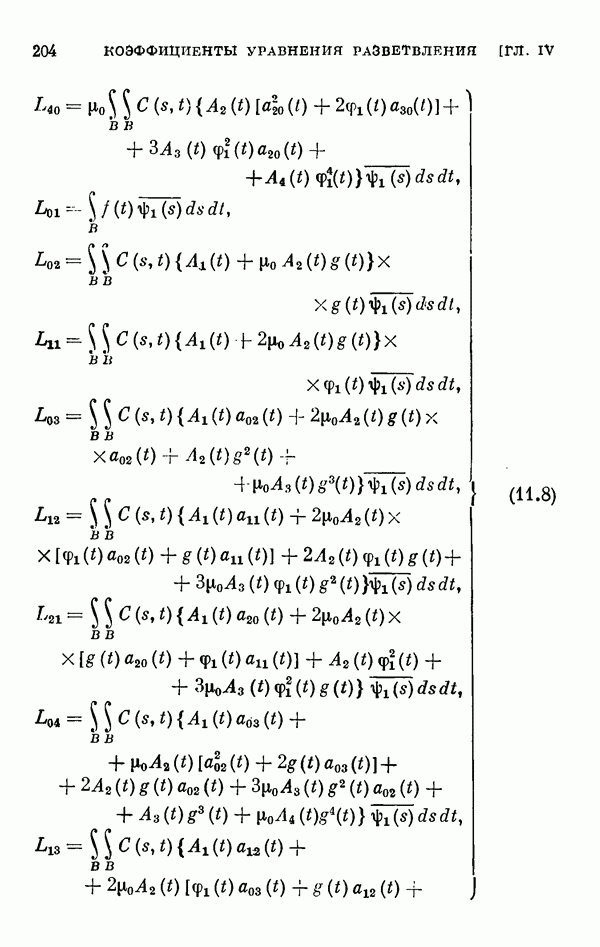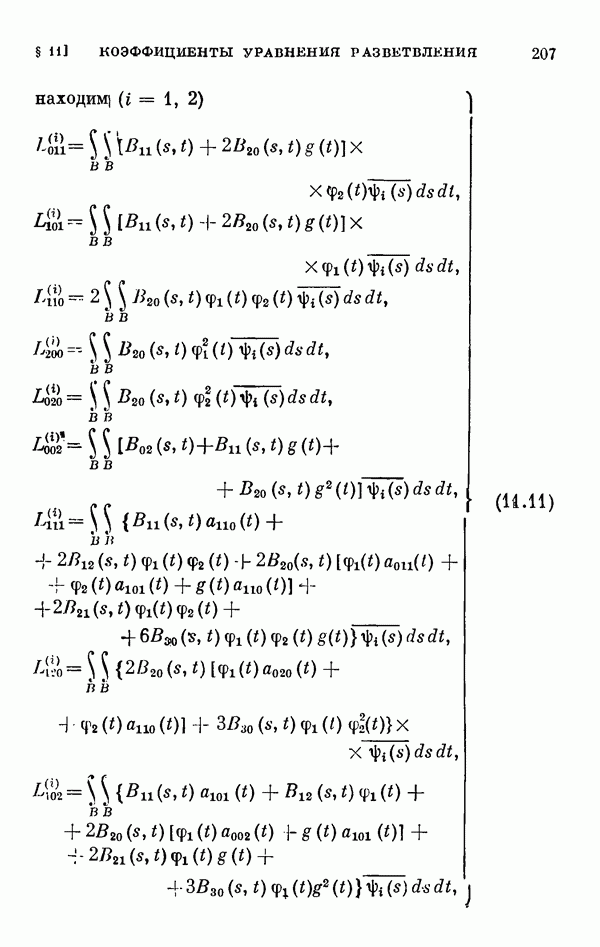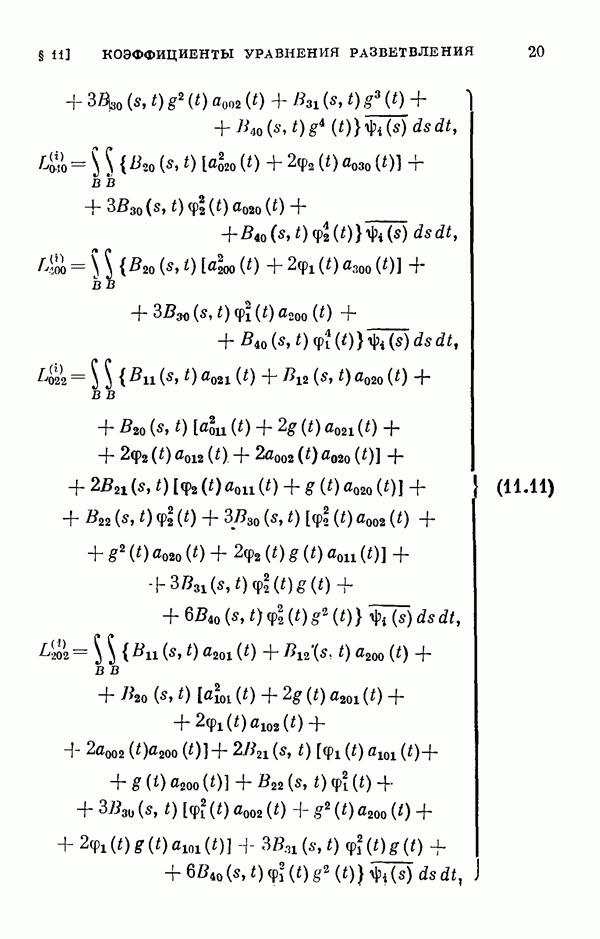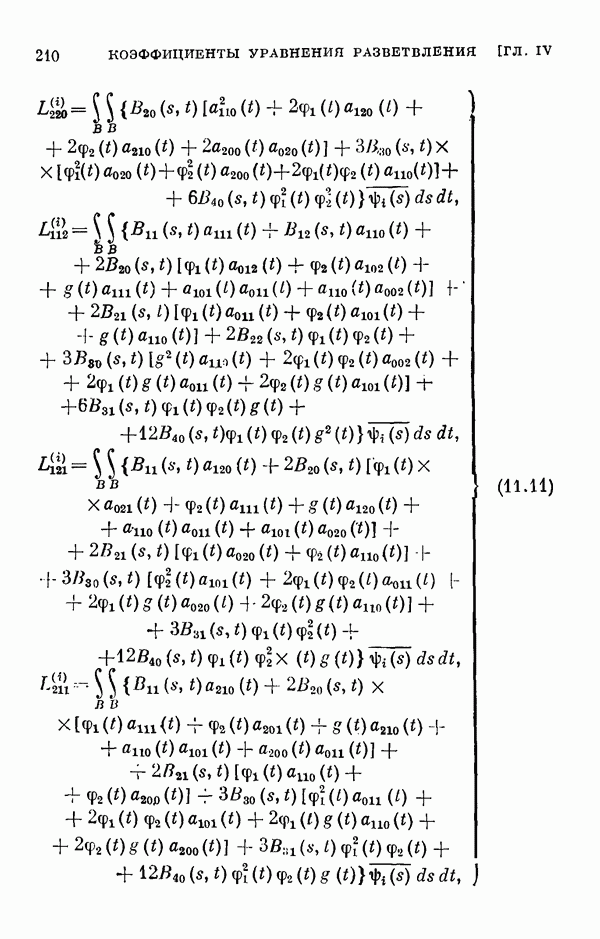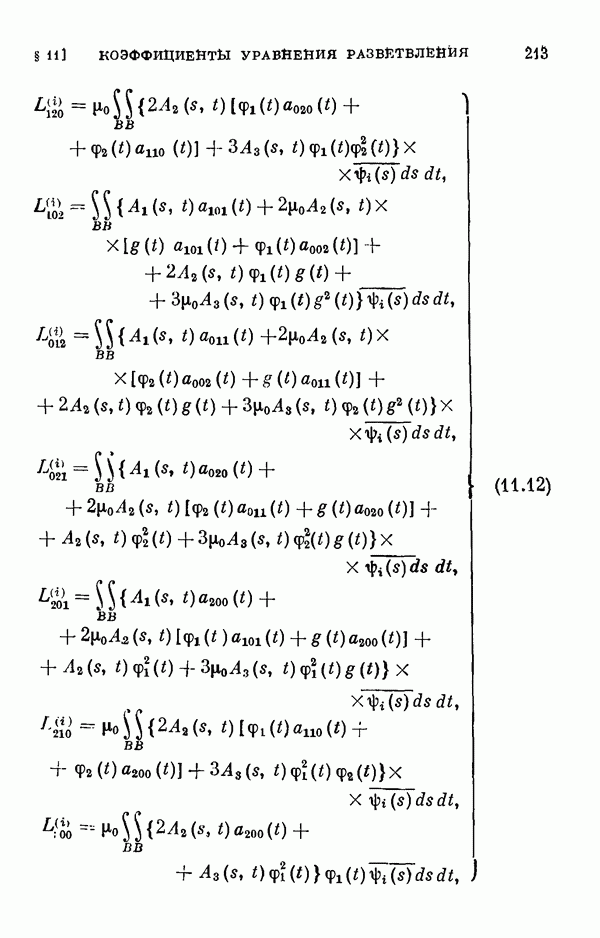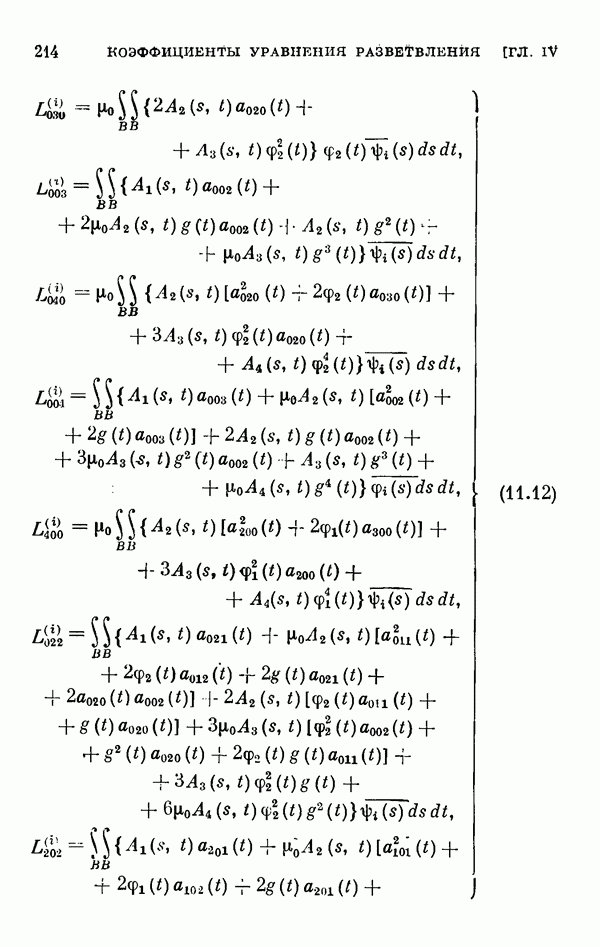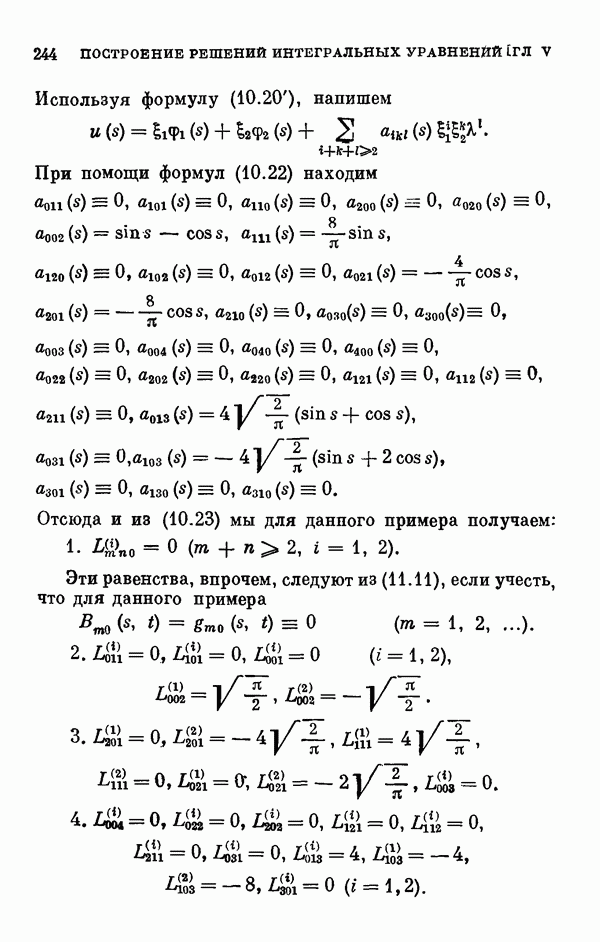| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
22.3 Теоремы о неявных операторах.
Приведем две теоремы о неявных операторах. Первая из них была установлена Ламсоном [1] и обобщена Гильдебрандтом и Грэйвсом [1], вторая, по-видимому, принадлежит Майклу и Клиффорду [1].
Рассмотрим задачу о нахождении решений  (у играет роль параметра) уравнения
(у играет роль параметра) уравнения

удовлетворяющих условию

если оператор  удовлетворяет условию
удовлетворяет условию

Теоремы о неявных операторах позволяют изучить простейший случай этой задачи, когда она имеет (локально) единственное решение. Общий случай приводит к теории ветвления решений нелинейных уравнений и будет изучен в последующих параграфах.
Теорема 22.1, Пусть оператор  непрерывен в некоторой окрестности
непрерывен в некоторой окрестности  точки
точки  со
со
значениями в  и удовлетворяет условию (22.11). Пусть, далее, в
и удовлетворяет условию (22.11). Пусть, далее, в  существует непрерывная частная производная
существует непрерывная частная производная  причем оператор
причем оператор

имеет ограниченный обратный оператор.
Тогда существуют положительные числа  такие, что в шаре
такие, что в шаре  существует единственное решение
существует единственное решение

уравнения (22.9). Это решение определено при  непрерывно в этом шаре и удовлетворяет условию (22.10).
непрерывно в этом шаре и удовлетворяет условию (22.10).
Доказательство этой теоремы содержится в различных книгах (см., например,  Канторович, Г. П. Акилов [I], теорема 2 (4.17) или Л. А. Люстерник, В. И. Соболев (II), и мы его приводить не будем.
Канторович, Г. П. Акилов [I], теорема 2 (4.17) или Л. А. Люстерник, В. И. Соболев (II), и мы его приводить не будем.
Теорема 22.2. Пусть  — аналитический оператор в
— аналитический оператор в  со значениями в
со значениями в  причем оператор В имеет ограниченный обратный. Тогда существуют положительные числа
причем оператор В имеет ограниченный обратный. Тогда существуют положительные числа  такие, что в
такие, что в  существует единственное решение (22.13) уравнения (22.9). Это решение определено в
существует единственное решение (22.13) уравнения (22.9). Это решение определено в  , аполитично в этом шаре и удовлетворяет условию (22.10).
, аполитично в этом шаре и удовлетворяет условию (22.10).
Доказательство. Сначала заметим, что выполнены все условия теоремы 2.1, поэтому справедлив вывод зтой теоремы. Положим

и запишем уравнение (22.9) так:

где

Решение уравнения (22.15) будем искать в виде

где  — степенной оператор порядка к. Подставляя (22.17) в (22.15) и приравнивая, согласно теореме единственности аналитических функций, члены одинаковых порядков по
— степенной оператор порядка к. Подставляя (22.17) в (22.15) и приравнивая, согласно теореме единственности аналитических функций, члены одинаковых порядков по  получим рекуррентную систему для определения
получим рекуррентную систему для определения 

Оказывается, что

Из системы (22.18) последовательно определяем  и получаем формальное решение в виде ряда (22.17). Это решение окажется настоящим, если удастся доказать сходимость ряда (22.17).
и получаем формальное решение в виде ряда (22.17). Это решение окажется настоящим, если удастся доказать сходимость ряда (22.17).
Сходимость этого ряда устанавливается при помощи метода мажорант Коши — Гурса (см. Гурса [2]). Ряд, стоящий в правой части уравнения (22.15), если учесть формулы (22.16) и неравенства Коши (22.8), мажорируется следующей функцией (кратной прогрессией):

где 
Как и в классическом случае (Гурса 11], стр. 78—82), легко убеждаемся, что уравнение

будет мажорантным для уравнения (22.15). Это квадратное уравнение относительно  имеет единственный корень
имеет единственный корень  удовлетворяющий условию
удовлетворяющий условию 

где

так что ряд (22.17) сходится при

Итак, в качестве  можно выбрать любое число из
можно выбрать любое число из  . Заметим еще, что
. Заметим еще, что  — монотонно возрастающая функция
— монотонно возрастающая функция  на
на  , поэтому в качестве
, поэтому в качестве  можно принять
можно принять 
Теорема доказана.
В заключение приведем более общую теорему о неявных операторах, позволяющую привлечь к рассмотрению и неограниченные операторы. Близкие результаты получены А. Е. Гельманом [1].
Теорема 22.3. Пусть  — линейное множество, плотное в
— линейное множество, плотное в  и пусть
и пусть  — нелинейный оператор со значениями в
— нелинейный оператор со значениями в  определенный при
определенный при

удовлетворяющий условию  и имеющий на
и имеющий на  производную в смысле Гато
производную в смысле Гато  . Пусть, далее, оператор
. Пусть, далее, оператор  имеет ограниченный обратный оператор, причем операторы
имеет ограниченный обратный оператор, причем операторы

непрерывны по  , где
, где 
Тогда найдутся положительные числа и  такие, что в шаре
такие, что в шаре  уравнение (22.9) имеет при
уравнение (22.9) имеет при  единственное решение (22.13). Это решение удовлетворяет условию (22.10) и непрерывно в
единственное решение (22.13). Это решение удовлетворяет условию (22.10) и непрерывно в  . Если дополнительно оператор
. Если дополнительно оператор  аналитичен при
аналитичен при  , то найдется число
, то найдется число  такое, что в шаре
такое, что в шаре  указанное решение аполитично.
указанное решение аполитично.
Доказательство. Уравнение (22.9) эквивалентно, очевидно, уравнению (замена 

где

Для уравнения (22.20) выполнены все условия теоремы 22.1. Так, условие (22.11) принимает вид  Далее, здесь
Далее, здесь  оператор
оператор  непрерывен и, наконец,
непрерывен и, наконец,

так как есть линейный (возможно, неограниченный) оператор с областью определения  не зависящей от
не зависящей от  в окрестности точки
в окрестности точки  Таким образом, существование и единственность непрерывного (при дополнительном предположении — аналитического) решения
Таким образом, существование и единственность непрерывного (при дополнительном предположении — аналитического) решения  удовлетворяющего условию и
удовлетворяющего условию и  следуют из теорем 22.1 и 22.2. Очевидно,
следуют из теорем 22.1 и 22.2. Очевидно,  и
и  и теорема доказана.
и теорема доказана.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ГЛАВА I. Системы неявных функций и классическая теория ветвления
- § 1. Задача о неявных функциях
- 1.2. Общее исследование задачи о неявных функциях.
- 1.3. Аналитический случай.
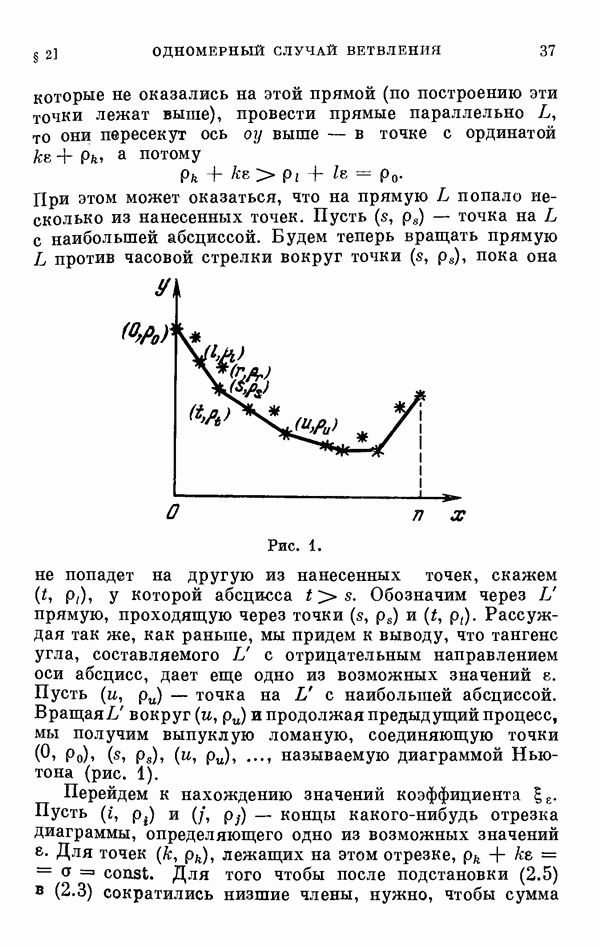
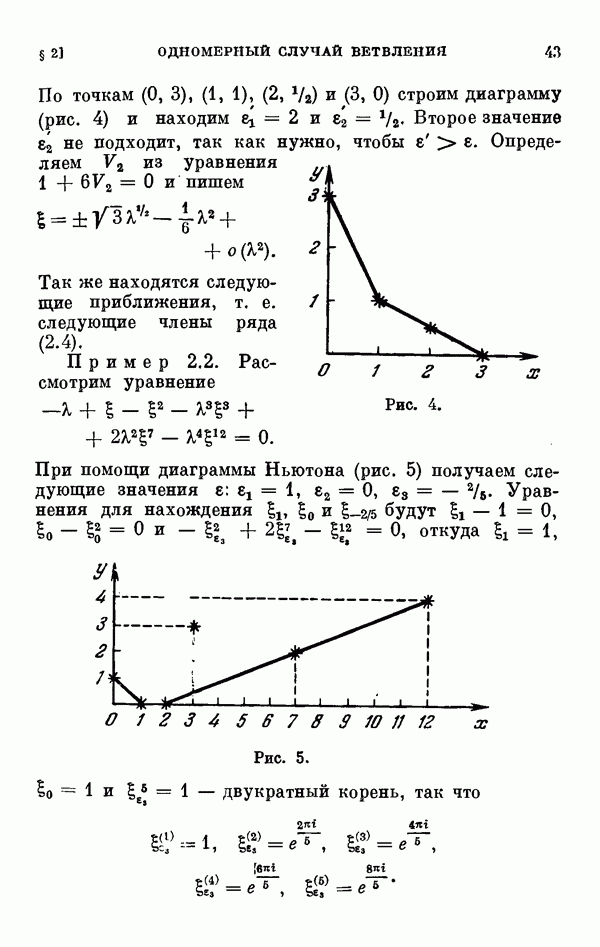
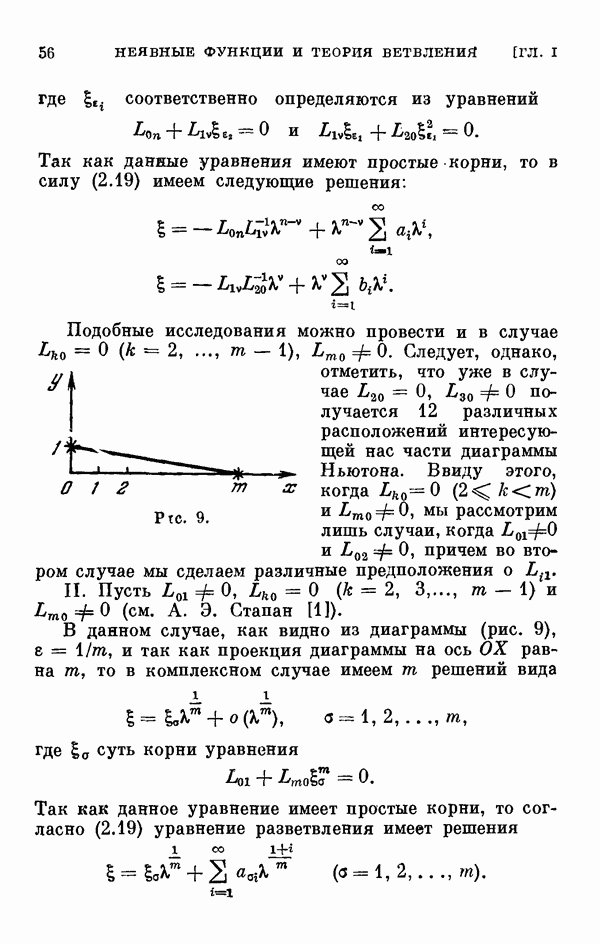
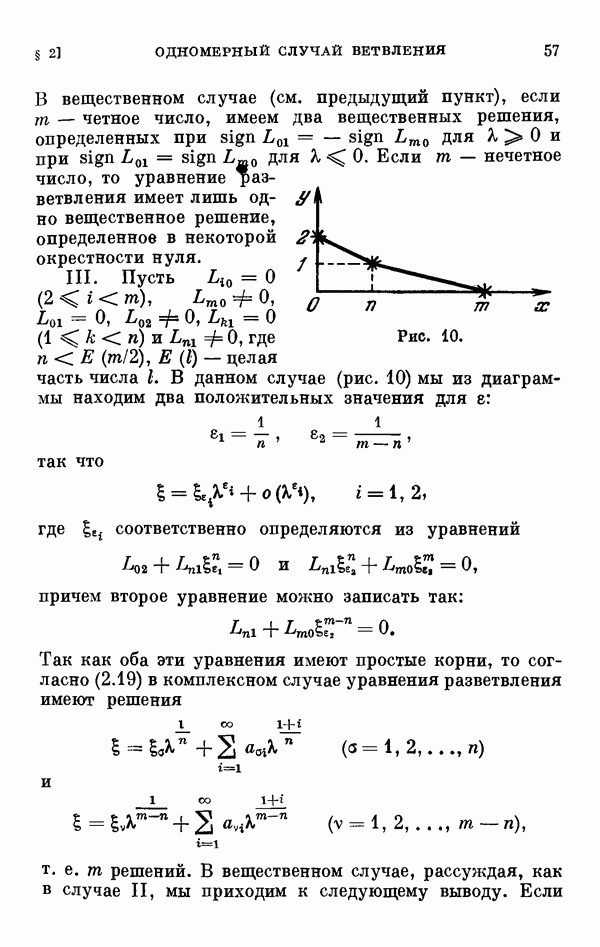
- § 2. Одномерный сличай ветвления и диаграмма Ньютона
- 2.2. О свойствах решений.
- 2.3. Примеры.
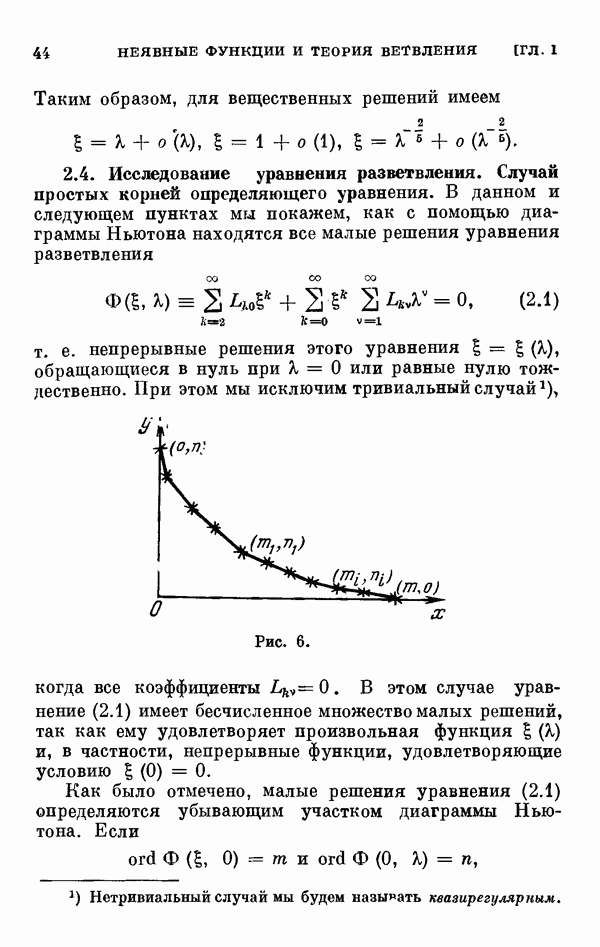
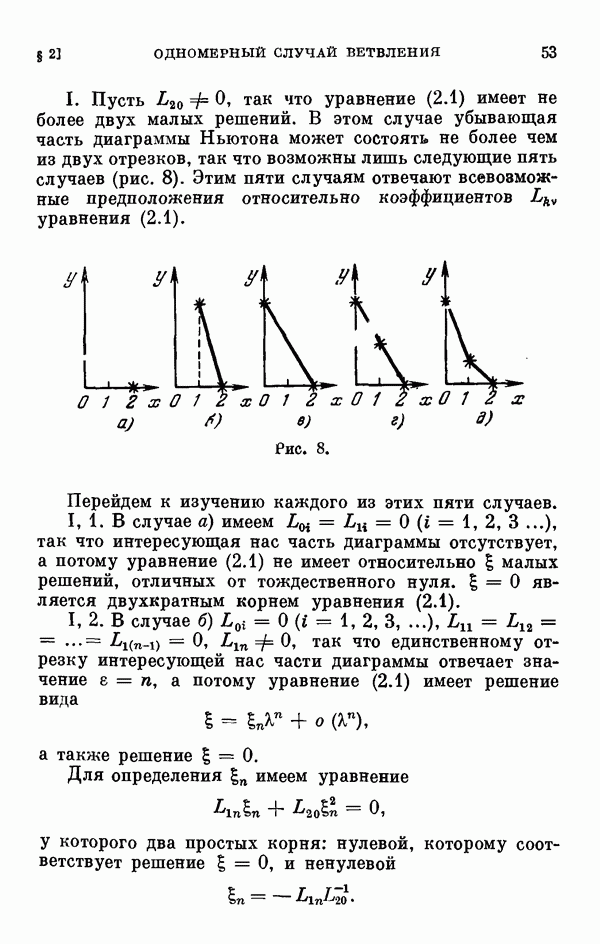
- 2.4. Исследование уравнения разветвления. Случай простых корней определяющего уравнения.
- 2.5. Случай кратных корней определяющего уравнения.
- 2.6. О вещественных решениях.
- 2.7. Некоторые частные случаи расположения диаграммы Ньютона.
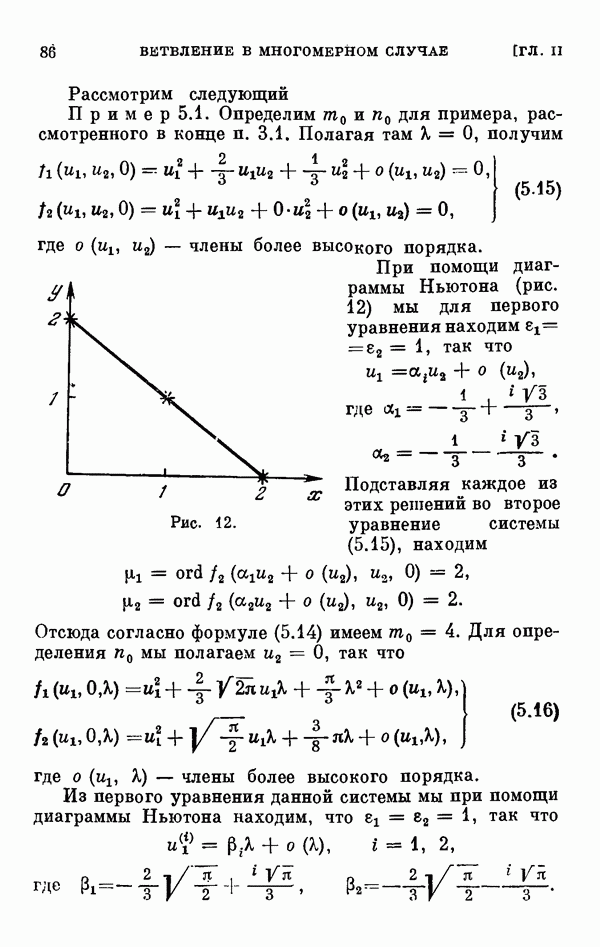
- ГЛАВА II. Исследование уравнения разветвления в многомерном случае
- 3.2. Приведение к нормальному виду.
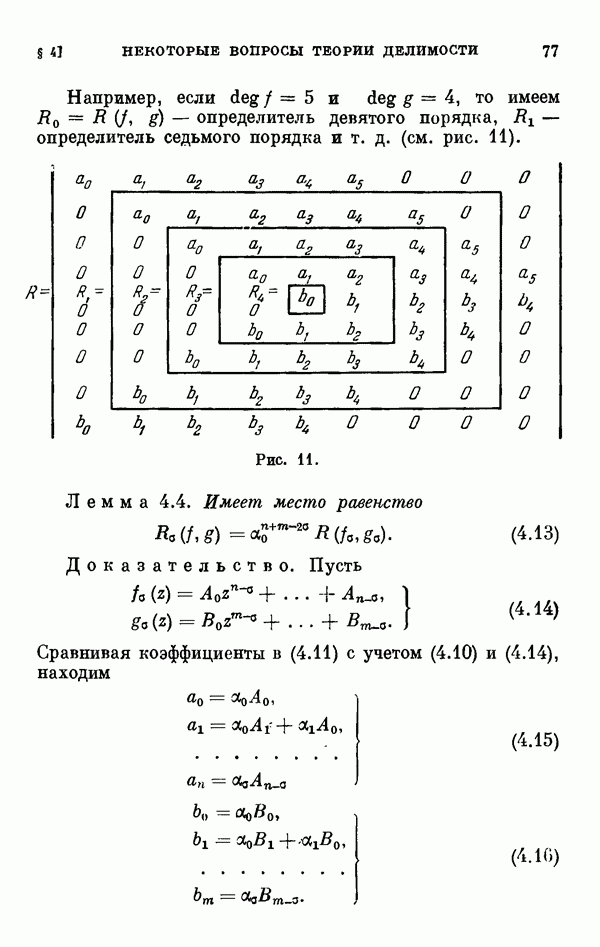
- § 4. Некоторые вопросы теории делимости
- 4.2. Общий делитель и аналог алгоритма Евклида.
- 4.3. Примитивный ОНД.
- 4.4. Применение к отмеченным многочленам.
- § 5. Двумерный случай ветвления
- 5.2. Указатели двумерного случая ветвления.
- 5.3. Частные случаи.
- § 6. Многомерный случай ветвления
- 6.2. Малые решения уравнения разветвления и метод исключения неизвестных.
- 6.3. Квазирегулярный случай ветвления.
- 6.4. Вырожденный случай ветвления.
- 6.5. Об изолированности нулевого решения.
- ГЛАВА III. Уравнение разветвления для нелинейных интегральных и интегро-дифференциальных уравнений
- § 7. Интегральные уравнения Ляпунова — Шмидта
- 7.2. Интегро-степенные ряды от многих функциональных аргументов.
- 7.3. Интегро-степенные ряды от интегро-степенных рядов.
- 7.4. Сжатость оператора Ляпунова—Шмидта.
- 7.5. Простейшее уравнение.
- 7.6. Последовательные приближения Лихтенштейна.
- 7.7. Применение метода мажорант.
- 7.8. Простейшее уравнение в случае равномерной сходимости.
- § 8. Общее интегральное уравнение Ляпунова—Шмидта
- 8.2. Регулярный случай при наличии многих аргументов.
- 8.3. Лемма Шмидта.
- 8.4. Одномерный случай ветвления.
- 8.5. Многомерный случай ветвления.
- 8.6. Возможные обобщения.
- § 9. Системы уравнений Ляпунова—Шмидта и некоторые интегро-дифференциальные уравнения
- 9.2. Регулярный случай.
- 9.3. Случай ветвления.
- 9.4. Некоторые нелинейные интегро-дифференциальные уравнения первого порядка.
- 9.5. Другие виды интегро-дифференциальных уравнений.
- 9.6. Другой способ построения уравнения разветвления
- ГЛАВА IV. Общее интегральное уравнение и коэффициенты уравнения разветвления
- 10.2. Регулярный случай.
- 10.3. Одномерный случай ветвления.
- 10.4. Многомерный случай ветвления.
- 10.5 Частный случай.
- 10.6. Уравнение Гаммерштейна.
- § 11. Коэффициенты уравнения разветвления
- 11.2. Коэффициенты одиомерного уравнения разветвления нелинейного интегрального уравнения Гаммерштейна.
- 11.3. Коэффициенты двумерного уравнения разветвления общего нелинейного интегрального уравнения.
- 11.4. Коэффициенты двумерного уравнения разветвления для частных случаев.
- 11.5. Некоторые свойства коэффициентов уравнения разветвления.
- ГЛАВА V. Описание и построение решений нелинейных интегральных уравнений
- § 12. Описание решений нелинейных интегральных уравнений
- 12.2. Описание решении в одномерном случае ветвления.
- 12.3. О точках бифуркации в одномерном случае ветвления.
- 12.4. Описание решений в двумерном случае ветвления.
- 12.5. Описание решений в многомерном случае ветвления.
- 12.6. О ветвлении изолированного решения.
- 12.7. Точки бифуркации в многомерном случае ветвления.
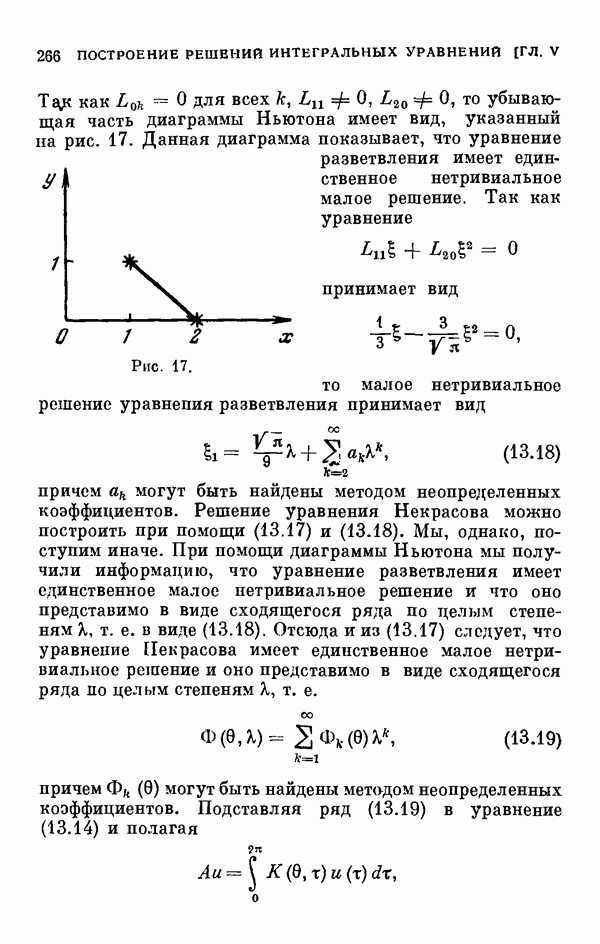
- § 13. Построение решений нелинейных интегральных уравнений
- 13.3. Двумерный случай ветвления.
- 13.4. Уравнение Некрасова.
- 13.5. Уравнение разветвления для уравнения Некрасова.
- § 14. Особые решения нелинейных интегральных уравнений
- 14.2. Сведение к малым решениям.
- 14.3. Особые решения в регулярном случае.
- 14.4. Исследование вспомогательного уравнения.
- 14.5. Ветвление решений основного уравнения.
- 14.6 Особые решения в пространствах Лебега.
- ГЛАВА VI. Ветвление периодических решений дифференциальных уравнений
- § 15. Периодические решения неавтономных систем
- 15.2. Метод Пуанкаре.
- 15.3. Условия периодичности и уравненне разветвления.
- 15.4. Описание решений в регулярном случае.
- 15.5. Описание решений в одномерном случае ветвления.
- 15.6. Описание решений в многомерном случае ветвления.
- § 16. Периодические решения квазилинейных систем
- 16.2. Условия периодичности.
- 16.3. Вывод уравнения разветвления.
- 16.4. Описание решений и дополнительные замечания.
- § 17. Периодические решения автономных систем
- 17.2. Уравнение разветвления.
- 17.3. Основные выводы.
- 17.4. Метод неопределенных коэффициентов.
- 17.5. Автономные системы с одной степенью свободы.
- § 18. Примеры
- 18.1. Неавтономные системы с одной степенью свободы.
- 18.2 Автономные системы с одной степенью свободы.
- § 19. Другие задачи о периодических решениях
- 19.1. Особые периодические решения неавтономных систем.
- 19.2. Ветвление периодических решений в банаховых пространствах
- § 20. Об устойчивости периодических решений, зависящих от малого параметра
- 20.2. Устойчивость решений задачи Пуанкаре.
- ГЛАВА VII. Нелинейные уравнения в банаховых пространствах
- § 21. Некоторые вопросы теории линейных операторов в банаховых пространствах
- 21.2. Специальные разложения пространств в прямые суммы подпространств.
- 21.3. Сужение оператора и обобщенная лемма Шмидта.
- 21.4 Связь с сопряженным оператором.
- 21.5. Неограниченные фредгольмовские операторы.
- § 22. Степенные операторы, ряды Тейлора, теоремы о неявных операторах
- 22.2 Степенные ряды. Ряды Тейлора.
- 22.3 Теоремы о неявных операторах.
- § 23. Уравнение разветвления Ляпунова — Шмидта
- 23.2. Вывод уравнения разветвления с помощью сужения оператора B.
- 23.3. Вывод уравнения разветвления с помощью леммы Шмидта.
- 23.4. Основная теорема об уравнении разветвления.
- 23.5. Уравление разветвления в аналитическом случае.
- 23.6. Уравнение разветвления для неограниченных операторов.
- § 24. Исследование одномерного случая ветвления
- 24.2. Вырожденный случай.
- 24.3. Квазирегулярный случай (задача А).
- 24.4. Задача Б (невырожденный случай).
- 24.5 Вещественный случай.
- 24.6. О ветвлении решений уравнений о достаточно гладкими операторами.
- 24.7 Случай функционального параметра. Ряды по однородным операторам.
- 24.8. Случай двух числовых параметров.
- § 25. Многомерный случай ветвления
- 25.2. Коэффициенты двумерного уравнения разветвления.
- 25.3. Двумерный случай ветвления.
- 25.4 Общий случай.
- 25.5. О ветвлении изолированного решения.
- 25.6. О точках бифуркации.
- ГЛАВА VIII. Ветвление решений нелинейных уравнений в сингулярном случае
- 26.2. Разложение пространств в прямые суммы подпространств.
- 26.3. Теорема Аткинсона.
- 23.4. О нетеровских неограниченных операторах.
- § 27. Теоремы о ветвлении решений
- 27.2. Случай n > 0, m = 0.
- 27.3. Случай n = 0, m > 0.
- 27.4. Основной случай. Уравнение разветвления.
- 27.5. О ветвлении решений уравнения с неограниченным оператором.
- § 28. Ветвление решений нелинейных сингулярных интегральных уравнений.
- 28.2. Нелинейные сингулярные интегральные уравнения с ядром типа Коши в пространствах Гёльдера.
- 28.3. Аналитический случай.
- 28.4. Нелинейные сингулярные интегральные уравнения с ядром Гильберта в пространствах Лебега.
- § 29. Ветвление решений краевых задач для нелинейных эллиптических уравнений
- 29.2. Краевые задачи на плоскости для эллиптических систем k-го порядка в пространстве Гёльдера.
- 29.3. Краевые задачи для эллиптических уравнений в пространстве суммируемых функций.
- ГЛАВА IX. Некоторые задачи теории вовмущений
- § 30. Жордановы цепочки и наборы фредгольмовских операторов
- 30.2. А-жордановы цепочки и наборы при n > 1.
- 30.3. Условия полноты А-жорданова набора.
- 30.4. Пример.
- § 31. Возмущение линейного уравнения малым линейным слагаемым
- 31.2. Случай n > 1.
- 31.3. Метод неопределенных коэффициентов.
- § 32. Ветвление собственных значений и собственных элементов фредгольмовских операторов
- 32.2. Уравнение разветвления в аналитическом случае.
- 32.3. Вырожденный и невырожденный случаи.
- 32.4. Одномерный случай.
- 32.5. Метод неопределенных коэффициентов.
- 32.6. Многомерный случай.
- 32.7. Некоторые обобщения.
- § 33. Особые решения нелинейных уравнений
- 33.2. Задача о возмущении линейного уравнения малым нелинейным слагаемым.
- 33.3. Понятие обобщенной жордановой цепочки.
- 33.4. Свойства некоторых многочленов.
- 33.5 Основной случай задачи о возмущении.
- 33.6. Случаи возмущения второго порядка.
- 33.7. Решения порядка …
- ГЛАВА X. Некоторые прикладные задачи
- § 34. О малых изгибах прямолинейного стержня под действием постоянной нагрузки
- § 35. К теории малых прогибов гибких пластин
- 35.2. Случай круглой пластины.
- 35.3. Исследование уравнения разветвления.
- 35.4. Круглая пластина с нулевой внешней нагрузкой.
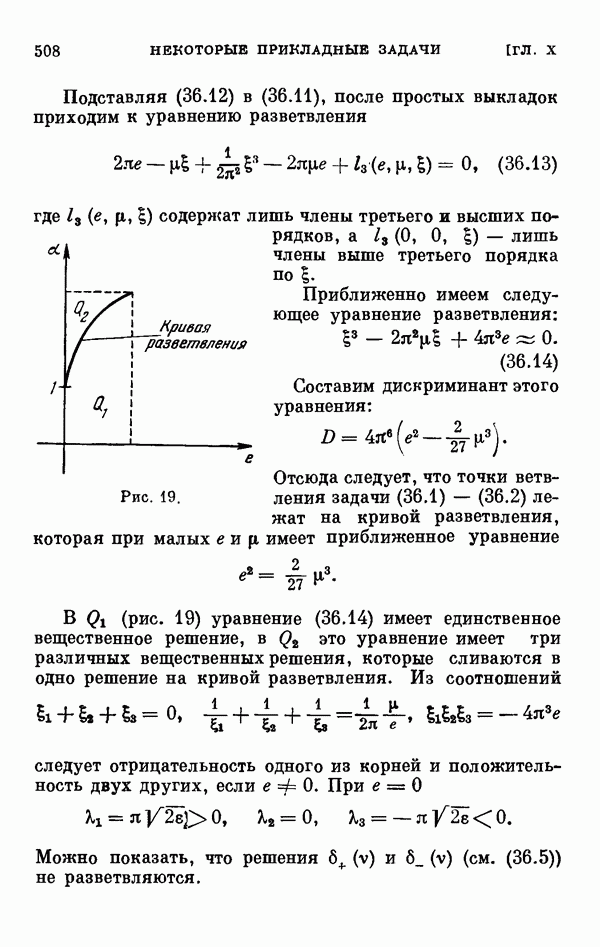
- § 36. О колебаниях спутника в плоскости эллиптической орбиты
- § 37. Об одном виде установившихся волн
- 37.2. Сведение к системе.
- 37.3. Регулярный случай.
- 37.4. Случай ветвления.
- Литература