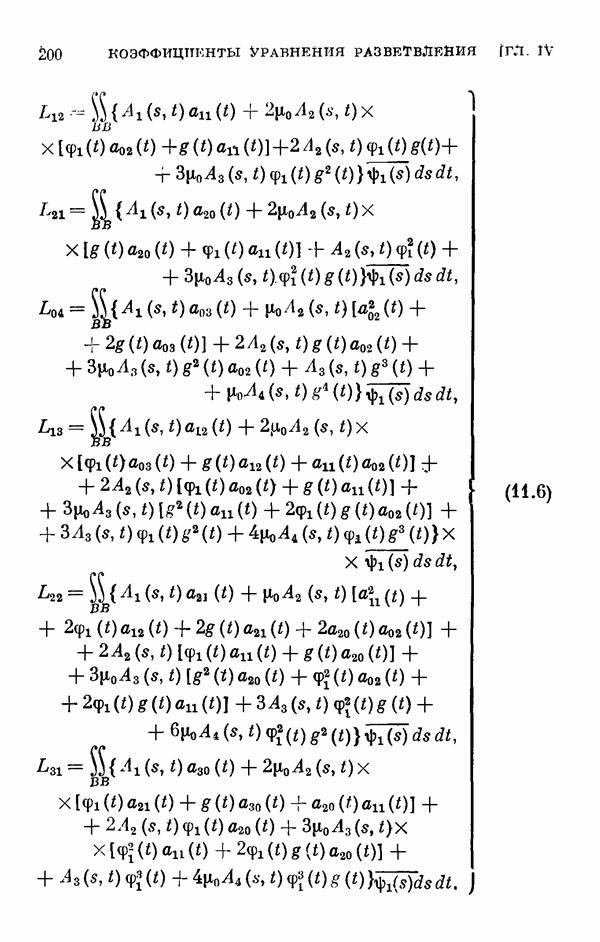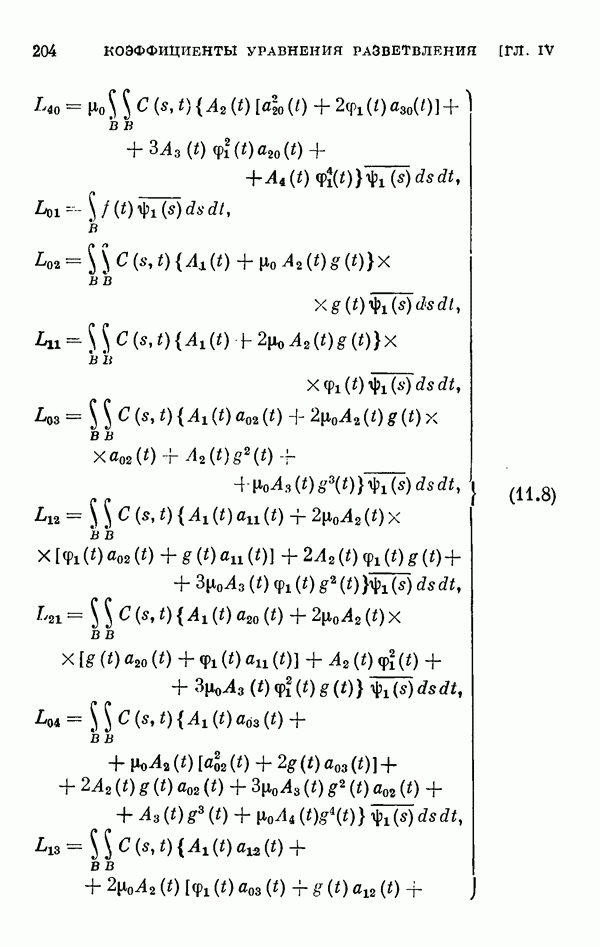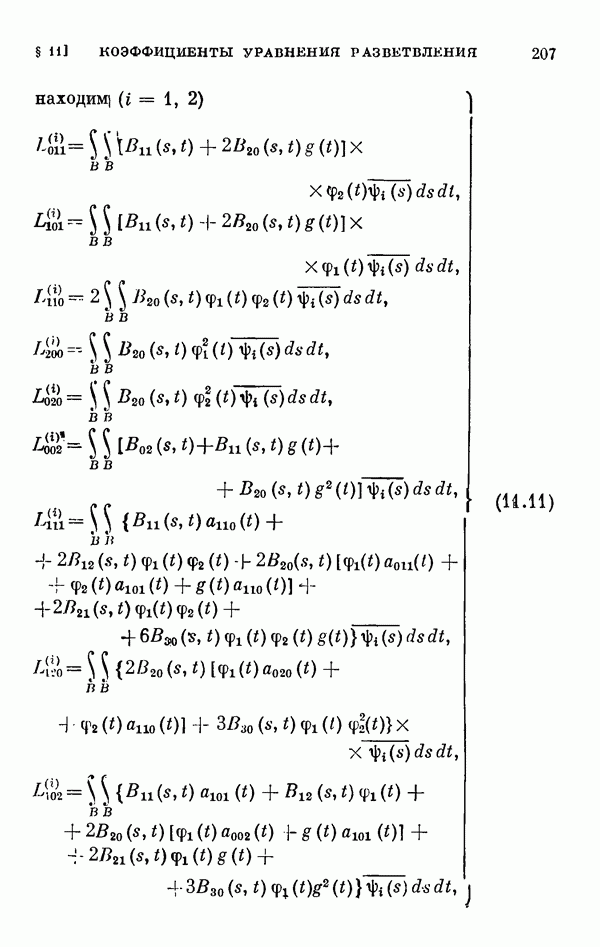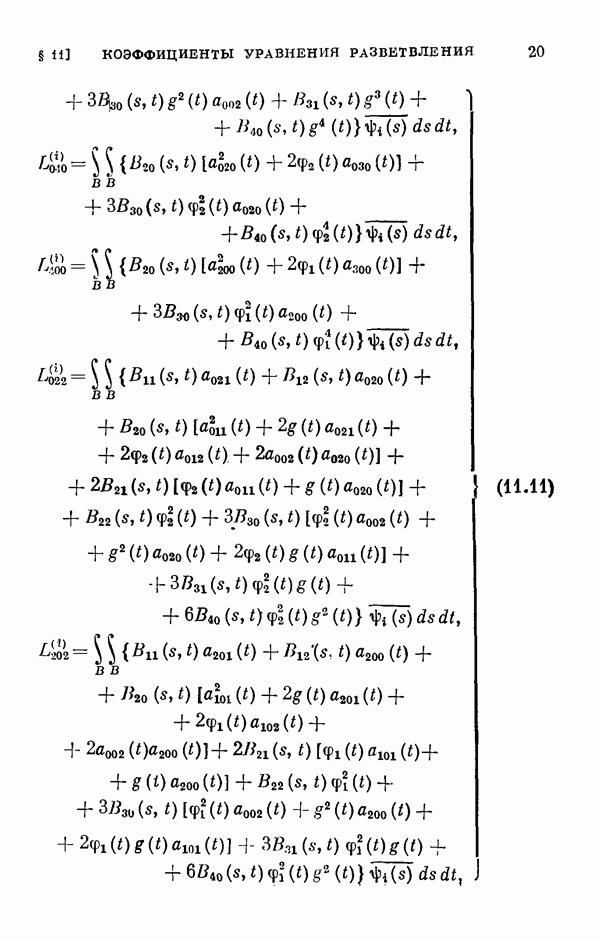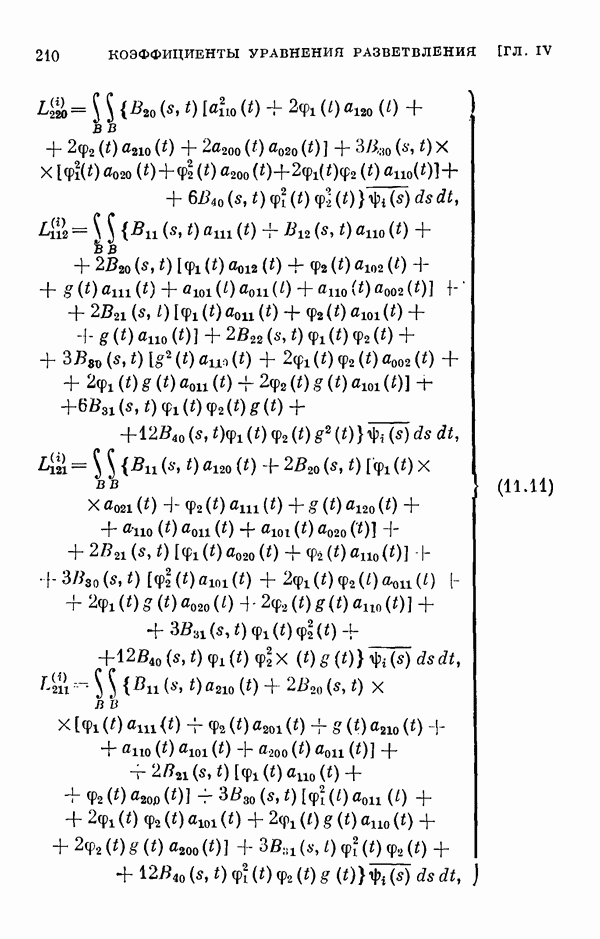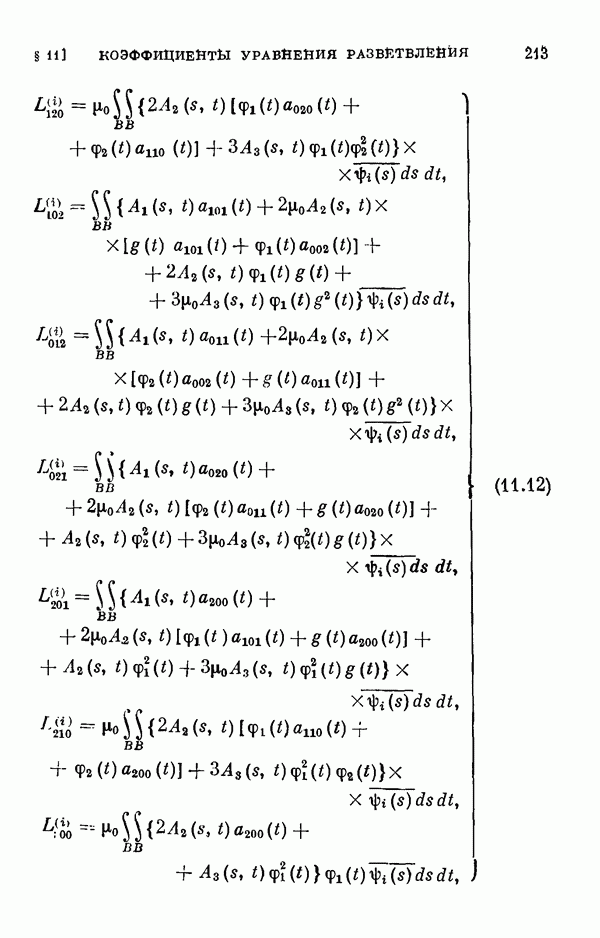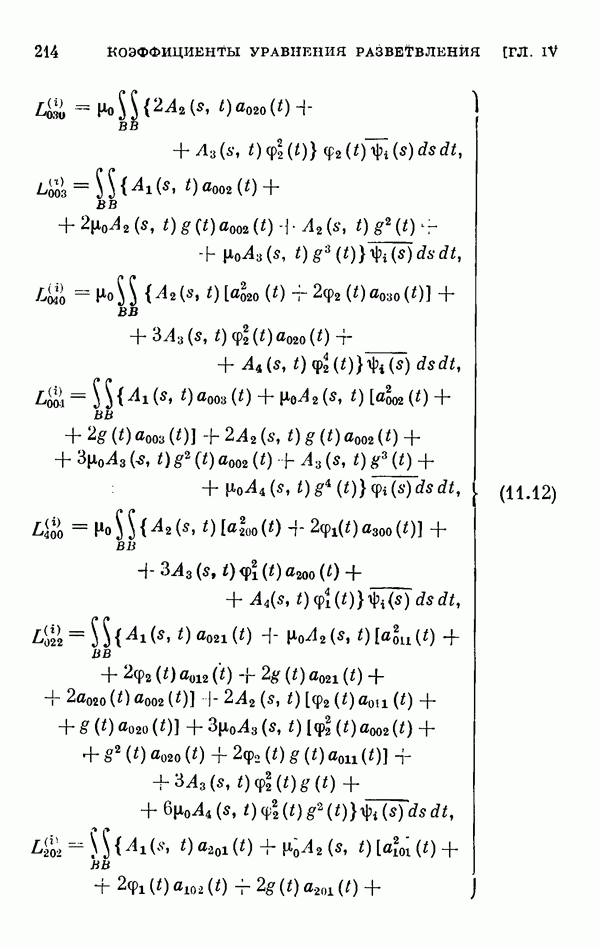| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
20.2. Устойчивость решений задачи Пуанкаре.
Рассмотрим теперь случай, когда дифференциальное уравнение зависит от малого вещественного числового параметра X. Пусть

есть уравнение, рассмотренное в § 16, причем для удобства предполагается также, что коэффициенты рядов  суть вещественные функции аргумента
суть вещественные функции аргумента 
Выберем одно из  -периодических решений
-периодических решений  задачи Пуанкаре для уравнения (20.4) и для малых значений
задачи Пуанкаре для уравнения (20.4) и для малых значений  исследуем его устойчивость.
исследуем его устойчивость.
Допустим, что компоненты вектора  вещественны и имеют вид
вещественны и имеют вид

где  — натуральное число), причем имеется в виду арифметическое значение корня
— натуральное число), причем имеется в виду арифметическое значение корня  , и
, и  -периодическое решение порождающего уравнения
-периодическое решение порождающего уравнения

Отметим, что если для уравнения (20.4) имеет место квазирегулярный случай (см. § 16), то число всех решений задачи Пуанкаре конечно и каждое из них представляется в виде (20.5).
Полагая в  , сведем поставленную задачу к задаче об устойчивости тривиального решения
, сведем поставленную задачу к задаче об устойчивости тривиального решения  уравнения
уравнения

где

и

Исследуем по первому приближению устойчивость тривиального решения уравнения (20.7). С этой целью построим сначала матрицу монодромии линейного уравнения

соответствующего уравнению (20.7). Для построения матрицы монодромии  уравнения (20.8) достаточно (см., например, И. Г. Малкин
уравнения (20.8) достаточно (см., например, И. Г. Малкин  решить начальную задачу (20.9) — (20.10):
решить начальную задачу (20.9) — (20.10):

и в полученном решении  (оно будет единственным и аналитическим по
(оно будет единственным и аналитическим по  ) положить
) положить  .
.
Решение  задачи (20.9) -(20.10) будем искать в виде матричного ряда
задачи (20.9) -(20.10) будем искать в виде матричного ряда

Коэффициенты ряда (20.11) определяются подстановкой (20.11) в (20.9) и решением получающейся рекуррентной системы уравнений при следующих начальных условиях (согласованных с  — нулевая матрица,
— нулевая матрица, 
Имеем

Решение задачи (20.12) — (20.10) принимает вид 

Таким образом, матрица монодромии уравнения (20.8) представляется в виде ряда

где

Обозначим через  мультипликаторы уравнения (20.8) и отметим следующие их два свойства.
мультипликаторы уравнения (20.8) и отметим следующие их два свойства.
Теорема 20.3. Все мультипликаторы  уравнения (20.8) суть непрерывные функции в некоторой полуокрестности справа
уравнения (20.8) суть непрерывные функции в некоторой полуокрестности справа  точки
точки 
Действительно, это утверждение непосредственно следует из того, что все элементы матрицы монодромии  уравнения (20.8) являются непрерывными функциями и старший коэффициент характеристического уравнения
уравнения (20.8) являются непрерывными функциями и старший коэффициент характеристического уравнения

не зависит от 
Теорема 20.4. Справедливы соотношения

где  суть собственные значения матрицы А-Действительно, так как
суть собственные значения матрицы А-Действительно, так как  — собственные значения матрицы А, то (см., например, Ф. Р. Гантмахер [1]) — собственные значения матрицы
— собственные значения матрицы А, то (см., например, Ф. Р. Гантмахер [1]) — собственные значения матрицы  Поэтому в силу соотношений (20.13), (20.14) и теоремы 20.3 приходим к (20.15). Из теорем 20.3 и 20.4 вытекает
Поэтому в силу соотношений (20.13), (20.14) и теоремы 20.3 приходим к (20.15). Из теорем 20.3 и 20.4 вытекает
Следствие 20.1. Все мультипликаторы уравнения (20.8) представляются в виде

где  определяются
определяются  формулам (20.15), а добавки
формулам (20.15), а добавки  непрерывны в некоторой полуокрестности справа точки
непрерывны в некоторой полуокрестности справа точки  и удовлетворяют условиям
и удовлетворяют условиям

Учитывая следствие 20.1, приходим к следующему выводу:
Если для некоторого собственного значения у матрицы  (соответственно
(соответственно  ), то отвечающий этому собственному значению мультипликатор
), то отвечающий этому собственному значению мультипликатор  уравнения (20.8) удовлетворяет (в некоторой полуокрестности справа точки
уравнения (20.8) удовлетворяет (в некоторой полуокрестности справа точки  неравенству
неравенству  (соответственно
(соответственно 
Отсюда на основании теоремы 20.2, в частности, следует, что если хотя бы одно собственное значение матрицы А имеет положительную вещественную часть, то для малых  тривиальное решение уравнения (20.7) неустойчиво.
тривиальное решение уравнения (20.7) неустойчиво.
Ввиду этого в дальнейшем будем предполагать, что собственные значения матрицы А удовлетворяют неравенствам  причем подлежат исследованию лишь добавки а
причем подлежат исследованию лишь добавки а  к тем
к тем  которые отвечают критическим собственным значениям
которые отвечают критическим собственным значениям  (т. е. нулевым и чисто мнимым). Для определения указанных добавок составим уравнение (см. также п.п. 32.1 и 32.2)
(т. е. нулевым и чисто мнимым). Для определения указанных добавок составим уравнение (см. также п.п. 32.1 и 32.2)

где

 — вектор-столбец
— вектор-столбец  -мерного евклидова пространства
-мерного евклидова пространства 
Исследуем сначала добавки а к тем  которые отвечают резонансным критическим собственным значениям
которые отвечают резонансным критическим собственным значениям  матрицы А, т. е. собственным значениям вида
матрицы А, т. е. собственным значениям вида

где  — натуральные числа.
— натуральные числа.
В силу (20.15) всей совокупности (20.20) отвечает лишь единственное собственное значение  матрицы
матрицы 
Обозначим через I кратность собственного значения  матрицы
матрицы  и через
и через  — размерность подпространства решений уравнения
— размерность подпространства решений уравнения  где
где  Как известно (см., например, А. И. Мальцев [1]), число
Как известно (см., например, А. И. Мальцев [1]), число  равно дефекту матрицы С.
равно дефекту матрицы С.
Для сравнения чисел  приведем следующий подсчет.
приведем следующий подсчет.
Обозначим через  число всех элементарных делителей матрицы А, отвечающих собственному значению
число всех элементарных делителей матрицы А, отвечающих собственному значению  и
и  — число всех элементарных делителей этой матрицы, отвечающих каждому собственному значению из пары
— число всех элементарных делителей этой матрицы, отвечающих каждому собственному значению из пары  Тогда согласно теоремам 9 и 8 главы VI
Тогда согласно теоремам 9 и 8 главы VI
монографии Ф. Р. Гантмахера [1] имеем

С другой стороны, согласно указанной теореме 9 и теореме Жордана число I равно сумме показателей всех упомянутых выше элементарных делителей матрицы А. Отсюда следует что

причем соотношение (20.21) переходит в равенство лишь в случае, когда все указанные элементарные делители простые.
Отметим также, что рассматриваемый в настоящем параграфе подход не связан с какими-либо априорными ограничениями на числа  и I.
и I.
Обозначим соответственно через

и

ортонормированные базисы подпространств решений уравнений  где С — матрица, сопряженная с С. В рассматриваемом случае С — матрица, транспонированная по отношению к С, ибо С — вещественная матрица.
где С — матрица, сопряженная с С. В рассматриваемом случае С — матрица, транспонированная по отношению к С, ибо С — вещественная матрица.
Введем в рассмотрение матрицу

и обозначим через скалярные произведения

Используя обозначения (20.22) и (20.23), перепишем уравнение (20.18) в виде

где

Покажем, что матрица  обратима. Для этого, как известно, достаточно установить, что уравнение
обратима. Для этого, как известно, достаточно установить, что уравнение

имеет единственное нулевое решение 
Пусть  — любое решение этого уравнения. Тогда в силу (20.24) выполняется соотношение
— любое решение этого уравнения. Тогда в силу (20.24) выполняется соотношение

которое после скалярного умножения обеих частей на  принимает вид
принимает вид

Упростим соотношения (20.25).
Так как 

Учитывая, далее, обозначение (20.22) и используя ортинормированность системы векторов  имеем
имеем

Таким образом, в силу (20.26) и (20.27) соотношения (20.25) принимают вид

т. е. вектор  ортогонален ко всем векторам базиса
ортогонален ко всем векторам базиса  подпространства решений уравнения
подпространства решений уравнения  принадлежит этому подпространству. Поэтому он равен нулю.
принадлежит этому подпространству. Поэтому он равен нулю.
Умножая теперь слева обе части уравнения (20.18) на матрицу  получаем
получаем

Преобразуем последние  слагаемых уравнения (20.28). Для этого покажем сначала, что
слагаемых уравнения (20.28). Для этого покажем сначала, что

Действительно, используя соотношения

и

и учитывая (20.24) и (20.22), имеем

Умножая теперь слева обе части полученных равенств  на матрицу
на матрицу  приходим к соотношениям (20.29). Итак, в силу (20.29) уравнение (20.28) принимает вид
приходим к соотношениям (20.29). Итак, в силу (20.29) уравнение (20.28) принимает вид

Отметим, что матрица Якоби уравнения (20.30) при  является единичной матрицей и, следовательно, для этого уравнения применима теорема о неявных функциях. Так как, кроме этого, правая часть (20.30) зависит аналитически от
является единичной матрицей и, следовательно, для этого уравнения применима теорема о неявных функциях. Так как, кроме этого, правая часть (20.30) зависит аналитически от  (причем от
(причем от  и
и  линейно), то уравнение (20.30) имеет единственное локальное решение
линейно), то уравнение (20.30) имеет единственное локальное решение

Коэффициенты ряда (20.31) последовательно определяются подстановкой (20.31) в (20.30) и сравнением коэффициентов в обеих частях получаемых тождеств при одинаковых одночленах относительно 
Подставляя ряд (20.31) в условия разрешимости уравнения (20.18):

приходим к однородному линейному уравнению отнеся тельно 1:

где через 1 обозначен вектор-столбец 
Отметим (см. (20.23)), что  является собственным значением матрицы монодромии тогда и только тогда, когда уравнение
является собственным значением матрицы монодромии тогда и только тогда, когда уравнение  допускает ненулевое решение
допускает ненулевое решение  т. е. лишь при условии, что
т. е. лишь при условии, что

Уравнение (20.32) можно представить в виде

причем

где I — кратность собственного значения матрицы 
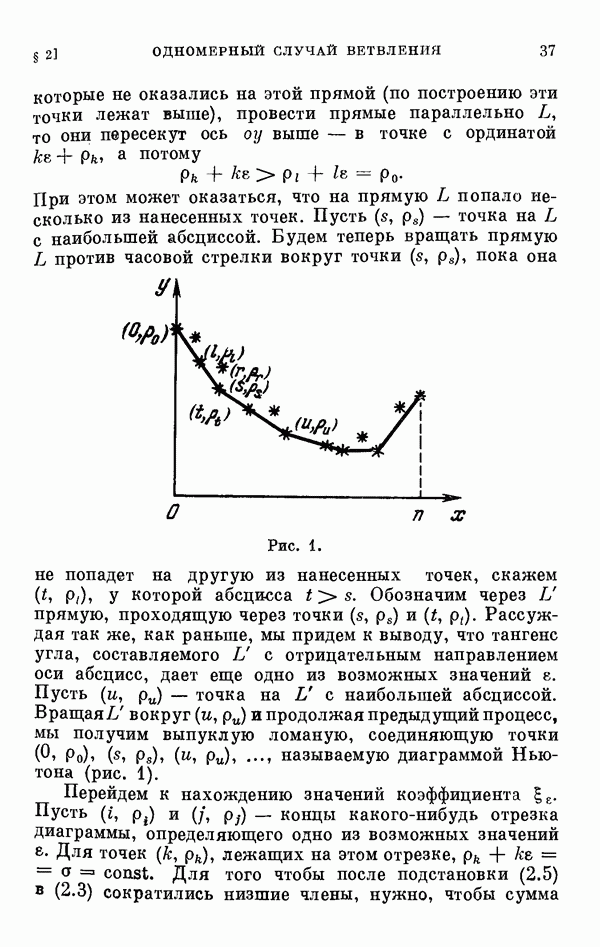
Для нахождения всех малых решений  уравнения (20.32) применим метод диаграммы Ньютона (см. § 2). Так как
уравнения (20.32) применим метод диаграммы Ньютона (см. § 2). Так как  то все нетривиальные малые решения этого уравнения представляются сходящимися рядами
то все нетривиальные малые решения этого уравнения представляются сходящимися рядами

где  — тангенс угла между соответствующим звеном диаграммы Ньютона и отрицательным направлением оси
— тангенс угла между соответствующим звеном диаграммы Ньютона и отрицательным направлением оси
абсцисс,  корень определяющего уравнения (см.п. 2.4) для этого звена:
корень определяющего уравнения (см.п. 2.4) для этого звена:

при этом (см. § 2) все коэффициенты уравнения (20.35) отличны от нуля и индексы к и  удовлетворяют соотношениям
удовлетворяют соотношениям

Для дальнейшего преобразуем определяющее уравнение (20.35). С этой целью предварительно перепишем соот ношения (20.37) в виде

откуда следует

и так как  имеем
имеем

т. е.

где  — натуральные числа, удовлетворяющие в силу (20.36) неравенствам
— натуральные числа, удовлетворяющие в силу (20.36) неравенствам 
Таким образом, определяющее уравнение (20.35) можно записать в виде

Запись определяющего уравнения в виде (20.35) делает совершенно прозрачными следующие два предложения.
Лемма 20.1. Если  — корень определяющего уравнения (20.35), то
— корень определяющего уравнения (20.35), то  где
где  — любой корень степени
— любой корень степени  из 1, также является корнем уравнения (20.35). Доказательство очевидно.
из 1, также является корнем уравнения (20.35). Доказательство очевидно.
Лемма 20.2. Пусть  Тогда, если уравнение (20.35) имеет корень с отрицательной вещественной частью, то оно обладает также корнем, у которого вещественная часть неотрицательна.
Тогда, если уравнение (20.35) имеет корень с отрицательной вещественной частью, то оно обладает также корнем, у которого вещественная часть неотрицательна.
Доказательство. Для  лемма очевидна. Действительно, если в этом случае число с
лемма очевидна. Действительно, если в этом случае число с  является корнем уравнения (20.35), то
является корнем уравнения (20.35), то  также является корнем этого уравнения.
также является корнем этого уравнения.
Пусть  Тогда существуют по крайней мере два корня степени
Тогда существуют по крайней мере два корня степени  из единицы
из единицы

такие, что 
Допустим, что  является корнем уравнения (20.35). Тогда по лемме 20.1 величины и
является корнем уравнения (20.35). Тогда по лемме 20.1 величины и  также служат корнями уравнения (20.35), причем, очевидно, хотя бы один из этих корней имеет неотрицательную вещественную часть. Лемма доказана.
также служат корнями уравнения (20.35), причем, очевидно, хотя бы один из этих корней имеет неотрицательную вещественную часть. Лемма доказана.
Наряду с мультипликатором

(см. (20.16) и (20.34), рассмотрим также его приближенное значение

Из (20.38) и (20.39) следует
Лемма 20.3. Для малых выражения  одновременно больше или меньше единицы.
одновременно больше или меньше единицы.
Отметим также, что в силу леммы 20.1 при нахождении приближенных значений  всех мультипликаторов
всех мультипликаторов  достаточно ограничиться лишь арифметическим значением корня
достаточно ограничиться лишь арифметическим значением корня 
С помощью лемм  и равенства (20.39) мы приходим к различным предложениям об устойчивости тривиального решения, из которых приведем следующие.
и равенства (20.39) мы приходим к различным предложениям об устойчивости тривиального решения, из которых приведем следующие.
Теорема 20.5. Если в резонансном случае хотя бы один корень определяющего уравнения какого-либо звена диаграммы Ньютона имеет неотрицательную вещественную часть, то для малых 0 тривиальное решение уравнения (20.7) неустойчиво.
Доказательство. Пусть С — корень с неотрицательной вещественной частью одного из определяющих
уравнений. Обозначим через  мультипликатор, отвечающий этому корню:
мультипликатор, отвечающий этому корню:

и запишем также его приближенное значение

Так как 

Отсюда согласно лемме 20.3 для малых  выполняется неравенство
выполняется неравенство

Для завершения доказательства остается лишь сослаться на теорему 20.2.
В приложениях удобна также следующая
Теорема 20.6. Если в резонансном случае хотя бы для одного звена диаграммы Ньютона число  то для малых
то для малых  тривиальное решение уравнения (20.7) неустойчиво.
тривиальное решение уравнения (20.7) неустойчиво.
Доказательство непосредственно вытекает из леммы 20.2. и теоремы 20.5.
Из теоремы 20.6, в частности, следует, что для асимптотической устойчивости тривиального решения уравнения (20.7) необходимо, чтобы числа  для всех звеньев диаграммы Ньютона равнялись единице.
для всех звеньев диаграммы Ньютона равнялись единице.
Приведем также один достаточный признак асимптотической устойчивости.
Выделим класс  дифференциальных уравнений (20.7), для которых собственные значения у матрицы А обладают неположительными вещественными частями, причем те у, для которых
дифференциальных уравнений (20.7), для которых собственные значения у матрицы А обладают неположительными вещественными частями, причем те у, для которых  являются резонансными и составленное для них уравнение (20.32) не имеет нулевых решений о
являются резонансными и составленное для них уравнение (20.32) не имеет нулевых решений о 
Теорема 20.7. Для асимптотической устойчивости тривиального решения уравнения (20.7), принадлежащего
к классу  достаточно, чтобы корни всех определяющих уравнений диаграммы Ньютона, построенной для (20.32), имели отрицательные вещественные части. Доказательство следует из леммы 20.3 и теоремы 20.1. Исследование устойчивости тривиального решения уравнения (20.7) в случае, когда матрица .4 имеет нерезонансные критические собственные значения у, не приводит к дополнительным трудностям.
достаточно, чтобы корни всех определяющих уравнений диаграммы Ньютона, построенной для (20.32), имели отрицательные вещественные части. Доказательство следует из леммы 20.3 и теоремы 20.1. Исследование устойчивости тривиального решения уравнения (20.7) в случае, когда матрица .4 имеет нерезонансные критические собственные значения у, не приводит к дополнительным трудностям.
Так же, как и в случае резонансных собственных значений, для определения добавок а приходим к уравнению вида (20.32), которое исследуется с помощью диаграммы Ньютона. На основании леммы 20.3 при малых  для оценки модуля мультипликатора
для оценки модуля мультипликатора

 — корень определяющего уравнения) можно ограничиться его приближенным значением
— корень определяющего уравнения) можно ограничиться его приближенным значением

При этом оказывается полезным следующее
Замечание 20.2. Неравенства  принимают соответственно вид
принимают соответственно вид

и

где

Так как  то для малых и при
то для малых и при  неравенства (20.40) и (20.41) равносильны соответственно неравенствам
неравенства (20.40) и (20.41) равносильны соответственно неравенствам

и

С помощью неравенств (20.40) и (20.41) или (20.42) и (20.43) устанавливаются различные признаки как неустойчивости, так и асимптотической устойчивости.
В заключение отметим, что изложенный в настоящем параграфе подход к задаче об устойчивости тривиального решения уравнения (20.7) целесообразно применять в случае, когда матрица А имеет резонансные собственные значения с непростыми элементарными делителями. Если  — непрерывная и
— непрерывная и  -периодическая матрица, то предложенный метод также применим. При этом он легко реализуется, когда уравнение
-периодическая матрица, то предложенный метод также применим. При этом он легко реализуется, когда уравнение

интегрируется в замкнутой форме.
Отметим еще, что результаты данного параграфа распространяются на дифференциально-разностные системы, но процедура вывода уравнения (20.32) иная.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА I. Системы неявных функций и классическая теория ветвления
- § 1. Задача о неявных функциях
- 1.2. Общее исследование задачи о неявных функциях.
- 1.3. Аналитический случай.
- § 2. Одномерный сличай ветвления и диаграмма Ньютона
- 2.2. О свойствах решений.
- 2.3. Примеры.
- 2.4. Исследование уравнения разветвления. Случай простых корней определяющего уравнения.
- 2.5. Случай кратных корней определяющего уравнения.
- 2.6. О вещественных решениях.
- 2.7. Некоторые частные случаи расположения диаграммы Ньютона.
- ГЛАВА II. Исследование уравнения разветвления в многомерном случае
- 3.2. Приведение к нормальному виду.
- § 4. Некоторые вопросы теории делимости
- 4.2. Общий делитель и аналог алгоритма Евклида.
- 4.3. Примитивный ОНД.
- 4.4. Применение к отмеченным многочленам.
- § 5. Двумерный случай ветвления
- 5.2. Указатели двумерного случая ветвления.
- 5.3. Частные случаи.
- § 6. Многомерный случай ветвления
- 6.2. Малые решения уравнения разветвления и метод исключения неизвестных.
- 6.3. Квазирегулярный случай ветвления.
- 6.4. Вырожденный случай ветвления.
- 6.5. Об изолированности нулевого решения.
- ГЛАВА III. Уравнение разветвления для нелинейных интегральных и интегро-дифференциальных уравнений
- § 7. Интегральные уравнения Ляпунова — Шмидта
- 7.2. Интегро-степенные ряды от многих функциональных аргументов.
- 7.3. Интегро-степенные ряды от интегро-степенных рядов.
- 7.4. Сжатость оператора Ляпунова—Шмидта.
- 7.5. Простейшее уравнение.
- 7.6. Последовательные приближения Лихтенштейна.
- 7.7. Применение метода мажорант.
- 7.8. Простейшее уравнение в случае равномерной сходимости.
- § 8. Общее интегральное уравнение Ляпунова—Шмидта
- 8.2. Регулярный случай при наличии многих аргументов.
- 8.3. Лемма Шмидта.
- 8.4. Одномерный случай ветвления.
- 8.5. Многомерный случай ветвления.
- 8.6. Возможные обобщения.
- § 9. Системы уравнений Ляпунова—Шмидта и некоторые интегро-дифференциальные уравнения
- 9.2. Регулярный случай.
- 9.3. Случай ветвления.
- 9.4. Некоторые нелинейные интегро-дифференциальные уравнения первого порядка.
- 9.5. Другие виды интегро-дифференциальных уравнений.
- 9.6. Другой способ построения уравнения разветвления
- ГЛАВА IV. Общее интегральное уравнение и коэффициенты уравнения разветвления
- 10.2. Регулярный случай.
- 10.3. Одномерный случай ветвления.
- 10.4. Многомерный случай ветвления.
- 10.5 Частный случай.
- 10.6. Уравнение Гаммерштейна.
- § 11. Коэффициенты уравнения разветвления
- 11.2. Коэффициенты одиомерного уравнения разветвления нелинейного интегрального уравнения Гаммерштейна.
- 11.3. Коэффициенты двумерного уравнения разветвления общего нелинейного интегрального уравнения.
- 11.4. Коэффициенты двумерного уравнения разветвления для частных случаев.
- 11.5. Некоторые свойства коэффициентов уравнения разветвления.
- ГЛАВА V. Описание и построение решений нелинейных интегральных уравнений
- § 12. Описание решений нелинейных интегральных уравнений
- 12.2. Описание решении в одномерном случае ветвления.
- 12.3. О точках бифуркации в одномерном случае ветвления.
- 12.4. Описание решений в двумерном случае ветвления.
- 12.5. Описание решений в многомерном случае ветвления.
- 12.6. О ветвлении изолированного решения.
- 12.7. Точки бифуркации в многомерном случае ветвления.
- § 13. Построение решений нелинейных интегральных уравнений
- 13.3. Двумерный случай ветвления.
- 13.4. Уравнение Некрасова.
- 13.5. Уравнение разветвления для уравнения Некрасова.
- § 14. Особые решения нелинейных интегральных уравнений
- 14.2. Сведение к малым решениям.
- 14.3. Особые решения в регулярном случае.
- 14.4. Исследование вспомогательного уравнения.
- 14.5. Ветвление решений основного уравнения.
- 14.6 Особые решения в пространствах Лебега.
- ГЛАВА VI. Ветвление периодических решений дифференциальных уравнений
- § 15. Периодические решения неавтономных систем
- 15.2. Метод Пуанкаре.
- 15.3. Условия периодичности и уравненне разветвления.
- 15.4. Описание решений в регулярном случае.
- 15.5. Описание решений в одномерном случае ветвления.
- 15.6. Описание решений в многомерном случае ветвления.
- § 16. Периодические решения квазилинейных систем
- 16.2. Условия периодичности.
- 16.3. Вывод уравнения разветвления.
- 16.4. Описание решений и дополнительные замечания.
- § 17. Периодические решения автономных систем
- 17.2. Уравнение разветвления.
- 17.3. Основные выводы.
- 17.4. Метод неопределенных коэффициентов.
- 17.5. Автономные системы с одной степенью свободы.
- § 18. Примеры
- 18.1. Неавтономные системы с одной степенью свободы.
- 18.2 Автономные системы с одной степенью свободы.
- § 19. Другие задачи о периодических решениях
- 19.1. Особые периодические решения неавтономных систем.
- 19.2. Ветвление периодических решений в банаховых пространствах
- § 20. Об устойчивости периодических решений, зависящих от малого параметра
- 20.2. Устойчивость решений задачи Пуанкаре.
- ГЛАВА VII. Нелинейные уравнения в банаховых пространствах
- § 21. Некоторые вопросы теории линейных операторов в банаховых пространствах
- 21.2. Специальные разложения пространств в прямые суммы подпространств.
- 21.3. Сужение оператора и обобщенная лемма Шмидта.
- 21.4 Связь с сопряженным оператором.
- 21.5. Неограниченные фредгольмовские операторы.
- § 22. Степенные операторы, ряды Тейлора, теоремы о неявных операторах
- 22.2 Степенные ряды. Ряды Тейлора.
- 22.3 Теоремы о неявных операторах.
- § 23. Уравнение разветвления Ляпунова — Шмидта
- 23.2. Вывод уравнения разветвления с помощью сужения оператора B.
- 23.3. Вывод уравнения разветвления с помощью леммы Шмидта.
- 23.4. Основная теорема об уравнении разветвления.
- 23.5. Уравление разветвления в аналитическом случае.
- 23.6. Уравнение разветвления для неограниченных операторов.
- § 24. Исследование одномерного случая ветвления
- 24.2. Вырожденный случай.
- 24.3. Квазирегулярный случай (задача А).
- 24.4. Задача Б (невырожденный случай).
- 24.5 Вещественный случай.
- 24.6. О ветвлении решений уравнений о достаточно гладкими операторами.
- 24.7 Случай функционального параметра. Ряды по однородным операторам.
- 24.8. Случай двух числовых параметров.
- § 25. Многомерный случай ветвления
- 25.2. Коэффициенты двумерного уравнения разветвления.
- 25.3. Двумерный случай ветвления.
- 25.4 Общий случай.
- 25.5. О ветвлении изолированного решения.
- 25.6. О точках бифуркации.
- ГЛАВА VIII. Ветвление решений нелинейных уравнений в сингулярном случае
- 26.2. Разложение пространств в прямые суммы подпространств.
- 26.3. Теорема Аткинсона.
- 23.4. О нетеровских неограниченных операторах.
- § 27. Теоремы о ветвлении решений
- 27.2. Случай n > 0, m = 0.
- 27.3. Случай n = 0, m > 0.
- 27.4. Основной случай. Уравнение разветвления.
- 27.5. О ветвлении решений уравнения с неограниченным оператором.
- § 28. Ветвление решений нелинейных сингулярных интегральных уравнений.
- 28.2. Нелинейные сингулярные интегральные уравнения с ядром типа Коши в пространствах Гёльдера.
- 28.3. Аналитический случай.
- 28.4. Нелинейные сингулярные интегральные уравнения с ядром Гильберта в пространствах Лебега.
- § 29. Ветвление решений краевых задач для нелинейных эллиптических уравнений
- 29.2. Краевые задачи на плоскости для эллиптических систем k-го порядка в пространстве Гёльдера.
- 29.3. Краевые задачи для эллиптических уравнений в пространстве суммируемых функций.
- ГЛАВА IX. Некоторые задачи теории вовмущений
- § 30. Жордановы цепочки и наборы фредгольмовских операторов
- 30.2. А-жордановы цепочки и наборы при n > 1.
- 30.3. Условия полноты А-жорданова набора.
- 30.4. Пример.
- § 31. Возмущение линейного уравнения малым линейным слагаемым
- 31.2. Случай n > 1.
- 31.3. Метод неопределенных коэффициентов.
- § 32. Ветвление собственных значений и собственных элементов фредгольмовских операторов
- 32.2. Уравнение разветвления в аналитическом случае.
- 32.3. Вырожденный и невырожденный случаи.
- 32.4. Одномерный случай.
- 32.5. Метод неопределенных коэффициентов.
- 32.6. Многомерный случай.
- 32.7. Некоторые обобщения.
- § 33. Особые решения нелинейных уравнений
- 33.2. Задача о возмущении линейного уравнения малым нелинейным слагаемым.
- 33.3. Понятие обобщенной жордановой цепочки.
- 33.4. Свойства некоторых многочленов.
- 33.5 Основной случай задачи о возмущении.
- 33.6. Случаи возмущения второго порядка.
- 33.7. Решения порядка …
- ГЛАВА X. Некоторые прикладные задачи
- § 34. О малых изгибах прямолинейного стержня под действием постоянной нагрузки
- § 35. К теории малых прогибов гибких пластин
- 35.2. Случай круглой пластины.
- 35.3. Исследование уравнения разветвления.
- 35.4. Круглая пластина с нулевой внешней нагрузкой.
- § 36. О колебаниях спутника в плоскости эллиптической орбиты
- § 37. Об одном виде установившихся волн
- 37.2. Сведение к системе.
- 37.3. Регулярный случай.
- 37.4. Случай ветвления.
- Литература