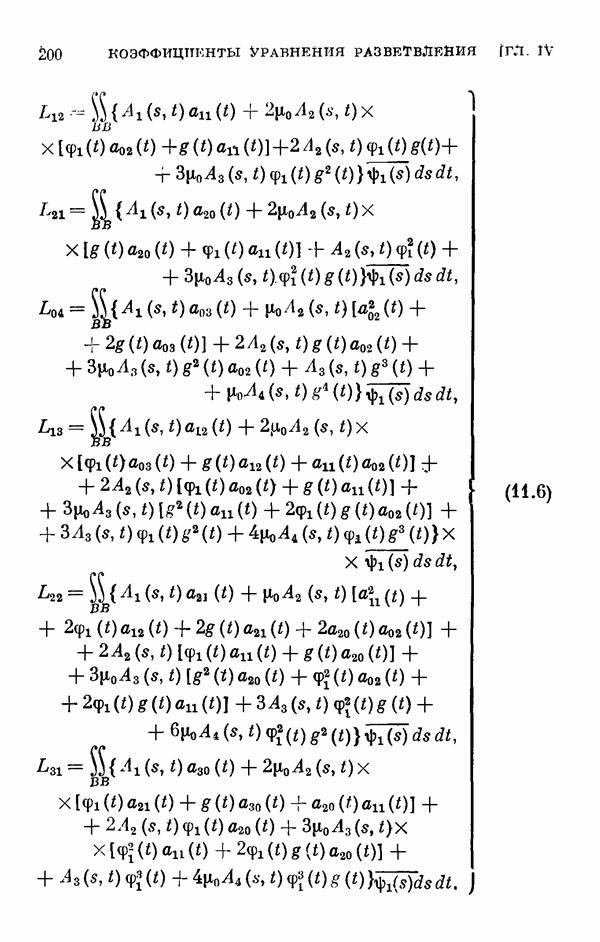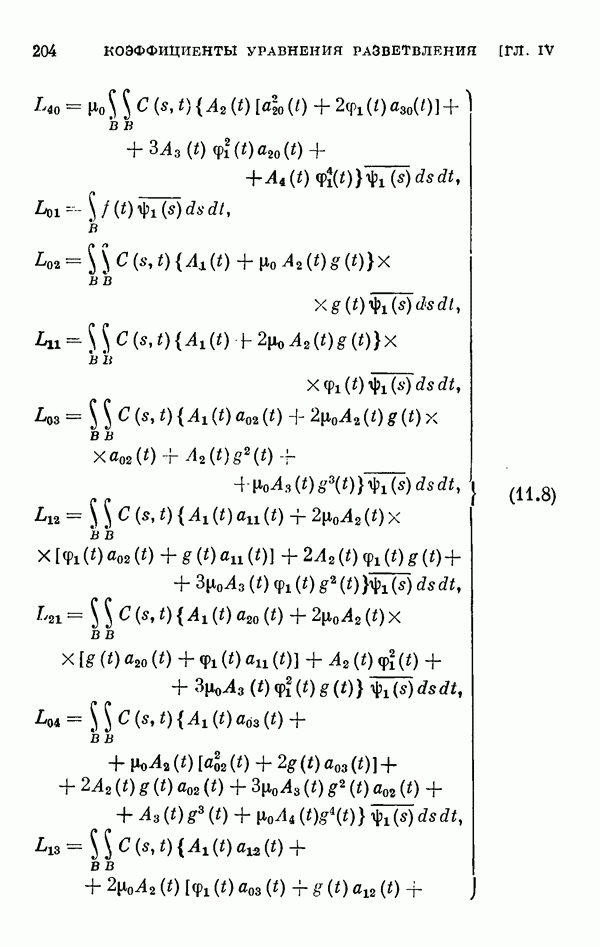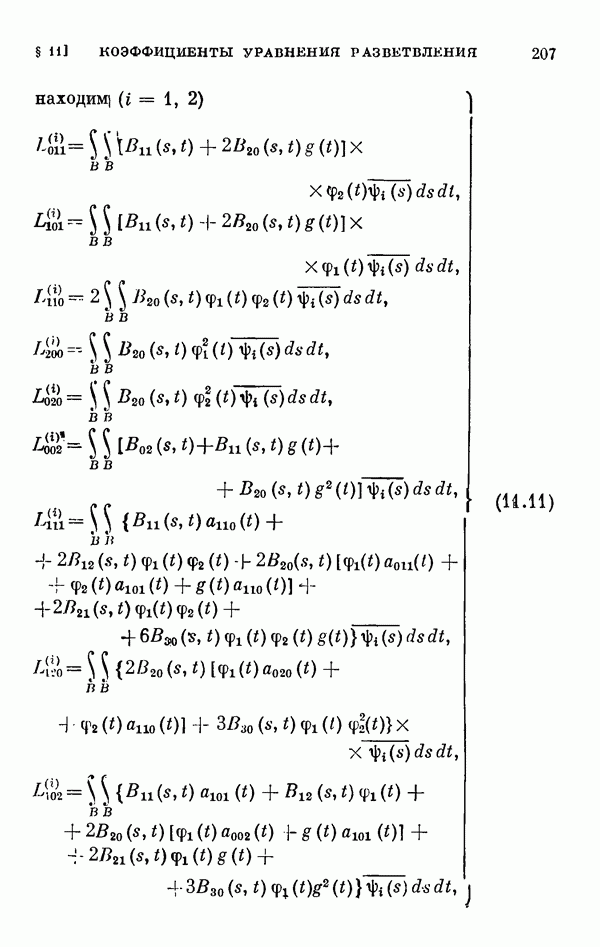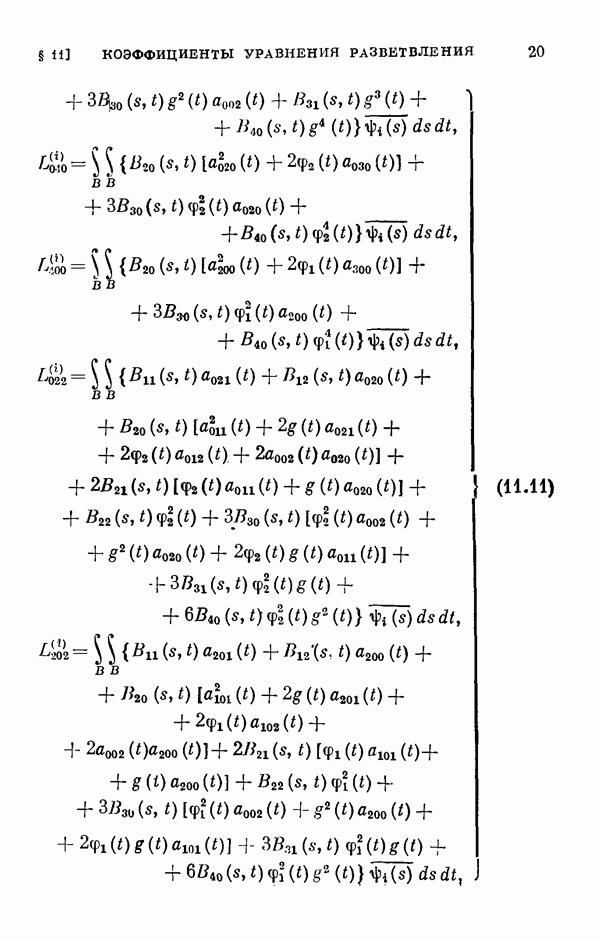| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
29.3. Краевые задачи для эллиптических уравнений в пространстве суммируемых функций.
Пусть  — ограниченная область в евклидовом пространстве
— ограниченная область в евклидовом пространстве  с бесконечно дифференцируемой границей Г (класса
с бесконечно дифференцируемой границей Г (класса  Рассмотрим дифференциальное выражение
Рассмотрим дифференциальное выражение

где  — мультииндекс, т. е. последовательность индексов
— мультииндекс, т. е. последовательность индексов 

а функции  бесконечно дифференцируемы в
бесконечно дифференцируемы в 
Дифференциальное выражение  называется эллиптическим в
называется эллиптическим в  если его характеристический полином
если его характеристический полином

всюду в  отличен от нуля при любом вещественном
отличен от нуля при любом вещественном
векторе  отличном от нуля. Под
отличном от нуля. Под  понимается выражение
понимается выражение 
Дифференциальное выражение  называется сильно эллиптическим (М. И. Вишик [1]), если существует комплексная функция
называется сильно эллиптическим (М. И. Вишик [1]), если существует комплексная функция  непрерывная в
непрерывная в  и такая, что полином
и такая, что полином  при
при  и любом вещественном векторе
и любом вещественном векторе  .
.
Наконец, эллиптическое в  дифференциальное выражение
дифференциальное выражение  назовем правильно эллиптическим в
назовем правильно эллиптическим в  если для каждого вещественного вектора
если для каждого вещественного вектора  , параллельного Г в точке х, и каждого вещественного вектора
, параллельного Г в точке х, и каждого вещественного вектора  , нормального к Г в х, полином от
, нормального к Г в х, полином от  имеет ровно
имеет ровно  корней
корней  с положительными мнимыми частями (остальные
с положительными мнимыми частями (остальные  корней вследствие эллиптичности имеют отрицательные мнимые части).
корней вследствие эллиптичности имеют отрицательные мнимые части).
Всякий эллиптический оператор в  при
при  правильно эллиптичен (Я. Б. Лопатинский [1]). Наряду с дифференциальным выражением (29.12) рассмотрим также граничные дифференциальные выражения
правильно эллиптичен (Я. Б. Лопатинский [1]). Наряду с дифференциальным выражением (29.12) рассмотрим также граничные дифференциальные выражения

где  коэффициенты
коэффициенты  бесконечно дифференцируемы на Г. (Естественно, можно ослабить ограничения на гладкость границы Г и коэффициентов
бесконечно дифференцируемы на Г. (Естественно, можно ослабить ограничения на гладкость границы Г и коэффициентов  Для граничных дифференциальных выражений составим их характеристические полиномы
Для граничных дифференциальных выражений составим их характеристические полиномы

Будем говорить, что система граничных дифференциальных выражений (29.13) дополнительна к правильно эллиптическому дифференциальному выражению (29.12), если для каждого вещественного вектора  , параллельного Г в точке х, и для каждого вещественного вектора
, параллельного Г в точке х, и для каждого вещественного вектора  , нормального к Г в х, полиномы от
, нормального к Г в х, полиномы от  линейно независимы по
линейно независимы по
модулю полинома

где  — корни полинома
— корни полинома  с положительными мнимыми частями, т. е. тождество вида
с положительными мнимыми частями, т. е. тождество вида

где  — полином, возможно лишь при
— полином, возможно лишь при  Отметим, что требование дополнительности
Отметим, что требование дополнительности  , к
, к  является видоизменением на рассматриваемый случай условия Шапиро — Лопатинского (см. предыдущий пункт).
является видоизменением на рассматриваемый случай условия Шапиро — Лопатинского (см. предыдущий пункт).
Система граничных дифференциальных выражений (29.13) называется нормальной, если

2)  при всех
при всех  и
и  , где
, где  вектор, нормальный к Г в точке х (это условие эквивалентно тому, что Г не является характеристикой ни для одного из
вектор, нормальный к Г в точке х (это условие эквивалентно тому, что Г не является характеристикой ни для одного из 
Введем банахово пространство  состоящее из функций и
состоящее из функций и  пространства
пространства  (см. С. Л. Соболев [1]) и удовлетворяющих граничным условиям
(см. С. Л. Соболев [1]) и удовлетворяющих граничным условиям  (граничные значения эти имеют смысл для функций из
(граничные значения эти имеют смысл для функций из  и понимаются в смысле обобщенных производных С. Л. Соболева).
и понимаются в смысле обобщенных производных С. Л. Соболева).
Пусть  — правильно эллиптическое дифференциальное выражение, а
— правильно эллиптическое дифференциальное выражение, а  — дополнительная к
— дополнительная к  и нормальная система граничных дифференциальных выражений. Тогда имеет место неравенство коэрцитивности (см., например, М. Шехтер [11)
и нормальная система граничных дифференциальных выражений. Тогда имеет место неравенство коэрцитивности (см., например, М. Шехтер [11)

Из этого неравенства следует, что дифференциальный оператор В, задаваемый на функциях из  формулой
формулой  является ограниченным оператором (оператором из
является ограниченным оператором (оператором из  причем число его нулей
причем число его нулей  конечно.
конечно.
Пусть  формально сопряженное к
формально сопряженное к  дифференциальное выражение:
дифференциальное выражение:

Можно определить также сопряженную к  нормальную систему граничных дифференциальных выражений
нормальную систему граничных дифференциальных выражений  определяется, как обычно, с помощью интегрирования по частям).
определяется, как обычно, с помощью интегрирования по частям).
Рассмотрим теперь граничную задачу

Если задача (29.14) имеет лишь тривиальное решение, то задача  разрешима при любой правой части
разрешима при любой правой части  Шехтер [1]). Если же задача (29.14) имеет нетривиальные решения, то для того, чтобы уравнение
Шехтер [1]). Если же задача (29.14) имеет нетривиальные решения, то для того, чтобы уравнение  было разрешимо, необходимо и достаточно, чтобы
было разрешимо, необходимо и достаточно, чтобы  для каждого решения
для каждого решения  задачи (29.14) (см. М. Шехтер [2]). Это означает нормальную разрешимость оператора В. Далее, неравенство коэрцитивности справедливо, конечно, и для сопряженной задачи, и потому задача (29.14) имеет конечное число линейно независимых решений. Таким образом, В есть нетеровский оператор.
задачи (29.14) (см. М. Шехтер [2]). Это означает нормальную разрешимость оператора В. Далее, неравенство коэрцитивности справедливо, конечно, и для сопряженной задачи, и потому задача (29.14) имеет конечное число линейно независимых решений. Таким образом, В есть нетеровский оператор.
В ряде случаев В оказывается фредгольмовским оператором. Так будет, например, в случае задачи Дирихле, когда  (производная по нормали к Г). Фредгольмовость оператора В, порожденного некоторыми краевыми задачами для сильно эллиптических дифференциальных выражений, установлена М. И. Вишиком [1]. Отметим, что при
(производная по нормали к Г). Фредгольмовость оператора В, порожденного некоторыми краевыми задачами для сильно эллиптических дифференциальных выражений, установлена М. И. Вишиком [1]. Отметим, что при  всякое правильно эллиптическое дифференциальное выражение
всякое правильно эллиптическое дифференциальное выражение  является сильно эллиптическим.
является сильно эллиптическим.
Рассмотрим теперь нелинейную краевую задачу с малым комплексным параметром X:

где  правильно эллиптично,
правильно эллиптично,  дополнительная к
дополнительная к  нормальная система.
нормальная система.
(Запись  — сокращенная запись, которая означает, что функция
— сокращенная запись, которая означает, что функция  может зависеть от и и ее производных до порядка
может зависеть от и и ее производных до порядка  . Также под
. Также под  будем понимать набор производных
будем понимать набор производных  по всем ее аргументам
по всем ее аргументам 
Пусть функция  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1)  непрерывны по совокупности переменных
непрерывны по совокупности переменных  , где
, где  любое, а
любое, а  почти при каждом фиксированном
почти при каждом фиксированном  и измеримы по х при фиксированных
и измеримы по х при фиксированных 
2)  почти для всех
почти для всех  ;
;
3)  есть непрерывный оператор, отображающий сферу в пространство
есть непрерывный оператор, отображающий сферу в пространство  и имеющий в указанной сфере непрерывную производную Фреше. (Если
и имеющий в указанной сфере непрерывную производную Фреше. (Если  зависит только от и, X, х, то достаточное условие для выполнимости 3) можно дать, повторяя рассуждения
зависит только от и, X, х, то достаточное условие для выполнимости 3) можно дать, повторяя рассуждения 
Эти условия обеспечивают применимость к задаче (29.15) теории § 27, а в случае фредгольмости оператора В — теории главы VII. Можно сформулировать соответствующие теоремы.
Заметим в заключение, что иногда удобно рассматривать задачу (29.15) как задачу с неограниченными операторами. Пусть в дополнение к перечисленным выше условиям выполнено неравенство  (к — число измерений), тогда вследствие теорем вложения Соболева — Кондрашева пространство
(к — число измерений), тогда вследствие теорем вложения Соболева — Кондрашева пространство  вполне непрерывно вложено в
вполне непрерывно вложено в  и поэтому В можно рассматривать как замкнутый линейный неограниченный оператор с плотной в
и поэтому В можно рассматривать как замкнутый линейный неограниченный оператор с плотной в  областью определения
областью определения  Оператор
Оператор  очевидно, подчинен В, так как имеет более широкую область определения. По-прежнему В есть Н-оператор, и, следовательно, можно воспользоваться теперь результатами пп. 26.4 и 27.5.
очевидно, подчинен В, так как имеет более широкую область определения. По-прежнему В есть Н-оператор, и, следовательно, можно воспользоваться теперь результатами пп. 26.4 и 27.5.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ГЛАВА I. Системы неявных функций и классическая теория ветвления
- § 1. Задача о неявных функциях
- 1.2. Общее исследование задачи о неявных функциях.
- 1.3. Аналитический случай.
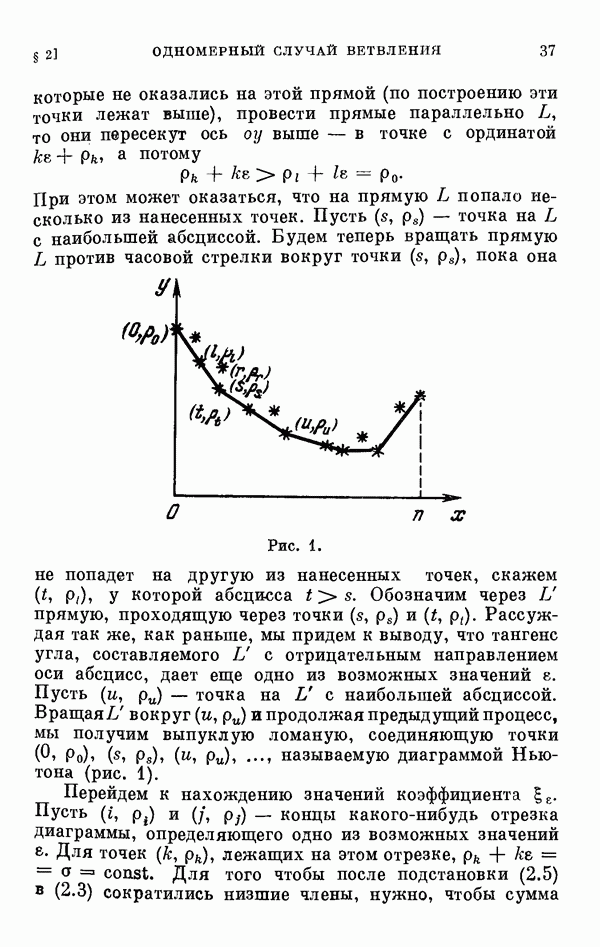
- § 2. Одномерный сличай ветвления и диаграмма Ньютона
- 2.2. О свойствах решений.
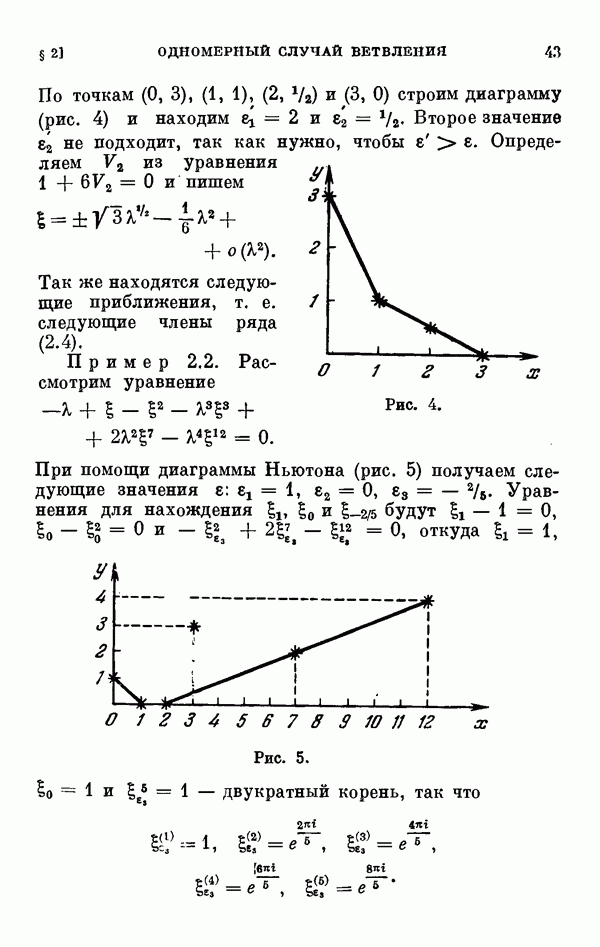
- 2.3. Примеры.
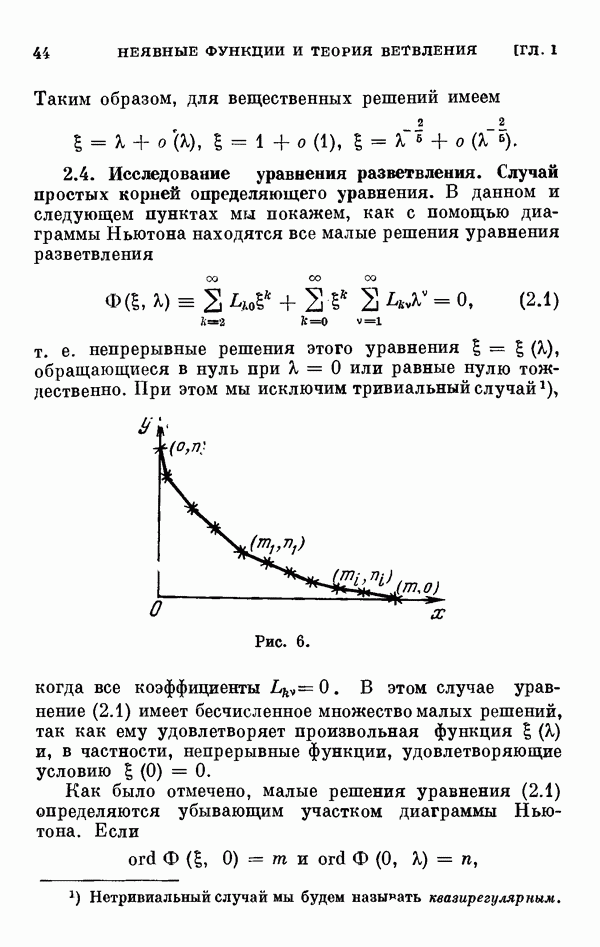
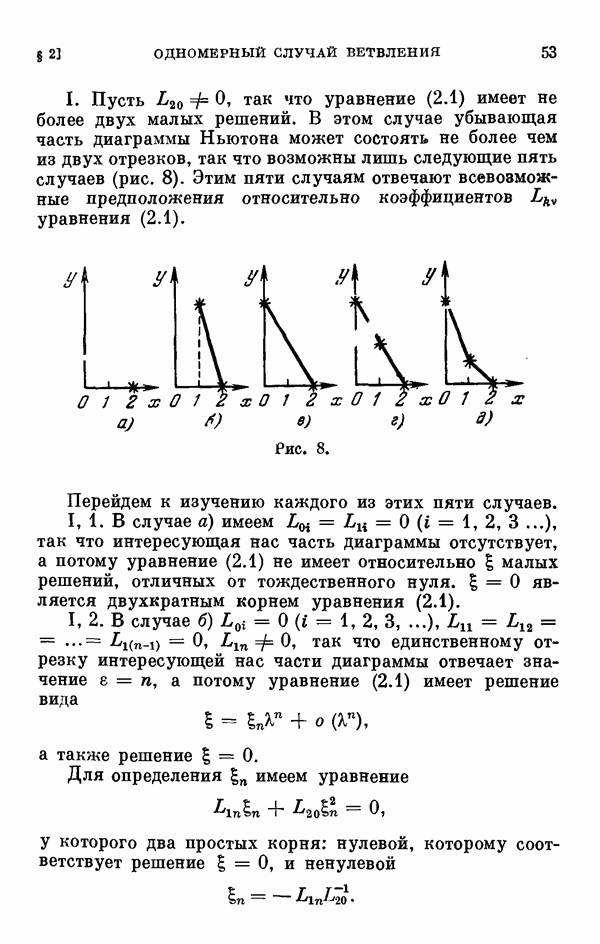
- 2.4. Исследование уравнения разветвления. Случай простых корней определяющего уравнения.
- 2.5. Случай кратных корней определяющего уравнения.
- 2.6. О вещественных решениях.
- 2.7. Некоторые частные случаи расположения диаграммы Ньютона.
- ГЛАВА II. Исследование уравнения разветвления в многомерном случае
- 3.2. Приведение к нормальному виду.
- § 4. Некоторые вопросы теории делимости
- 4.2. Общий делитель и аналог алгоритма Евклида.
- 4.3. Примитивный ОНД.
- 4.4. Применение к отмеченным многочленам.
- § 5. Двумерный случай ветвления
- 5.2. Указатели двумерного случая ветвления.
- 5.3. Частные случаи.
- § 6. Многомерный случай ветвления
- 6.2. Малые решения уравнения разветвления и метод исключения неизвестных.
- 6.3. Квазирегулярный случай ветвления.
- 6.4. Вырожденный случай ветвления.
- 6.5. Об изолированности нулевого решения.
- ГЛАВА III. Уравнение разветвления для нелинейных интегральных и интегро-дифференциальных уравнений
- § 7. Интегральные уравнения Ляпунова — Шмидта
- 7.2. Интегро-степенные ряды от многих функциональных аргументов.
- 7.3. Интегро-степенные ряды от интегро-степенных рядов.
- 7.4. Сжатость оператора Ляпунова—Шмидта.
- 7.5. Простейшее уравнение.
- 7.6. Последовательные приближения Лихтенштейна.
- 7.7. Применение метода мажорант.
- 7.8. Простейшее уравнение в случае равномерной сходимости.
- § 8. Общее интегральное уравнение Ляпунова—Шмидта
- 8.2. Регулярный случай при наличии многих аргументов.
- 8.3. Лемма Шмидта.
- 8.4. Одномерный случай ветвления.
- 8.5. Многомерный случай ветвления.
- 8.6. Возможные обобщения.
- § 9. Системы уравнений Ляпунова—Шмидта и некоторые интегро-дифференциальные уравнения
- 9.2. Регулярный случай.
- 9.3. Случай ветвления.
- 9.4. Некоторые нелинейные интегро-дифференциальные уравнения первого порядка.
- 9.5. Другие виды интегро-дифференциальных уравнений.
- 9.6. Другой способ построения уравнения разветвления
- ГЛАВА IV. Общее интегральное уравнение и коэффициенты уравнения разветвления
- 10.2. Регулярный случай.
- 10.3. Одномерный случай ветвления.
- 10.4. Многомерный случай ветвления.
- 10.5 Частный случай.
- 10.6. Уравнение Гаммерштейна.
- § 11. Коэффициенты уравнения разветвления
- 11.2. Коэффициенты одиомерного уравнения разветвления нелинейного интегрального уравнения Гаммерштейна.
- 11.3. Коэффициенты двумерного уравнения разветвления общего нелинейного интегрального уравнения.
- 11.4. Коэффициенты двумерного уравнения разветвления для частных случаев.
- 11.5. Некоторые свойства коэффициентов уравнения разветвления.
- ГЛАВА V. Описание и построение решений нелинейных интегральных уравнений
- § 12. Описание решений нелинейных интегральных уравнений
- 12.2. Описание решении в одномерном случае ветвления.
- 12.3. О точках бифуркации в одномерном случае ветвления.
- 12.4. Описание решений в двумерном случае ветвления.
- 12.5. Описание решений в многомерном случае ветвления.
- 12.6. О ветвлении изолированного решения.
- 12.7. Точки бифуркации в многомерном случае ветвления.
- § 13. Построение решений нелинейных интегральных уравнений
- 13.3. Двумерный случай ветвления.
- 13.4. Уравнение Некрасова.
- 13.5. Уравнение разветвления для уравнения Некрасова.
- § 14. Особые решения нелинейных интегральных уравнений
- 14.2. Сведение к малым решениям.
- 14.3. Особые решения в регулярном случае.
- 14.4. Исследование вспомогательного уравнения.
- 14.5. Ветвление решений основного уравнения.
- 14.6 Особые решения в пространствах Лебега.
- ГЛАВА VI. Ветвление периодических решений дифференциальных уравнений
- § 15. Периодические решения неавтономных систем
- 15.2. Метод Пуанкаре.
- 15.3. Условия периодичности и уравненне разветвления.
- 15.4. Описание решений в регулярном случае.
- 15.5. Описание решений в одномерном случае ветвления.
- 15.6. Описание решений в многомерном случае ветвления.
- § 16. Периодические решения квазилинейных систем
- 16.2. Условия периодичности.
- 16.3. Вывод уравнения разветвления.
- 16.4. Описание решений и дополнительные замечания.
- § 17. Периодические решения автономных систем
- 17.2. Уравнение разветвления.
- 17.3. Основные выводы.
- 17.4. Метод неопределенных коэффициентов.
- 17.5. Автономные системы с одной степенью свободы.
- § 18. Примеры
- 18.1. Неавтономные системы с одной степенью свободы.
- 18.2 Автономные системы с одной степенью свободы.
- § 19. Другие задачи о периодических решениях
- 19.1. Особые периодические решения неавтономных систем.
- 19.2. Ветвление периодических решений в банаховых пространствах
- § 20. Об устойчивости периодических решений, зависящих от малого параметра
- 20.2. Устойчивость решений задачи Пуанкаре.
- ГЛАВА VII. Нелинейные уравнения в банаховых пространствах
- § 21. Некоторые вопросы теории линейных операторов в банаховых пространствах
- 21.2. Специальные разложения пространств в прямые суммы подпространств.
- 21.3. Сужение оператора и обобщенная лемма Шмидта.
- 21.4 Связь с сопряженным оператором.
- 21.5. Неограниченные фредгольмовские операторы.
- § 22. Степенные операторы, ряды Тейлора, теоремы о неявных операторах
- 22.2 Степенные ряды. Ряды Тейлора.
- 22.3 Теоремы о неявных операторах.
- § 23. Уравнение разветвления Ляпунова — Шмидта
- 23.2. Вывод уравнения разветвления с помощью сужения оператора B.
- 23.3. Вывод уравнения разветвления с помощью леммы Шмидта.
- 23.4. Основная теорема об уравнении разветвления.
- 23.5. Уравление разветвления в аналитическом случае.
- 23.6. Уравнение разветвления для неограниченных операторов.
- § 24. Исследование одномерного случая ветвления
- 24.2. Вырожденный случай.
- 24.3. Квазирегулярный случай (задача А).
- 24.4. Задача Б (невырожденный случай).
- 24.5 Вещественный случай.
- 24.6. О ветвлении решений уравнений о достаточно гладкими операторами.
- 24.7 Случай функционального параметра. Ряды по однородным операторам.
- 24.8. Случай двух числовых параметров.
- § 25. Многомерный случай ветвления
- 25.2. Коэффициенты двумерного уравнения разветвления.
- 25.3. Двумерный случай ветвления.
- 25.4 Общий случай.
- 25.5. О ветвлении изолированного решения.
- 25.6. О точках бифуркации.
- ГЛАВА VIII. Ветвление решений нелинейных уравнений в сингулярном случае
- 26.2. Разложение пространств в прямые суммы подпространств.
- 26.3. Теорема Аткинсона.
- 23.4. О нетеровских неограниченных операторах.
- § 27. Теоремы о ветвлении решений
- 27.2. Случай n > 0, m = 0.
- 27.3. Случай n = 0, m > 0.
- 27.4. Основной случай. Уравнение разветвления.
- 27.5. О ветвлении решений уравнения с неограниченным оператором.
- § 28. Ветвление решений нелинейных сингулярных интегральных уравнений.
- 28.2. Нелинейные сингулярные интегральные уравнения с ядром типа Коши в пространствах Гёльдера.
- 28.3. Аналитический случай.
- 28.4. Нелинейные сингулярные интегральные уравнения с ядром Гильберта в пространствах Лебега.
- § 29. Ветвление решений краевых задач для нелинейных эллиптических уравнений
- 29.2. Краевые задачи на плоскости для эллиптических систем k-го порядка в пространстве Гёльдера.
- 29.3. Краевые задачи для эллиптических уравнений в пространстве суммируемых функций.
- ГЛАВА IX. Некоторые задачи теории вовмущений
- § 30. Жордановы цепочки и наборы фредгольмовских операторов
- 30.2. А-жордановы цепочки и наборы при n > 1.
- 30.3. Условия полноты А-жорданова набора.
- 30.4. Пример.
- § 31. Возмущение линейного уравнения малым линейным слагаемым
- 31.2. Случай n > 1.
- 31.3. Метод неопределенных коэффициентов.
- § 32. Ветвление собственных значений и собственных элементов фредгольмовских операторов
- 32.2. Уравнение разветвления в аналитическом случае.
- 32.3. Вырожденный и невырожденный случаи.
- 32.4. Одномерный случай.
- 32.5. Метод неопределенных коэффициентов.
- 32.6. Многомерный случай.
- 32.7. Некоторые обобщения.
- § 33. Особые решения нелинейных уравнений
- 33.2. Задача о возмущении линейного уравнения малым нелинейным слагаемым.
- 33.3. Понятие обобщенной жордановой цепочки.
- 33.4. Свойства некоторых многочленов.
- 33.5 Основной случай задачи о возмущении.
- 33.6. Случаи возмущения второго порядка.
- 33.7. Решения порядка …
- ГЛАВА X. Некоторые прикладные задачи
- § 34. О малых изгибах прямолинейного стержня под действием постоянной нагрузки
- § 35. К теории малых прогибов гибких пластин
- 35.2. Случай круглой пластины.
- 35.3. Исследование уравнения разветвления.
- 35.4. Круглая пластина с нулевой внешней нагрузкой.
- § 36. О колебаниях спутника в плоскости эллиптической орбиты
- § 37. Об одном виде установившихся волн
- 37.2. Сведение к системе.
- 37.3. Регулярный случай.
- 37.4. Случай ветвления.
- Литература