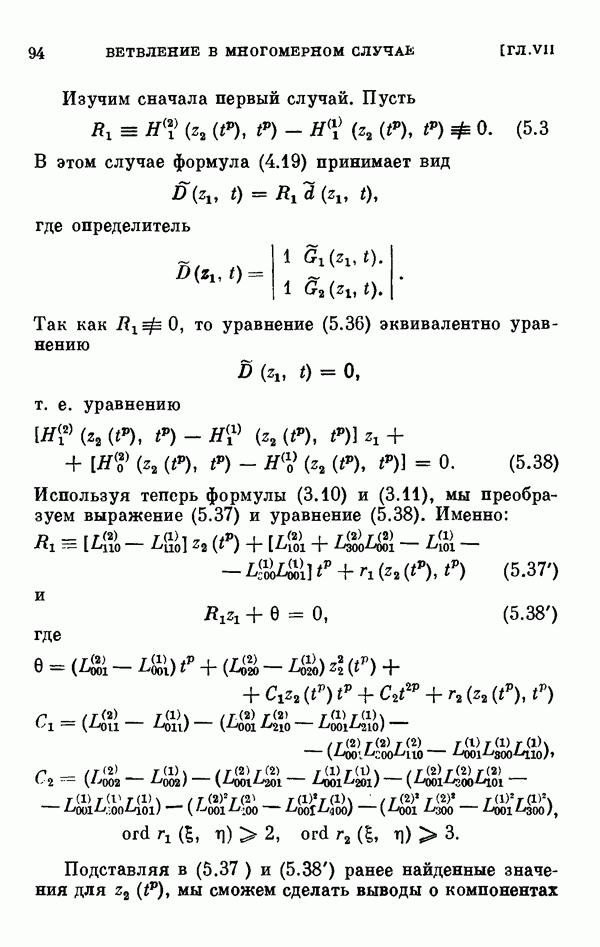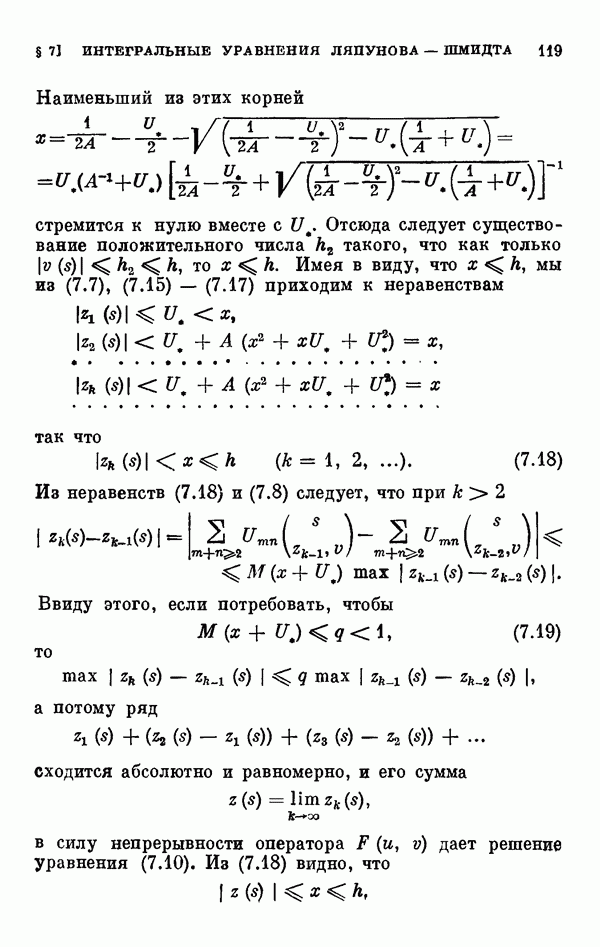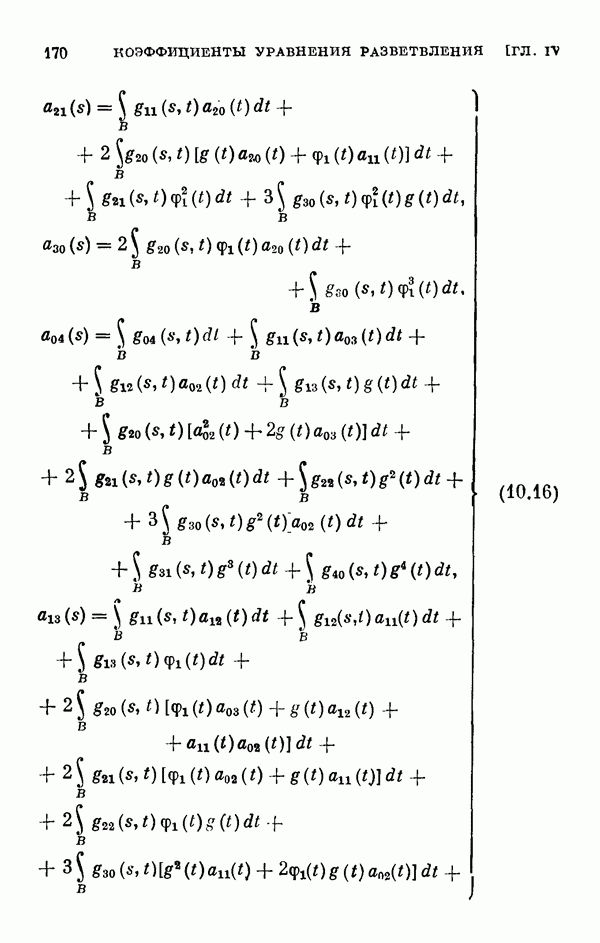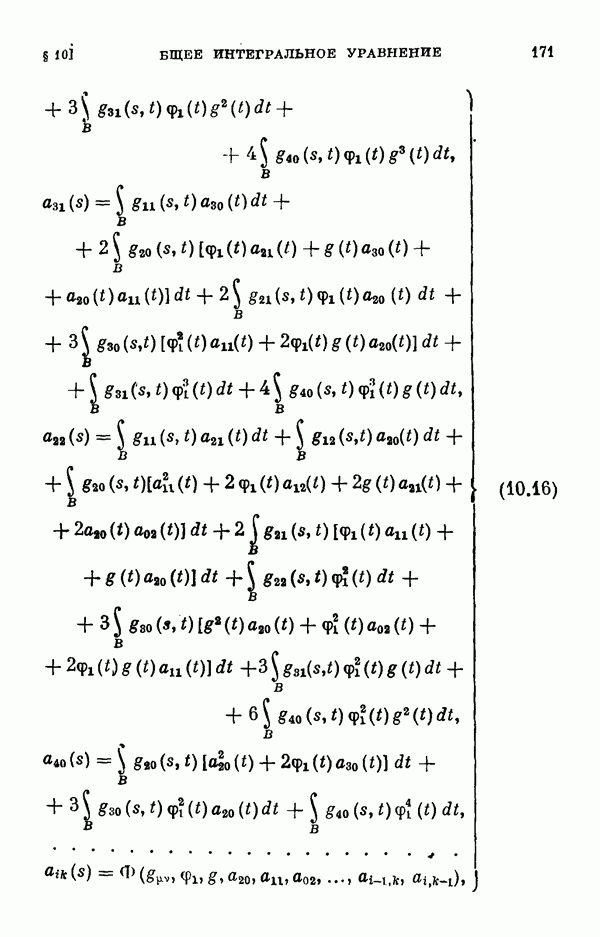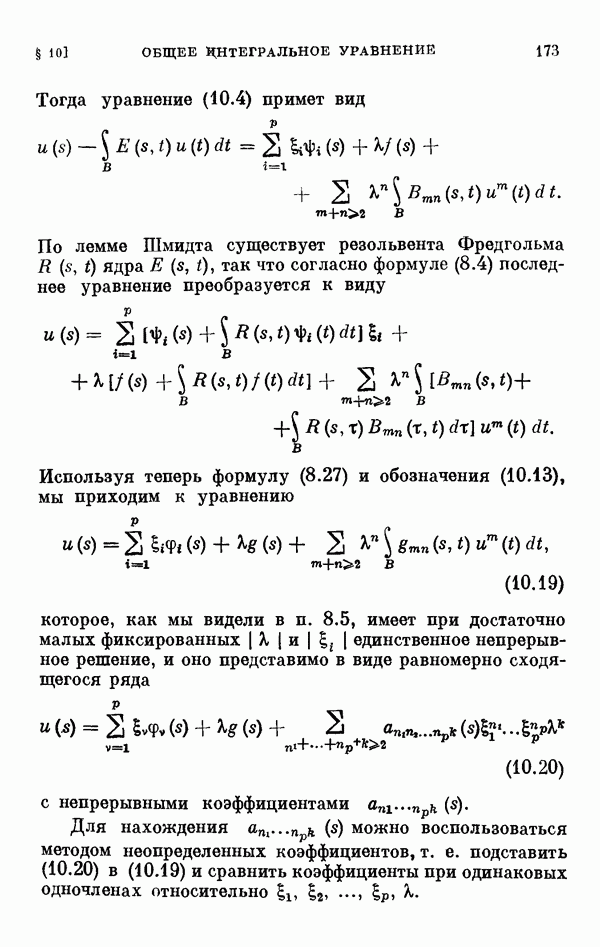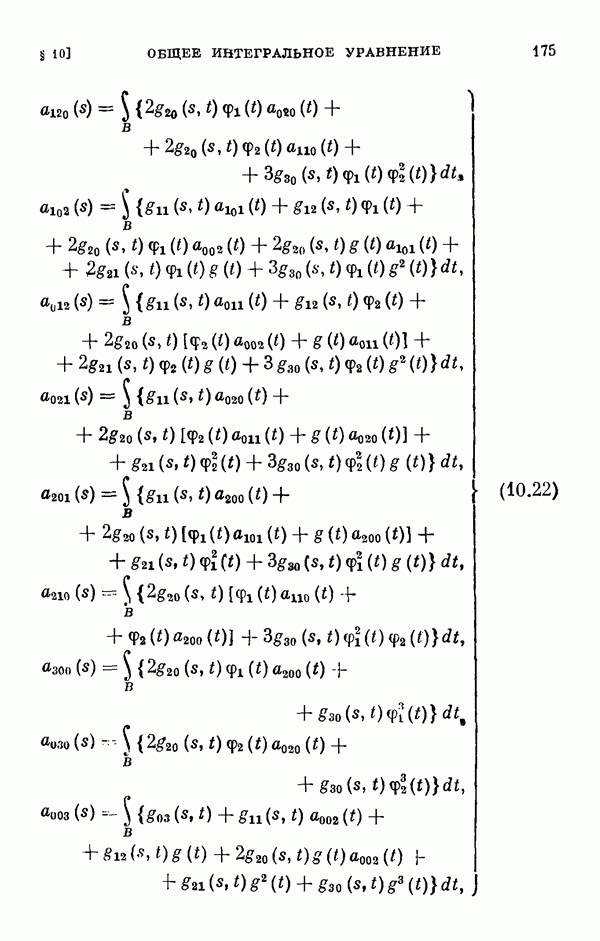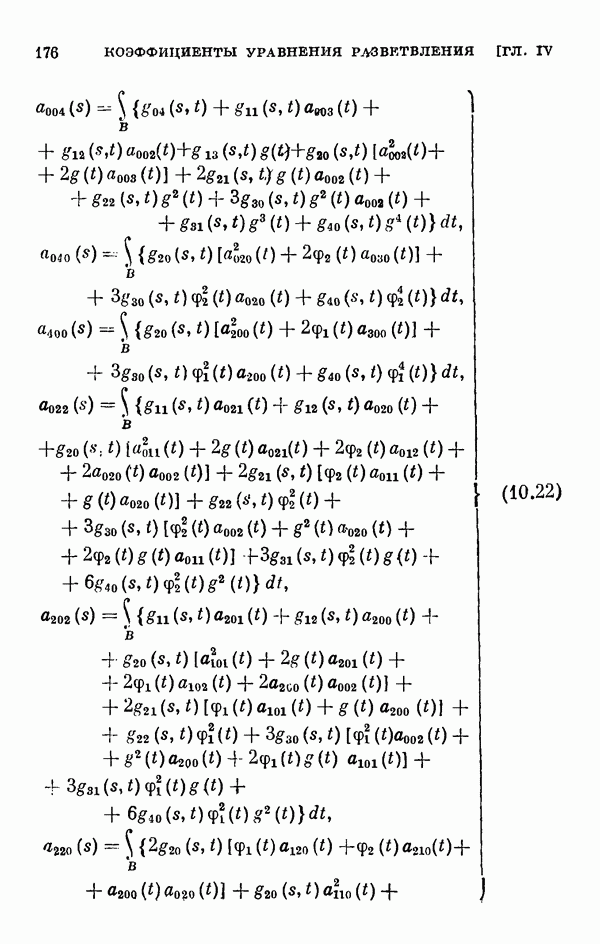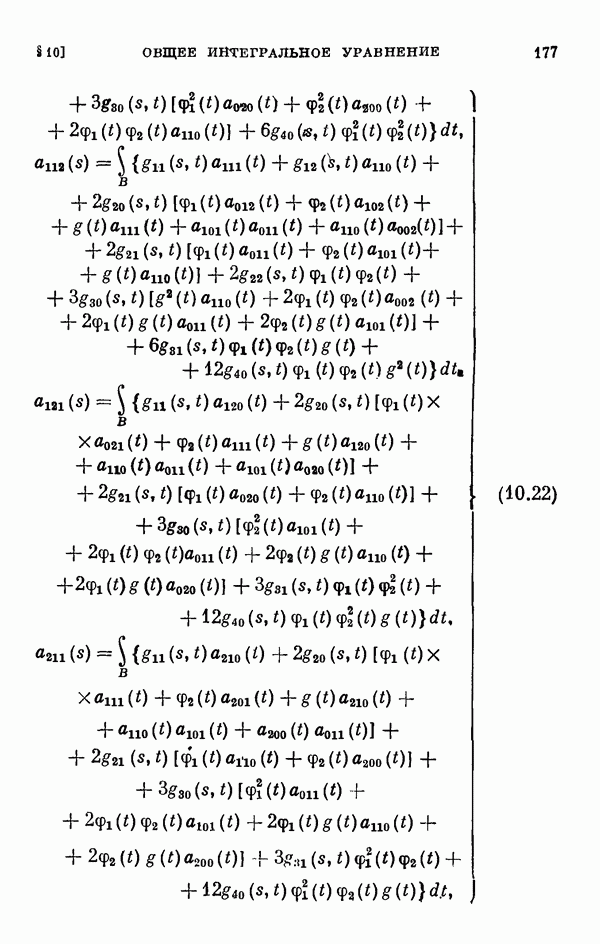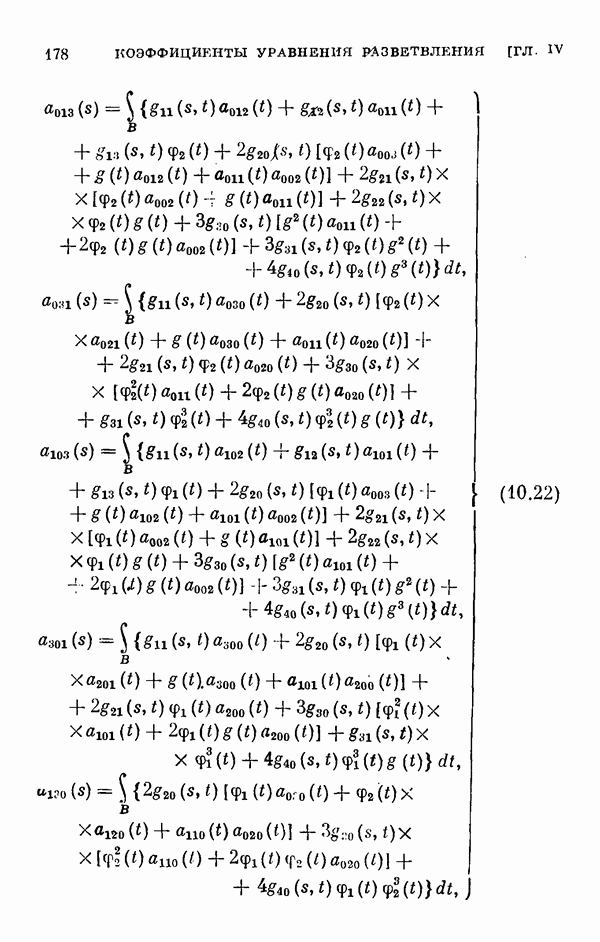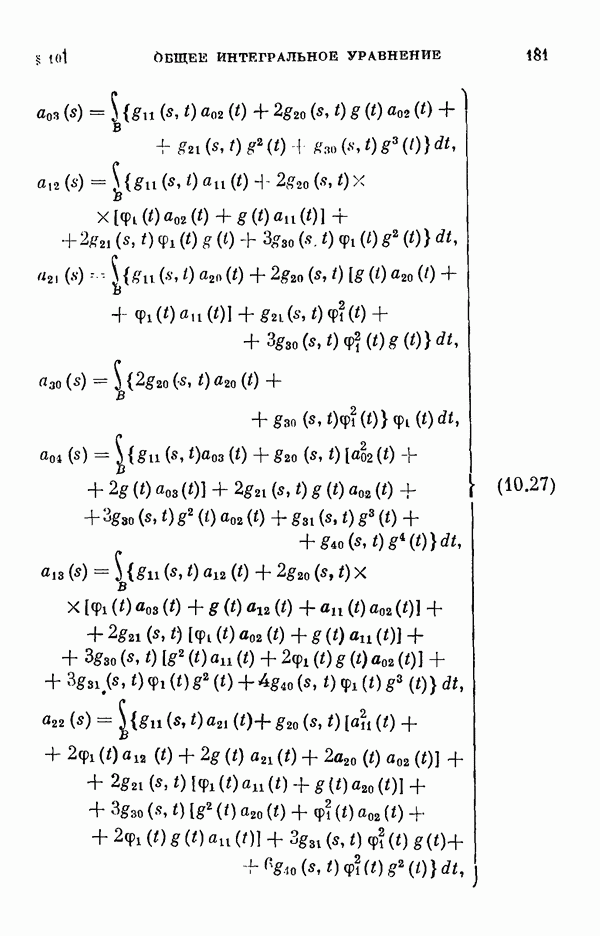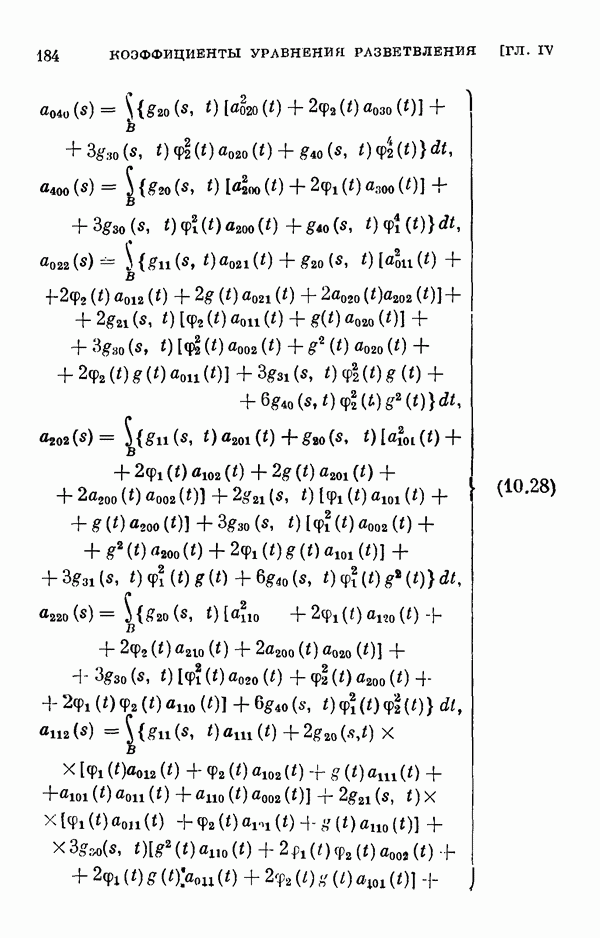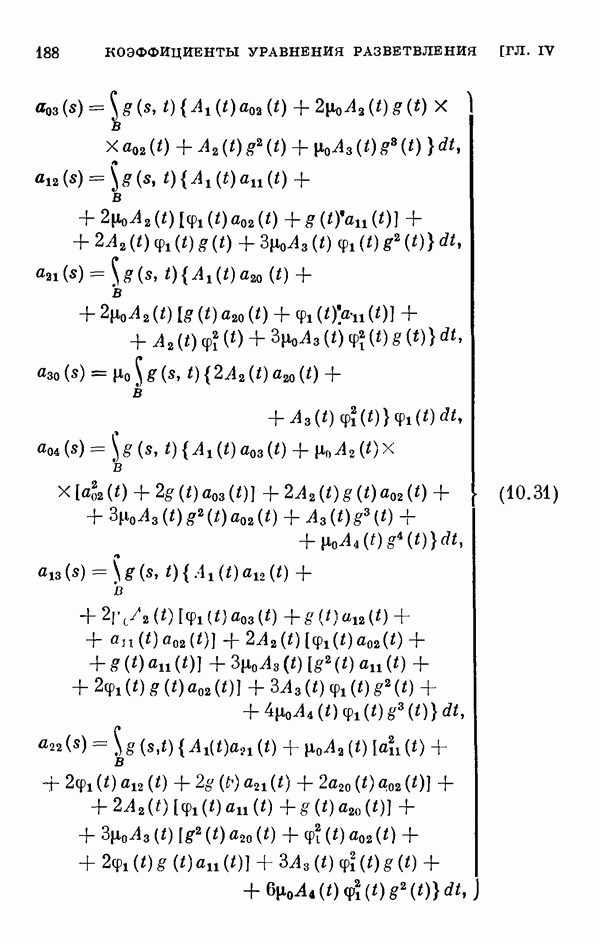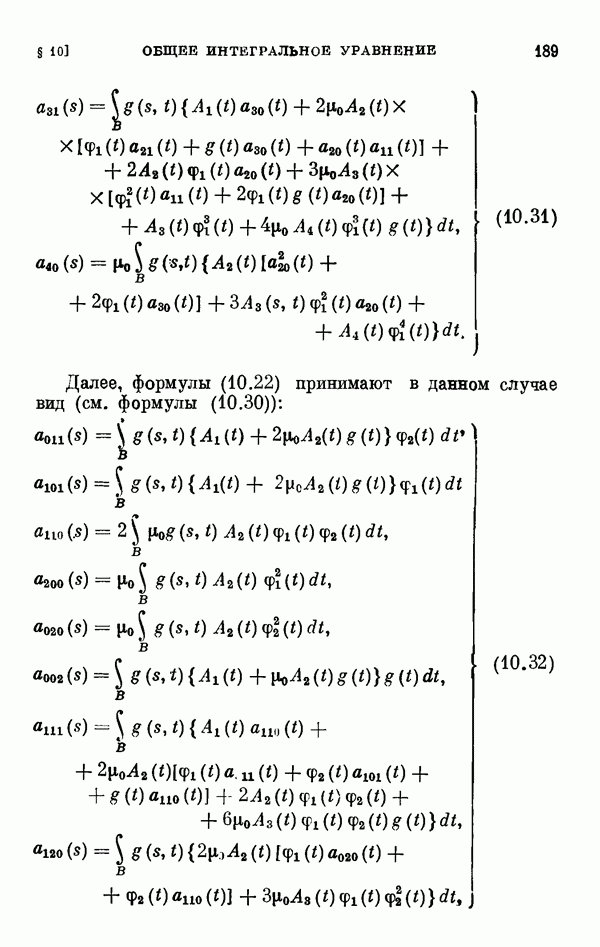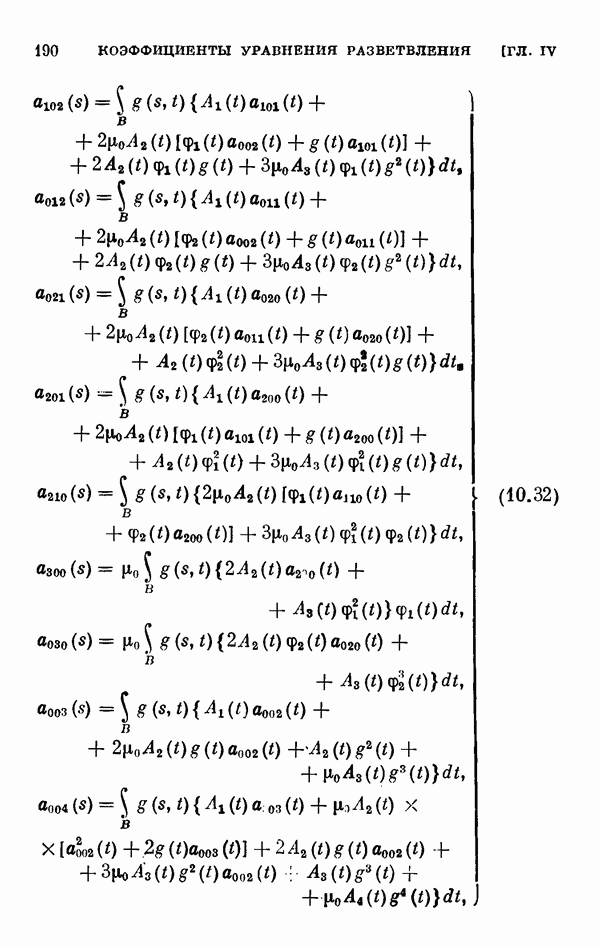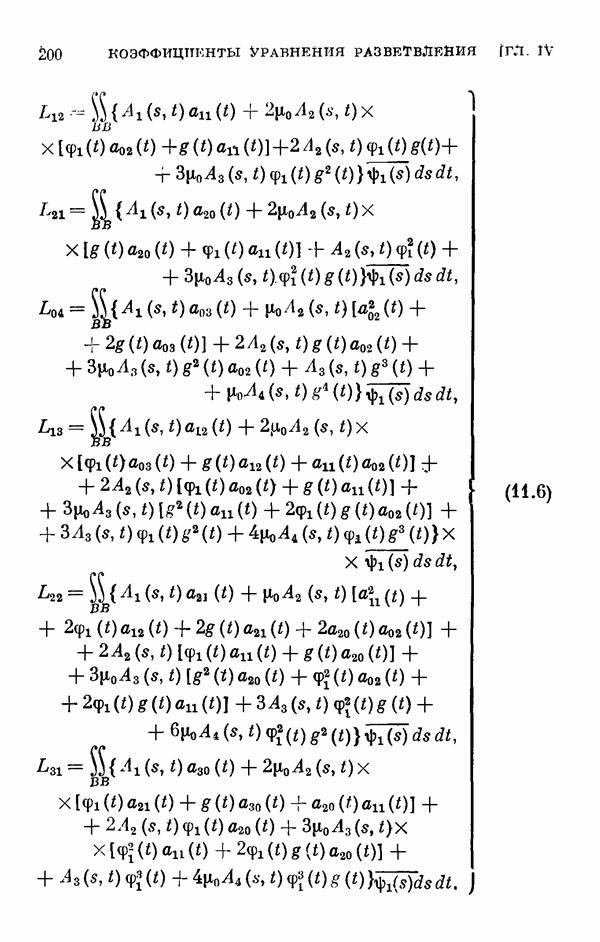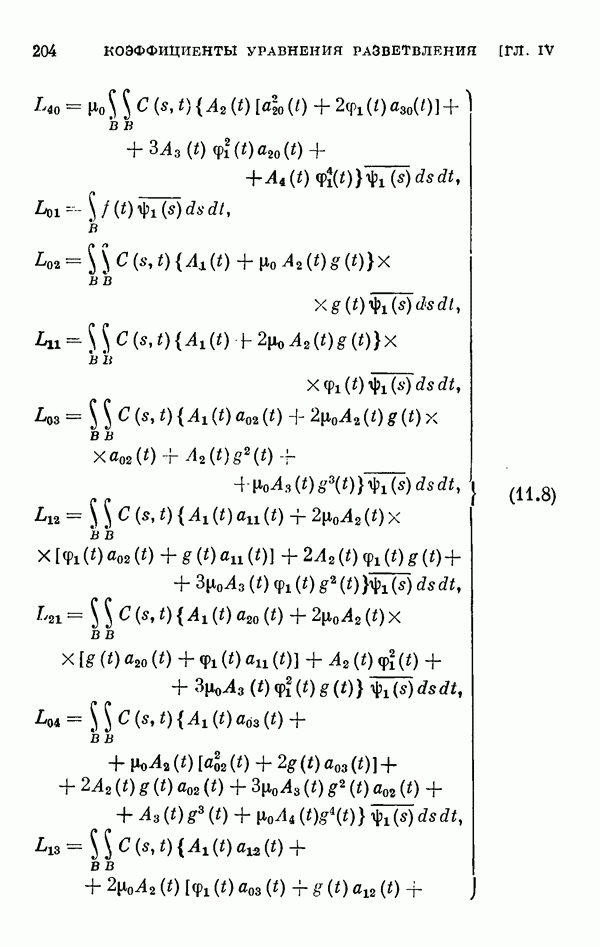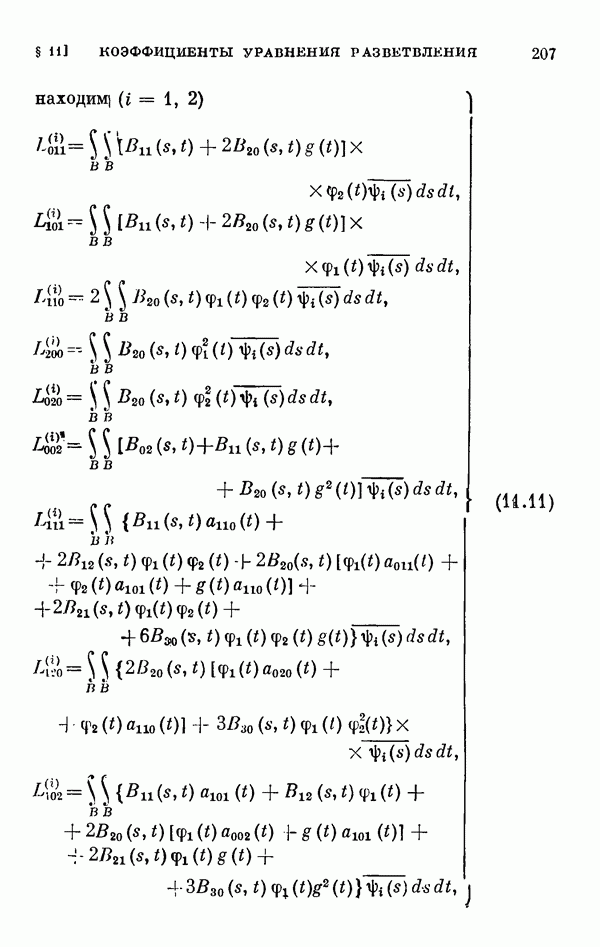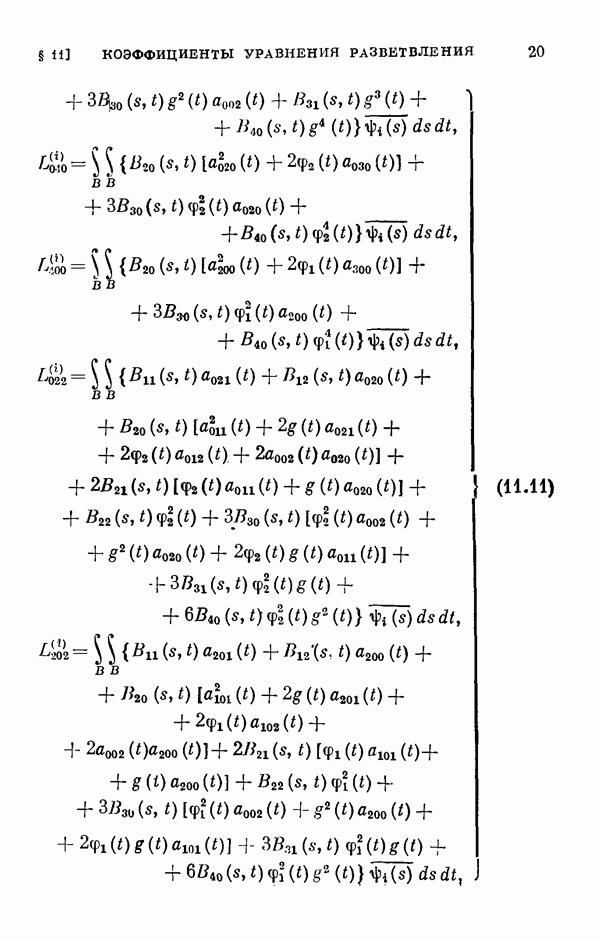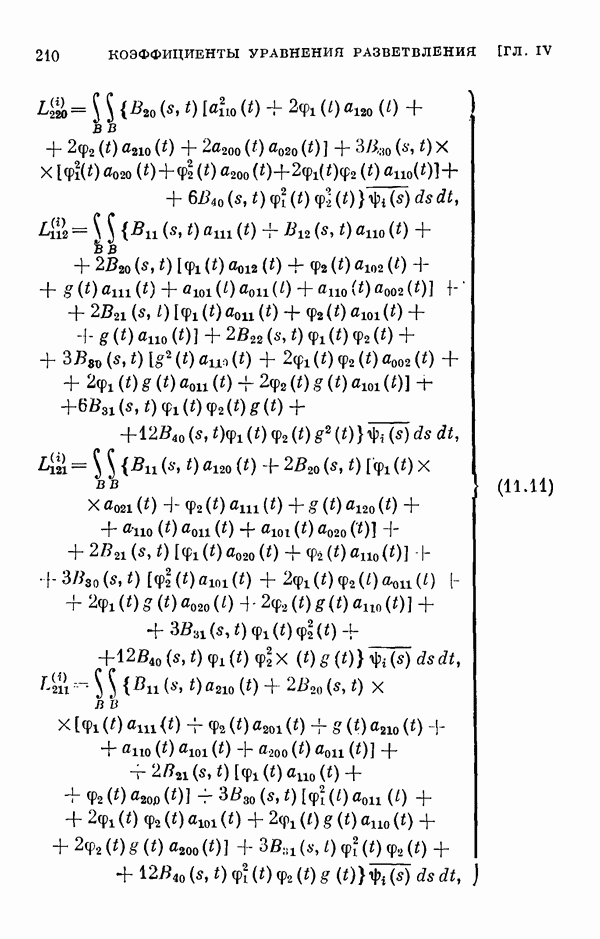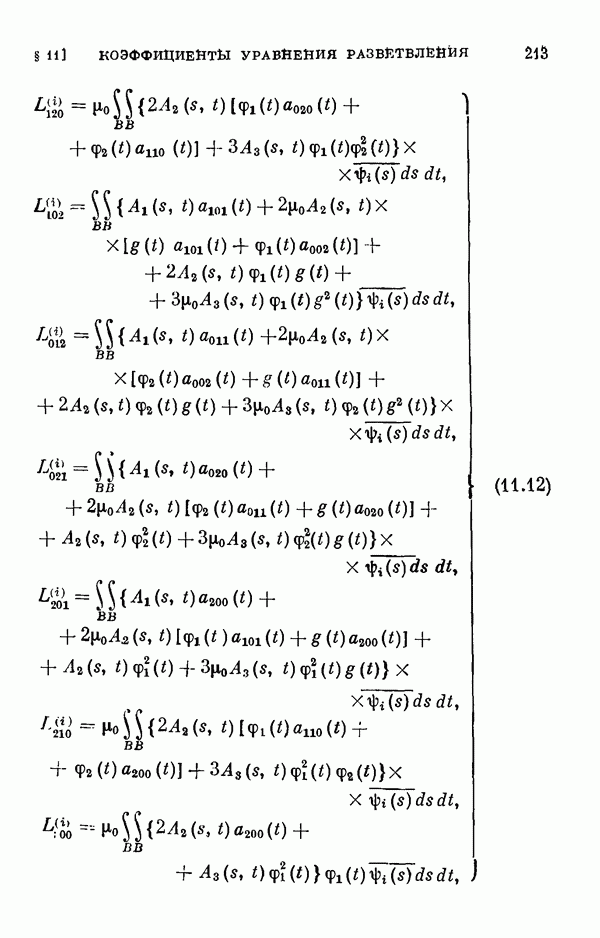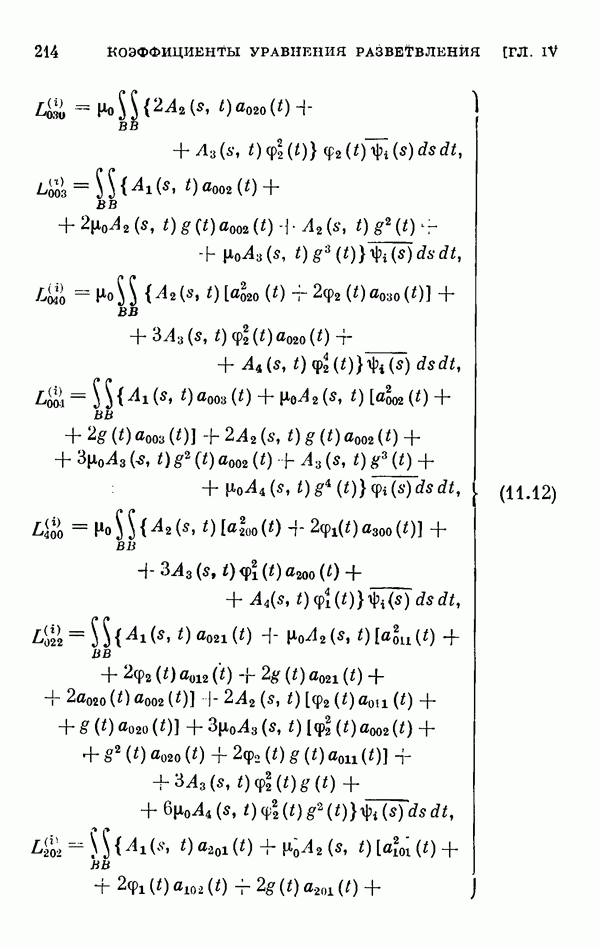| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА VI. Ветвление периодических решений дифференциальных уравнений
Основное содержание данной главы связано с решением задачи Пуанкаре о периодических решениях систем обыкновенных дифференциальных уравнений.
§ 15. Периодические решения неавтономных систем
15.1. Постановка задачи.
Пусть  — евклидово пространство (вещественное или комплексное) размерности
— евклидово пространство (вещественное или комплексное) размерности  — некоторая область пространства
— некоторая область пространства  — параметр (вещественный или комплексный),
— параметр (вещественный или комплексный),  — окрестность нуля комплексной плоскости, а в вещественном случае А — окрестность или полуокрестность нуля и
— окрестность нуля комплексной плоскости, а в вещественном случае А — окрестность или полуокрестность нуля и 
Рассмотрим систему дифференциальных уравнений, записанную в векторной форме:

где  — искомый вектор пространства
— искомый вектор пространства  — заданные вектор-функции со значениями в
— заданные вектор-функции со значениями в  непрерывные по совокупности аргументов
непрерывные по совокупности аргументов  и
и  -периодические по
-периодические по  Мы будем предполагать,
Мы будем предполагать, 
— голоморфная по х функция в области 
— голоморфная функция по  т. е. что компоненты этих функций разлагаются в сходящиеся ряды
т. е. что компоненты этих функций разлагаются в сходящиеся ряды


в некоторой окрестности произвольной точки  и
и  . Пусть
. Пусть  — какое-нибудь
— какое-нибудь  -периодическое решение порождающей системы
-периодическое решение порождающей системы

Ставится задача о нахождении при достаточно малых  всех непрерывных и
всех непрерывных и  -периодических решений
-периодических решений  системы (15.1), удовлетворяющих условию
системы (15.1), удовлетворяющих условию

Данная задача восходит к Пуанкаре [1], предложившему общий подход для ее решения. Сам Пуанкаре и многие другие авторы ограничились в своих исследованиях рассмотрением различных частных случаев сформулированной задачи (см. И. Г. Малкин [1], а также Чезари [1], где указана библиография). Сравнительно недавно Лефшец [1, 2] предложил воспользоваться некоторым видоизменением кронекеровского метода исключения для решения сформулированной задачи в общей постановке. Эта идея Лефшеда была развига для решения поставленной задачи в работах П. Г. Айзенгендлера и М. М. Вайнберга [2—4], в которых существенно использовался алгебраический аппарат, изложенный в §§ 2—6.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ГЛАВА I. Системы неявных функций и классическая теория ветвления
- § 1. Задача о неявных функциях
- 1.2. Общее исследование задачи о неявных функциях.
- 1.3. Аналитический случай.
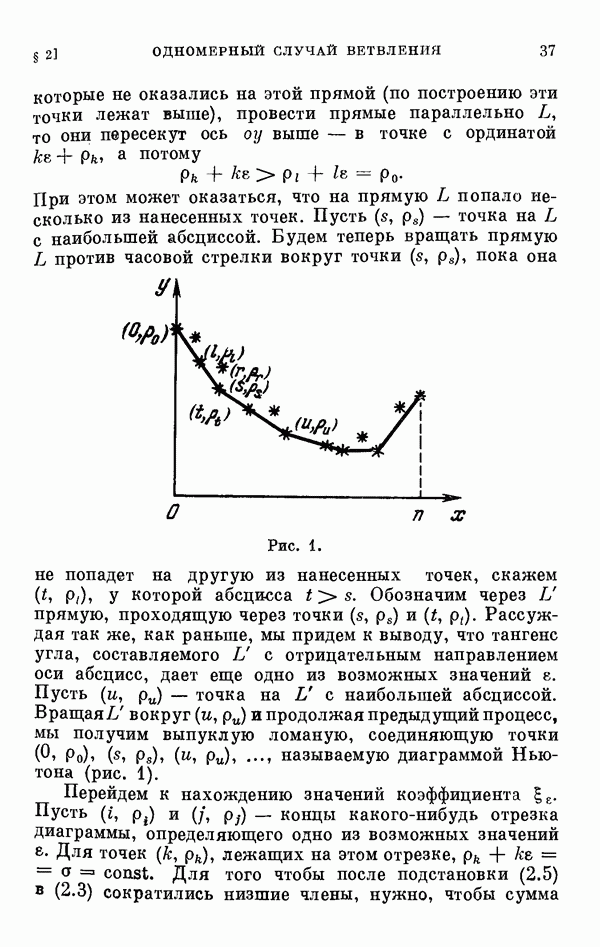
- § 2. Одномерный сличай ветвления и диаграмма Ньютона
- 2.2. О свойствах решений.
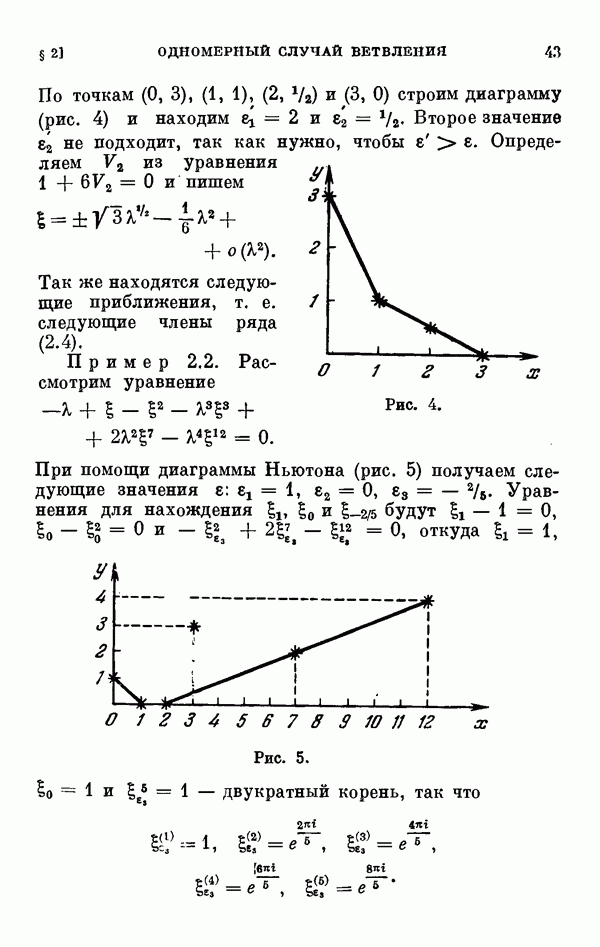
- 2.3. Примеры.
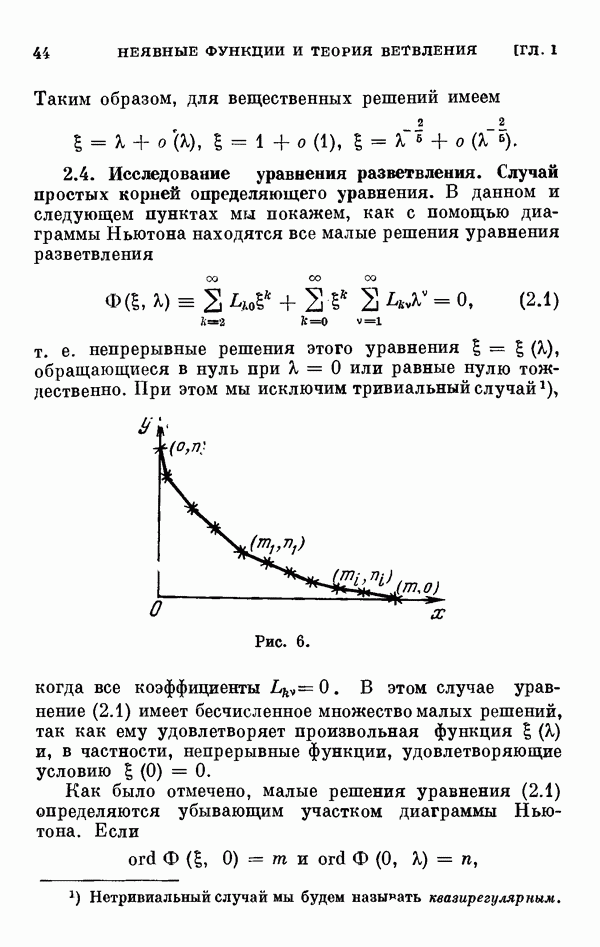
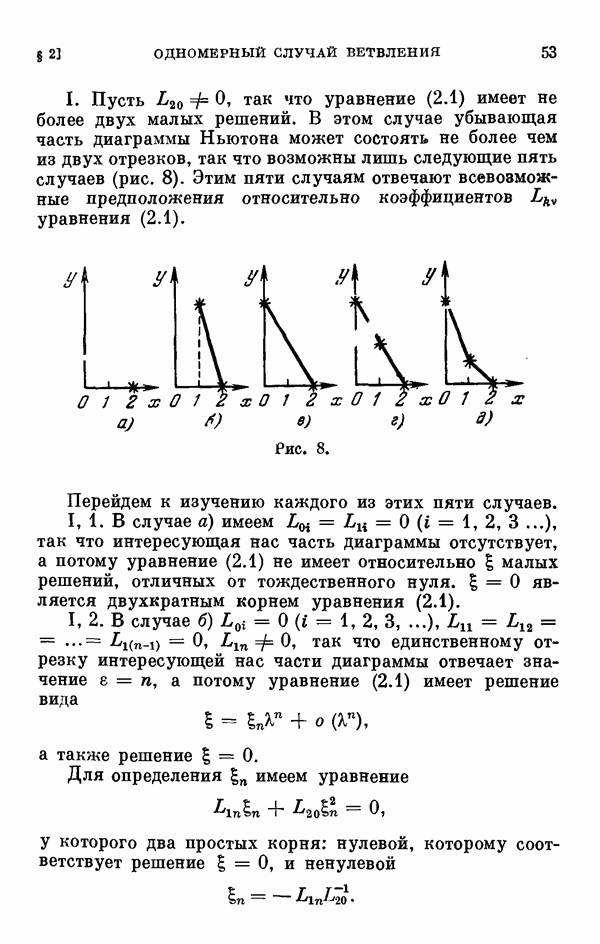
- 2.4. Исследование уравнения разветвления. Случай простых корней определяющего уравнения.
- 2.5. Случай кратных корней определяющего уравнения.
- 2.6. О вещественных решениях.
- 2.7. Некоторые частные случаи расположения диаграммы Ньютона.
- ГЛАВА II. Исследование уравнения разветвления в многомерном случае
- 3.2. Приведение к нормальному виду.
- § 4. Некоторые вопросы теории делимости
- 4.2. Общий делитель и аналог алгоритма Евклида.
- 4.3. Примитивный ОНД.
- 4.4. Применение к отмеченным многочленам.
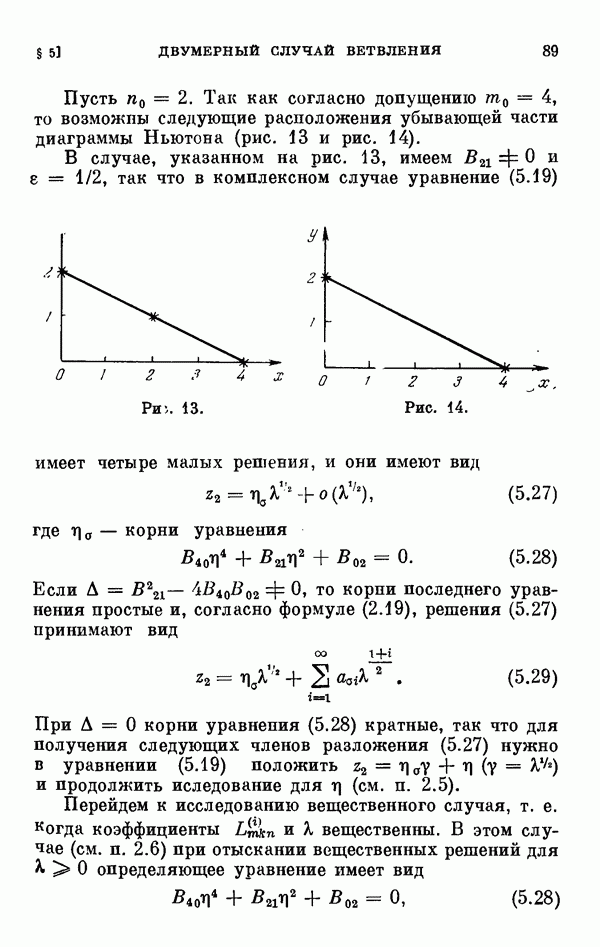
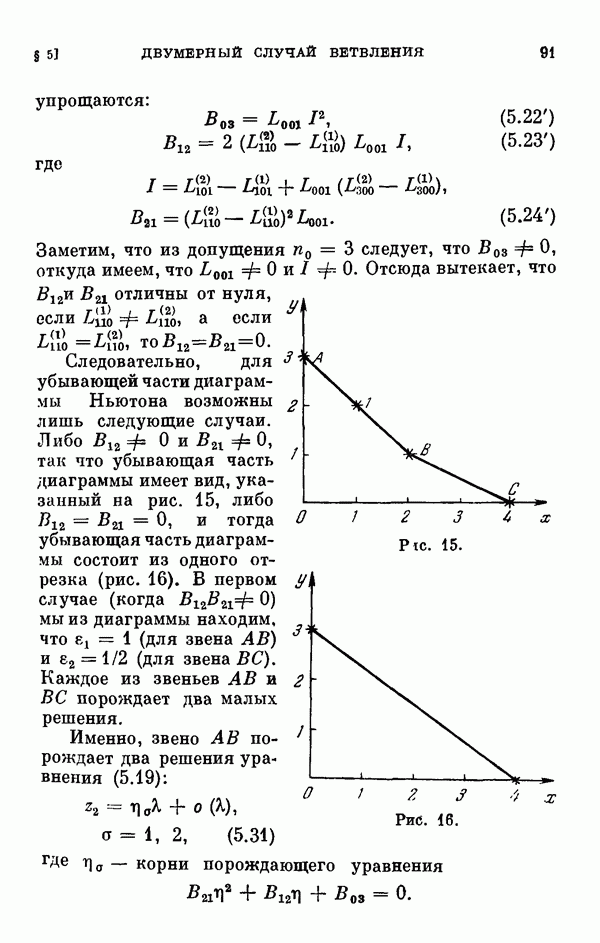
- § 5. Двумерный случай ветвления
- 5.2. Указатели двумерного случая ветвления.
- 5.3. Частные случаи.
- § 6. Многомерный случай ветвления
- 6.2. Малые решения уравнения разветвления и метод исключения неизвестных.
- 6.3. Квазирегулярный случай ветвления.
- 6.4. Вырожденный случай ветвления.
- 6.5. Об изолированности нулевого решения.
- ГЛАВА III. Уравнение разветвления для нелинейных интегральных и интегро-дифференциальных уравнений
- § 7. Интегральные уравнения Ляпунова — Шмидта
- 7.2. Интегро-степенные ряды от многих функциональных аргументов.
- 7.3. Интегро-степенные ряды от интегро-степенных рядов.
- 7.4. Сжатость оператора Ляпунова—Шмидта.
- 7.5. Простейшее уравнение.
- 7.6. Последовательные приближения Лихтенштейна.
- 7.7. Применение метода мажорант.
- 7.8. Простейшее уравнение в случае равномерной сходимости.
- § 8. Общее интегральное уравнение Ляпунова—Шмидта
- 8.2. Регулярный случай при наличии многих аргументов.
- 8.3. Лемма Шмидта.
- 8.4. Одномерный случай ветвления.
- 8.5. Многомерный случай ветвления.
- 8.6. Возможные обобщения.
- § 9. Системы уравнений Ляпунова—Шмидта и некоторые интегро-дифференциальные уравнения
- 9.2. Регулярный случай.
- 9.3. Случай ветвления.
- 9.4. Некоторые нелинейные интегро-дифференциальные уравнения первого порядка.
- 9.5. Другие виды интегро-дифференциальных уравнений.
- 9.6. Другой способ построения уравнения разветвления
- ГЛАВА IV. Общее интегральное уравнение и коэффициенты уравнения разветвления
- 10.2. Регулярный случай.
- 10.3. Одномерный случай ветвления.
- 10.4. Многомерный случай ветвления.
- 10.5 Частный случай.
- 10.6. Уравнение Гаммерштейна.
- § 11. Коэффициенты уравнения разветвления
- 11.2. Коэффициенты одиомерного уравнения разветвления нелинейного интегрального уравнения Гаммерштейна.
- 11.3. Коэффициенты двумерного уравнения разветвления общего нелинейного интегрального уравнения.
- 11.4. Коэффициенты двумерного уравнения разветвления для частных случаев.
- 11.5. Некоторые свойства коэффициентов уравнения разветвления.
- ГЛАВА V. Описание и построение решений нелинейных интегральных уравнений
- § 12. Описание решений нелинейных интегральных уравнений
- 12.2. Описание решении в одномерном случае ветвления.
- 12.3. О точках бифуркации в одномерном случае ветвления.
- 12.4. Описание решений в двумерном случае ветвления.
- 12.5. Описание решений в многомерном случае ветвления.
- 12.6. О ветвлении изолированного решения.
- 12.7. Точки бифуркации в многомерном случае ветвления.
- § 13. Построение решений нелинейных интегральных уравнений
- 13.3. Двумерный случай ветвления.
- 13.4. Уравнение Некрасова.
- 13.5. Уравнение разветвления для уравнения Некрасова.
- § 14. Особые решения нелинейных интегральных уравнений
- 14.2. Сведение к малым решениям.
- 14.3. Особые решения в регулярном случае.
- 14.4. Исследование вспомогательного уравнения.
- 14.5. Ветвление решений основного уравнения.
- 14.6 Особые решения в пространствах Лебега.
- ГЛАВА VI. Ветвление периодических решений дифференциальных уравнений
- § 15. Периодические решения неавтономных систем
- 15.2. Метод Пуанкаре.
- 15.3. Условия периодичности и уравненне разветвления.
- 15.4. Описание решений в регулярном случае.
- 15.5. Описание решений в одномерном случае ветвления.
- 15.6. Описание решений в многомерном случае ветвления.
- § 16. Периодические решения квазилинейных систем
- 16.2. Условия периодичности.
- 16.3. Вывод уравнения разветвления.
- 16.4. Описание решений и дополнительные замечания.
- § 17. Периодические решения автономных систем
- 17.2. Уравнение разветвления.
- 17.3. Основные выводы.
- 17.4. Метод неопределенных коэффициентов.
- 17.5. Автономные системы с одной степенью свободы.
- § 18. Примеры
- 18.1. Неавтономные системы с одной степенью свободы.
- 18.2 Автономные системы с одной степенью свободы.
- § 19. Другие задачи о периодических решениях
- 19.1. Особые периодические решения неавтономных систем.
- 19.2. Ветвление периодических решений в банаховых пространствах
- § 20. Об устойчивости периодических решений, зависящих от малого параметра
- 20.2. Устойчивость решений задачи Пуанкаре.
- ГЛАВА VII. Нелинейные уравнения в банаховых пространствах
- § 21. Некоторые вопросы теории линейных операторов в банаховых пространствах
- 21.2. Специальные разложения пространств в прямые суммы подпространств.
- 21.3. Сужение оператора и обобщенная лемма Шмидта.
- 21.4 Связь с сопряженным оператором.
- 21.5. Неограниченные фредгольмовские операторы.
- § 22. Степенные операторы, ряды Тейлора, теоремы о неявных операторах
- 22.2 Степенные ряды. Ряды Тейлора.
- 22.3 Теоремы о неявных операторах.
- § 23. Уравнение разветвления Ляпунова — Шмидта
- 23.2. Вывод уравнения разветвления с помощью сужения оператора B.
- 23.3. Вывод уравнения разветвления с помощью леммы Шмидта.
- 23.4. Основная теорема об уравнении разветвления.
- 23.5. Уравление разветвления в аналитическом случае.
- 23.6. Уравнение разветвления для неограниченных операторов.
- § 24. Исследование одномерного случая ветвления
- 24.2. Вырожденный случай.
- 24.3. Квазирегулярный случай (задача А).
- 24.4. Задача Б (невырожденный случай).
- 24.5 Вещественный случай.
- 24.6. О ветвлении решений уравнений о достаточно гладкими операторами.
- 24.7 Случай функционального параметра. Ряды по однородным операторам.
- 24.8. Случай двух числовых параметров.
- § 25. Многомерный случай ветвления
- 25.2. Коэффициенты двумерного уравнения разветвления.
- 25.3. Двумерный случай ветвления.
- 25.4 Общий случай.
- 25.5. О ветвлении изолированного решения.
- 25.6. О точках бифуркации.
- ГЛАВА VIII. Ветвление решений нелинейных уравнений в сингулярном случае
- 26.2. Разложение пространств в прямые суммы подпространств.
- 26.3. Теорема Аткинсона.
- 23.4. О нетеровских неограниченных операторах.
- § 27. Теоремы о ветвлении решений
- 27.2. Случай n > 0, m = 0.
- 27.3. Случай n = 0, m > 0.
- 27.4. Основной случай. Уравнение разветвления.
- 27.5. О ветвлении решений уравнения с неограниченным оператором.
- § 28. Ветвление решений нелинейных сингулярных интегральных уравнений.
- 28.2. Нелинейные сингулярные интегральные уравнения с ядром типа Коши в пространствах Гёльдера.
- 28.3. Аналитический случай.
- 28.4. Нелинейные сингулярные интегральные уравнения с ядром Гильберта в пространствах Лебега.
- § 29. Ветвление решений краевых задач для нелинейных эллиптических уравнений
- 29.2. Краевые задачи на плоскости для эллиптических систем k-го порядка в пространстве Гёльдера.
- 29.3. Краевые задачи для эллиптических уравнений в пространстве суммируемых функций.
- ГЛАВА IX. Некоторые задачи теории вовмущений
- § 30. Жордановы цепочки и наборы фредгольмовских операторов
- 30.2. А-жордановы цепочки и наборы при n > 1.
- 30.3. Условия полноты А-жорданова набора.
- 30.4. Пример.
- § 31. Возмущение линейного уравнения малым линейным слагаемым
- 31.2. Случай n > 1.
- 31.3. Метод неопределенных коэффициентов.
- § 32. Ветвление собственных значений и собственных элементов фредгольмовских операторов
- 32.2. Уравнение разветвления в аналитическом случае.
- 32.3. Вырожденный и невырожденный случаи.
- 32.4. Одномерный случай.
- 32.5. Метод неопределенных коэффициентов.
- 32.6. Многомерный случай.
- 32.7. Некоторые обобщения.
- § 33. Особые решения нелинейных уравнений
- 33.2. Задача о возмущении линейного уравнения малым нелинейным слагаемым.
- 33.3. Понятие обобщенной жордановой цепочки.
- 33.4. Свойства некоторых многочленов.
- 33.5 Основной случай задачи о возмущении.
- 33.6. Случаи возмущения второго порядка.
- 33.7. Решения порядка …
- ГЛАВА X. Некоторые прикладные задачи
- § 34. О малых изгибах прямолинейного стержня под действием постоянной нагрузки
- § 35. К теории малых прогибов гибких пластин
- 35.2. Случай круглой пластины.
- 35.3. Исследование уравнения разветвления.
- 35.4. Круглая пластина с нулевой внешней нагрузкой.
- § 36. О колебаниях спутника в плоскости эллиптической орбиты
- § 37. Об одном виде установившихся волн
- 37.2. Сведение к системе.
- 37.3. Регулярный случай.
- 37.4. Случай ветвления.
- Литература