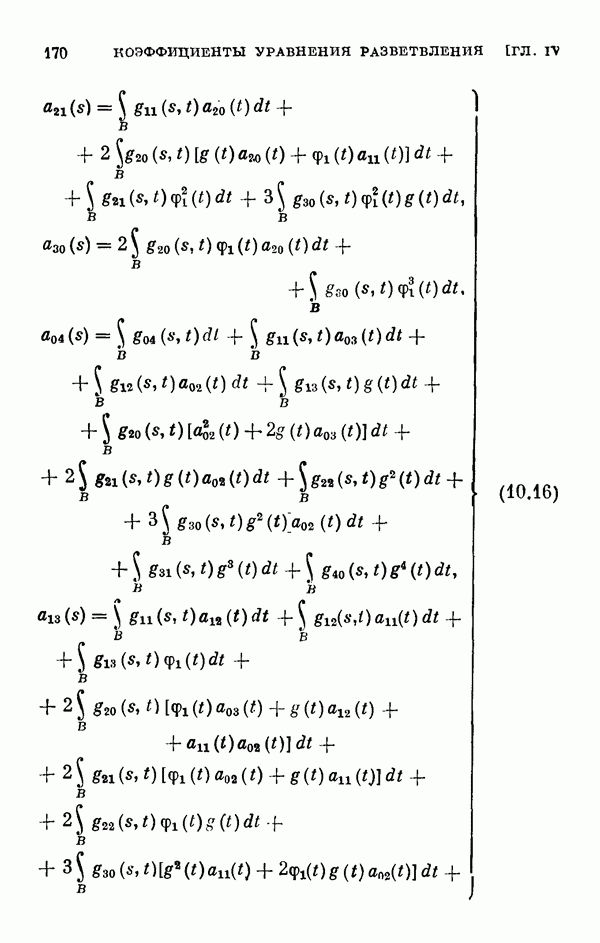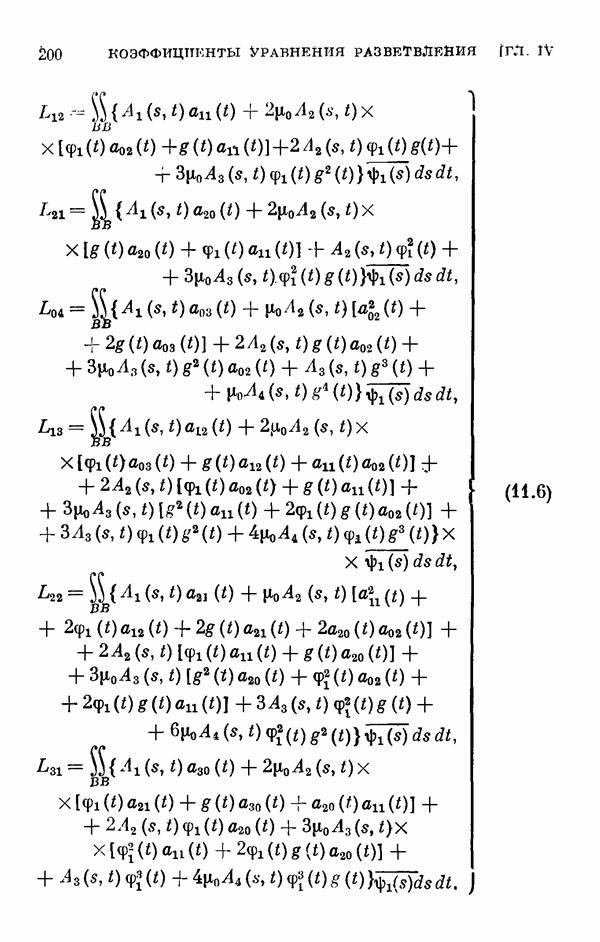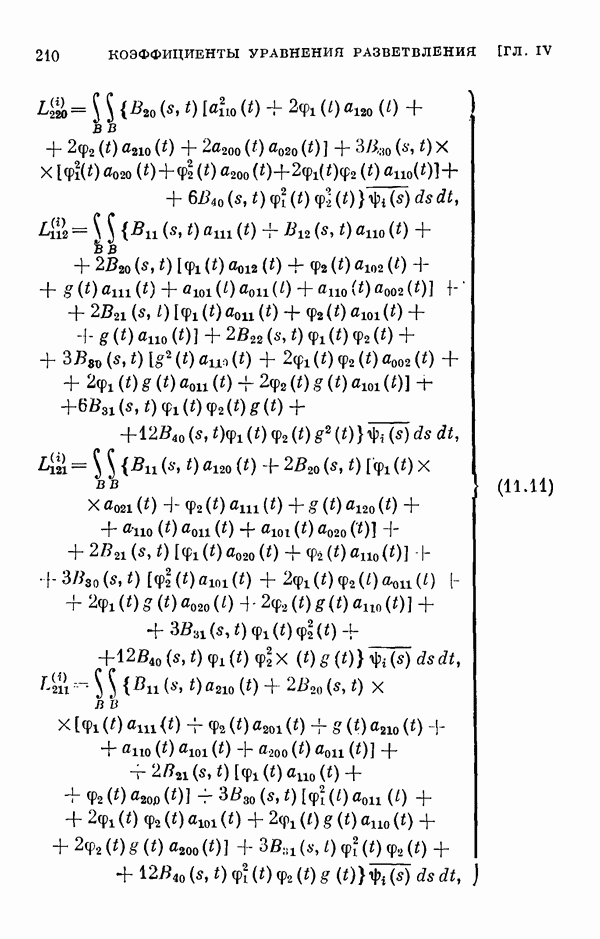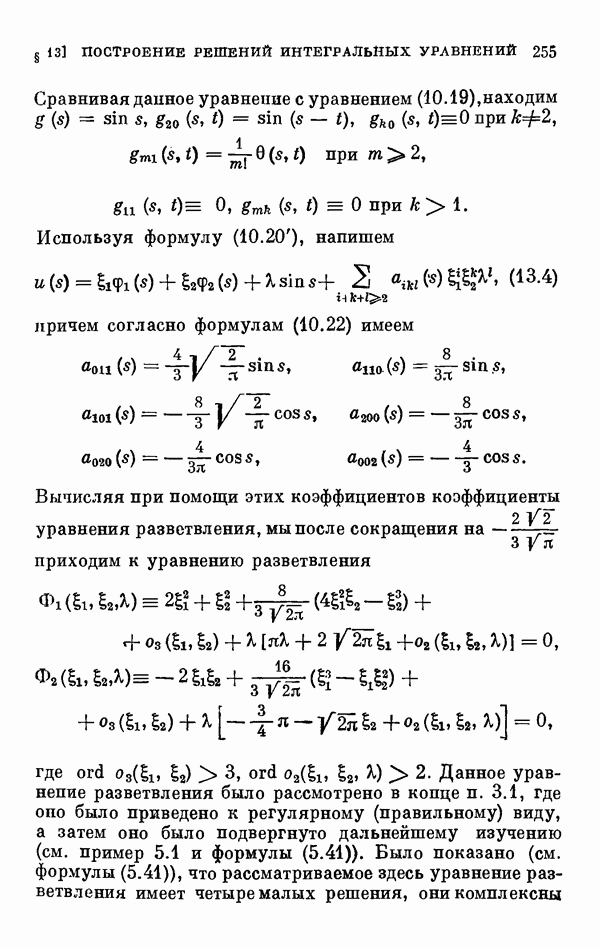| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
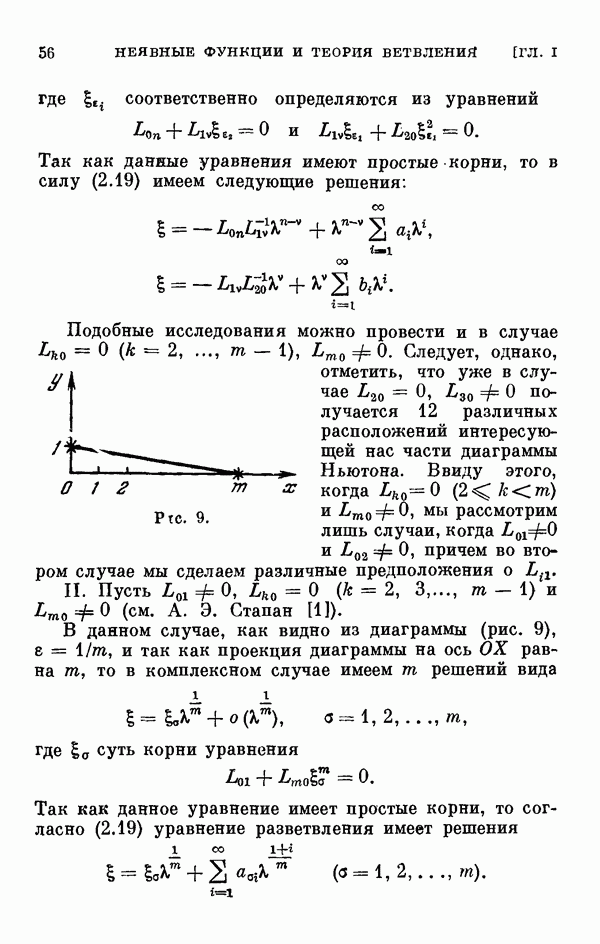
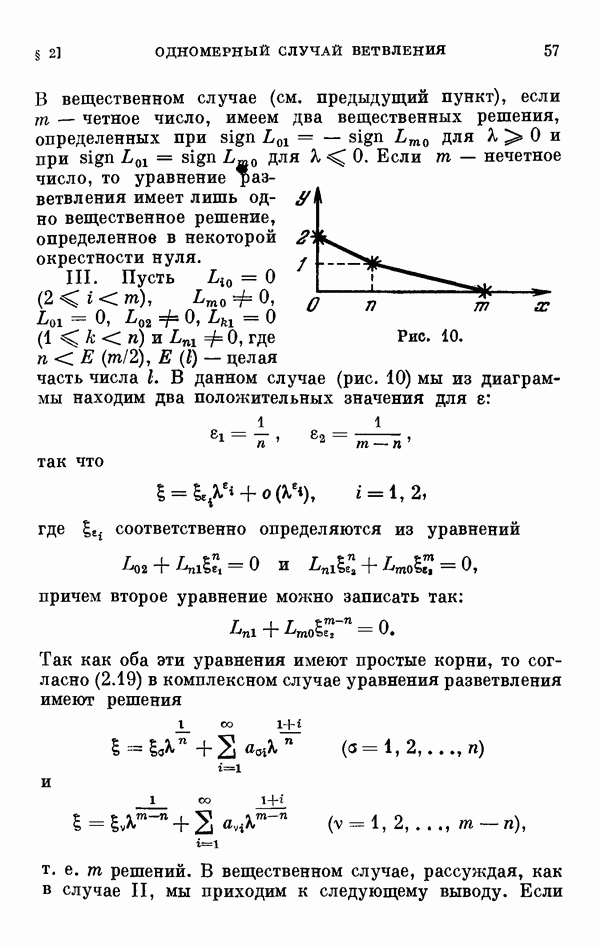
§ 2. Одномерный сличай ветвления и диаграмма Ньютона
Здесь мы исследуем уравнение разветвления (1.11) когда  . В этом случае оно принимает вид
. В этом случае оно принимает вид

Числа  называются коэффициентами уравнения разветвления. К такому уравнению разветвления мы приходим, когда в задаче о неявных функциях (1.1) — (1.2) с аналитическими
называются коэффициентами уравнения разветвления. К такому уравнению разветвления мы приходим, когда в задаче о неявных функциях (1.1) — (1.2) с аналитическими  выполняются условия:
выполняются условия: 
Для исследования уравнения (2.1) мы воспользуемся диаграммой Ньютона.
Ньютон, по-видимому, впервые исследовал вопрос об отыскании неявных функций, когда частная производная может обращаться в нуль. В одной из своих работ (Ньютон [1], стр. 33—44) он рассматривает уравнение

между вещественными переменными х и у, предполагая, что  и что
и что  разлагается в ряд по целым положительным степеням
разлагается в ряд по целым положительным степеням  без требования того, что
без требования того, что  Решение уравнения (2.2) он ищет в виде ряда
Решение уравнения (2.2) он ищет в виде ряда

где  — возрастающая последовательность рациональных чисел. Для нахождения возможных значений
— возрастающая последовательность рациональных чисел. Для нахождения возможных значений  Ньютон дал геометрический прием, получивший название диаграммы Ньютона (или многоугольника Ньютона, или параллелограмма Ньютона). Развитие метода Ньютона и его роль в современном развитии
Ньютон дал геометрический прием, получивший название диаграммы Ньютона (или многоугольника Ньютона, или параллелограмма Ньютона). Развитие метода Ньютона и его роль в современном развитии
математики прекрасно освещены в статье Н. Г. Чеботарева [1]. Результаты Ньютона были получены для уравнения (2.2) и в случае комплексных  При этом было установлено, что никаких других решений, кроме тех, которые были указаны Ньютоном, нет (А. И. Маркушевич [1]).
При этом было установлено, что никаких других решений, кроме тех, которые были указаны Ньютоном, нет (А. И. Маркушевич [1]).
Нас, однако, будут интересовать лишь малые решения уравнения (2.1), т. е. непрерывные решения  удовлетворяющие условию
удовлетворяющие условию 
2.1. Диаграмма Ньютона
Рассмотрим сначала случай, когда  является псевдомногочленом относительно т. е.
является псевдомногочленом относительно т. е.

 — комплексные числа,
— комплексные числа,  — комплексные переменные,
— комплексные переменные,  — неотрицательные рациональные числа,
— неотрицательные рациональные числа,  — любое натуральное число,
— любое натуральное число,  Из нашего допущения о представлении функции
Из нашего допущения о представлении функции  вытекает, что если
вытекает, что если  то можно считать
то можно считать  Следовательно, без ограничения общности можно считать
Следовательно, без ограничения общности можно считать 
Будем рассматривать уравнение

решение которого относительно  будем искать в виде ряда
будем искать в виде ряда

где  или, кратко,
или, кратко,

где 
Для нахождения возможных значений  и мы подставим (2.5) в (2.3), соберем члены с одинаковымы степенями
и мы подставим (2.5) в (2.3), соберем члены с одинаковымы степенями  и приравняем нулю коэффициенты при этих степенях. Начнем с члена наинизшей степени. Пока
и приравняем нулю коэффициенты при этих степенях. Начнем с члена наинизшей степени. Пока  не
не
определено, мы не знаем, какие из полученных членов имеют наинизпшй порядок по Можно лишь утверждать, что низшие члены находятся среди следующих:

если все  или среди членов
или среди членов

где к принимает те из значений  для которых
для которых  Так как в (2.6) все коэффициенты
Так как в (2.6) все коэффициенты  то для сокращения членов низшего порядка необходимо, чтобы по крайней мере два из показателей
то для сокращения членов низшего порядка необходимо, чтобы по крайней мере два из показателей

совпали, а остальные были бы не меньше их. Приравнивая показатели, мы определим все возможные значения  а затем подберем значения так, чтобы сумма коэффициентов членов (2.6), имеющих равные показатели, была равна нулю. Таким образом,
а затем подберем значения так, чтобы сумма коэффициентов членов (2.6), имеющих равные показатели, была равна нулю. Таким образом,  должен быть корнем одного из линейных уравнений
должен быть корнем одного из линейных уравнений

причем из всех корней только те дают решение задачи, подстановка которых в остальные выражения (2.7) дает не меньшее значение, чем 
Для нахождения этих значений используется следующий геометрический прием, принадлежащий Ньютону и носящий название диаграммы Ньютона.
Выберем в плоскости прямоугольную систему координат и построим точки  где к принимает те же значения, что и в (2.6).
где к принимает те же значения, что и в (2.6).
Проведем через точку  прямую, совпадающую с осью ординат, и станем ее вращать вокруг точки
прямую, совпадающую с осью ординат, и станем ее вращать вокруг точки  против часовой стрелки до тех пор, пока она не заденет какую-нибудь из других построенных точек, например
против часовой стрелки до тех пор, пока она не заденет какую-нибудь из других построенных точек, например  Тангенс угла, составляемого прямой
Тангенс угла, составляемого прямой  проходящей через точки
проходящей через точки  с отрицательным направлением оси абсцисс, равен одному из возможных значений
с отрицательным направлением оси абсцисс, равен одному из возможных значений  так как, во-первых, для этого
так как, во-первых, для этого  имеем
имеем  , во-вторых, если через точки
, во-вторых, если через точки 
которые не оказались на этой прямой (по построению эти точки лежат выше), провести прямые параллельно  то они пересекут ось
то они пересекут ось  выше — в точке с ординатой
выше — в точке с ординатой  а потому
а потому

При этом может оказаться, что на прямую  попало несколько из нанесенных точек. Пусть
попало несколько из нанесенных точек. Пусть  — точка на
— точка на  с наибольшей абсциссой. Будем теперь вращать прямую
с наибольшей абсциссой. Будем теперь вращать прямую  против часовой стрелки вокруг точки
против часовой стрелки вокруг точки  пока она не попадет на другую из нанесенных точек, скажем
пока она не попадет на другую из нанесенных точек, скажем  которой абсцисса
которой абсцисса 

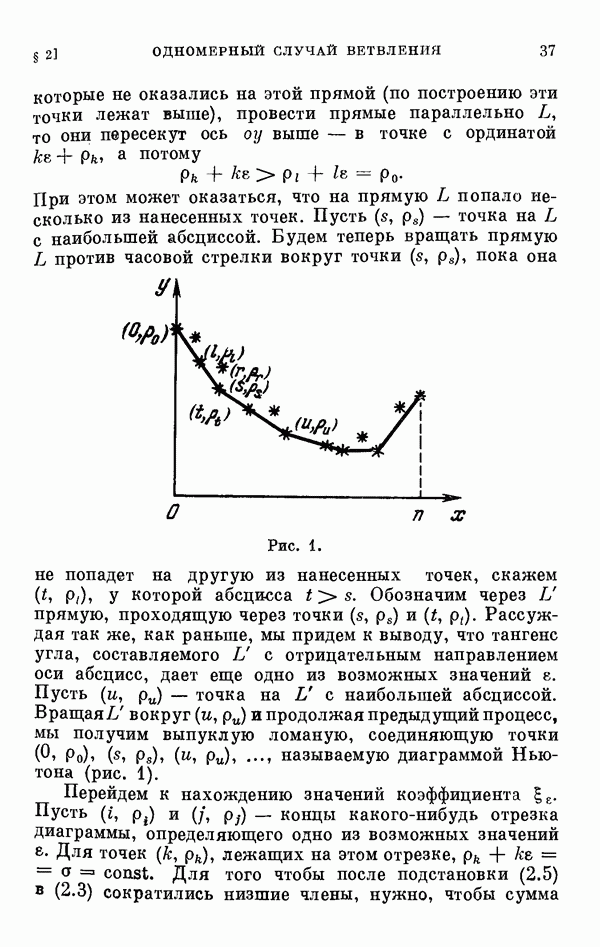
Рис. 1.
Обозначим через  прямую, проходящую через точки
прямую, проходящую через точки  Рассуждая так же, как раньше, мы придем к выводу, что тангенс угла, составляемого
Рассуждая так же, как раньше, мы придем к выводу, что тангенс угла, составляемого  с отрицательным направлением оси абсцисс, дает еще одно из возможных значений е. Пусть
с отрицательным направлением оси абсцисс, дает еще одно из возможных значений е. Пусть  — точка на
— точка на  с наибольшей абсциссой. Вращая
с наибольшей абсциссой. Вращая  вокруг
вокруг  и продолжая предыдущий процесс, мы получим выпуклую ломаную, соединяющую точки
и продолжая предыдущий процесс, мы получим выпуклую ломаную, соединяющую точки  называемую диаграммой Ньютона (рис. 1).
называемую диаграммой Ньютона (рис. 1).
Перейдем к нахождению значений коэффициента  Пусть
Пусть  — концы какого-нибудь отрезка диаграммы, определяющего одно из возможных значений
— концы какого-нибудь отрезка диаграммы, определяющего одно из возможных значений  Для точек
Для точек  лежащих на этом отрезке,
лежащих на этом отрезке,  Для того чтобы после подстановки (2.5) в (2.3) сократились низшие члены, нужно, чтобы сумма
Для того чтобы после подстановки (2.5) в (2.3) сократились низшие члены, нужно, чтобы сумма
коэффициентов при  равнялась нулю, т. е. чтобы
равнялась нулю, т. е. чтобы

где  означает, что суммирование проводится лишь по тем к, для которых
означает, что суммирование проводится лишь по тем к, для которых  Это уравнение имеет
Это уравнение имеет  отличных от нуля корней (различных или частично совпадающих), т. е. столько корней, какова длина проекции взятого отрезка диаграммы. Отсюда видно, что этим методом мы получим все
отличных от нуля корней (различных или частично совпадающих), т. е. столько корней, какова длина проекции взятого отрезка диаграммы. Отсюда видно, что этим методом мы получим все  значений главного члена
значений главного члена  в разложении (2.5).
в разложении (2.5).
Для нахождения следующего члена разложения  нужно подставить (2.5) в (2.3) и тем же приемом найти низший член разложения для V. Продолжая данный процесс вычисления, мы придем к разложению (2.4) для каждого из
нужно подставить (2.5) в (2.3) и тем же приемом найти низший член разложения для V. Продолжая данный процесс вычисления, мы придем к разложению (2.4) для каждого из  решений уравнения (2.3).
решений уравнения (2.3).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ГЛАВА I. Системы неявных функций и классическая теория ветвления
- § 1. Задача о неявных функциях
- 1.2. Общее исследование задачи о неявных функциях.
- 1.3. Аналитический случай.
- § 2. Одномерный сличай ветвления и диаграмма Ньютона
- 2.2. О свойствах решений.
- 2.3. Примеры.
- 2.4. Исследование уравнения разветвления. Случай простых корней определяющего уравнения.
- 2.5. Случай кратных корней определяющего уравнения.
- 2.6. О вещественных решениях.
- 2.7. Некоторые частные случаи расположения диаграммы Ньютона.
- ГЛАВА II. Исследование уравнения разветвления в многомерном случае
- 3.2. Приведение к нормальному виду.
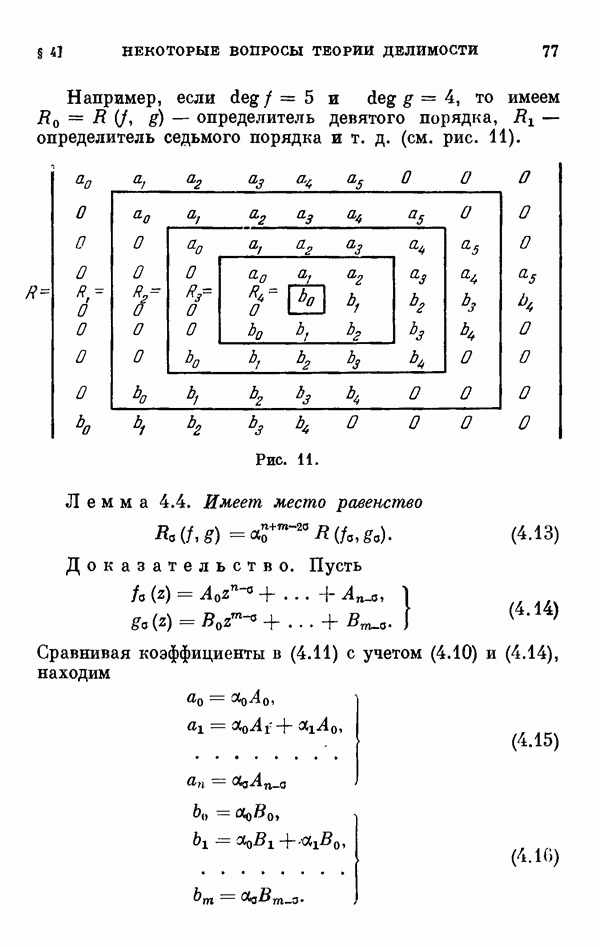
- § 4. Некоторые вопросы теории делимости
- 4.2. Общий делитель и аналог алгоритма Евклида.
- 4.3. Примитивный ОНД.
- 4.4. Применение к отмеченным многочленам.
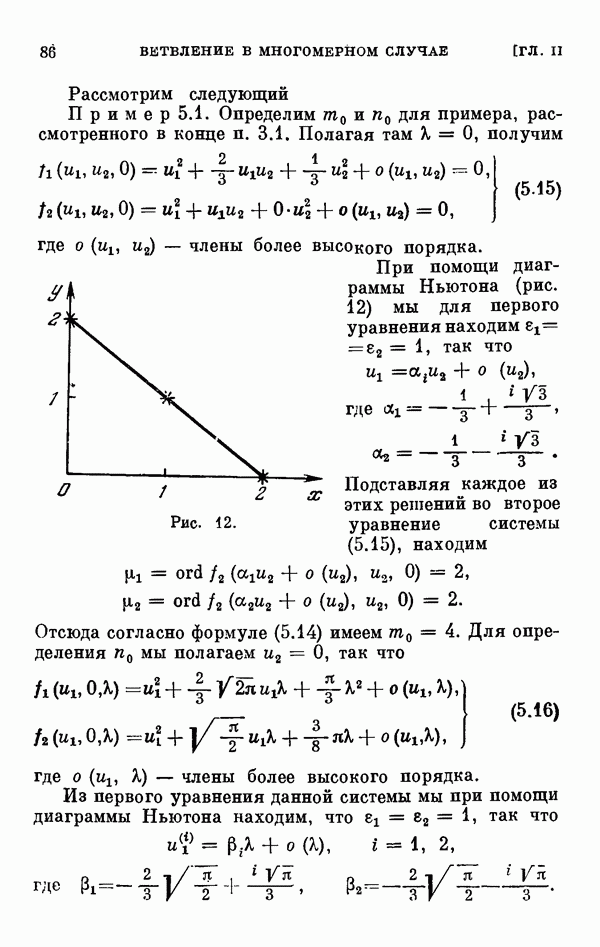
- § 5. Двумерный случай ветвления
- 5.2. Указатели двумерного случая ветвления.
- 5.3. Частные случаи.
- § 6. Многомерный случай ветвления
- 6.2. Малые решения уравнения разветвления и метод исключения неизвестных.
- 6.3. Квазирегулярный случай ветвления.
- 6.4. Вырожденный случай ветвления.
- 6.5. Об изолированности нулевого решения.
- ГЛАВА III. Уравнение разветвления для нелинейных интегральных и интегро-дифференциальных уравнений
- § 7. Интегральные уравнения Ляпунова — Шмидта
- 7.2. Интегро-степенные ряды от многих функциональных аргументов.
- 7.3. Интегро-степенные ряды от интегро-степенных рядов.
- 7.4. Сжатость оператора Ляпунова—Шмидта.
- 7.5. Простейшее уравнение.
- 7.6. Последовательные приближения Лихтенштейна.
- 7.7. Применение метода мажорант.
- 7.8. Простейшее уравнение в случае равномерной сходимости.
- § 8. Общее интегральное уравнение Ляпунова—Шмидта
- 8.2. Регулярный случай при наличии многих аргументов.
- 8.3. Лемма Шмидта.
- 8.4. Одномерный случай ветвления.
- 8.5. Многомерный случай ветвления.
- 8.6. Возможные обобщения.
- § 9. Системы уравнений Ляпунова—Шмидта и некоторые интегро-дифференциальные уравнения
- 9.2. Регулярный случай.
- 9.3. Случай ветвления.
- 9.4. Некоторые нелинейные интегро-дифференциальные уравнения первого порядка.
- 9.5. Другие виды интегро-дифференциальных уравнений.
- 9.6. Другой способ построения уравнения разветвления
- ГЛАВА IV. Общее интегральное уравнение и коэффициенты уравнения разветвления
- 10.2. Регулярный случай.
- 10.3. Одномерный случай ветвления.
- 10.4. Многомерный случай ветвления.
- 10.5 Частный случай.
- 10.6. Уравнение Гаммерштейна.
- § 11. Коэффициенты уравнения разветвления
- 11.2. Коэффициенты одиомерного уравнения разветвления нелинейного интегрального уравнения Гаммерштейна.
- 11.3. Коэффициенты двумерного уравнения разветвления общего нелинейного интегрального уравнения.
- 11.4. Коэффициенты двумерного уравнения разветвления для частных случаев.
- 11.5. Некоторые свойства коэффициентов уравнения разветвления.
- ГЛАВА V. Описание и построение решений нелинейных интегральных уравнений
- § 12. Описание решений нелинейных интегральных уравнений
- 12.2. Описание решении в одномерном случае ветвления.
- 12.3. О точках бифуркации в одномерном случае ветвления.
- 12.4. Описание решений в двумерном случае ветвления.
- 12.5. Описание решений в многомерном случае ветвления.
- 12.6. О ветвлении изолированного решения.
- 12.7. Точки бифуркации в многомерном случае ветвления.
- § 13. Построение решений нелинейных интегральных уравнений
- 13.3. Двумерный случай ветвления.
- 13.4. Уравнение Некрасова.
- 13.5. Уравнение разветвления для уравнения Некрасова.
- § 14. Особые решения нелинейных интегральных уравнений
- 14.2. Сведение к малым решениям.
- 14.3. Особые решения в регулярном случае.
- 14.4. Исследование вспомогательного уравнения.
- 14.5. Ветвление решений основного уравнения.
- 14.6 Особые решения в пространствах Лебега.
- ГЛАВА VI. Ветвление периодических решений дифференциальных уравнений
- § 15. Периодические решения неавтономных систем
- 15.2. Метод Пуанкаре.
- 15.3. Условия периодичности и уравненне разветвления.
- 15.4. Описание решений в регулярном случае.
- 15.5. Описание решений в одномерном случае ветвления.
- 15.6. Описание решений в многомерном случае ветвления.
- § 16. Периодические решения квазилинейных систем
- 16.2. Условия периодичности.
- 16.3. Вывод уравнения разветвления.
- 16.4. Описание решений и дополнительные замечания.
- § 17. Периодические решения автономных систем
- 17.2. Уравнение разветвления.
- 17.3. Основные выводы.
- 17.4. Метод неопределенных коэффициентов.
- 17.5. Автономные системы с одной степенью свободы.
- § 18. Примеры
- 18.1. Неавтономные системы с одной степенью свободы.
- 18.2 Автономные системы с одной степенью свободы.
- § 19. Другие задачи о периодических решениях
- 19.1. Особые периодические решения неавтономных систем.
- 19.2. Ветвление периодических решений в банаховых пространствах
- § 20. Об устойчивости периодических решений, зависящих от малого параметра
- 20.2. Устойчивость решений задачи Пуанкаре.
- ГЛАВА VII. Нелинейные уравнения в банаховых пространствах
- § 21. Некоторые вопросы теории линейных операторов в банаховых пространствах
- 21.2. Специальные разложения пространств в прямые суммы подпространств.
- 21.3. Сужение оператора и обобщенная лемма Шмидта.
- 21.4 Связь с сопряженным оператором.
- 21.5. Неограниченные фредгольмовские операторы.
- § 22. Степенные операторы, ряды Тейлора, теоремы о неявных операторах
- 22.2 Степенные ряды. Ряды Тейлора.
- 22.3 Теоремы о неявных операторах.
- § 23. Уравнение разветвления Ляпунова — Шмидта
- 23.2. Вывод уравнения разветвления с помощью сужения оператора B.
- 23.3. Вывод уравнения разветвления с помощью леммы Шмидта.
- 23.4. Основная теорема об уравнении разветвления.
- 23.5. Уравление разветвления в аналитическом случае.
- 23.6. Уравнение разветвления для неограниченных операторов.
- § 24. Исследование одномерного случая ветвления
- 24.2. Вырожденный случай.
- 24.3. Квазирегулярный случай (задача А).
- 24.4. Задача Б (невырожденный случай).
- 24.5 Вещественный случай.
- 24.6. О ветвлении решений уравнений о достаточно гладкими операторами.
- 24.7 Случай функционального параметра. Ряды по однородным операторам.
- 24.8. Случай двух числовых параметров.
- § 25. Многомерный случай ветвления
- 25.2. Коэффициенты двумерного уравнения разветвления.
- 25.3. Двумерный случай ветвления.
- 25.4 Общий случай.
- 25.5. О ветвлении изолированного решения.
- 25.6. О точках бифуркации.
- ГЛАВА VIII. Ветвление решений нелинейных уравнений в сингулярном случае
- 26.2. Разложение пространств в прямые суммы подпространств.
- 26.3. Теорема Аткинсона.
- 23.4. О нетеровских неограниченных операторах.
- § 27. Теоремы о ветвлении решений
- 27.2. Случай n > 0, m = 0.
- 27.3. Случай n = 0, m > 0.
- 27.4. Основной случай. Уравнение разветвления.
- 27.5. О ветвлении решений уравнения с неограниченным оператором.
- § 28. Ветвление решений нелинейных сингулярных интегральных уравнений.
- 28.2. Нелинейные сингулярные интегральные уравнения с ядром типа Коши в пространствах Гёльдера.
- 28.3. Аналитический случай.
- 28.4. Нелинейные сингулярные интегральные уравнения с ядром Гильберта в пространствах Лебега.
- § 29. Ветвление решений краевых задач для нелинейных эллиптических уравнений
- 29.2. Краевые задачи на плоскости для эллиптических систем k-го порядка в пространстве Гёльдера.
- 29.3. Краевые задачи для эллиптических уравнений в пространстве суммируемых функций.
- ГЛАВА IX. Некоторые задачи теории вовмущений
- § 30. Жордановы цепочки и наборы фредгольмовских операторов
- 30.2. А-жордановы цепочки и наборы при n > 1.
- 30.3. Условия полноты А-жорданова набора.
- 30.4. Пример.
- § 31. Возмущение линейного уравнения малым линейным слагаемым
- 31.2. Случай n > 1.
- 31.3. Метод неопределенных коэффициентов.
- § 32. Ветвление собственных значений и собственных элементов фредгольмовских операторов
- 32.2. Уравнение разветвления в аналитическом случае.
- 32.3. Вырожденный и невырожденный случаи.
- 32.4. Одномерный случай.
- 32.5. Метод неопределенных коэффициентов.
- 32.6. Многомерный случай.
- 32.7. Некоторые обобщения.
- § 33. Особые решения нелинейных уравнений
- 33.2. Задача о возмущении линейного уравнения малым нелинейным слагаемым.
- 33.3. Понятие обобщенной жордановой цепочки.
- 33.4. Свойства некоторых многочленов.
- 33.5 Основной случай задачи о возмущении.
- 33.6. Случаи возмущения второго порядка.
- 33.7. Решения порядка …
- ГЛАВА X. Некоторые прикладные задачи
- § 34. О малых изгибах прямолинейного стержня под действием постоянной нагрузки
- § 35. К теории малых прогибов гибких пластин
- 35.2. Случай круглой пластины.
- 35.3. Исследование уравнения разветвления.
- 35.4. Круглая пластина с нулевой внешней нагрузкой.
- § 36. О колебаниях спутника в плоскости эллиптической орбиты
- § 37. Об одном виде установившихся волн
- 37.2. Сведение к системе.
- 37.3. Регулярный случай.
- 37.4. Случай ветвления.
- Литература