6.3. Задача Дирихле

Рассмотрим задачу Дирихле для уравнения в ограниченной области пространства Используемая здесь процедура ее решения для уравнения с переменными коэффициентами состоит в сведении с помощью метода продолжения по параметру к случаю постоянных коэффициентов. Коротко говоря, применяемый здесь метод отправляется от решения задачи для уравнения Пуассона затем уравнения непрерывно соединяются семейством эллиптических уравнений.

Рассмотрим сначала задачу Дирихле для достаточно гладких областей и граничных данных. В этой ситуации связь между разрешимостью

уравнения Пуассона и уравнения в котором описывается следующей теоремой.

Теорема 6.8. Пусть область в класса и пусть сильно эллиптический оператор в с коэффициентами из причем с Тогда если задача Дирихле для уравнения Пуассона на 912) имеет для любой функции и любой функции , то задача

также имеет (единственное) решение из для всех таких функций

Доказательство. В силу условий теоремы мы можем считать, что коэффициенты оператора удовлетворяют условиям

с положительными постоянными (В написанных нормах мы для краткости опускаем индекс Так как задача (6.39) эквивалентна задаче на , то достаточно ограничиться рассмотрением случая нулевых граничных значений. Рассмотрим семейство уравнений

Заметим, что и что коэффициенты оператора удовлетворяют (6.40) с постоянными

Оператор можно рассматривать как линейный ограниченный оператор из банахова пространства на банахово пространство Однозначная разрешимость задачи Дирихле на для эквивалентна взаимной однозначности отображения на Обозначим через решение этой задачи. В силу теоремы 3.7 справедлива оценка

в которой постоянная С зависит только от и диаметра области Следовательно, из (6.36) следует, что

т. е.

где постоянная С не зависит от Так как по условию оператор отображает на все то применим метод продолжения по параметру (теорема 5.2), откуда и следует утверждение теоремы.

Одним из условий теоремы 6.8 является условие разрешимости в пространстве задачи Дирихле для уравнения Пуассона в случае, когда

область и граничные данные принадлежат классу В действительности это условие не является ограничением: факт соответствующей разрешимости задачи Дирихле — теорема Келлога — может быть установлен непосредственно методами теории потенциала. Однако мы здесь не будем ни предполагать, ни доказьюать его, а получим его позднее из общей эллиптической теории. В специальном случае, когда есть шар, теорема Келлога была нами доказана в следствии 4.14. Таким образом, для случая, когда область является шаром, мы доказали следующую теорему существования.

Следствие 6.9. Пусть в теореме 6.8 область является шаром В и пусть оператор удовлетворяет условиям теоремы 6.8. Тогда если то задача Дирихле имеет (единственное) решение и

Условия на граничные данные можно ослабить в рамках следующего обобщения, которое будет использовано далее.

Лемма 6.10. Пусть кусок границы (возможно, пустой) шара и пусть Тогда если оператор удовлетворяет в шаре В условиям теоремы то задача Дирихле на имеет (единственное) решение и

Доказательство. Пусть произвольная точка если непусто. Мы можем предполагать, что граничная функция у непрерывно продолжена по радиусу и продолженная функция (обозначим ее также через принадлежит где шар, содержащий В (см. замечание 2 после леммы 6.38). Пусть — последовательность достаточно гладких в В (например, из класса функций таких, что

с постоянной С, не зависящей от к. (По поводу существования такой аппроксимации см. обсуждение после леммы 7.1.) Для каждого к обозначим через соответствующее решение задачи Дирихле на В силу следствия 6.9 функции существуют и принадлежат Из принципа максимума следует, что последовательность равномерно сходится к функции и такой, что на Компактность семейства обеспечивается следствием 6.3, гарантирующим также, что последовательность сходится к решению уравнения на компактных подмножествах В и, следовательно, предельная функция и будет решением класса уравнения в В. Кроме того, в силу следствия 6.7 в области . В функции удовлетворяют оценке

Из (6.43) и теоремы Арцела следует, что функция и удовлетворяет такой же оценке (с заменой на частности, что и Таким образом, функция и , и лемма доказана.

Специально отметим, что из этой леммы следует существование решения задачи Дирихле в шаре, если граничные значения просто непрерывны. Решение в этом случае будет принадлежать

Теперь мы можем перенести на рассматриваемую ситуацию изложенный в гл. II метод Перрона субгармонических функций, а полученные там для гармонических функций результаты распространить на задачу Дирихле для уравнения Функцию и класса будем называть субрешением суперрешением) уравнения в области если для любого шара и любого решения такого, что в В, из неравенства выполняющегося на следует неравенство и во всем шаре В. Если мы предположим, что оператор удовлетворяет условиям сильного принципа максимума и задача Дирихле для уравнения разрешима в шарах для непрерывных граничных функций, то субрешения и субгармонические функции обладают многими одинаковыми свойствами. Мы сформулируем эти свойства без доказательств. Доказательства этих утверждений по существу те же, что и для субгармонических функций. Если функция и коэффициенты оператора принадлежат то в этих доказательствах следует теоремы 2.2 и 2.6 заменить теоремой 3.5 и леммой 6.10 соответственно.

(i) Функция и является субрешением тогда и только тогда, когда

Если функция и является субрешением в ограниченной области а функция является суперрешением в причем на выполняется неравенство то либо всюду в либо

Пусть функция и является субрешением в и В — такой шар, что Обозначим через и решение уравнения в В, удовлетворяющее условию и — и на Тогда функция определенная равенством

является субрешением в

Пусть и субрешения в области Тогда функция является также субрешением в

Аналогичные свойства имеют место, очевидно, и для суперрешений.

Пусть ограниченная область, а ограниченная функция на Функцию и будем называть субфункцией (суперфункцией) относительно если и является субрешением (суперрешением) в и выполняется неравенство и на . В силу свойства (ii) каждая субфункция не превосходит произвольную суперфункцию. Обозначим через множество субфункций в относительно Предположим, что непусто и ограничено сверху. Такова ситуация, например, в случае, когда оператор строго эллиптичен в и его коэффициенты и функция ограничены. Действительно, если лежит в полосе то функции

являются соответственно суперфункцией и субфункцией, если постоянная у

достаточно велика (см. теорему 3.7). Суперфункция ограничивает сверху функции из а существование субфункции гарантирует непустоту

Мы можем теперь сформулировать основной результат о существовании решения, получаемого процессом Перрона, для уравнения в предположении, что и коэффициенты оператора принадлежат и что

Теорема 6.11. Если функция ограничена, она принадлежит и является решением уравнения в области

Доказательство этой теоремы лишь незначительно отличается от доказательства теоремы 2.12, и мы оставляем его читателю. При этом обратим внимание на то, что используемая в доказательстве компактность решений обеспечивается внутренней оценкой следствия 6.3, а подходящая форма принципа максимума дается теоремой 3.5.

Перейдем теперь к описанию условий, гарантирующих непрерывное принятие построенным в теореме 6.11 решением граничного значения Как и в случае гармонических функций, эта задача может быть решена на основе барьерной концепции, которую мы изложим в случае уравнения ограниченной области. Пусть — определенная и ограниченная на функция, непрерывная в точке Последовательность функций из назьюается верхним (нижним) барьером в в точке если:

(i) является суперфункцией (субфункцией) относительно у и

Если оба — верхний и нижний — барьера существуют в точке, мы будем, для краткости, говорить просто о барьере в точке.

Основное свойство барьеров дано в следующей лемме.

Лемма 6.12. Пусть функция у ограничена на 912 и непрерывна в точке а и - определенное в теореме 6.11 решение в уравнения Тогда если в точке существует барьер, то при

Доказательство. Из определения и из того, что любая субфункция не превосходит любую суперфункцию, мы имеем для всех Для произвольного и для всех достаточно больших из условия (ii) следуют неравенства Отсюда следовательно, при

Мы расширим концепцию барьеров с помощью следующих замечаний.

Замечание 1. Во многих интересных случаях специальная структура уравнения упрощает определение барьера. Например, в случае ситуация аналогична ситуации для уравнения Лапласа, для которого барьер в точке определяется просто как суперрешение обладающее свойством: на Покажем это. Возьмем произвольное тогда в силу ограниченности и непрерывности в точке функции у существует такая положительная постоянная что

функции

будут соответственно суперфункцией и субфункцией в по отношению к причем, очевидно, при Таким образом, семейства определяют барьер.

Рассмотрим другой класс уравнений. Предположим, что функция и коэффициенты оператора ограничены в . В этом случае одна функция определяет барьер в точке если она удовлетворяет условиям:

Действительно, для найдем, как и ранее, положительную постоянную такую, что

Если теперь мы возьмем то функции

будут соответственно суперфункцией и субфункцией и определят барьер в точке Действительно, на 912 и, так как то

Аналогично Поэтому семейства функций определяют барьер относительно в точке

В случае, когда, как и в рассмотренных примерах, барьер в точке строится с помощью фиксированного зависящего только от! и области суперрешения уравнения мы будем говорить, что функция определяет барьер в точке

Замечание 2. Введенное определение барьера нередко трудно использовать в приложениях, так как при этом требуется построение глобальных суб- и суперрешений, определенных во всей области Поэтому возникает потребность в построении локальных барьеров, позволяющих получать нужные результаты. Пусть верхняя (нижняя) грань множества значений решения в поведение которого изучается вблизи точки Последовательность функций будем называть локальным верхним (нижним) барьером относительно в точке если существует окрестность точки такая, что:

(i) является супер (суб) решением в

(В частности, если то функции определяют барьер в точке в введенном ранее глобальном смысле; в этом случае условие (iii) может быть опущено.) Непосредственно видно, что если решение существование которого установлено в теореме 6.11, удовлетворяет в

неравенству то лемма 6.12 остается справедливой в предположении, что существует локальный барьер в точке относительно граней

Локальные барьеры будут играть далее в этой книге важную роль при изучении граничного поведения решений.

Замечание 3. Так же, как и в лемме 6.12, показывается, что барьер определяет вблизи границы модуль непрерывности решения, непрерывно принимающего свое граничное значение. Тем самым в рассмотренных в замечании 1 случаях справедливо следующее утверждение: если - ограниченное решение уравнения такое, что при то для произвольного существует положительная постоянная такая, что в выполняется неравенство Если функция определяет локальный барьер в точке то такое же неравенство выполняется в фиксированной окрестности точки (не зависящей от ).

Для уравнения как и для уравнения Лапласа, существование барьеров и методы их построения тесно связаны с локальными свойствами границы. Проиллюстрируем сказанное примером, интересным для дальнейших приложений. Пусть заданный в ограниченной области строго эллиптический оператор с коэффициентом и пусть функция и коэффициенты оператора ограничены в Предположим, что область удовлетворяет условию внешней сферы в точке т.е. найдется шар такой, что выполняется соотношение Покажем, что при некоторых положительных постоянных и а функция

удовлетворяет в II неравенству а следовательно, определяет барьер в точке Полагая для простоты из (6.40) и из неравенства с мы получаем в точках

Так как область и коэффициенты оператора 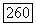ограничены, то правая часть полученного неравенства при достаточно большом значении о будет отрицательна и; более того, будет строго меньше отрицательной постоянной. Поэтому, как и утверждалось, для достаточно больших 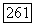и а будет выполняться неравенство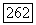

Таким образом, если уравнение 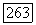удовлетворяет перечисленным выше условиям, а ограниченная область 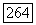удовлетворяет в каждой точке 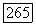условию внешней сферы (это имеет место, например, для любой области класса 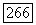для каждой граничной точки существует барьер и применима поэтому лемма 6.12, если только заданные граничные значения являются непрерывной функцией. Объединяя этот результат с теоремой 6.11, мы получаем следующую общую теорему существования.

Теорема 6.13. Пусть оператор 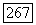строго эллиптичен в ограниченной области 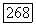коэффициент с 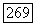и пусть функция 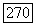и коэффициенты оператора 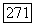ограничены и принадлежат 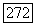Предположим также, что область 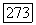удовлетворяет условию внешней сферы в любой граничной точке. Тогда

если функция 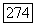непрерывна на 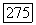то задача Дирихле

имеет (единственное) решение и, принадлежащее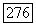

Эта теорема может быть обобщена на более широкий класс областей. В частности, при тех же самых условиях на 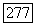можно доказать утверждение теоремы для областей, удовлетворяющих условию внешнего конуса (см. задачу 6.3).

Если требования теоремы несколько усилить, например, если предположить, что функциями коэффициенты оператора 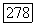принадлежат 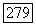то можно доказать, что классы областей, для которых задача Дирихле разрешима при произвольных непрерывных граничных значениях для оператора Лапласа и для оператора 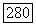совпадают (см. примечания).

Вернемся теперь к вопросу о глобальной регулярности построенных выше решений для достаточно гладких граничных данных. Мы видели, что при выполнении условий теоремы 6.8 решение задачи Дирихле для уравнения 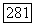принадлежит 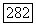если только справедлив соответствующий результат (теорема Келлога) для уравнения Лапласа.

Сейчас мы докажем теорему о регулярности непосредствено из результатов этого раздела.

Теорема 6.14. Пусть оператор 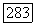строго эллиптичен в ограниченной области коэффициент 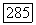и пусть функция 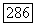и коэффициенты оператора 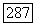принадлежат Предположим, что 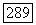область класса 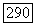и что функция Тогда задача Дирихле

имеет (единственное) решение, принадлежащее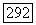

Доказательство. Так как выполнены условия теоремы 6.13, то решение и задачи Дирихле существует. Из теоремы 6.13 мы знаем, что и 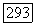так что остается только показать, что для каждой точки 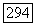и для некоторой окрестности 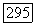этой точки и 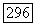Так как 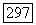есть область класса 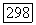то существует такая окрестность Лоточки 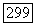которая при диффеоморфизме 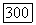класса отображается в окрестность таким образом, что содержит замыкание шара В, а содержащая точку часть пересечения отображается этим преобразованием в часть границы шара В. При этом отображении уравнение переходит в уравнение определенное в шаре В. Так как отображение принадлежит классу то а функция и оператор удовлетворяют в В тем же условиям, которым в удовлетворяли функциям оператор Это значит, что оператор строго эллиптичен в В, коэффициент , функциям и коэффициенты оператора принадлежат (см. лемму 6.5). Рассмотрим решение задачи Дирихле: на Так как на то и на Следовательно, в силу единственности задачи Дирихле и леммы 6.10 решение и . Возвращаясь в обозначим Получим, что

и произвольная точка то мы заключаем, что и

Полученный результат может быть обобщен на случай более слабых требований о регулярности коэффициентов, области и граничных значений (см. примечания).

Если оператор не удовлетворяет условию то, как показывают несложные примеры, задача Дирихле для уравнения может, вообще говоря, не иметь решения. Однако можно утверждать справедливость альтернативы Фредгольма, которую мы сформулируем в следующем виде.

Теорема 6.15. Пусть оператор с строго эллиптичен, его коэффициенты принадлежат и пусть область является областью класса Тогда или

а) однородная задача имеет только тривиальное решение в этом случае неоднородная задача на имеет единственное решение класса для произвольных или

б) однородная задача имеет нетривиальные решения, которые образуют конечномерное подпространство пространства .

Доказательство. При сделанных предположениях относительно функций неоднородная задача на эквивалентна задаче Будем рассматривать далее задачу Дирихле с нулевым краевым условием: на и поэтому достаточно рассматривать оператор на линейном пространстве на Пусть — какая-то постоянная удовлетворяющая неравенству Пусть . В силу теоремы 6.14 отображение обратимо. Кроме того, в силу оценок (6.36) и теоремы 3.7 обратное отображение является компактным отображением пространства в пространство и потому является компактным отображением и как отображение С (12) в Рассмотрим уравнение

в котором оператор является компактным.

По теореме 5.3 о компактных операторах в банаховых пространствах имеет место альтернатива Фредгольма, и уравнение (6.46) имеет решение и из если только однородное уравнение и имеет лишь тривиальное решение Если же последнее условие не выполняется, то нуль-пространство оператора тождественный оператор) является конечномерным подпространством пространства (теорема 5.5).

Для того чтобы перенести эти утверждения на задачу Дирихле для уравнения прежде ьсего заметим, что, так как оператор отображает , любое решение и уравнения (6.46) принадлежит также и . Следовательно, действуя на (6.46) оператором 2а, мы получим

Ясно, что имеется взаимно однозначное соответствие между решениями

уравнения (6.46) и решениями краевой задачи (6.47). Отсюда следует утверждение теоремы.

Важность установленной альтернативы для задачи Дирихле состоит в том, что вопрос о существовании сводится к изучению вопроса о единственности. Отметим, что в силу леммы 6.18 (которая будет доказана в следующем разделе) решения уравнения из класса принадлежат и поэтому нуль-пространство оператора также конечномерно. Отметим также, что из теоремы 5.5 следует, что множество вещественных чисел а, для которых однородная задача имеет нетривиальные решения, является не более чем счетным и дискретным. Кроме того (по теореме 5.3), если то любое решение задачи Дирихле удовлетворяет оценке с постоянной С, не зависящей от