12.4. Неравномерно эллиптические уравнения

Мы увидим при изучении неравномерно эллиптических уравнений, что, в отличие от предыдущего раздела, в котором рассматриваемая область достаточно произвольна, разрешимость задачи Дирихле в общем случае тесно связана с геометрией области. Эта особенность неравномерно эллиптических задач уже обсуждалась ранее в линейной теории (раздел 6.6). В настоящем разделе выясняется важная роль выпуклости области для разрешимости задачи Дирихле для общего квазилинейного эллиптического уравнения вида

Пусть ограниченная область функция, заданная на Задачу Дирихле для уравнения (12.40) будем формулировать в терминах граничной кривой

Напомним (см. раздел 11.3), что кривая и функция удовлетворяют условию ограниченности наклона (с постоянной К), если для любой точки существуют плоскости в описываемые уравнениями

проходящие через точку и такие, что

Условие (i) означает, что для каждой точки кривая ограничена сверху и снизу на цилиндре плоскостями совпадает с ними в точке

Условие (ii) означает, что наклоны этих плоскостей равномерно по Ограничены постоянной К. Ясно, что из условия ограниченности наклона следует непрерывность функции

Относительно условия ограниченности наклона сделаем следующие заметания.

(1) Для произвольной области кривая лежит в плоскости (и удовлетворяет условию ограниченности наклона) тогда и только тогда, когда функция является следом линейной на функции. Однако если не яежит в плоскости и удовлетворяет условию ограниченности наклона, область должна быть выпуклой. Чтобы убедиться в этом, запишем на основании (12.41) соотношения

Из него следует, что в каждой точке имеется опорная линия а это и означает выпуклость

(2) Предположим, что граница выпукла и кривая удовлетворяет условию ограниченности наклона. Пусть - три различные точки на Если точки коллинеарны, то точки также коллинеарны на ибо для точек, расположенных иначе, соответствующая плоскость будет вертикальной, что противоречит неравенствам (21.41). Таким образом, функция линейна на прямолинейных отрезках .

(3) С условием ограниченности наклона тесно связано и по существу ему эквивалентно так называемое условие трех точек, которое часто встречается в литературе о минимальных поверхностях и непараметрических вариационных задачах с двумя переменными. Пусть ограниченная выпуклая область. Будем говорить, что кривая удовлетворяет условию трех точек с постоянной К, если любое множество из трех различных точек на лежит в плоскости, наклон которой не превосходит К. В конце этого раздела мы докажем эквивалентность условий ограниченности наклона и трех точек с одной и той же постоянной К.

Из условия трех точек следует, что плоскость, определенная любыми тремя неколлинеарными точками должна иметь наклон, не превосходящий К. Таким образом, если область строго выпукла (т.е. любой прямолинейный интервал, соединяющий две точки целиком лежит в то наклон любой плоскости, пересекающей по крайней мере в трех точках, не превосходит К. Верно и обратное утверждение: из такого более сильного варианта условия трех точек следует, что строго выпукла.

(4) Нетрудно показать, что если кривизна всюду положительна, то удовлетворяет условию ограниченности наклона, с постоянной, зависящей от минимума кривизны и верхних граней первых и вторых производных функции (см. [345], [321]).

При изучении задачи Дирихле для уравнения (12.40) необходима априорная оценка градиента следующего вида.

Лемма Пусть ограниченная область в а ее граница и определенная на ней функция удовлетворяют условию ограниченности наклона с постоянной К. Предположим, что функция и удовлетворяет линейному эллиптическому уравнению

в и равенству на . Тогда

Подчеркнем, что предполагается только, что оператор является эллиптическим. Условия на его коэффициенты не накладываются. Примечательно, что сформулированный результат справедлив при весьма общих обстоятельствах, для произвольных седловых поверхностей (см. [245], [213]).

Доказательство леммы Рассмотрим сначала случай, когда функция у является следом линейной функции на . В силу теоремы единственности (теорема 3.3) решение и в этом случае совпадает с линейной функцией в и условие (12.43) при этом выполняется автоматически. Как следует из предшествующего замечания (1), область можно считать выпуклой.

Из (12.42) и эллиптичности оператора имеем:

Следовательно, и равенство имеет место только в точках, в которых (заметим, что поверхность является седловой поверхностью). Рассмотрим теперь произвольную точку в которой и пусть уравнением определяется плоскость касательная к поверхности в точке . Функция является решением уравнения (12.42) в и множество точек, в которых разделяет некоторый малый круг с центром ровно на четыре области в которых функция непоследовательно положительна и отрицательна, например, Пусть связные компоненты того множества в где и пусть аналогичные компоненты множества в где Тогда каждая из областей имеет по крайней мере две граничные точки на , в которых в противном случае из слабого принципа максимума (теорема 3.1) следовало бы, что в области. Итак, плоскость пересекает граничную кривую по крайней мере в четырех точках. Из предшествующего замечания (3) следует, что если любые три из этих точек неколлинеарны, то плоскость имеет наклон, не превышающий К. С другой стороны, если точки на , в которых образуют коллинеарное множество 2, то в силу замечания (2) функции линейны и совпадают с на прямолинейном отрезке , содержащем 2. Тем самым получаем, что в одной из

областей Пришли к противоречию. Следовательно, наклон касательной плоскости к поверхности решения не может превзойти К в точках, в которых

Рассмотрим теперь множество на котором Мы можем предполагать, что ибо в противном случае функция была бы линейной и утверждение становилось бы тривиальным. Если точка является пределом точек, в которых то в силу непрерывности касательная плоскость в точке должна иметь наклон, не превышающий К. Если же точка является внутренней точкой множества то точка принадлежит открытой связной компоненте того множества, на котором На этой компоненте функция и линейна, а касательная плоскость совпадает с самой поверхностью Так как любая граничная точка является внутренней точкой и является пределом точек, в которых то получаем, что Лвсюду на в частности, в точке Этим завершается доказательство.

Теперь мы можем доказать следующую теорему существования для уравнения (12.40), обобщающую относящееся к случаю утверждение теоремы 11.5.

Теорема 12.7. Пусть выпуклая область в Предположим, что уравнение

эллиптично в с коэффициенты для некоторого Пусть и определенная на ней функция удовлетворяют условию ограниченности наклона с постоянной К. Тогда задача Дирихле

имеет решение и причем

Доказательство. Достаточно предполагать, что область выпукла, так как в противном случае функция является следом линейной функции и результат тривиален. Поделим коэффициенты с на максимальное собственное значение и обозначим получившееся уравнение снова через Оператор имеет теперь максимальное собственное значение, равное единице, но его минимальное собственное значение X может приближаться к нулю в Рассмотрим семейство уравнений

с граничным условием Для каждого это уравнение равномерно эллиптично, а в силу теоремы существует решение такое, что на (для этого достаточно утверждения из первой части теорем доказательства теоремы 12.5). В силу леммы 12.6 имеет место равномерная оценка градиента решений вида

не зависящая от Из принципа максимума следует, что Таким образом, в произвольной подобласти минимальное собственное значение линейного уравнения

получающегося при подстановке в коэффициенты:

где равномерно положительно в ограничено снизу постоянной зависящей только от Максимальное собственное значение ограничено сверху числом 2 при всех . В силу теоремы решения уравнения (12.46) равные функции на в частности, решения , на подмножествах удовлетворяют равномерной (по ) оценке Гёльдера градиента:

где Поэтому коэффициенты локально непрерьюны по Гёльдеру в с показателем и равномерно ограничены в Так как произвольны, то из следствия 6.3 и замечения к нему следует, что семейство решений уравнения (12.46) равностепенно непрерывно вместе с их первыми и вторыми производными на компактных подмножествах и поэтому, используя известный диагональный процесс, можно выделить последовательность из семейства сходящуюся в к решению уравнения при Равномерная оценка градиента (12.45) гарантирует, что сходимость будет равномерной на следовательно, на Этим завершается доказательство теоремы.

Замечания. (1) Необходимость выполнения некоторых геометрических условий на таких, например, как выпуклость, демонстрирует классический пример уравнения минимальных поверхностей

в кольце Если граничная функция равна положительной постоянной при и равна нулю при а величина достаточно мала, то краевая граничная задача имеет хорошо известное решение (катеноид). Однако если величина достаточно велика, то не существует решений, принимающих заданные граничные значения. В гл. 14 мы увидим, что задача Дирихле для уравнения минимальных поверхностей (12.47) разрешима для произвольных граничных значений класса тогда и только тогда, когда область выпукла.

(2) Условия гладкостй, косвенным образом содержащиеся в условии ограниченности наклона, не могут быть заменены в общем случае на условие непрерывности граничных значений Контрпримеры показьюают, что задача Дирихле может не иметь решения для непрерывных граничных значений, даже если граничная кривая является окружностью, а коэффициенты уравнения являются бесконечно дифференцируемыми функциями

(см. [304]). Разрешимость для непрерывных граничных значений будет обсуждаться в гл. 15 и 16.

(3) Существенный шаг доказательства теоремы 12.7 состоит в сведении к равномерно эллиптическому случаю, а это возможно в силу наличия глобальной оценки градиента (лемма 12.6). Такие оценки градаента справедливы и при других структурных условиях на оператор и других требованиях относительно геометрии области Они обсуждаются в гл. 14 и 15. Например, если область выпукла, а оператор таков, что то задача Дирихле для уравнения (12.40) разрешима для произвольной функции , независимо от того, выполняется или нет условие ограниченности наклона (см. раздел 14.2). Такому условию удовлетворяет, например, уравнение минимальных поверхностей (12.47).

(4) Если оператор граница и функция у удовлетворяют тем же дополнительным условиям гладкости, что и в теореме 11.4, т. е. если

то решение, существующее в силу теоремы 12.7, принадлежит Доказательство этого результата по существу то же, что и доказательство замечания 1 к теореме 12.5, если воспользоваться тем, что оценка градиента делает уравнение равномерно эллиптическим.

Эквивалентность условия ограниченности наклона и условия трех точек. Предположим сначала, что кривая удовлетворяет условию ограниченности наклона с постоянной К и что область выпукла. Пусть - три неколлинеарные точки на 912. Пусть

— верхняя и соответственно нижняя плоскости в удовлетворяющие (12.41). Пусть

- плоскости, проходящие через Мы ходам показать, что (Если точки следовательно, точки коллинеарны, то плоскость с наклоном, не превосходящим К, определяется по непрерьюности.) Из (12.41) следует, что

Так как точки являются вершинами невырожденного треугольника и - вектор в то для некоторого или 3 имеет место равенство

Из (12.48) следует, что или

или

и поэтому Таким образом, из выполнения условия ограниченности наклона следует выполнение условия трех точек с той же постоянной К.

Обратно, пусть кривая удовлетворяет условию трех точек с постоянной К и пусть область выпукла. Пусть - произвольная точка кривой такая, что не является внутренней точкой прямолинейного отрезка на Тогда существует последовательность треугольников с вершинами в неколлинеарных точках таких, что при и плоскости проходящие через сходятся к предельной плоскости Можно предполагать, что отрезки имеют предельное направление, которое определяет прямую линию проходящую через точку А и лежащую в плоскости А, причем проекция прямой на z-плоскость является опорной линией области Ясно, что прямая совпадает с касательной к в точке А, если эта касательная существует. Пусть и пусть плоскость, проходящая через точку и прямую Наклон плоскости не превосходит К, так как он равен пределу последовательности наклонов плоскостей, проходящих через точки Рассмотрим множество плоскостей, проходящих через и точки и пусть эти плоскости определяются линейными функциями Обозначим через Я ту полуплоскость z-плоскости с границей которая содержит область Если в некоторой точке то то же неравенство имеет место и для всех точек в частности, для Таким образом, в точке А имеются верхняя и нижняя плоскости, определяемые равенствами

Плоскости и в силу предыдущих замечаний имеют наклоны, не превосходящие К, и лежат выше и ниже соответственно (над Следовательно, они удовлетворяют условию ограниченности наклона в точке А с постоянной К. Ясно, что если точка А лежит на прямолинейном отрезке кривой то линия, содержащая этот отрезок, может заменить прямую в предыдущих рассуждениях. Таким образом, из условия трех точек следует выполнимость условия ограниченности наклона с той же самой постоянной К.

Примечания

Оценки Гёльдера для квазиконформных отображений (раздел были получены различными способами и впервые — Морри [204] (ссылки см. [302]). Изложенные в этом разделе оценки получены Финном и Серрином [309]. Ими же получена оценка (12.14) с наилучшим показателем Гёльдера, а в случае, когда в (12.2) постоянная получен соответствующий результат с коэффициентом Гёльдера в котором С - абсолютная постоянная.

Основные оценки Гёльдера в решений линейных уравнений, изложенные в разделе получены Морри [204] и, в более простом виде, Ниренбергом [215]. Описанный выше вариант — более поздний по

времени, однако в нем, следуя Морри, используются оценки роста интеграла Дирихле. Идея применения таких априорных оценок в для линейных уравнений к изучению задачи Дирихле для квазилинейного уравнения (12.40) появилась в работе [204], однако в этой работе имеется ошибка. Идея была реализована и упрощена в деталях Ниренбергом, который, используя теорему Шаудера о неподвижной точке, доказал, общую теорему существования. Его метод является основой построений разделов 12.3 и 12.4,

До 1950 г. теория задачи Дирихле для нелинейных эллиптических уравнений была развита в основном в случае двух независимых переменных. Пионерские работы Бернштейна достаточно ограничительные по своим условиям, были обобщены Лере и Шаудером [160], [345], доказавшими существование решения задачи Дирихле для уравнения (12.40) в предположении, что коэффициенты принадлежат С и что граничные значения достаточно гладкие. Они использовали метод, основанный (как и в работах Бернштейна) на априорных оценках вторых производных решений. Эти результаты были усилены и упрощены в указанных выше работах Морри и Ниренберга. Ниренберг доказал, что если уравнение (12.40) эллиптично в его коэффициенты принадлежат 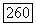граница 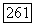является равномерно выпуклой кривой класса 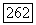а функция 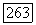принадлежит 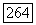то задача Дирихле для (12.40) имеет решение, принадлежащее 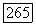(если же 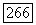то решение существует и принадлежит 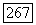В теореме 12.7 этот результат обобщается на случай более слабых требований о коэффициентах и граничных данных: требуется лишь выполнение условия ограниченности наклона без дополнительных условий регулярности. Решения, получающиеся при этом, также принадлежат 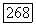если выполнены те же условия, что и в теореме Ниренберга (см. замечание 4 после теоремы 12.7). Доказательство теоремы 12.7 использует только внутренние априорные оценки в 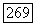для линейных уравнений (теорема 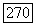То, что таких оценок достаточно для доказательства теоремы существования, было отмечено ранее Ниренбергом .

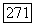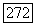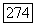Задаче Дирихле для равномерно эллиптического уравнения (12.25) посвящены работы Берса и Ниренберга [31], Ладыженской и Уральцевой [147] и Фон Валя [51]. В работе [31] теоремы существования для задач Дирихле и Неймана были получены для решений класса (в случае, когда коэффициенты в (12.25) принадлежат эти решения из принадлежат также и 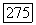Доказательства в [31] и теоремы 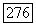осуществлены в предположении линейного роста функции 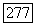аналогичного (12.27), и основаны на оценках в 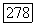для линейных уравнений и теореме Шаудера о неподвижной точке. И в [31], и в теореме 12.5 не делаются априорные предположения о решениях. В предположении, что выполнена равномерная оценка 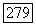для всех решений уравнения (12.29) при следующих условиях: 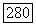(это условие слабее условия (12.27)), Фон Валь в работе [51] доказал априорную оценку решений задачи Дирихле, обобщив тем самым аналогичные результаты из

[147]. (Эти оценки не следуют из методов настоящего раздела без априорной оценки градиента.) Существование решений класса 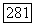задачи Дирихле (12.29) может быть получено теперь с помощью применения теоремы Лере - Шаудера о неподвижной точке.

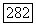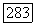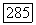Доказательство оценки градиента в лемме было подсказано вводными замечаниями Финна в [304]. Обычно такую оценку выводят из теоремы Радо [245], утверждающей, что если функция ощюделяет седловую поверхность над выпуклой областью непрерывную в и если ее граничные значения удовлетворяют в 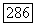условию трех точек с постоянной К, то функция и удовлетворяет в 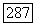условию Липшица с постоянной К. В этой теореме слова функция определяет седловую поверхность понимаются в следующем смысле: функция 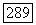непрерывна и функция и 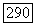удовлетворяет слабому принципу максимума - минимума для произвольных коэффициентов а, b, с. В частности, это имеет место в случаях, когда функция и удовлетворяет уравнению (12.42) или является поверхностью с неположительной гауссовой кривизной. Элементарное (но непростое) доказательство этого факта было дано фон Нейманом 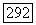Хартман и Ниренберг [322], [218] обобщили результат на случай больших размерностей.

Касаясь условия ограниченности наклона, Хартман [321] анализирует связь между свойствами регулярности функции 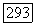в случае, когда 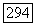удовлетворяет условию ограниченности наклона на границе 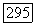ограниченной выпуклой области 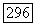В результате он доказывает эквивалентность условия ограниченности наклона и условия 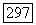точки при 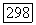однако связь между постоянными в этих двух условиях при 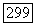остается невыясненной. Из других результатов мы отметим следующие.

(i) Если 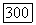и функция удовлетворяют условию ограниченности наклона на то

(ii) Если граница принадлежит классу и равномерно выпукла, то функция удовлетворяет условию ограниченности наклона на тогда и только тогда, когда Последний результат вытекает из и того факта, что если произвольная равномерно выпуклая область и функция является следом на функции из то функция удовлетворяет условию ограниченности наклона на

Задачи

(см. скан)

(см. скан)