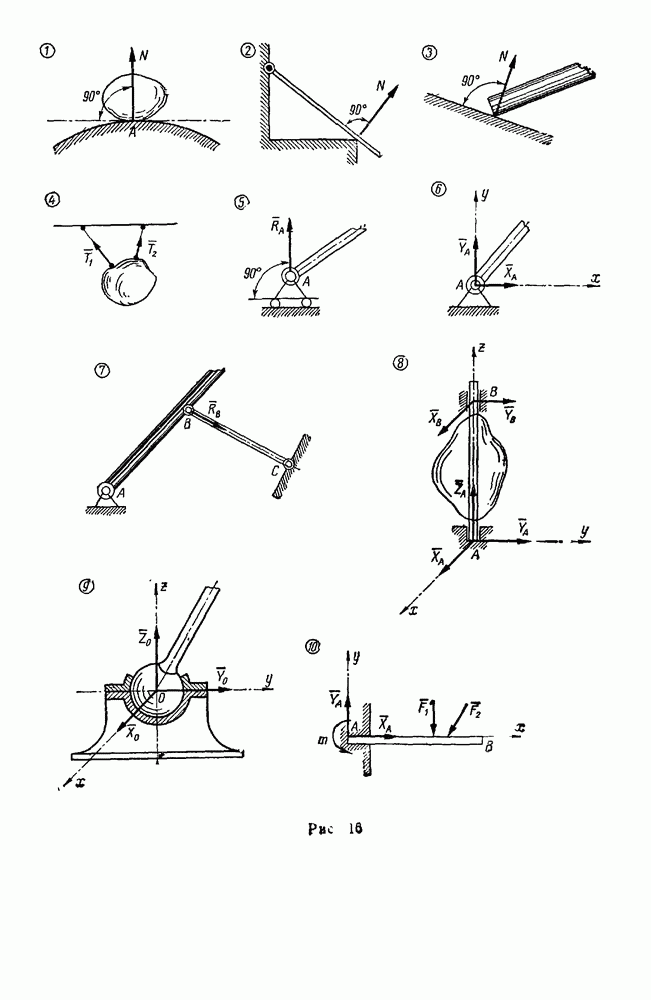
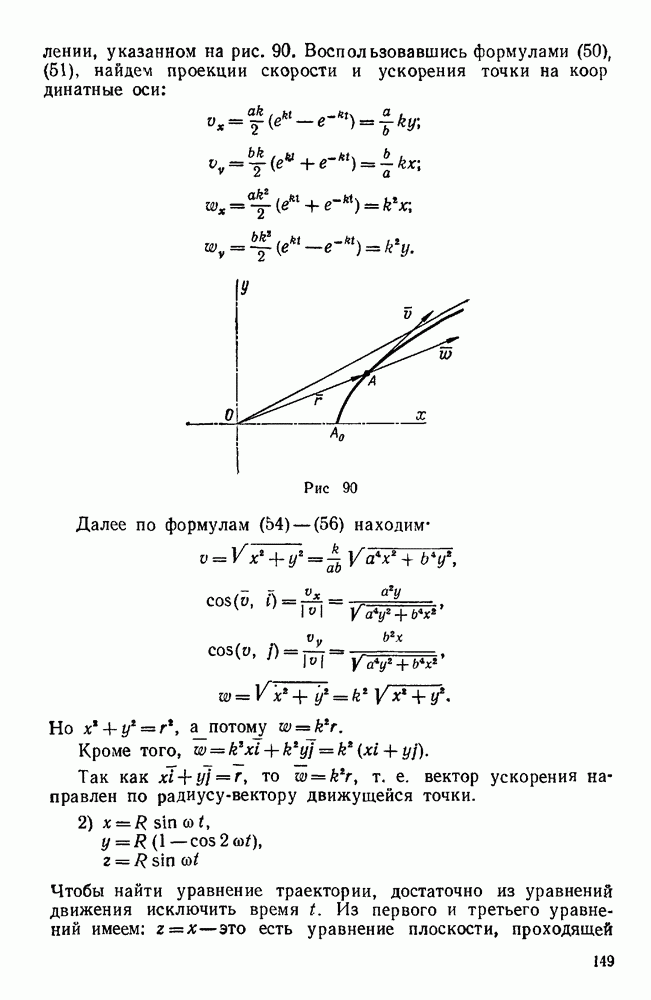
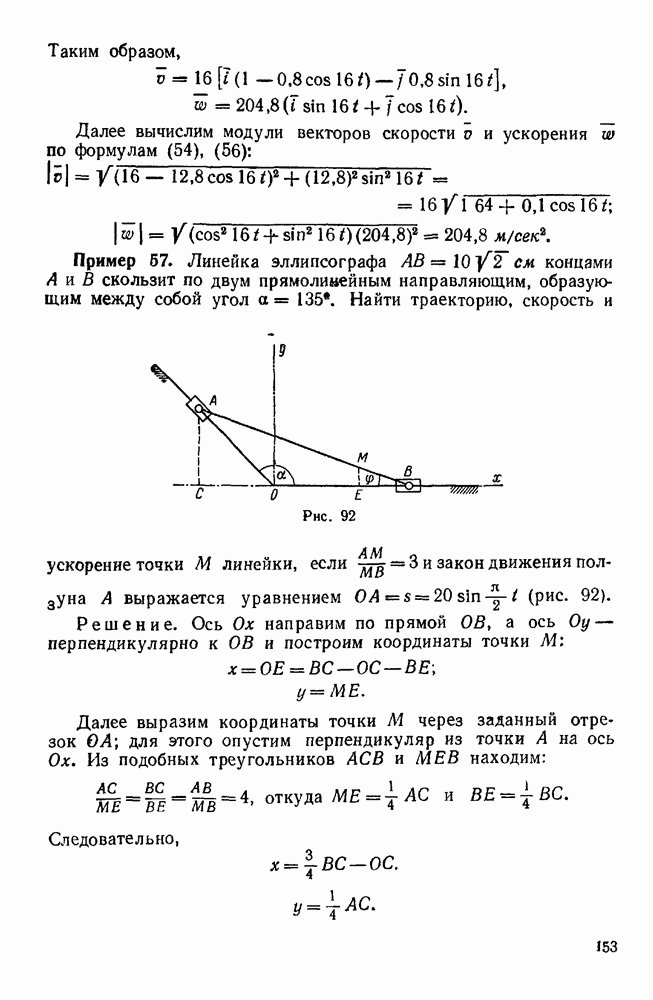
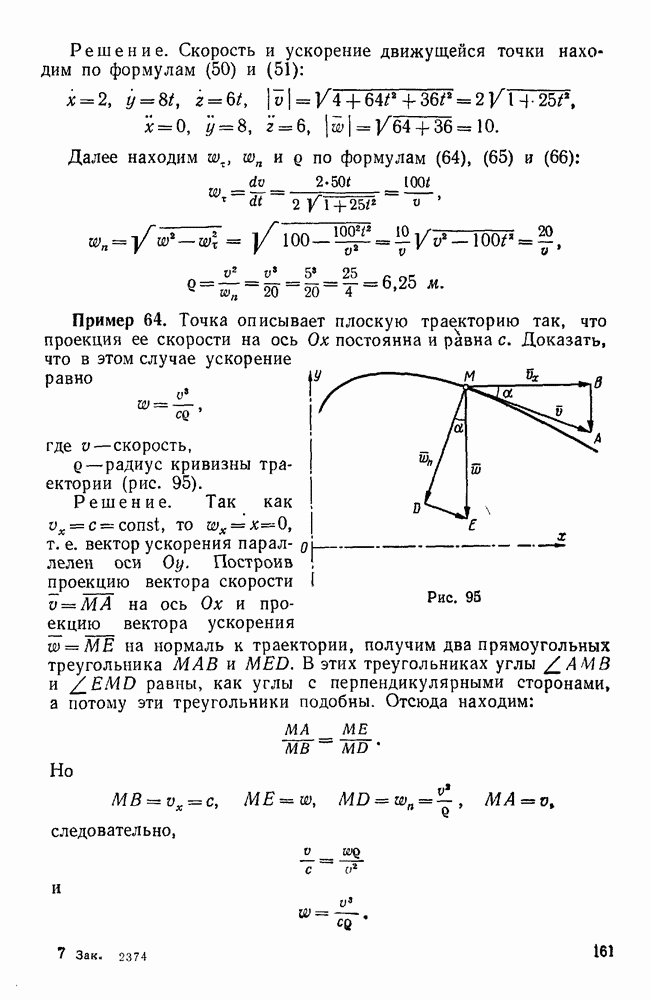
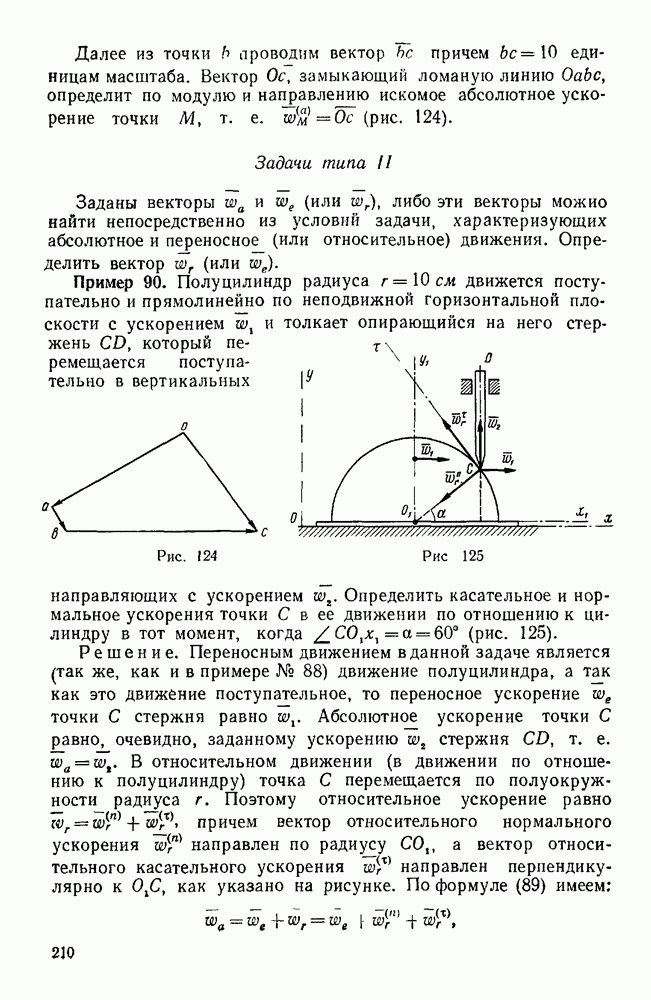
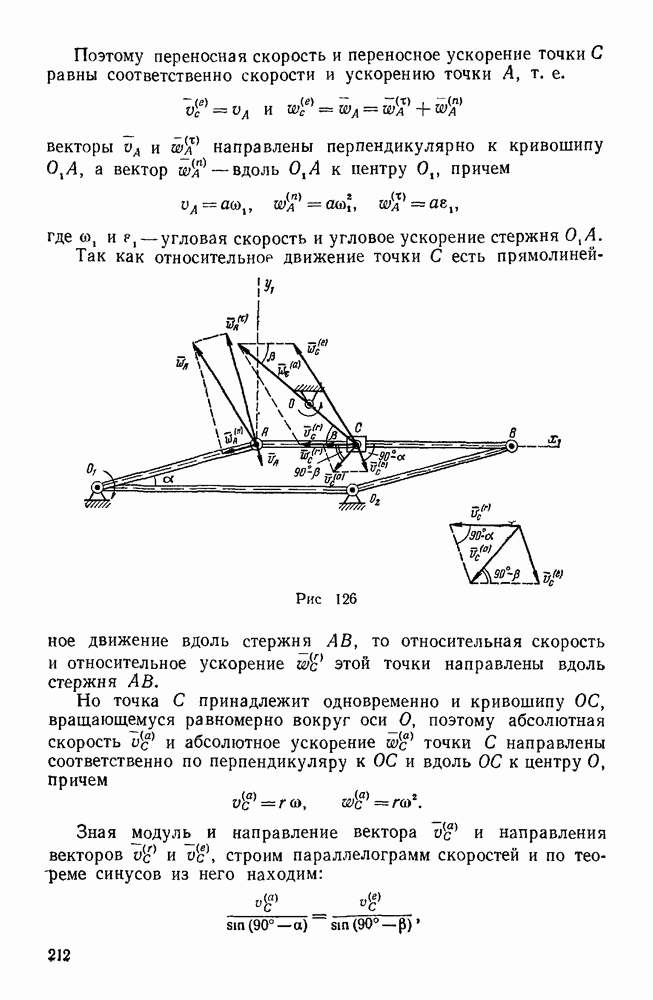
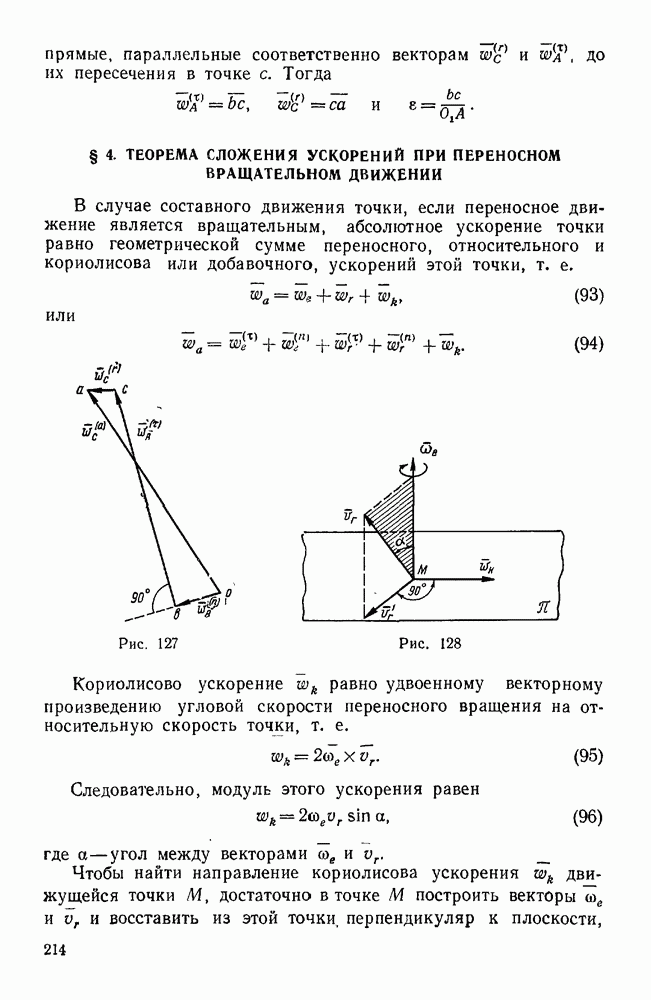
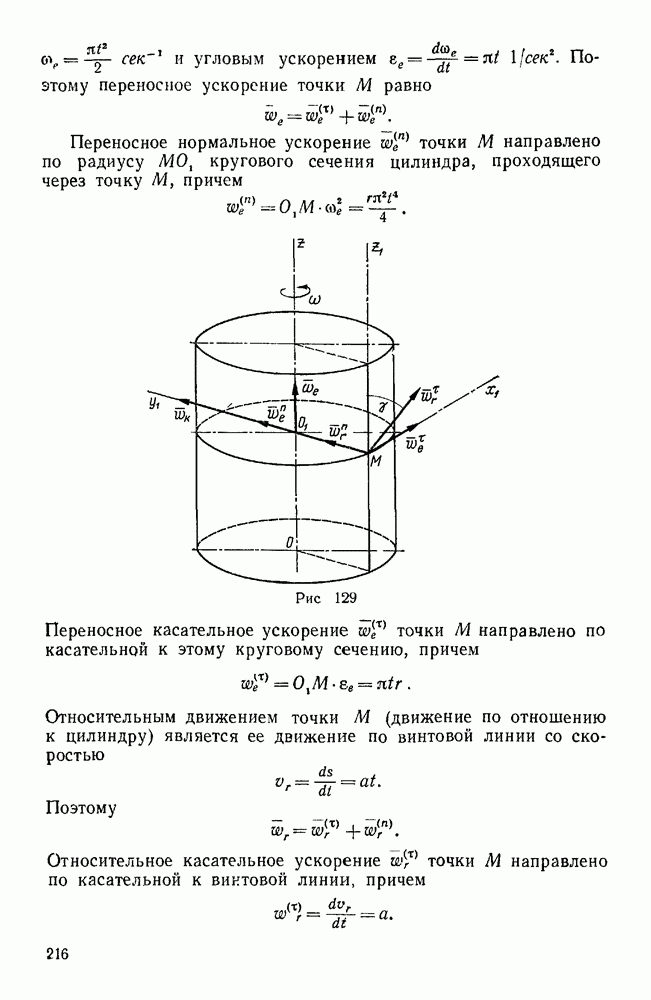
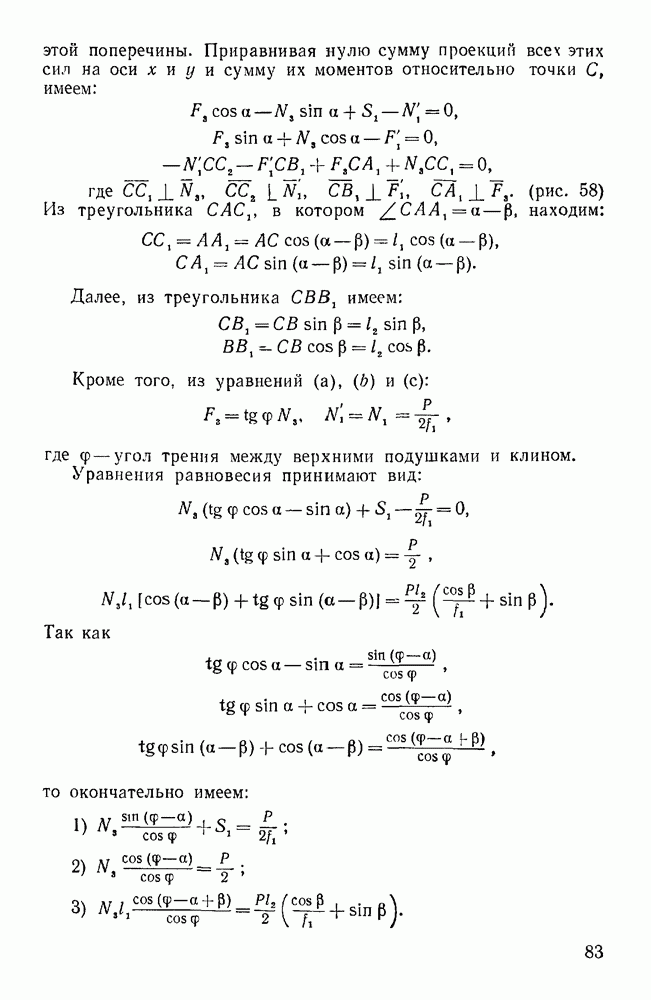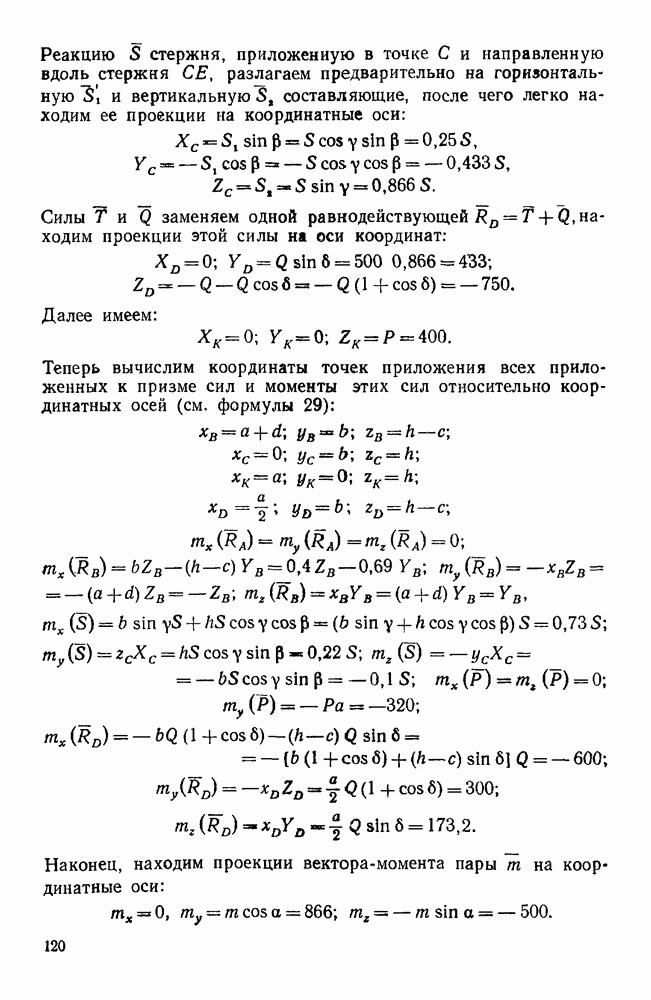| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
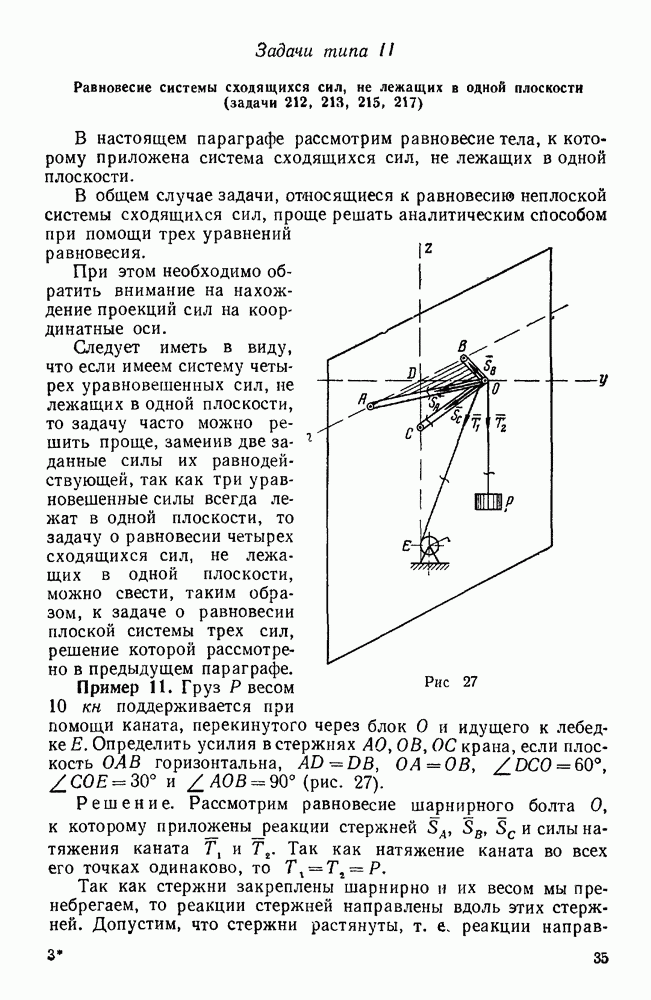
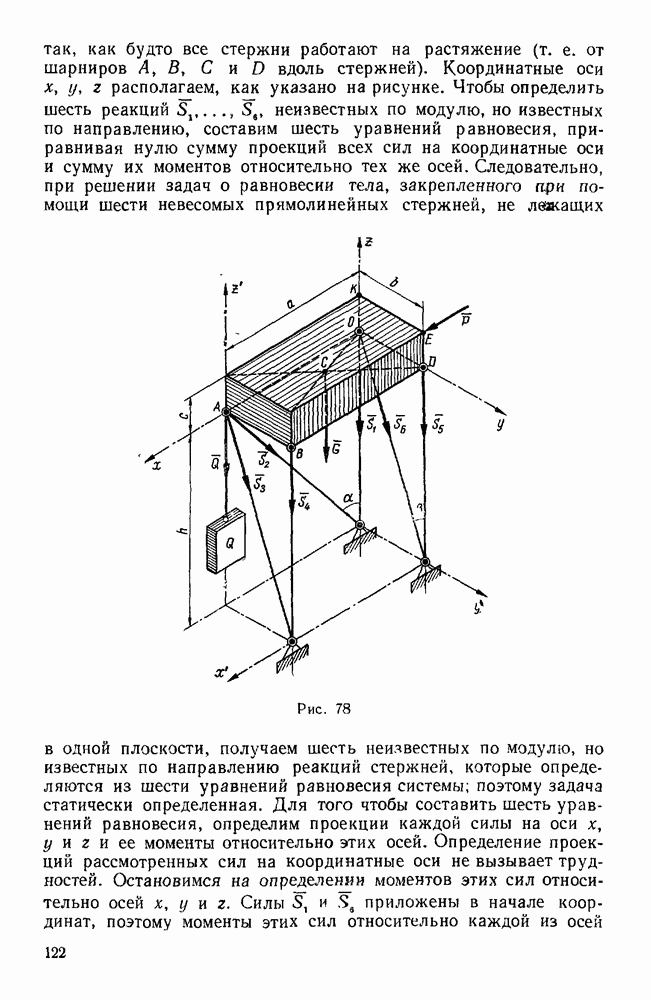
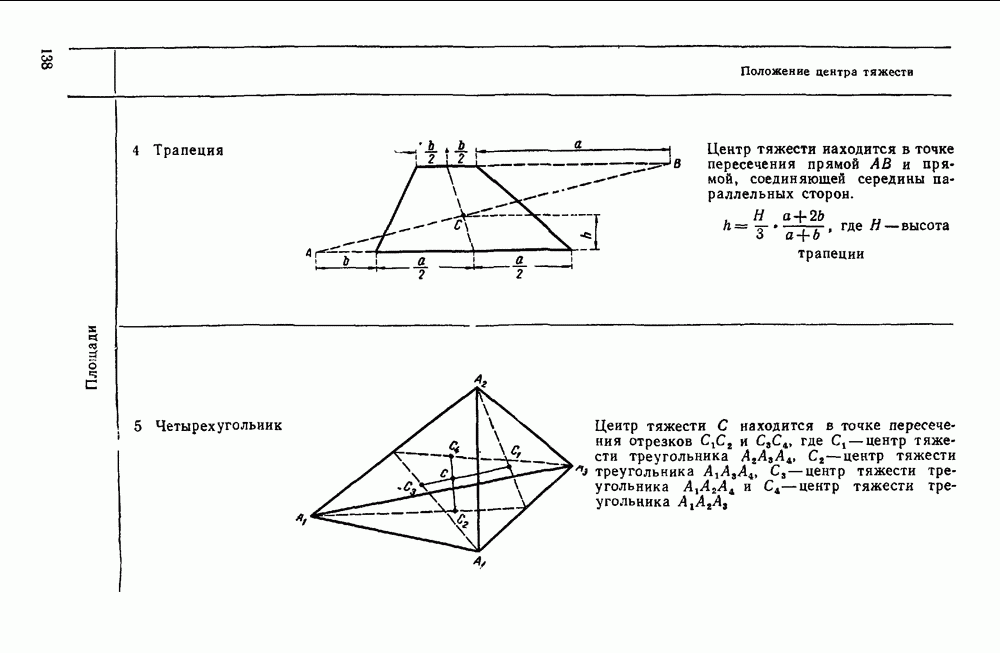
Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
В настоящем параграфе рассмотрим равновесие тела, к которому приложена система сходящихся сил, не лежащих в одной плоскости.
В общем случае задачи, относящиеся к равновесию неплоской системы сходящихся сил, проще решать аналитическим способом при помощи трех уравнений равновесия.
При этом необходимо обратить внимание на нахождение проекций сил на координатные оси.
Следует иметь в виду, что если имеем систему четырех уравновешенных сил, не лежащих в одной плоскости, то задачу часто можно решить проще, заменив две заданные силы их равнодействующей, так как три уравновешенные силы всегда лежат в одной плоскости, то задачу о равновесии четырех сходящихся сил, не лежащих в одной плоскости, можно свести, таким образом, к задаче о равновесии плоской системы трех сил, решение которой рассмотрено в предыдущем параграфе.

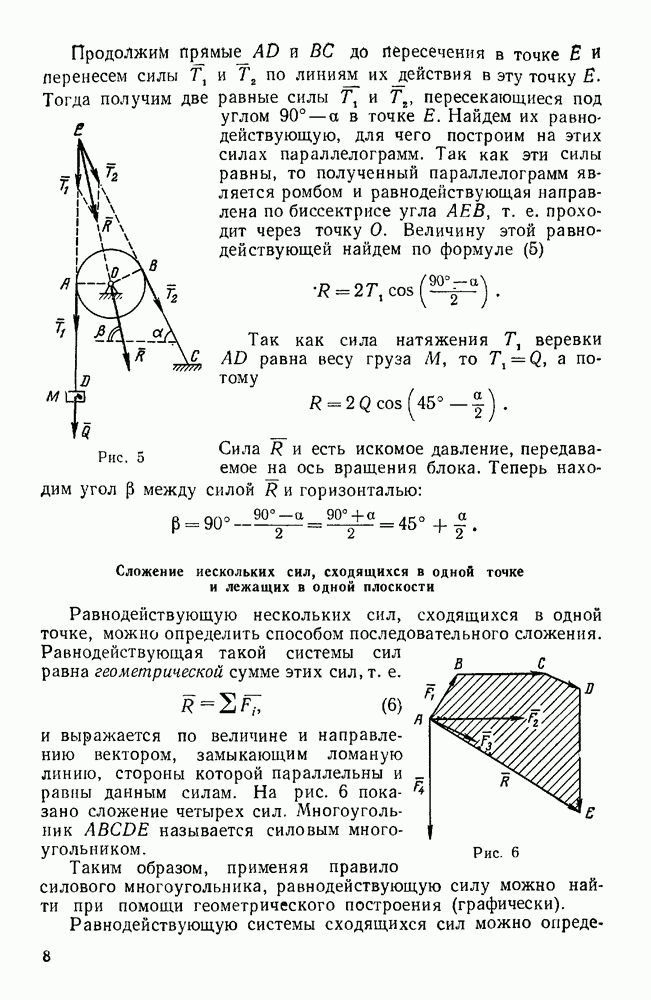
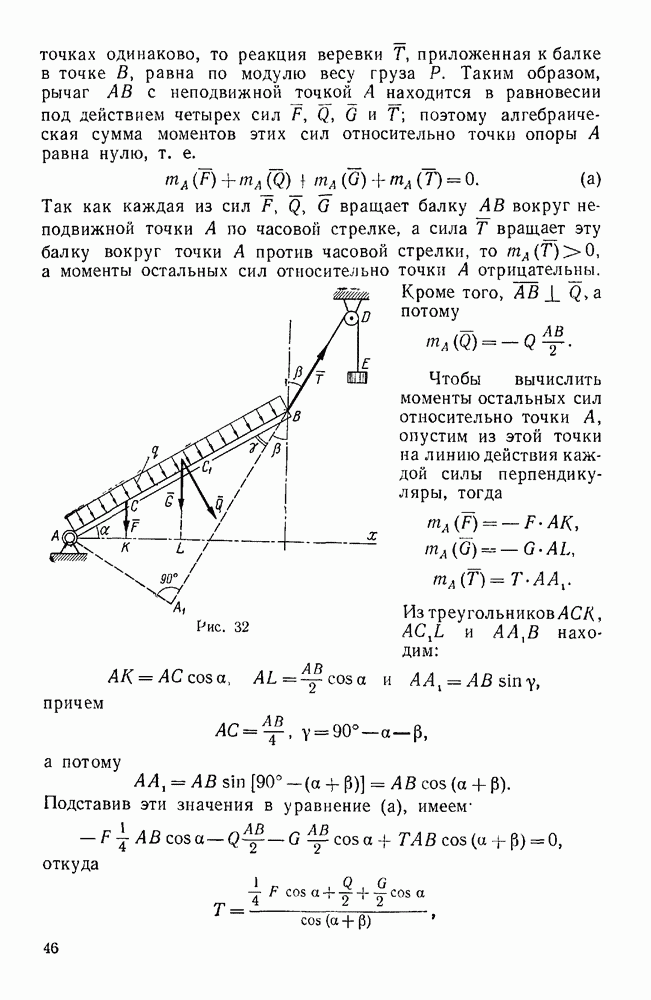
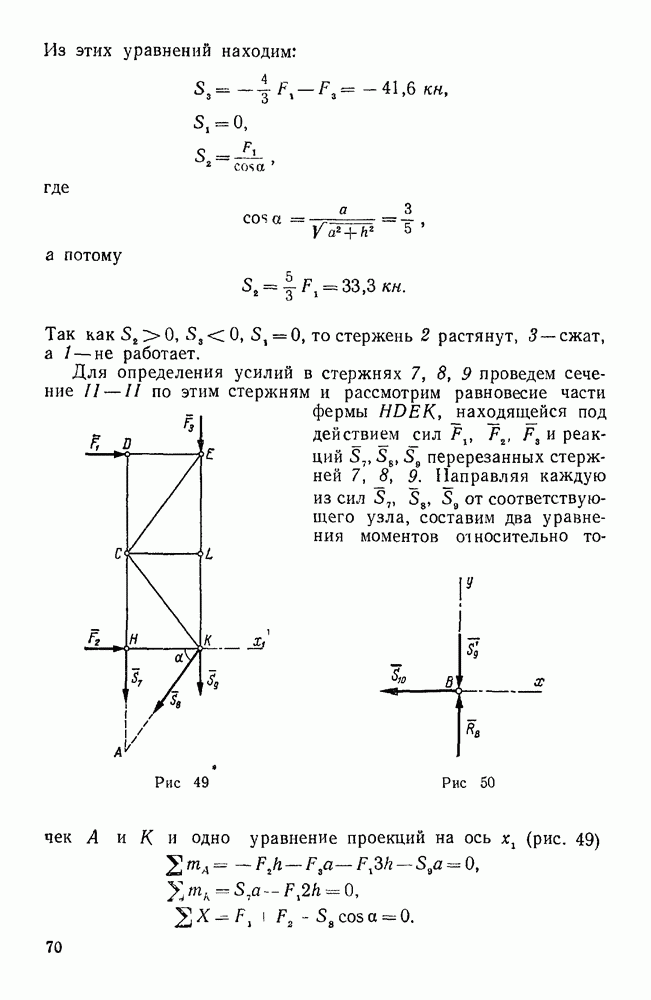
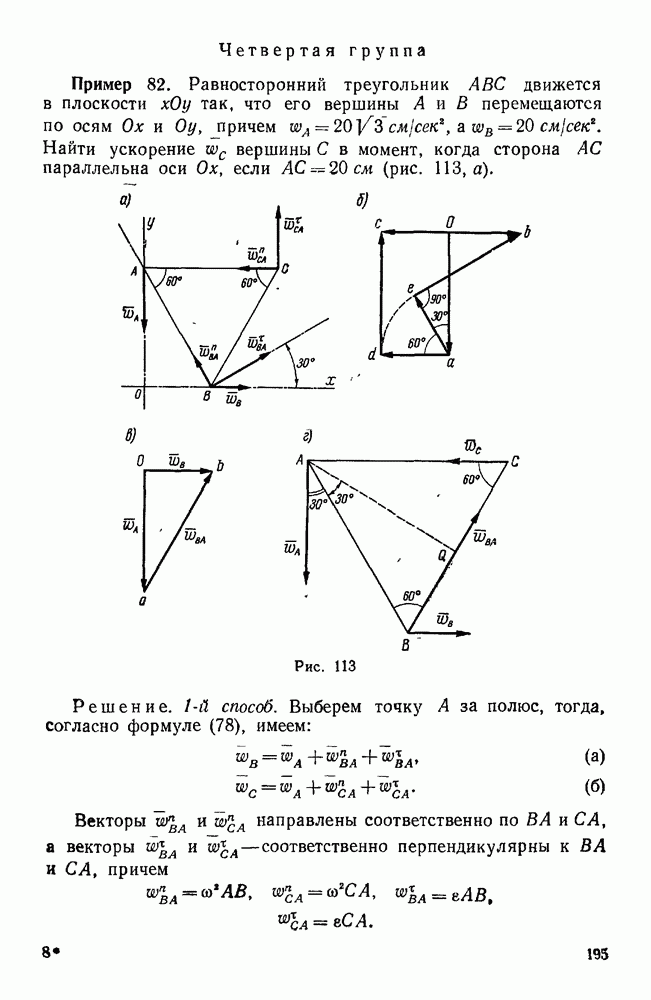
Рис. 27.
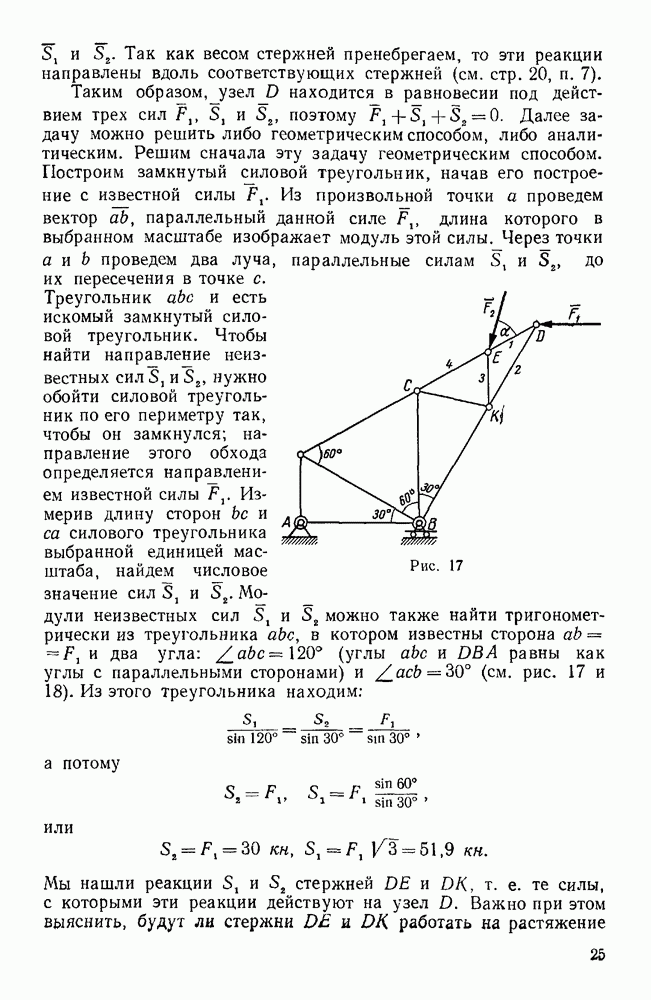
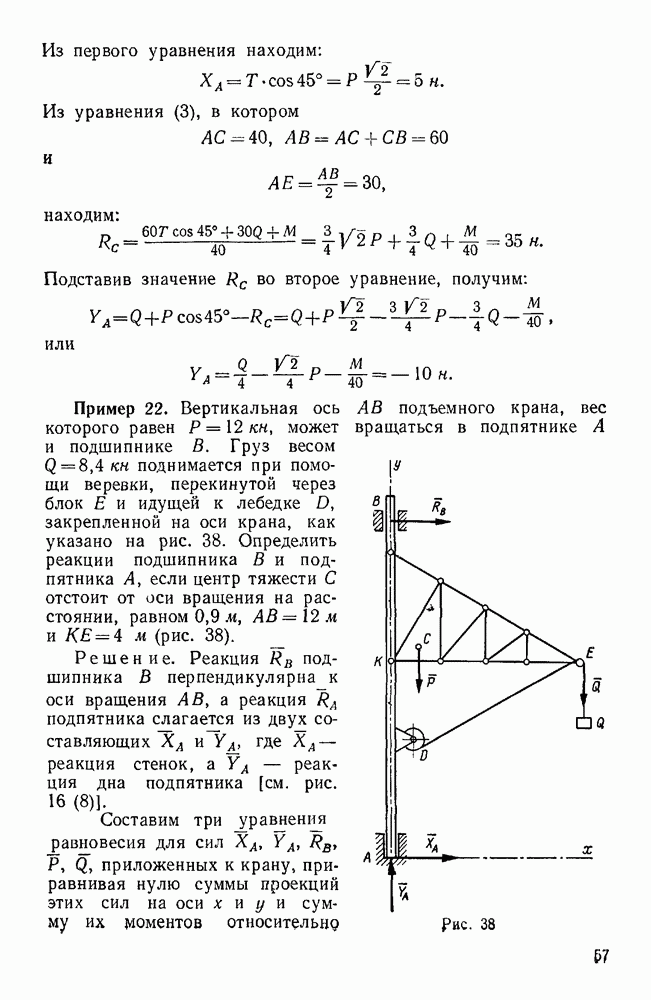
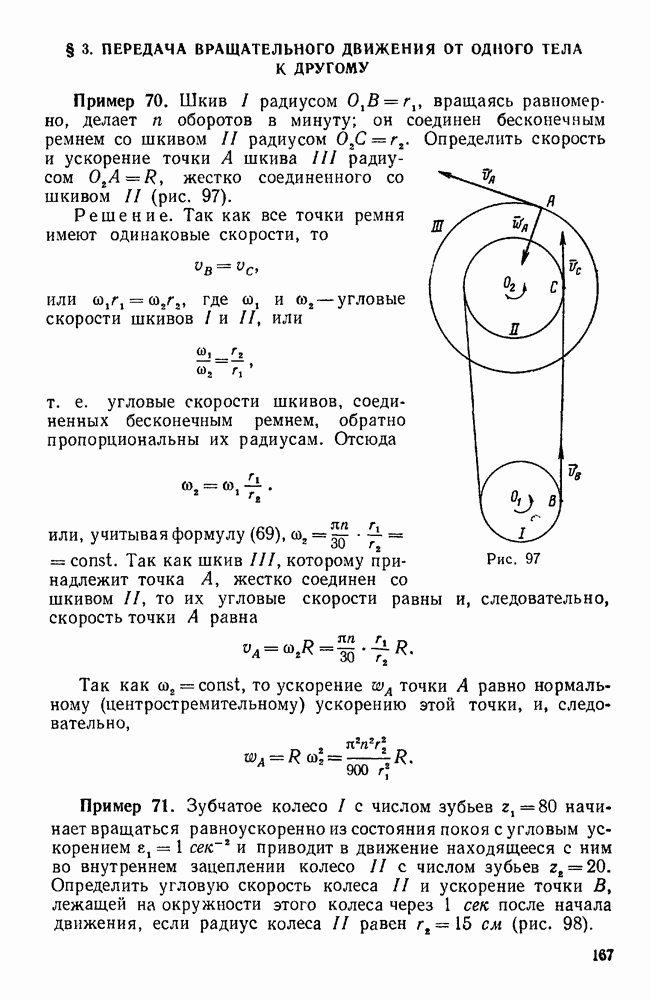
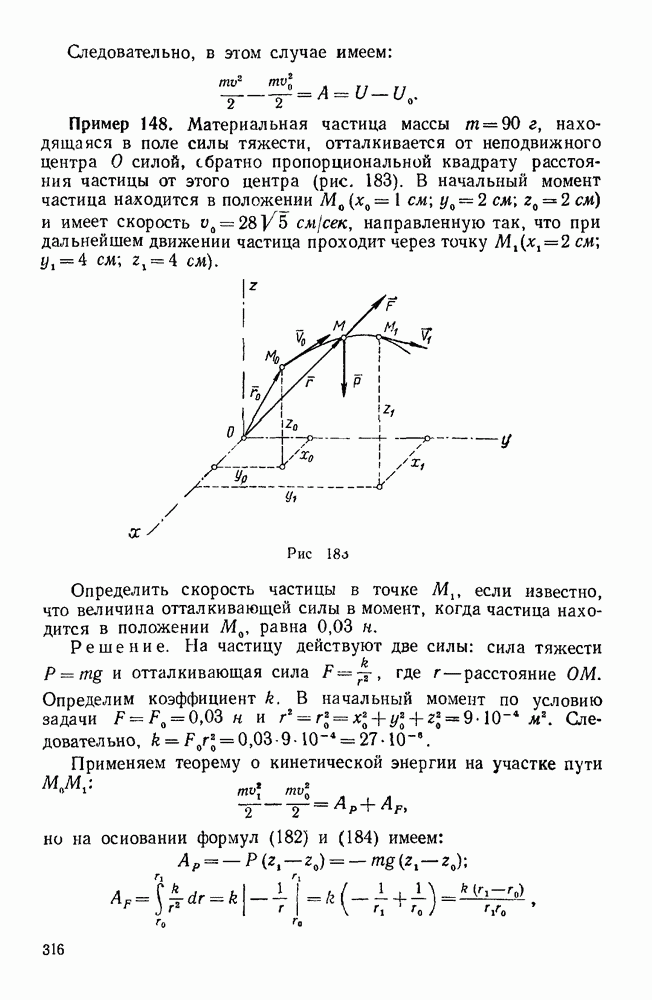
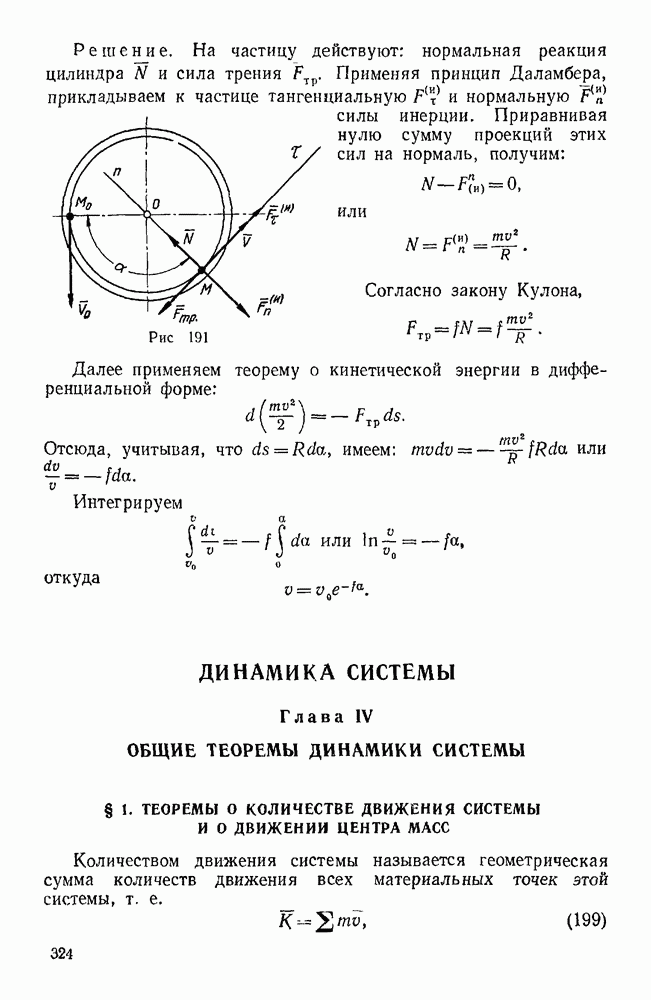
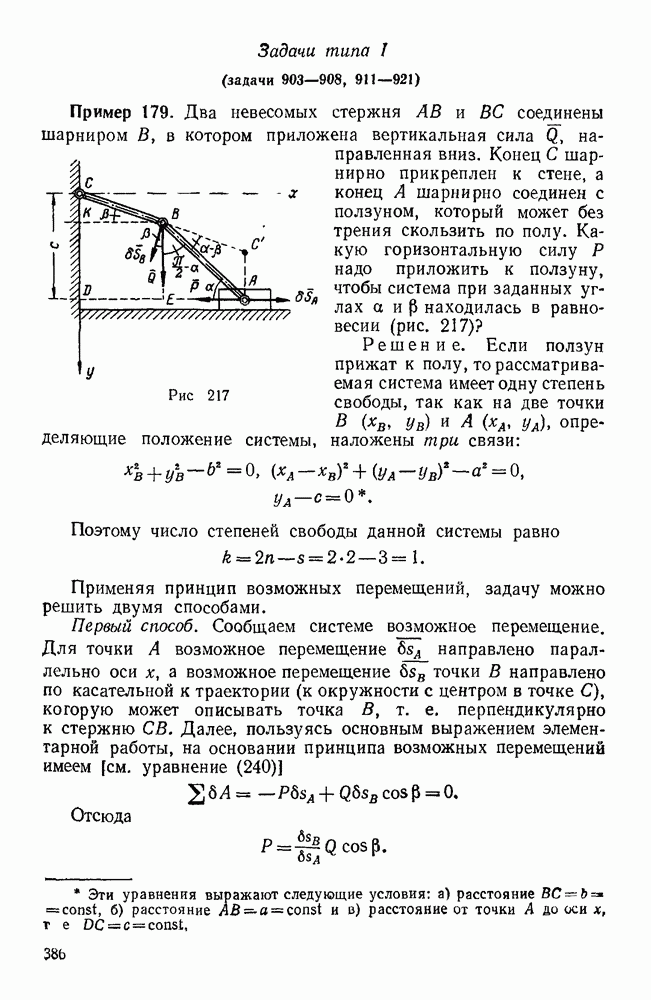
Пример 11. Груз  весом
весом  поддерживается при помощи каната, перекинутого через блок О и идущего к лебедке Е. Определить усилия в стержнях АО, ОВ, ОС крана, если плоскость ОАВ горизонтальна, AD=DB,
поддерживается при помощи каната, перекинутого через блок О и идущего к лебедке Е. Определить усилия в стержнях АО, ОВ, ОС крана, если плоскость ОАВ горизонтальна, AD=DB,  . (рис. 27).
. (рис. 27).
Решение. Рассмотрим равновесие шарнирного болта О, к которому  стержней
стержней  и силы натяжения каната
и силы натяжения каната  и
и  . Так как натяжение каната во всех его точках одинаково, то
. Так как натяжение каната во всех его точках одинаково, то  .
.
Так как стержни закреплены шарнирно и их весом мы пренебрегаем, то реакции стержней направлены вдоль этих стержней. Допустим, что стержни растянуты, т. е. реакции направлены от узла О.
Силы  не лежат в одной плоскости.
не лежат в одной плоскости.
Составим три уравнения равновесия этих сил, для чего выберем сначала систему координатных осей  , у z так, чтобы силы
, у z так, чтобы силы  лежали в координатных плоскостях; ось
лежали в координатных плоскостях; ось  направим перпендикулярно к плоскости АОВ; начало координат выберем в точке D, а оси х и у направим соответственно по прямым АВ и OD. Тогда силы
направим перпендикулярно к плоскости АОВ; начало координат выберем в точке D, а оси х и у направим соответственно по прямым АВ и OD. Тогда силы  будут расположены в плоскости
будут расположены в плоскости  , а силы
, а силы  — в вертикальной плоскости
— в вертикальной плоскости  . При
. При  выборе координатных осей легко определить углы каждой силы с координатными осями, а следовательно, и ее проекции на эти оси. Так как силы и
выборе координатных осей легко определить углы каждой силы с координатными осями, а следовательно, и ее проекции на эти оси. Так как силы и  лежат в плоскости
лежат в плоскости  , то
, то  . Найдем углы, составляемые этими силами с осями х и у. По условию задачи
. Найдем углы, составляемые этими силами с осями х и у. По условию задачи  , а потому треугольник АОВ равнобедренный; кроме того,
, а потому треугольник АОВ равнобедренный; кроме того,  — 90°. Следовательно, прямая OD есть биссектриса угла АОВ и
— 90°. Следовательно, прямая OD есть биссектриса угла АОВ и  45°.
45°.
Теперь находим проекции сил  и
и  на координатные оси
на координатные оси  .
.
Проекции  , очевидно, отрицательны, так как силы
, очевидно, отрицательны, так как силы  и
и  образуют острые углы с отрицательным направлением оси
образуют острые углы с отрицательным направлением оси  , а сила
, а сила  образует острый угол и с отрицательным направлением оси
образует острый угол и с отрицательным направлением оси  :
:

Силы  лежат в плоскости
лежат в плоскости  , а потому они перпендикулярны к оси
, а потому они перпендикулярны к оси  и, следовательно,
и, следовательно,

Сила  параллельна оси
параллельна оси  , а потому
, а потому  . Углы между силой
. Углы между силой  и осями у и z заданы по условию задачи, а потому находим:
и осями у и z заданы по условию задачи, а потому находим:

Остается найти углы силы  с осями у и z. Для этого рассмотрим треугольник ОСЕ. Угол
с осями у и z. Для этого рассмотрим треугольник ОСЕ. Угол  — внешний угол этого треугольника, а потому он равен сумме углов СОЕ и CEO, т. е. 60°
— внешний угол этого треугольника, а потому он равен сумме углов СОЕ и CEO, т. е. 60°  , откуда
, откуда  30°. Из прямоугольного треугольника ODE находим, что
30°. Из прямоугольного треугольника ODE находим, что  60°. Таким образом,
60°. Таким образом,  образует острый угол в 30° с отрицательным направлением оси z и острый угол в 60° с отрицательным направлением оси у, а потому
образует острый угол в 30° с отрицательным направлением оси z и острый угол в 60° с отрицательным направлением оси у, а потому

Указанные значения проекций можно расположить в виде табл. 2.
Составим теперь три уравнения равновесия, для чего достаточно приравнять нулю сумму проекций всех сил на каждую координатную ось:

Таблица 2

или

Решая эту систему трех уравнений относительно неизвестных  , получим:
, получим:

или

и

или

Так как мы получили отрицательное значение для силы  , то выбранное нами направление этой силы нужно изменить на противоположное; следовательно, стержень СО не растянут, как мы предполагали, а сжат.
, то выбранное нами направление этой силы нужно изменить на противоположное; следовательно, стержень СО не растянут, как мы предполагали, а сжат.

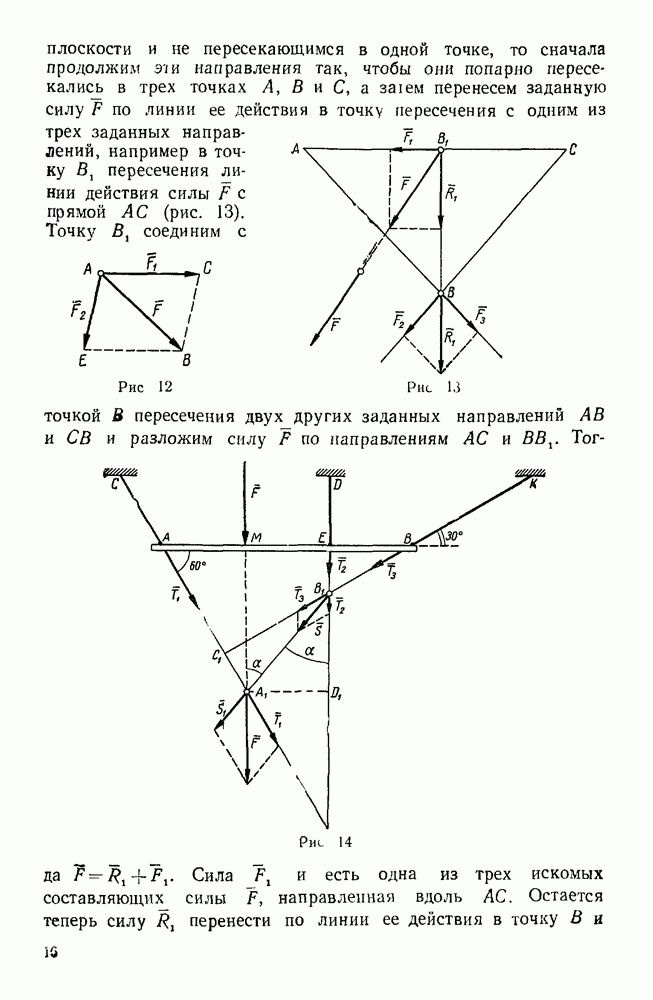
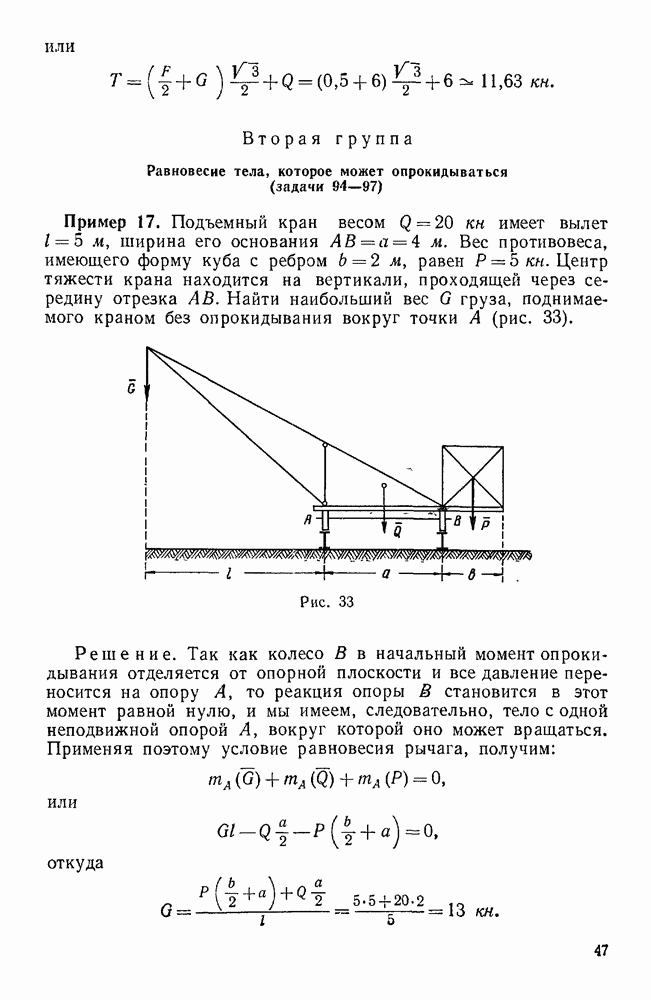
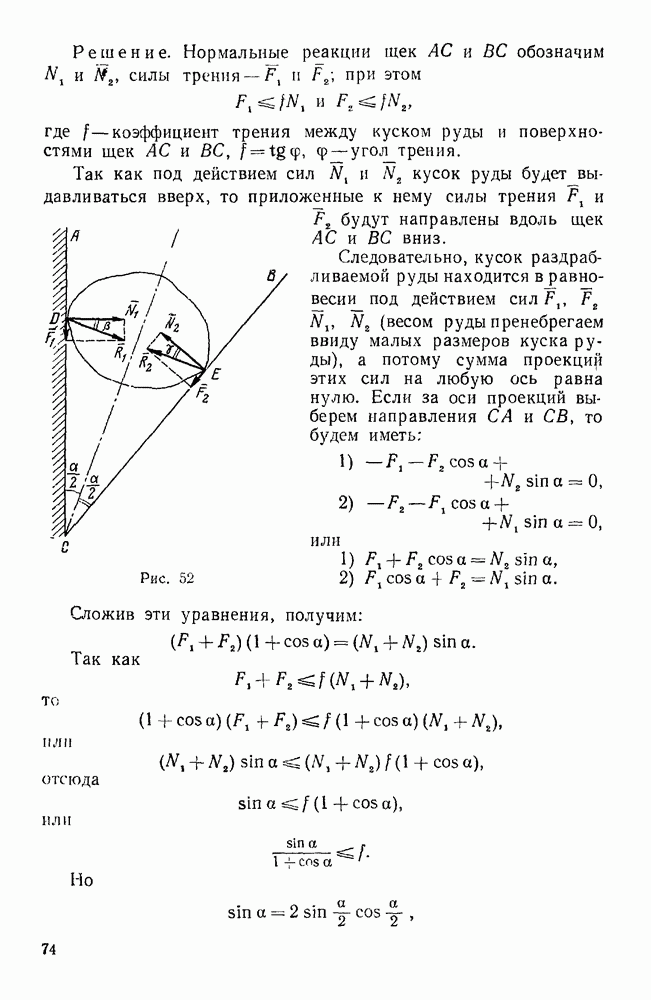
Рис 28.
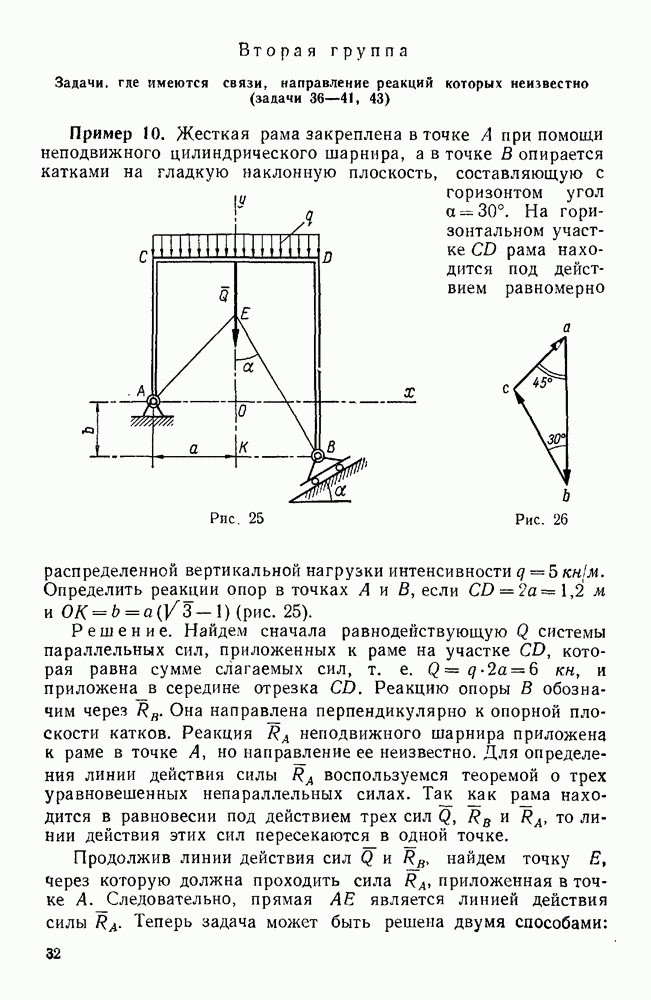
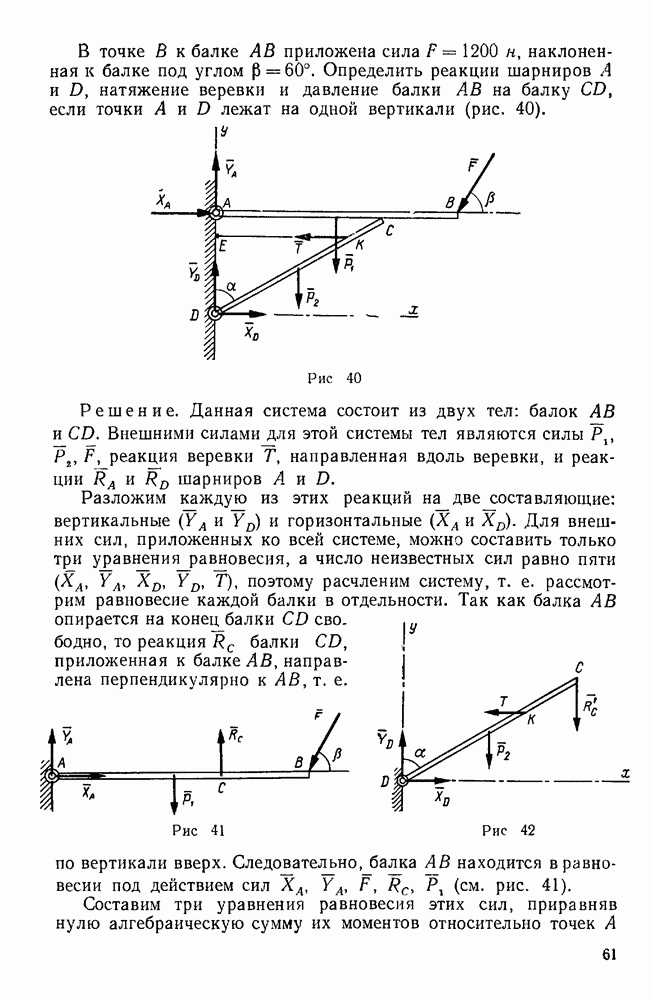
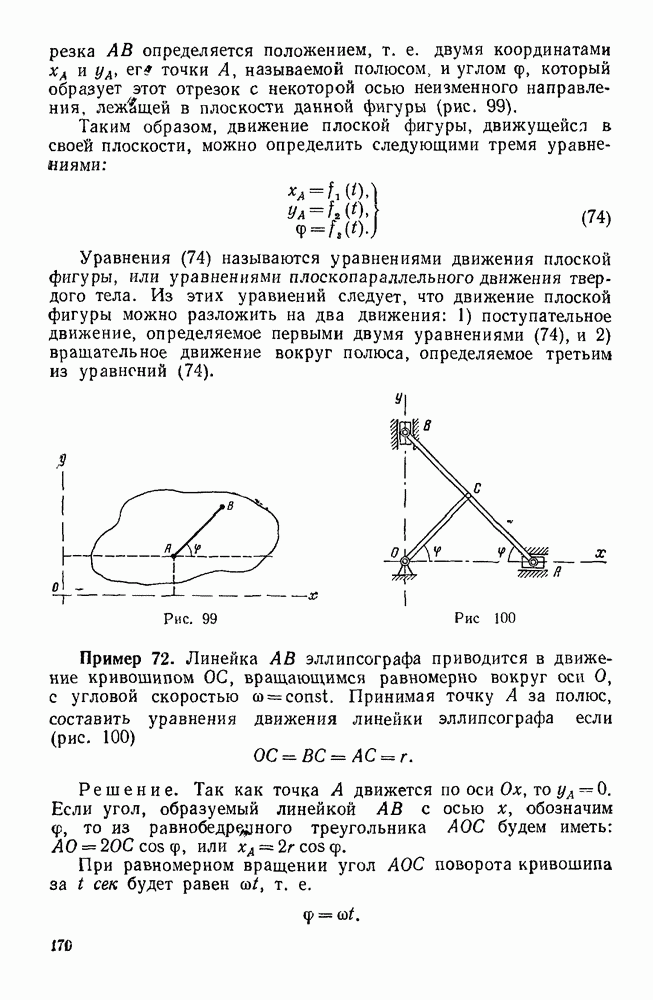
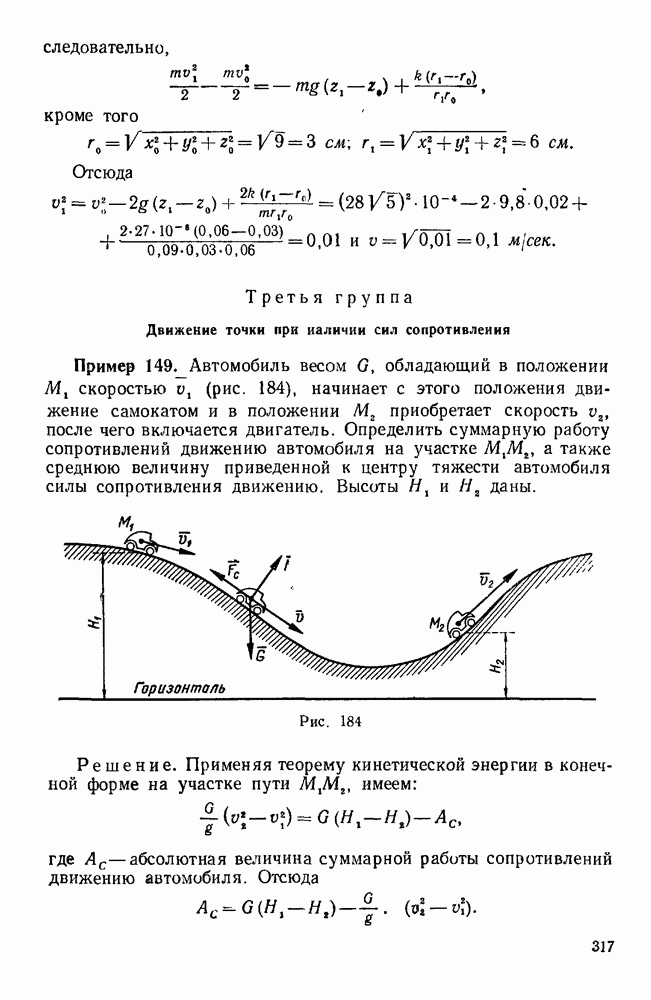
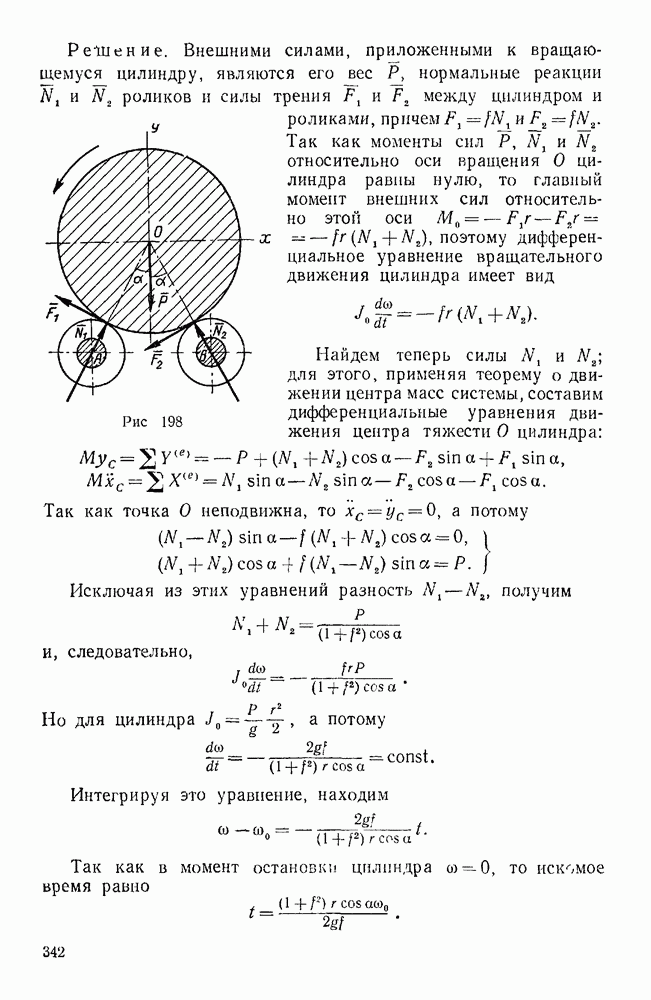
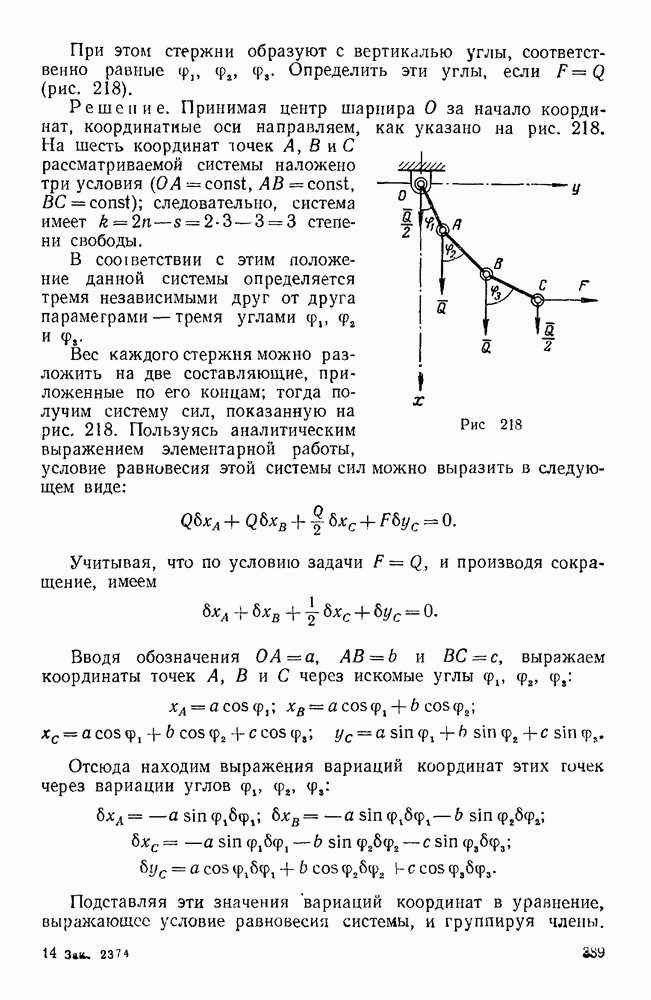
Пример 12. Невесомые стержни АС, АВ и AD соединены шарнирно между тобой в точке Лис неподвижными опорами в точках С, D и В. К узлу А приложена сила  , составляющая с координатными осями х и у углы
, составляющая с координатными осями х и у углы  60°. Определить реакции стержней АС, АВ и AD, если
60°. Определить реакции стержней АС, АВ и AD, если  45° (рис. 28).
45° (рис. 28).
Решение. Рассмотрим равновесие узла А, к которому приложены заданная сила F и реакции  , стержней AC, АВ и AD, направленные вдоль этих стержней. Допустим, что эти реакции направлены от узла А. Так как линии действия сил
, стержней AC, АВ и AD, направленные вдоль этих стержней. Допустим, что эти реакции направлены от узла А. Так как линии действия сил  , пересекаются в одной точке А, то имеем четыре уравновешенные сходящиеся силы, не лежащие в одной плоскости, а потому вычислим проекции этих сил на выбранные координатные оси и составим три уравнения равновесия.
, пересекаются в одной точке А, то имеем четыре уравновешенные сходящиеся силы, не лежащие в одной плоскости, а потому вычислим проекции этих сил на выбранные координатные оси и составим три уравнения равновесия.
Силы  и
и  параллельны соответственно осям х и у, а потому
параллельны соответственно осям х и у, а потому  . Так как углы
. Так как углы  между силой F и положительными направлениями осей х и у заданы, то
между силой F и положительными направлениями осей х и у заданы, то  .
.
Угол  между силой F и осью
между силой F и осью  мы найдем из соотношения
мы найдем из соотношения  , откуда
, откуда  .
.
Так как сила F составляет острый угол с отрицательным направлением оси  , то
, то  . Угол
. Угол  между силой
между силой  и положительным направлением оси
и положительным направлением оси  задан, а потому
задан, а потому  . Углы между силой
. Углы между силой  и осями
и осями  и у не заданы и их нельзя определить непосредственно из чертежа, а потому спроектируем эту силу на плоскость
и у не заданы и их нельзя определить непосредственно из чертежа, а потому спроектируем эту силу на плоскость  и полученную проекцию, которую обозначим через
и полученную проекцию, которую обозначим через  , спроектируем затем на оси х и у. Тогда
, спроектируем затем на оси х и у. Тогда  . Приравнивая нулю сумму проекций всех сил на оси
. Приравнивая нулю сумму проекций всех сил на оси  , получим следующие три уравнення равновесия:
, получим следующие три уравнення равновесия:

Из третьего уравнения находим:  .
.
Из первых двух уравнений имеем:

Так как мы получили отрицательные значения для сил и  то выбранные нами направления для этих сил следует изменить на противоположные; следовательно, стержни АВ и АС сжаты, а стержень AD растянут, так как реакция этого стержня, как мы и предполагали, направлена от узла А.
то выбранные нами направления для этих сил следует изменить на противоположные; следовательно, стержни АВ и АС сжаты, а стержень AD растянут, так как реакция этого стержня, как мы и предполагали, направлена от узла А.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
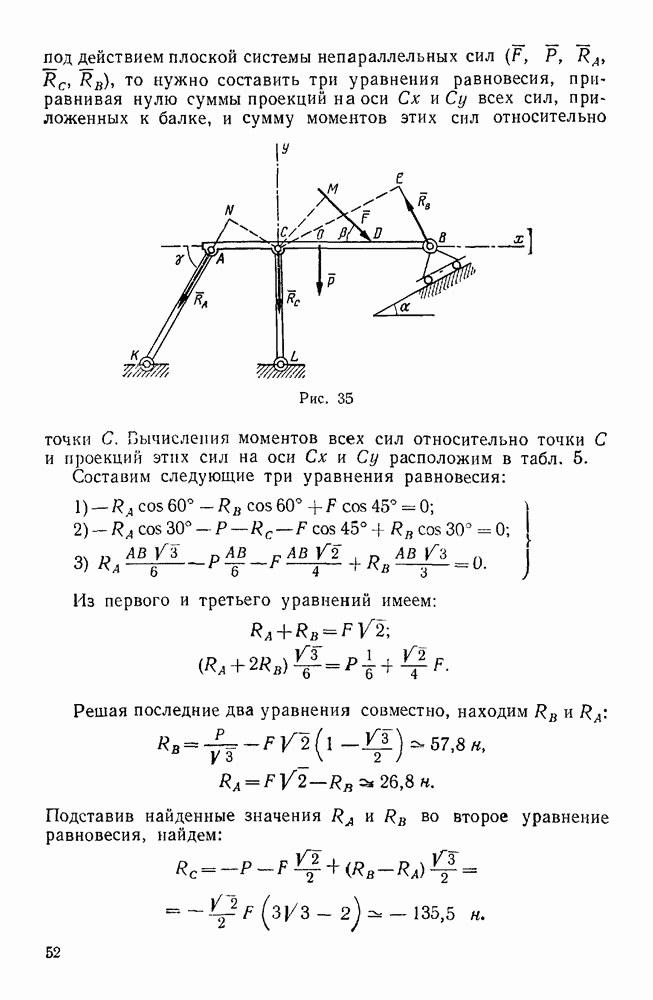
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
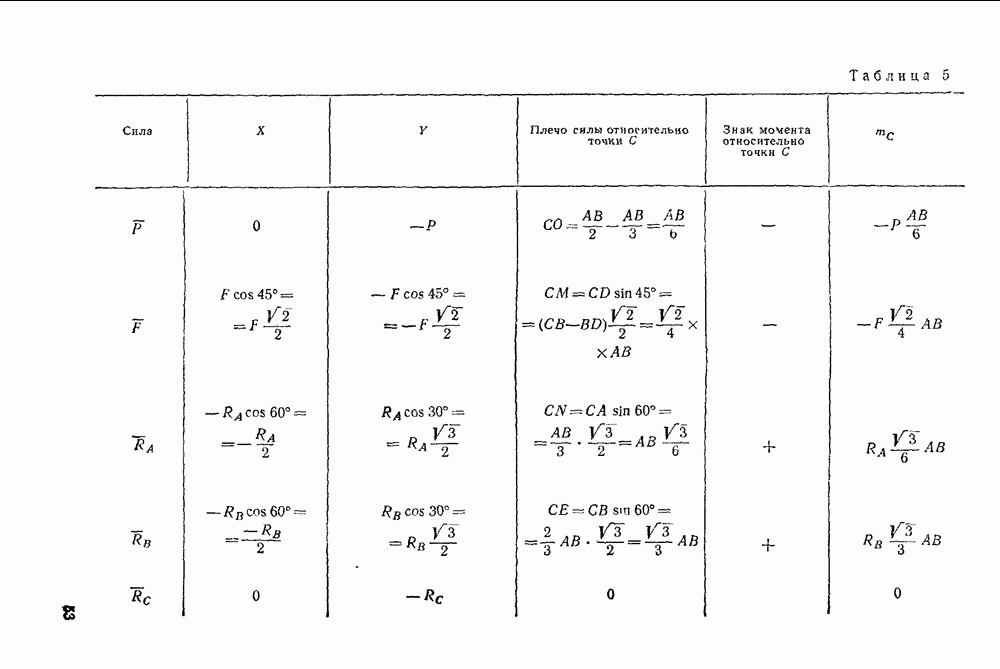
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
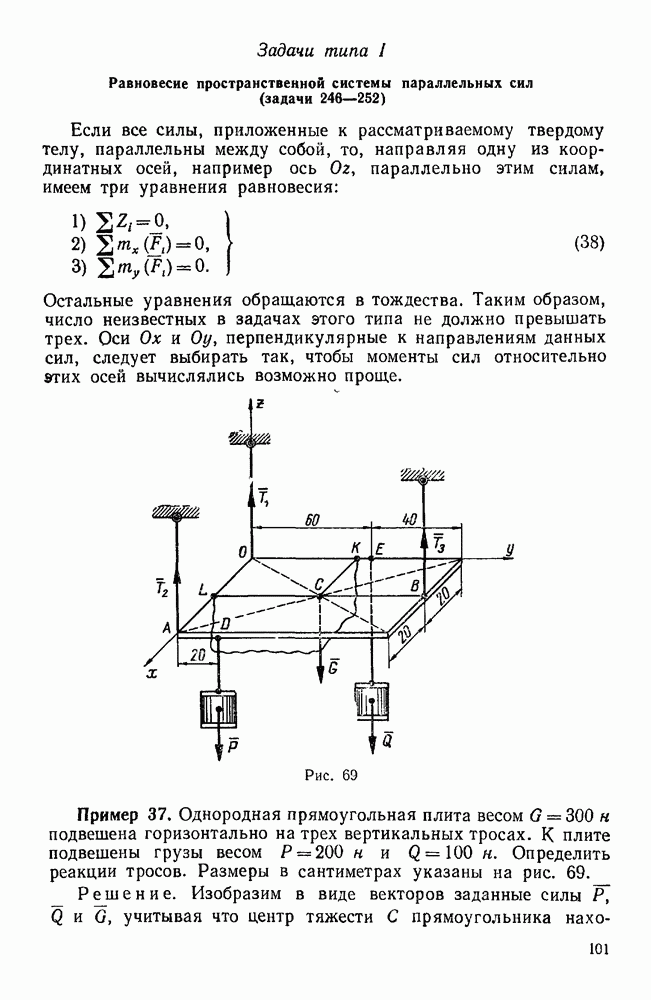
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
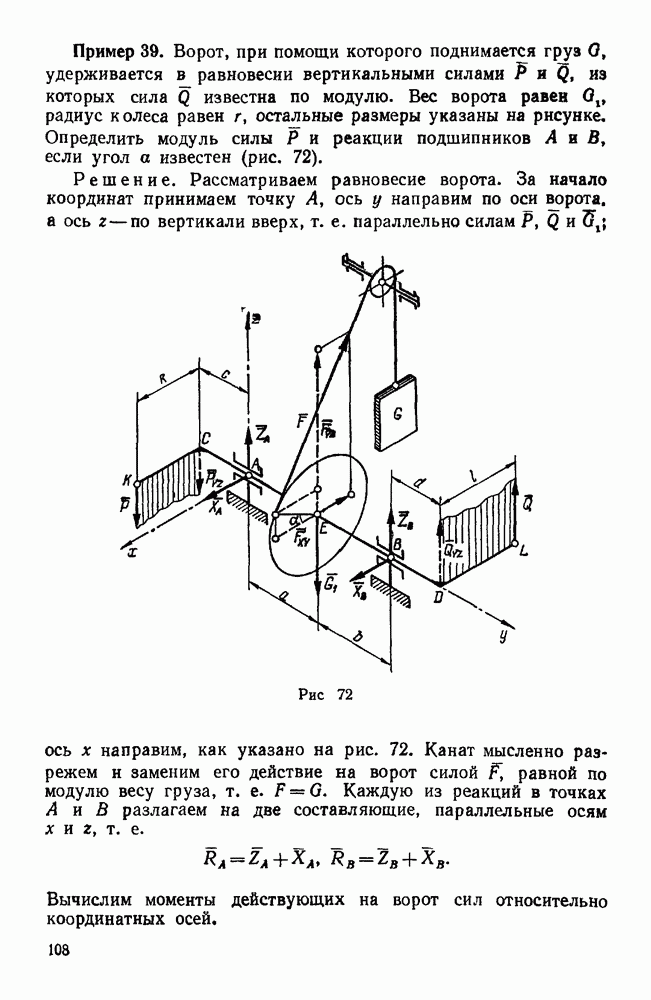
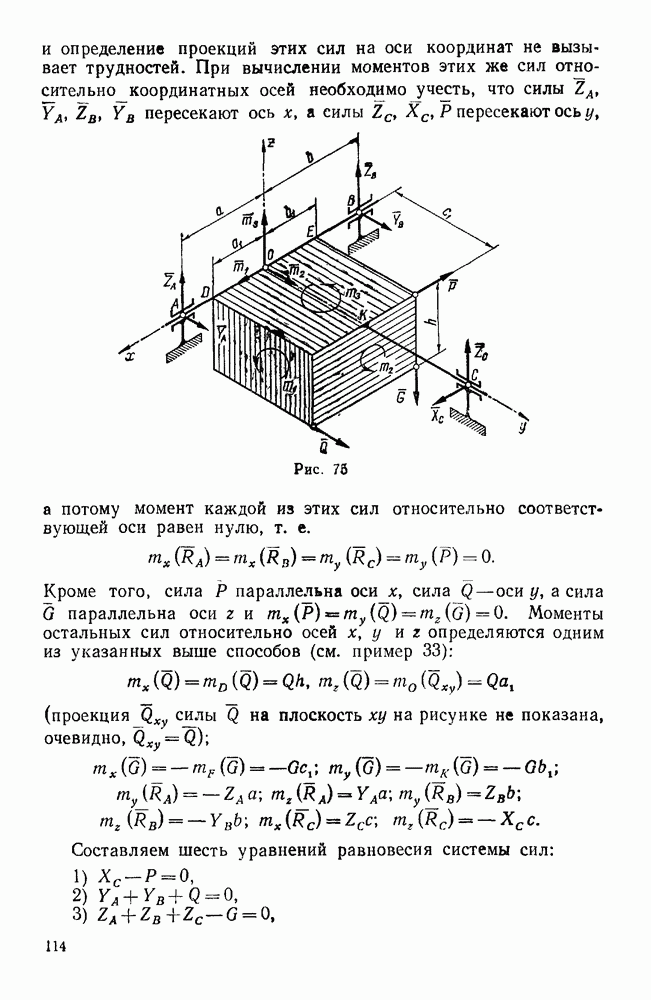
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
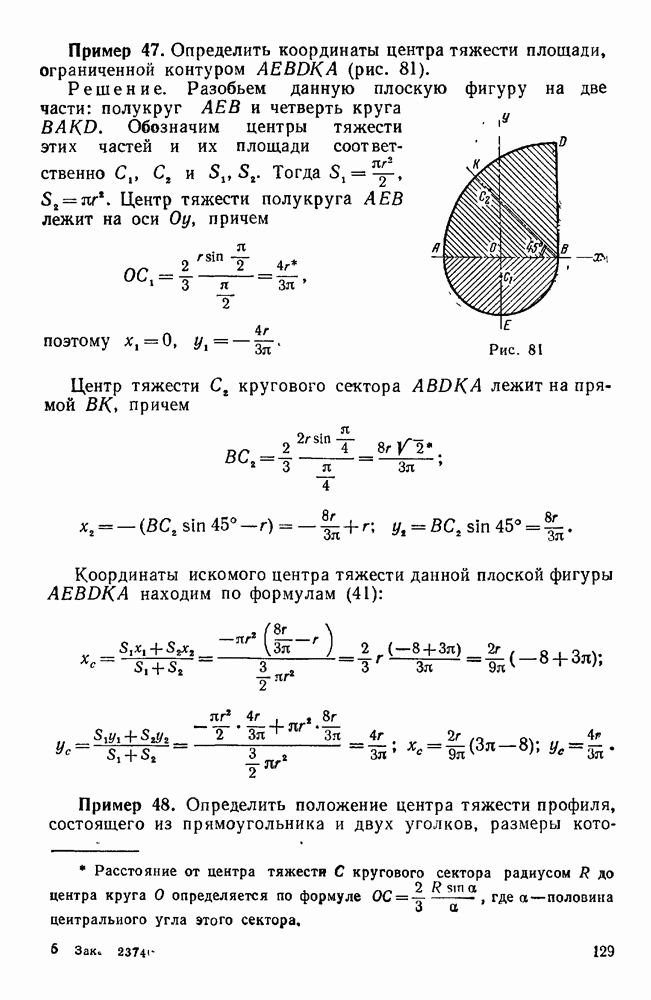
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
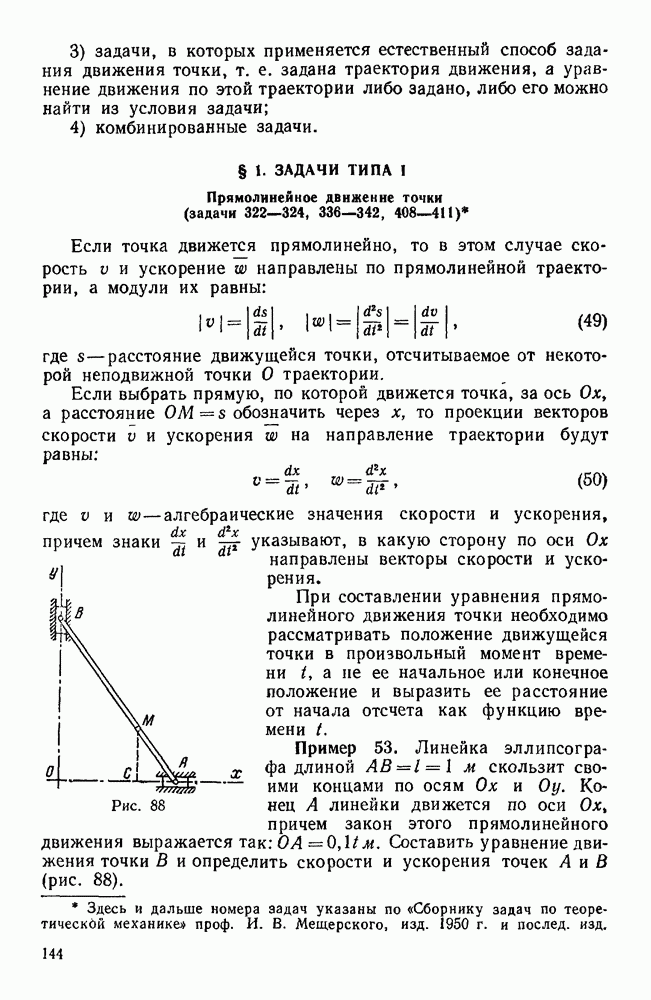
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
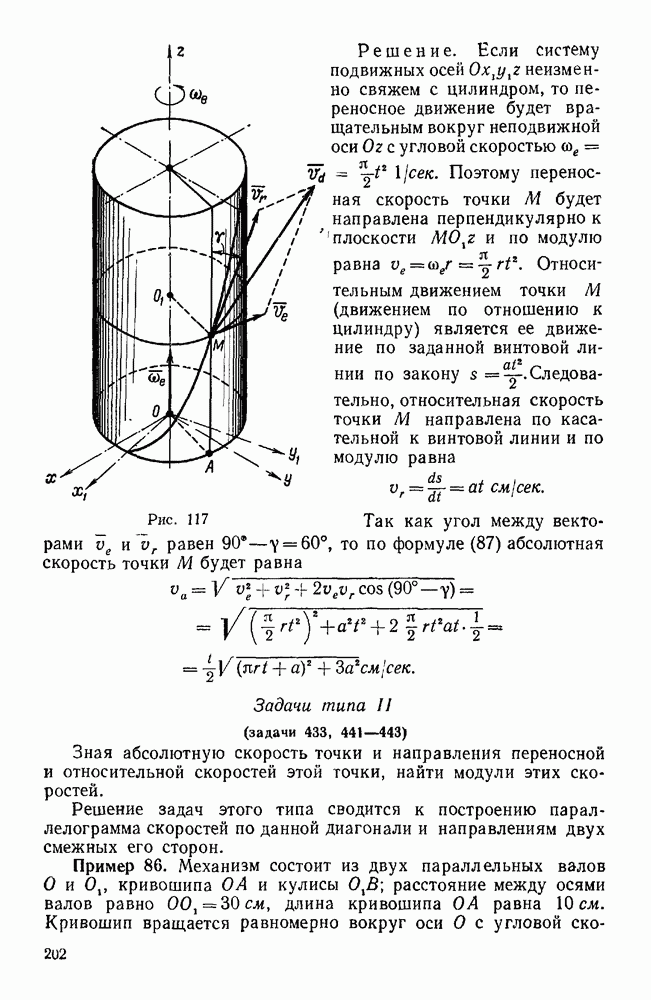
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
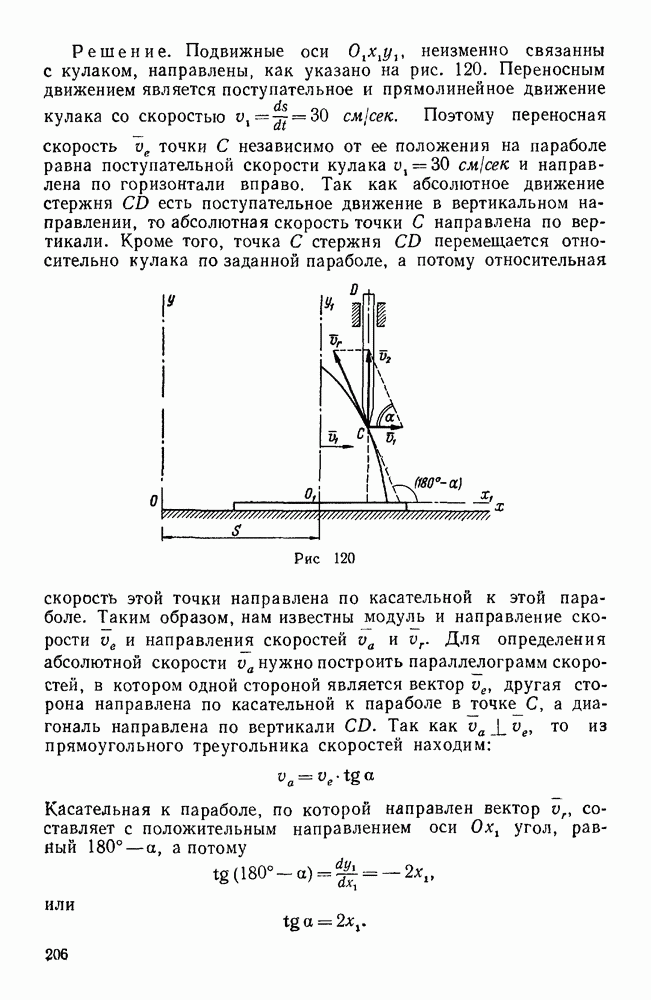
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
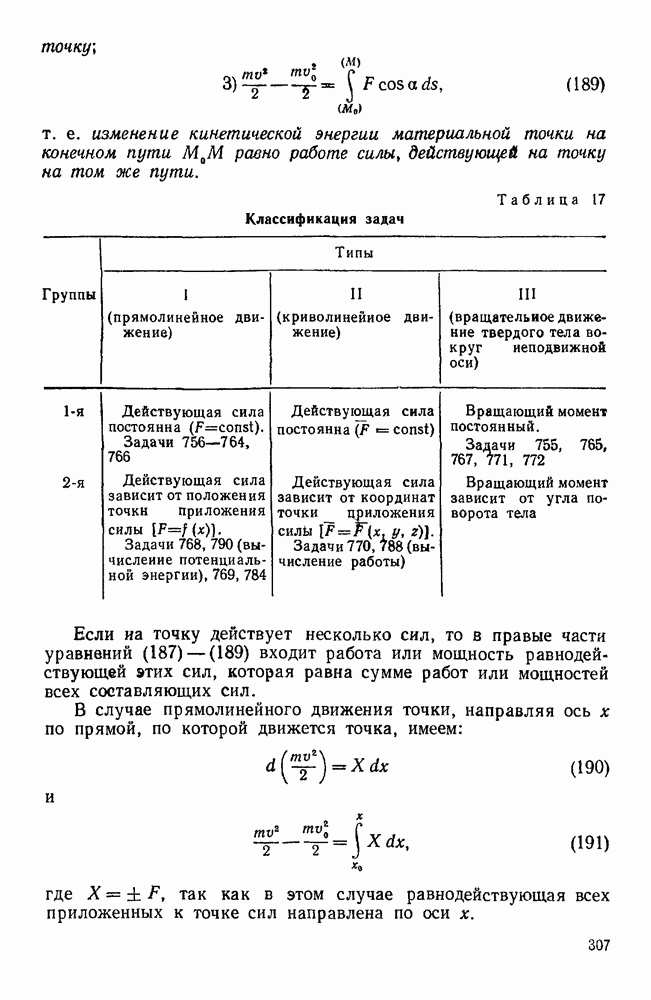
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
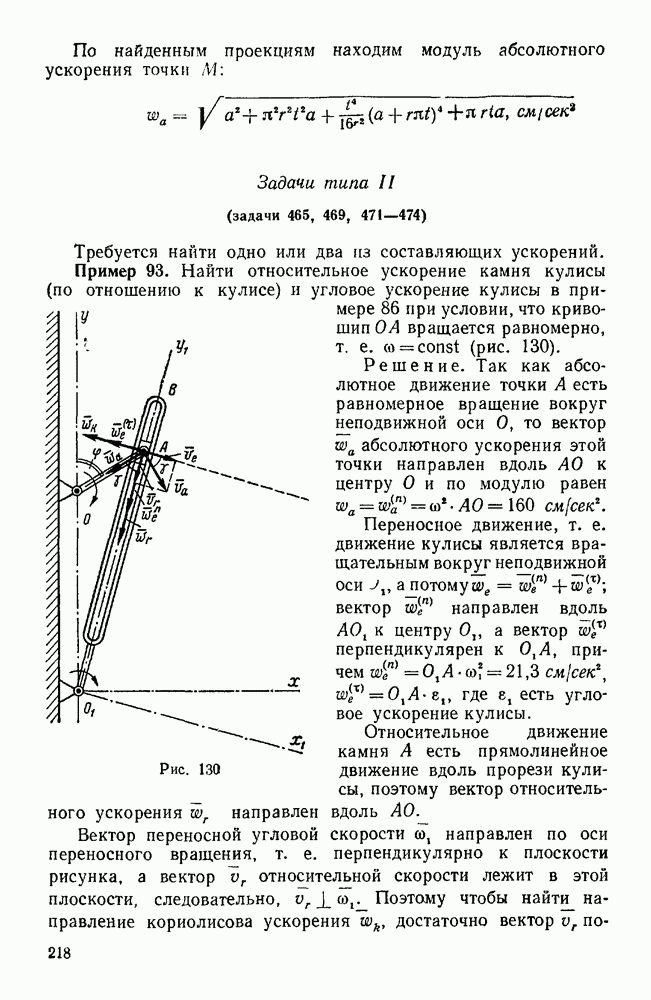
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
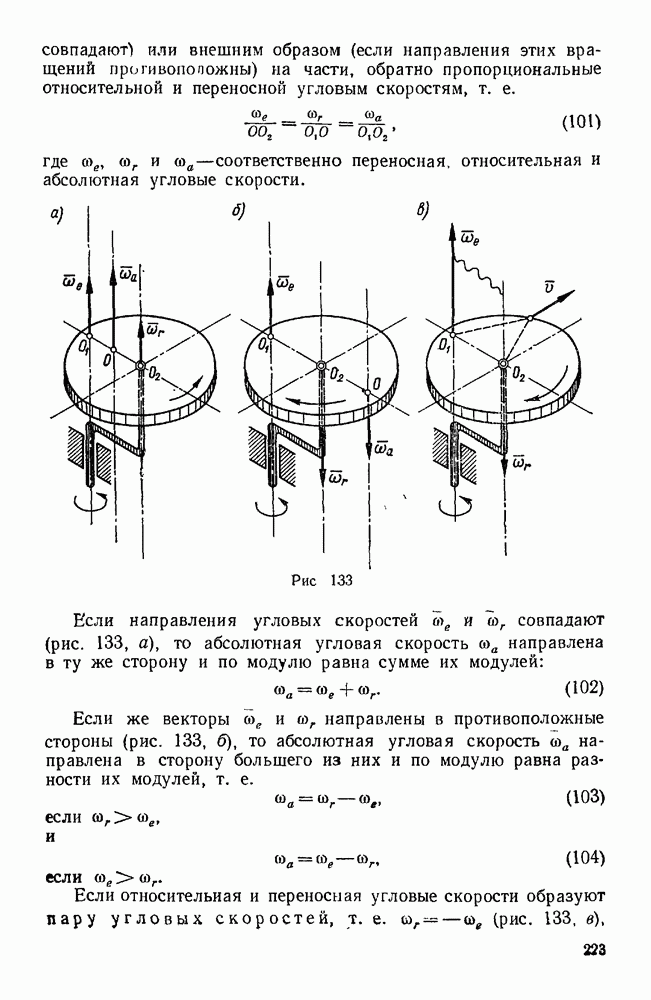
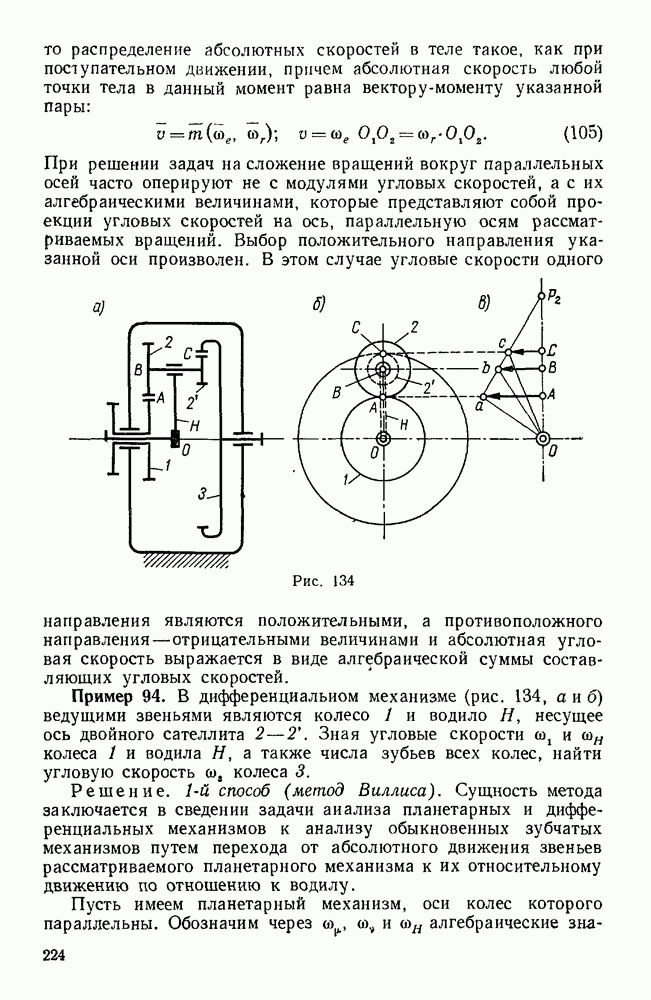
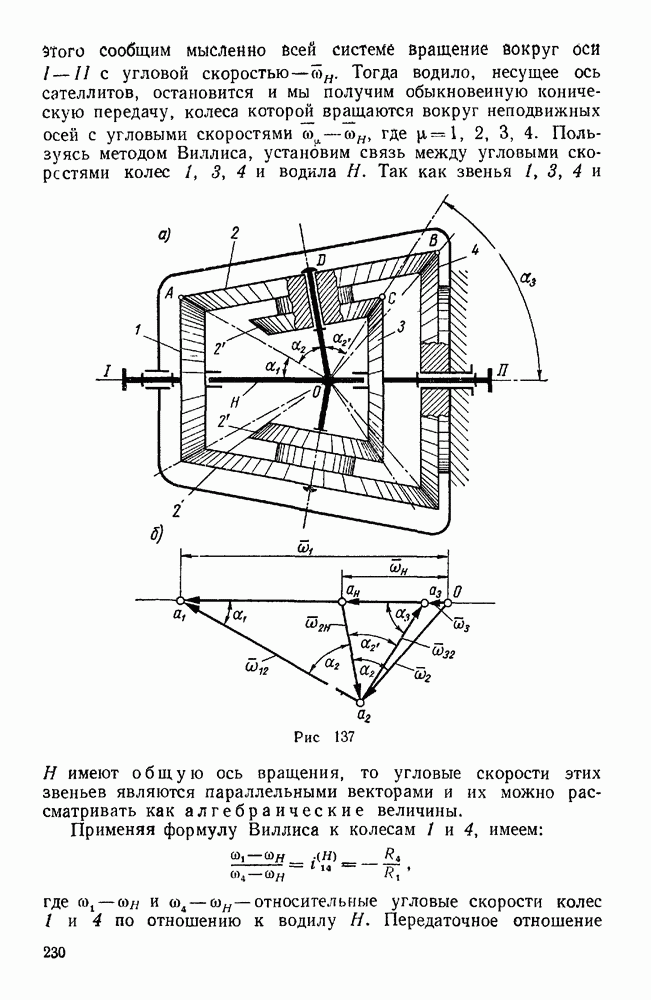
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
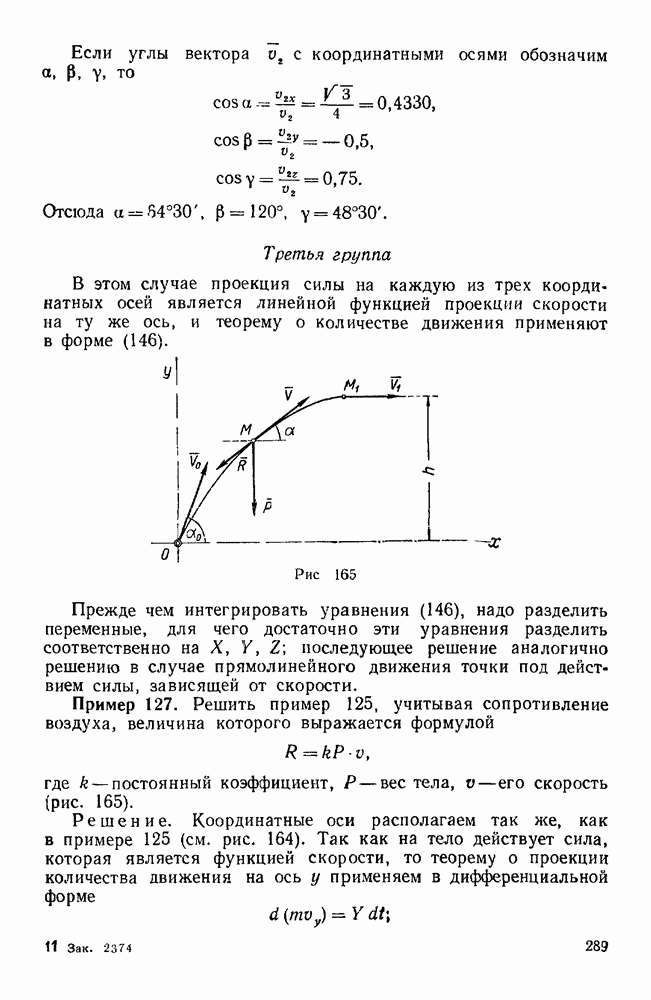
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
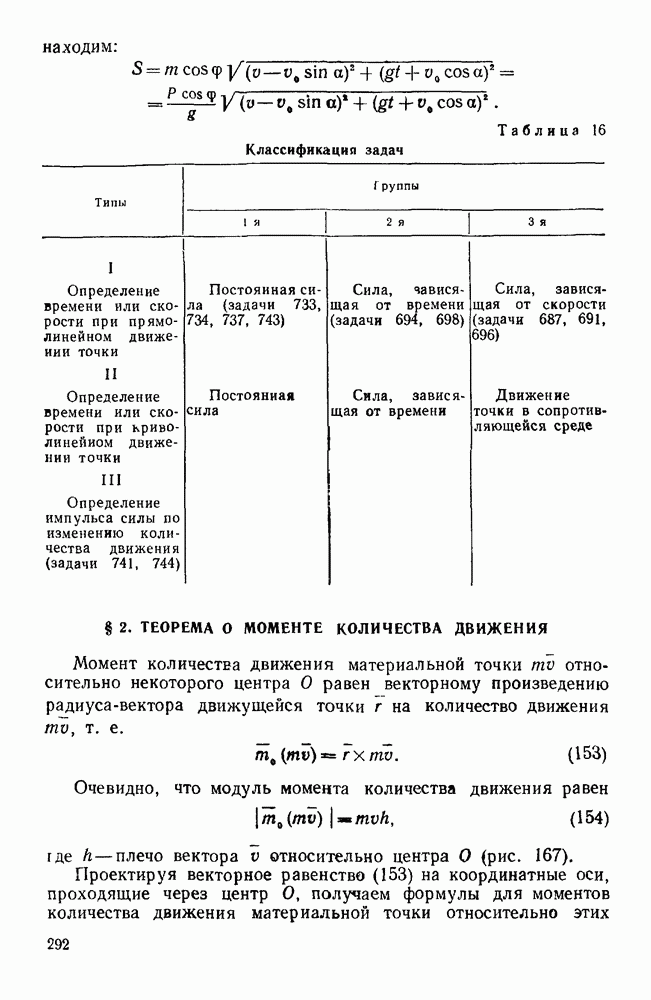
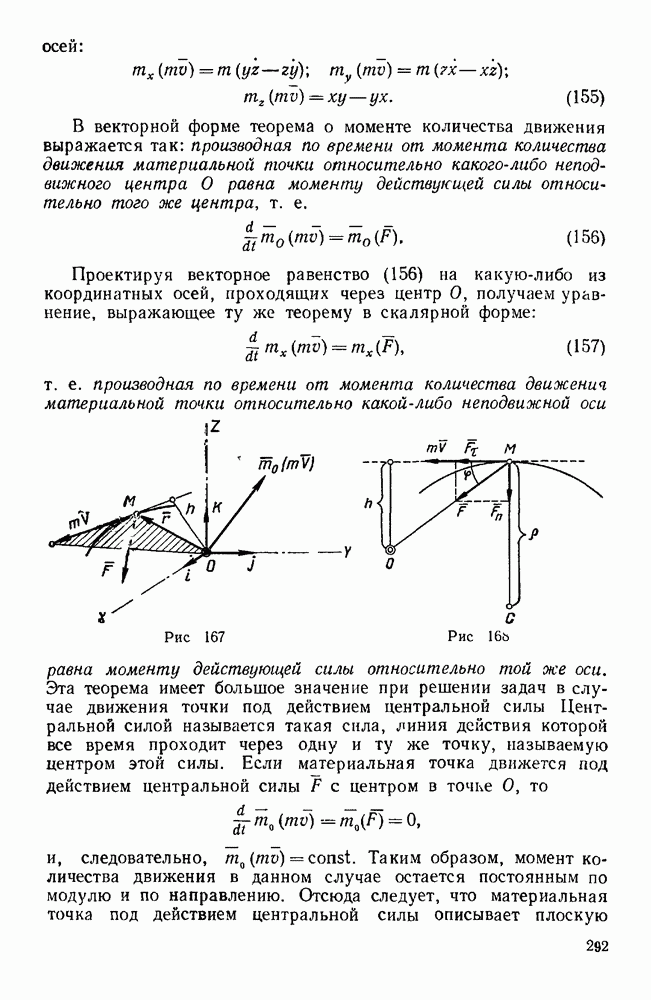
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
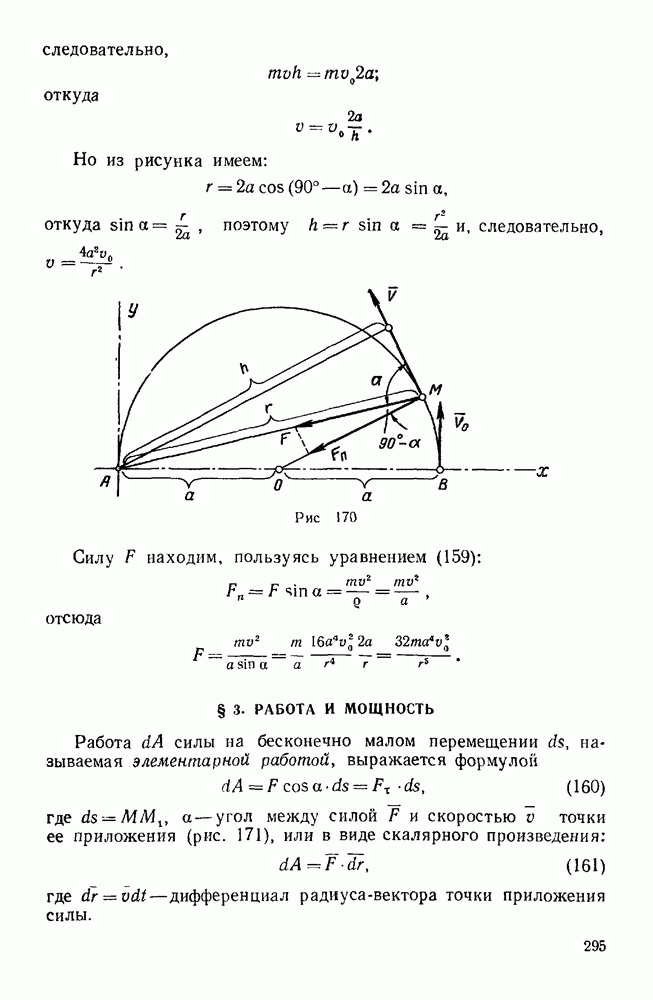
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА