| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Задачи типа III
Задачи этого типа, в которых рассматривается движение несвободной материальной точки, можно разделить на две группы.
Первая группа
Задачи, в которых рассматривается движение несвободной точки по заданной неподвижной линии.

Рис. 147.

Рис. 148.
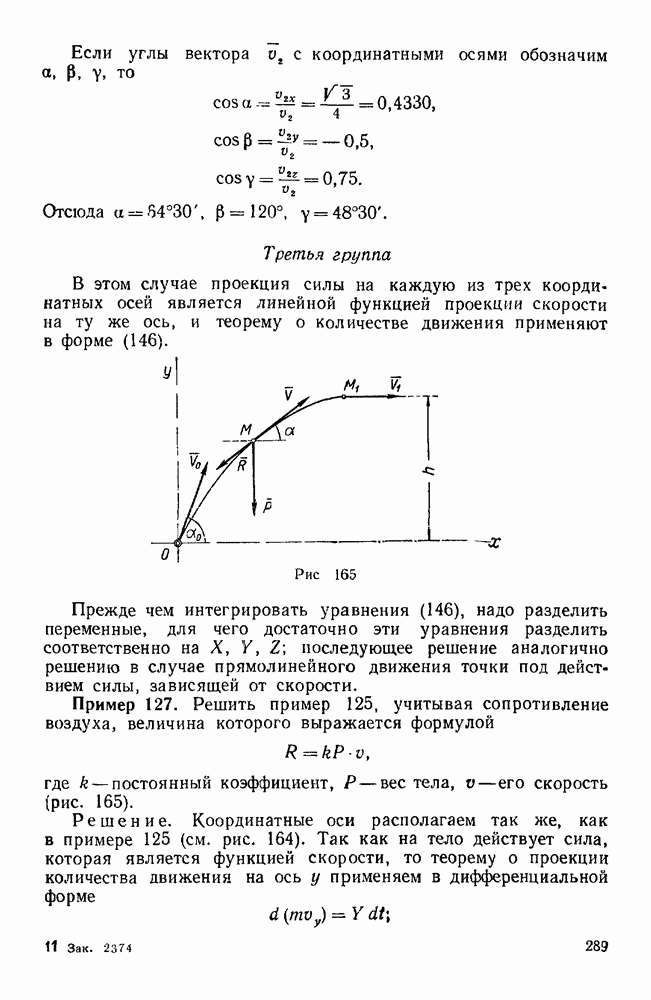
В этом случае, поскольку траектория точки известна, проще воспользоваться дифференциальными уравнениями движения точки в естественной форме (112); при этом необходимо учесть реакции связей, т. е. нормальную реакцию и силу трения (если трение учитывается).
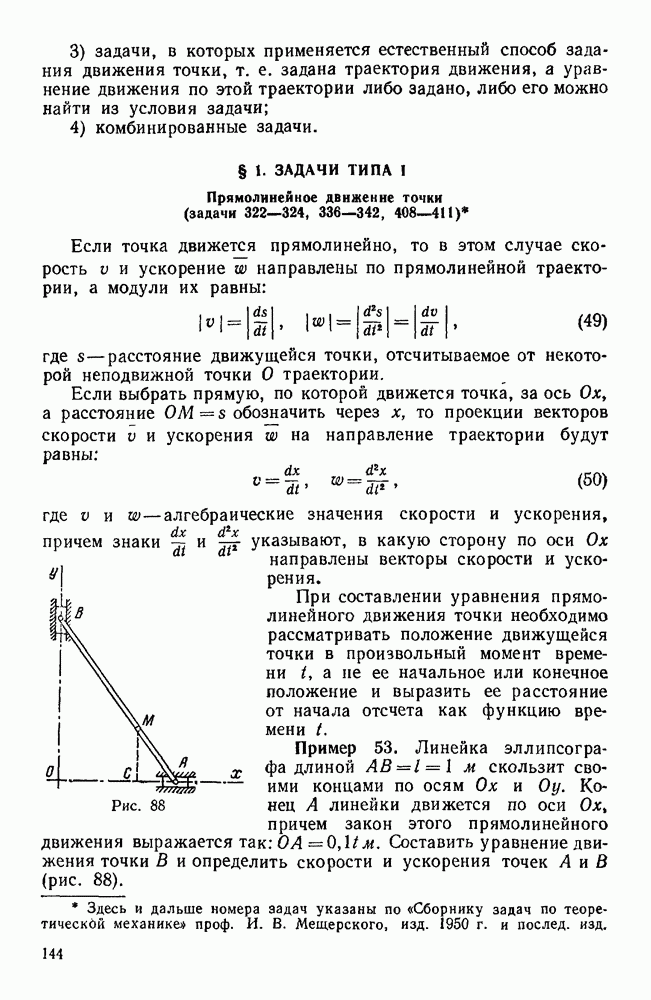
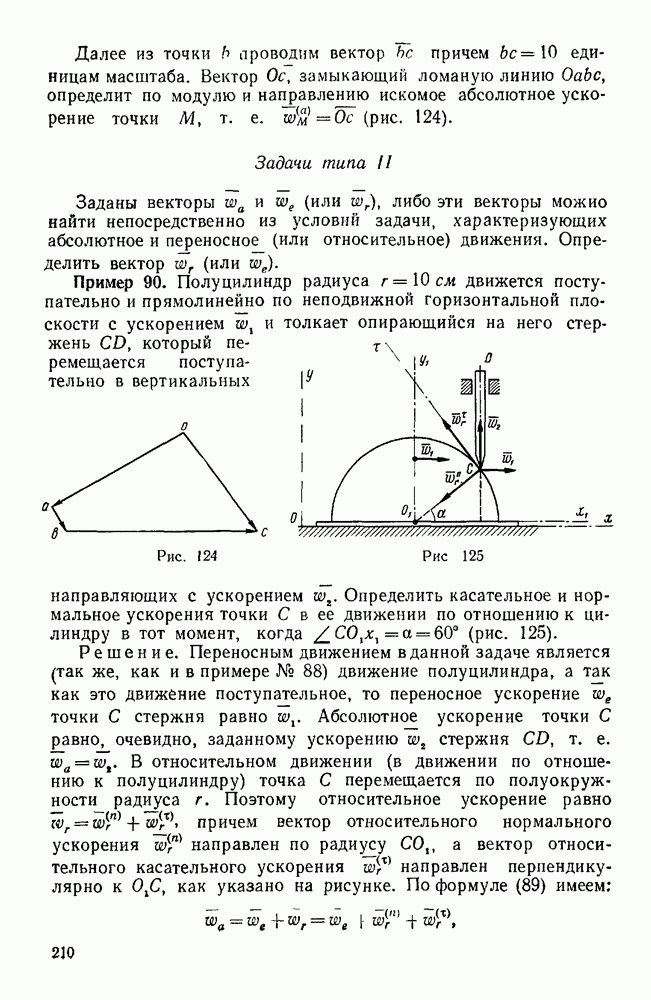
Пример 112. Известно, что на прямолинейном участке железнодорожного пути с углом наклона а вагон, получив некоторую начальную скорость вниз по уклону, движется затем равномерно.
Считая сопротивление движению пропорциональным нормальному давлению колес на рельсы, определить закон движения этого вагона, если он будет двигаться вниз без начальной скорости по прямолинейному участку пути с углом наклона  (рис. 147 и 148).
(рис. 147 и 148).
Решение. Вагон движется поступательно под действием неса Р, нормальной реакции N и силы сопротивления F, которая направлена по наклонной плоскости вверх, противоположно движению вагона.
Сначала рассмотрим равномерное движение вагона по пути с углом наклона  .
.
Согласно уравнениям (ПО), имеем:

Так как вагон движется прямолинейно и равномерно, то  поэтому
поэтому  .
.
Согласно условию,

где  - коэффициент сопротивления. Следовательно,
- коэффициент сопротивления. Следовательно,

откуда

Теперь рассмотрим второй случай, когда вагон движется по участку пути с углом наклона  .
.
Аналогично предыдущему на основании уравнений (110) имеем (см. рис. 148):

Так как ускорение w вагона параллельно оси  (рис. 148), то
(рис. 148), то  , поэтому
, поэтому  , следовательно,
, следовательно,  , или, подставляя значение f и сокращая на
, или, подставляя значение f и сокращая на  , получим:
, получим:

или

Следовательно, вагон движется с постоянным ускорением  . Поэтому по формуле для пройденного пути при равномерно ускоренном движении без начальной скорости имеем:
. Поэтому по формуле для пройденного пути при равномерно ускоренном движении без начальной скорости имеем:

Это и есть искомый закон движения вагона.
Пример 113. Материальная точка весом  , лежащая на горизонтальной поверхности стола, привязана к неподвижной точке О нитью длиной
, лежащая на горизонтальной поверхности стола, привязана к неподвижной точке О нитью длиной  . Точке сообщена начальная скорость
. Точке сообщена начальная скорость  , перпендикулярная к направлению натянутой нити, вследствие чего точка описывает на столе окружность (рис. 149).
, перпендикулярная к направлению натянутой нити, вследствие чего точка описывает на столе окружность (рис. 149).
Найти скорость точки и силу натяжения нити через 1 сек после начала движения, если коэффициент трения  .
.
Решение. К данной материальной точке приложены силы: вес  , нормальная реакция стола N, сила трения
, нормальная реакция стола N, сила трения  и натяжение
и натяжение  .
.

Рис. 149.
Составляем уравнения движения точки в фюрме Эйлера (в проекциях на касательную, нормаль и бинормаль):

Из последнего уравнения  следовательно,
следовательно,  , откуда
, откуда  . Так как
. Так как  , при
, при  , то
, то  поэтому
поэтому  . При
. При  и при числовых данных задачи имеем:
и при числовых данных задачи имеем:  .
.
Из второго уравнения Эйлера, учитывая, что  , находим натяжение нити в момент
, находим натяжение нити в момент  сек:
сек:

Вторая группа
Ко второй группе относятся задачи, в которых рассматривается криволинейное движение точки по данной неподвижной поверхности.
В этих задачах следует составлять дифференциальные уравнения движения точки в координатной форме, учитывая при этом, кроме равнодействующей F заданных сил, приложенных к движущейся точке, нормальную реакцию N поверхности и силу трения  . Поэтому дифференциальные уравнения движения точки имеют вид:
. Поэтому дифференциальные уравнения движения точки имеют вид:

Если к этим уравнениям присоединить уравнение Кулона

где f — коэффициент трения, и уравнение связи (т. е. уравнение поверхности  , по которой перемещается точка, то получим систему пяти уравнений, из которых можно определить все пять искомых величин:
, по которой перемещается точка, то получим систему пяти уравнений, из которых можно определить все пять искомых величин:  .
.
Если трение отсутствует, то последние члены в правых частях уравнений (124) исчезают.
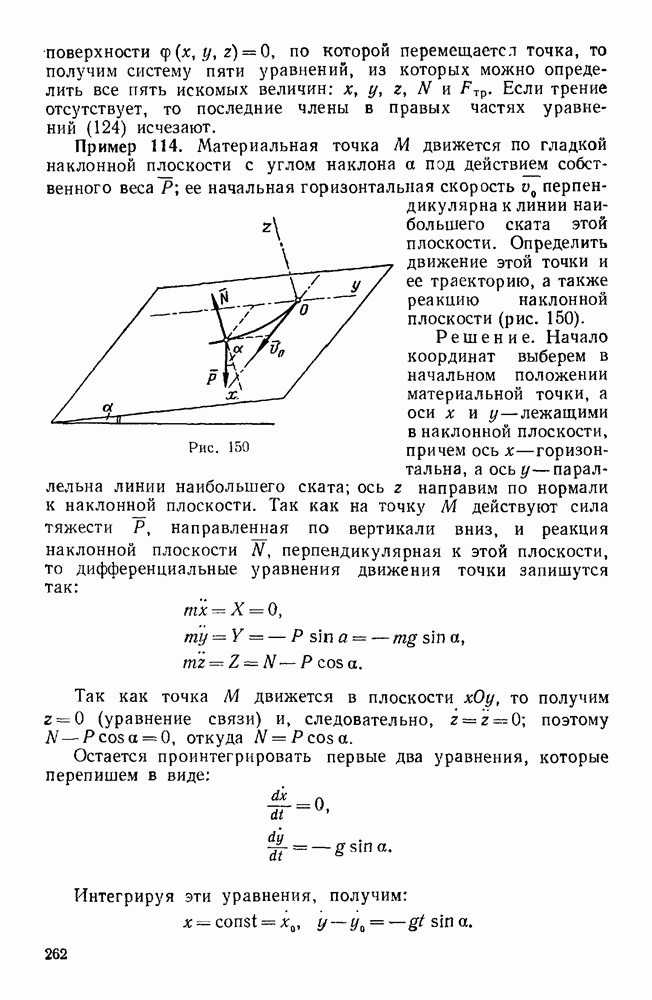
Пример 114. Материальная точка М. движется по гладкой наклонной плоскости с углом наклона а под действием собственного веса  ее начальная горизонтальная скорость перпендикулярна к линии наибольшего ската этой плоскости. Определить
ее начальная горизонтальная скорость перпендикулярна к линии наибольшего ската этой плоскости. Определить  , движение этой точки и ее траекторию, а также реакцию наклонной плоскости (рис. 150).
, движение этой точки и ее траекторию, а также реакцию наклонной плоскости (рис. 150).

Рис. 150.
Решение. Начало координат выберем в начальном положении материальной точки, а оси х и у — лежащими в наклонной плоскости, причем ось х — горизонтальна, а ось у — параллельна линии наибольшего ската; ось z направим по нормали к наклонной плоскости. Так как на точку М действуют сила тяжести  , направленная по вертикали вниз, и реакция наклонной плоскости N, перпендикулярная к этой плоскости, то дифференциальные уравнения движения точки запишутся так:
, направленная по вертикали вниз, и реакция наклонной плоскости N, перпендикулярная к этой плоскости, то дифференциальные уравнения движения точки запишутся так:

Так как точка М движется в плоскости  , то получим
, то получим  (уравнение связи) и, следовательно,
(уравнение связи) и, следовательно,  поэтому
поэтому  , откуда
, откуда  .
.
Остается проинтегрировать первые два уравнения, которые перепишем в виде:

Интегрируя эти уравнения, получим:

Но

а поэтому

Отсюда, интегрируя и принимая во внимание, что  находим:
находим:

Эти уравнения определяют движение точки М по наклонной плоскости.
Исключая отсюда параметр t, находим траекторию этой точки:

Это — парабола, расположенная под осью  .
.
Посмотрим теперь, как изменится решение этой задачи, если учесть силу трения между материальной точкой и наклонной плоскостью, равную

где  - коэффициент трения.
- коэффициент трения.
Третье дифференциальное уравнение движения точки М (относящееся к оси z) остается, очевидно, без изменения; поэтому  и, следовательно,
и, следовательно,  . Так как сила трения направлена противоположно скорости v, то
. Так как сила трения направлена противоположно скорости v, то

Отсюда

Следовательно, дифференциальные уравнения движения точки М в плоскости  после сокращения на m имеют вид:
после сокращения на m имеют вид:

Интегрирование этих дифференциальных уравнений можно выполнить, пользуясь приближенными методами.
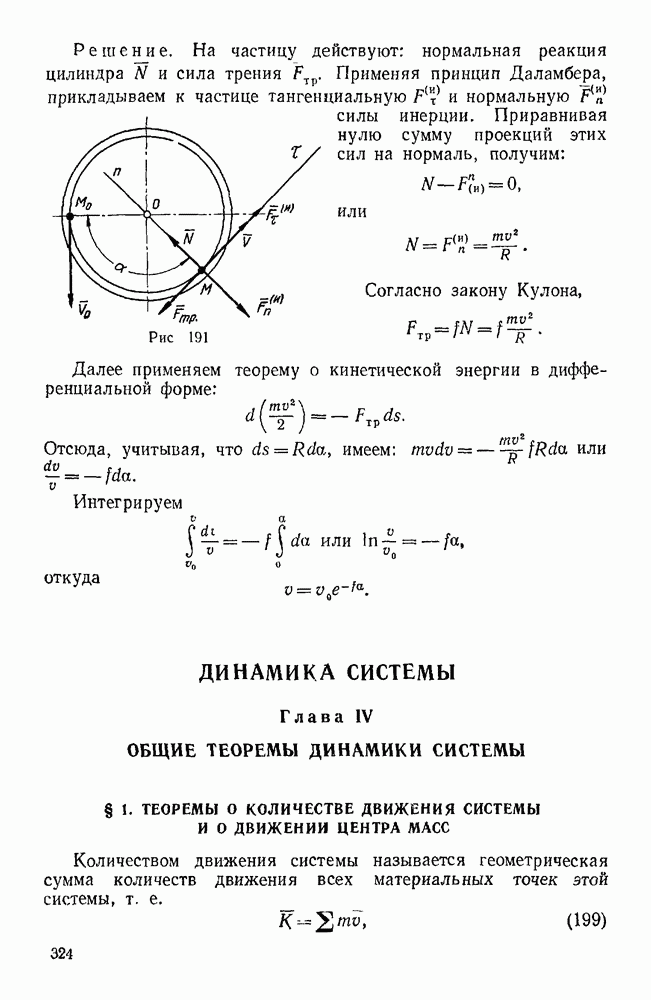
Пример 115. Тяжелая материальная частица массы  движется по внутренней поверхности шероховатого круглого цилиндра
движется по внутренней поверхности шероховатого круглого цилиндра  .
.
Коэффициент трения между частицей и цилиндром равен k. В начальный момент частица находится на оси  и получает скорость
и получает скорость  , перпендикулярную к оси
, перпендикулярную к оси  и составляющую с плоскостью
и составляющую с плоскостью  угол
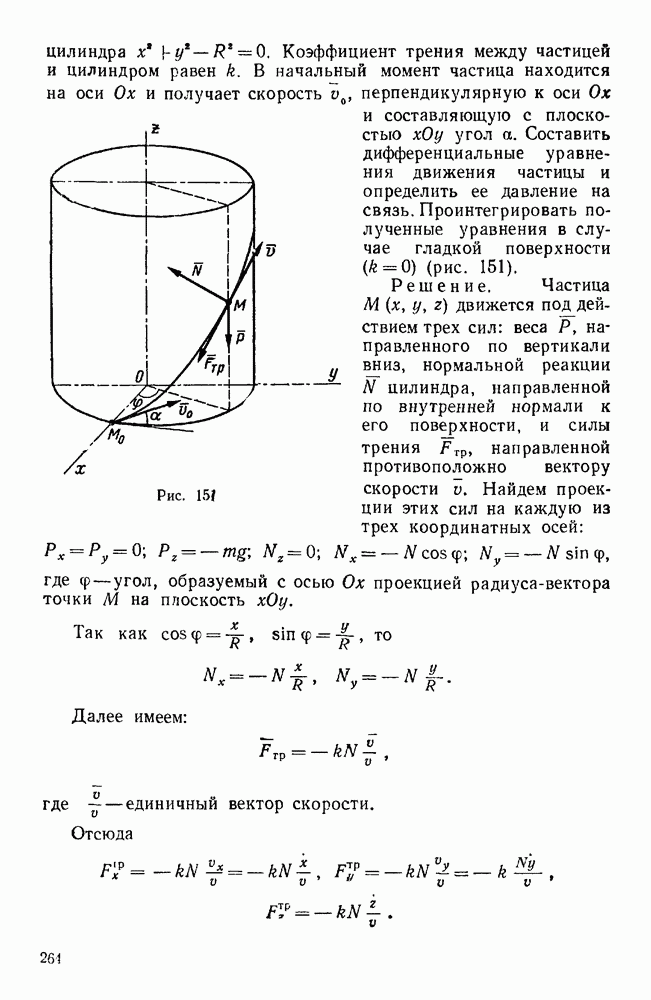
угол  . Составить дифференциальные уравнения движения частицы и определить ее давление на связь. Проинтегрировать полученные уравнения в случае гладкой поверхности
. Составить дифференциальные уравнения движения частицы и определить ее давление на связь. Проинтегрировать полученные уравнения в случае гладкой поверхности  (рис. 151).
(рис. 151).

Рис. 151.
Решение. Частица М(х, у, z) движется под действием трех сил: веса  , направленного по вертикали вниз, нормальной реакции N цилиндра, направленной по внутренней нормали к его поверхности, и силы трения
, направленного по вертикали вниз, нормальной реакции N цилиндра, направленной по внутренней нормали к его поверхности, и силы трения  , направленной противоположно вектору скорости
, направленной противоположно вектору скорости  . Найдем проекции этих сил на каждую из трех координатных осей:
. Найдем проекции этих сил на каждую из трех координатных осей:

где  — угол, образуемый с осью
— угол, образуемый с осью  проекцией радиуса-вектора точки М на плоскость
проекцией радиуса-вектора точки М на плоскость  .
.

Далее имеем:

где  — единичный вектор скорости.
— единичный вектор скорости.
Отсюда

Следовательно, уравнения (124) принимают вид:

Присоединяя к этим уравнениям уравнение связи

мы получили систему четырех уравнений с четырьмя неизвестными х, у, z и N. Продифференцируем дважды уравнение связи:

Умножим первое из уравнений (а) на х, второе — на у и сложим их почленно:

Учитывая соотношения (в) и (г), получим:

или

Подставляя найденное значение N в уравнения (а), получим систему нелинейных дифференциальных уравнений, содержащих координаты х, у и z, а также первые и вторые производные от этих координат по времени.
Так как решение этой системы дифференциальных уравнений представляет собой сложную математическую задачу, то рассмотрим частный случай, когда поверхность цилиндра гладкая.
Тогда система (а) принимает вид:

Чтобы исключить из первых двух уравнений силу N, поделим почленно первое уравнение на второе;
Тогда имеем:

откуда

Но

а поэтому

Так как

то

Следовательно,

Постоянную С, находим из начальных условий движения:

Отсюда

или

Таким образом

Интегрируя третье уравнение системы (а) и определяя произвольную постоянную интегрирования, получим:

Подставляя найденные значения  и
и  в равенство (е), имеем:
в равенство (е), имеем:

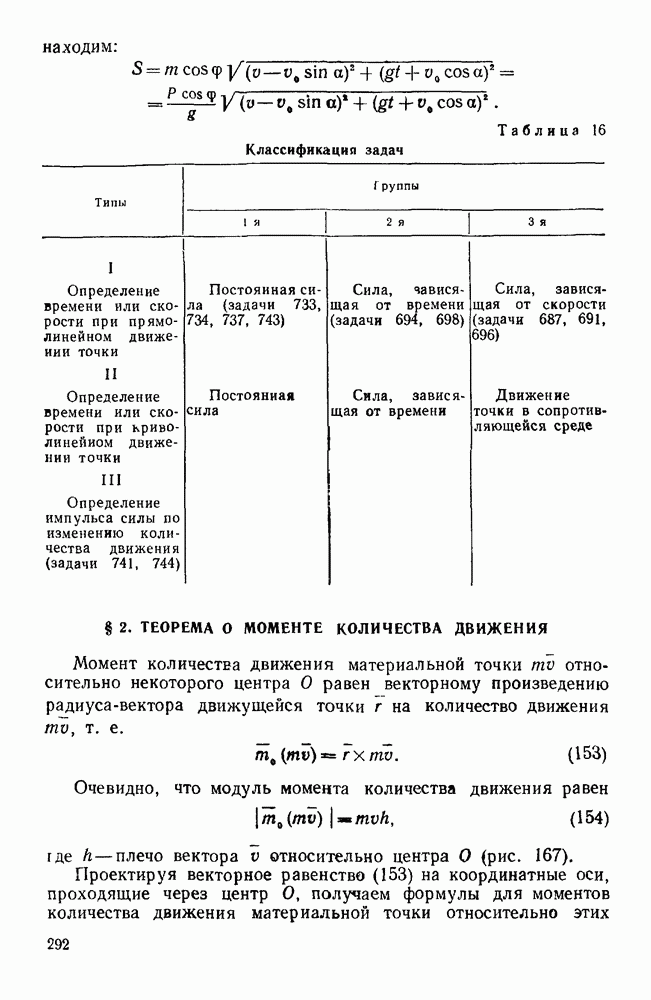
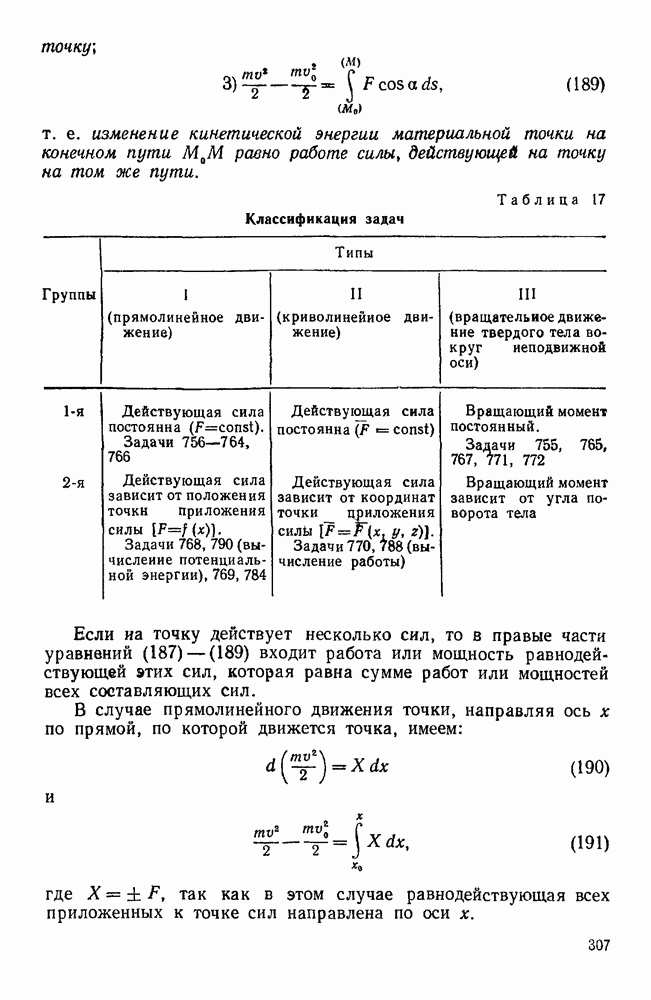
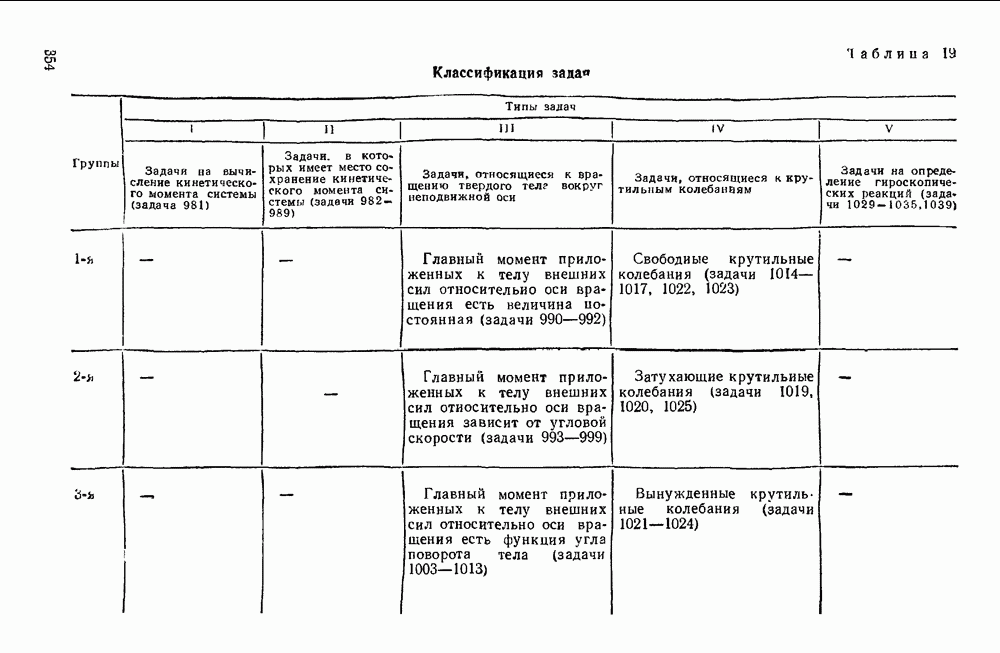
Таблица 15. Классификация задач

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
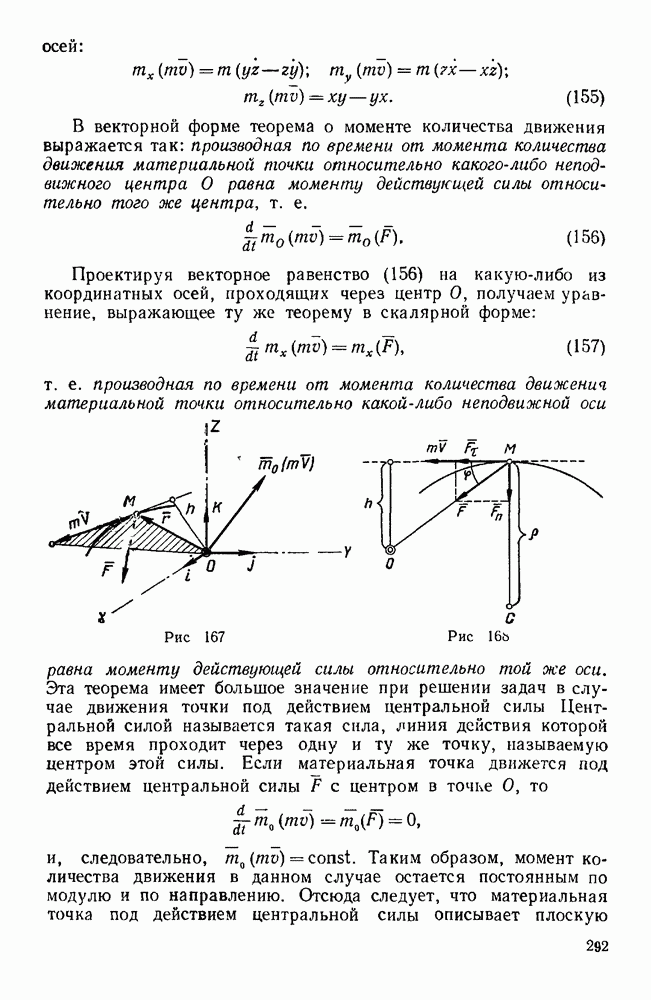
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
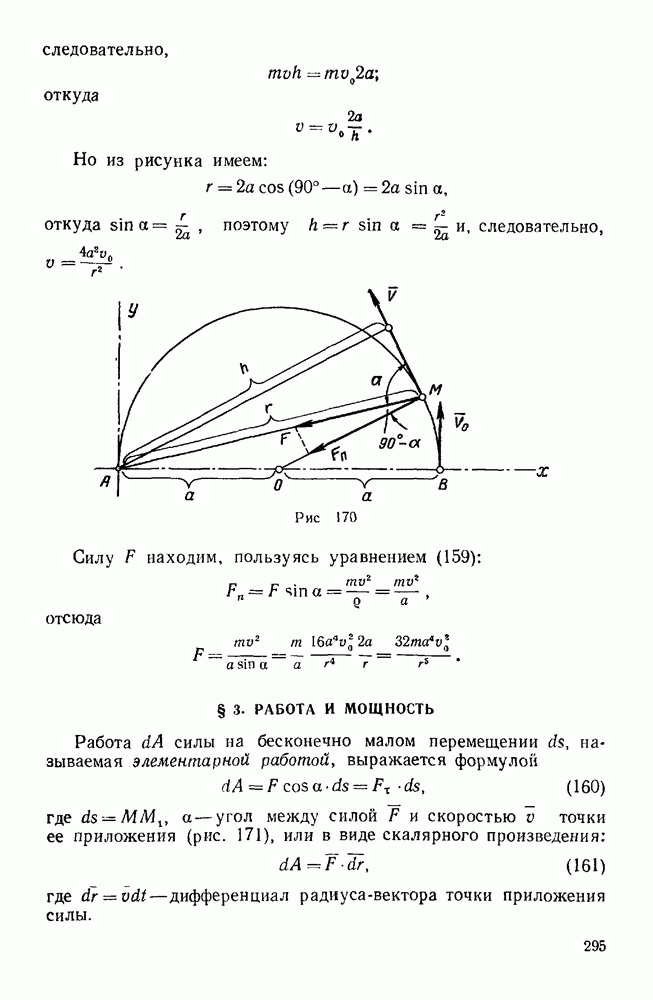
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
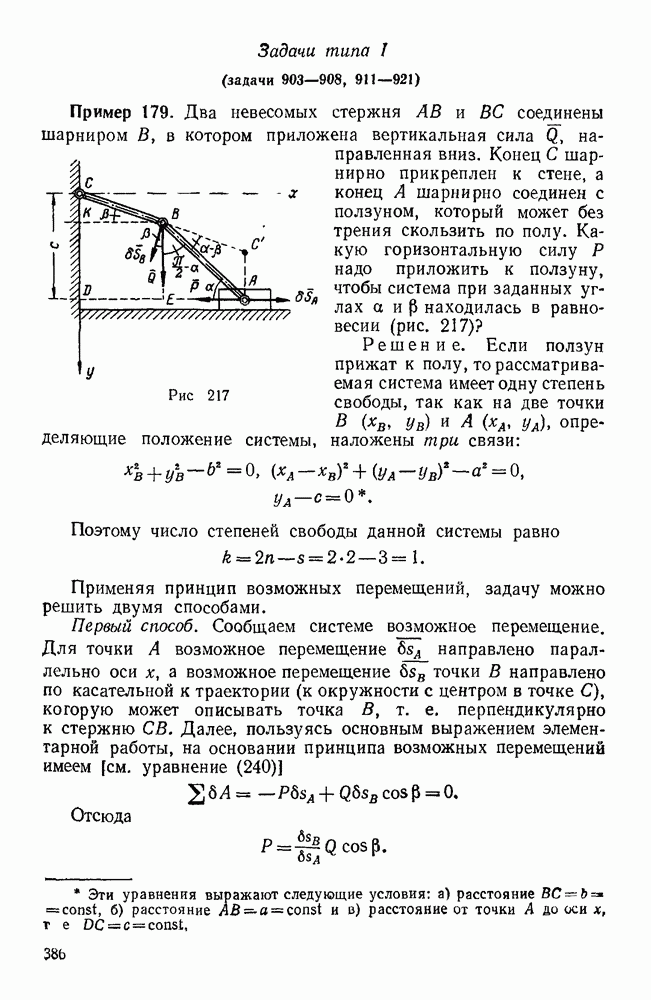
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
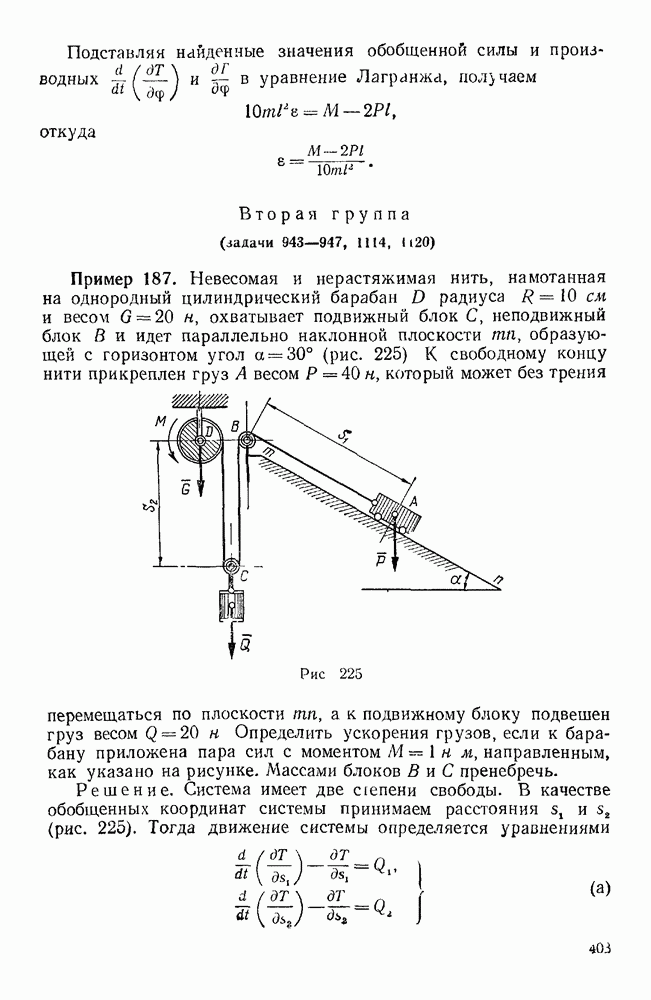
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА