Вторая группа (задачи 1219, 1301, 1303, 1304)

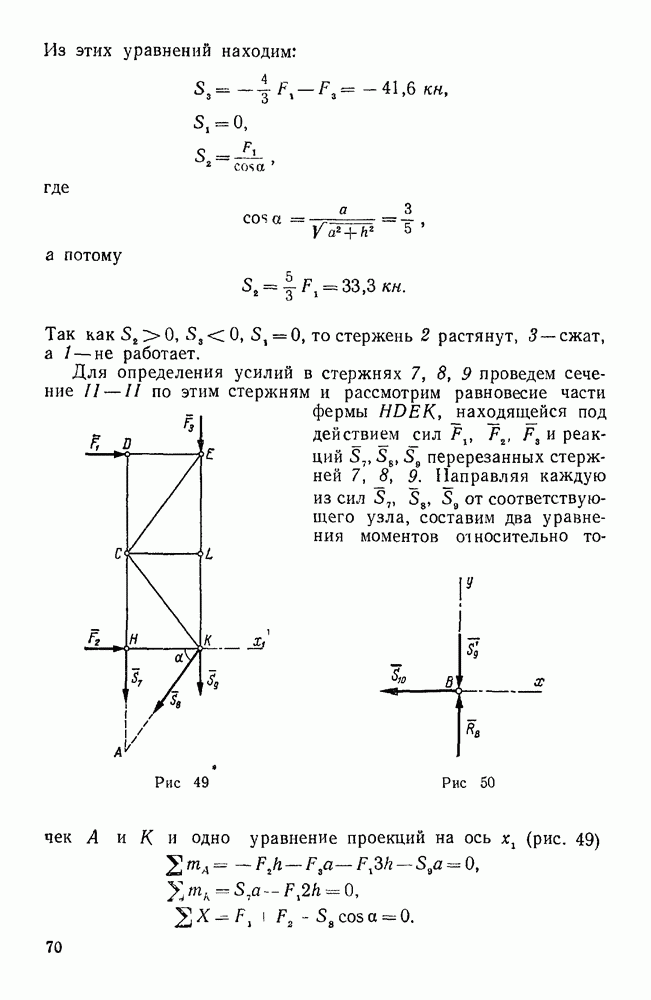
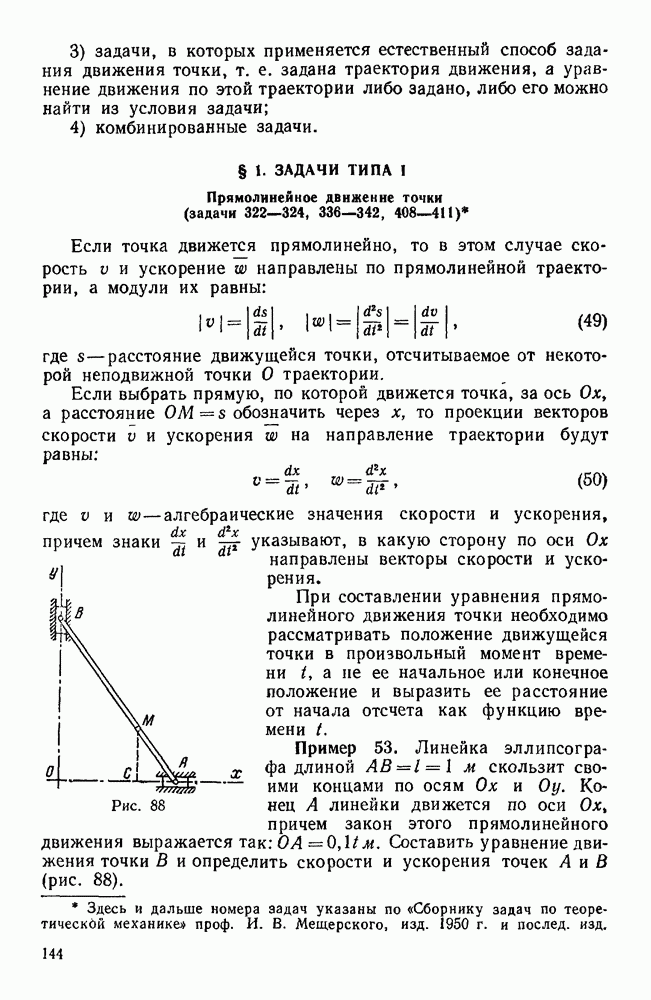
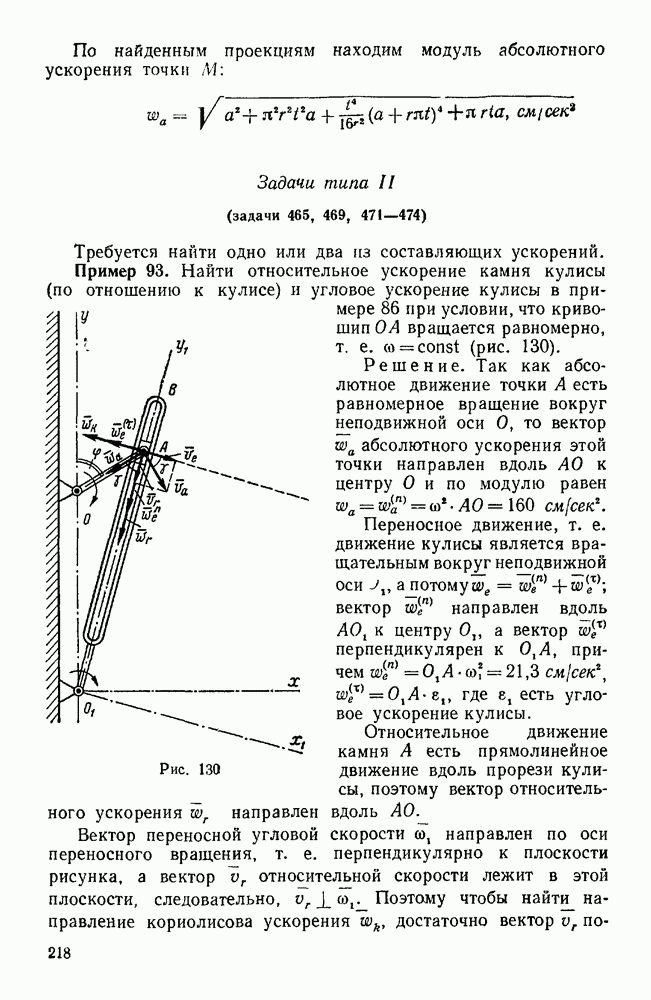
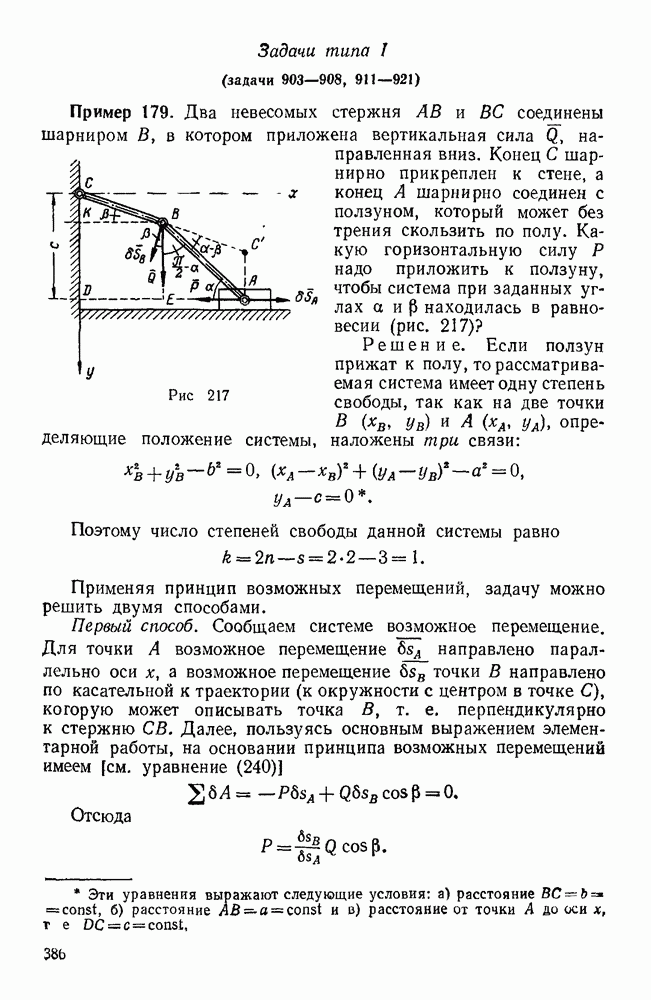
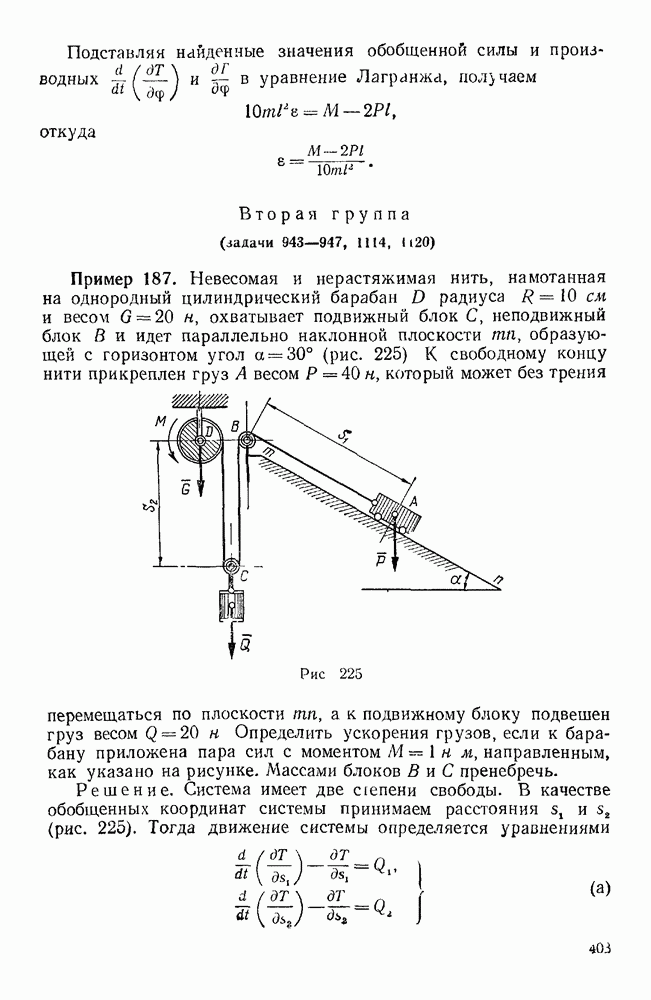
Пример 189. Два однородных сплошных цилиндра общим весом , жестко закрепленные на оси, толщиной и массой которой можно пренебречь, образуют скат, опирающийся на горизонтальные опоры (рис. 227). На той же оси свободно насажен тонкий стержень длиной , несущий на конце точечный груз А весом . Определить движение этой системы, пренебрегая массой стержня и предполагая, что отклонения маятника СА от вертикали весьма малы; трение в узле С отсутствует и цилиндры катятся по опорам без скольжения (рис. 227).

Решение. В данном случае рассматривается система с двумя степенями свободы. Координатные оси располагаем так, как указано на рис. 227.

Рис. 227.

В качестве обобщенных координат выбираем абсциссу точки С и угол отклонения стержня СА от вертикали. В соответствии с этим в данной задаче составляем два уравнения Лагранжа:

Обозначив общую массу цилиндров через , а массу груза А через , вычисляем кинетическую энергию Т системы, которая слагается из кинетической энергии Т, цилиндров и кинетической энергии груза А, причем

где и - скорости точек С и А, — угловая скорость цилиндров, a - момент инерции цилиндров относительно оси вращения, проходящей через точку С. Следовательно,

При этом

где R — радиус цилиндров.

Для определения скорости точки А выразим ее декартовы координаты через выбранные обобщенные координаты

Отсюда

Следовательно, . Теперь получаем

Отсюда

Обобщенные силы и Q находим по общим формулам (247). Замечая, что ,

на основании этих формул получаем

Так как в данной задаче система находится под действием сил тяжести, для которых существует силовая функция, обобщенные силы можно и по формулам (249). Силовая функция для сил , и имеет вид

Следовательно,

Таким образом, уравнения Лагранжа принимают вид

Так как по условию задачи отклонения маятника СА от вертикали весьма малы (т. е. координата и ее первая производная по времени являются весьма малыми величинами), то полученные точные дифференциальные уравнения движения системы можно заменить более простыми приближенными уравнениями, полагая . Кроме того, произведение является малой величиной более высокого порядка, чем остальные члены; поэтому можно положить тогда получаем приближенные уравнения Лагранжа:

Из уравнения (а) имеем

Первое интегрирование этого уравнения дает

После вторичного интегрирования получаем

Для того чтобы определить функцию , из уравнений (а) и (б) исключаем х:

или

или

Вводя обозначение

имеем

Общее решение этого уравнения будет

откуда

Следовательно,

Полученные уравнения, выражающие координаты как функции времени t, и определяют движение рассматриваемой системы. Произвольные постоянные определяются по начальным условиям движения системы.

В начальный момент при имеем

Пусть

Тогда

и, следовательно,

где

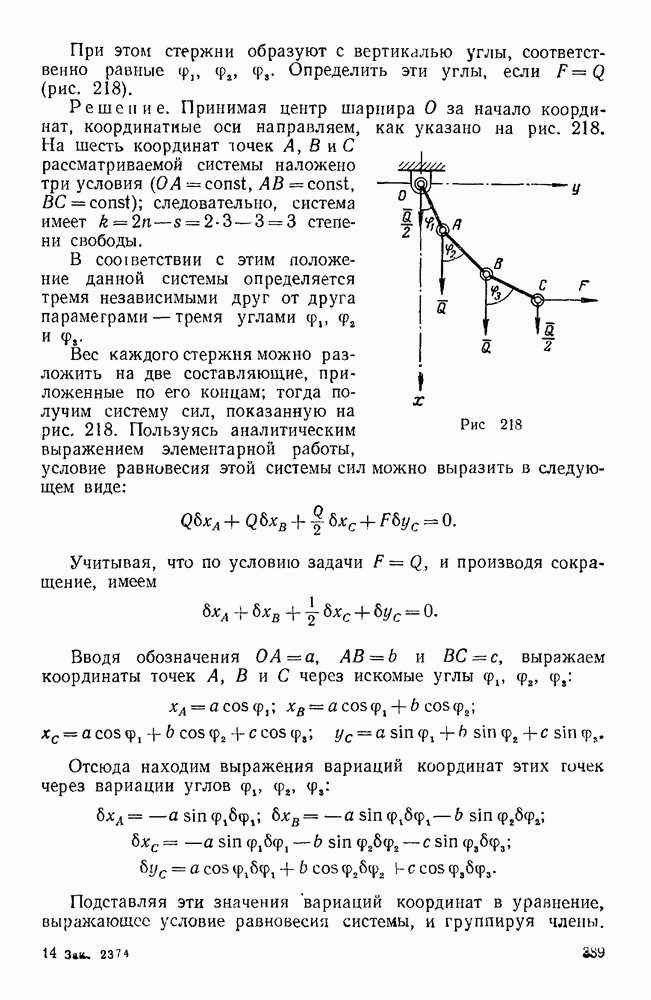
Пример 190. Крановая тележка (рис. 228) массой кг наезжает со скоростью на упругий буфер, жесткость которого . В центре тяжести А тележки подвешен груз В массой кг на канате длиной . Определить движение тележки и груза после соприкосновендя тележки с упором, пренебрегая массой каната.

Рис. 228.

Решение. В качестве обобщенных координат данной системы с двумя степенями свободы принимаем перемещение s тележки с момента соприкосновения с упором и угол отклонения каната от вертикали, который в начальный момент равен нулю. Если рассматривать груз как материальную гочку, то кинетическая энергия системы равна

где скорость тележки , а скорость груза — геометрическая сумма переносной скорости, равной , и относительной скорости (по отношению к тележке) и направленной перпендикулярно к АВ. Поэтому

и, следовательно,

Так как сжатие пружины равно, очевидно, , то потенциальная энергия данной системы равна

Отсюда

Составляя теперь для данной системы два уравнения Лагранжа, получаем

Считая, что в данном случае угловая скорость и угол отклонения каната от вертикали при движении остаются небольшими, полученные уравнения можно заменить приближенными уравнениями, полагая и пренебрегая членом, содержащим . Тогда получаем следующую систему двух линейных дифференциальных уравнений:

где .

Частные решения уравнений (а) ищем в виде

Подставляя эти выражения и их вторые производные в уравнения (а) и сокращая эти уравнения на , имеем

или

Отсюда получаем следующее уравнение частот:

После упрощении это уравнение принимает вид

или

где

Решая уравнение частот, находим

откуда

Таким образом, для отношения амплитуд получаем два значения:

Обозначая через и амплитуды, соответствующие первой частоте , а через амплитуды, соответствующие второй частоте , имеем

Итак, получаем две системы частных решений уравнений (а). Первая система:

Вторая система:

где — начальные фазы, соответствующие частотам .

Первая система частных решений соответствует так называемому первому главному колебанию рассматриваемой механической системы, вторая сисгема частных решений соответствует второму главному колебанию.

В силу линейности исходных дифференциальных уравнений (а) общее решение этих уравнений складывается из частных решений, т. е.

В этих уравнениях являются произвольными постоянными, которые определяются по начальным условиям движения системы.

Дифференцируя уравнения (б) по времени t, имеем

В рассматриваемом примере при .

Подставляя эти значения в уравнения (б) и (в), имеем

Из этих уравнений находим

Таким образом,

Рассмотрим еще второй способ решения полученной системы (а) двух линейных дифференциальных уравнений второго порядка:

Путем последовательного дифференцирования каждого из уравнений этой системы находим

Исключая сначала из этих шести уравнений обобщенную координату и ее производные, а затем координату s и ее производные, получаем два независимых друг от друга линейных дифференциальных уравнений четвертого порядка:

или, введя опять обозначения

Составим характеристическое уравнение, соответствующее каждому из уравнений этой системы.

Корни этого уравнения равны:

Следовательно, решение уравнений (е) имеет вид

где — произвольные постоянные. Перейдем к определению этих постоянных, для чего воспользуемся начальными условиями движения. Полагая в уравнениях (а) и (г) и учитывая, что по условиям задачи имеем

Решая каждую из этих систем в отдельности, получим

Теперь определяем постоянные .

Для этого вычислим из первого из уравнений (ж) производные

Полагая в этих равенствах и в первом из уравнений (ж), получим следующую систему четырех уравнений относительно неизвестных :

Решая совместно первое и третье уравнения, находим . Из второго и четвертого уравнений имеем

откуда

Таким образом,

Аналогично, для определения постоянных получим следующую систему четырех уравнений:

Отсюда находим и, следовательно,

Подставляя в полученные уравнения числовые данные, приходим к прежним результатам.