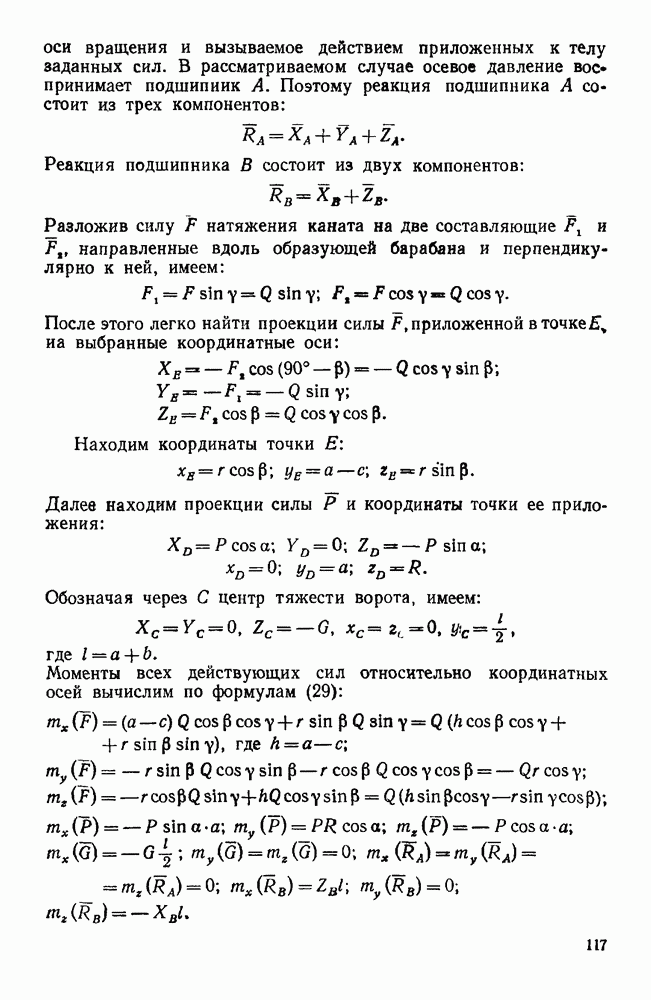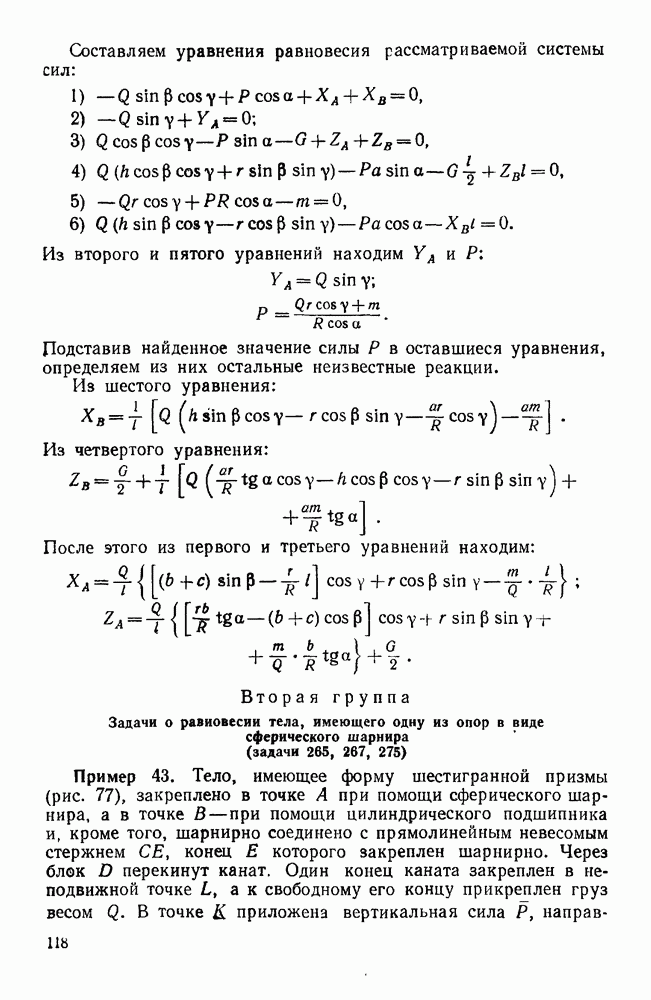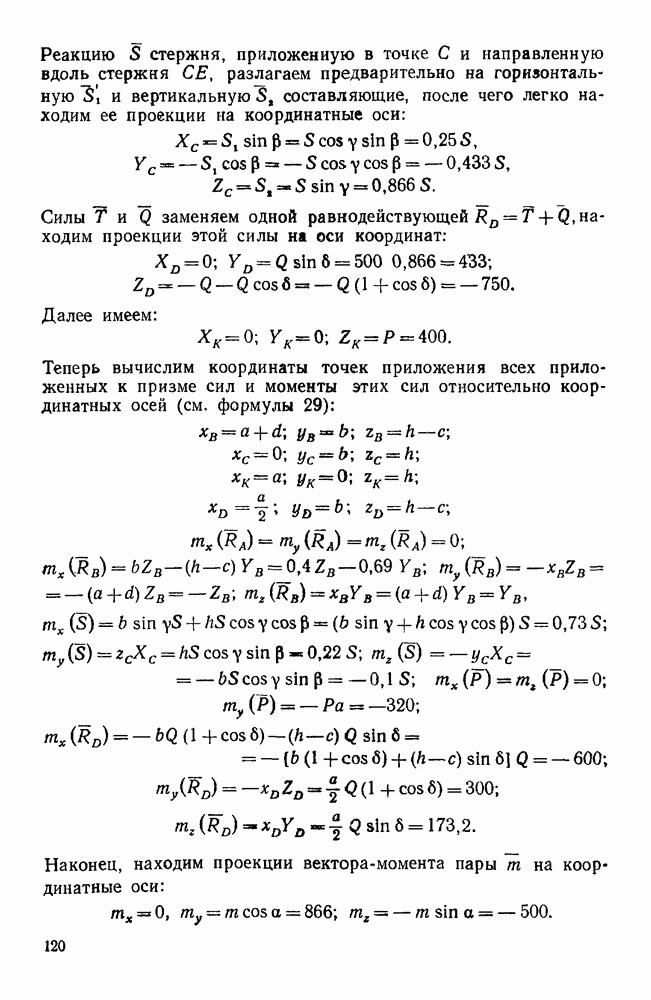| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Вторая группа
К этой группе относятся задачи, в которых требуется определить реакции двух закрепленных точек твердого тела (двух подшипников или подшипника и подпятника), возникающие при вращении твердого тела вокруг неподвижной оси, проходящей через эти закрепленные точки.
При решении этих задач по принципу Даламбера нужно разбить вращающееся твердое тело на элементарные материальные частицы и к каждой такой частице приложить касательную и нормальную силы инерции этой частицы. Так как, согласно принципу Даламбера, все эти силы инерции уравновешиваются заданными силами, приложенными к телу, и реакциями закрепленных точек, то в общем случае имеем шесть известных из статики уравнений равновесия (три уравнения проекций и три уравнения моментов). В эти уравнения войдут, во-первых, сумма проекций всех сил инерции на каждую из трех выбранных координатных осей, или, что то же, проекции главного вектора сил инерции на каждую из этих осей, и, во-вторых, суммы моментов всех сил инерции относительно каждой координатной оси, или, что то же, главные моменты сил инерции относительно каждой из этих осей. Если ось вращения тела причем за координатную ось z, то проекции главного вектора сил инерции на координатные оси будут равны (см., например, «Курс теоретической механики» И. М. Воронкова, § 139)

а главные моменты сил инерции относительно координатных осей выразятся так:

В этих формулах М — масса тела,  — соответственно угловая скорость и угловое ускорение тела,
— соответственно угловая скорость и угловое ускорение тела,  координаты центра тяжести С тела,
координаты центра тяжести С тела,  - центробежные моменты инерции тела и
- центробежные моменты инерции тела и  - момент инерции тела относительно оси вращения.
- момент инерции тела относительно оси вращения.
Отметим некоторые частные случаи:
1. Тело вращается равномерно. Тогда  .
.
2. Центр тяжести тела лежит на оси вращения. Тогда  и, следовательно,
и, следовательно,

В этом случае все силы инерции приводятся к одной паре, проекции вектора - момента которой на координатные оси определяются по формулам (235).
3. Координатная плоскость  является плоскостью симметрии тела. Тогда центр тяжести тела лежит в этой плоскости, и ось вращения
является плоскостью симметрии тела. Тогда центр тяжести тела лежит в этой плоскости, и ось вращения  как ось, перпендикулярная к плоскости симметрии, является главной осью инерции тела в точке О, поэтому
как ось, перпендикулярная к плоскости симметрии, является главной осью инерции тела в точке О, поэтому  . Если при этом
. Если при этом  , то
, то

и

В этом случае все силы инерции  одной равнодействующей, равной
одной равнодействующей, равной  , где
, где  — радиус-вектор точки С, т. е. приводятся к одной силе, равной центробежной силе центра тяжести, если предположить, что в этом центре сосредоточена вся масса тела; при этом линия действия этой равнодействующей
— радиус-вектор точки С, т. е. приводятся к одной силе, равной центробежной силе центра тяжести, если предположить, что в этом центре сосредоточена вся масса тела; при этом линия действия этой равнодействующей  проходит через центр тяжести тела.
проходит через центр тяжести тела.
4. Если ось вращения z является главной центральной осью инерции тела и если при этом тело вращается равномерно, то  , а потому
, а потому  , т. е. система сил инерции является в этом случае уравновешенной системой. Следовательно, в уравнения равновесия, составленные на основании принципа Даламбера, силы инерции не войдут; эти уравнения будут совпадать с уравнениями статики, которые используются при равновесии тела под действием приложенных к нему заданных сил. Поэтому искомые реакции закрепленных точек будут в этом случае равны статическим реакциям.
, т. е. система сил инерции является в этом случае уравновешенной системой. Следовательно, в уравнения равновесия, составленные на основании принципа Даламбера, силы инерции не войдут; эти уравнения будут совпадать с уравнениями статики, которые используются при равновесии тела под действием приложенных к нему заданных сил. Поэтому искомые реакции закрепленных точек будут в этом случае равны статическим реакциям.
При решении задач этой группы по принципу Даламбера следует иметь в виду, что в уравнение моментов относительно оси вращения  искомые реакции закрепленных точек не
искомые реакции закрепленных точек не  , так как их моменты относительно этой оси равны нулю. Поэтому эти реакции определяются из остальных пяти уравнений равновесия. Если в данной задаче, как это нередко бывает, требуется найти только реакции, перпендикулярные к оси вращения
, так как их моменты относительно этой оси равны нулю. Поэтому эти реакции определяются из остальных пяти уравнений равновесия. Если в данной задаче, как это нередко бывает, требуется найти только реакции, перпендикулярные к оси вращения  , то достаточно составить четыре уравнения равновесия (два уравнения проекций на оси v и у и два уравнения моментов относительно этих осей).
, то достаточно составить четыре уравнения равновесия (два уравнения проекций на оси v и у и два уравнения моментов относительно этих осей).
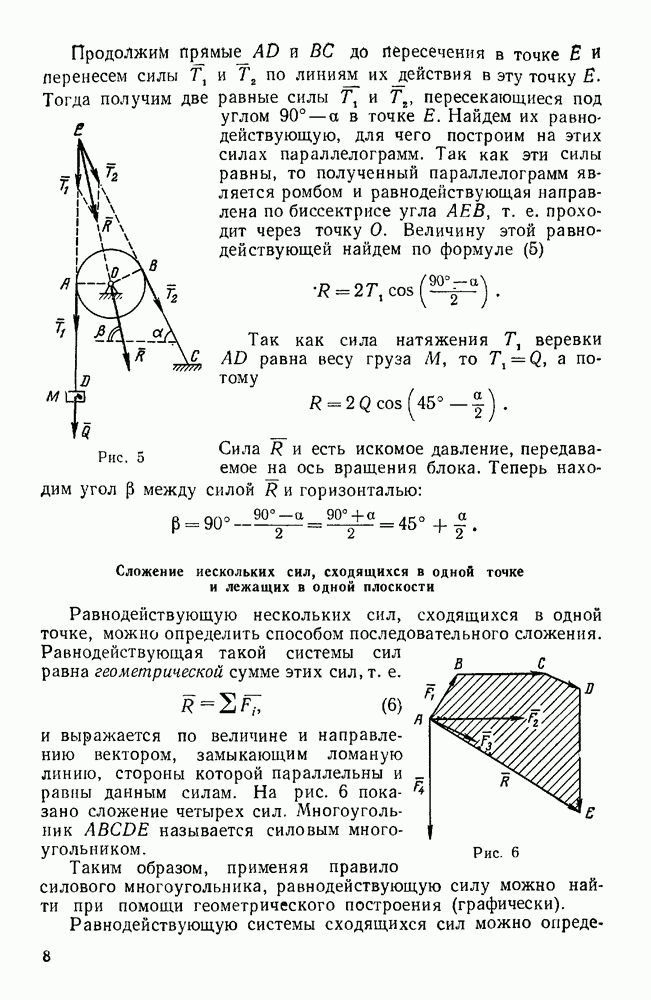
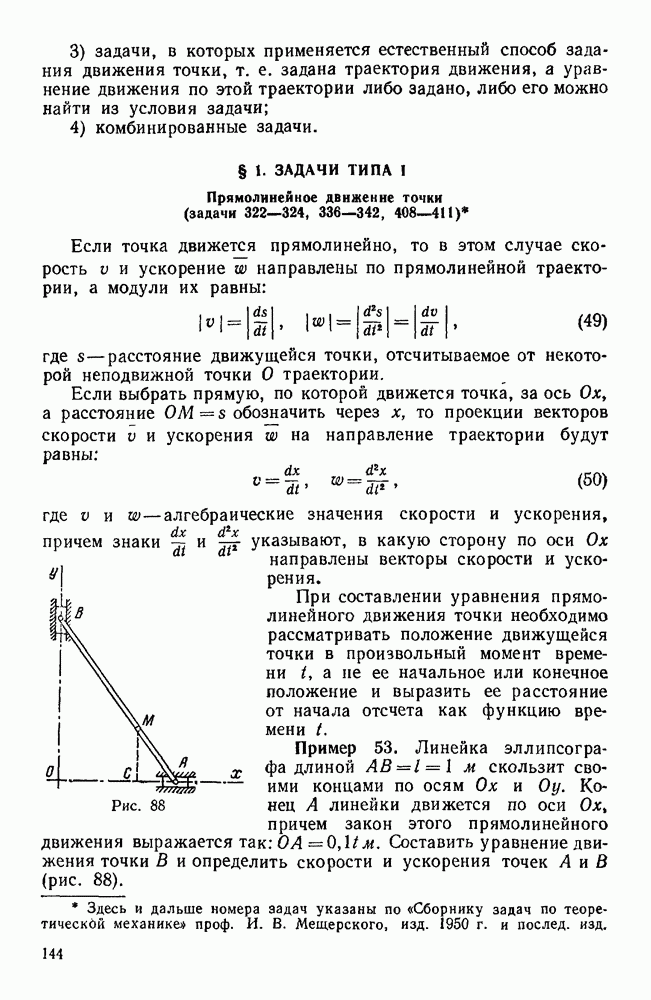
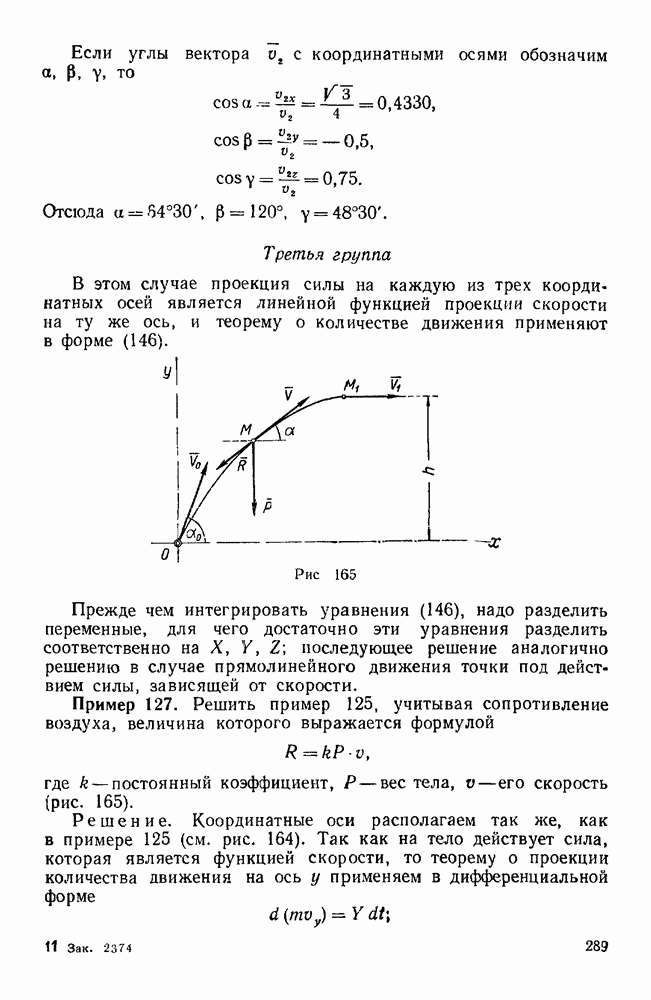
Пример 177. Однородный тонкий диск радиусом R и весом Р насажен на горизонтальный вал под углом а к оси вала и жестко скреплен с валом, причем центр тяжести О диска лежит на оси вала.
Определить реакции подшипников А и В, если вал вращается с постоянной угловой скоростью  и
и  весом вала и трением в подшипниках можно пренебречь (рис. 214).
весом вала и трением в подшипниках можно пренебречь (рис. 214).

Рис. 214.
Решение. Реакция каждого из подшипников перпендикулярна к оси вращения вала и равна геометрической сумме двух сил: статической реакции, вызываемой весом  диска, и инерционной реакции, возникающей при вращении диска и обусловленной проявлением инерции материальных частиц вращающегося диска.
диска, и инерционной реакции, возникающей при вращении диска и обусловленной проявлением инерции материальных частиц вращающегося диска.
Каждая из статических реакций равна, очевидно,  и направлена по вертикали вверх. Для определения инерционных реакций применим принцип Даламбера. Составляющие инерционной реакции по координатным осям х и у, приложенные в точке А, обозначим
и направлена по вертикали вверх. Для определения инерционных реакций применим принцип Даламбера. Составляющие инерционной реакции по координатным осям х и у, приложенные в точке А, обозначим  и
и  , а инерционные реакции, приложенные в точке В, обозначим
, а инерционные реакции, приложенные в точке В, обозначим  . При этом ось х лежит в одной плоскости с осью вращения вала и с нормалью
. При этом ось х лежит в одной плоскости с осью вращения вала и с нормалью  к плоскости диска, ось у — в плоскости диска; ось z направим по оси вращения вала. Оси х и у связаны с диском и вращаются вместе с ним. Диаметр
к плоскости диска, ось у — в плоскости диска; ось z направим по оси вращения вала. Оси х и у связаны с диском и вращаются вместе с ним. Диаметр  , диска лежит в плоскости
, диска лежит в плоскости  и, следовательно, перпендикулярен к оси у.
и, следовательно, перпендикулярен к оси у.
Так как сила  уравновешивается статическими реакциями подшипников, то, согласно принципу Даламбера, силы инерции материальных частиц диска будут уравновешиваться инерционными реакциями
уравновешивается статическими реакциями подшипников, то, согласно принципу Даламбера, силы инерции материальных частиц диска будут уравновешиваться инерционными реакциями  .
.
Поэтому имеем следующие четыре уравнения равновесия: уравнение проекций на ось х

уравнение проекций на ось у

уравнение моментов относительно оси х

уравнение моментов относительно оси у

В этих уравнениях, как было уже указано выше,  — проекции на оси х и у, главного вектора сил инерции материальных частиц диска,
— проекции на оси х и у, главного вектора сил инерции материальных частиц диска,  — главные моменты этих сил относительно тех же осей. Так как в данной задаче центр тяжести диска лежит на оси вращения z и
— главные моменты этих сил относительно тех же осей. Так как в данной задаче центр тяжести диска лежит на оси вращения z и  , то
, то  , поэтому из формул (234) и (235) имеем:
, поэтому из формул (234) и (235) имеем:

Кроме того, так как ось у, направленная по диаметру диска, есть ось симметрии диска, то она является его главной центральной осью инерции, а поэтому  .
.
Следовательно, предыдущие уравнения принимают вид:

Из этих уравнений находим:

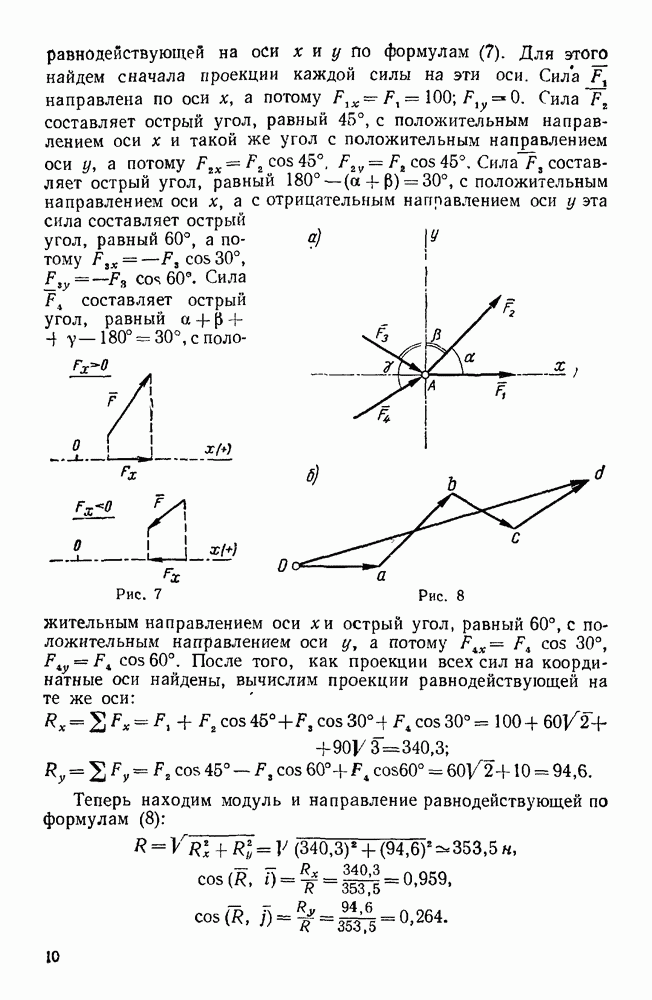
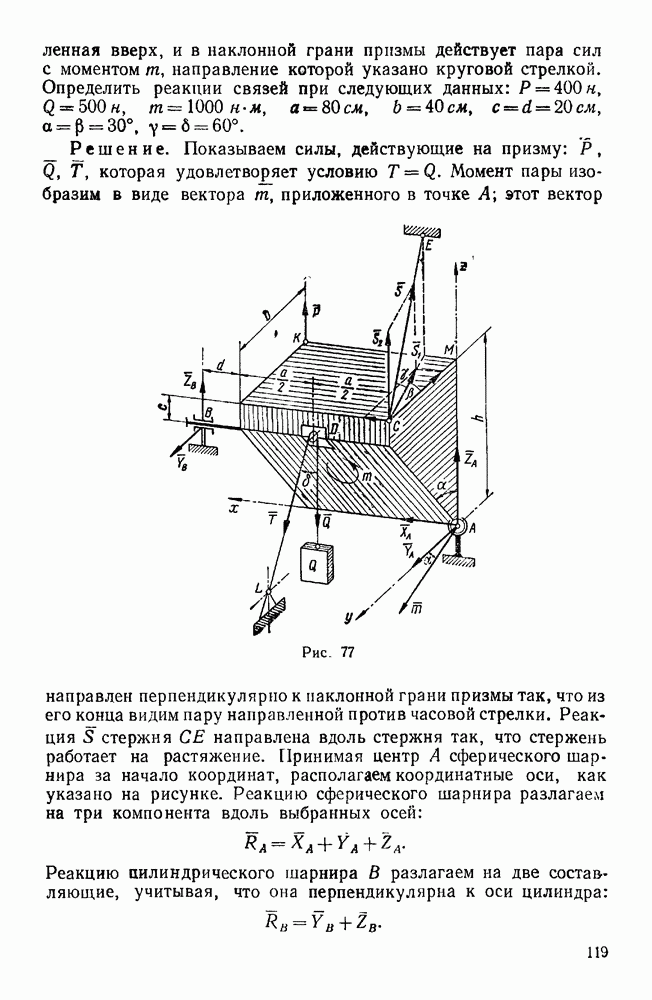
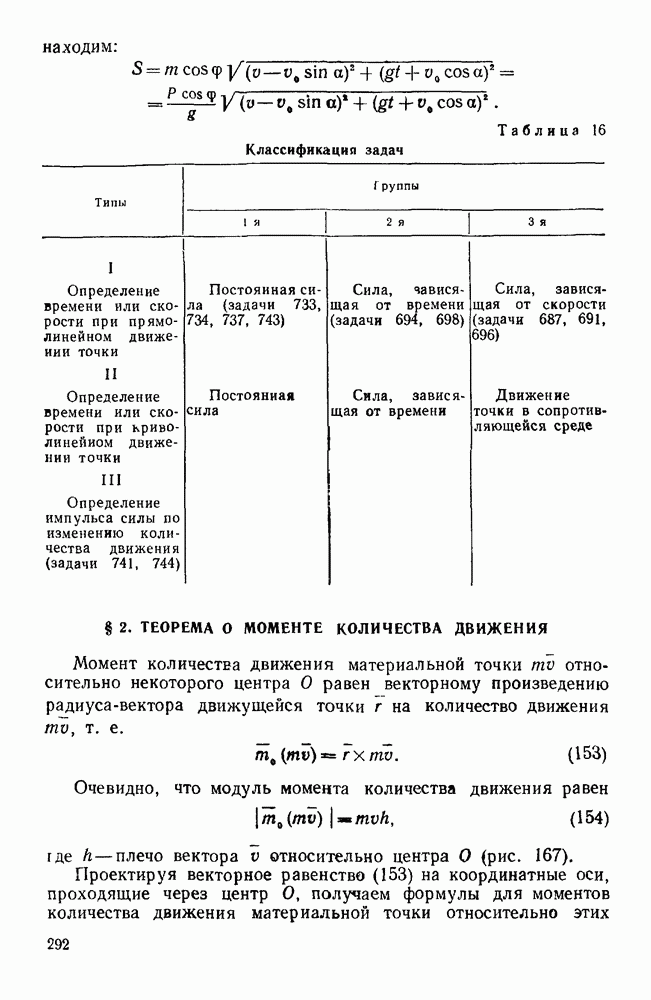
Вычислим центробежный момент инерции  . Если рассмотрим материальную частицу диска с массой
. Если рассмотрим материальную частицу диска с массой  , то, как видно из рис. 215, координаты этой частицы будут равны
, то, как видно из рис. 215, координаты этой частицы будут равны

где h — расстояние этой частицы от оси у. Следовательно,

момент инерции диска относительно оси у (относительно диаметра), равный  , поэтому
, поэтому  .
.
Таким обрчзом, окончательно получаем:

Отсюда видно, что инерционные реакции подшипников параллельны оси х; следовательно, эти реакции, сохраняя постоянную величину, непрерывно изменяют свое направление, так как ось х вращается вместе с диском. Отрицательное значение силы  указывает на то, что эта сила имеет направление, противоположное принятому на рис. 214, а поэтому реакции
указывает на то, что эта сила имеет направление, противоположное принятому на рис. 214, а поэтому реакции  образуют пару сил, лежащую в плоскости, проходящей через ось вращения и нормаль
образуют пару сил, лежащую в плоскости, проходящей через ось вращения и нормаль  к плоскости диска.
к плоскости диска.

Рис. 215.

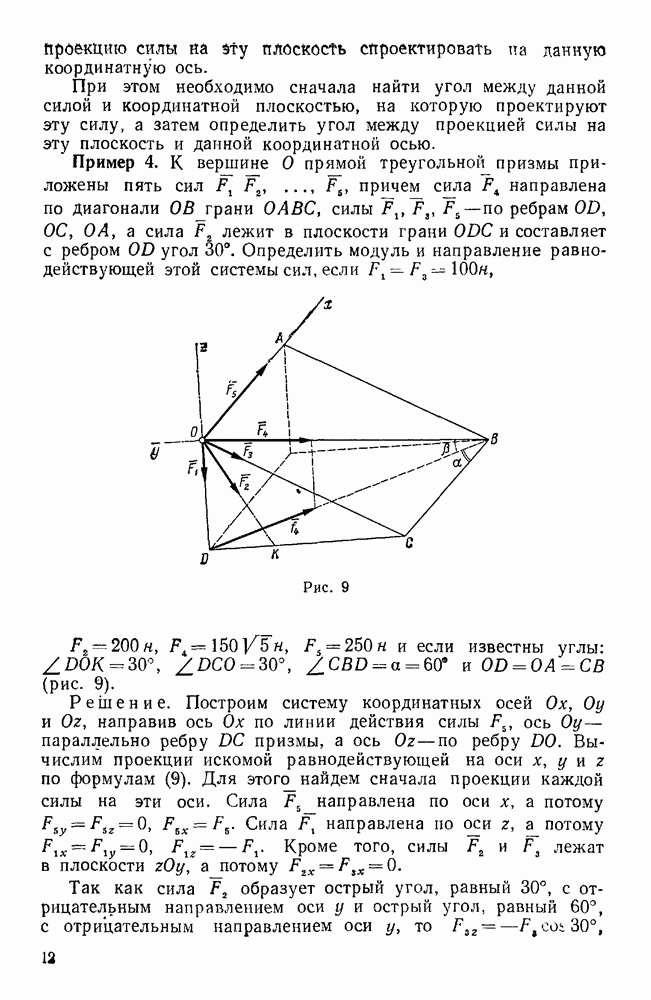
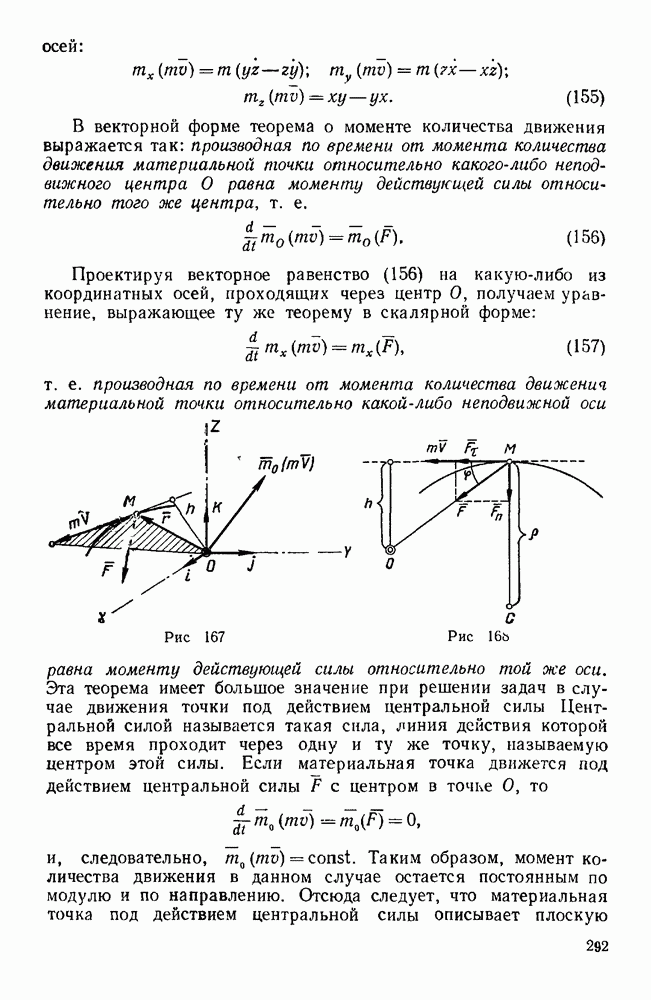
Рис. 216.
Пример 178. С вертикальной осью, укрепленной в подшипнике А и подпятнике В, жестко соединены перпендикулярный к этой оси тонкий стержень DE длиной  и весом
и весом  , и круглый однородный цилиндр весом
, и круглый однородный цилиндр весом  . образующие которого параллельны оси АВ. При этом цилиндр насажен эксцентрично так, что его центр тяжести
. образующие которого параллельны оси АВ. При этом цилиндр насажен эксцентрично так, что его центр тяжести  находится от оси АВ на расстоянии
находится от оси АВ на расстоянии  Цилиндр и стержень вращаются вокруг оси АВ с данной угловой скоростью
Цилиндр и стержень вращаются вокруг оси АВ с данной угловой скоростью  . Найти реакции подшипника А и подпятника В, если
. Найти реакции подшипника А и подпятника В, если  (рис. 216).
(рис. 216).
Решение. Проведем координатные оси, связанные с цилиндром, как указано на рис. 216, т. е. ось z направим по оси вращения ВА, ось у — по прямой ОС, и ось х — параллельно стержню ED.
Составляющие реакции подшипника А по осям х и у обозначим  , а составляющие реакции подпятника В по координатным осям —
, а составляющие реакции подпятника В по координатным осям —  и
и  .
.
Применяя принцип Даламбера, разобьем стержень DE на бесконечно малые элементы и к каждому такому элементу приложим соответствующую силу инерции.
Так как  , то
, то  и, следовательно, касательные силы инерции всех элементов стержня будут равны нулю, а их нормальные силы инерции (центробежные силы) будут направлены вдоль стержня от оси вращения.
и, следовательно, касательные силы инерции всех элементов стержня будут равны нулю, а их нормальные силы инерции (центробежные силы) будут направлены вдоль стержня от оси вращения.
Равнодействующая этих центробежных сил имеет то же направление и по модулю равна

где  - масса элемента,
- масса элемента,  — расстояние от элемента до оси вращения. Но
— расстояние от элемента до оси вращения. Но  , где
, где  — расстояние центра тяжести С, стержня от оси АВ, равное у, поэтому
— расстояние центра тяжести С, стержня от оси АВ, равное у, поэтому  . Так как плоскость
. Так как плоскость  является для цилиндра плоскостью симметрии и цилиндр вращается равномерно, то, как было указано выше, силы инерции материальных частиц цилиндра приводятся в этом случае к одной равнодействующей
является для цилиндра плоскостью симметрии и цилиндр вращается равномерно, то, как было указано выше, силы инерции материальных частиц цилиндра приводятся в этом случае к одной равнодействующей  , равной центробежной силе центра тяжести
, равной центробежной силе центра тяжести  цилиндра в предположении, что в этом центре сосредоточена вся масса цилиндра. Следовательно,
цилиндра в предположении, что в этом центре сосредоточена вся масса цилиндра. Следовательно,  эта сила
эта сила  приложена в точке
приложена в точке  и направлена по
и направлена по  , т. е. по оси у.
, т. е. по оси у.
Согласно принципу Даламбера, заданные силы  реакции
реакции  и силы инерции
и силы инерции  взаимно уравновешиваются; поэтому для этой системы сил можно составить следующие пять уравнений равновесия (три уравнения проекций на оси х, у, z и два уравнения моментов относительно осей х и у):
взаимно уравновешиваются; поэтому для этой системы сил можно составить следующие пять уравнений равновесия (три уравнения проекций на оси х, у, z и два уравнения моментов относительно осей х и у):

или

Из этих уравнений находим

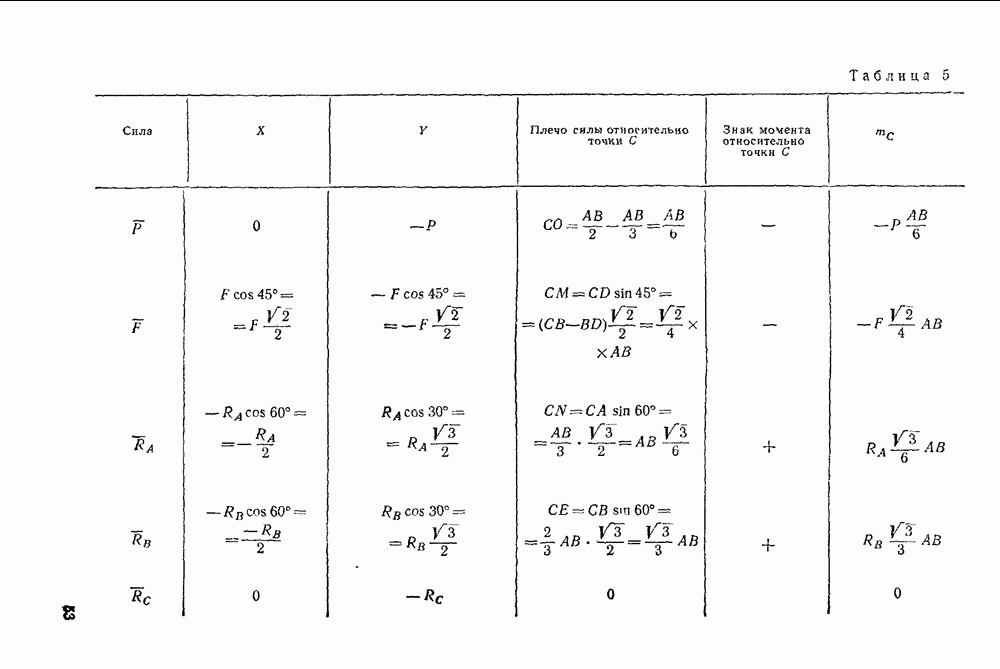
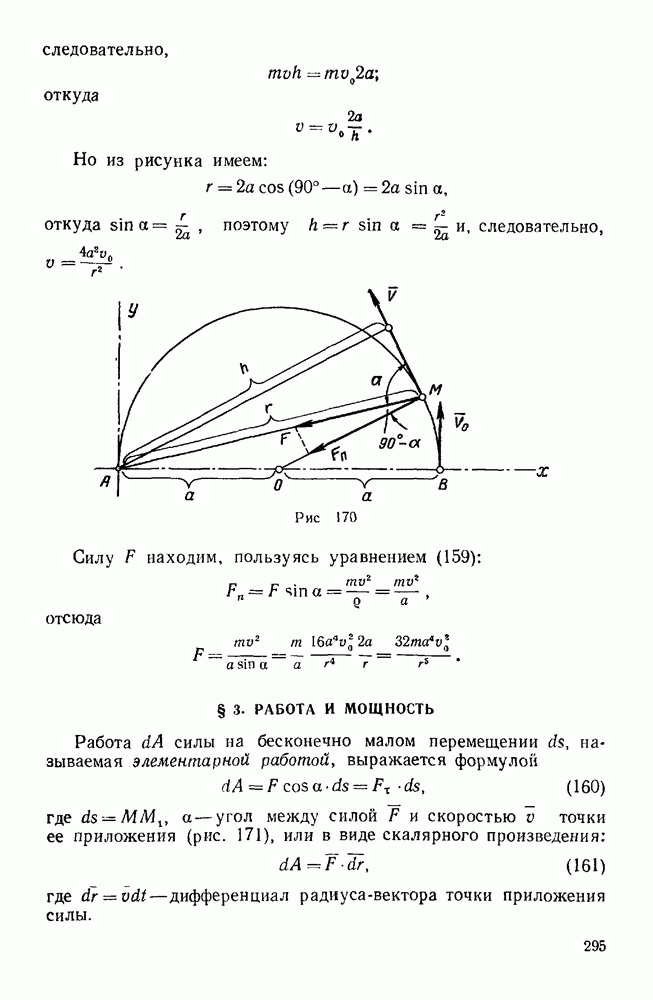
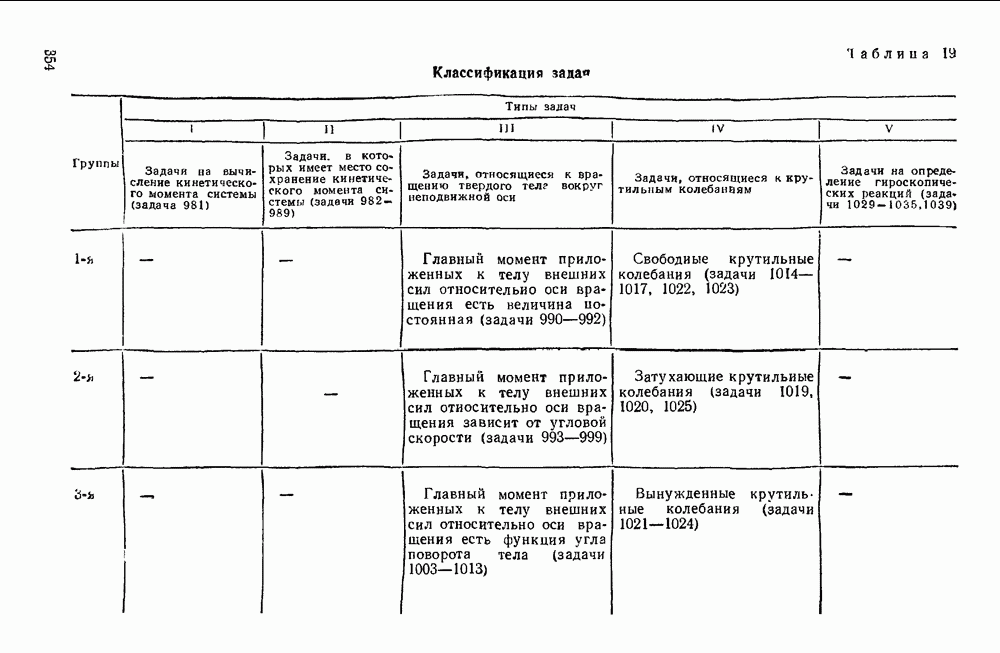
Таблица 21. Классификация задач

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
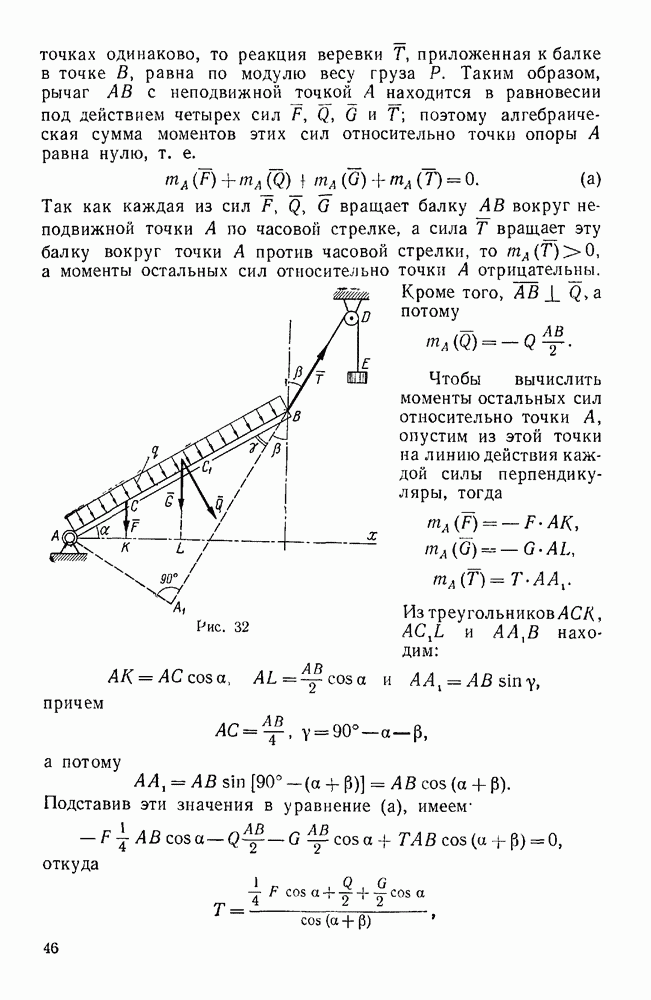
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
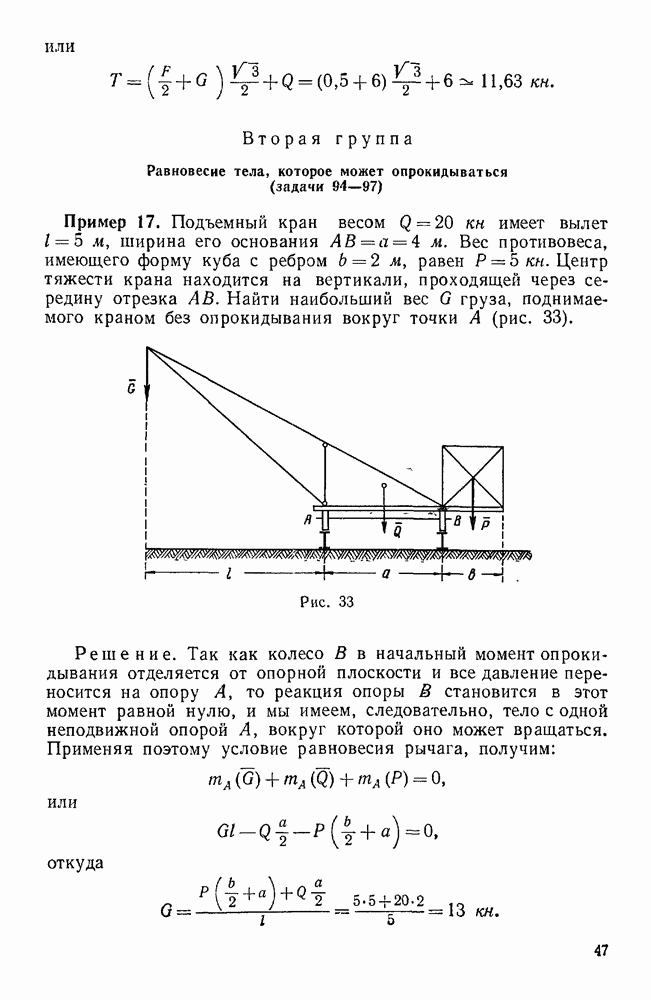
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
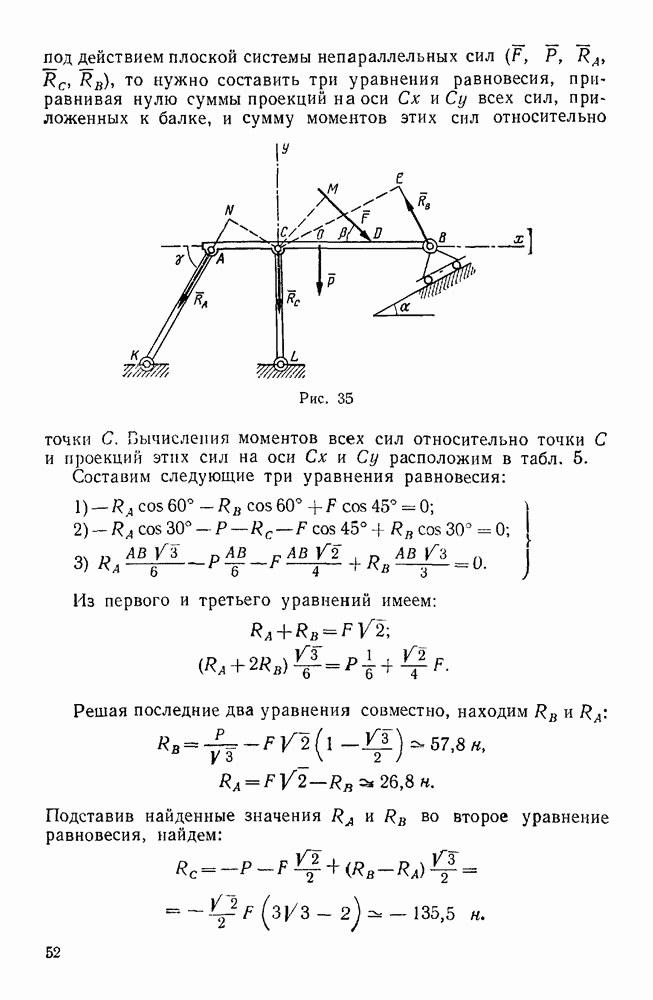
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
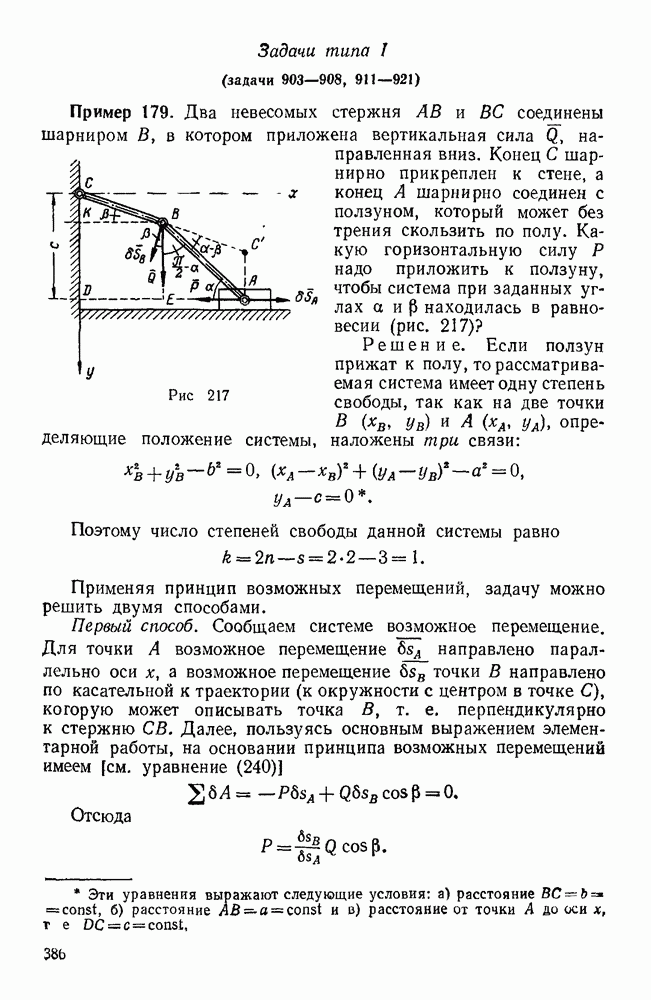
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
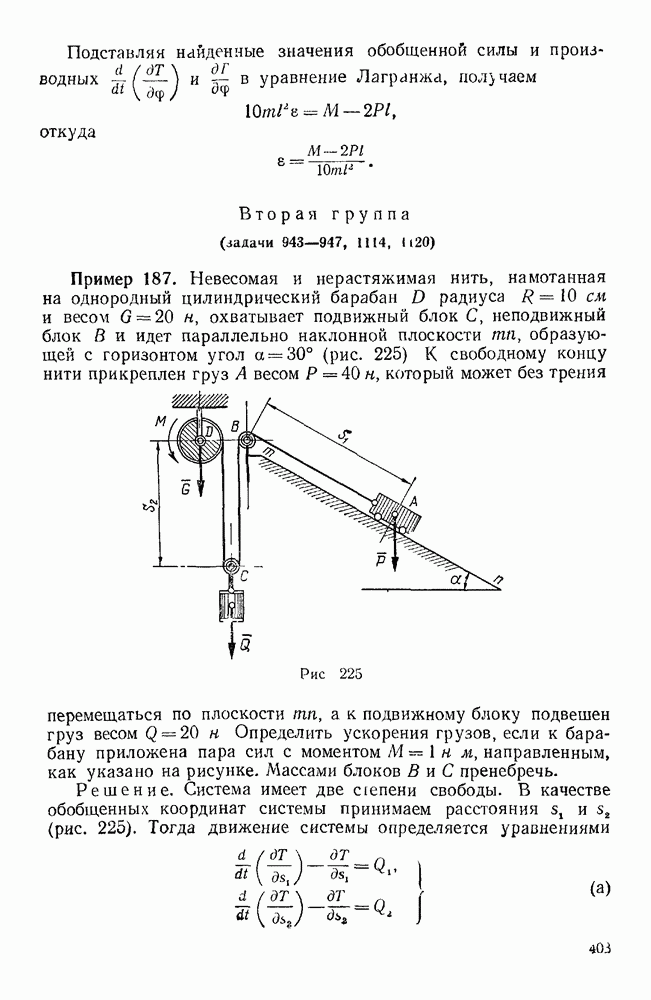
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА