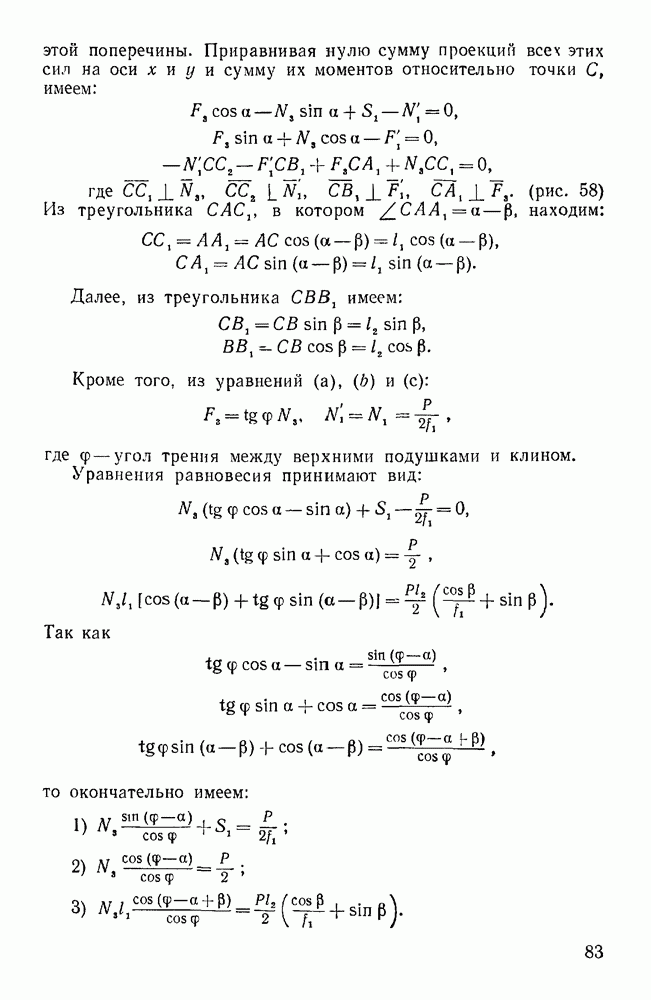| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
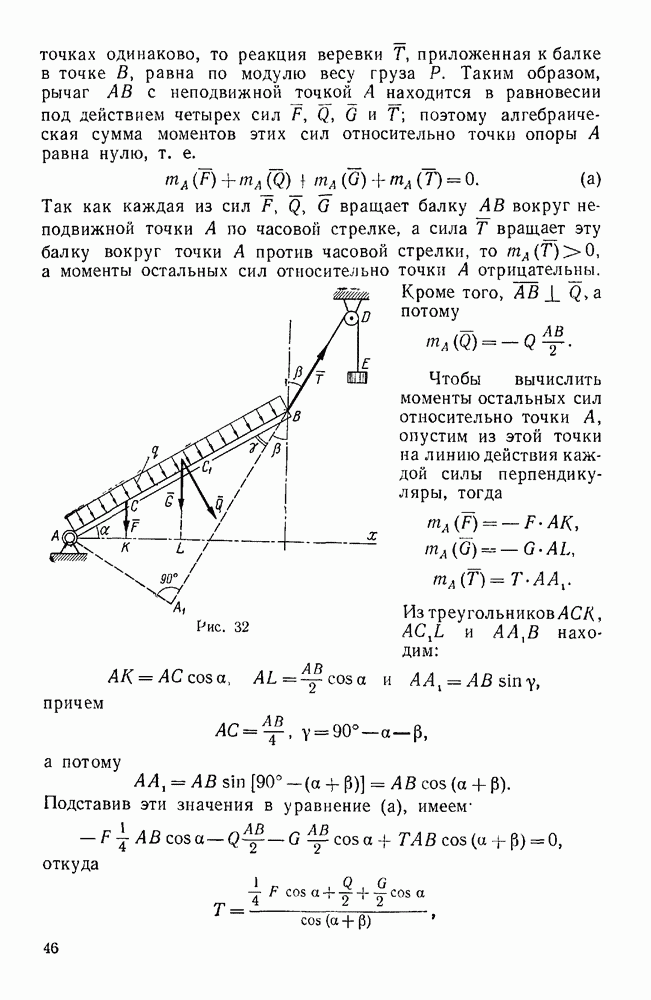
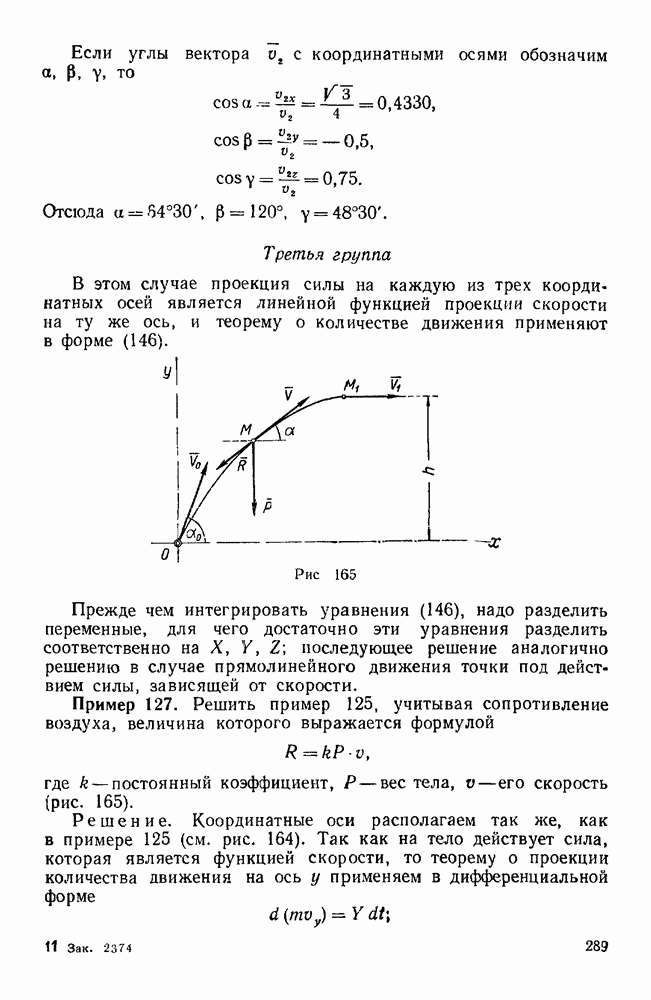
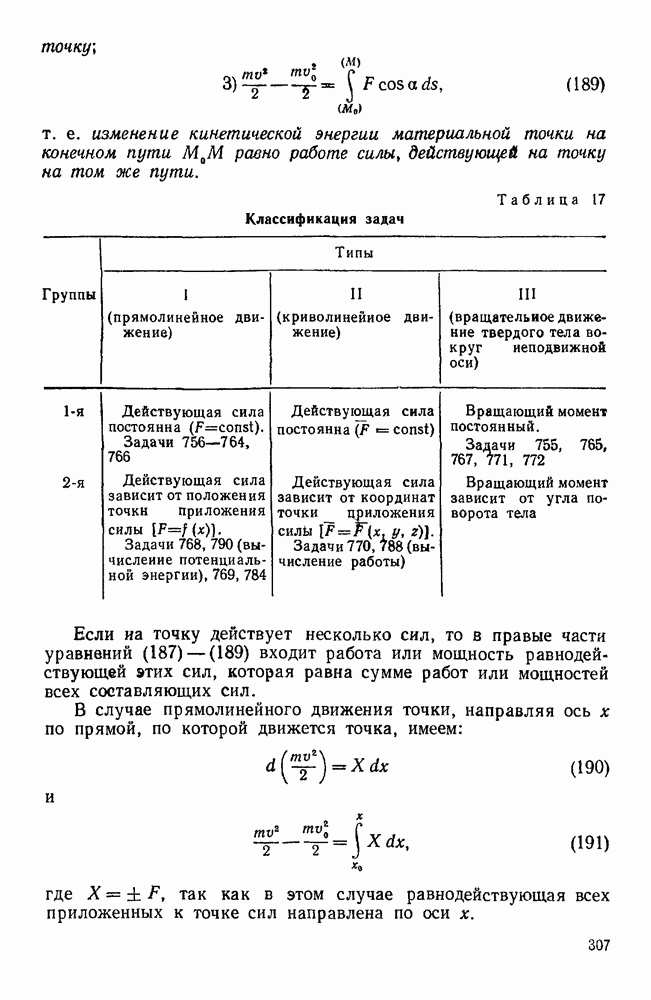
Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
В рассматриваемом случае одну из трех координатных осей например, ось х располагают перпендикулярно к данным силам. Еумма проекций этих сил на выбранную таким образом ось тождественно равна нулю  , поэтому из шести уравнений равновесия пространственной системы сил остается только пять:
, поэтому из шести уравнений равновесия пространственной системы сил остается только пять:

Следовательно, число неизвестных в задаче на равновесие одного тела не должно превышать пяти. Обычно в задачах данного типа приходится рассматривать равновесие тела, имеющего неподвижную ось вращения.
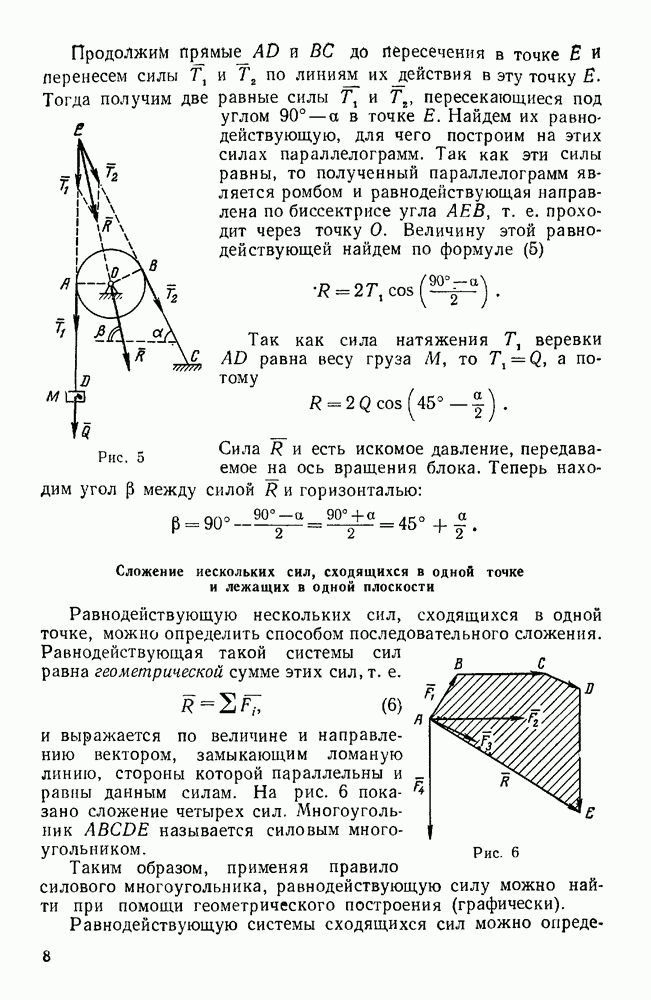
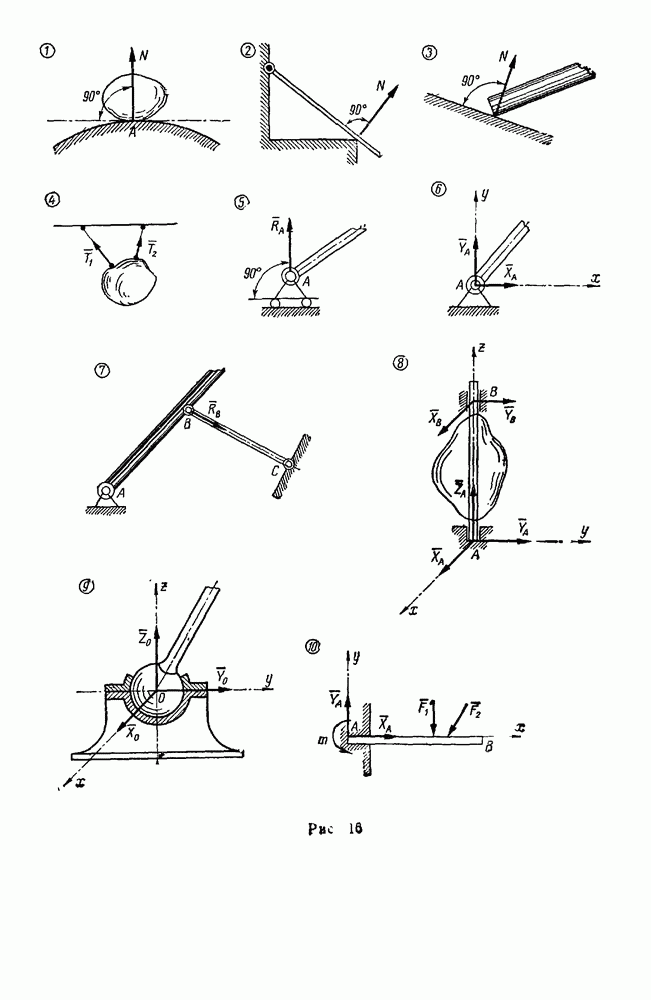
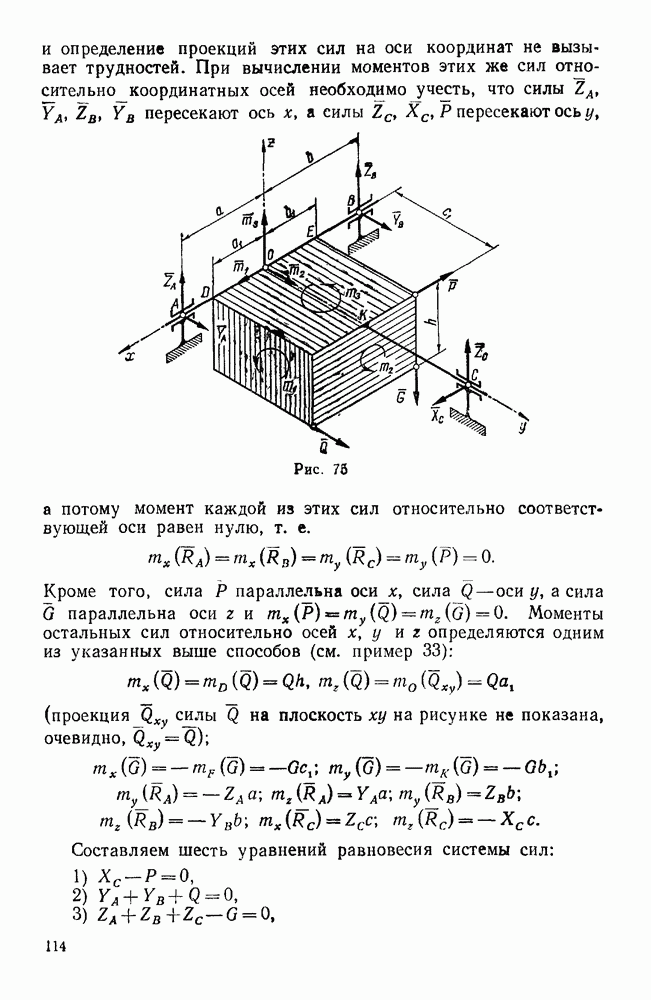
Так, например, тело может быть закреплено на валу, который опирается на два цилиндрических подшипника (рис. 70), причем на тело действуют силы, перпендикулярные к оси вращения. Обычно подшипники конструктивно оформляются так, что препятствуют осевым перемещениям вала (рис.  применяются также упорные подшипники (рис. 70, б). Однако, если на тело действуют силы, перпендикулярные к оси вала, то вдоль этой оси никаких реакций не возникает и реакции подшипников направлены тоже перпендикулярно к оси вала, т. е. опоры, показанные на рис. 70, а и 70, б, в рассматриваемом частном случае эквивалентны опорам, изображенным на рис. 70, в, где никаких устройств, фиксирующих вал в осевом направлении, нет.
применяются также упорные подшипники (рис. 70, б). Однако, если на тело действуют силы, перпендикулярные к оси вала, то вдоль этой оси никаких реакций не возникает и реакции подшипников направлены тоже перпендикулярно к оси вала, т. е. опоры, показанные на рис. 70, а и 70, б, в рассматриваемом частном случае эквивалентны опорам, изображенным на рис. 70, в, где никаких устройств, фиксирующих вал в осевом направлении, нет.

Рис. 70.
Ось вала следует принять за одну из координатных осей например, ось  , тогда две другие оси (у и z) располагаются перпендикулярно к оси вала и реакция каждого подшипника разлагается на два компонента вдоль этих двух осей (см. рис. 70). В некоторых случаях координатные оси можно выбрать так, чтобы каждая сила, действующая на тело, была параллельна одной из координатных осей [см. задачи № 254—256, 261].
, тогда две другие оси (у и z) располагаются перпендикулярно к оси вала и реакция каждого подшипника разлагается на два компонента вдоль этих двух осей (см. рис. 70). В некоторых случаях координатные оси можно выбрать так, чтобы каждая сила, действующая на тело, была параллельна одной из координатных осей [см. задачи № 254—256, 261].
Пример 38. Груз Q опускается равномерно при помощи каната, навернутого на барабан радиуса  . На общем валу с барабаном заклинено колесо Е и тормозной шкив С радиуса
. На общем валу с барабаном заклинено колесо Е и тормозной шкив С радиуса  . К колесу Е приложена пара сил, тормозящая вращение вала, момент которой равен
. К колесу Е приложена пара сил, тормозящая вращение вала, момент которой равен  (силы, образующие эту пару, на рисунке не показаны, а направление ее указано круговой стрелкой). Ввиду того, что этот момент не обеспечивает равномерного спуска груза, осуществляется еще притормаживание системы при помощи колодочного тормоза, причем колодка тормоза при жимается к тормозному шкиву силой Р.
(силы, образующие эту пару, на рисунке не показаны, а направление ее указано круговой стрелкой). Ввиду того, что этот момент не обеспечивает равномерного спуска груза, осуществляется еще притормаживание системы при помощи колодочного тормоза, причем колодка тормоза при жимается к тормозному шкиву силой Р.
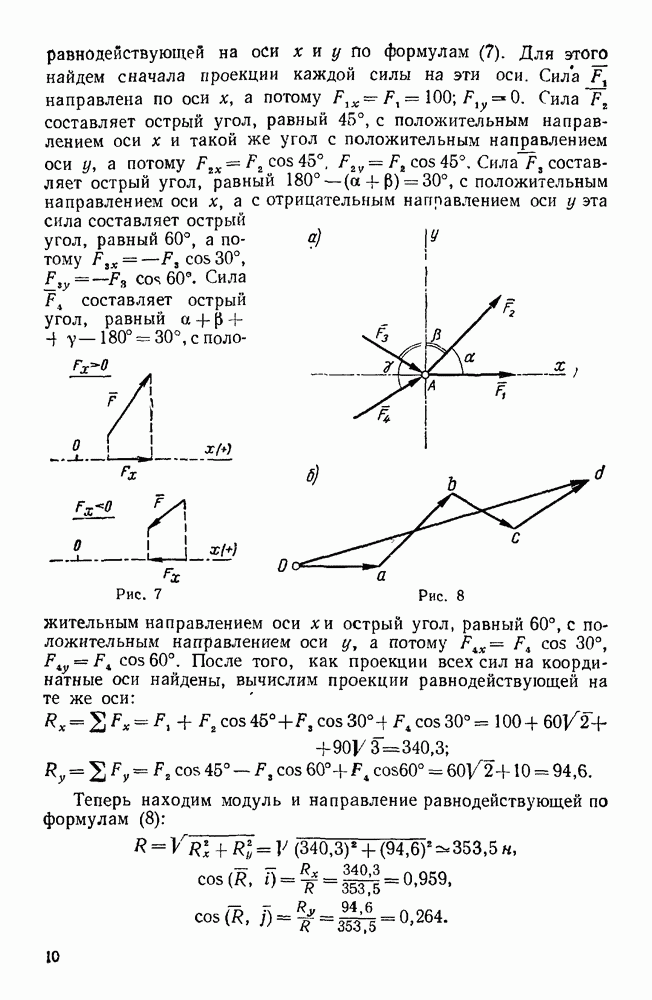
Определить эту силу, а также реакции подшипников, если коэффициент трения между колодкой и тормозным шкивом равен  . Размеры указаны на рисунке (рис 71).
. Размеры указаны на рисунке (рис 71).

Рис. 71.
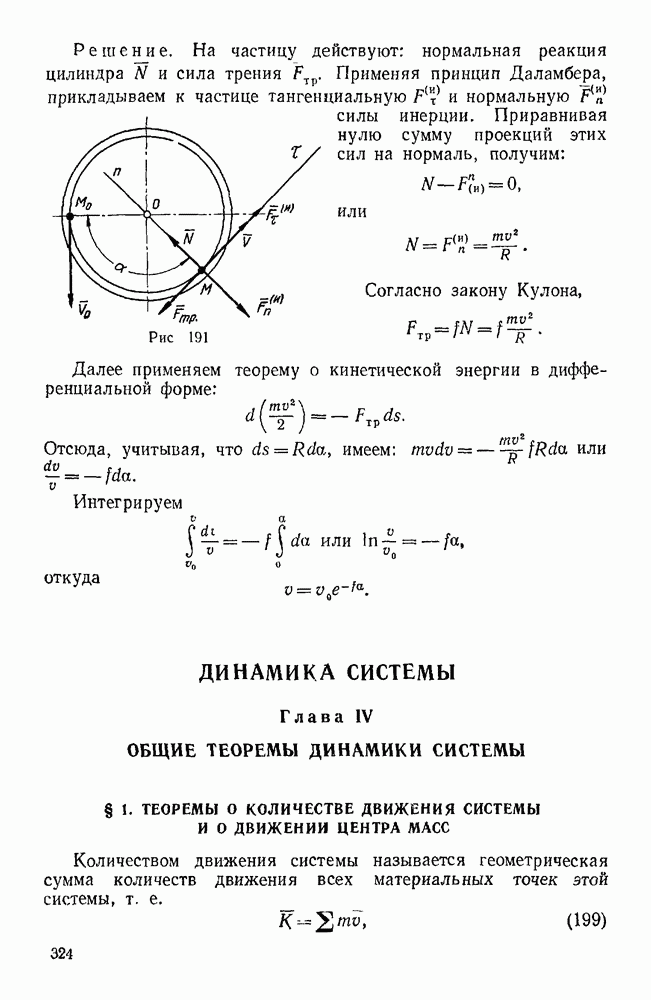
Решение. Рассмотрим равновесие вала с закрепленными на нем телами. На вал, кроме реакций подшипников, действуют: вертикальная сила  каната, равная весу груза Q; вертикальная сила Р давления колодки на тормозной шкив; сила трения F, направленная по касательной к тормозному шкиву (т. е. в данном случае горизонтально), и, наконец, тормозящий момент
каната, равная весу груза Q; вертикальная сила Р давления колодки на тормозной шкив; сила трения F, направленная по касательной к тормозному шкиву (т. е. в данном случае горизонтально), и, наконец, тормозящий момент  , который можно изобразить в виде вектора, направленного по оси вала. Рассмотренные силы образуют систему вертикальных и горизонтальных векторов, перпендикулярных к оси вала (силы, образующие заданную пару, можно направить параллельно оси у, или оси 2, так как пару можно расположить как угодно в ее плоскости).
, который можно изобразить в виде вектора, направленного по оси вала. Рассмотренные силы образуют систему вертикальных и горизонтальных векторов, перпендикулярных к оси вала (силы, образующие заданную пару, можно направить параллельно оси у, или оси 2, так как пару можно расположить как угодно в ее плоскости).
Поэтому, принимая точку А за начало координат, ось х направим по оси вала, а две другие оси располагаем, как указано на рисунке (горизонтально и вертикально). Учитывая, что реакции подшипников направлены перпендикулярно к оси вала, разлагаем каждую из них на два компонента вдоль осей у и z. Таким образом, получаем систему сил, расположенных параллельно плоскости  , причем каждая из них параллельна одной из координатных осей. Поэтому в данной задаче можно составить пять уравнений равновесия по формулам (39). При этом вычисления проекции сил на координатные оси не вызывает трудностей. Остановимся на определении
, причем каждая из них параллельна одной из координатных осей. Поэтому в данной задаче можно составить пять уравнений равновесия по формулам (39). При этом вычисления проекции сил на координатные оси не вызывает трудностей. Остановимся на определении  сил относительно этих осей. Силы
сил относительно этих осей. Силы  и Р пересекают ось х, поэтому их моменты относительно этой оси равны нулю. Точно так же силы
и Р пересекают ось х, поэтому их моменты относительно этой оси равны нулю. Точно так же силы  и
и  пересекают каждую из осей у и z, а потому их моменты относительно этих осей равны нулю.
пересекают каждую из осей у и z, а потому их моменты относительно этих осей равны нулю.
Силы  параллельны оси z, а силы F и
параллельны оси z, а силы F и  параллельны оси у, поэтому
параллельны оси у, поэтому

Следовательно, уравнения равновесия (39) принимают вид:

При составлении этих уравнений учтено, что сумма моментов сил, образующих пару, относительно какой-либо оси равна проекции вектора-момента пары на эту ось. Поэтому тормозящий момент m вошел лишь в уравнение (3), так как вектор  проектируется на ось
проектируется на ось  в свою натуральную величину, а на остальные две оси его проекции равны нулю.
в свою натуральную величину, а на остальные две оси его проекции равны нулю.
Найдем теперь моменты сил F и Q относительно оси х; эти силы расположены в плоскостях, перпендикулярных к оси х, поэтому

и

Далее вычислим моменты сил  относительно оси у; силы
относительно оси у; силы  и
и  расположены в плоскости
расположены в плоскости  , перпендикулярной к оси у, поэтому
, перпендикулярной к оси у, поэтому

Чтобы вычислить момент силы Q относительно оси у, достаточно эту силу спроектировать на плоскость  , тогда
, тогда

гак как  (проекция силы Q на плоскость
(проекция силы Q на плоскость  показана пунктиром).
показана пунктиром).
Теперь находим моменты сил F и  относительно оси z:
относительно оси z:

Так как  (проекция силы F на плоскость
(проекция силы F на плоскость  показана пунктиром),
показана пунктиром),

Таким образом, получим следующие пять уравнений равновесия рассматриваемой системы сил:

К составленным выше пяти уравнениям равновесия присоединяется еще одно уравнение, выражающее закон Кулона:

Из третьего уравнения находим:

Тогда из шестого уравнения имеем:

Из четвертого уравнения:

где

Из пятого уравнения:

После этого из первого и второго уравнений нетрудно найти

В ряде случаев координатные оси невозможно выбрать так, чтобы каждая из действующих на тело сил была параллельна одной из осей (см. задачи № 251, 257, 260, 262—264, 266, 276, 279—281). Тогда координатные оси следует выбрать так, чтобы наибольшее число сил удовлетворяло этому условию.
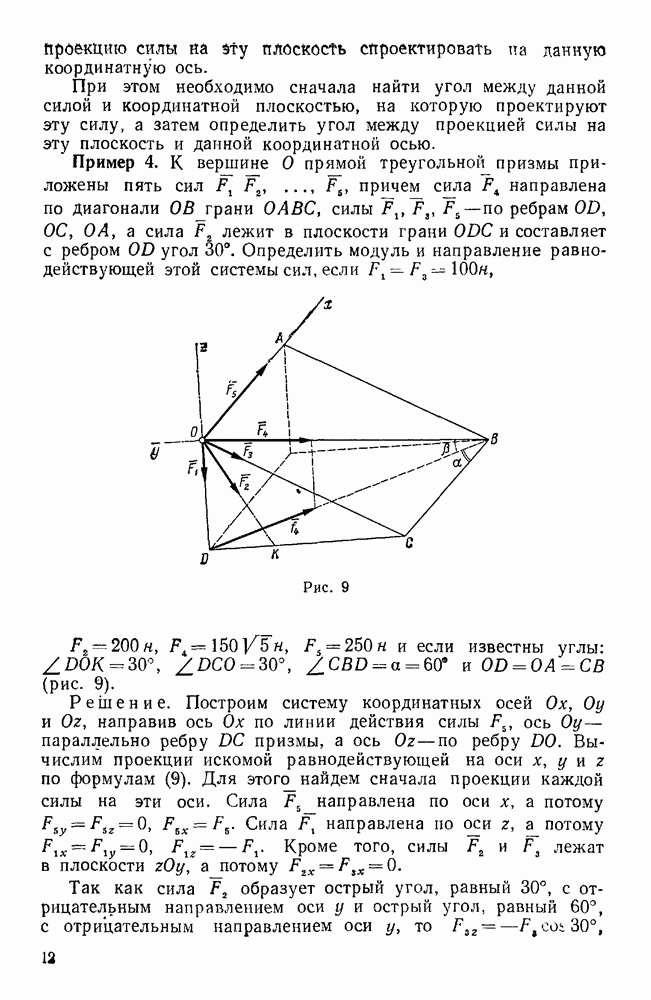
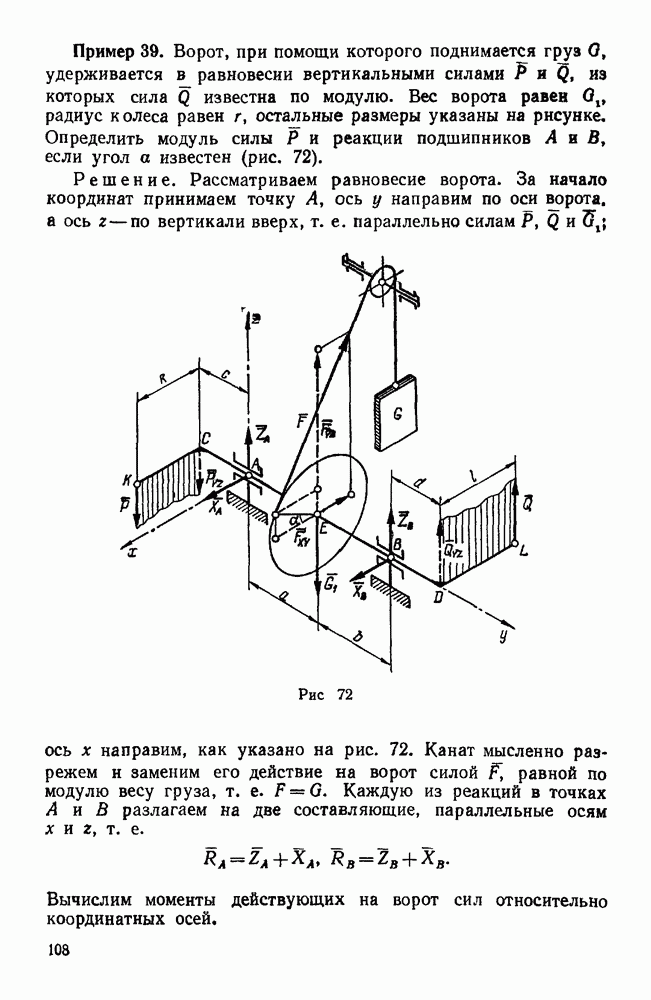
Пример 39. Ворот, при помощи которого поднимается груз О, удерживается в равновесии вертикальными силами Р и Q, из которых сила Q известна по модулю. Вес ворота равен радиус колеса равен  , остальные размеры указаны на рисунке. Определить модуль силы Р и реакции подшипников А и В, если угол а известен (рис. 72).
, остальные размеры указаны на рисунке. Определить модуль силы Р и реакции подшипников А и В, если угол а известен (рис. 72).
Решение. Рассматриваем равновесие ворота. За начало координат принимаем точку А, ось у направим по оси ворота, а ось z — по вертикали вверх, т. е. параллельно силам Р, Q и  ось х направим, как указано на рис. 72.
ось х направим, как указано на рис. 72.

Рис. 72.
Канат мысленно разрежем и заменим его действие на ворот силой F, равной по модулю весу груза, т. е.  . Каждую из реакций в точках А и В разлагаем на две составляющие, параллельные осям х и z, т. е.
. Каждую из реакций в точках А и В разлагаем на две составляющие, параллельные осям х и z, т. е.

Вычислим моменты действующих на ворот сил относительно координатных осей.
Относительно оси  :
:

(Проекция силы Р на плоскость  , перпендикулярную к оси
, перпендикулярную к оси  , показана пунктиром; очевидно,
, показана пунктиром; очевидно,  )
)

(Проекция силы F на плоскость  показана на рисунке пунктиром; сила F образует с плоскостью
показана на рисунке пунктиром; сила F образует с плоскостью  угол, равный углу
угол, равный углу  , а потому
, а потому  )
)

 . Относительно оси у:
. Относительно оси у:

Относительно оси  :
:

Учитывая, что  , составим пять уравнений равновесия рассматриваемой системы сил:
, составим пять уравнений равновесия рассматриваемой системы сил:

Из пятого уравнения имеем:

Из четвертого уравнения находим:

Из третьего уравнения:

Подставив найденные значения  и
и  в первые два уравнения равновесия, находим из этих уравнений
в первые два уравнения равновесия, находим из этих уравнений  и
и  :
:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
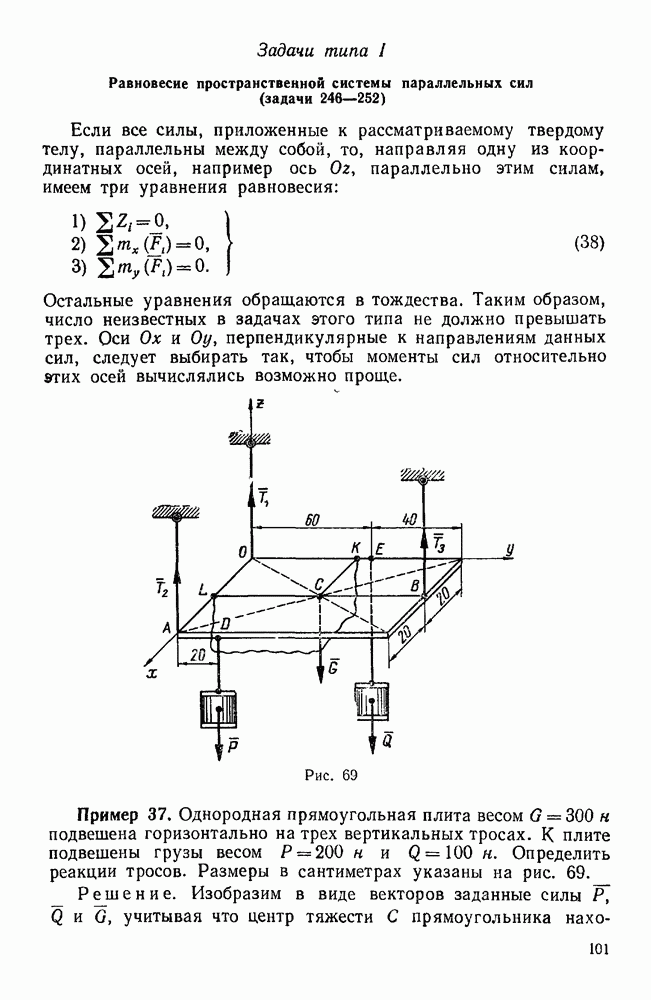
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
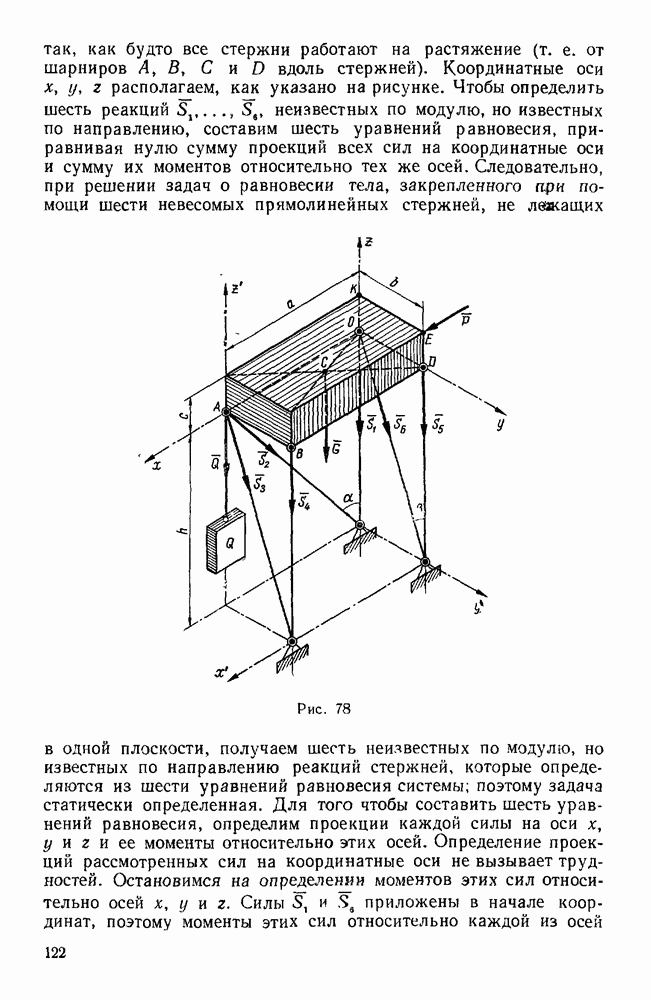
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
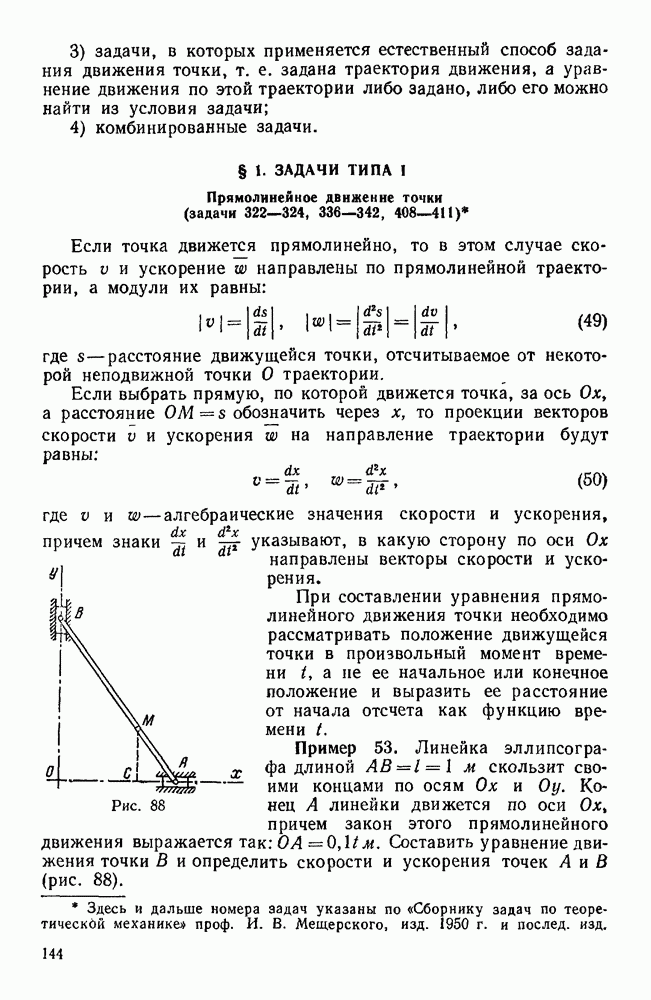
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
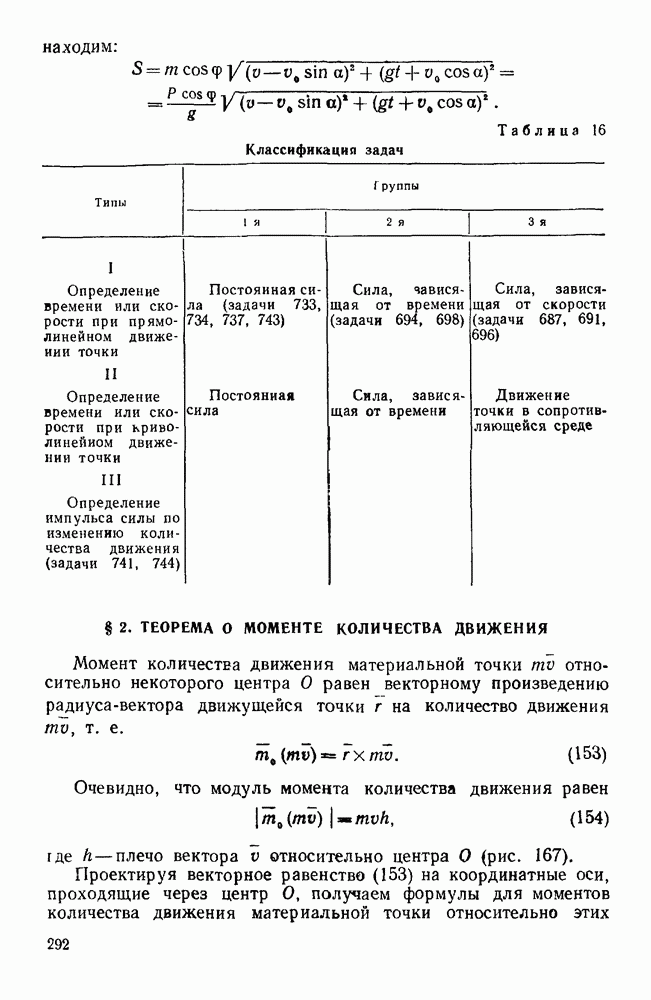
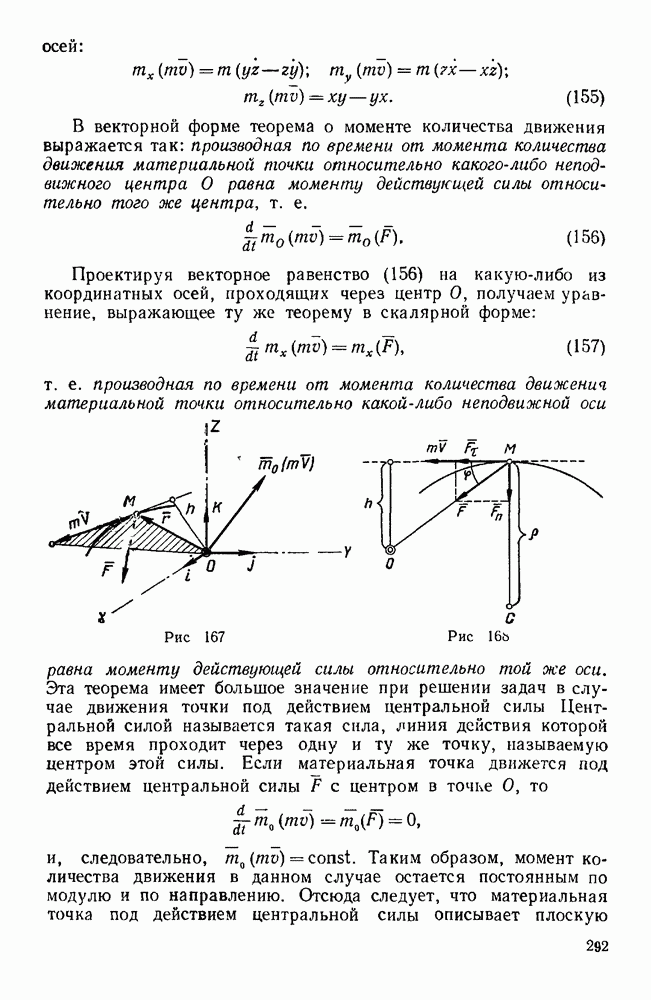
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
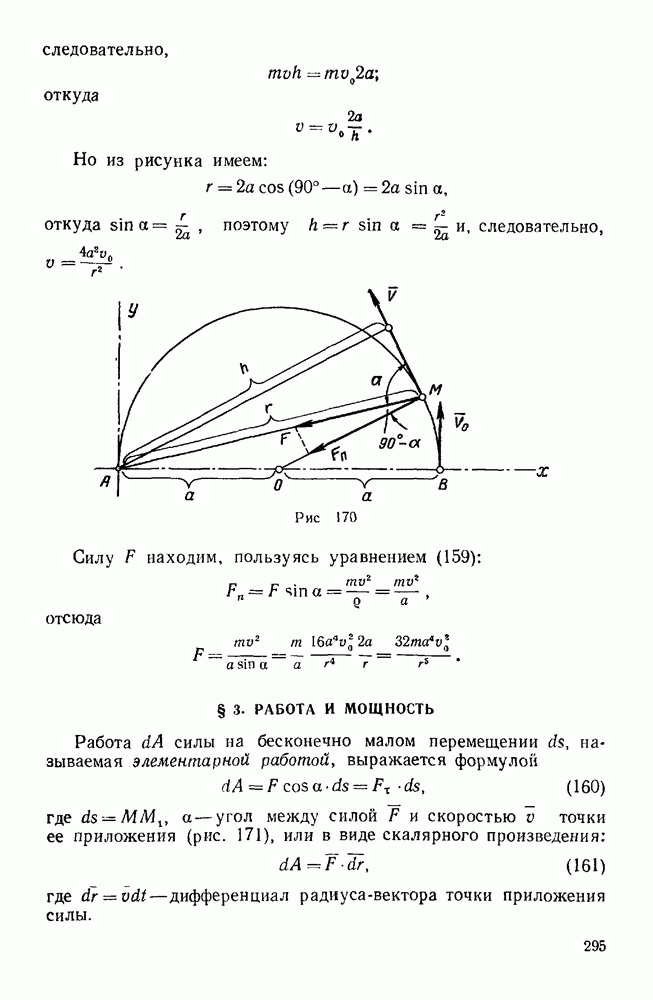
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
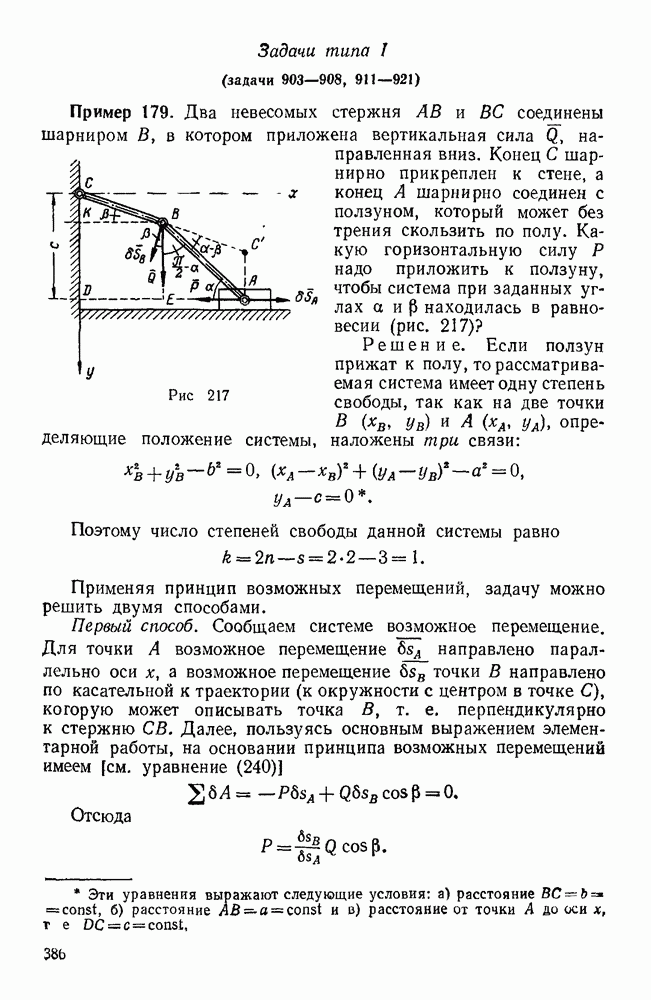
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
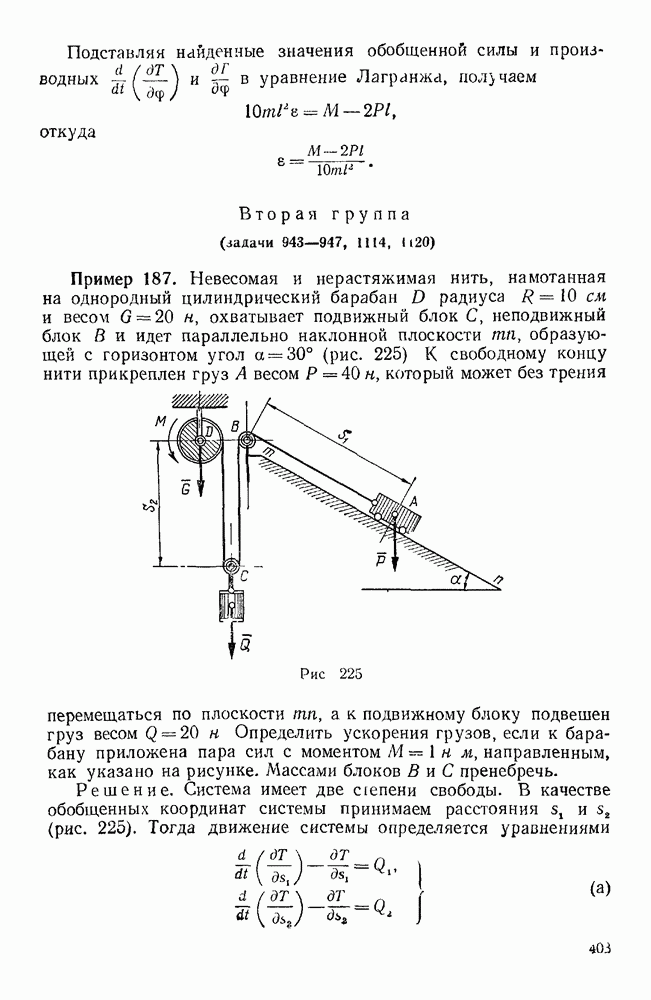
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА