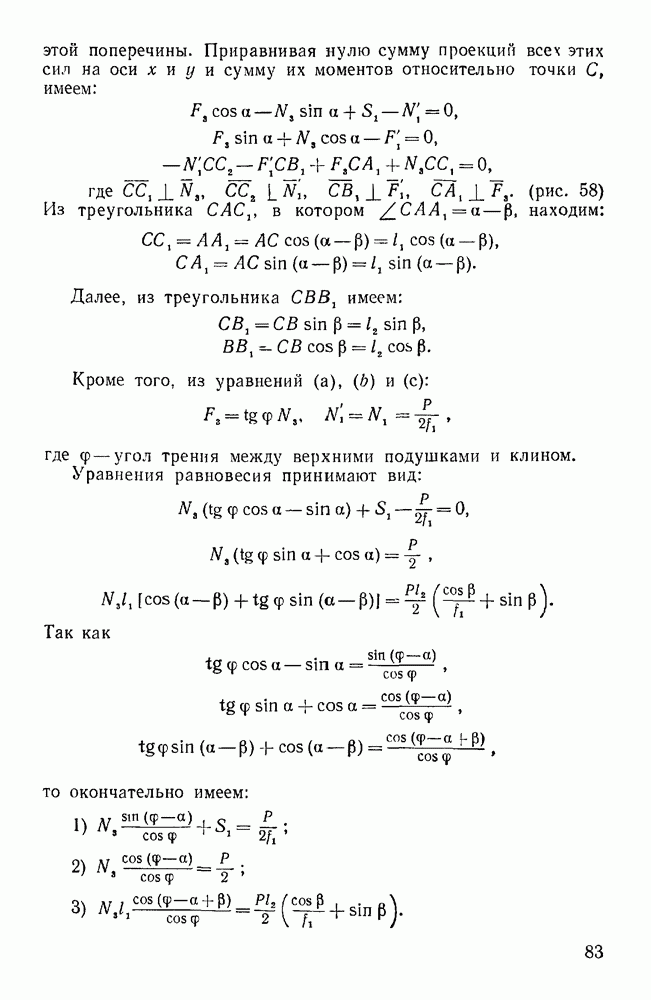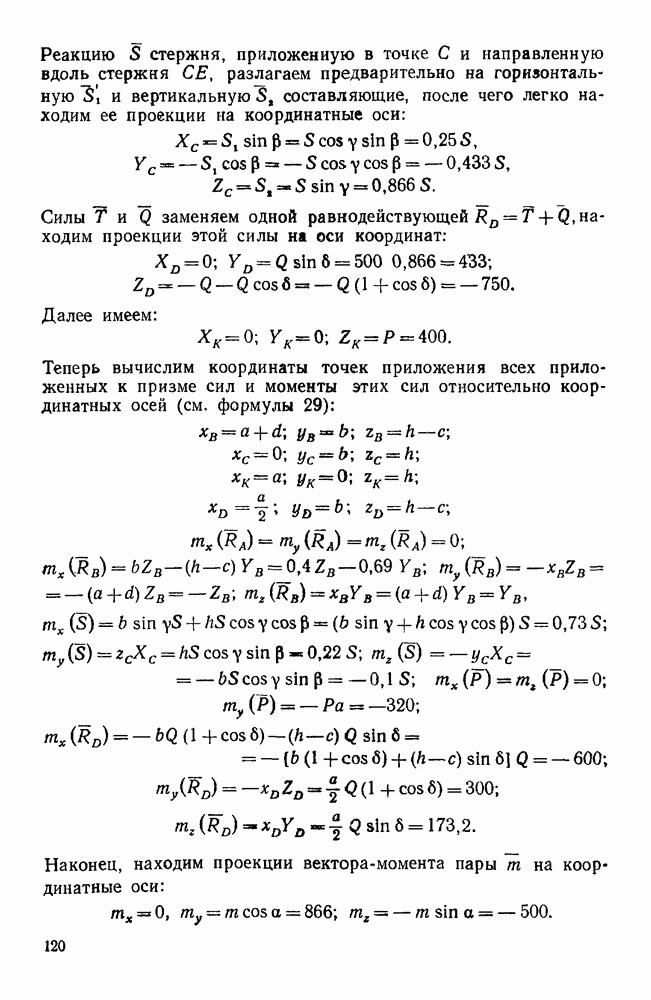| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
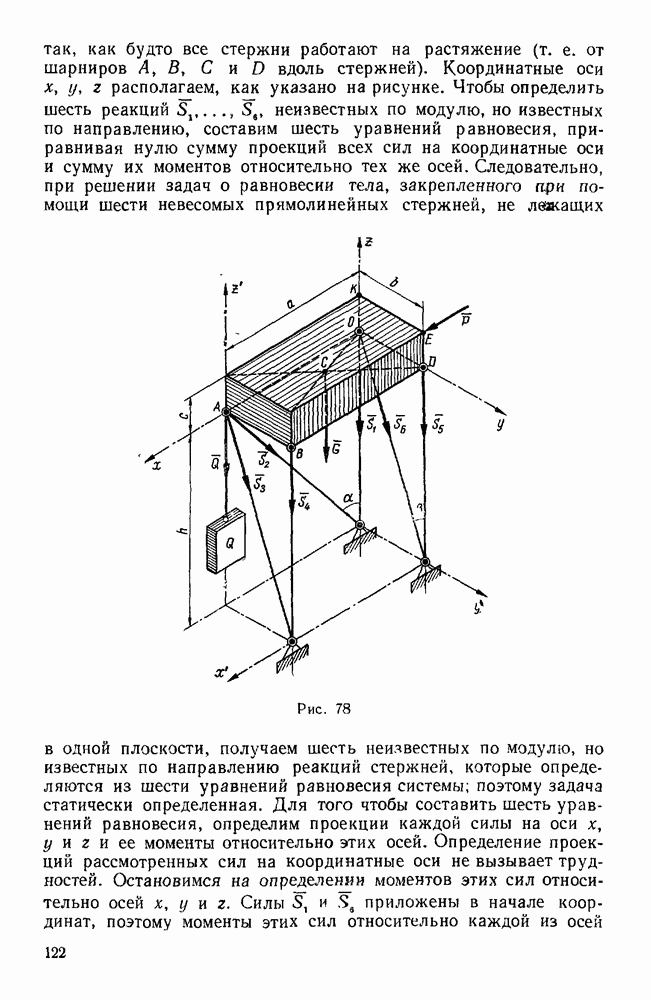
§ 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
(задачи 232—240)
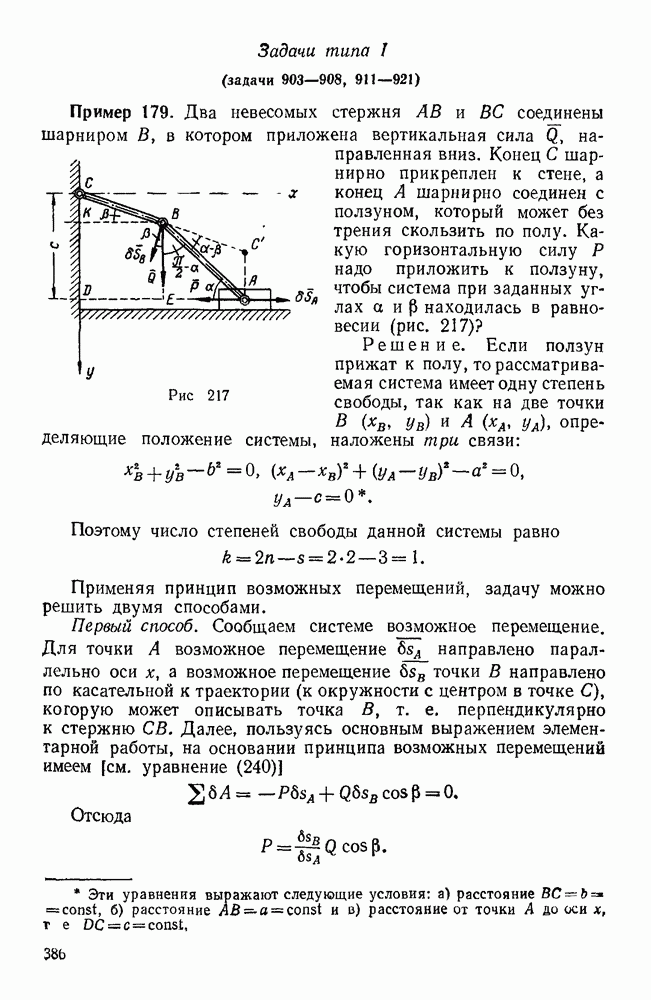
Если задана система сил  , расположенных
, расположенных
как угодно в пространстве, то эти силы можно привести к произвольно выбранному центру О. В результате такого приведения, как и в случае плоской системы сил, получим одну силу R, приложенную в центре приведения О и равную главному вектору данной системы сил, и одну пару с вектором-моментом  , равным главному моменту этой системы сил относительно центра О.
, равным главному моменту этой системы сил относительно центра О.
Следовательно, будем иметь:

Аналитически модуль и направление векторов R и  определяются по их проекциям на координатные оси
определяются по их проекциям на координатные оси  , начало которых находится в центре приведения О, причем
, начало которых находится в центре приведения О, причем

Отсюда имеем:
 (31)
(31)
Модуль и направление главного вектора не зависят от выбора центра приведения. Поэтому главный вектор является первым инвариантом данной системы сил. Модуль и направление главйого момента  изменяются с изменением центра приведения.
изменяются с изменением центра приведения.

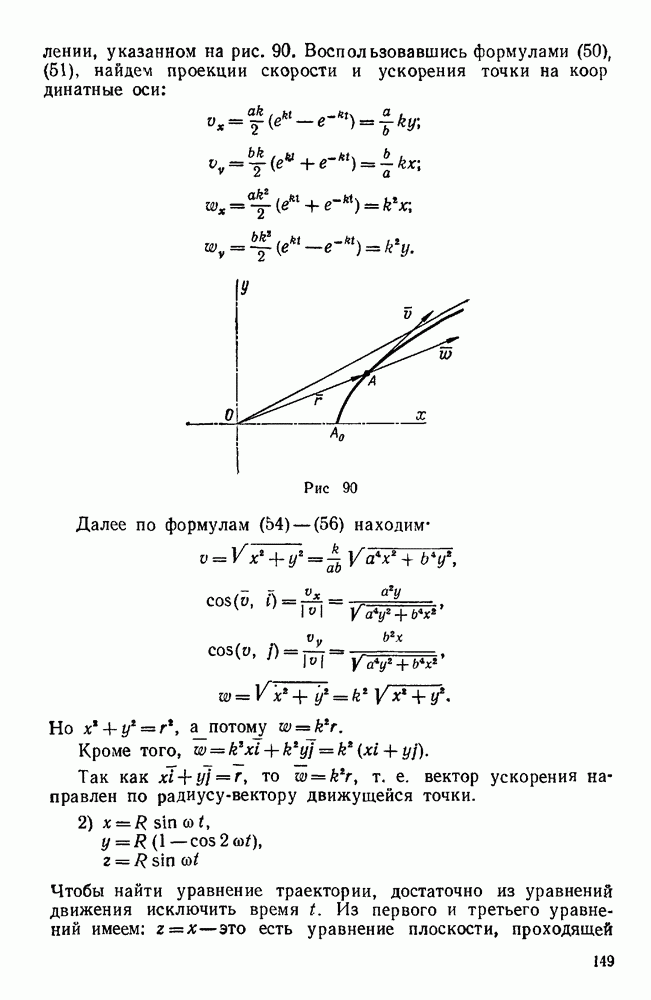
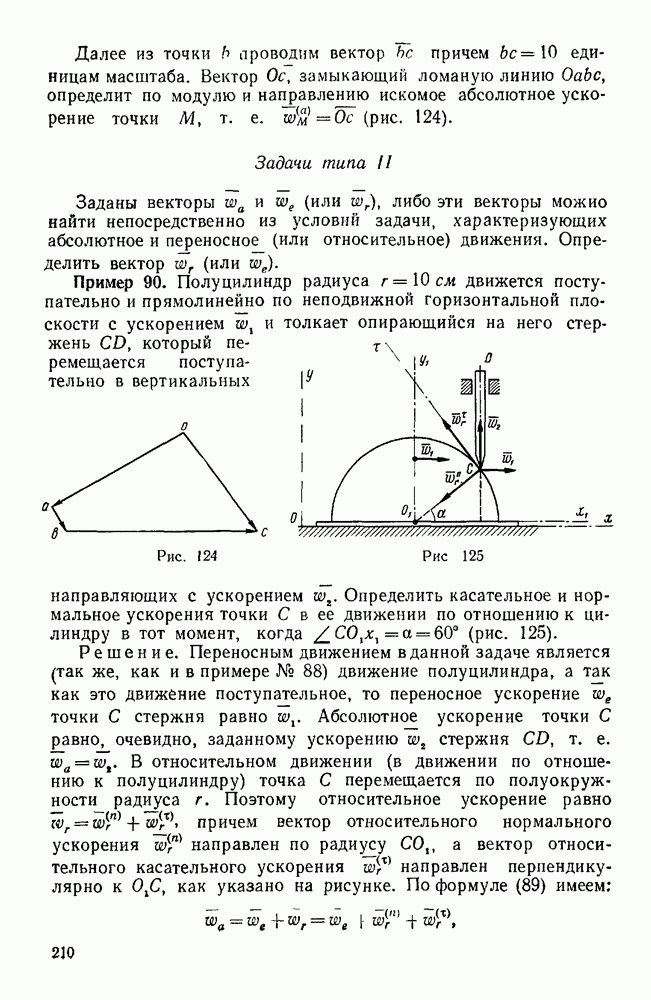
Рис. 63.
Но скалярное произведение  главного вектора и главного момента не зависит от выбора центра приведения, т. е. является вторым инвариантам данной системы сил. При этом
главного вектора и главного момента не зависит от выбора центра приведения, т. е. является вторым инвариантам данной системы сил. При этом  , где
, где  — угол между направлениями главного вектора R и главного момента
— угол между направлениями главного вектора R и главного момента  . Выражая это скалярное произведение через проекции векторов R и
. Выражая это скалярное произведение через проекции векторов R и  , имеем:
, имеем:

Если второй инвариант данной системы сил не равен нулю, то эта система приводится к динаме, т. е. к паре и к силе, перпендикулярной к плоскости этой пары (рис. 63).
Прямая, проходящая через точку  , по которой направлены векторы R и
, по которой направлены векторы R и  называется центральной осью данной системы сил. При этом отрезок
называется центральной осью данной системы сил. При этом отрезок  перпендикулярен к векторам
перпендикулярен к векторам 
 , а его длина равна:
, а его длина равна:

При перемещении центра приведения по центральной оси главный момент данной системы не изменяется, т. е. остается равным  , причем его модуль является наименьшим по сравнению с модулем главного момента данной системы сил относительно всякого другого центра приведения, не лежащего на центральной оси.
, причем его модуль является наименьшим по сравнению с модулем главного момента данной системы сил относительно всякого другого центра приведения, не лежащего на центральной оси.
Величина этого наименьшего момента определяется по формуле

Аналитически положение центральной оси определяется ее двумя уравнениями, которые имеют следующий вид:

где x, у и z - текущие координаты точки, лежащей на центральной оси.

Рис. 64.
Может оказаться, что скалярное произведение  равно нулю, но каждый из сомножителей отличен от нуля. В этом случае главный момент перпендикулярен главному вектору, т. е. сила и пара, получающаяся в результате приведения данной системы сил к центру О, лежат в одной плоскости.
равно нулю, но каждый из сомножителей отличен от нуля. В этом случае главный момент перпендикулярен главному вектору, т. е. сила и пара, получающаяся в результате приведения данной системы сил к центру О, лежат в одной плоскости.

Рис. 65.
В этом случае, как уже было  § 1 гл. II, система приводится к равнодействующей,
§ 1 гл. II, система приводится к равнодействующей,  , которая проходет через точку
, которая проходет через точку  , лежащую на перпендикуляре, к векторам
, лежащую на перпендикуляре, к векторам  на расстоянии
на расстоянии  (рис. 64). Если
(рис. 64). Если  то система сил приводится, очевидно, к одной равнодействующей силе R, проходящей через центр приведения О.
то система сил приводится, очевидно, к одной равнодействующей силе R, проходящей через центр приведения О.
Если же  , то заданная система сил приводится к одной паре с моментом
, то заданная система сил приводится к одной паре с моментом  в этом случае главный момент системы не изменяется с изменением центра приведения, т. е. относительно любого центра приведения главный момент будет равен
в этом случае главный момент системы не изменяется с изменением центра приведения, т. е. относительно любого центра приведения главный момент будет равен  (рис. 65).
(рис. 65).
Наконец, если главный вектор R и главный момент  одновременно равны нулю, то данная система находится в равновесии.
одновременно равны нулю, то данная система находится в равновесии.
Эти результаты можно расположить в табл. 8.
Таблица 8

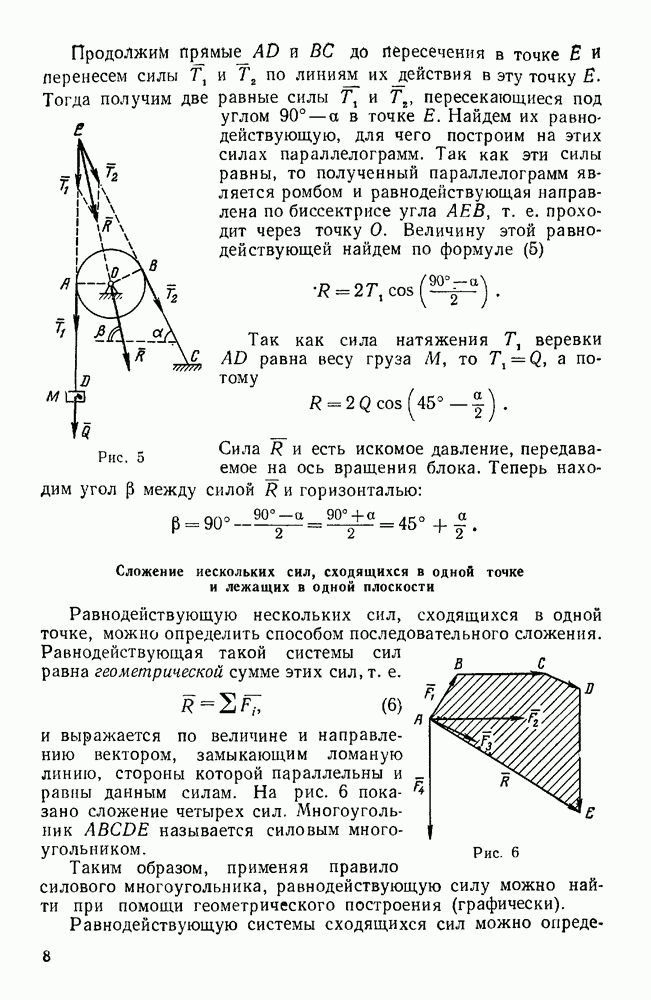
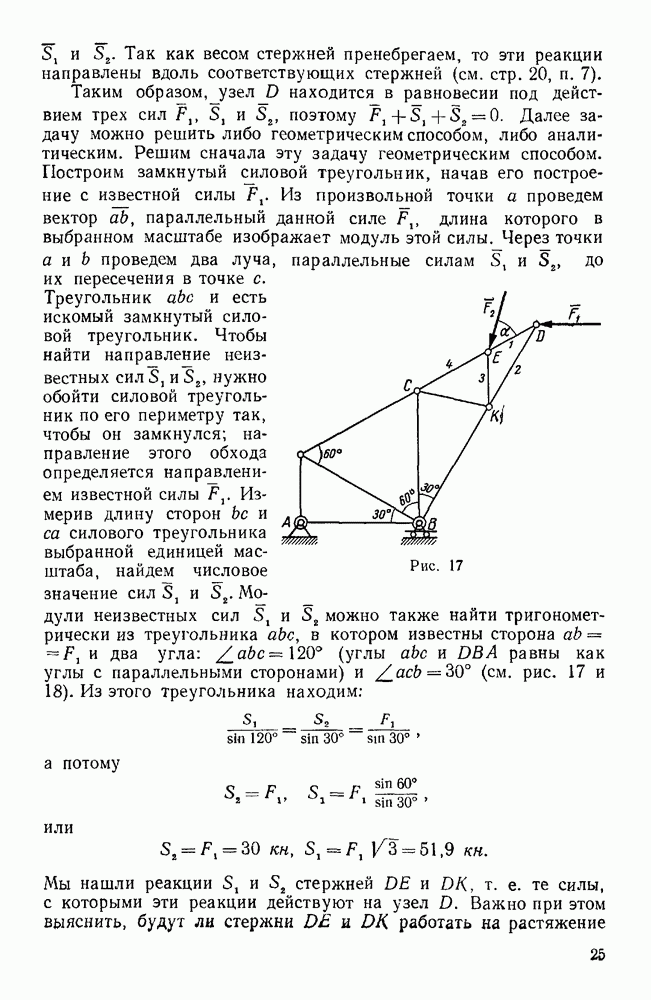
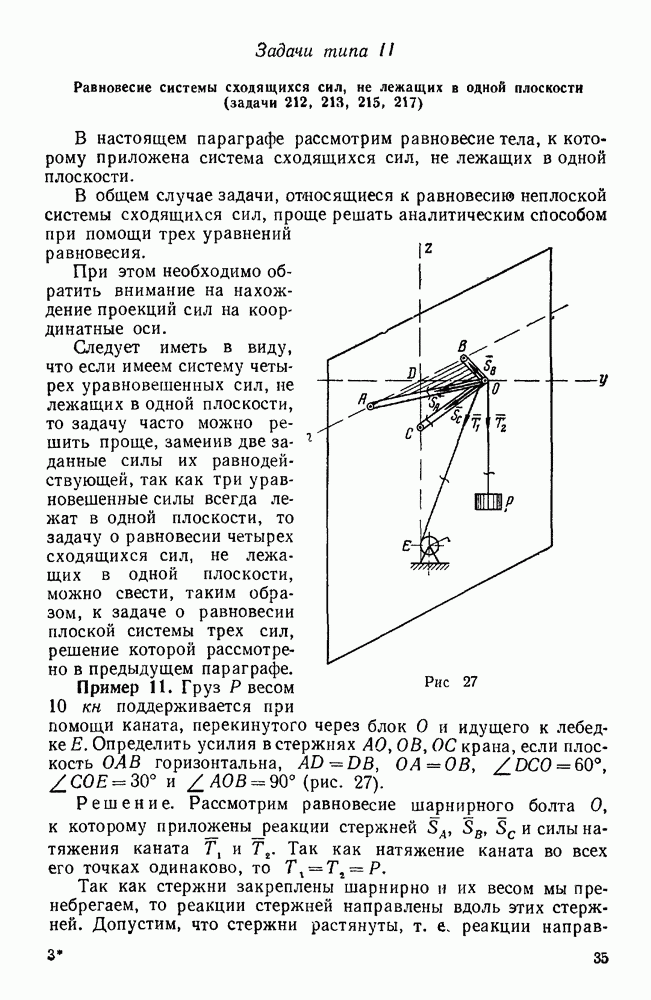
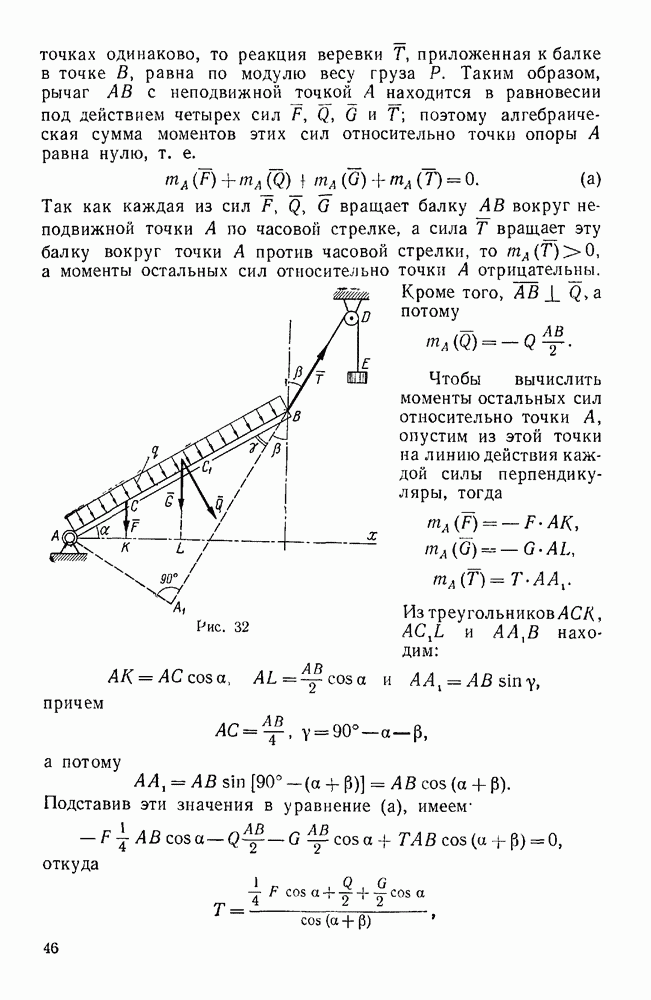
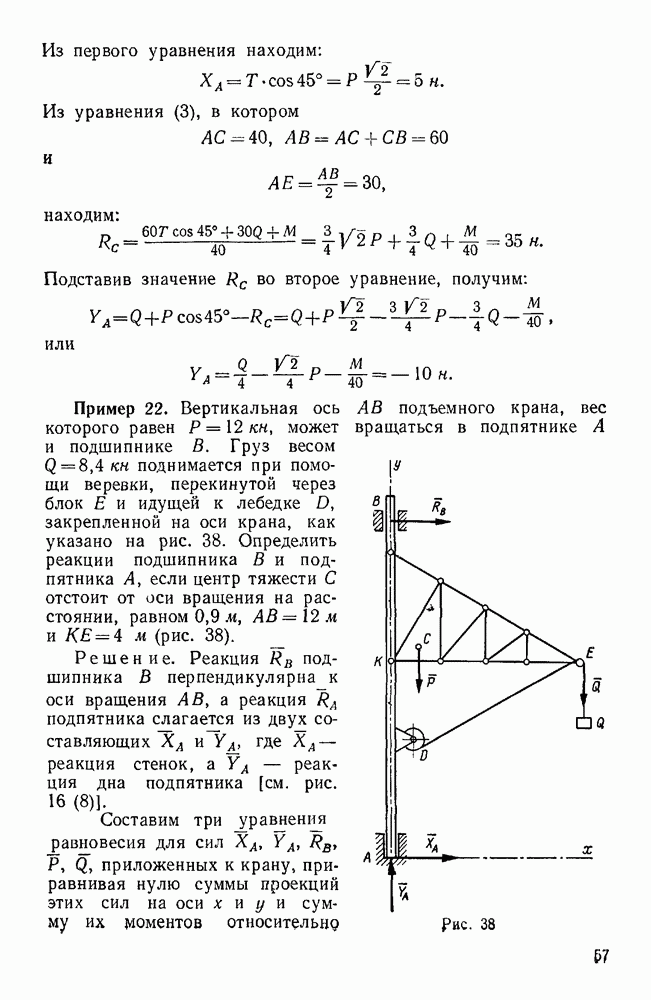
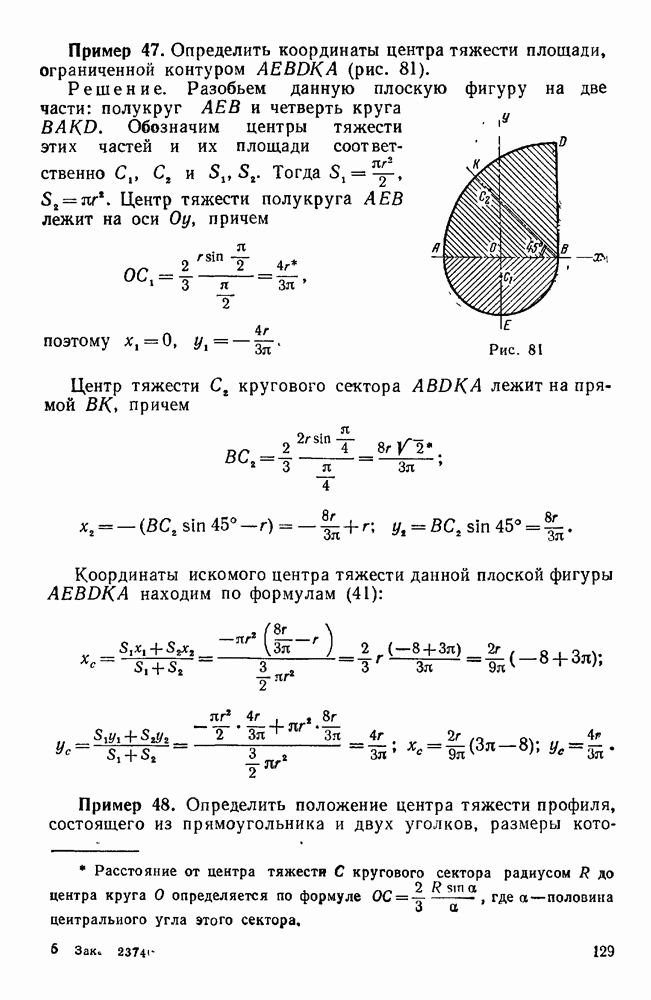
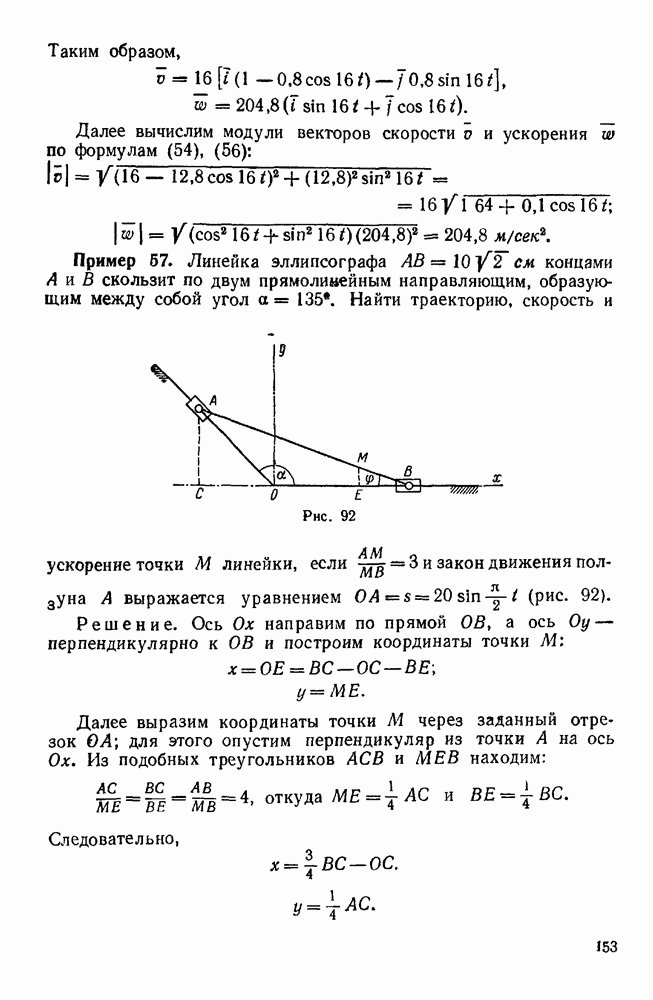
Пример 34. Даны три силы  , приложенные в точках
, приложенные в точках  (0; 2; 1),
(0; 2; 1),  (1;-1;3),
(1;-1;3),  (2; 3; 1), и их проекции на координатные оси (в ньютонах).
(2; 3; 1), и их проекции на координатные оси (в ньютонах).

Привести эту систему сил к началу координат.
Решение. Определим сначала проекции главного вектора и главного момента на координатные оси:

Для вычисления моментов сил  относительно координатных осей воспользуемся формулами (29). Тогда имеем:
относительно координатных осей воспользуемся формулами (29). Тогда имеем:

Теперь по найденным проекциям определяем величину главного вектора и главного момента:

Для определения направления главного момента находим его направляющие косинусы:

Так как главный вектор данной системы сил равен нулю, то эта система сил приводится к одной паре с моментом  , причем этот момент не изменяется с изменением центра приведения.
, причем этот момент не изменяется с изменением центра приведения.
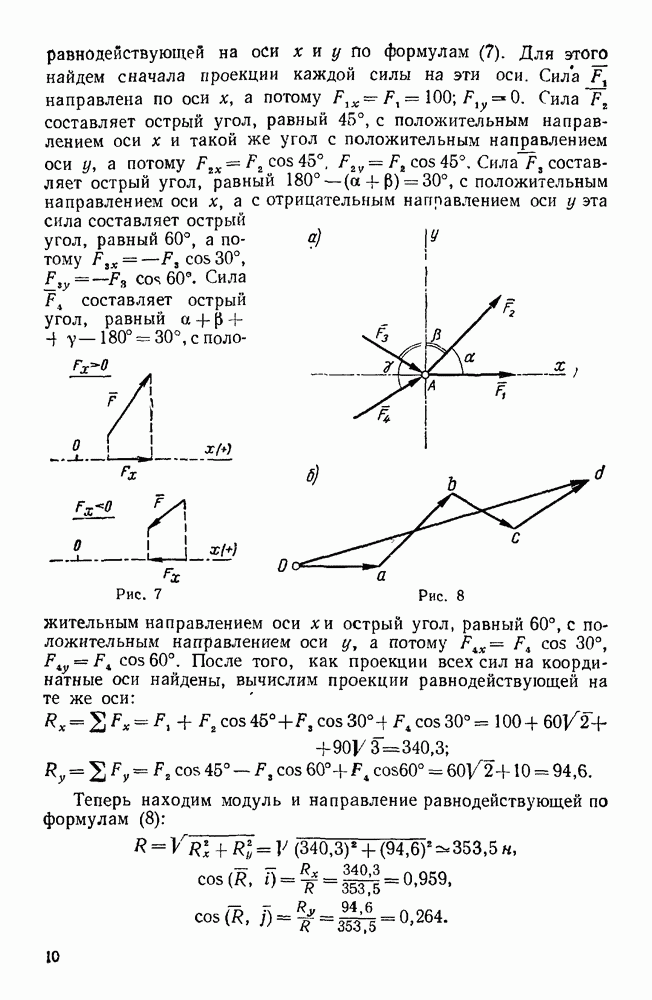
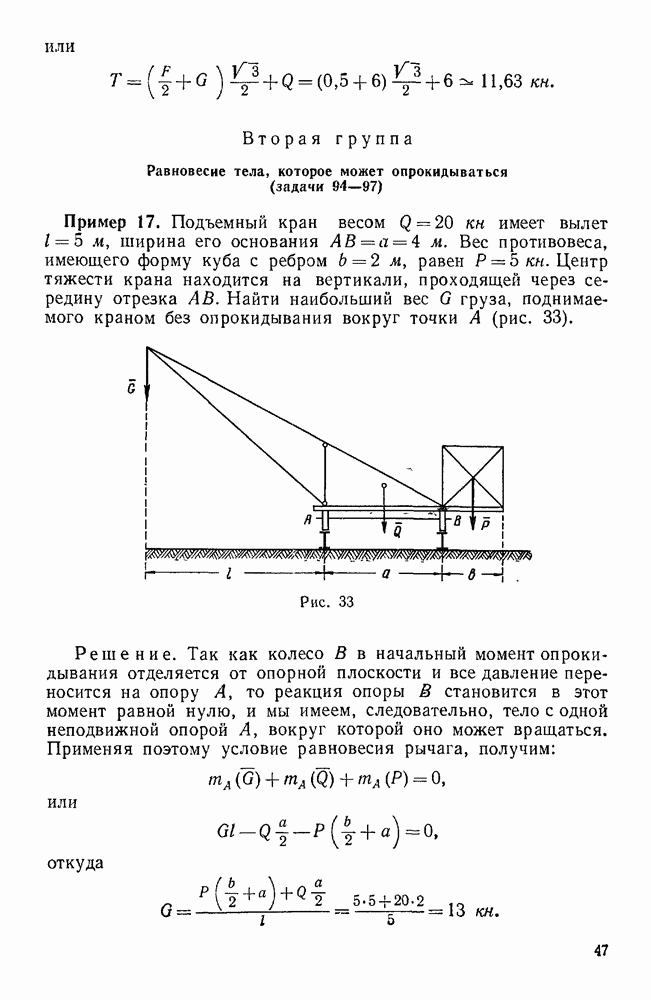
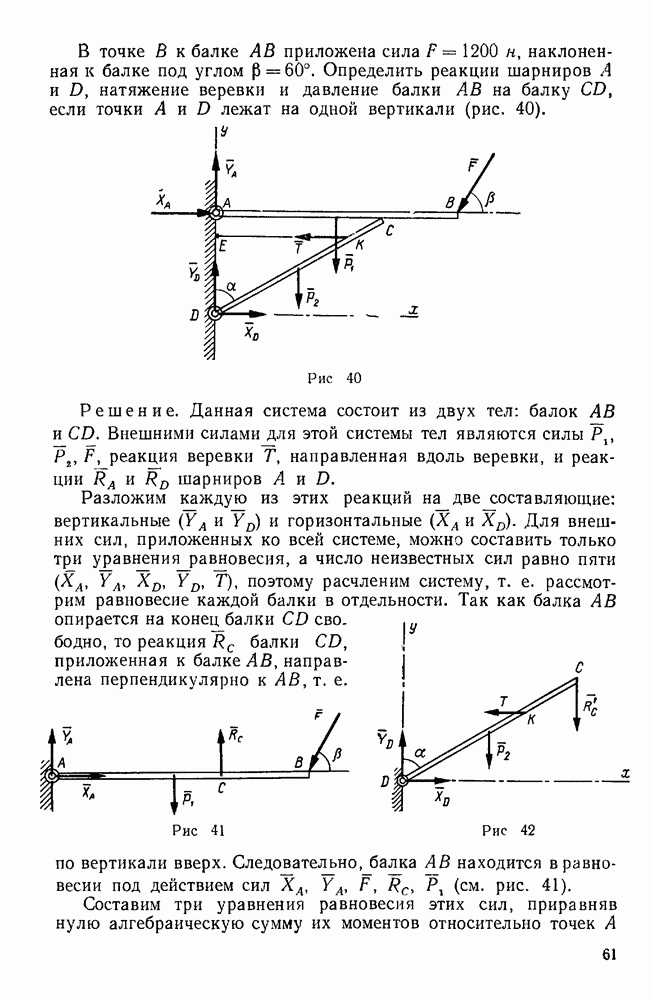
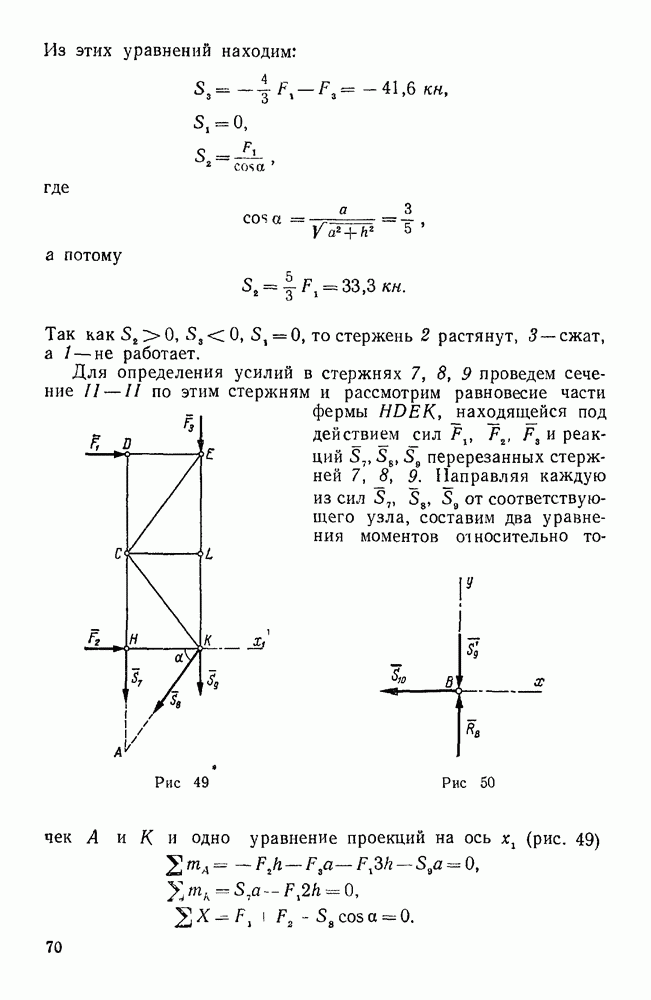
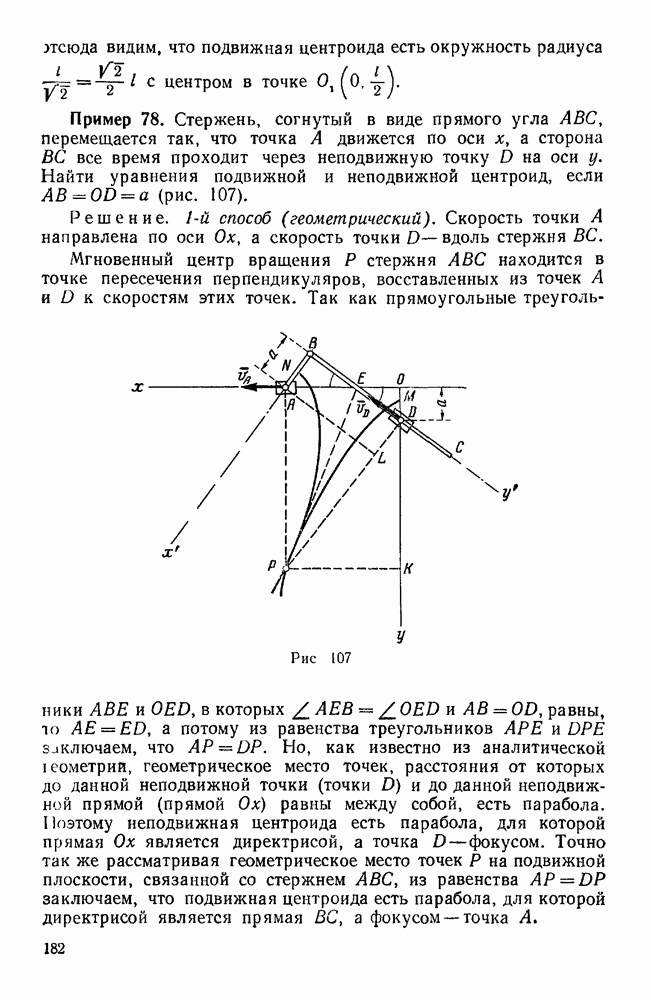
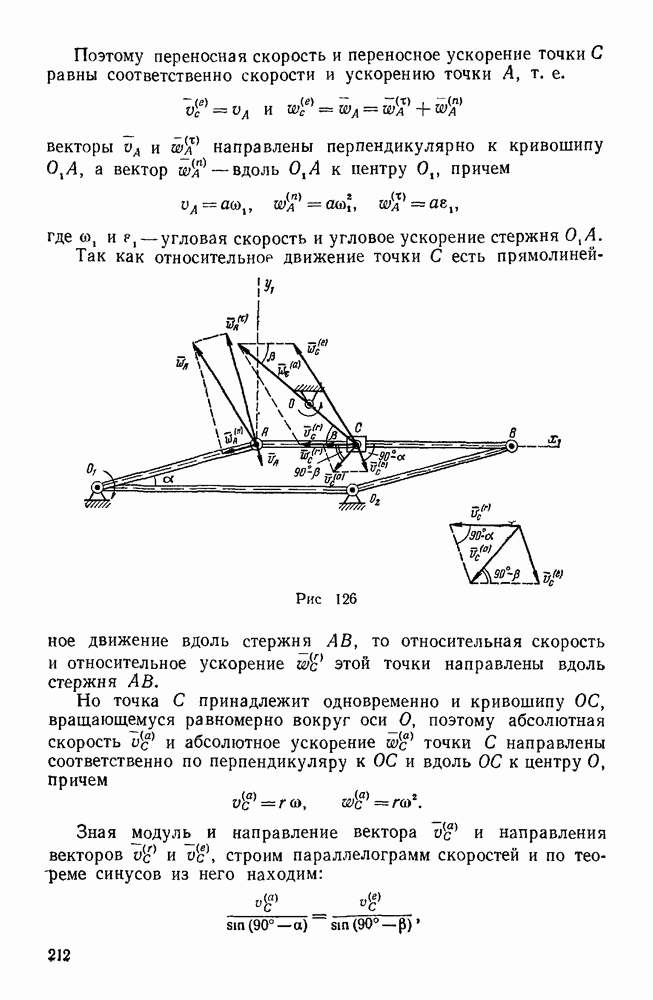
Пример 35. По ребрам призмы действуют, как указано на рис. 66, силы  . Кроме того, дано
. Кроме того, дано  . Привести эту систему сил к простейшему виду.
. Привести эту систему сил к простейшему виду.

Рис. 66.
Решение. Выберем систему координатных осей, как указано на рисунке, и найдем проекции главного вектора на координатные оси.

Отсюда следует, что главный вектор направлен по оси у и равен  .
.
Приводя данную систему сил к началу координат, найдем проекции  на оси х, у, z главного момента
на оси х, у, z главного момента  относительно точки О:
относительно точки О:

Так как силы  пересекают ось
пересекают ось  , а силы
, а силы  параллельна этой оси, то моменты этих сил относительно оси х равны нулю и, следовательно,
параллельна этой оси, то моменты этих сил относительно оси х равны нулю и, следовательно,

Сила  лежит в плоскости
лежит в плоскости  , причем наблюдатель, смотрящий с положительного конца этой оси, видит силу
, причем наблюдатель, смотрящий с положительного конца этой оси, видит силу  направленной относительно точки О по часовой стрелке, поэтому
направленной относительно точки О по часовой стрелке, поэтому

Далее

Силы  пересекают ось у, поэтому их моменты относительно этой оси равны нулю.
пересекают ось у, поэтому их моменты относительно этой оси равны нулю.
Следовательно,

Силы  лежат в плоскости хz, поэтому
лежат в плоскости хz, поэтому

и

Итак,

Так как силы  пересекают ось z, а сила
пересекают ось z, а сила  параллельна этой оси, а потому момент каждой из этих сил относительно оси z равен нулю, следовательно,
параллельна этой оси, а потому момент каждой из этих сил относительно оси z равен нулю, следовательно,

Так как

то главный момент  направлен по оси х и
направлен по оси х и

Таким образом, данная система сил эквивалентна силе R, приложенной в точке О, и паре с моментом  .
.
Остается теперь выяснить, к какому простейшему виду можно привести данную систему сил: к одной равнодействующей силе или к динаме. Так как  перпендикулярен главному моменту
перпендикулярен главному моменту  , то сила R и пара (с моментом
, то сила R и пара (с моментом  ) лежат в одной плоскости
) лежат в одной плоскости  , поэтому они приводятся к одной равнодействующей силе
, поэтому они приводятся к одной равнодействующей силе  , равной и параллельной силе R и приложенной в точке
, равной и параллельной силе R и приложенной в точке  . Найдем эту точку
. Найдем эту точку  .
.
Для этого нужно на прямой, проведенной из точки О и перпендикулярной к векторам R и  , т. е. в данном случае на оси z, отложить отрезок, равный
, т. е. в данном случае на оси z, отложить отрезок, равный

При этом отрезок  следует отложить на оси в таком направлении, чтобы, смотря с конца вектора-момента
следует отложить на оси в таком направлении, чтобы, смотря с конца вектора-момента  , можно было видеть равнодействующую силу
, можно было видеть равнодействующую силу  , приложенную в точке
, приложенную в точке  , направленной по отношению к точке О против часовой стрелки. Так как
, направленной по отношению к точке О против часовой стрелки. Так как  , то точка
, то точка  совпадает с данной точкой К.
совпадает с данной точкой К.
Точка К и будет точкой приложения  , данная система
, данная система  приводится к равнодействующей силе
приводится к равнодействующей силе  , приложенной в точке К и направленной параллельно оси у, причем
, приложенной в точке К и направленной параллельно оси у, причем

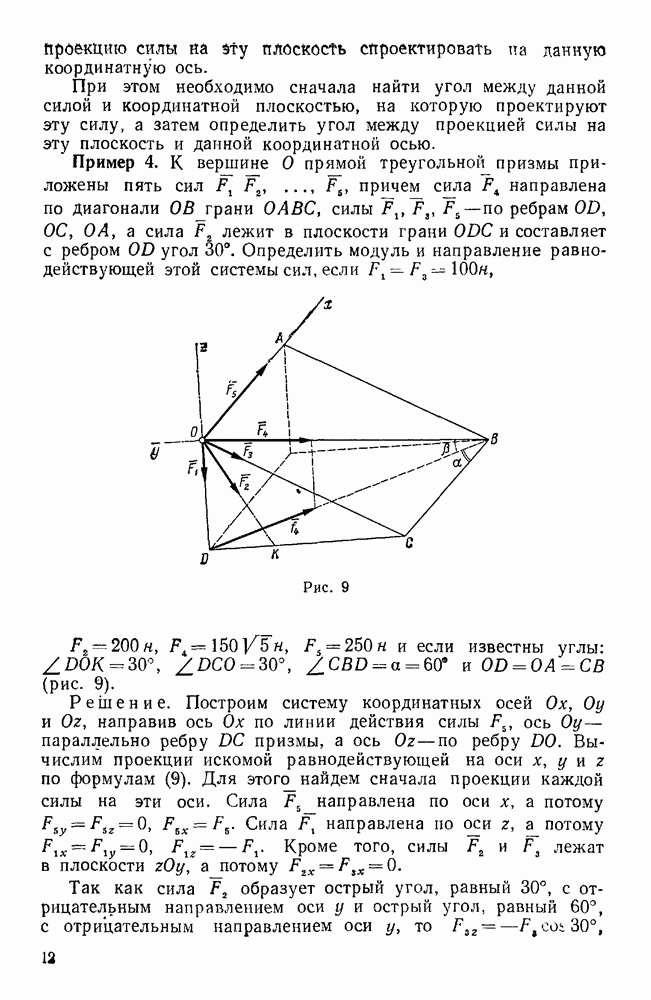
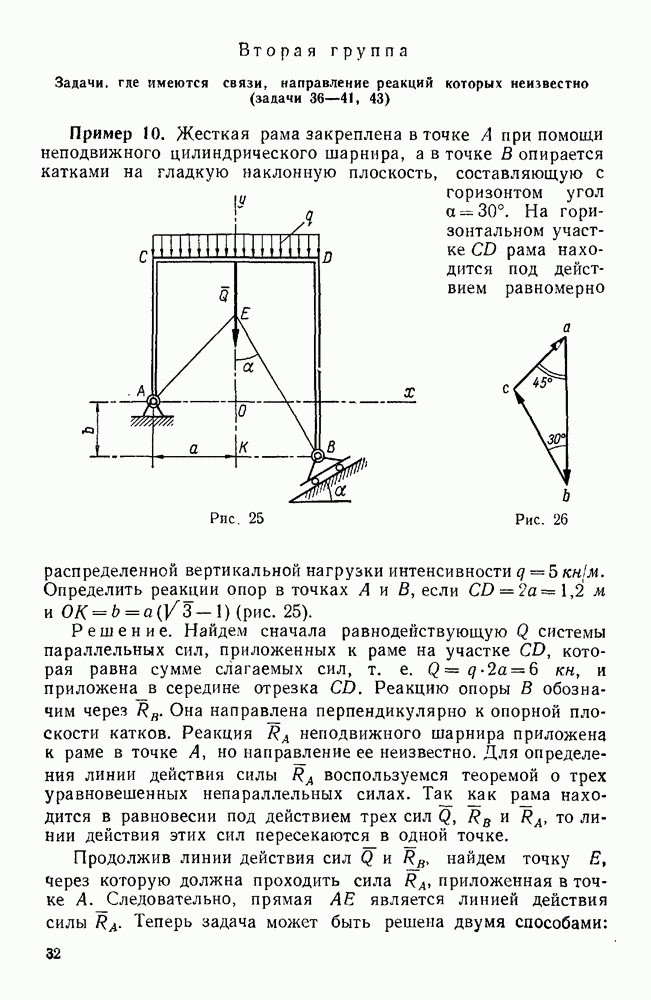
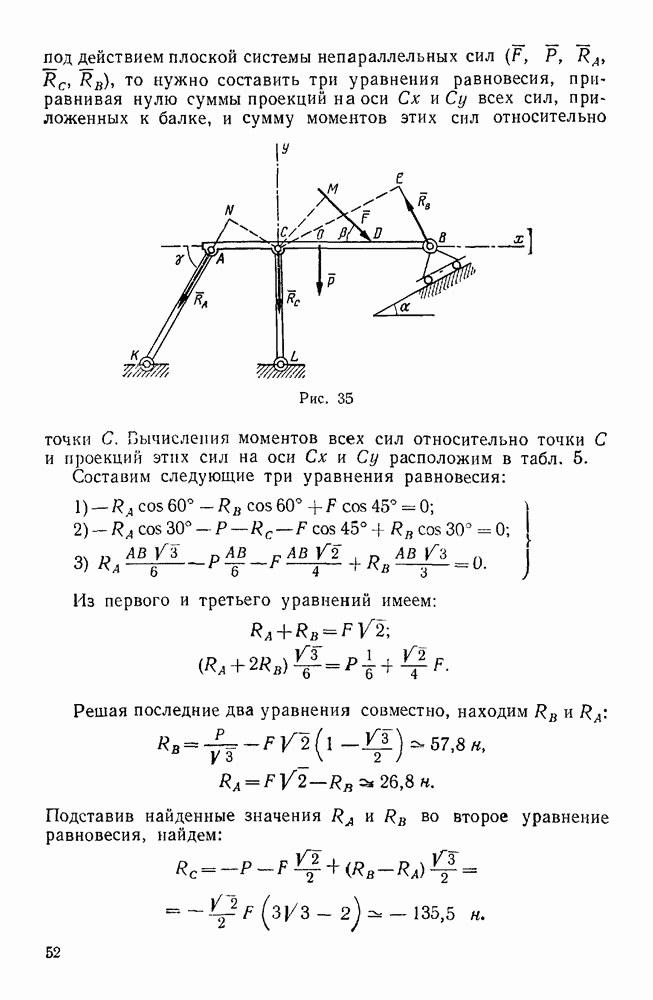
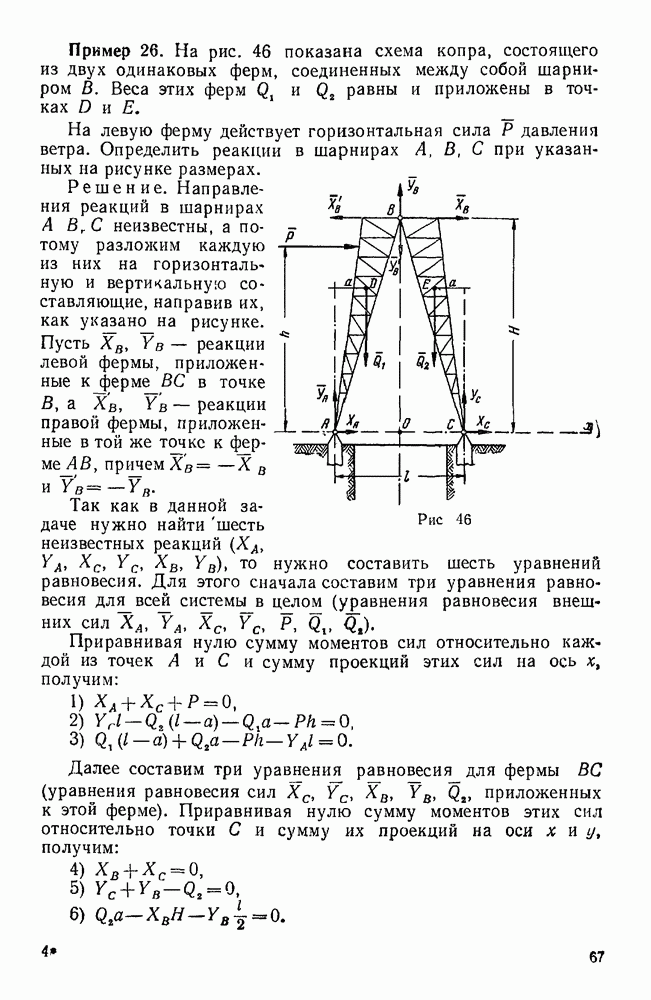
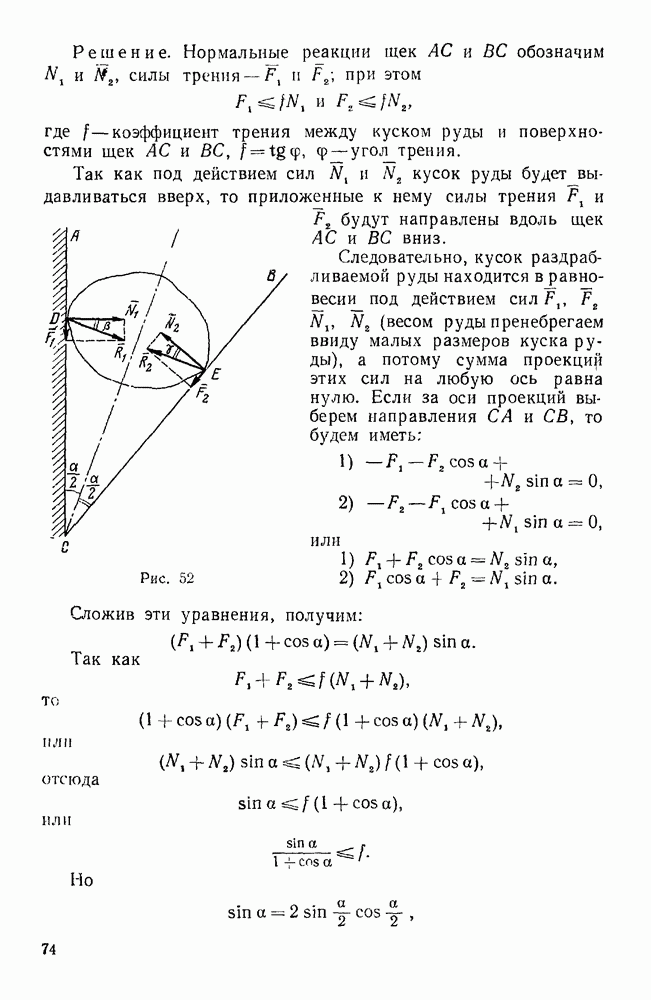
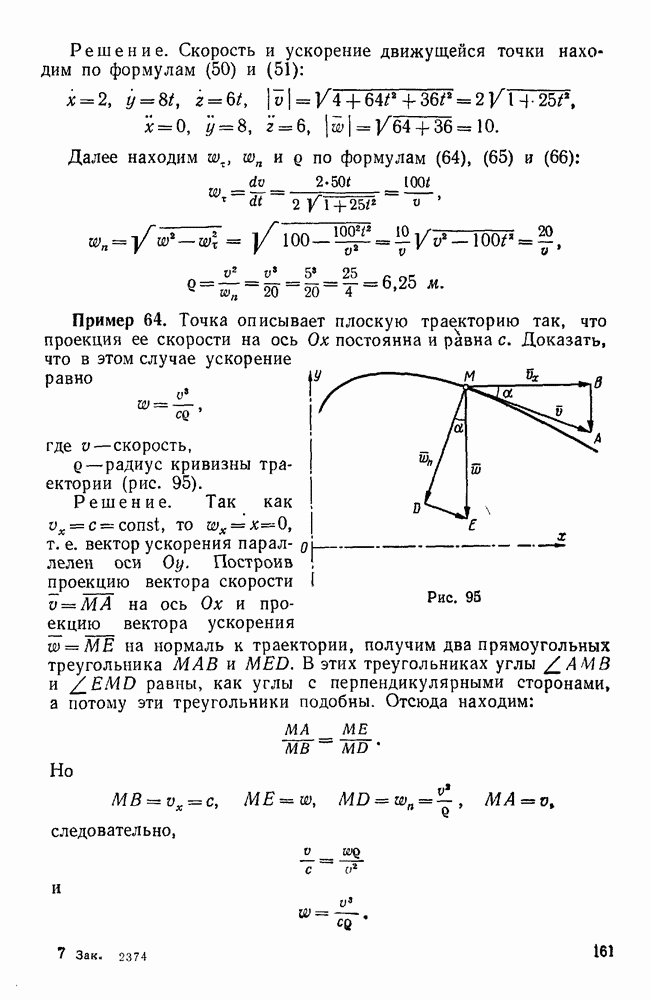
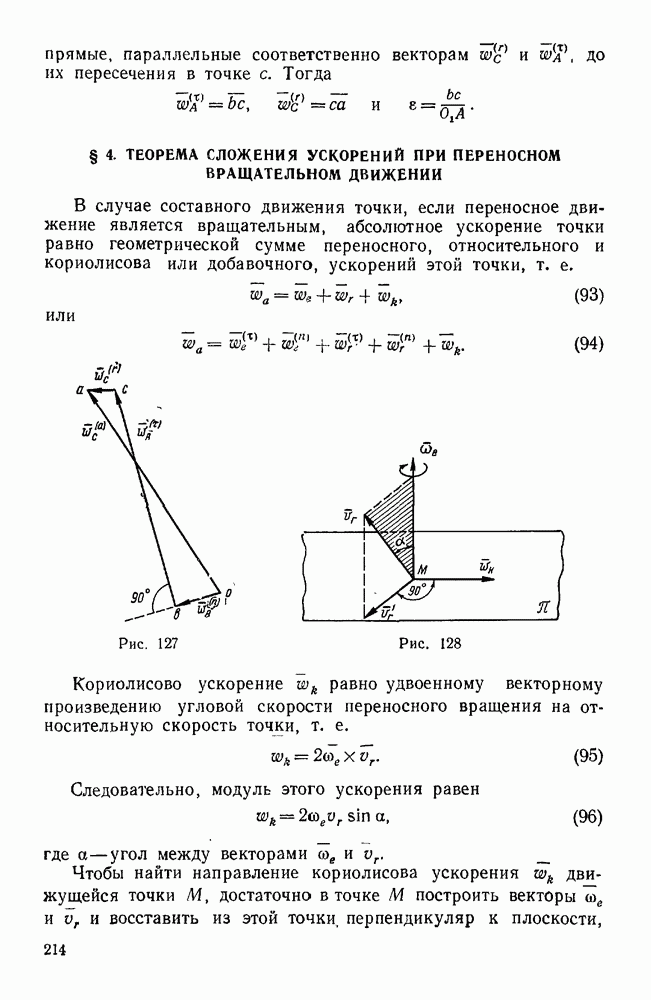
Пример 36. Дана система сил  , приложенных в вершинах прямоугольного параллелепипеда и направленных, как указано на рис. 67, причем
, приложенных в вершинах прямоугольного параллелепипеда и направленных, как указано на рис. 67, причем

Привести эту систему сил к простейшему виду.

Рис. 67.
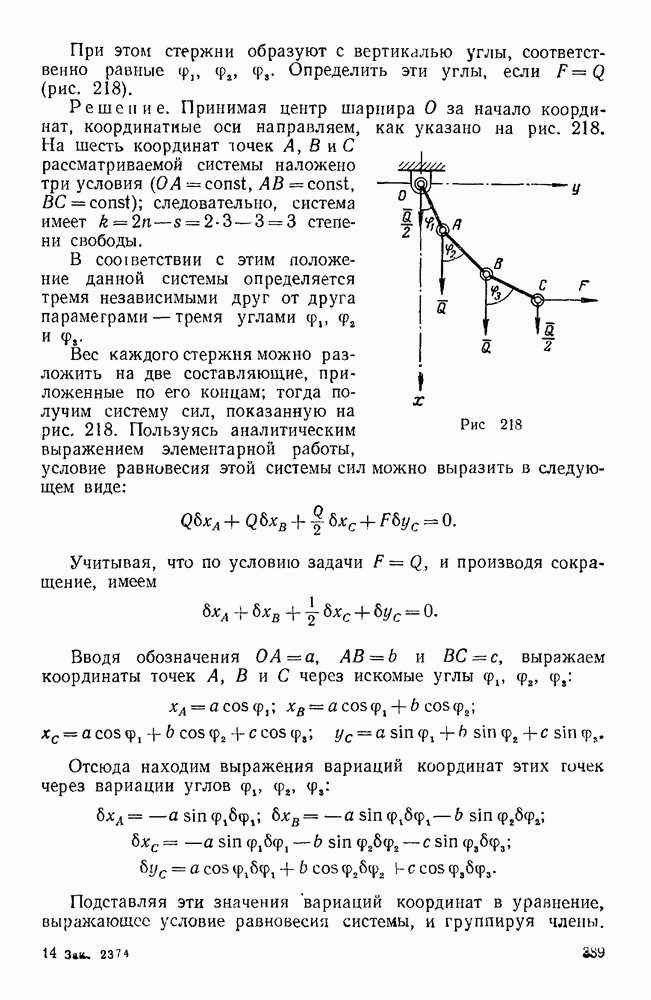
Решение. Координатные оси х, у, z направим, как указано на чертеже, и введем следующие обозначения: угол ODK обозначим  , угол КОВ —
, угол КОВ —  и угол АОЕ —
и угол АОЕ —  .
.
При вычислении проекций заданных сил на координатные оси заметим, что проекции силы  на оси х и у нужно находить так же, как это было указано в примере № 12, т. е. сначала силу
на оси х и у нужно находить так же, как это было указано в примере № 12, т. е. сначала силу  следует спроектировать на плоскость
следует спроектировать на плоскость  и полученную проекцию
и полученную проекцию  спроектировать затем на оси х и у.
спроектировать затем на оси х и у.
Значения проекций всех заданных сил и координаты их точек приложения расположим в виде табл. 9.
Таблица 9

Из прямоугольных треугольников ODK, ОСЕ и ОВК находим:

Теперь вычислим проекции главного вектора на координатные оси:

Отсюда видим, что главный вектор  направлен по оси у влево и по величине равен 30 н.
направлен по оси у влево и по величине равен 30 н.
Переходим к вычислению главного момента  относительно центра приведения О.
относительно центра приведения О.
Сила  параллельна оси х, а остальные силы пересекают эту ось, поэтому момент каждой силы относительно оси х равен нулю. Следовательно,
параллельна оси х, а остальные силы пересекают эту ось, поэтому момент каждой силы относительно оси х равен нулю. Следовательно,  .
.
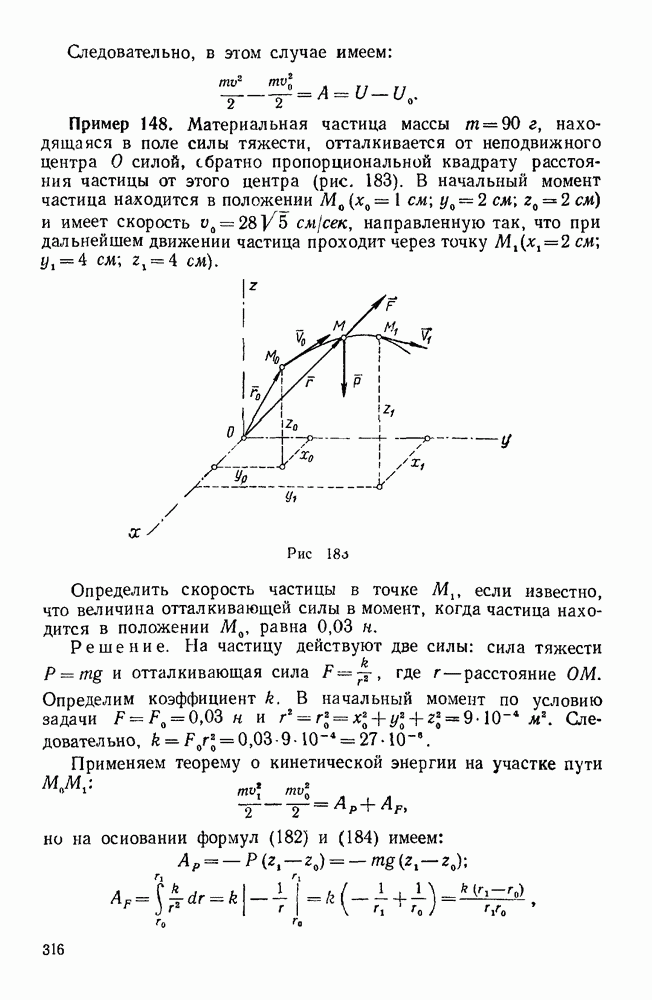
Точно так же момент каждой из сил  , относительно оси у равен нулю, а потому
, относительно оси у равен нулю, а потому

Моменты сил  относительно оси z равны нулю, так как эти силы пересекают эту ось, следовательно,
относительно оси z равны нулю, так как эти силы пересекают эту ось, следовательно,

Так как  , то главный момент
, то главный момент  лежит в плоскости
лежит в плоскости  и по величине равен
и по величине равен

Так как главный вектор и главный момент отличны от нуля, то необходимо выяснить, приводится ли данная система сил к динаме или к одной равнодействующей силе. Для этого вычислим скалярное произведение главного вектора и главного момента:

Так как это произведение не равно нулю, то векторы R и  не перпендикулярны и, следовательно, данная система сил приводится к динаме.
не перпендикулярны и, следовательно, данная система сил приводится к динаме.
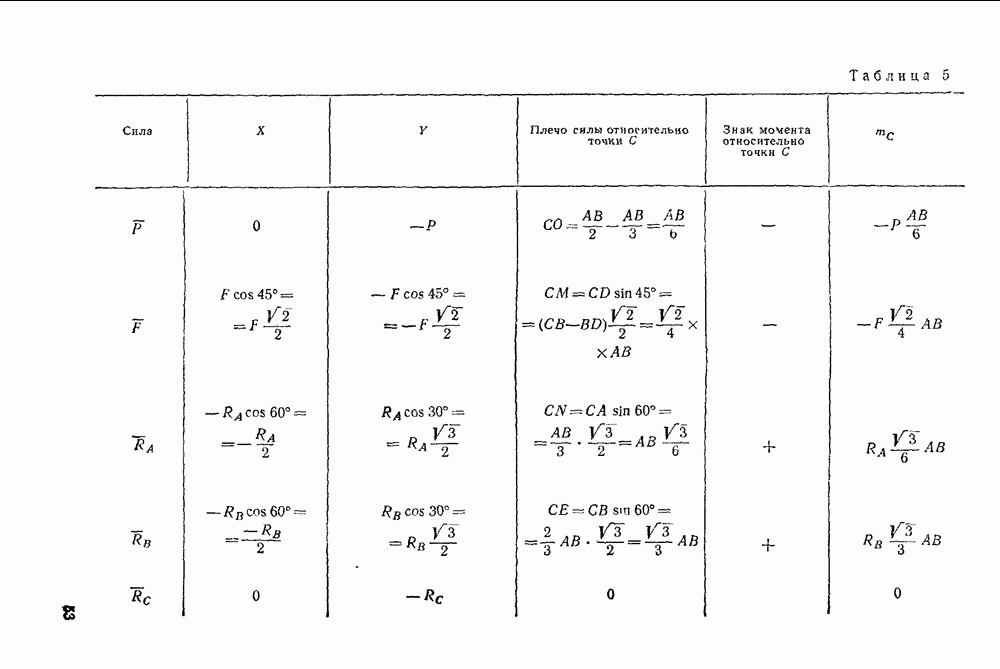
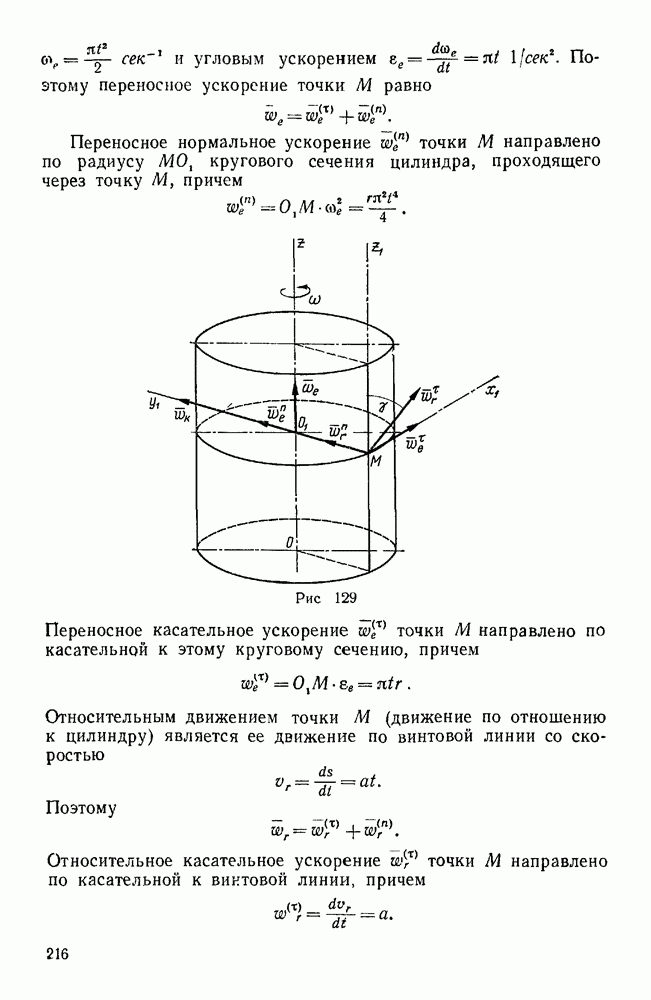
Найдем точку, через которую проходит центральная ось данной системы сил, а также величину главного момента относительно этой точки.
Для этого построим главный вектор R и главный момент  по их проекциям на координатные оси и разложим главный момент по правилу параллелограмма на два составляющих момента М и
по их проекциям на координатные оси и разложим главный момент по правилу параллелограмма на два составляющих момента М и  , из которых М направлен вдоль главного вектора, т. е. по оси у, а
, из которых М направлен вдоль главного вектора, т. е. по оси у, а  перпендикулярен к нему, т. е. направлен по оси z.
перпендикулярен к нему, т. е. направлен по оси z.
Следовательно,

Пара, имеющая момент  , лежит в плоскости
, лежит в плоскости  , т. е. в одной плоскости с главным вектором R, поэтому одну из сил R этой пары можно выбрать равной по величине силе R и направленной прямо противоположно этой силе.
, т. е. в одной плоскости с главным вектором R, поэтому одну из сил R этой пары можно выбрать равной по величине силе R и направленной прямо противоположно этой силе.
Тогда вторая сила этой пары  будет приложена в точке
будет приложена в точке  , лежащей на оси
, лежащей на оси  , причем плечо пары будет равно
, причем плечо пары будет равно

Система, состоящая из силы R и пары  , очевидно, эквивалентна одной силе
, очевидно, эквивалентна одной силе  . Таким образом, заданная система сил эквивалентна силе
. Таким образом, заданная система сил эквивалентна силе  и паре с моментом
и паре с моментом  , причем Следовательно, заданная система сил приводится к динаме, а точка
, причем Следовательно, заданная система сил приводится к динаме, а точка  находится на центральной оси.
находится на центральной оси.
 есть наименьший главный момент данной системы сил, т. е.
есть наименьший главный момент данной системы сил, т. е.

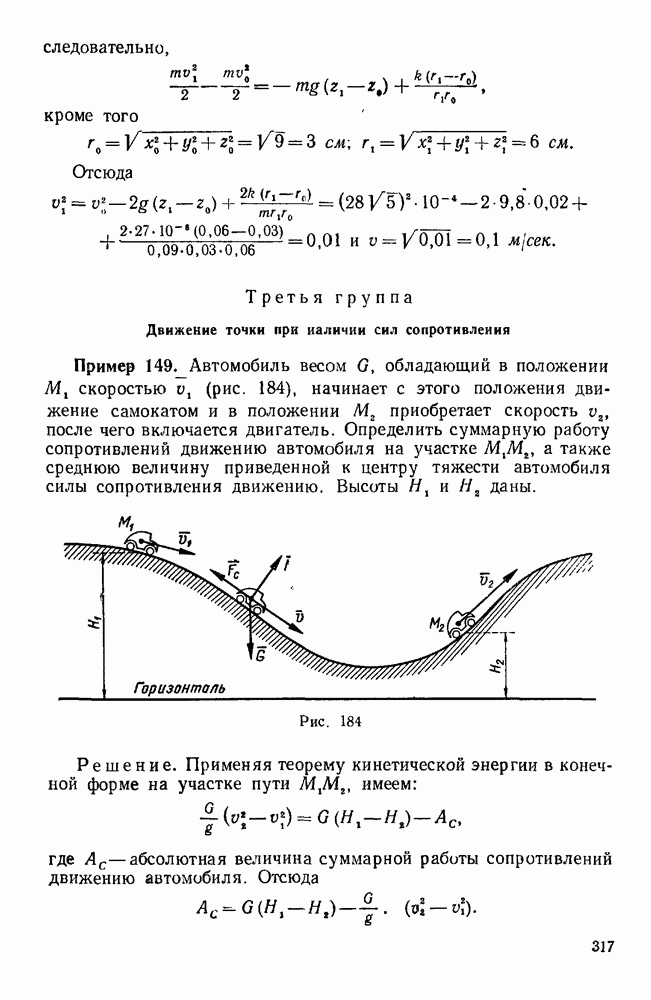
Эту же задачу можно решить другим способом.
После того как определим проекции на координатные оси главного вектора и главного момента, можно составить уравнения центральной оси данной системы сил:

Подставляя сюда значения  , получим:
, получим:

откуда

т. е.

Эти равенства показывают, что центральная ось проходит через точку  и параллельна оси у.
и параллельна оси у.

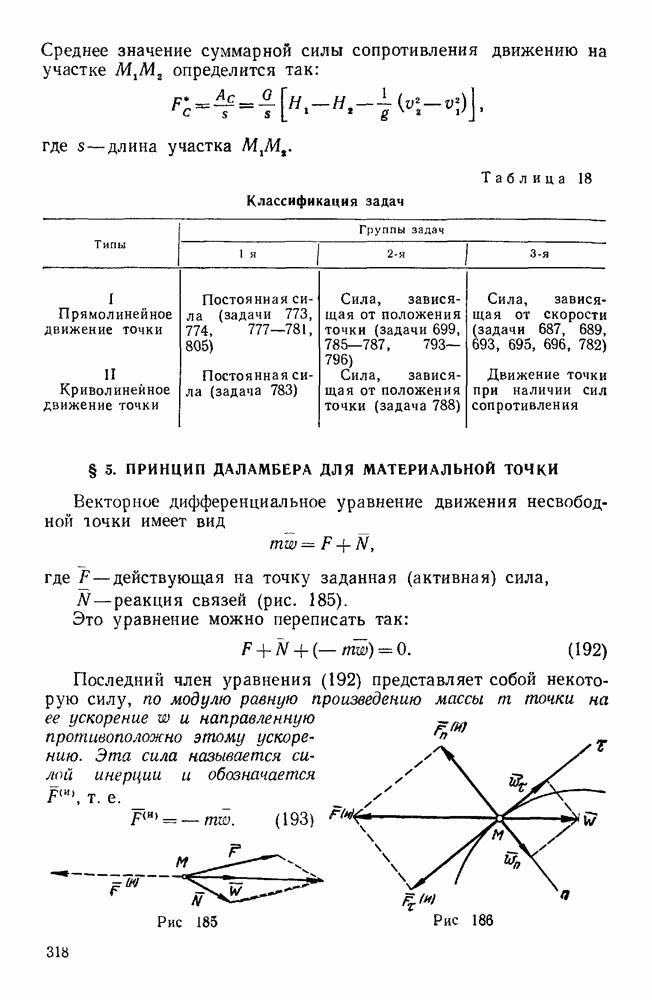
Рис. 68.
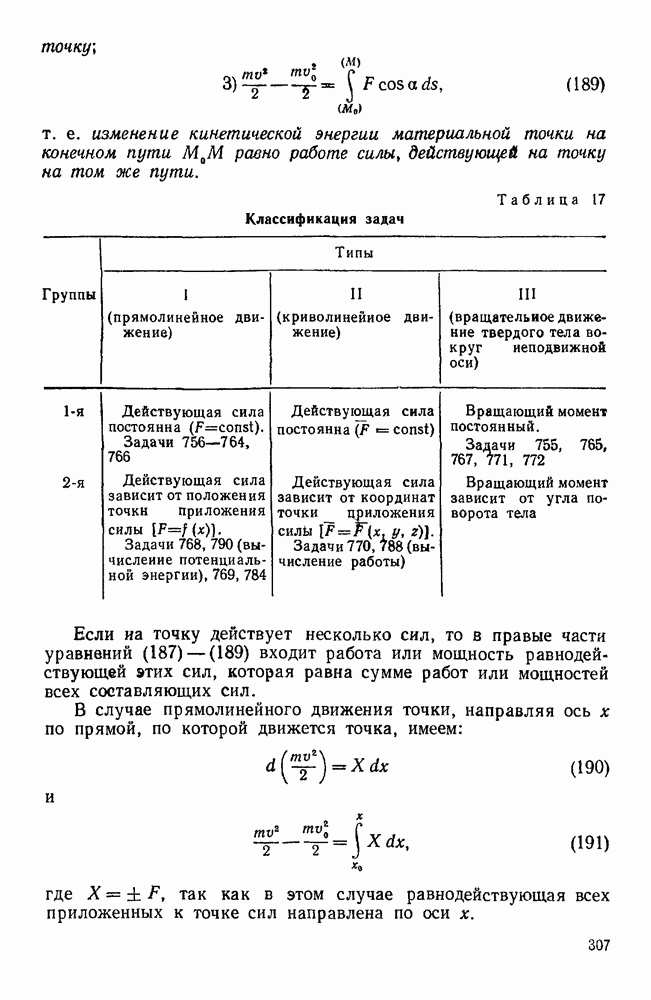
Чтобы найти модуль наименьшего главного момента, достаточно скалярное произведение  разделить на величину главного вектора, т. е.
разделить на величину главного вектора, т. е.

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
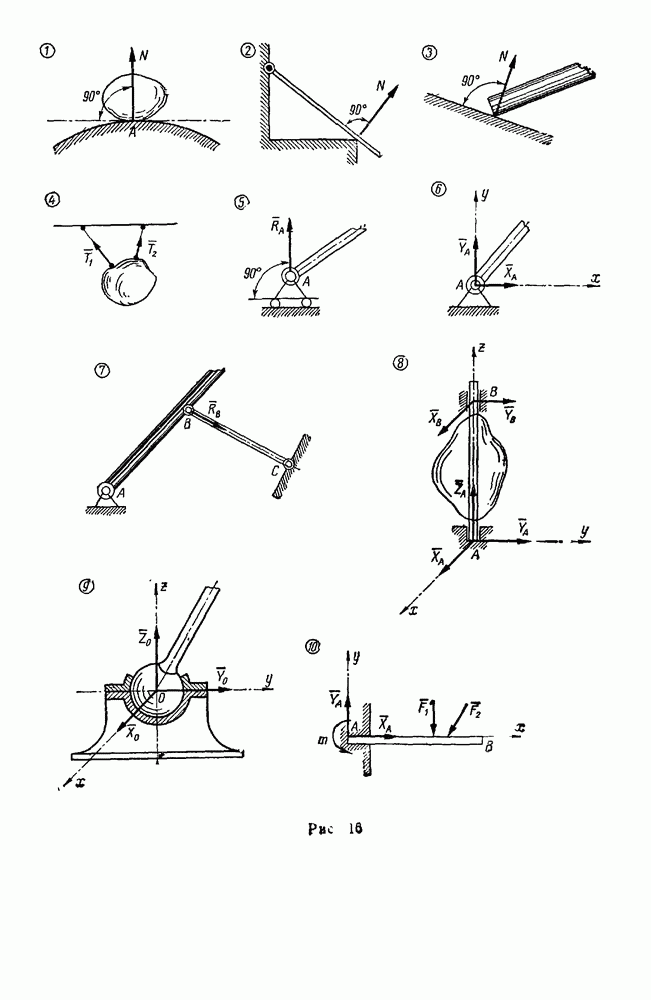
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
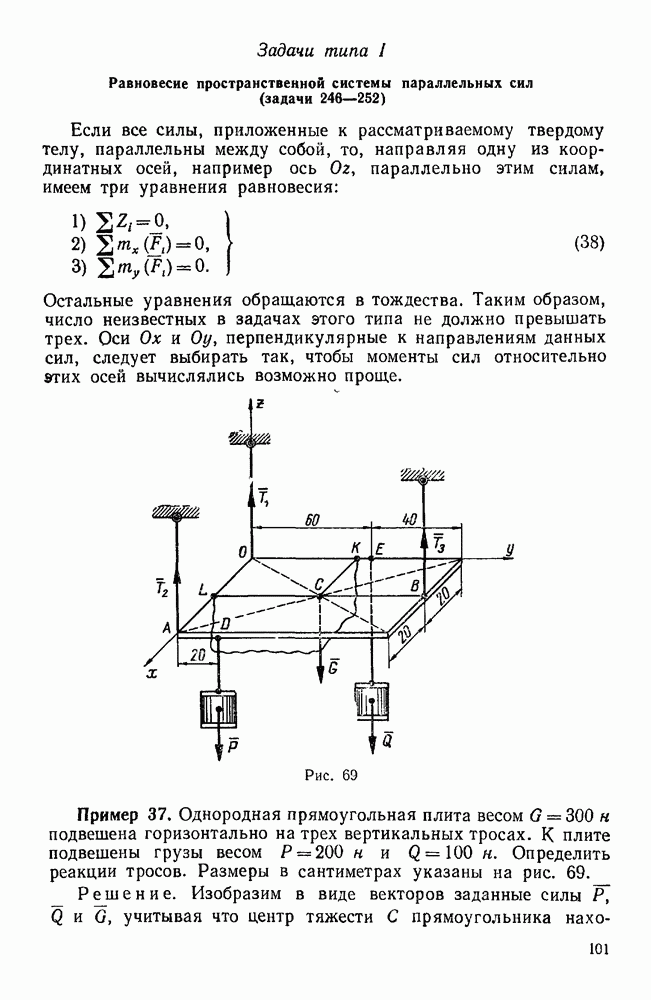
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
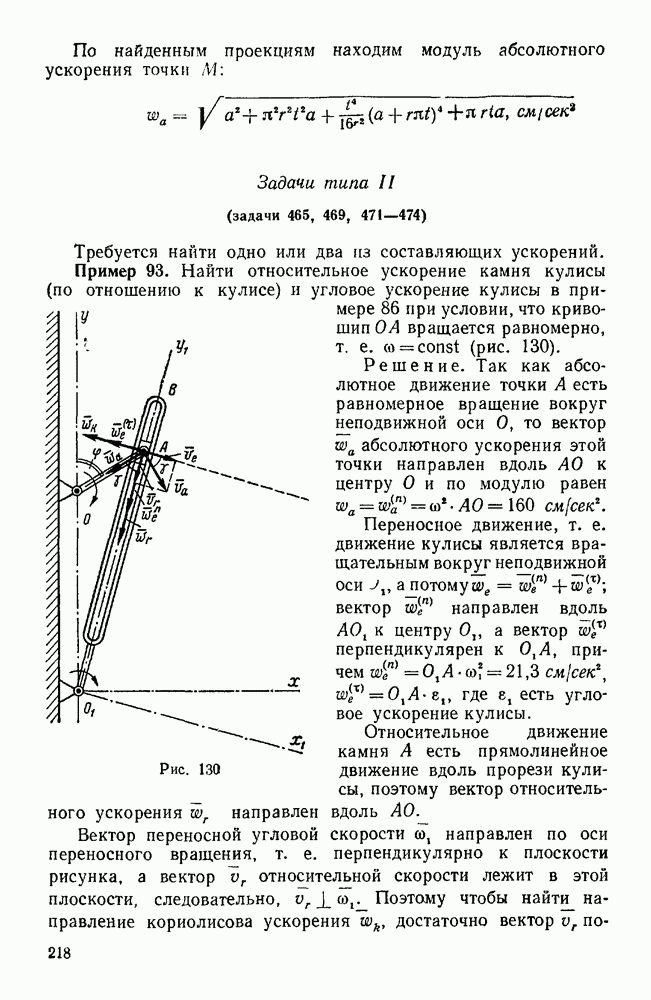
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
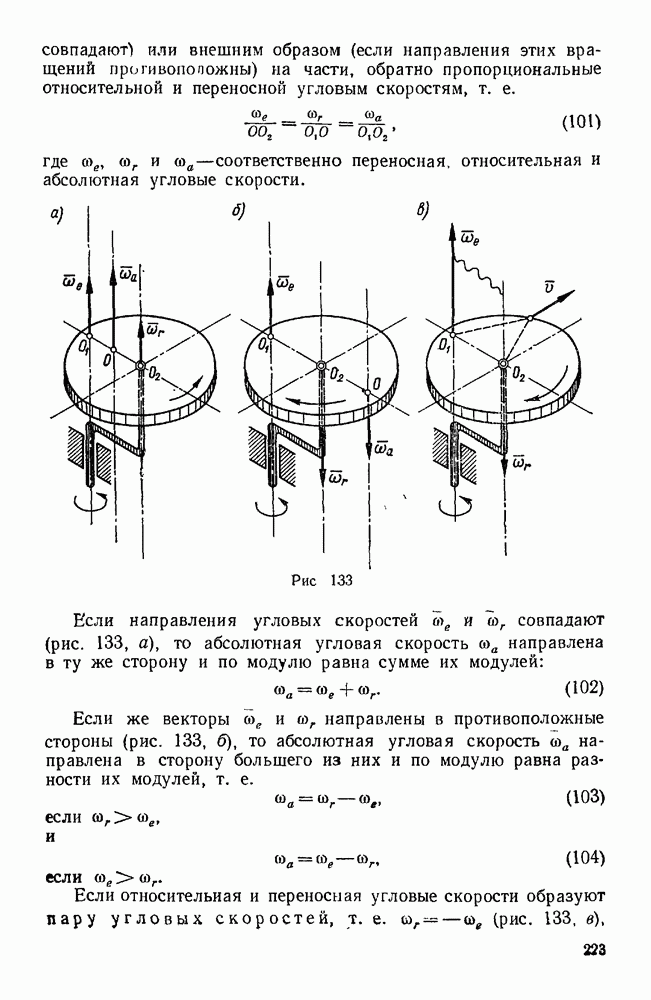
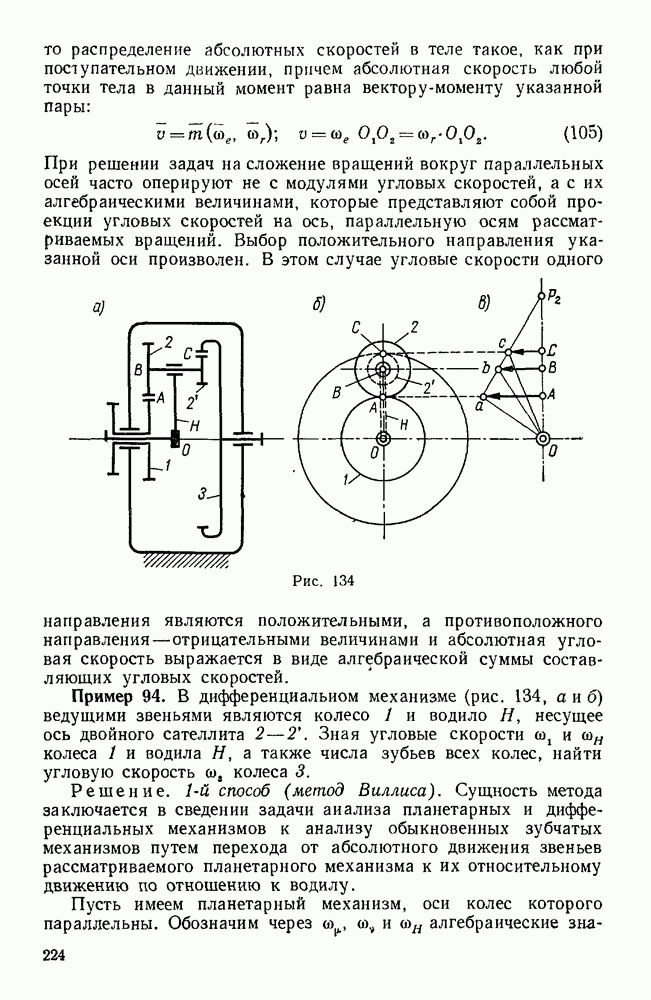
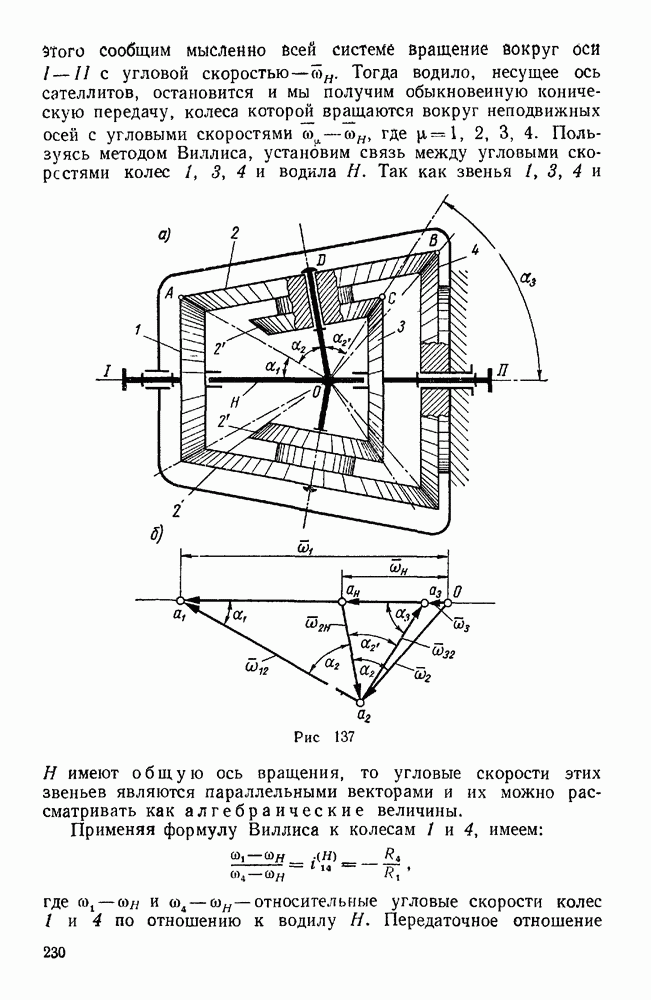
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
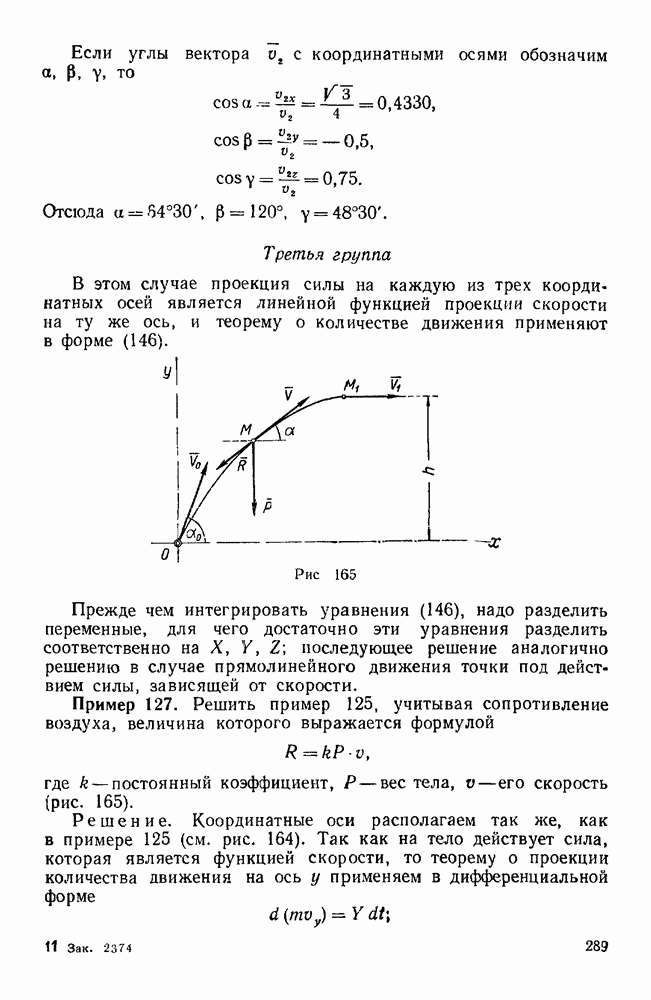
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
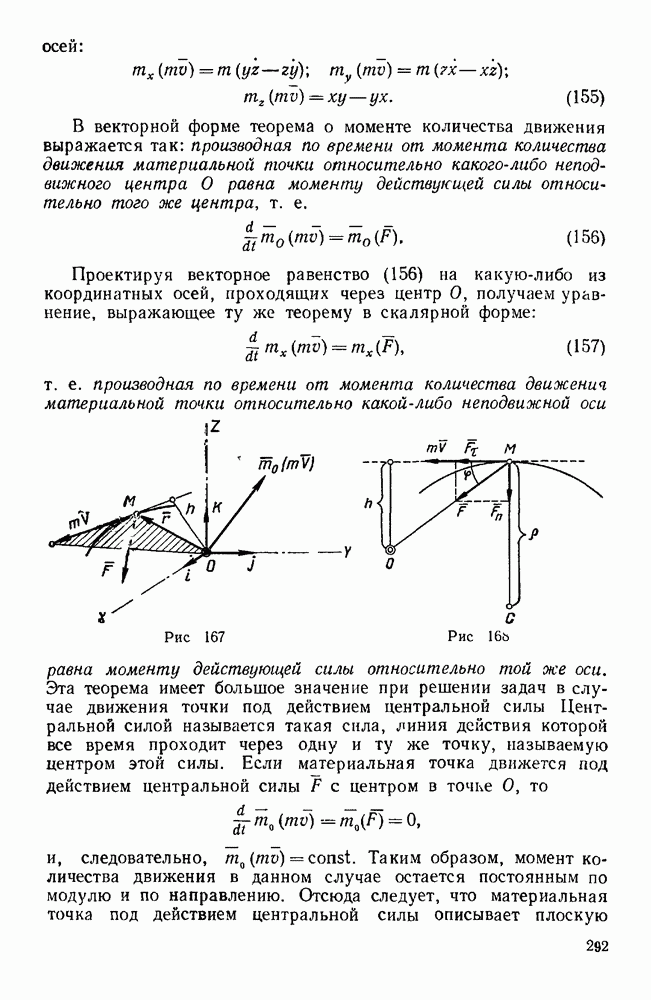
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
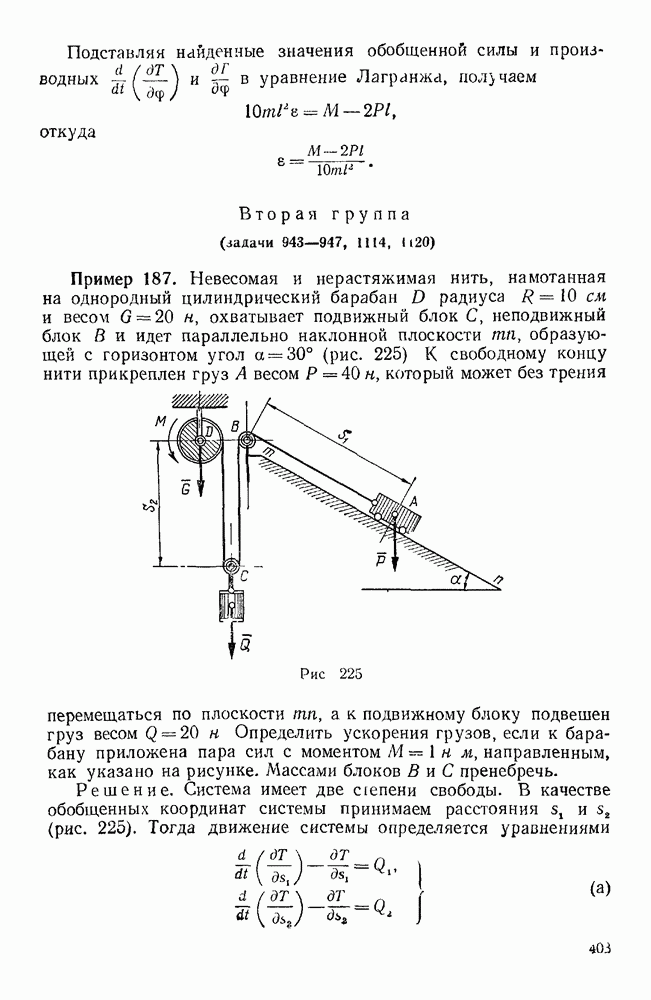
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА