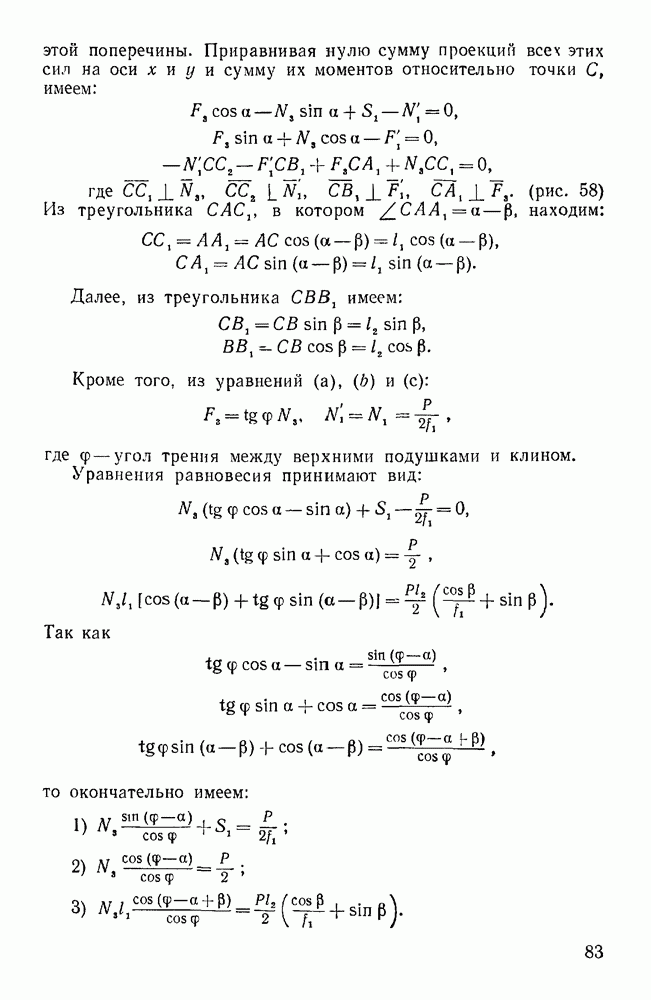| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
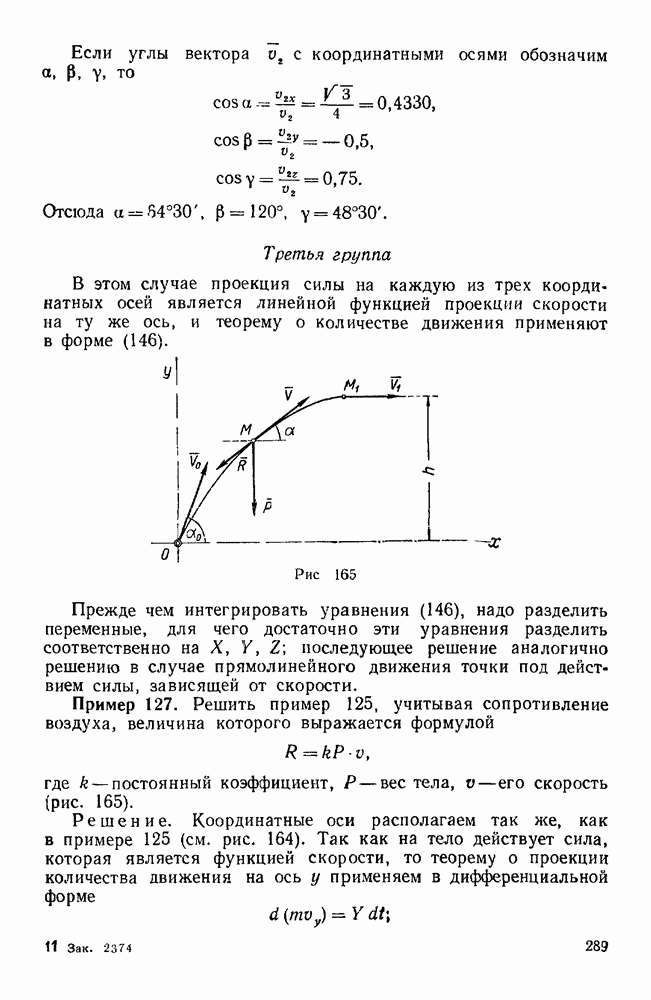
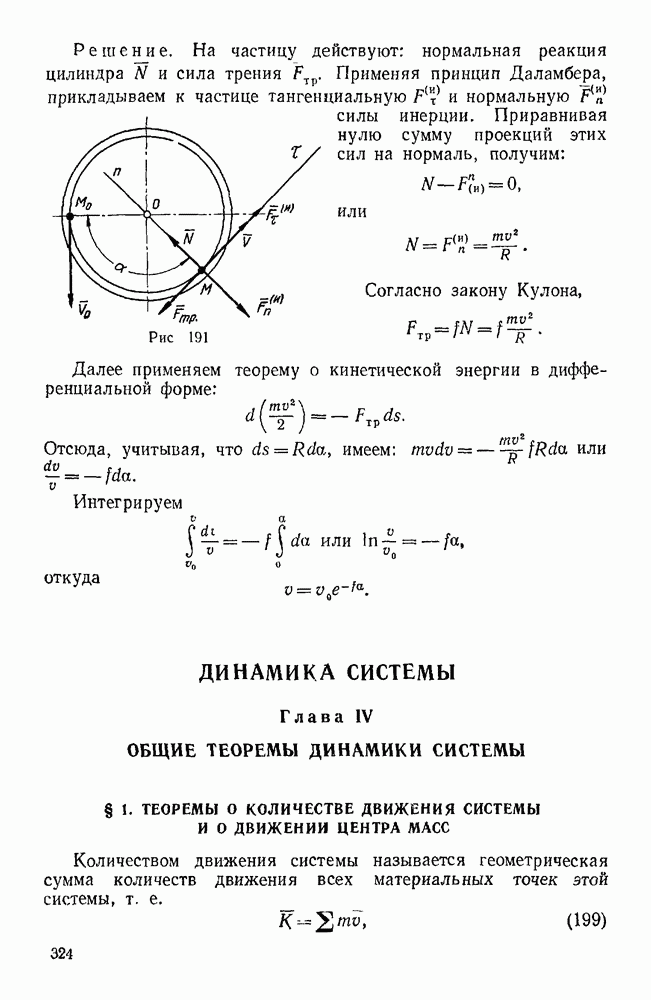
Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
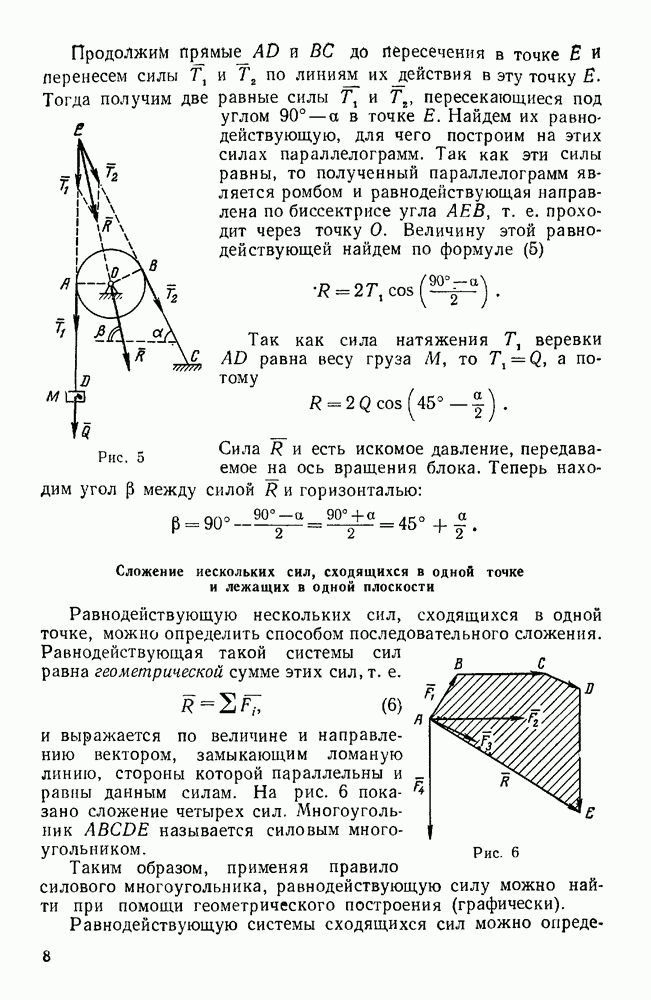
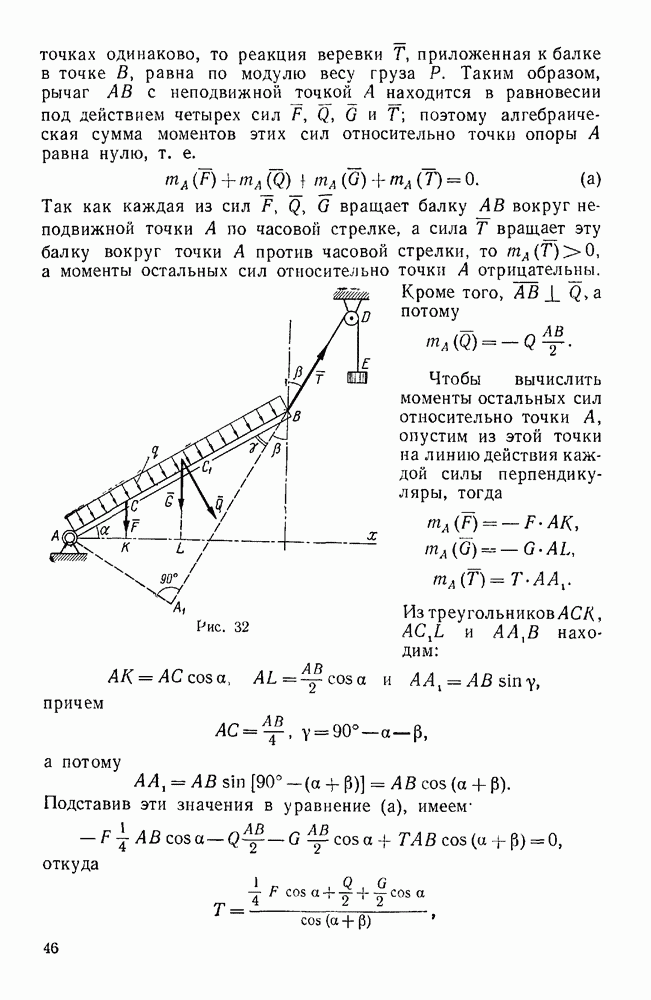
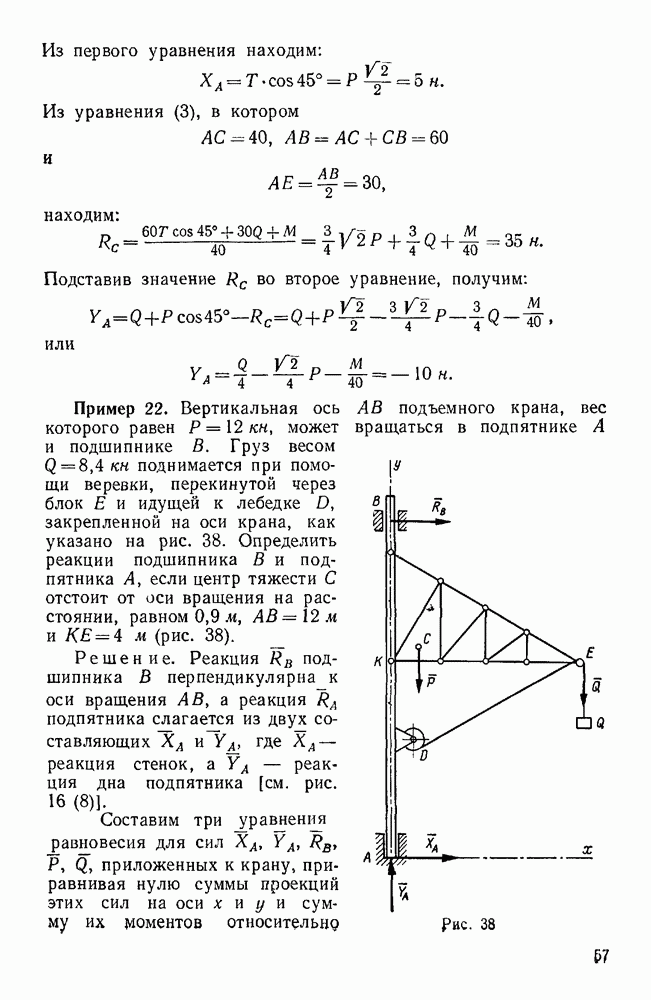
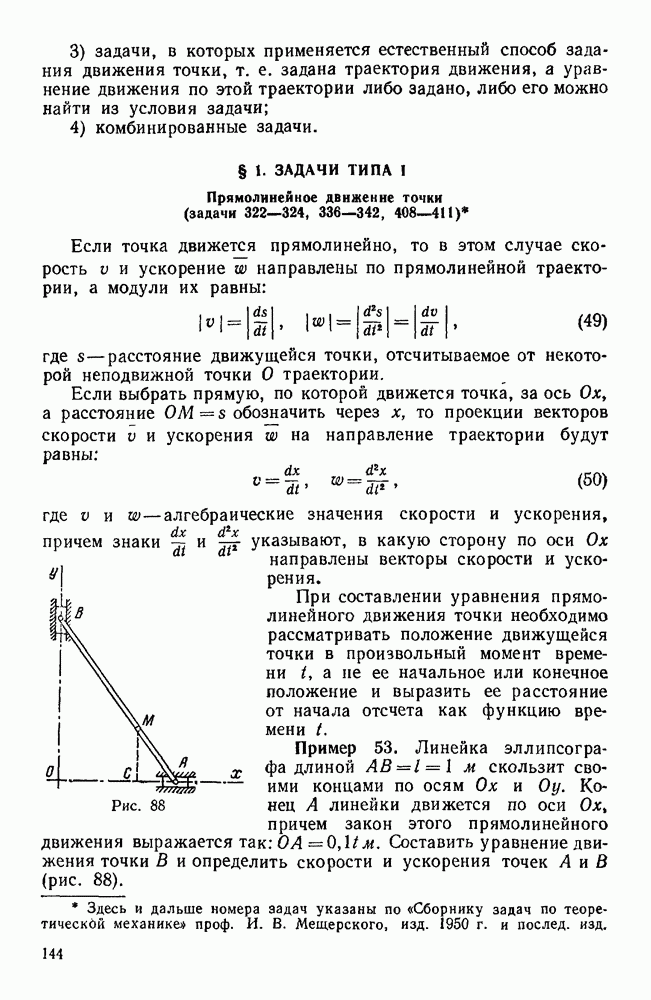
Пример 30. Два груза А и В, веса которых равны Р и Q, лежащие на наклонных плоскостях с углами  , связаны веревкой, перекинутой через блок О.
, связаны веревкой, перекинутой через блок О.
Найти отношение весов при равновесии, если угол трения грузов о плоскость равен  (рис. 54).
(рис. 54).
Решение. Найдем наибольшую величину отношения  , при которой еще возможно равновесие, предполагая, что дальнейшее увеличение этого отношения вызовет движение груза А по наклонной плоскости вниз, а, следовательно, груз В начнет двигаться вверх. В этом случае силы трения
, при которой еще возможно равновесие, предполагая, что дальнейшее увеличение этого отношения вызовет движение груза А по наклонной плоскости вниз, а, следовательно, груз В начнет двигаться вверх. В этом случае силы трения  , приложенные к грузам А и В, будут направлены вдоль соответствующих наклонных плоскостей, как указано на рисунке. Нормальные реакции наклонных плоскостей,
, приложенные к грузам А и В, будут направлены вдоль соответствующих наклонных плоскостей, как указано на рисунке. Нормальные реакции наклонных плоскостей,  к грузам, обозначим
к грузам, обозначим  и
и  . Рассмотрим равновесие груза А, к которому приложены силы
. Рассмотрим равновесие груза А, к которому приложены силы  , а также сила натяжения Т, веревки.
, а также сила натяжения Т, веревки.

Рис. 54.
Проектируя эти силы на направление АО и направление, перпендикулярное к АО, получим два уравнения равновесия:

Аналогично, рассматривая равновесие груза В, к которому приложены силы  , и сила
, и сила  натяжения веревки, и проектируя эти силы на направление ОВ и направление, перпендикулярное к ОВ, получим еще два уравнения равновесия:
натяжения веревки, и проектируя эти силы на направление ОВ и направление, перпендикулярное к ОВ, получим еще два уравнения равновесия:

Учитывая, что  , исключим эти две неизвестные силы, сложив первое уравнение с третьим.
, исключим эти две неизвестные силы, сложив первое уравнение с третьим.
Тогда получим:

Но

а

поэтому

С другой стороны, из первого равнения имеем:

Следовательно,

Разделив это уравнение на Q, получим:

Отсюда

и

Таким образом, мы нашли наибольшее значение отношения  , при котором еще возможно равновесие, т. е.
, при котором еще возможно равновесие, т. е.

Найдем теперь наименьшее значение отношения  , при котором существует равновесие, но так, что дальнейшее уменьшение этого отношения вызовет опускание груза В и поднятие груза А,
, при котором существует равновесие, но так, что дальнейшее уменьшение этого отношения вызовет опускание груза В и поднятие груза А,
В этом случае направления сил трения  будут противоположны направлениям этих сил в предыдущем случае.
будут противоположны направлениям этих сил в предыдущем случае.
Поэтому, чтобы получить наименьшее значение отношения  , достаточно в первом и третьем уравнениях равновесия изменить знаки при
, достаточно в первом и третьем уравнениях равновесия изменить знаки при  и на обратные, что равносильно изменению знака при
и на обратные, что равносильно изменению знака при  в четвертом уравнении.
в четвертом уравнении.
Следовательно, будем иметь:

Таким образом, равновесие данной системы возможно при условии:

Пример 31. Два клина А и В, коэффициент трения между которыми  , могут двигаться без трения в своих направляющих. К клину А приложена сила
, могут двигаться без трения в своих направляющих. К клину А приложена сила  .
.
Какую силу Q нужно приложить к клину В, чтобы клин А двигался равномерно в направлении действия силы  , если углы
, если углы  известны? Весом клиньев пренебречь (рис. 55).
известны? Весом клиньев пренебречь (рис. 55).
Решение. Обозначим реакцию направляющих, приложенную к клину  через
через  , а реакцию направляющих, приложенную к клину
, а реакцию направляющих, приложенную к клину  через
через  . Так как каждый клин может двигаться в своих направляющих без трения, то реакции
. Так как каждый клин может двигаться в своих направляющих без трения, то реакции  и
и  направлены по нормали к поверхности соответствующего клина
направлены по нормали к поверхности соответствующего клина

Рис. 55.
При равномерном движении клина А в направлении силы Р клин В будет скользить по клину А вверх а потому сила трения  , приложенная к клину
, приложенная к клину  будет направлена по прямой CD вниз, т. е. в сторону, противоположную перемещению клина В относительно клина А. По закону равенства действия и противодействия сила трения
будет направлена по прямой CD вниз, т. е. в сторону, противоположную перемещению клина В относительно клина А. По закону равенства действия и противодействия сила трения  клина В, приложенная к клину А, будет равна по величине и направлена противоположно силе трения
клина В, приложенная к клину А, будет равна по величине и направлена противоположно силе трения  , а нормальная реакция
, а нормальная реакция  клина А, приложенная к клину В, равна по величине и направлена противоположно нормальной реакции N, клина В, приложенной к клину А, т. е.
клина А, приложенная к клину В, равна по величине и направлена противоположно нормальной реакции N, клина В, приложенной к клину А, т. е.

Так как клин Л движется равномерно, то силы  приложенные к этому клину, уравновешиваются. При этом клин В будет также двигаться равномерно, и, следовательно, силы
приложенные к этому клину, уравновешиваются. При этом клин В будет также двигаться равномерно, и, следовательно, силы  , приложенные к этому клину, тоже уравновешиваются. Поэтому сумма проекций всех сил, приложенных к каждому клину, на направление движения этого клина равна нулю, т. е.
, приложенные к этому клину, тоже уравновешиваются. Поэтому сумма проекций всех сил, приложенных к каждому клину, на направление движения этого клина равна нулю, т. е.

Кроме того,

где  — коэффициент динамического трения. Подставив эти значения сил трения в первое и второе уравнения, будем иметь:
— коэффициент динамического трения. Подставив эти значения сил трения в первое и второе уравнения, будем иметь:

Но

поэтому

откуда

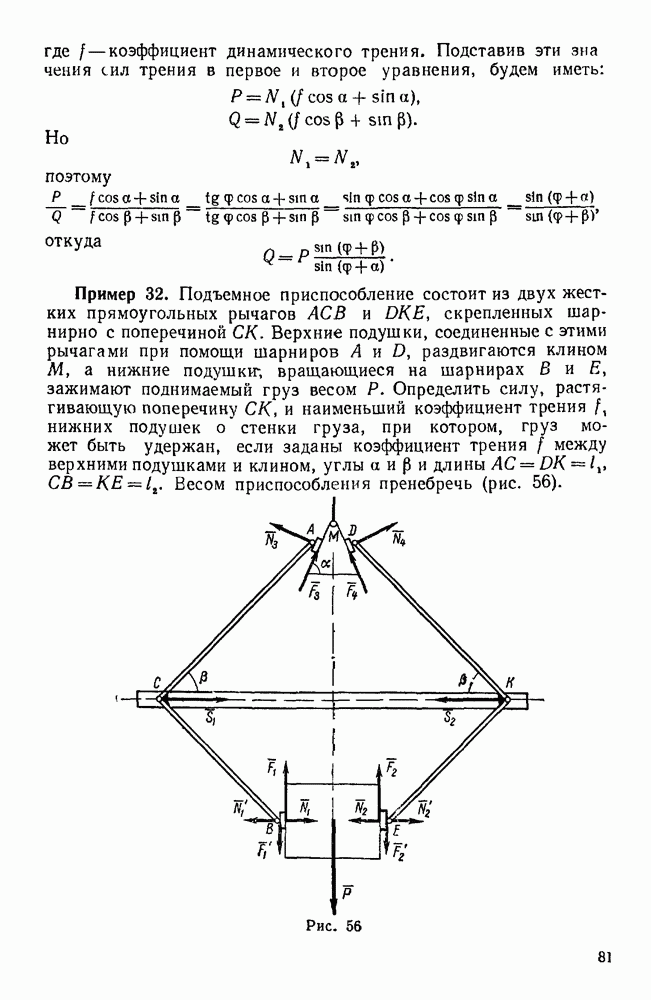
Пример 32. Подъемное приспособление состоит из двух жестких прямоугольных рычагов АСВ и DKE, скрепленных шарнирно с поперечиной СК. Верхние подушки, соединенные с этими рычагами при помощи шарниров А и D, раздвигаются клином М, а нижние подушки; вращающиеся на шарнирах В и Е, зажимают поднимаемый груз весом  . Определить силу, растягивающую поперечину
. Определить силу, растягивающую поперечину  и наименьший коэффициент трения
и наименьший коэффициент трения  , нижних подушек о стенки груза, при котором, груз может быть удержан, если заданы коэффициент трения f между верхними подушками и клином, углы
, нижних подушек о стенки груза, при котором, груз может быть удержан, если заданы коэффициент трения f между верхними подушками и клином, углы  и длины
и длины  . Весом приспособления пренебречь (рис. 56).
. Весом приспособления пренебречь (рис. 56).

Рис. 56.
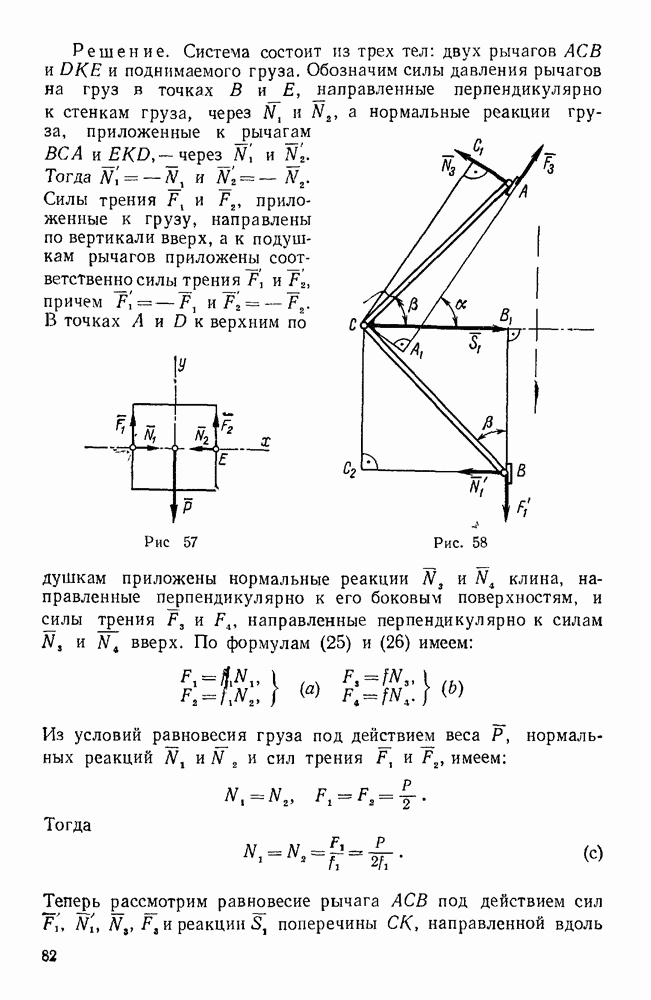
Решение. Система состоит из трех тел: двух рычагов АСВ и DKE и поднимаемого груза. Обозначим силы давления рычагов на груз в точках В и Е, направленные перпендикулярно к стенкам груза, через  и
и  , а нормальные реакции груза, приложенные к рычагам ВСА и EKD, — через
, а нормальные реакции груза, приложенные к рычагам ВСА и EKD, — через  .
.
Тогда  .
.

Рис. 57.
Силы трения F, и  , приложенные к грузу, направлены по вертикали вверх, а к подушкам рычагов приложены соответственно силы трения F, и
, приложенные к грузу, направлены по вертикали вверх, а к подушкам рычагов приложены соответственно силы трения F, и  причем
причем  .
.

Рис. 58.
В точках А и D к верхним подушкам приложены нормальные реакции  клина, направленные перпендикулярно к его боковым поверхностям, и силы трения
клина, направленные перпендикулярно к его боковым поверхностям, и силы трения  , направленные перпендикулярно к силам
, направленные перпендикулярно к силам  вверх. По формулам (25) и (26) имеем:
вверх. По формулам (25) и (26) имеем:

Из условий равновесия груза под действием веса  , нормальных реакций
, нормальных реакций  и
и  и сил трения F, и
и сил трения F, и  , имеем:
, имеем:

Тогда

Теперь рассмотрим равновесие рычага АСВ под действием сил  , и реакции
, и реакции  поперечины СК, направленной вдоль этой поперечины.
поперечины СК, направленной вдоль этой поперечины.
Приравнивая нулю сумму проекций всех этих сил на оси х и у и сумму их моментов относительно точки С, имеем:

где  (рис. 58). Из треугольника
(рис. 58). Из треугольника  , в котором
, в котором  , находим:
, находим:

Далее, из треугольника СВВ, имеем:

Кроме того, из уравнений (а),  и (с):
и (с):

где  — угол трения между верхними подушками и клином. Уравнения равновесия принимают вид:
— угол трения между верхними подушками и клином. Уравнения равновесия принимают вид:

Так как

то окончательно имеем:

Из уравнения (2) находим:

Подставив найденное значение  в уравнения 1 и 3, находим из этих уравнений
в уравнения 1 и 3, находим из этих уравнений  :
:

откуда

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
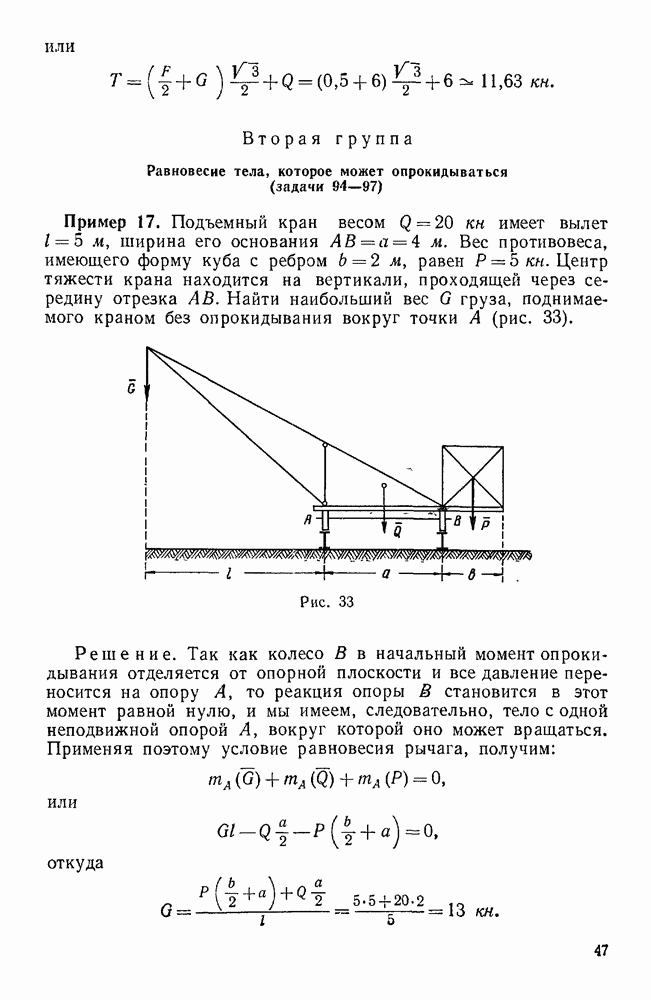
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
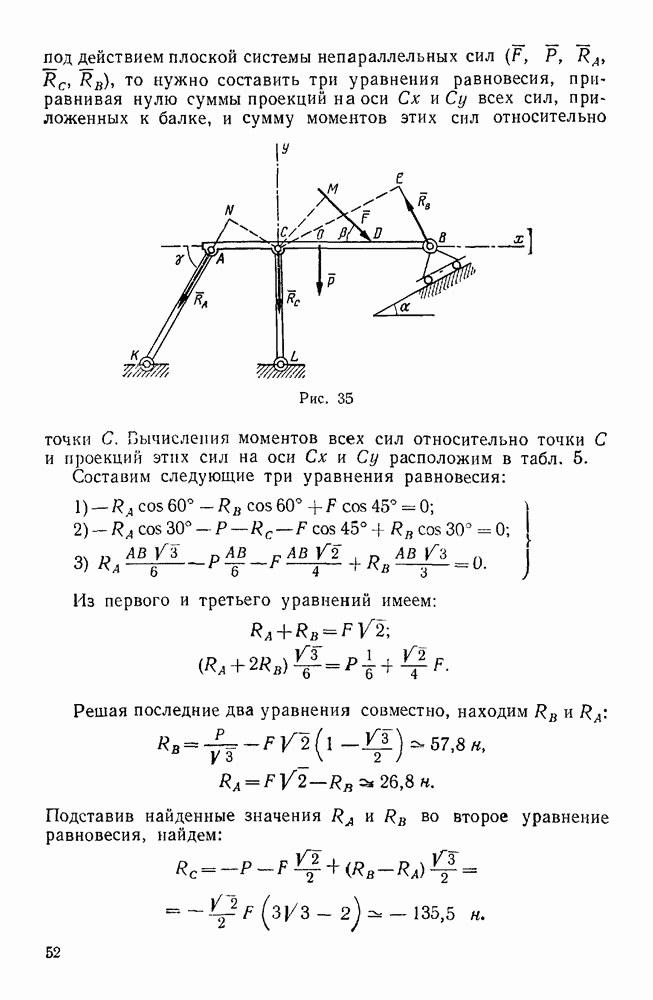
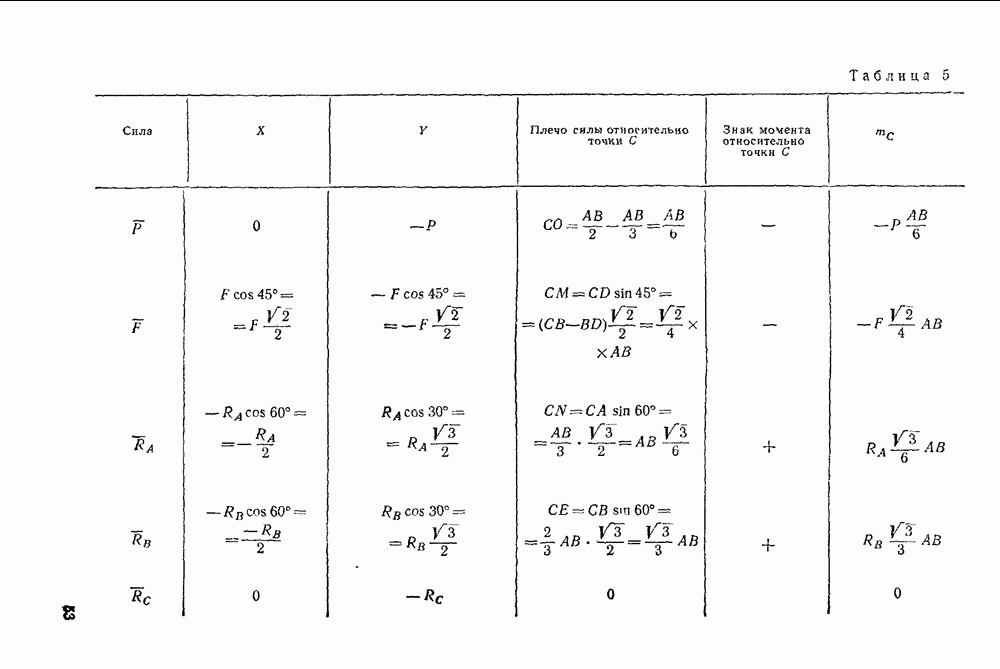
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
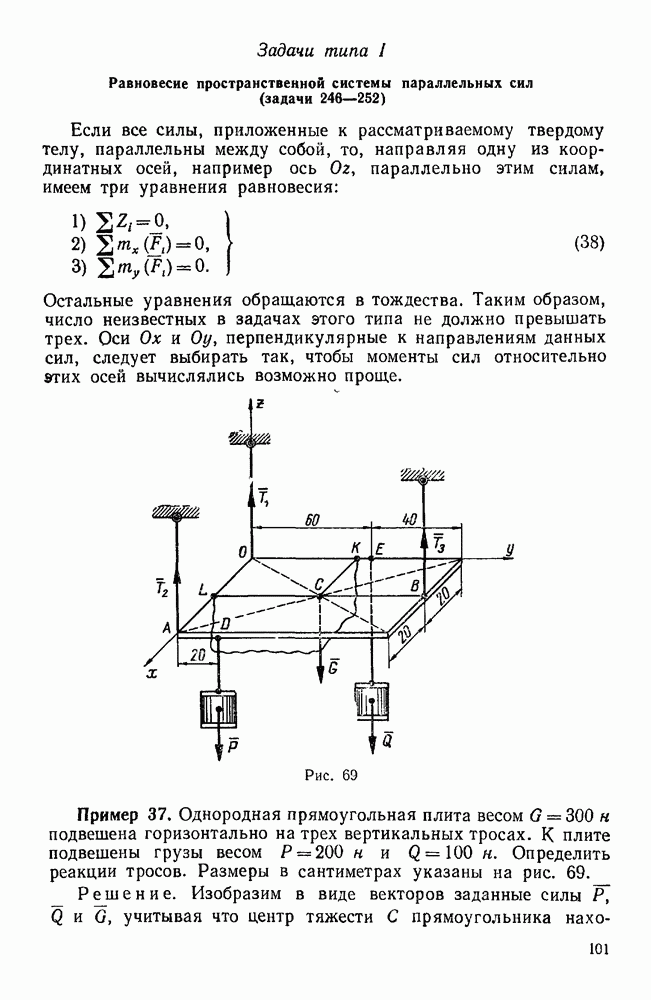
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
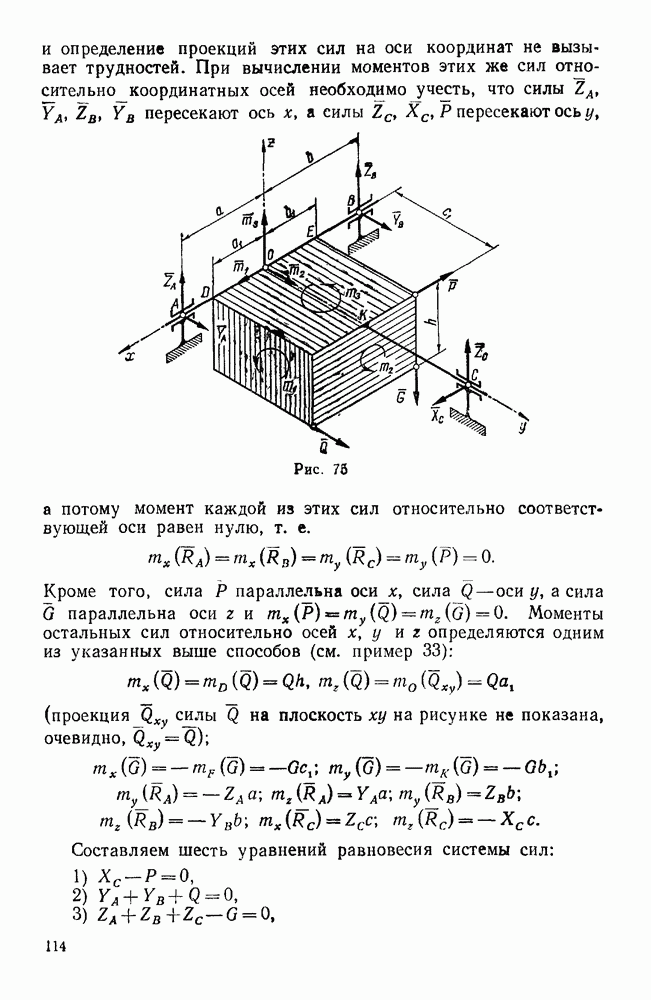
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
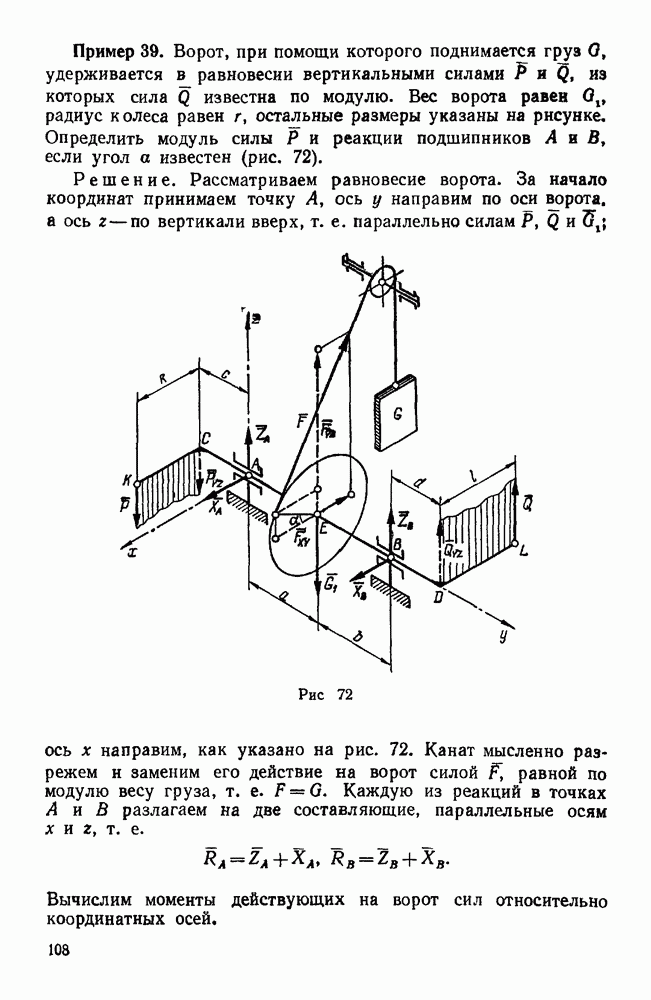
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
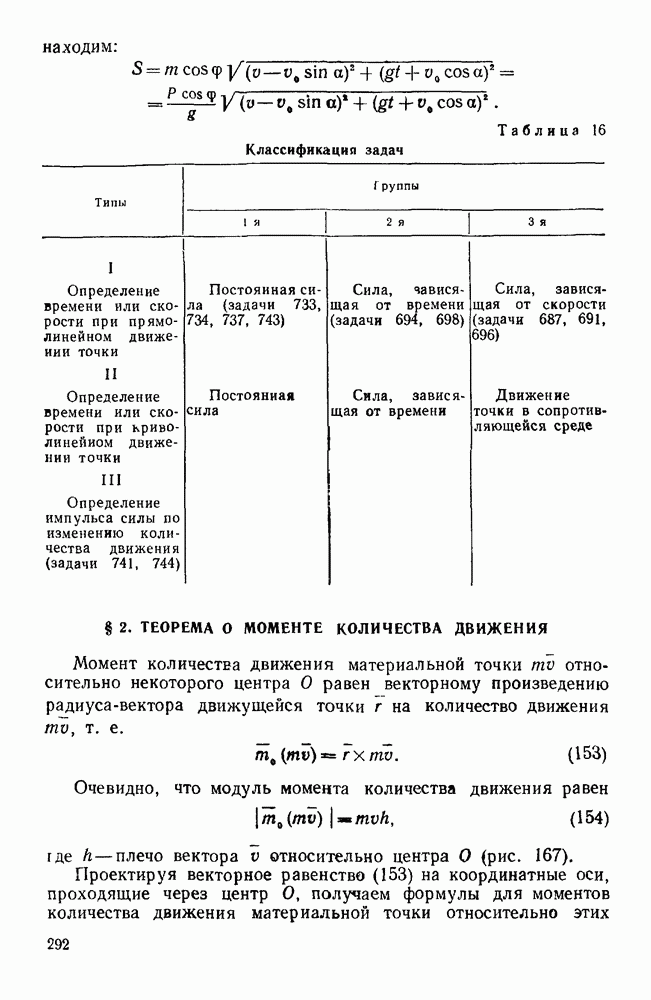
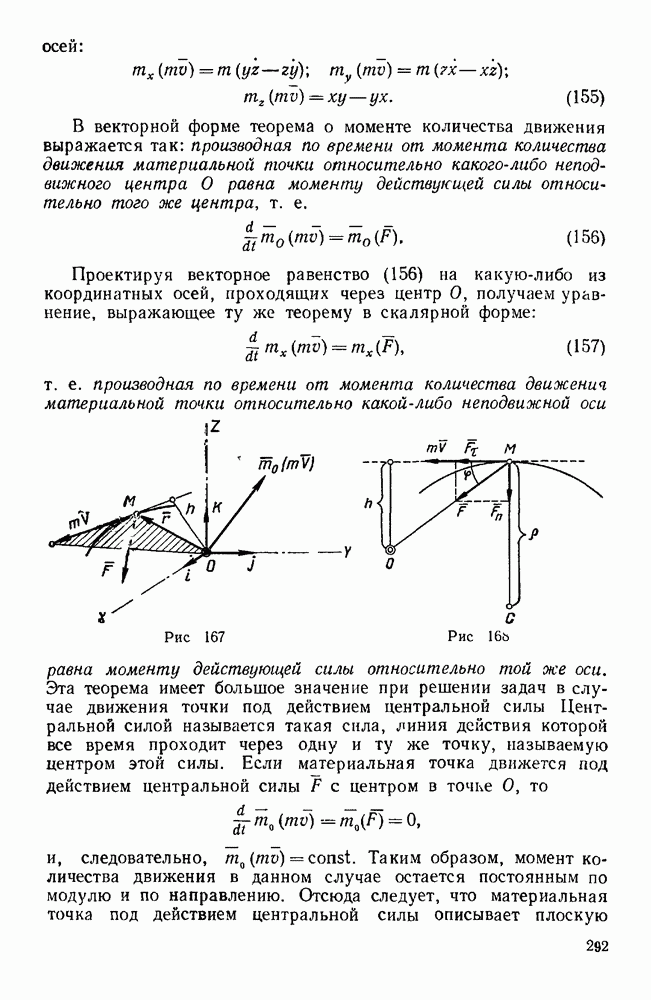
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
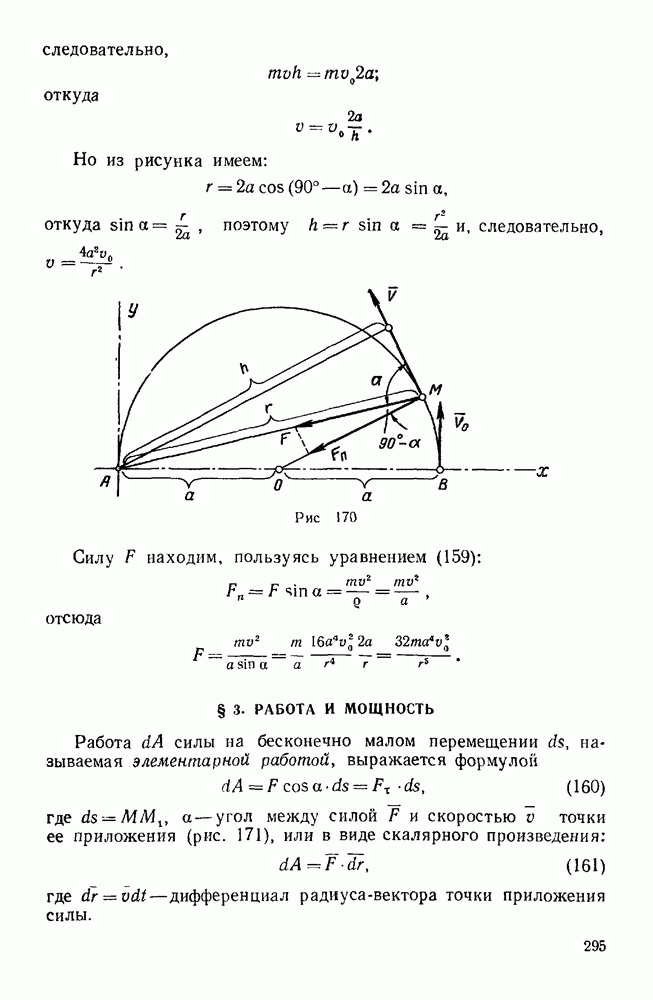
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
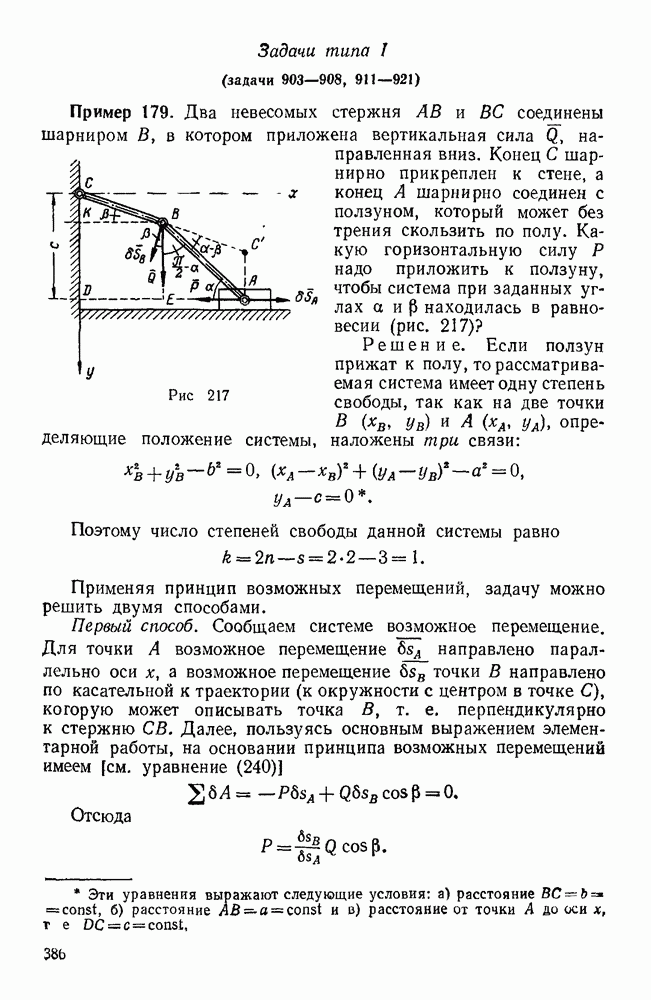
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
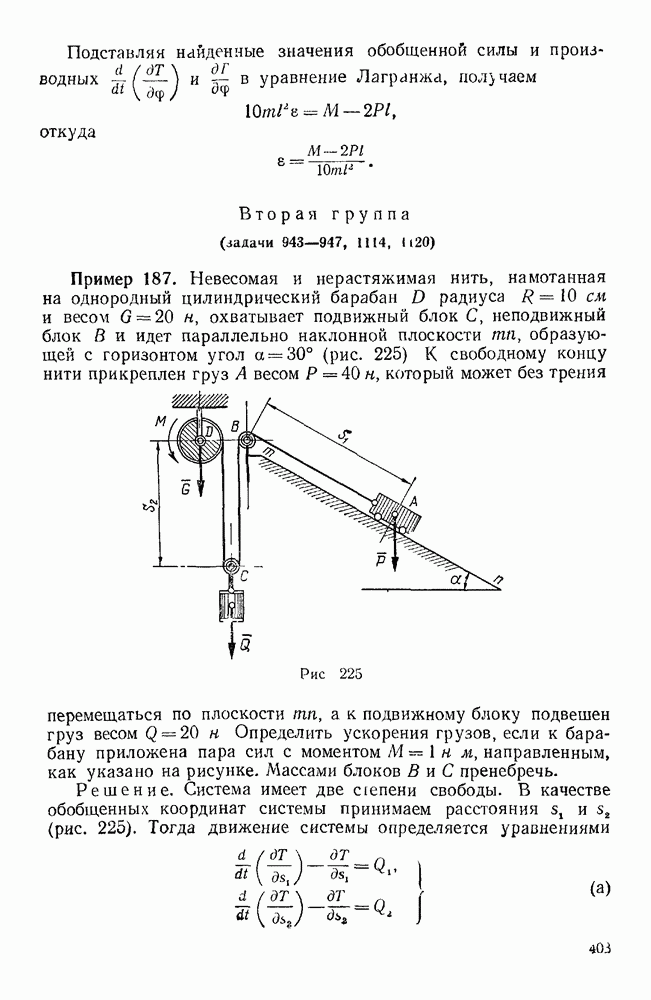
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА