| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
Эта задача заключается в том, что по заданному движению и известной массе материальной точки требуется определить силу, действующую на эту точку, или, если на материальную точку действует несколько сил, определить одну из них.
Решение этой задачи сводится к определению ускорения точки, которое в том случае, когда движение точки задано, нетрудно найти по правилам кинематики.
Задачи этого параграфа можно разделить на следующих два основных типа в зависимости от траектории движущейся точки:
I. Задачи, относящиеся к прямолинейному движению точки.
II. Задачи, относящиеся к криволинейному движению точки.
Задачи типа I
Задачи этого типа, в которых рассматривается прямолинейное движение точки, решаются при помощи уравнения (111); их можно разделить на две группы.
Первая группа
Задачи, в которых к движущейся материальной точке приложена одна сила. Необходимо определить эту силу.
Пример 98. Материальная точка массой  совершает гармонические колебания по горизонтальной оси
совершает гармонические колебания по горизонтальной оси  по закону
по закону  ( х выражено в см,
( х выражено в см,  сек). Найти силу, действующую на точку в функции от
сек). Найти силу, действующую на точку в функции от  .
.
Решение. Находим проекцию ускорения точки на ось  :
:

Далее находим проекцию на ось действующей силы:

Но  , а потому
, а потому  .
.
Так как проекция силы на ось  и координата
и координата  движущейся точки противоположны по знаку, то искомая сила направлена вдоль оси
движущейся точки противоположны по знаку, то искомая сила направлена вдоль оси  к началу координат О.
к началу координат О.
По модулю эта сила равна  , т. е. пропорциональна расстоянию от движущейся точки до начала О.
, т. е. пропорциональна расстоянию от движущейся точки до начала О.
Вторая группа
Ко второй группе относятся задачи, в которых к движущейся материальной точке приложено несколько сил, причем требуется найти одну из них.
К этой группе следует отнести такие задачи, в которых требуется определить неизвестную реакцию связи, что характерно для движения несвободной материальной точки.
Пример 99. Клеть весом  поднимается с помощью каната, навернутого на барабан радиуса R, вращающийся вокруг неподвижной горизонтальной оси по закону:
поднимается с помощью каната, навернутого на барабан радиуса R, вращающийся вокруг неподвижной горизонтальной оси по закону:

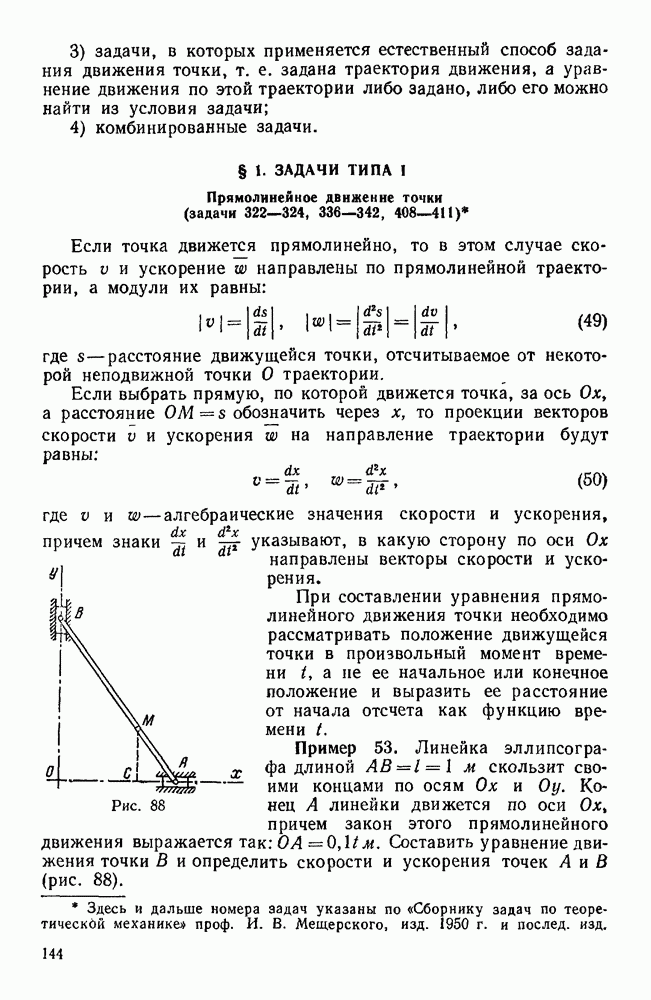
Определить натяжение каната как функцию высоты подъема h (рис. 139).
Решение. При повороте барабана на угол  клеть поднимается на высоту
клеть поднимается на высоту  . Силу натяжения каната обозначим через Т. На клеть действуют две силы: натяжение каната Т и вес клети
. Силу натяжения каната обозначим через Т. На клеть действуют две силы: натяжение каната Т и вес клети  , причем
, причем  , так как ускорение клети направлено вверх. Равнодействующая этих сил
, так как ускорение клети направлено вверх. Равнодействующая этих сил  . Применяя формулу (108), получим:
. Применяя формулу (108), получим:

откуда

Ускорение w клети найдем по формуле

или

Следовательно,

Задача типа II
Задачи этого типа, в которых рассматривается криволинейное движение материальной точки, можно также разделить на две группы, как и задачи первого типа.
Первая группа
Задачи, в которых к движущейся материальной точке приложена одна сила; требуется определить эту силу.
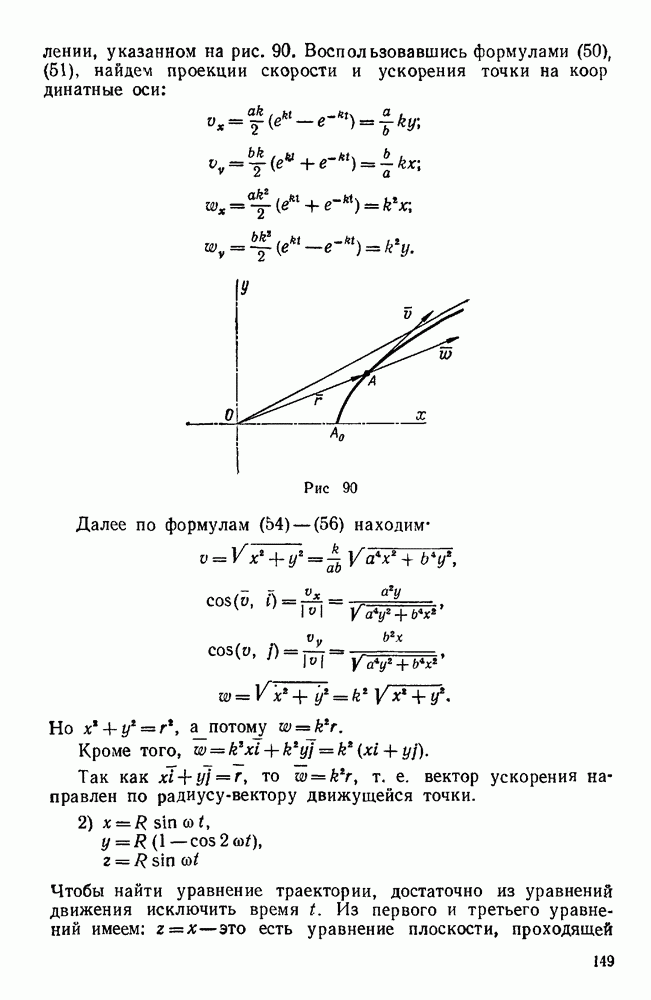
Если движение точки задано уравнениями в декартовых координатах:

где х, у, z — координаты точки; t — время, то на основании уравнений (110) находим проекции искомой силы на три координатные оси:


Рис. 139.
Затем нужно найти модуль действующей силы F и ее исправляющие косинусы по формулам:

Пример 100. Материальная точка массой  кг совершает движение согласно уравнениям:
кг совершает движение согласно уравнениям:

причем координаты точки выражены в метрах, время — в секундах. Определить величину и направление силы, действующей на точку, в момент  сек.
сек.
Решение. 1. Находим проекции скорости данной точки на оси координат:

2. Находим проекции ускорения точки на оси координат:

3. На основании уравнений (114) находим проекции силы на оси координат:

4. По формулам (115) и (116) находим модуль силы и направляющие косинусы:

откуда

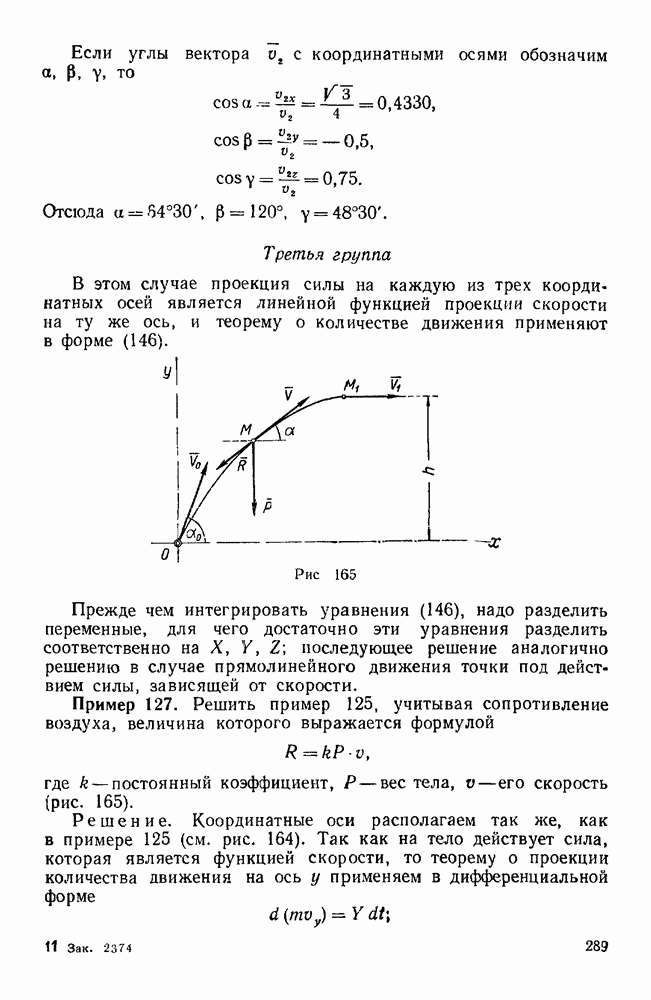
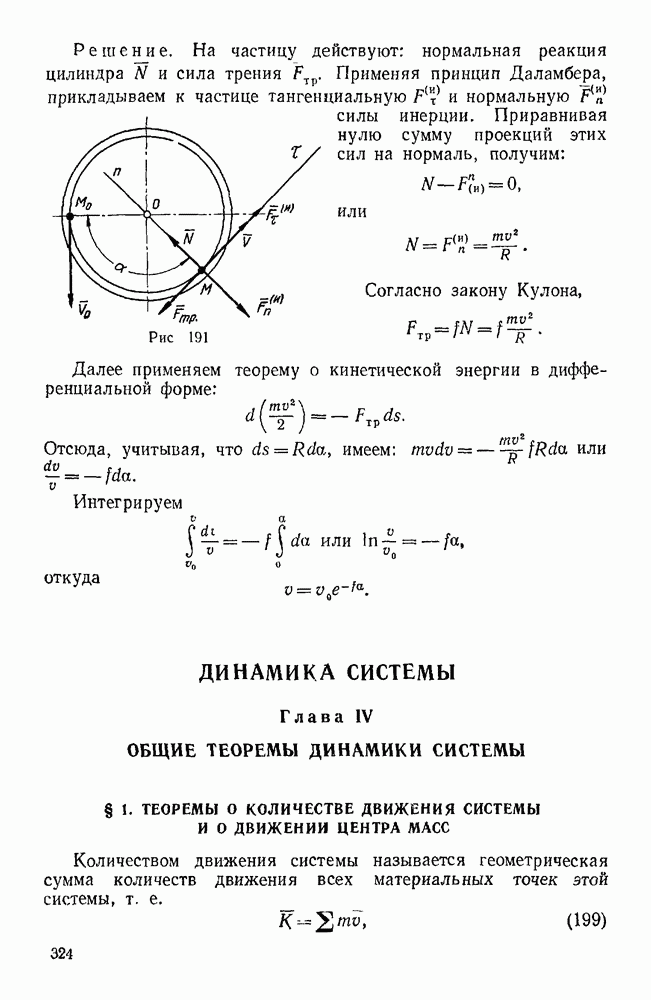
Если же движение точки задано естественным способом, т. е. задана траектория точки и закон ее движения по этой траектории s — то следует, воспользовавшись уравнениями (112), найти проекции искомой силы F на естественные оси, а затем по этим проекциям вычислить ее модуль.
Пример 101. Материальная точка массой  кг описывает криволинейную траекторию по закону
кг описывает криволинейную траекторию по закону  выражено в
выражено в  ,
,
— в сек). В данный момент она занимает положение М и имеет скорость  , причем радиус кривизны траектории в точке М равен
, причем радиус кривизны траектории в точке М равен  . Найти в этот момент силу, действующую на эту материальную точку.
. Найти в этот момент силу, действующую на эту материальную точку.
Решение. Находим скорость точки и проекции ее ускорения на касательную и главную нормаль траектории:

Согласно условию, в данный момент t имеем  поэтому
поэтому  , откуда
, откуда  или
или  .
.
Следовательно, в этот момент

Теперь на основании уравнений (112) находим проекции искомой силы на касательную и главную нормали:

Отсюда искомая сила

Вторая группа
Задачи, в которых к движущейся материальной точке приложено несколько сил и одну из них требуется найти.
В этой группе, так же как и в задачах второй группы типа 1, часто встречаются такие задачи, где требуется определить неизвестную реакцию связи при движении несвободной материальной точки.
Пример 102. Центробежный регулятор состоит из двух шаров А и В весом  каждый, муфты С весом Q и четырех одинаковых невесомых стержней
каждый, муфты С весом Q и четырех одинаковых невесомых стержней  , закрепленных по концам шарнирно. Регулятор вращается вокруг неподвижной вертикальной оси
, закрепленных по концам шарнирно. Регулятор вращается вокруг неподвижной вертикальной оси  .
.
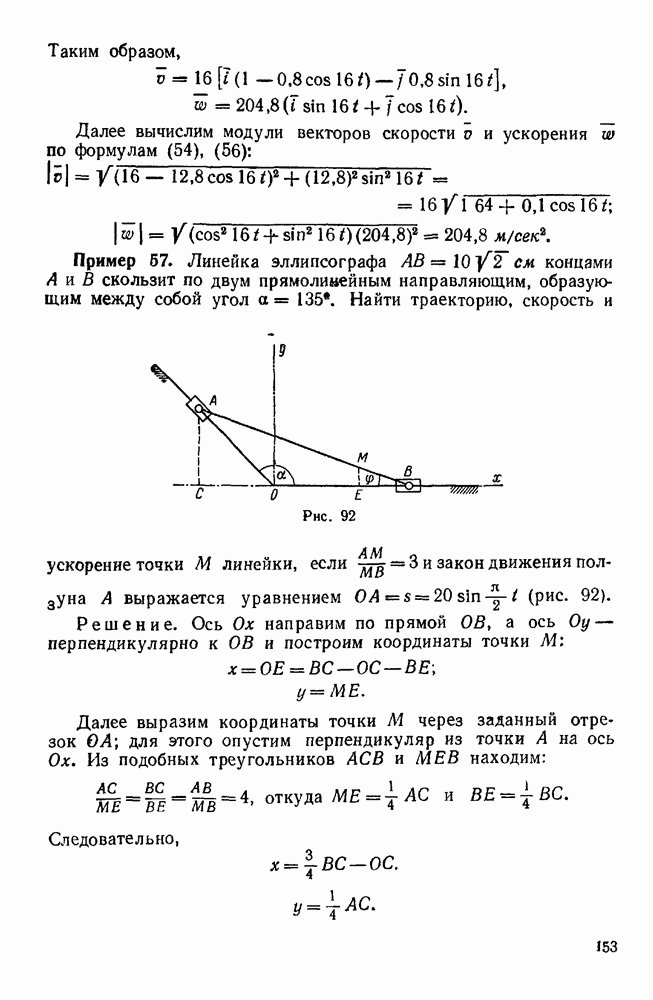
Определить усилия в стержнях и угловую скорость регулятора, предполагая, что угол  , образуемый каждым из стержней с вертикалью, имеет заданное постоянное значение
, образуемый каждым из стержней с вертикалью, имеет заданное постоянное значение  (рис. 140).
(рис. 140).

Рис. 140.
Решение. Рассмотрим движение шара А, принимая его за материальную точку, которая описывает окружность, расположенную в горизонтальной плоскости, с центром в точке О, и радиусом, равным R.
К этому шару приложены три силы: вес  и реакции
и реакции  и
и  стержней AD и АС, направленные вдоль этих стержней и равные искомым усилиям. Применяя уравнения движения материальной точки в естественной форме, т. е. уравнения (112), и проектируя все силы, приложенные к шару А, на естественные оси
стержней AD и АС, направленные вдоль этих стержней и равные искомым усилиям. Применяя уравнения движения материальной точки в естественной форме, т. е. уравнения (112), и проектируя все силы, приложенные к шару А, на естественные оси  , показанные
, показанные  рис. 140, имеем:
рис. 140, имеем:

 , или, учитывая, что
, или, учитывая, что  , получим:
, получим:

Следовательно,

Аналогичным соотношением удовлетворяют действующие на шар  реакции S, и
реакции S, и  стержней BD и СВ, причем, очевидно,
стержней BD и СВ, причем, очевидно,  . Рассмотрим теперь муфту С, к которой приложены вес Q и реакции
. Рассмотрим теперь муфту С, к которой приложены вес Q и реакции  стержней С А и СВ, равные по модулю и противоположные по направлению силам
стержней С А и СВ, равные по модулю и противоположные по направлению силам  . Так как при
. Так как при  муфта С по оси z не перемещается, то сумма проекций всех приложенных сил на ось z равна нулю, т. е.
муфта С по оси z не перемещается, то сумма проекций всех приложенных сил на ось z равна нулю, т. е.

Таким образом, мы получили следующие три уравнения для определения неизвестных  :
:

Решая эти уравнения, находим:

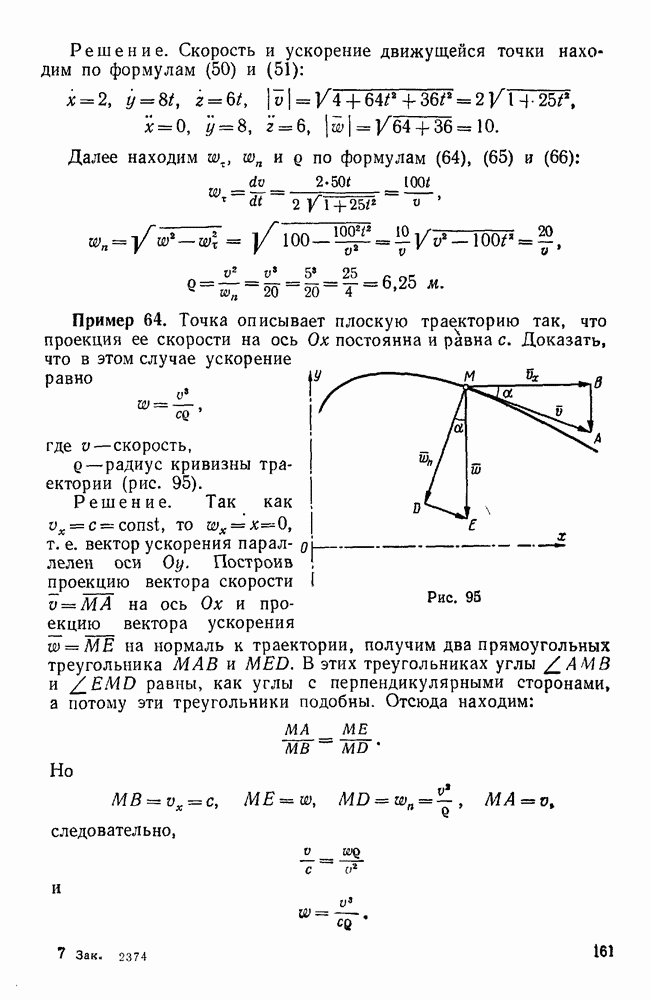
Пример 103. Материальная точка массы  движется в плоскости
движется в плоскости  в сопротивляющейся среде под действием силы притяжения к центру О, равной
в сопротивляющейся среде под действием силы притяжения к центру О, равной  , где
, где  ,
,  — радиус-вектор этой точки. Найти силу сопротивления среды
— радиус-вектор этой точки. Найти силу сопротивления среды  как функцию скорости, если известны уравнения движения точки:
как функцию скорости, если известны уравнения движения точки:

причем

Решение. 1. Находим проекции скорости и ускорения движущейся точки на ось  :
:

так

то

На основании уравнений (96) имеем:

но

а потому

или

откуда

Аналогично находим  . Следовательно, искомая сила
. Следовательно, искомая сила  , т. e. сила сопротивления среды, пропорциональна скорости точки и направлена противоположно этой скорости.
, т. e. сила сопротивления среды, пропорциональна скорости точки и направлена противоположно этой скорости.
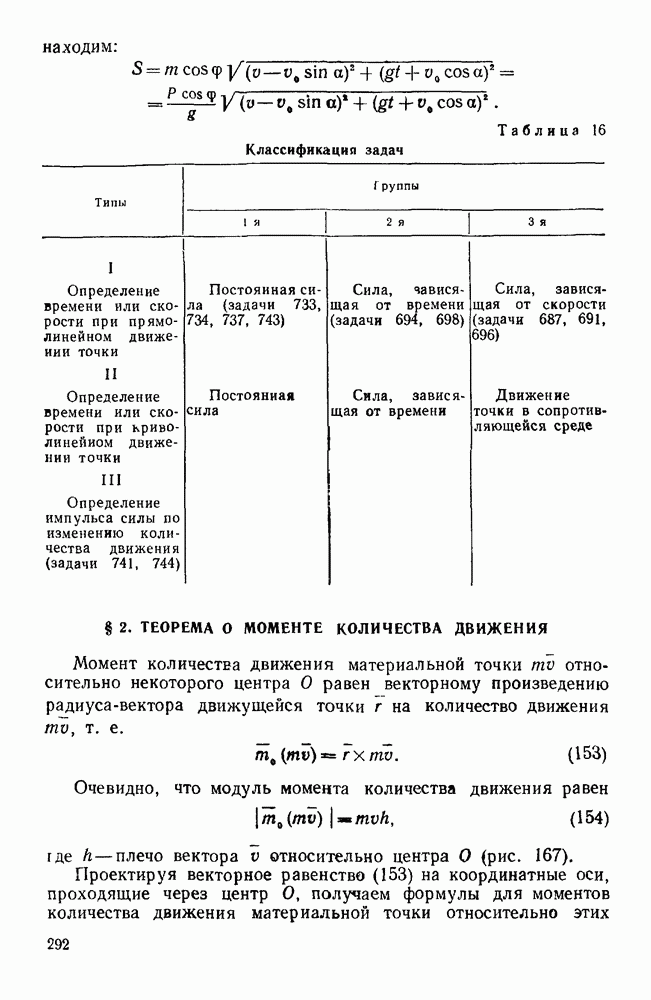
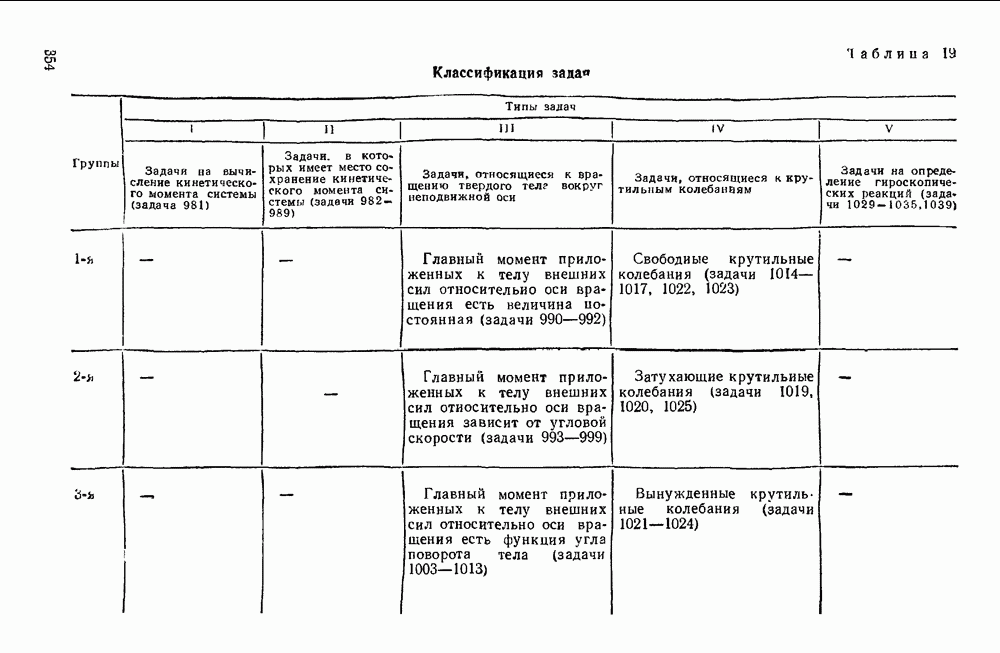
Таблица 14. Классификация задач

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
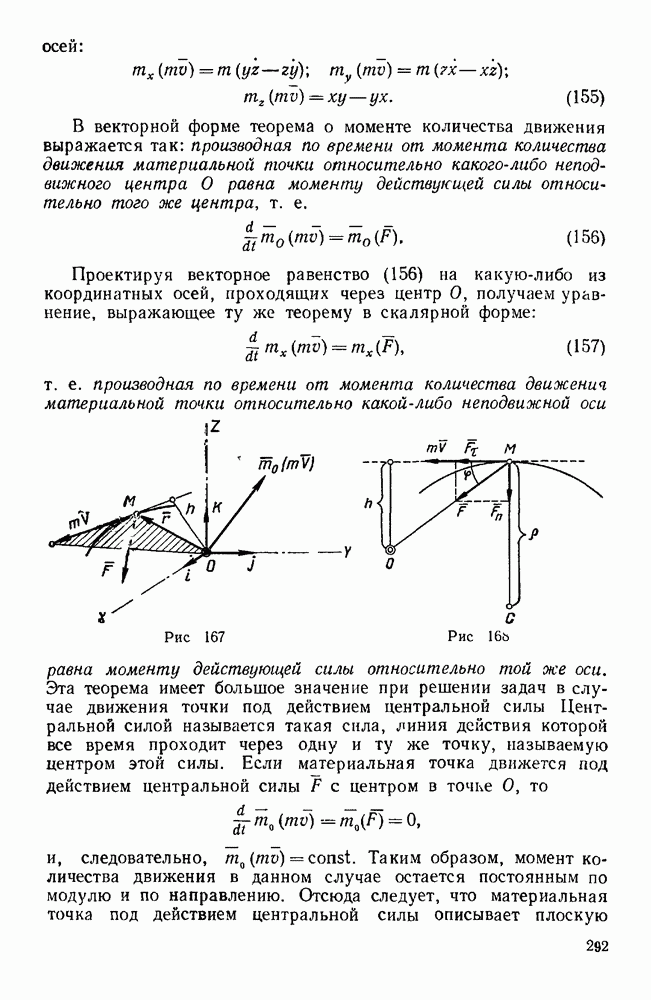
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
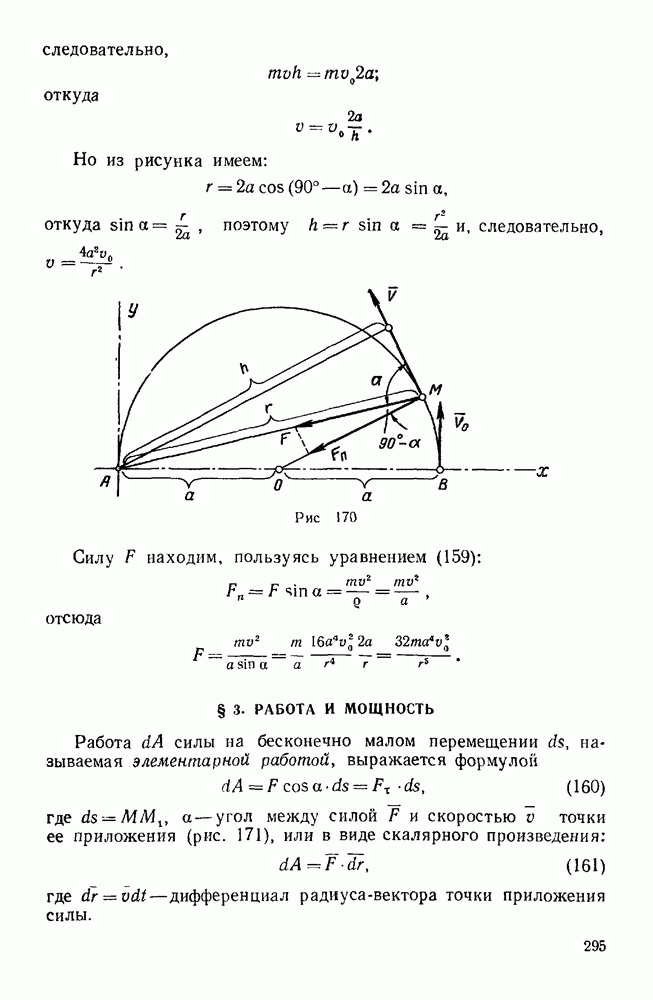
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
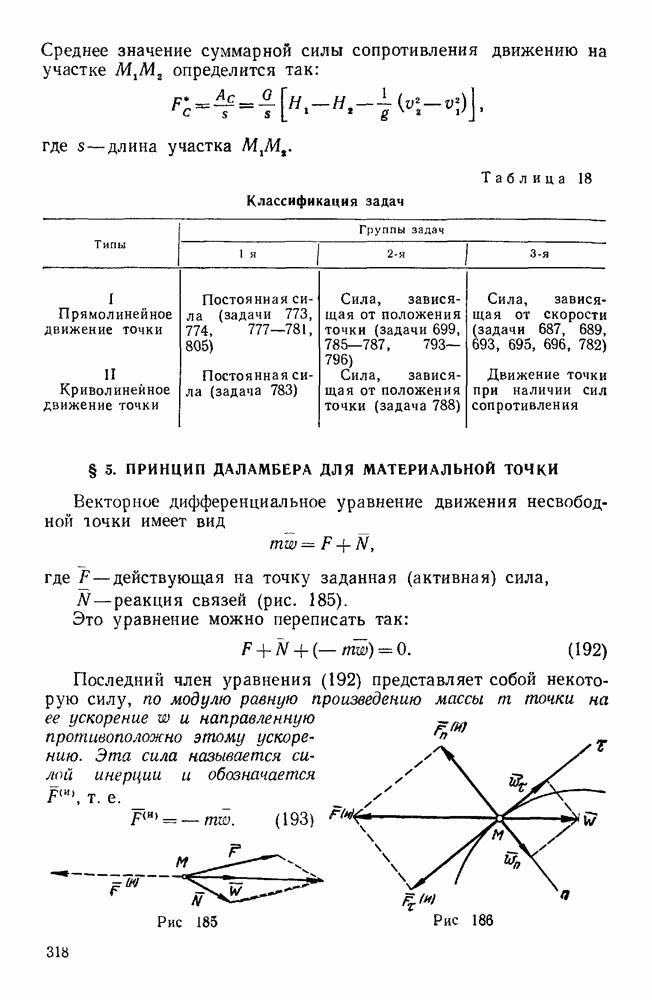
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
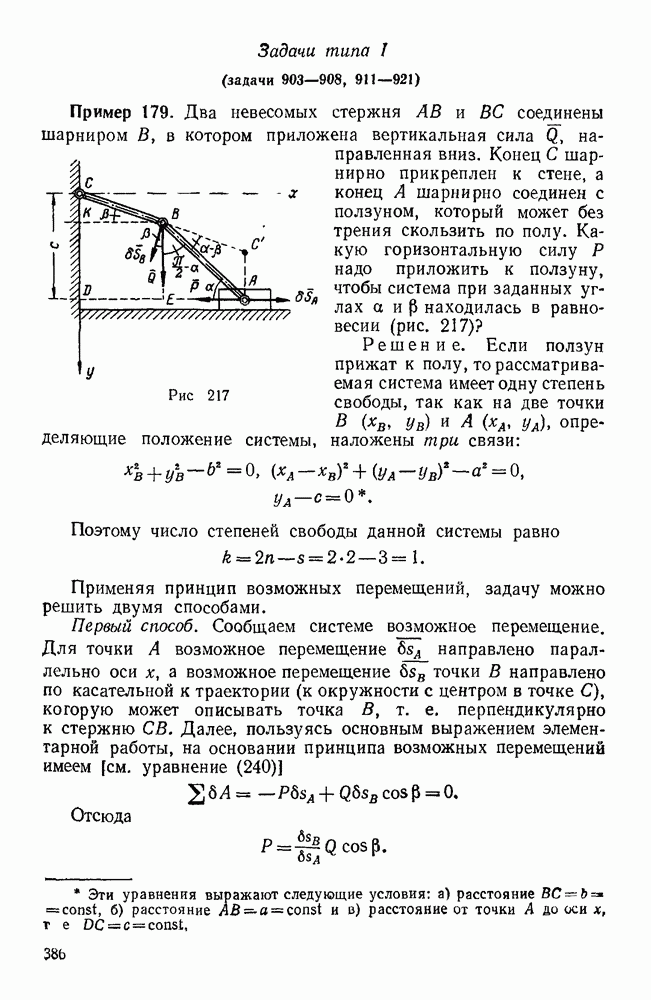
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
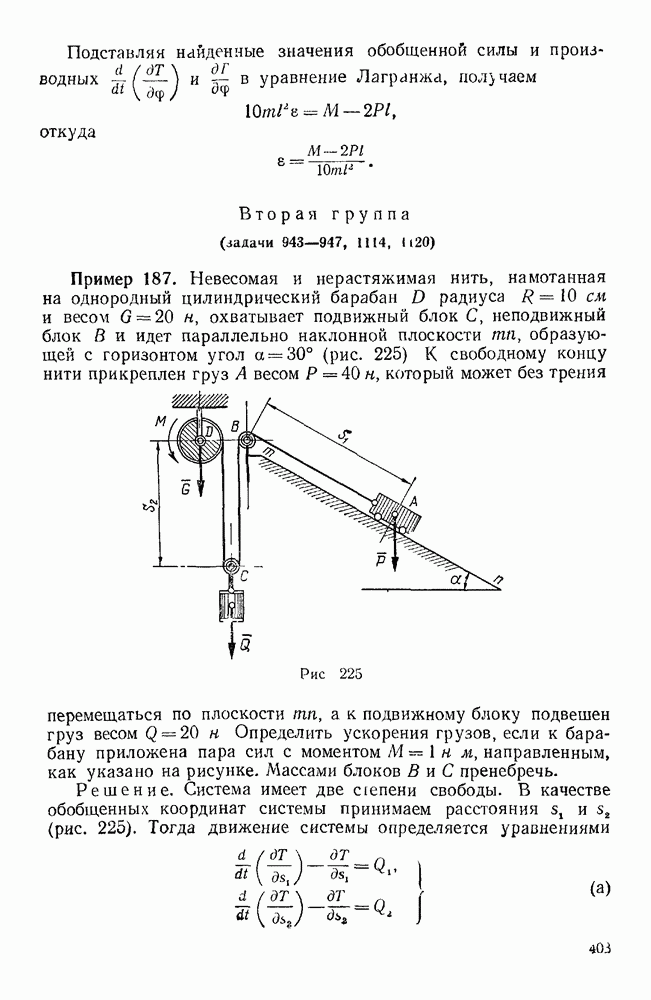
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА