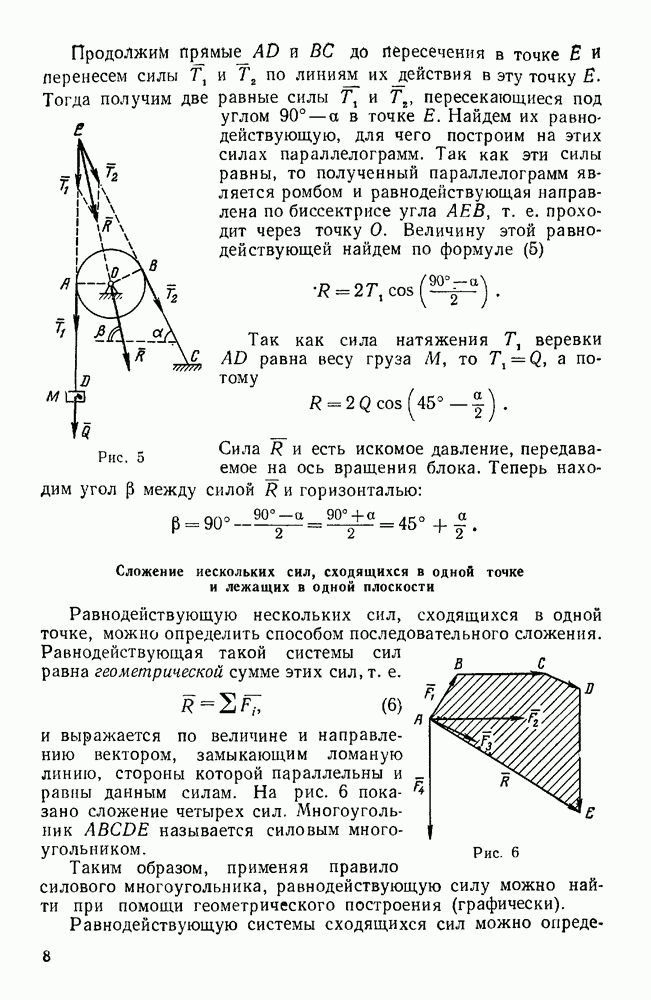
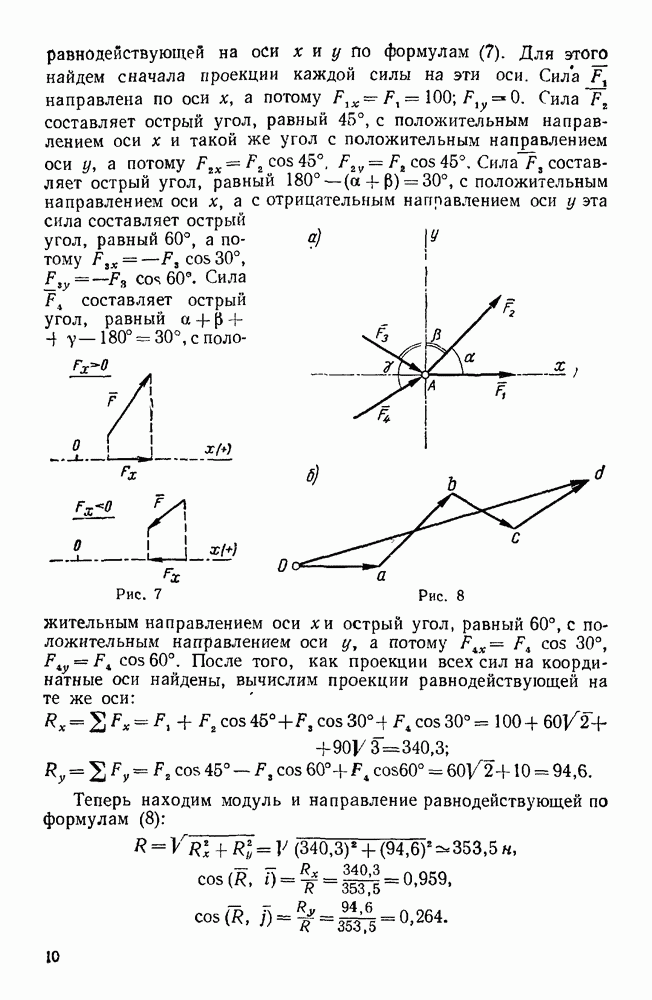
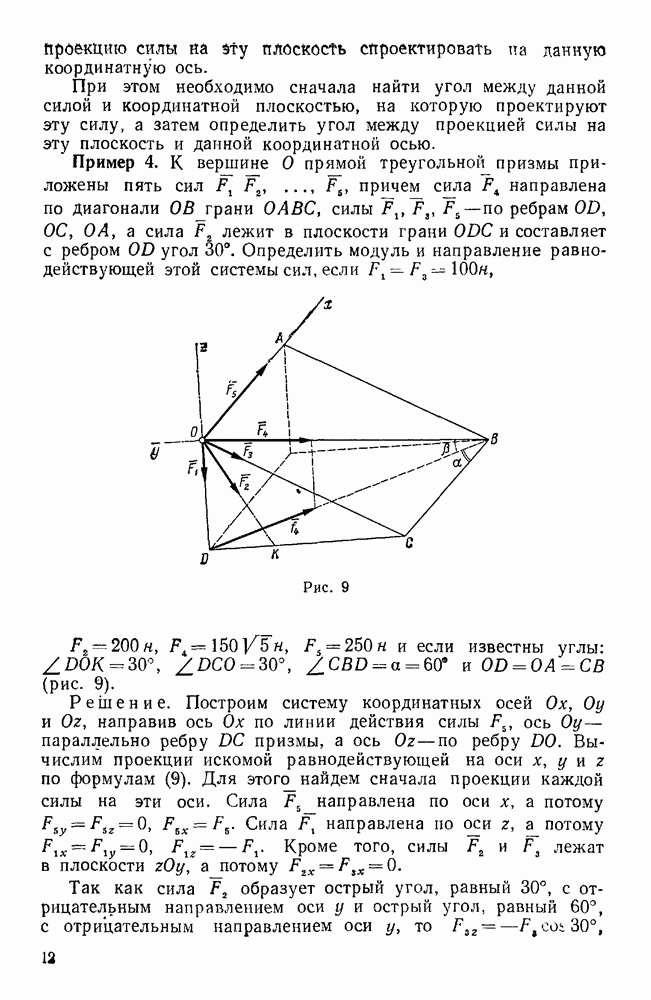
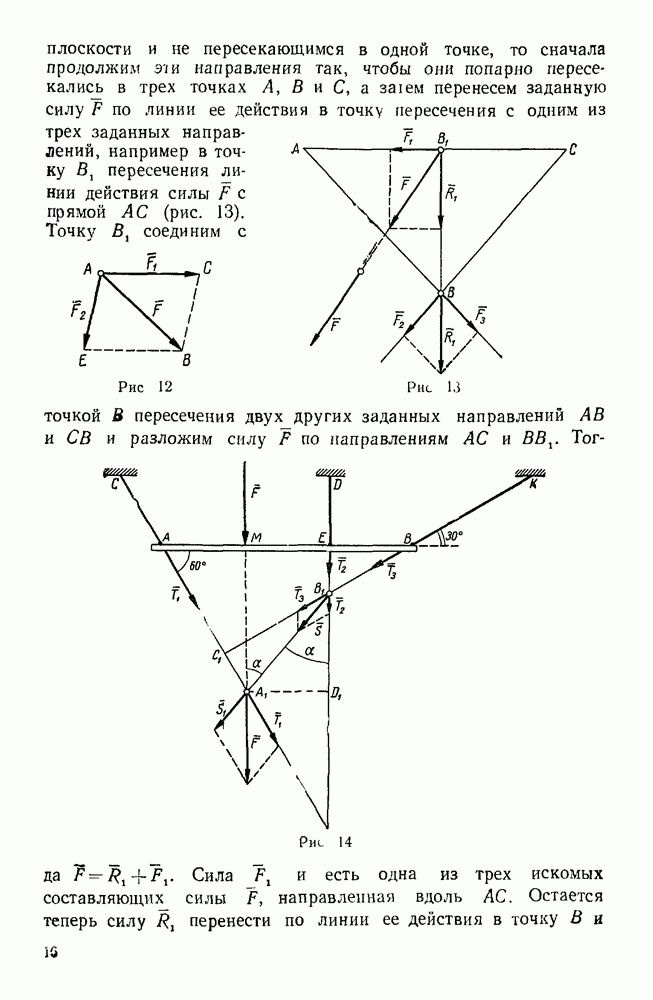
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. РАБОТА И МОЩНОСТЬ
Работа  силы на бесконечно малом перемещении
силы на бесконечно малом перемещении  , называемая элементарной работой, выражается формулой
, называемая элементарной работой, выражается формулой

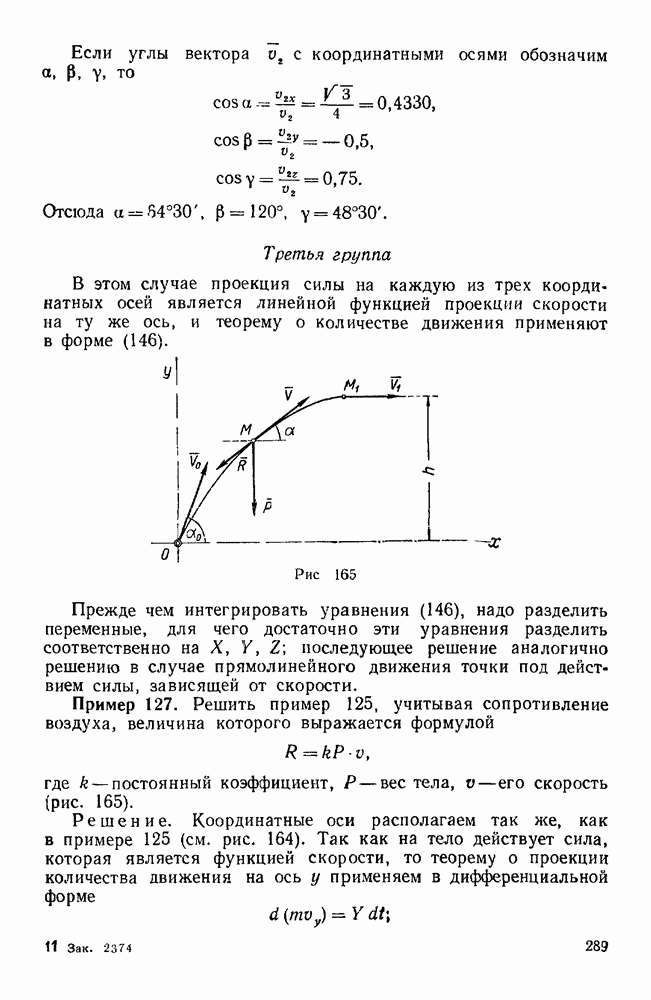
где  — угол между силой F и скоростью v точки ее приложения (рис. 171), или в виде скалярного произведения:
— угол между силой F и скоростью v точки ее приложения (рис. 171), или в виде скалярного произведения:

где  — дифференциал радиуса-вектора точки приложения силы.
— дифференциал радиуса-вектора точки приложения силы.
Выражая это скалярное произведение через проекции векторов F и  на координатные оси, получаем аналитическое выражение элементарной работы:
на координатные оси, получаем аналитическое выражение элементарной работы:

где X, Y, Z — проекции силы на координатные оси,  - бесконечно малые изменения (дифференциалы) координат точки приложения силы при элементарном перемещении этой точки.
- бесконечно малые изменения (дифференциалы) координат точки приложения силы при элементарном перемещении этой точки.

Рис. 171.
Если сила F приложена к твердому телу, вращающемуся вокруг неподвижной оси z, то

где  — элементарный угол поворота тела вокруг оси.
— элементарный угол поворота тела вокруг оси.
Если к телу, имеющему неподвижную ось вращения  приложена пара сил с моментом
приложена пара сил с моментом  , то элементарная работа этой пары выражается следующим образом:
, то элементарная работа этой пары выражается следующим образом:

где  — проекция вектора — момента пары на ось
— проекция вектора — момента пары на ось  .
.
Особый интерес представляет случай, когда сила является функцией координат точки и, кроме того,

В этом случае существует такая функция координат  , частные производные которой по координатам равны проекциям силы на соответствующие координатные оси, т. е.
, частные производные которой по координатам равны проекциям силы на соответствующие координатные оси, т. е.

Такая функция называется силовой, или потенциальной, функцией. Таким образом, если существует силовая функция, то

т. е. элементарная работа силы равна полному дифференциалу силовой функции. Ограниченная или неограниченная часть пространства, где проявляется действие силы, имеющей силовую функцию, называется силовым потенциальным полем.
Геометрическое место точек силового потенциального поля, в которых силовая функция сохраняет постоянное значение, называется эквипотенциальной поверхностью, или поверхностью уровня.
Работа А силы F на конечном пути определяется как предел суммы элементарных работ и выражается в виде криволинейного интеграла, взятого вдоль дуги  траектории от точки
траектории от точки  до точки М:
до точки М:
 (167)
(167)
Если произведение  а выражается известной функцией дуговой координаты s точки приложения силы, то переменной интегрирования является эта величина s и формула для вычисления работы принимает вид
а выражается известной функцией дуговой координаты s точки приложения силы, то переменной интегрирования является эта величина s и формула для вычисления работы принимает вид
 (168)
(168)
где  — значения дуговой координаты, соответствующие положениям
— значения дуговой координаты, соответствующие положениям  и М точки приложения силы,
и М точки приложения силы,  — проекция силы на касательную к траектории этой точки.
— проекция силы на касательную к траектории этой точки.
Если постоянная по модулю сила образует с прямой, по которой движется ее точка приложения, постоянный угол  , то
, то

В частном случае, когда точка М движется по прямой под действием постоянной силы F, направленной по той же прямой в сторону движения или против движения, то соответственно имеем:

где  - путь пройденный точкой.
- путь пройденный точкой.
Если при вращательном движении твердого тела вокруг неподвижной оси момент приложенной к нему силы является функцией угла  поворота тела, т. е.
поворота тела, т. е.

то

Аналогично определяется работа пары сил:

Работа силы, имеющей потенциальную функцию, на конечном перемещении выражается разностью значений этой функции в конечной и начальной точках пути:

т. е. в этом случае работа силы не зависит от кривой, по которой перемещается точка М, а зависит лишь от начального и конечного ее положений. При изучении движения материальной точки в силовом потенциальном поле весьма большое значение имеет понятие потенциальной энергии. Потенциальная энергия материальной точки представляет собой особый вид энергии, которым обладает точка, находящаяся в силовом потенциальном поле. Потенциальная энергия П равна работе, которую совершила бы сила поля при перемещении точки ее приложения из данного положения М(х, у, z) в положение  , принятое за нулевое, т. е.
, принятое за нулевое, т. е.

откуда

Работа силы на конечном пути через потенциальную энергию выражается так:

Если на точку действует несколько сил, то работа равнодействующей этих сил на каком-либо пути равна сумме работ составляющих сил на том же пути.
В технической системе единиц работа измеряется в килограмм-метрах  . В Международной системе единиц единицей работы является 1 джоуль
. В Международной системе единиц единицей работы является 1 джоуль  .
.
Мощность N характеризует быстроту, с которой совершается работа, и в общем случае определяется как производная от работы по времени:
 (177)
(177)
т. е. мощность равна скалярному произведению вектора силы на вектор скорости.
Если работа А производится равномерно, то мощность определяется так:

где  - время, в течение которого произведена работа.
- время, в течение которого произведена работа.
Таким образом, в этом частном случае мощность численно равна работе, производимой в единицу времени.
При вращательном движении твердого тела вокруг неподвижной оси  :
:

где  — главный момент приложенных к телу сил относительно оси вращения,
— главный момент приложенных к телу сил относительно оси вращения,  — угловая скорость тела.
— угловая скорость тела.
В технической системе единиц мощность измеряется в  или в лошадиных силах, причем
или в лошадиных силах, причем

В Международной системе единиц единицей мощности является

При решении задач на вычисление работы и мощности часто используют коэффициент полезного действия. Коэффициентом полезного действия  называется отношение полезной работы или мощности к работе или мощности движущих сил:
называется отношение полезной работы или мощности к работе или мощности движущих сил:

Так как вследствие вредных сопротивлений  , то
, то  .
.
При вычислении работы нужно различать следующие случаи.
1. Прямолинейное движение под действием постоянной по модулю и направлению силы, в задачах такого типа применяются формулы (169) и (170) (задачи 756, 762).
2. Прямолинейное движение под действием силы, проекция которой на направление прямолинейной траектории является функцией расстояния точки от некоторого неподвижного центра на этой прямой (задача № 768), в задачах этого типа применяется формула (167), которая, если направить ось  по траектории точки, принимает вид
по траектории точки, принимает вид

3. Криволинейное движение под действием постоянной по модулю и направлению силы, в этом случав можно использовать формулу (167).
4. Криволинейное движение под действием силы, которая является функцией координат точки приложения силы.
Здесь определение работы сводится к вычислению криволинейного интеграла по формуле (167). Если в рассматриваемом случае существует силовая функция, то работу определяют по формуле (173) или (176).
5. Вращательное движение твердого тела под действием постоянного момента или момента, являющегося функцией угла поворота тела; в этом случае для вычисления работы применяется формула (171).
Для вычисления мощности в зависимости от характера движения пользуемся формулой (177) при прямолинейном или криволинейном движении точки приложения силы (задачи 760, 764), или формулой (179) — в случае вращательного движения твердого тела (задачи 771, 772, 765). Среднюю мощность можно определять по формуле (178).
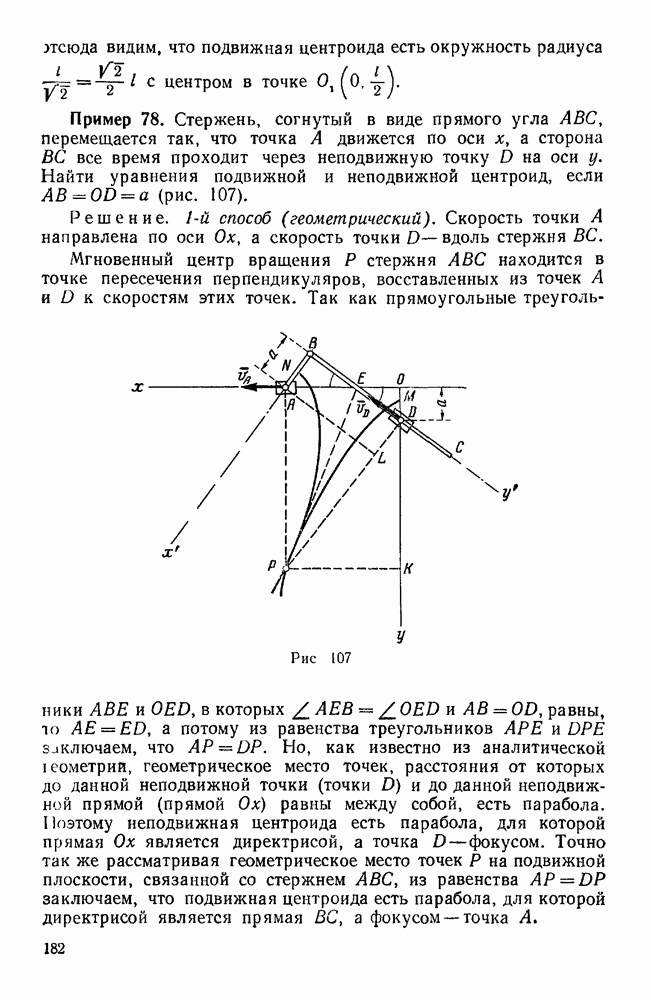
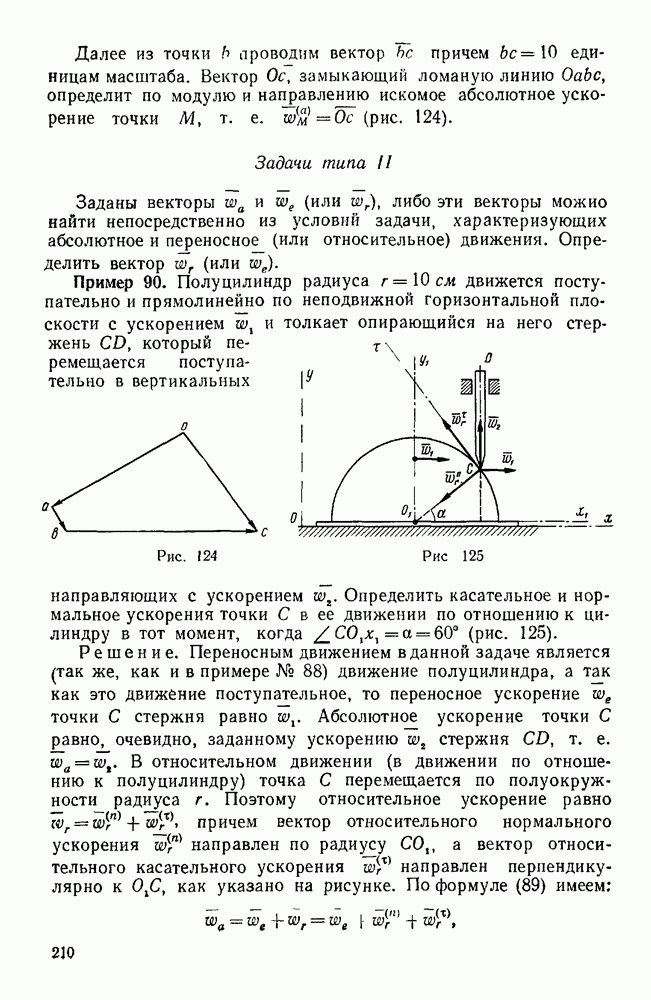
Пример 131. Вдоль тяги, при помощи которой тянут вагончик по горизонтальному пути, действует постоянная сила  (рис. 172). Тяга образует с горизонтом угол
(рис. 172). Тяга образует с горизонтом угол  . Определить работу, совершенную силой F на пути
. Определить работу, совершенную силой F на пути  .
.

Рис. 172.
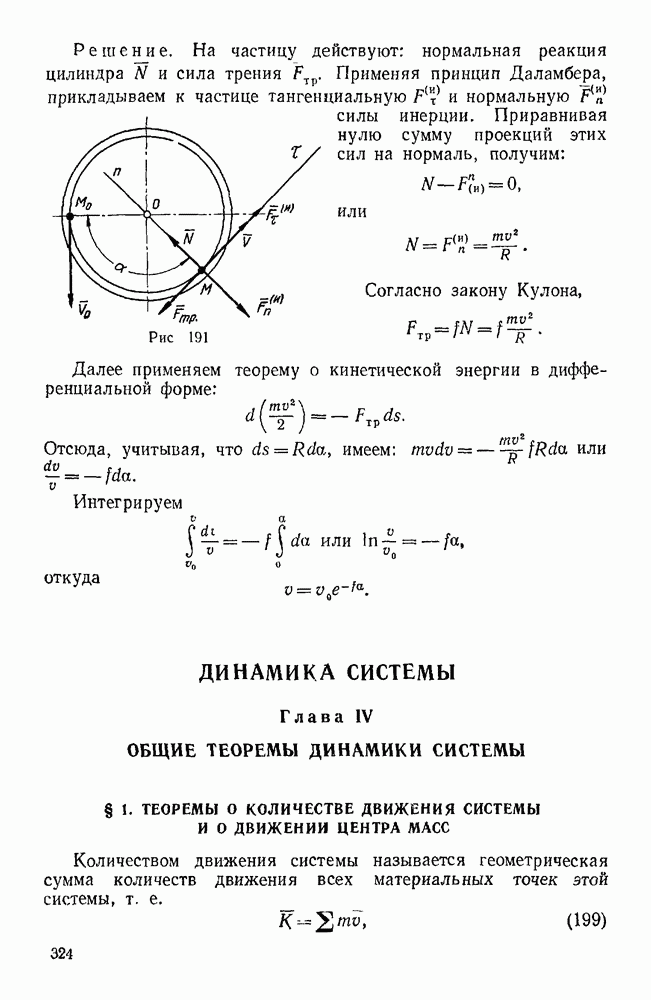
Решение. Здесь работу определяем по формуле (169):

Пример 132. Тело весом  передвигают по горизонтальному полу при помощи горизонтальной силы на расстояние
передвигают по горизонтальному полу при помощи горизонтальной силы на расстояние  . Определить работу, которую совершит при этом сила трения, если коэффициент трения между поверхностью тела и полом
. Определить работу, которую совершит при этом сила трения, если коэффициент трения между поверхностью тела и полом  .
.
Решение. Согласно закону Кулона, сила трения  , где N — нормальное давление тела на поверхность пола, причем в данном случае
, где N — нормальное давление тела на поверхность пола, причем в данном случае  . Так как сила трения направлена в сторону, противоположную движению, то работа этой силы отрицательна:
. Так как сила трения направлена в сторону, противоположную движению, то работа этой силы отрицательна:

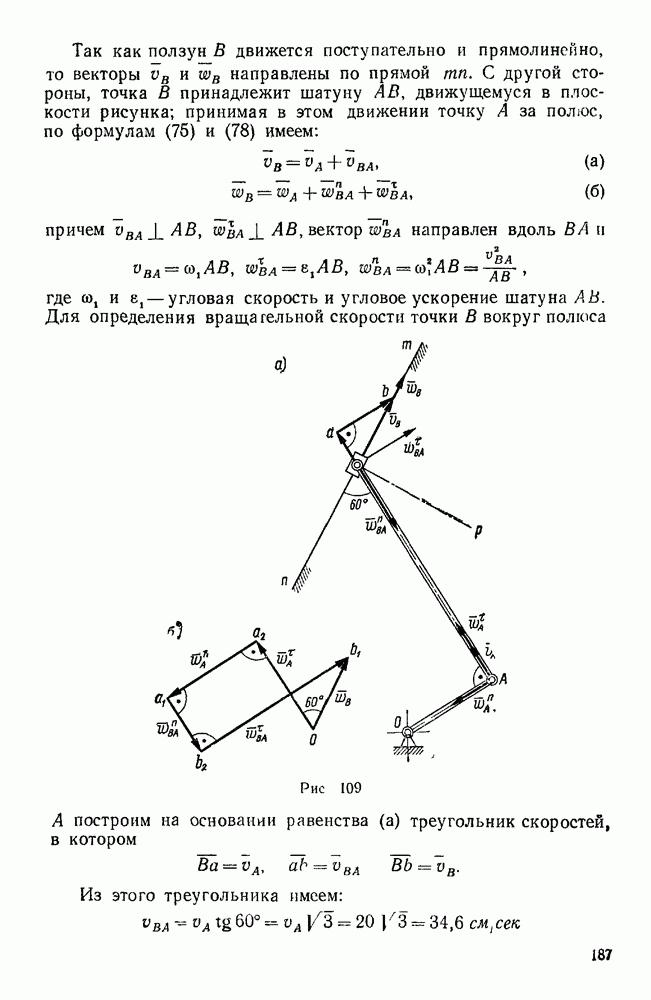
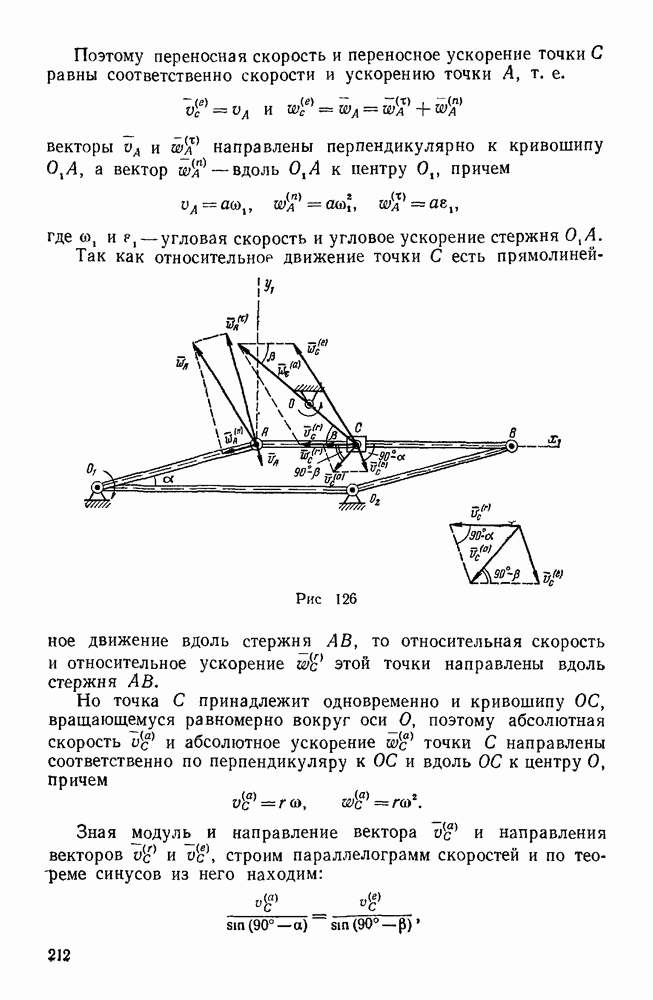
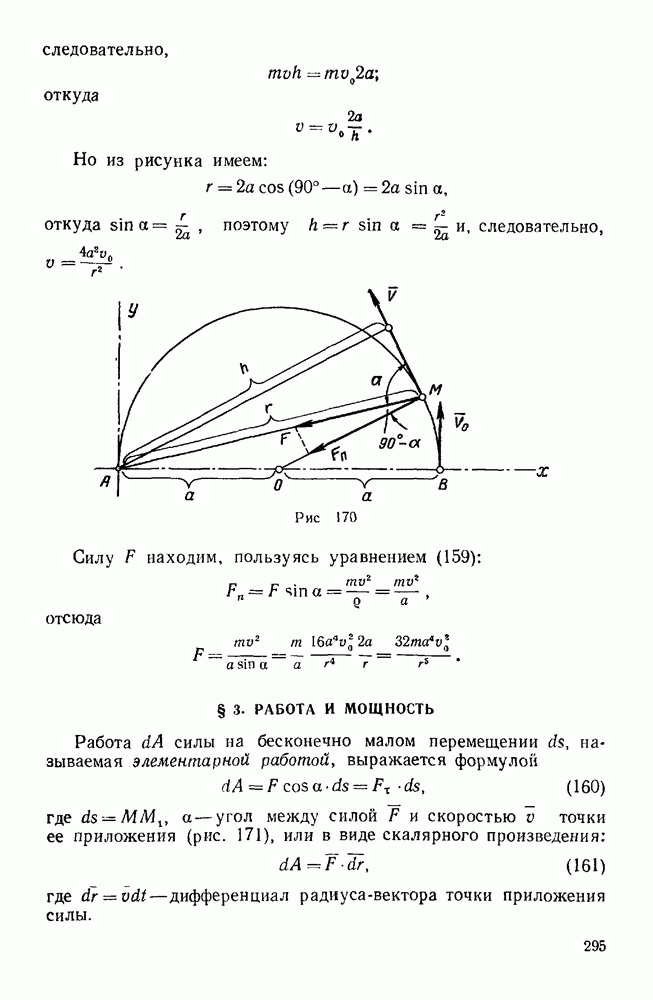
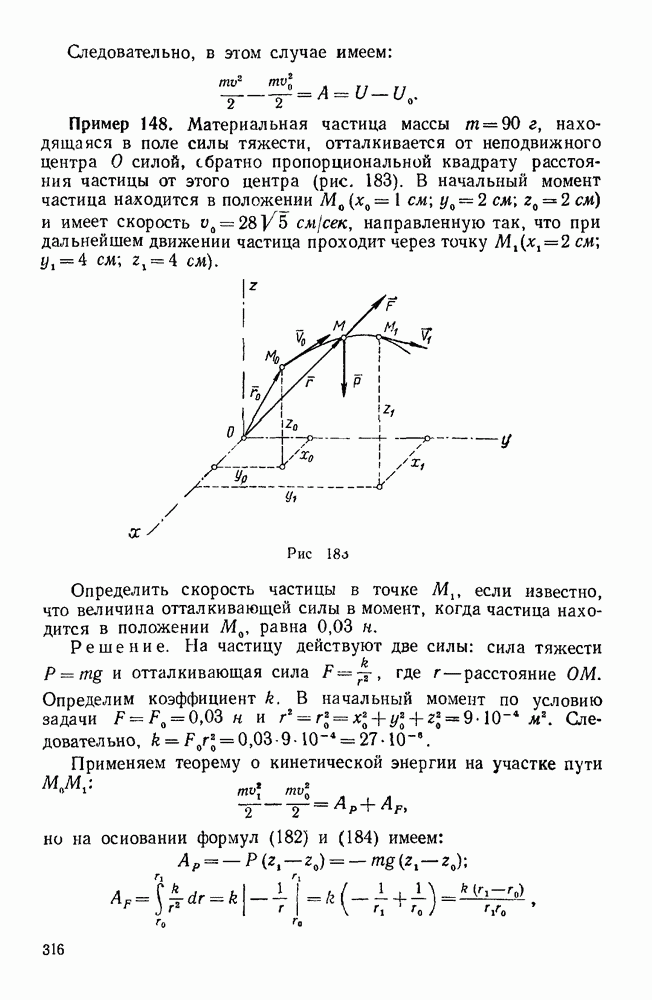
Пример 133. Найти работу силы тяжести при перемещении материальной точки из положения  в положение М (х, у, z), а также вычислить потенциальную энергию точки в положении М (рис. 173).
в положение М (х, у, z), а также вычислить потенциальную энергию точки в положении М (рис. 173).
Решение. Направляя ось z вертикально вверх, имеем:

где  — вес тела. Следовательно, по формуле (162)
— вес тела. Следовательно, по формуле (162)

откуда
 (182)
(182)
т. е. работа силы тяжести равна произведению веса материальной точки на разность ее высот в начальном и конечном положениях, причем эти высоты отсчитываются от произвольно выбранной горизонтальной плоскости.

Рис. 173.
Потенциальную энергию точки определим на основании формулы (175):

Отсюда

где С — произвольная постоянная интегрирования.
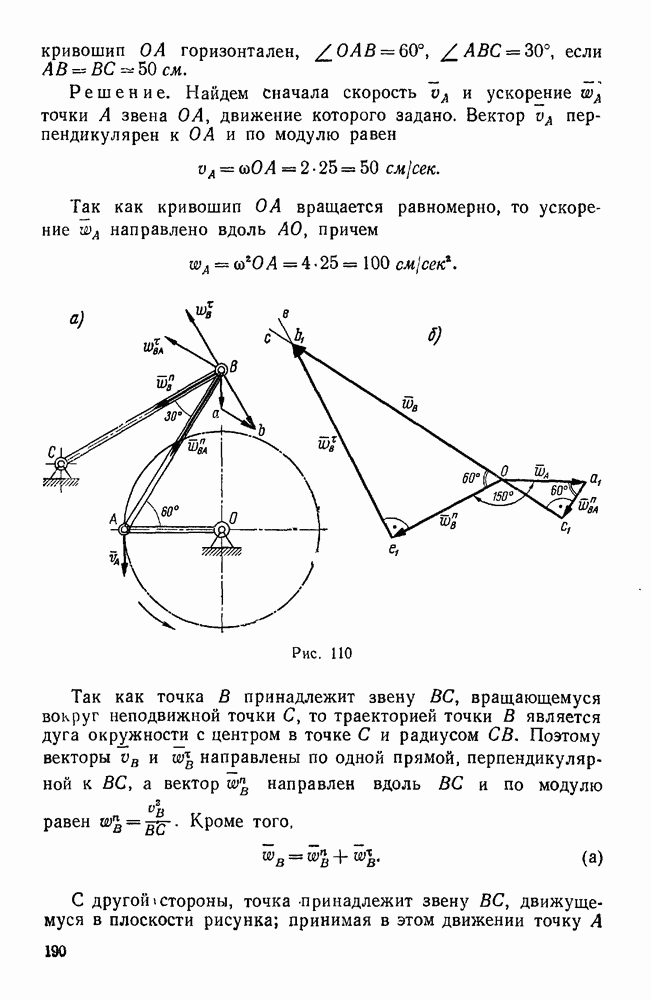
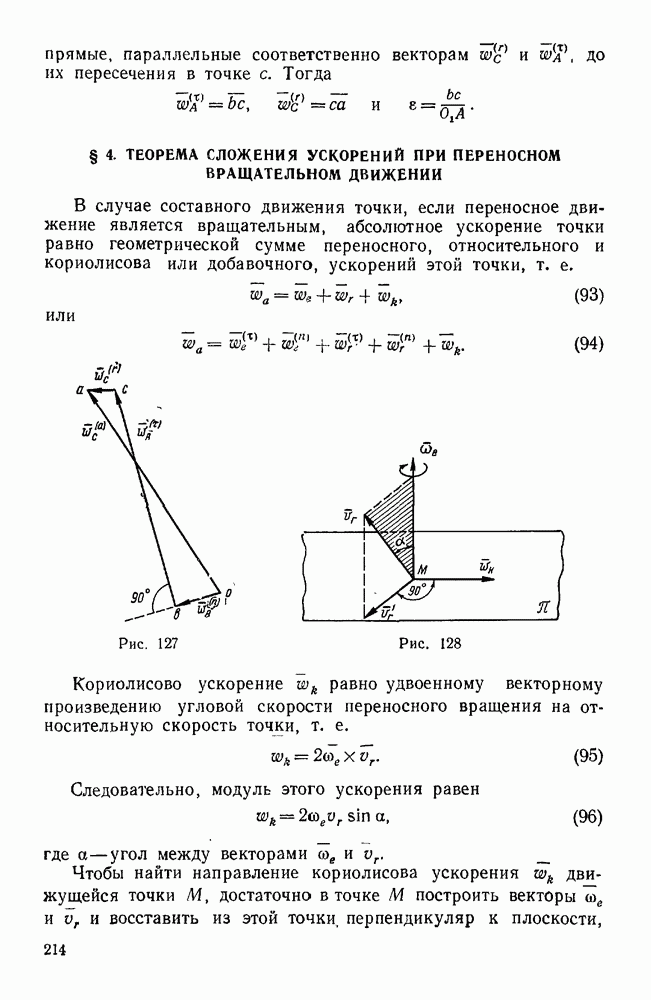
Пример 134. Определить работу силы упругости растянутого стержня, к концу которого подвешен груз М, при перемещении этого груза из положения  в положение М, если длина недеформированного стержня равна
в положение М, если длина недеформированного стержня равна  вычислить также потенциальную энергию точки в положении М (рис. 174).
вычислить также потенциальную энергию точки в положении М (рис. 174).

Рис. 174.
Решение. Обозначив силу упругости F и направив ось х по вертикали вниз, имеем:

где х — удлинение стержня, с — его жесткость.
Следовательно,

отсюда

Пример 135. На материальную точку действует сила, проекции которой на координатные оси выражаются так:

Определить работу этой силы при перемещении точки из положения  в положение
в положение  , если сила выражена в н, а координаты — в см.
, если сила выражена в н, а координаты — в см.
Решение. Выясним прежде всего, существует ли в данном случае силовая функция: для этого находим частные производные:

Отсюда получаем, что

т. е. условия (164) выполняются, и силовая функция существует. Полный дифференциал этой функции равен элементарной работе, т. е.  . Элементарную работу находим по формуле
. Элементарную работу находим по формуле  или, подставляя значения
или, подставляя значения  :
:

Это выражение действительно является полным дифференциалом

Итак

Отсюда

Значения функции  в точках
в точках  и М равны:
и М равны:

Следовательно, искомая работа равна

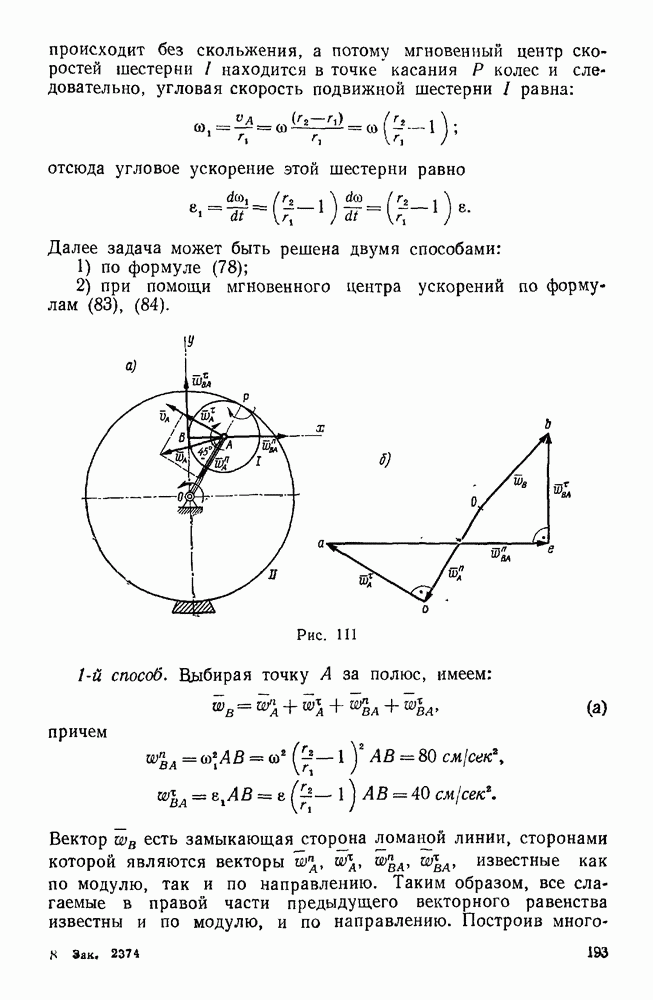
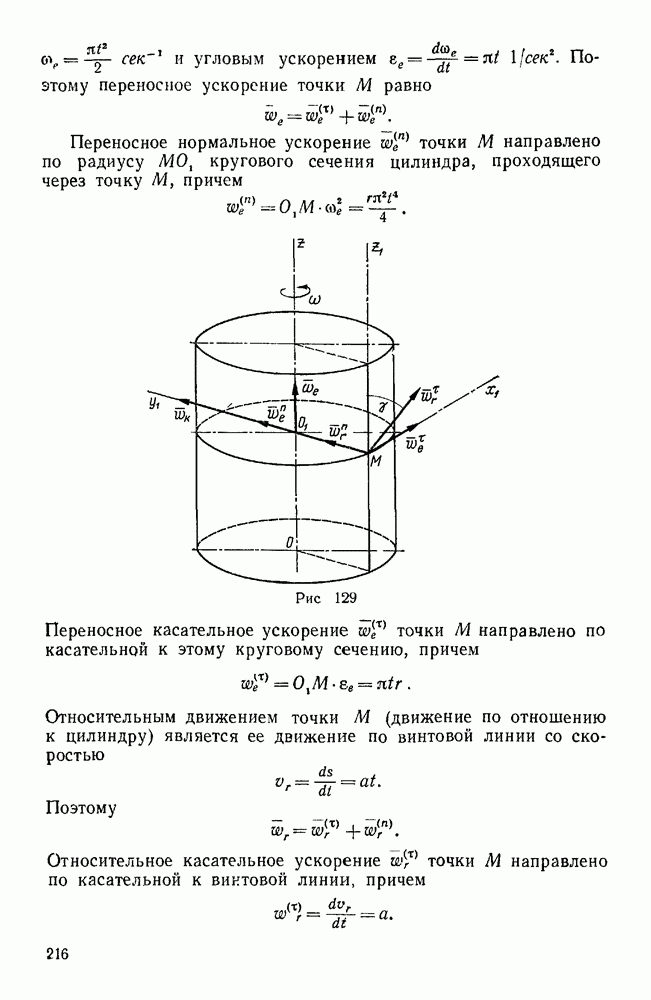
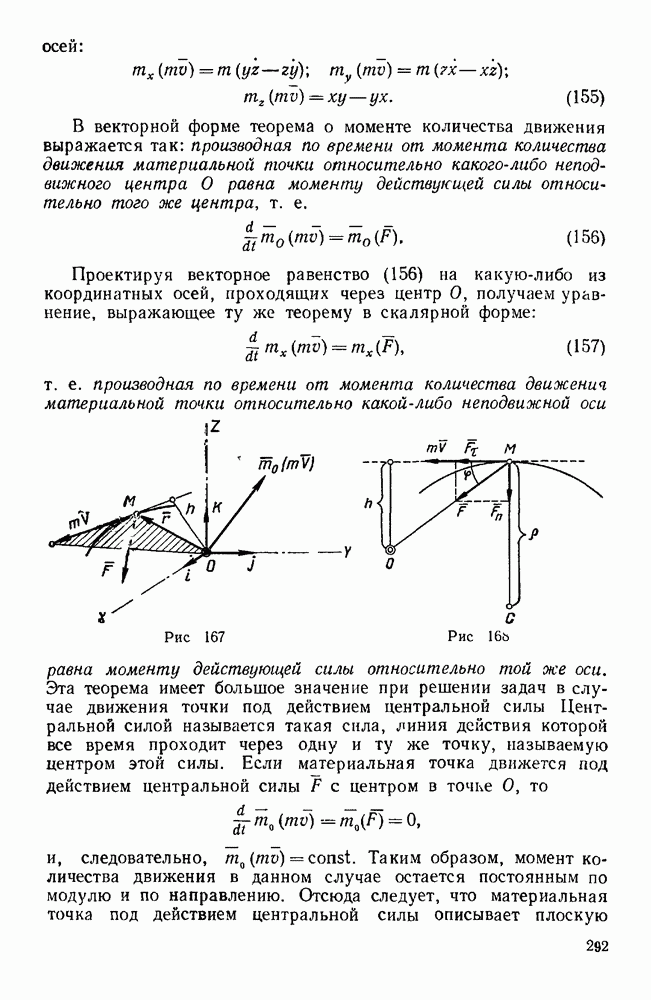
Пример 136. Определить работу центральной силы, модуль которой является функцией расстояния материальной точки от центра этой силы, т. е.  (рис. 175).
(рис. 175).
Решение. В данном случае единичный вектор силы  равен
равен
 , причем знак
, причем знак  выбирается в зависимости от того,отталкивается от центра силы или притягивается к нему точка М.
выбирается в зависимости от того,отталкивается от центра силы или притягивается к нему точка М.
Таким образом, вектор силы F выразится так:

Отсюда, пользуясь формулой (161), имеем:

Но

Следовательно,

откуда

т. е. элементарная работа является полным дифференциалом и, значит, существует силовая функция, причем

отсюда

Итак, в данном случае имеем общую формулу, по которой сразу можем определить силовую функцию в зависимости от радиуса-вектора точки приложения силы, а затем вычислить работу силы при перемещении этой точки из положения  в положение
в положение 

Пример 137. Один конец пружины закреплен шарнирно в точке О, а к другому концу ее прикреплен шарик Длина нерастянутой пружины —  , жесткость
, жесткость  . Шарик перемещают из положения
. Шарик перемещают из положения  в положение
в положение  , причем пружина растянута и не изгибается. Определить работу силы упругости пружины, если
, причем пружина растянута и не изгибается. Определить работу силы упругости пружины, если

Решение. Модуль силы упругости пружины в данном случае выражается так:


Рис. 175.
Следовательно, можно воспользоваться формулой (186):

Знак минус перед интегралом стоит потому, что сила притягивает шарик к центру О.

Рис. 176.
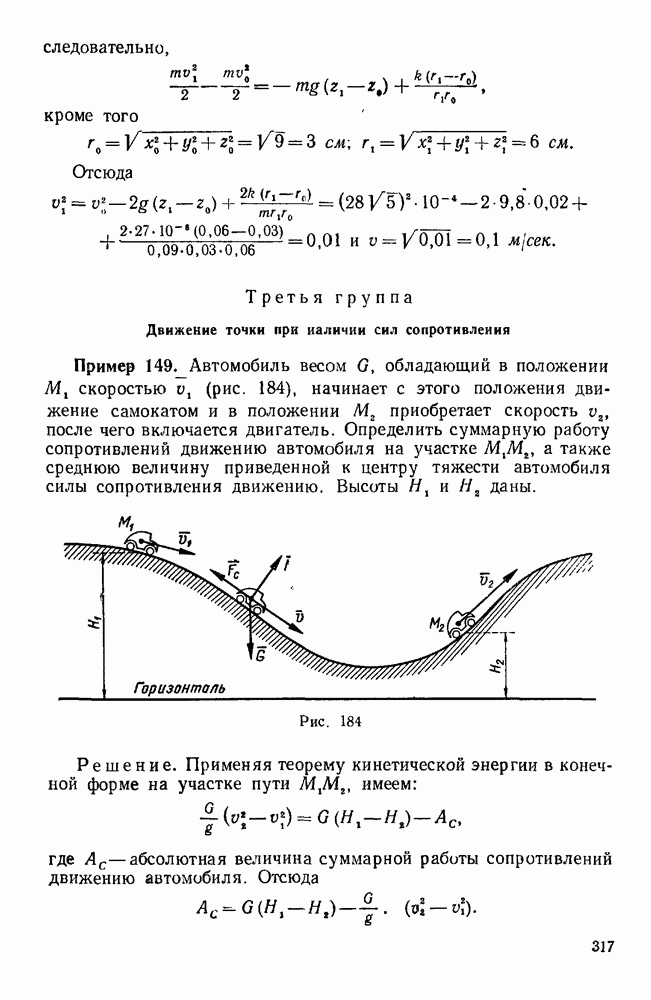
Пример 138. Колесо радиуса R катится без скольжения по горизонтальному рельсу. Найти работу трения качения при перемещении центра колеса на расстояние s, если вертикальная нагрузка на ось колеса равна  и коэффициент трения качения
и коэффициент трения качения  (Рис. 177).
(Рис. 177).

Рис. 177.
Решение. Трение качения возникает, как известно, вследствие деформаций колеса и рельса. Момент пары трения качения по закону Кулона будет равен

Так как эта пара стремится повернуть колесо в направлении, противоположном его вращению, то работа трения качения будет отрицательна и равна произведению постоянного момента  угол поворота
угол поворота  колеса [по формуле (172)]:
колеса [по формуле (172)]:

При качении колеса без скольжения имеем:  . Следовательно,
. Следовательно,

Пример 139. К валу длиною  , один конец которого закреплен жестко, приложен на свободном коице крутящий момент, который заставляет вал испытывать деформацию кручения. Определить работу возникающих при этом сил упругости, если суммарный момент упругих сил пропорционален углу закручивания, причем коэффициент пропорциональности (коэффициент жесткости вала на кручение) равен с.
, один конец которого закреплен жестко, приложен на свободном коице крутящий момент, который заставляет вал испытывать деформацию кручения. Определить работу возникающих при этом сил упругости, если суммарный момент упругих сил пропорционален углу закручивания, причем коэффициент пропорциональности (коэффициент жесткости вала на кручение) равен с.
Определить также потенциальную энергию этого вала в зависимости от угла закручивания (рис. 178).
Решение. Момент сил упругости выражается формулой

Отсюда, на основании формулы (172), имеем:

Следовательно,

Для потенциальной энергии имеем:

а потому

Пример 140. Для определения натяжений  ветвей конвейерной ленты привод А конвейера установлен на катки и включен динамометр D между приводом и неподвижной стойкой С.
ветвей конвейерной ленты привод А конвейера установлен на катки и включен динамометр D между приводом и неподвижной стойкой С.

Рис. 178.
Определить натяжения и  , если показание динамометра равно
, если показание динамометра равно  (в ньютонах), диаметр приводного барабана d, потребляемая электродвигателем привода мощность равна N и приводной барабан делает
(в ньютонах), диаметр приводного барабана d, потребляемая электродвигателем привода мощность равна N и приводной барабан делает  оборотов в минуту (рис. 179).
оборотов в минуту (рис. 179).

Рис. 179.
Решение. Рассматривал равновесие действующих на привод сил и пренебрегая трением между катками и опорной плоскостью, имеем:

откуда

Так как привод барабана вращается равномерно, то вращающий момент на валу двигателя, очевидно, определится так:

Но на основании формулы (179), мощность двигателя

Отсюда

II, следовательно,

Решая совместно уравнения (а) и (б), находим:

Пример 141. Найти мощность машины, поднимающей 100 раз в минуту молот весом  на высоту
на высоту  , если коэффициент полезного действия
, если коэффициент полезного действия 
Решение. Находим полезную работу за 1 мин:

Теперь по формуле (178) находим полезную мощность:

Далее, пользуясь формулой (180), определяем искомую мощность двигателя:

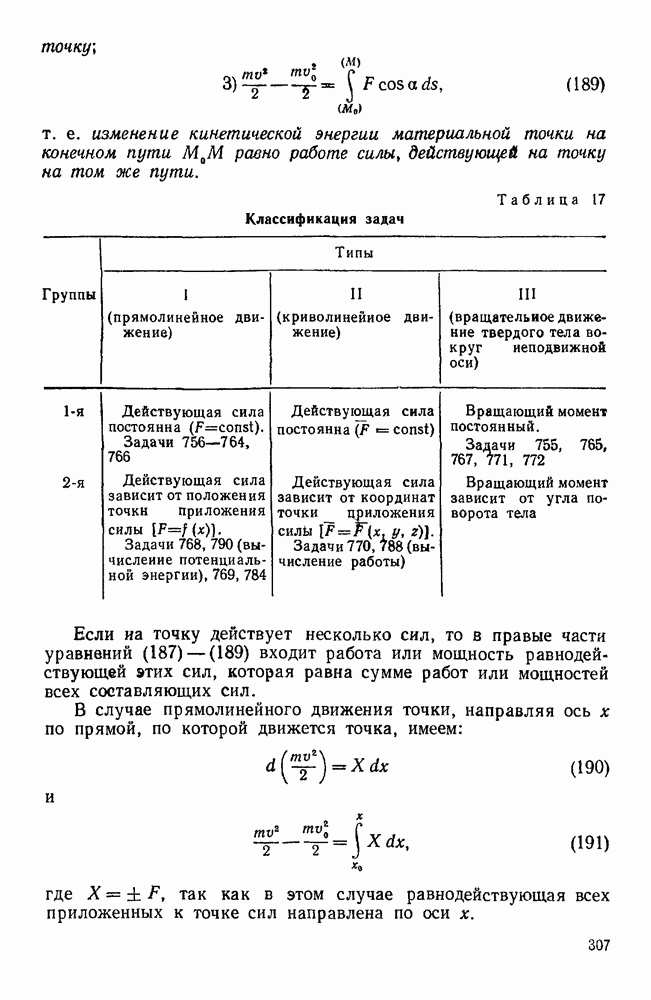
Классификация задач данного параграфа приведена в табл. 17.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
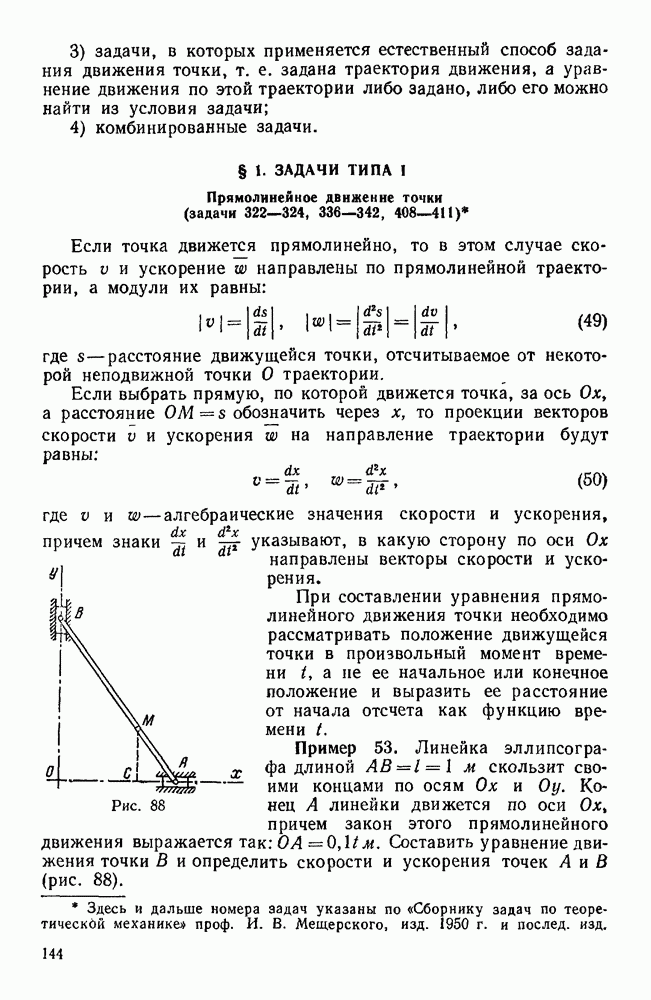
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
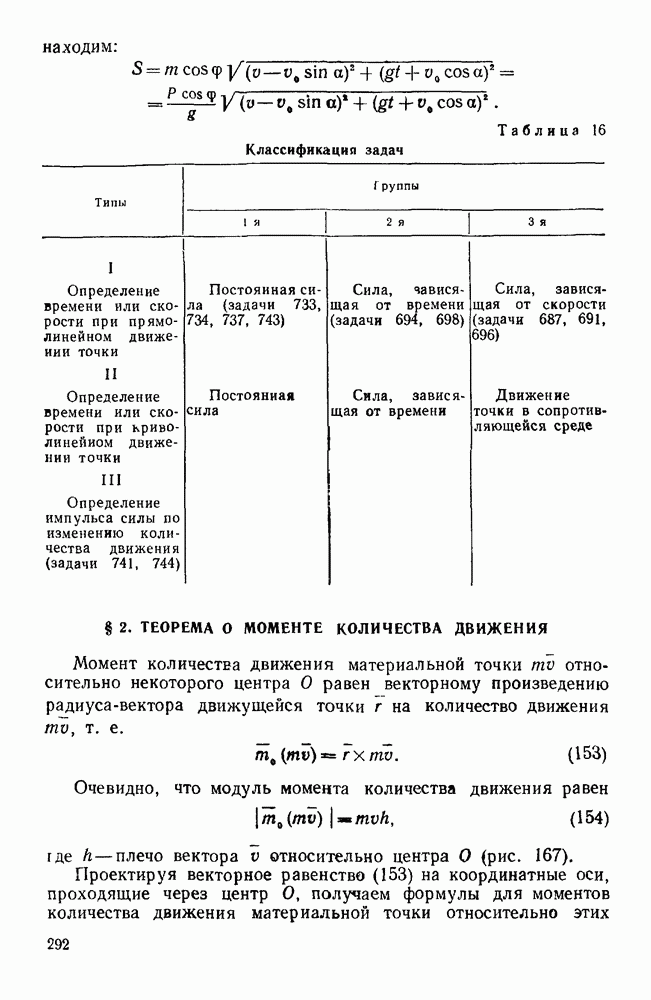
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
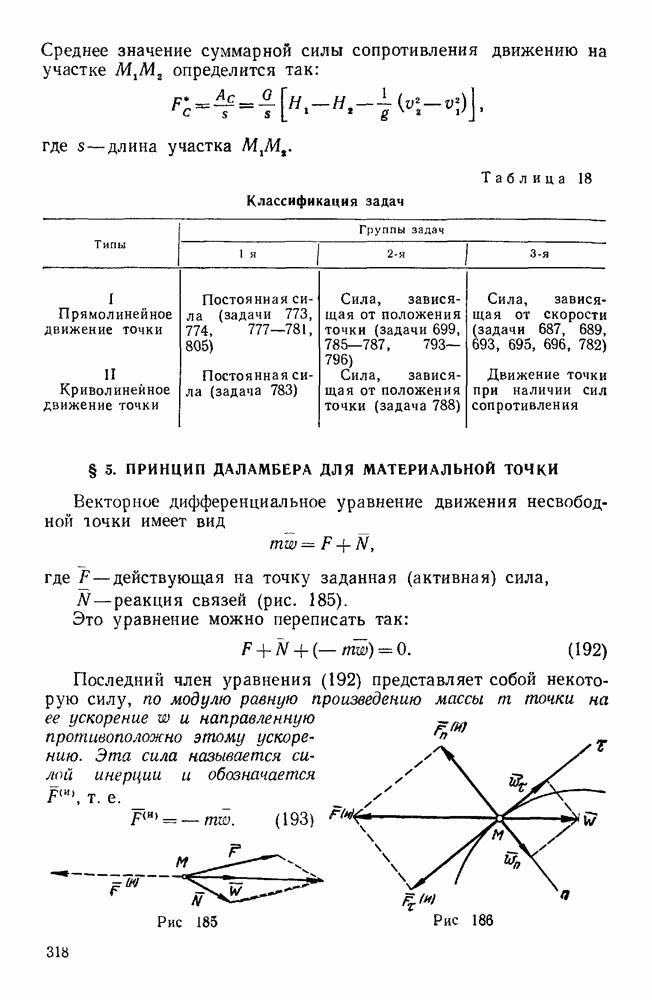
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
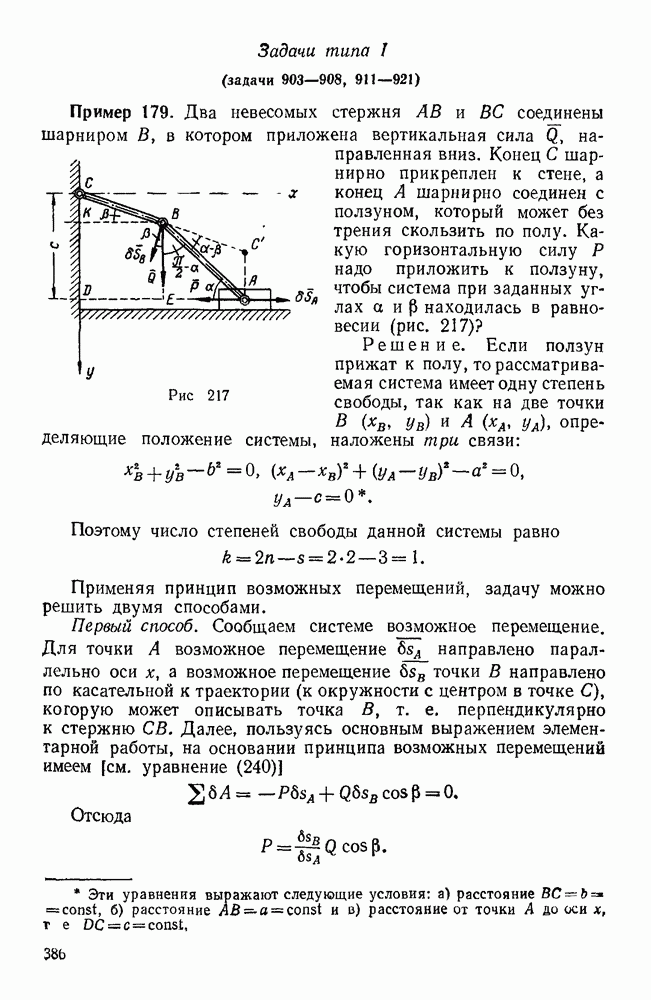
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА