| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Задачи типа V
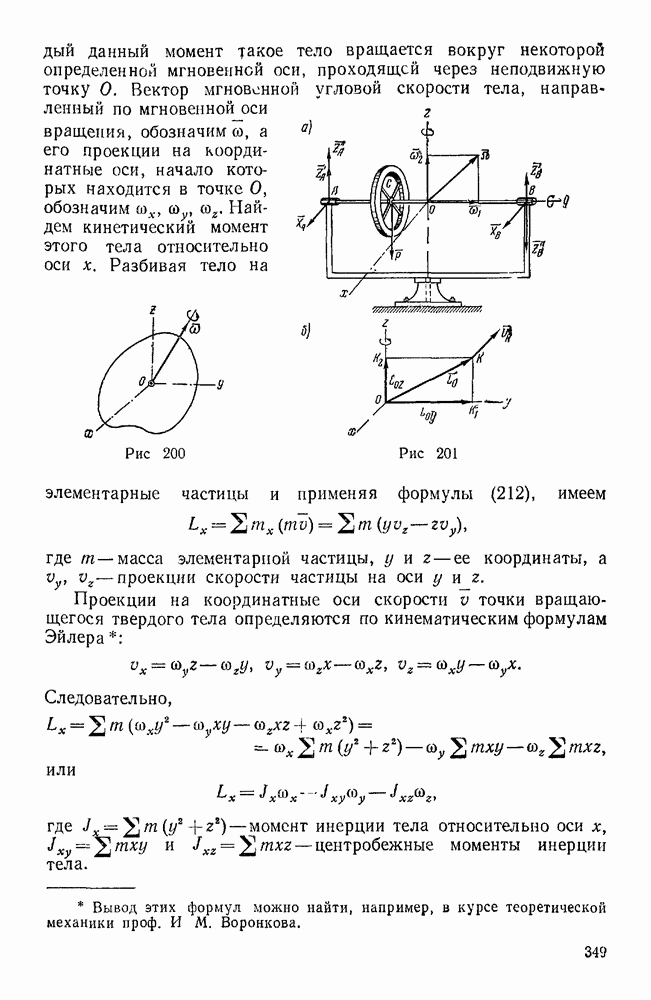
Представим себе движущееся твердое тело, одна точка О которого закреплена неподвижно, например при помощи сферического шарнира (рис. 200).
Как известно из кинематики, в каждый данный момент такое тело вращается вокруг некоторой определенной мгновенной оси, проходящей через неподвижную точку О. Вектор мгновенной угловой скорости тела, направленный по мгновенной оси вращения, обозначим  , а его проекции на координатные оси, начало которых находится в точке О, обозначим
, а его проекции на координатные оси, начало которых находится в точке О, обозначим  . Найдем кинетический момент этого тела относительно оси
. Найдем кинетический момент этого тела относительно оси  .
.

Рис. 200.

Рис. 201.
Разбивая тело на элементарные частицы и применяя формулы (212), имеем

где  — масса элементарной частицы, у и z — ее координаты, а
— масса элементарной частицы, у и z — ее координаты, а  проекции скорости частицы на оси у и z.
проекции скорости частицы на оси у и z.
Проекции на координатные оси скорости v точки вращающегося твердого тела определяются по кинематическим формулам Эйлера:

Следовательно,

или

где  — момент инерции тела относительно оси х,
— момент инерции тела относительно оси х,  — центробежные моменты инерции тела.
— центробежные моменты инерции тела.
Если координатные оси х, у, z направим по главным осям инерции данного тела в точке О, то  а потому в этом случае
а потому в этом случае  .
.
Аналогично найдем, что при этом условии кинетические моменты тела относительно осей у и z будут равны

Предположим теперь, что твердое тело, имеющее форму тела вращения вокруг оси АВ, например колесо или тор, равномерно вращается вокруг этой оси АВ с угловой скоростью  в то же время эта горизонтальная ось АВ вращается равномерно вокруг неподвижной вертикальной оси с угловой скоростью
в то же время эта горизонтальная ось АВ вращается равномерно вокруг неподвижной вертикальной оси с угловой скоростью  . Требуется определить реакции в подшипниках А и В, перпендикулярные к оси АВ, если вес тела равен
. Требуется определить реакции в подшипниках А и В, перпендикулярные к оси АВ, если вес тела равен  и
и  , причем С — центр тяжести данного тела (рис. 201, а и б). Такое тело представляет собой гироскоп с двумя степенями свободы.
, причем С — центр тяжести данного тела (рис. 201, а и б). Такое тело представляет собой гироскоп с двумя степенями свободы.
Вращение вокруг оси АВ с угловой скоростью  , называется собственным вращением гироскопа, а вращение с угловой скоростью
, называется собственным вращением гироскопа, а вращение с угловой скоростью  вокруг оси z называется прецессионным вращением, или прецессией гироскопа. Неподвижную точку пересечения осей вращения примем за начало координат О и направим координатные оси, как указано на рис. 201, а. Горизонтальные реакции подшипников А и В, параллельные оси х, обозначим
вокруг оси z называется прецессионным вращением, или прецессией гироскопа. Неподвижную точку пересечения осей вращения примем за начало координат О и направим координатные оси, как указано на рис. 201, а. Горизонтальные реакции подшипников А и В, параллельные оси х, обозначим  : вертикальные статические реакции подшипников, обусловленные только весом
: вертикальные статические реакции подшипников, обусловленные только весом  гироскопа, обозначим
гироскопа, обозначим  , причем очевидно
, причем очевидно  , а динамические вертикальные реакции обозначим
, а динамические вертикальные реакции обозначим  и
и 
Найдем кинетический момент  гироскопа относительно неподвижной точки О. Сложив векторы
гироскопа относительно неподвижной точки О. Сложив векторы  и
и  получим абсолютную мгновенную угловую скорость гироскопа Q [см. равенство (107)]. Так как гироскоп есть тело вращения вокруг оси
получим абсолютную мгновенную угловую скорость гироскопа Q [см. равенство (107)]. Так как гироскоп есть тело вращения вокруг оси  то эта ось и две перпендикулярные к ней оси х и z являются главными осями инерции гироскопа в точке О, а потому, как было указано выше, кинетические моменты гироскопа относительно этих осей равны
то эта ось и две перпендикулярные к ней оси х и z являются главными осями инерции гироскопа в точке О, а потому, как было указано выше, кинетические моменты гироскопа относительно этих осей равны

Учитывая, что  являются проекциями вектора
являются проекциями вектора  на координатные оси, по найденным проекциям строим вектор
на координатные оси, по найденным проекциям строим вектор  (рис. 201, б).
(рис. 201, б).
Применяя теперь теорему о кинетическом моменте системы относительно неподвижной точки О (см. уравнение 213), имеем

Так как производная  есть скорость
есть скорость  точки К, то
точки К, то

Это равенство выражает теорему Резаля, т. е. скорость, с которой перемещается конец вектора, изображающего кинетический момент системы относительно неподвижной точки О, равна главному моменту внешних сил, действующих на эту систему, относительно той же точки.
Так как  , то вектор OK, описывает круглый конус, вращаясь вокруг оси z с угловой скоростью
, то вектор OK, описывает круглый конус, вращаясь вокруг оси z с угловой скоростью  . Отсюда следует, что вращательная скорость
. Отсюда следует, что вращательная скорость  точки К направлена параллельно оси х, как показано на рис. 201, б и по модулю равна
точки К направлена параллельно оси х, как показано на рис. 201, б и по модулю равна

Применяя затем теорему о движении центра тяжести системы (см. уравнение 206), имеем

где  - главный вектор внешних сил, которыми в данной задаче являются вес
- главный вектор внешних сил, которыми в данной задаче являются вес  и искомые реакции подшипников
и искомые реакции подшипников  . Проектируя это векторное равенство и равенство (223) на оси х и z и учитывая, что силы
. Проектируя это векторное равенство и равенство (223) на оси х и z и учитывая, что силы  взаимно уравновешиваются, получим четыре уравнения:
взаимно уравновешиваются, получим четыре уравнения:

Так как скорость  параллельна оси х, а центростремительное ускорение точки С направлено по оси у (от С к О), то
параллельна оси х, а центростремительное ускорение точки С направлено по оси у (от С к О), то  . Поэтому предыдущие уравнения принимают вид
. Поэтому предыдущие уравнения принимают вид

Из этих уравнений находим:

Так как динамические реакции  и
и  равны по модулю и направлены противоположно, то они образуют пару с моментом, равным
равны по модулю и направлены противоположно, то они образуют пару с моментом, равным  , называемым гироскопическим моментом. Следовательно, обозначая этот момент
, называемым гироскопическим моментом. Следовательно, обозначая этот момент  , имеем
, имеем

Эта пара лежит в плоскости, в которой расположены векторы  . Учитывая направления векторов
. Учитывая направления векторов  , получаем векторное равенство:
, получаем векторное равенство:

Возникновение реакций  и
и  , а также гироскопического момента, обусловленное изменением направления оси АВ собственного вращения гироскопа, называется гироскопическим эффектом.
, а также гироскопического момента, обусловленное изменением направления оси АВ собственного вращения гироскопа, называется гироскопическим эффектом.
Пример 165. Турбина, вал которой параллелен продольной оси судна, делает 300 оборотов в минуту: вес вращающихся частей равен  , а их радиус инерции относительно оси вращения турбины равен
, а их радиус инерции относительно оси вращения турбины равен  . Определить гироскопические давления на подшипники, расстояние между которыми
. Определить гироскопические давления на подшипники, расстояние между которыми  , если судно поворачивается вокруг вертикальной оси на 15° в сек.
, если судно поворачивается вокруг вертикальной оси на 15° в сек.
Решение. Обозначая угловую скорость вращения судна вокруг вертикальной оси z через  , а угловую скорость вращения турбины вокруг горизонтальной оси у через
, а угловую скорость вращения турбины вокруг горизонтальной оси у через  , имеем:
, имеем:

По формуле (224) находим гироскопический момент

но

где  — вес вращающихся частей турбины и
— вес вращающихся частей турбины и  — их радиус инерции; поэтому
— их радиус инерции; поэтому  .
.
Искомые гироскопические давления образуют пару сил, лежащую в вертикальной плоскости, причем момент этой пары равен  , а ее плечо равно
, а ее плечо равно  , следовательно, вертикальное гироскопическое давление на каждый подшипник равно
, следовательно, вертикальное гироскопическое давление на каждый подшипник равно

Пример 166. С концом вертикального вала  шарнирно соединен горизонтальный стержень ОС, на который свободно насажен массивный цилиндрический каток (бегун).
шарнирно соединен горизонтальный стержень ОС, на который свободно насажен массивный цилиндрический каток (бегун).
При вращении вала  вокруг вертикальной оси z бегун катится без скольжения по горизонтальной плоскости, на которую закладывается измельчаемый материал (рис. 202, а и б). Определить гироскопические реакции в точках О и А, а также усилие в стержне ОС, если заданы вес
вокруг вертикальной оси z бегун катится без скольжения по горизонтальной плоскости, на которую закладывается измельчаемый материал (рис. 202, а и б). Определить гироскопические реакции в точках О и А, а также усилие в стержне ОС, если заданы вес  , длина
, длина  , радиус бегуна R и угловая скорость вала
, радиус бегуна R и угловая скорость вала  .
.

Рис. 202.
Решение. Обозначим угловую скорость собственного вращения бегуна вокруг оси ОС через  . Так как качение бегуна по горизонтальной плоскости происходит без скольжения, то скорость точки А равна нулю; поэтому мгновенная ось вращения бегуна проходит через точки О и А, а его абсолютная угловая скорость Q направлена по прямой ОА, причем
. Так как качение бегуна по горизонтальной плоскости происходит без скольжения, то скорость точки А равна нулю; поэтому мгновенная ось вращения бегуна проходит через точки О и А, а его абсолютная угловая скорость Q направлена по прямой ОА, причем  .
.
Построив параллелограмм угловых скоростей, из подобных треугольников ОАС и  имеем:
имеем:

Теперь по формуле (224) находим гироскопический момент

Рассматривая бегун как однородный цилиндр, имеем

и, следовательно,

Гироскопические реакции  в точках О и А образуют пару сил, момент которой равен
в точках О и А образуют пару сил, момент которой равен  и направлен, согласно формуле (224), по оси
и направлен, согласно формуле (224), по оси  , как указано на рис. 202, а. Отсюда следует, что, во-первых, силы
, как указано на рис. 202, а. Отсюда следует, что, во-первых, силы  и
и  имеют направления, указанные на рис. 202, а, и, во-вторых,
имеют направления, указанные на рис. 202, а, и, во-вторых,

Таким образом, полире давление бегуна на горизонтальную плоскость в точке А равно сумме двух сил: веса  и гироскопического давления, равного
и гироскопического давления, равного  , т. е.
, т. е.

Центростремительное ускорение центра тяжести С бегуна направлено вдоль оси у от С к О и по модулю равно —  . Поэтому, применяя теорему о движении центра тяжести системы, получим:
. Поэтому, применяя теорему о движении центра тяжести системы, получим:
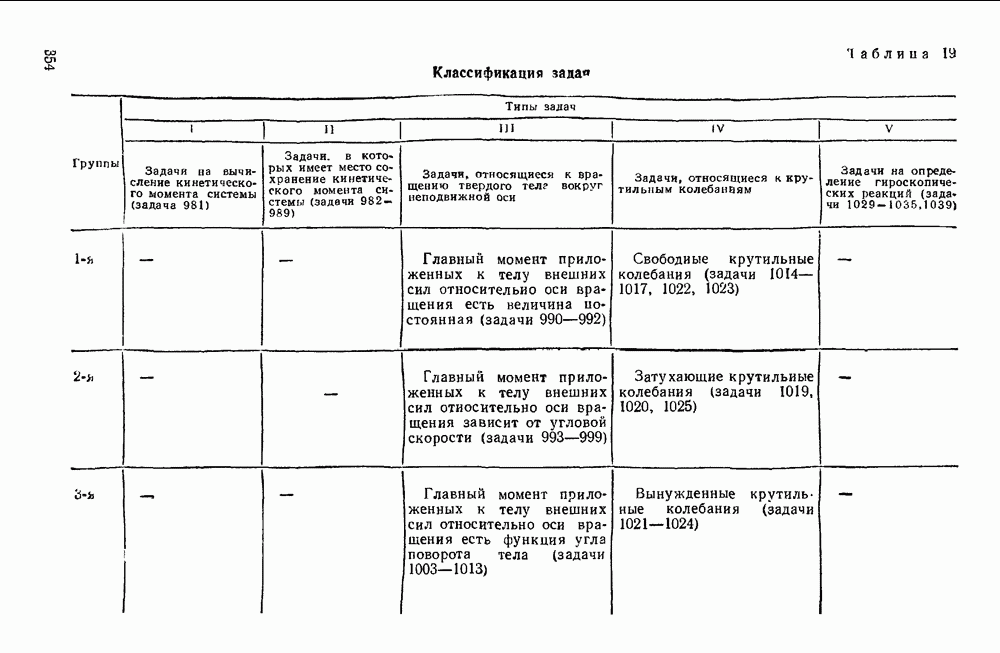
Таблица 19. Классификация задач
(см. оригинал)

где  — реакция в точке О по направлению оси у.
— реакция в точке О по направлению оси у.
Отсюда

Растягивающее усилие в стержне ОС, очевидно, равно этой реакции  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
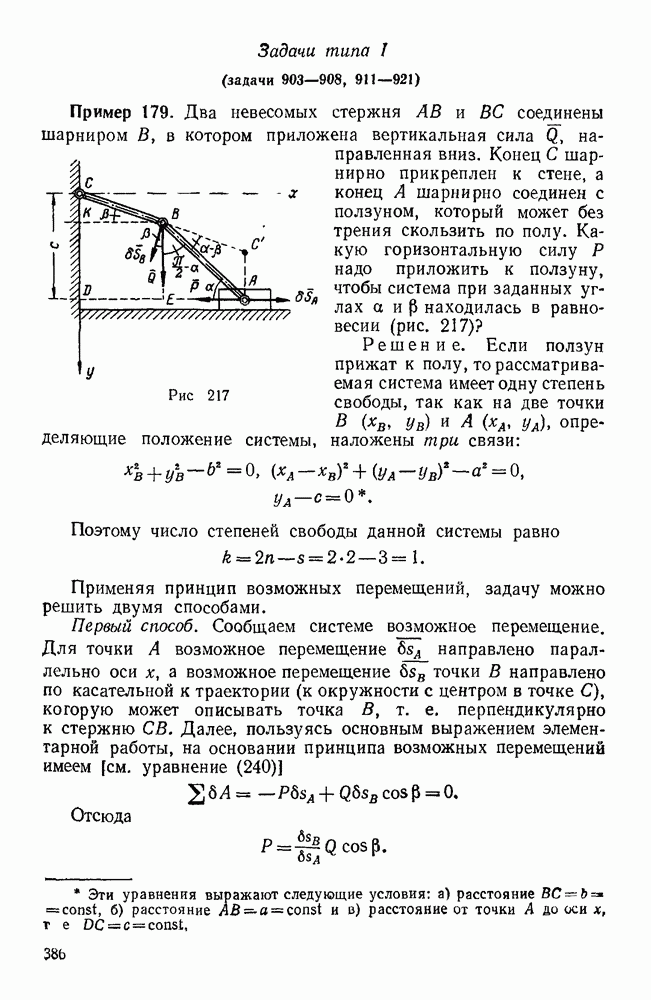
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
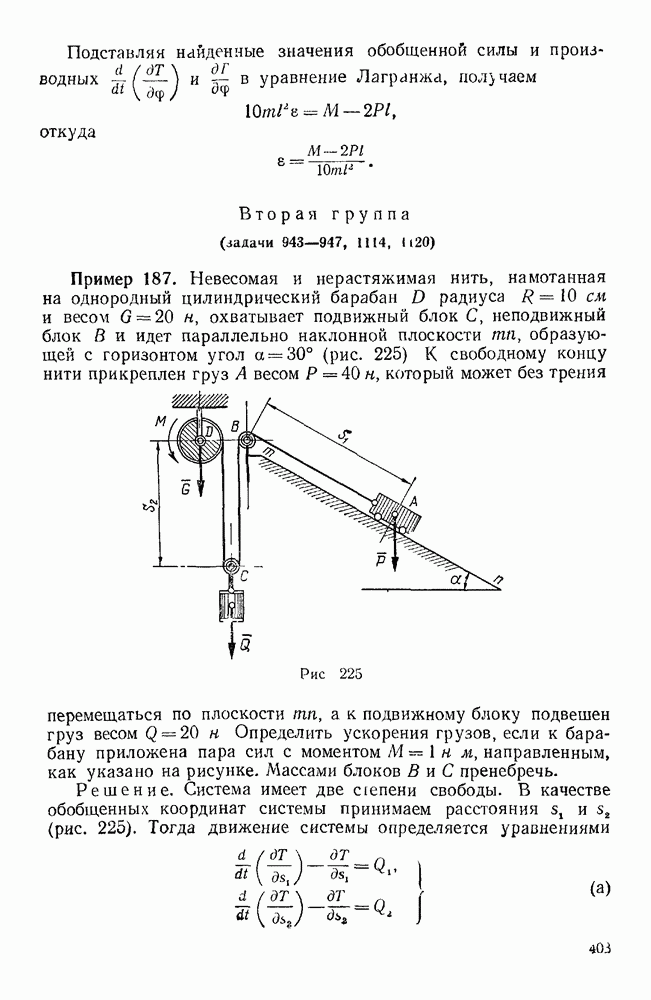
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА