| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
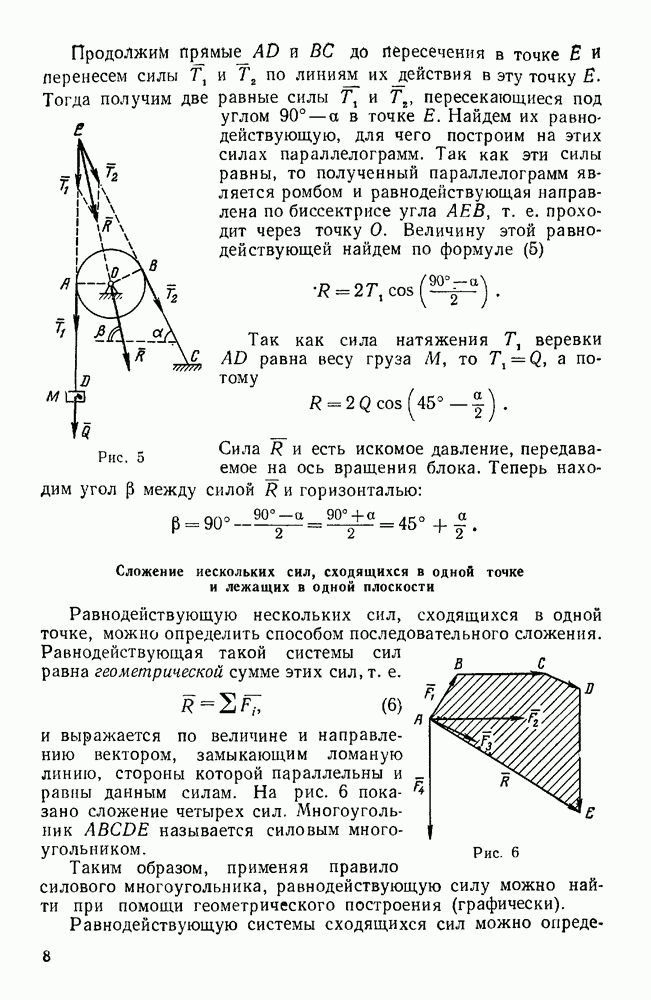
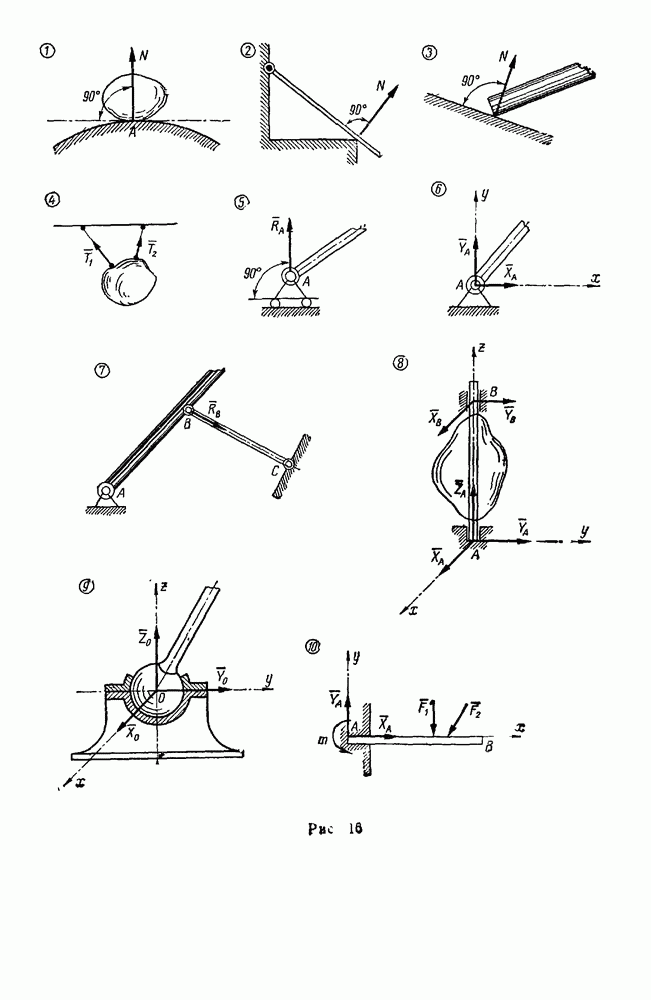
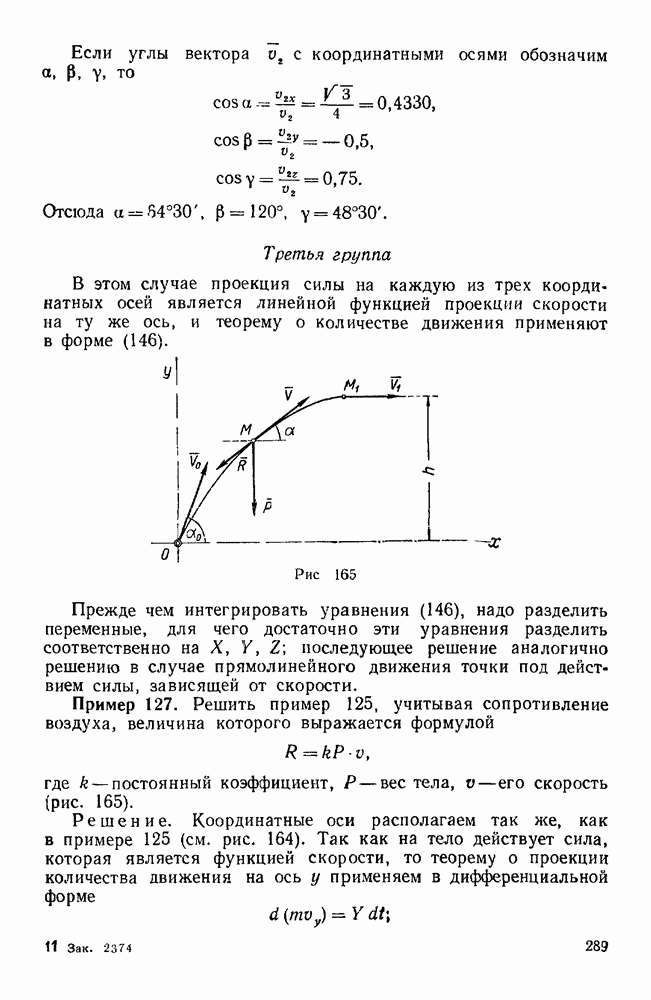
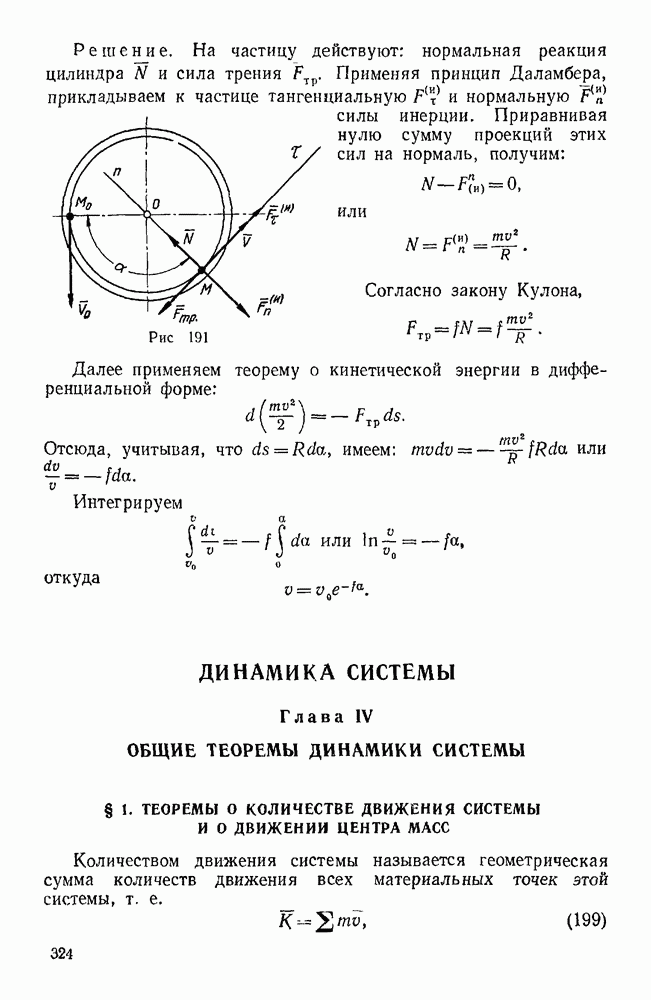
Задачи типа I. Равновесие плоской системы сходящихся сил
Первая группа
Задачи, в которых линии действия реакций всех связей известны (задачи 17—21, 26—32)
Пример 8. Плоская ферма, состоящая из невесомых стержней, соединенных между собой по концам шарнирно, находится в равновесии под действием сил  и
и  , причем сила F, горизонтальна, а сила
, причем сила F, горизонтальна, а сила  составляет со стержнем ED угол
составляет со стержнем ED угол  . Определить усилия в стержнях 1, 2, 3 и 4, если
. Определить усилия в стержнях 1, 2, 3 и 4, если  (рис. 17).
(рис. 17).
Решение. Рассмотрим сначала узел D; к этому узлу, находящемуся в равновесии, приложены заданная сила F, и неизвестные реакции стержней 1 и 2, которые обозначим через  и
и  .
.
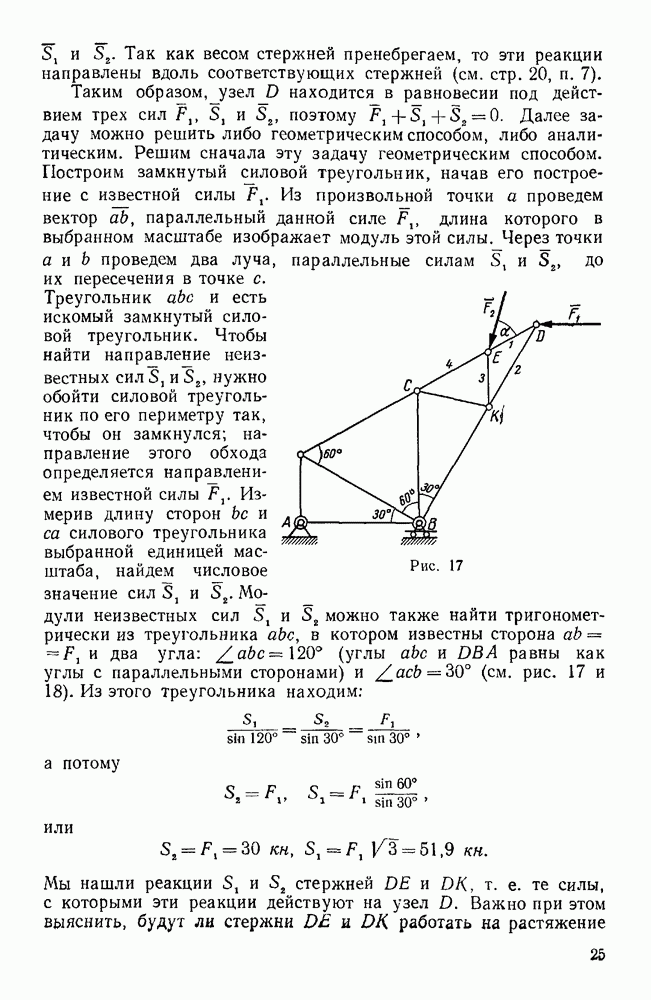
Так как весом стержней пренебрегаем, то эти реакции направлены вдоль соответствующих стержней (см. стр. 20, п. 7).
Таким  находится в равновесии под действием трех сил
находится в равновесии под действием трех сил  , поэтому
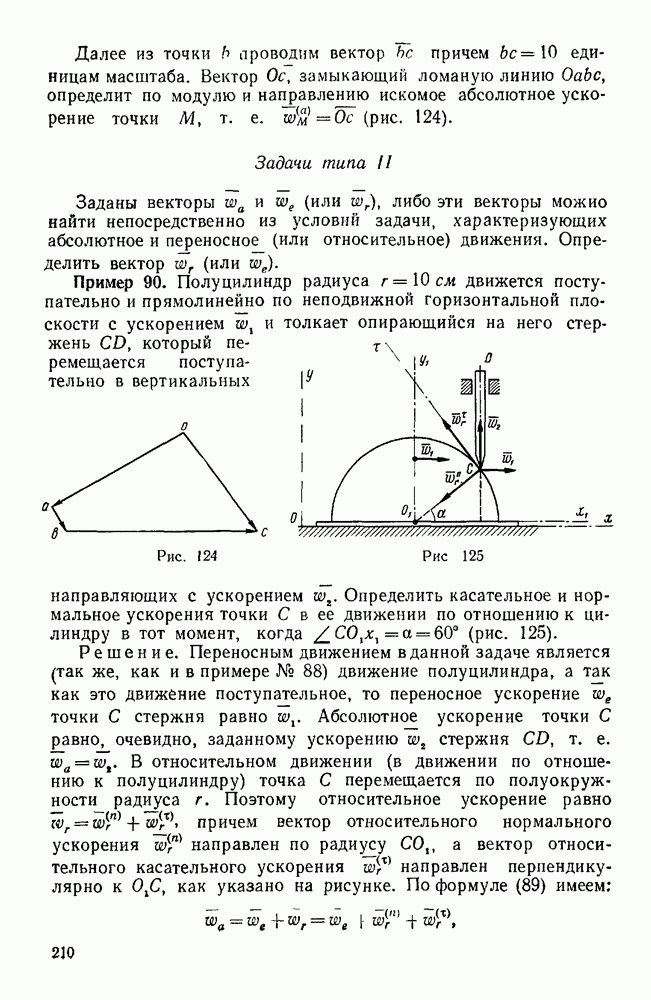
, поэтому  . Далее задачу можно решить либо геометрическим способом, либо аналитическим. Решим сначала эту задачу геометрическим способом. Построим замкнутый силовой треугольник, начав его построение с известной силы
. Далее задачу можно решить либо геометрическим способом, либо аналитическим. Решим сначала эту задачу геометрическим способом. Построим замкнутый силовой треугольник, начав его построение с известной силы  . Из произвольной точки а проведем вектор
. Из произвольной точки а проведем вектор  , параллельный данной силе
, параллельный данной силе  , длина которого в выбранном масштабе изображает модуль этой силы. Через точки а и b проведем два луча, параллельные силам
, длина которого в выбранном масштабе изображает модуль этой силы. Через точки а и b проведем два луча, параллельные силам  и
и  , до их пересечения в точке с.
, до их пересечения в точке с.
Треугольник  и есть искомый замкнутый силовой треугольник. Чтобы найти направление неизвестных сил S, и
и есть искомый замкнутый силовой треугольник. Чтобы найти направление неизвестных сил S, и  , нужно обойти силовой треугольник по его периметру так, чтобы он замкнулся; направление этого обхода определяется направлением известной силы
, нужно обойти силовой треугольник по его периметру так, чтобы он замкнулся; направление этого обхода определяется направлением известной силы  . Измерив длину сторон
. Измерив длину сторон  силового треугольника выбранной единицей масштаба, найдем числовое значение сил
силового треугольника выбранной единицей масштаба, найдем числовое значение сил  и
и  . Модули неизвестных сил S, и
. Модули неизвестных сил S, и  можно также найти тригонометрически из треугольника
можно также найти тригонометрически из треугольника  , в котором известны сторона
, в котором известны сторона  , и два угла:
, и два угла:  (углы
(углы  и DBA равны как углы с параллельными сторонами) и
и DBA равны как углы с параллельными сторонами) и  30° (см. рис. 17 и 18). Из этого треугольника находим:
30° (см. рис. 17 и 18). Из этого треугольника находим:

а потому

или

Мы нашли реакции  и
и  стержней DE и DK, т. е. те силы, с которыми эти реакции действуют на узел D. Важно при этом выяснить, будут ли стержни DE и DK работать на растяжение или на сжатие.
стержней DE и DK, т. е. те силы, с которыми эти реакции действуют на узел D. Важно при этом выяснить, будут ли стержни DE и DK работать на растяжение или на сжатие.

Рис. 17.
Для этого рассмотрим равновесие каждого стержня отдельно; начнем со стержня DK (рис. 19, а).

Рис. 18.
Реакция стержня DK, приложенная к узлу D, направлена от узла D внутрь отрезка DK. Но тогда сила  , с которой шарнир D действует на стержень DK, или иначе — реакция шарнира D, приложенная к стержню DK, равна по модулю и противоположна по направлению силе
, с которой шарнир D действует на стержень DK, или иначе — реакция шарнира D, приложенная к стержню DK, равна по модулю и противоположна по направлению силе  . Стержень DK находится в равновесии под действием двух сил: реакции 5г шарнира D и реакции шарнира К, которую обозначим через
. Стержень DK находится в равновесии под действием двух сил: реакции 5г шарнира D и реакции шарнира К, которую обозначим через  .
.

Рис. 19.
Отсюда следует, что силы  направленные по одной прямой, равны по модулю и противоположны по направлению, т. е.
направленные по одной прямой, равны по модулю и противоположны по направлению, т. е.  . Силы
. Силы  и приложенные к концам стержня KD, вызывают, очевидно, растяжение этого стержня. Отсюда заключаем, что если вектор
и приложенные к концам стержня KD, вызывают, очевидно, растяжение этого стержня. Отсюда заключаем, что если вектор  , изображающий реакцию стержня KD на шарнир D и показанный на самом стержне, направлен от узла D, то стержень растянут. Теперь рассмотрим стержень DE (рис. 19,6). Реакция S, этого стержня на шарнир D, начерченная на самом стержне DE, направлена, как видно, к шарниру D. Аналогично предыдущему заключаем, что реакция
, изображающий реакцию стержня KD на шарнир D и показанный на самом стержне, направлен от узла D, то стержень растянут. Теперь рассмотрим стержень DE (рис. 19,6). Реакция S, этого стержня на шарнир D, начерченная на самом стержне DE, направлена, как видно, к шарниру D. Аналогично предыдущему заключаем, что реакция  шарнира D на стержень DE, приложенная к этому стержню, будет равна по модулю и прямо противоположна по направлению силе
шарнира D на стержень DE, приложенная к этому стержню, будет равна по модулю и прямо противоположна по направлению силе  . Так как стержень DE находится в равновесии, то реакция S, шарнира Е, приложенная к этому стержню, равна по модулю и прямо противоположна по направлению силе
. Так как стержень DE находится в равновесии, то реакция S, шарнира Е, приложенная к этому стержню, равна по модулю и прямо противоположна по направлению силе  . Очевидно, что силы
. Очевидно, что силы  , приложенные к стержню DE, сжимают этот стержень. Поэтому можно сказать, что если вектор
, приложенные к стержню DE, сжимают этот стержень. Поэтому можно сказать, что если вектор  , изображающий реакцию стержня DE на шарнир D и начерченный на самом стержне, направлен к узлу D, то стержень сжат. Таким образом, сформулируем следующее правило:
, изображающий реакцию стержня DE на шарнир D и начерченный на самом стержне, направлен к узлу D, то стержень сжат. Таким образом, сформулируем следующее правило:
Если изображенный на самом стержне, вектор силы, с которой данный стержень действует на шарнир (узел), направлен от шарнира (от узла), то стержень растянут. Если же этот вектор направлен к шарниру (к узлу), то стержень сжат.
Рассмотрим далее аналитический способ решения этой задачи. Направим ось  по линии действия силы
по линии действия силы  а ось
а ось  перпендикулярно к ней, как показано на рис. 20, и найдем проекции всех сил, приложенных к шарниру D на эти оси. Известно, что абсолютное значение проекции силы на ось равно произведению модуля этой силы на косинус острого угла между направлением силы и осью проекций. При этом, если направление силы составляет острый угол с положительным направлением оси проекций, то проекция силы на эту ось
перпендикулярно к ней, как показано на рис. 20, и найдем проекции всех сил, приложенных к шарниру D на эти оси. Известно, что абсолютное значение проекции силы на ось равно произведению модуля этой силы на косинус острого угла между направлением силы и осью проекций. При этом, если направление силы составляет острый угол с положительным направлением оси проекций, то проекция силы на эту ось  же направление силы составляет острый угол с отрицательным направлением оси проекций, то проекция силы на эту ось отрицательна.
же направление силы составляет острый угол с отрицательным направлением оси проекций, то проекция силы на эту ось отрицательна.

Рис. 20.
Сила  совпадает с отрицательным направлением оси
совпадает с отрицательным направлением оси  , а потому проекция ее на эту ось равна модулю самой силы, взятому со знаком минус, а ее проекция на ось
, а потому проекция ее на эту ось равна модулю самой силы, взятому со знаком минус, а ее проекция на ось  равна нулю. Сила
равна нулю. Сила  составляет острый угол 30° с положительным направлением оси
составляет острый угол 30° с положительным направлением оси  и острый угол 60° с положительным направлением оси
и острый угол 60° с положительным направлением оси  , а потому
, а потому

Сила  составляет острый угол 60° с отрицательным направлением оси
составляет острый угол 60° с отрицательным направлением оси  и острый угол 30° с отрицательным направлением оси
и острый угол 30° с отрицательным направлением оси  , а потому
, а потому

При равновесии тела сумма проекций всех приложенных к телу сил на каждую из координатных осей равна нулю. Таким образом, получим два следующих уравнения равновесия:

или

Решим теперь эту систему уравнений относительно неизвестных  и
и  :
:

Чтобы определить усилия в стержнях 3 и 4, рассмотрим узел Е, находящийся в равновесии под действием заданной силы  и трех реакций стержней 1, 3, 4, направленных вдоль этих стержней. Неизвестные реакции стержней 3 и 4 обозначим через
и трех реакций стержней 1, 3, 4, направленных вдоль этих стержней. Неизвестные реакции стержней 3 и 4 обозначим через  , направив их от рассматриваемого узла Е. Что касается реакции стержня 1, приложенной к узлу Е, то по закону равенства действия и противодействия она равна по модулю и противоположна по направлению силе S, т. е. равна силе
, направив их от рассматриваемого узла Е. Что касается реакции стержня 1, приложенной к узлу Е, то по закону равенства действия и противодействия она равна по модулю и противоположна по направлению силе S, т. е. равна силе  . Следовательно,
. Следовательно,  . Для определения неизвестных сил применим сначала аналитический способ решения задачи. Для этого выберем оси координат, как указано на рис. 21, и найдем проекции каждой силы на эти оси.
. Для определения неизвестных сил применим сначала аналитический способ решения задачи. Для этого выберем оси координат, как указано на рис. 21, и найдем проекции каждой силы на эти оси.

Рис. 21
Тогда имеем:

Приравнивая нулю сумму проекций всех сил на каждую из координатных осей  , получим два уравнения равновесия:
, получим два уравнения равновесия:

Из этих уравнений находим:

или

т. е.

Так как после решения уравнений равновесия мы получили отрицательные значения для неизвестных реакций  , то эти силы имеют направления, противоположные выбранным нами на рис. 21, т. е. силы
, то эти силы имеют направления, противоположные выбранным нами на рис. 21, т. е. силы  направлены к узлу Е и стержни 3 и 4 сжаты. Полученные результаты проверим геометрически, т. е. рассмотрим геометрический способ решения этой задачи. Для этого построим замкнутый многоугольник сил
направлены к узлу Е и стержни 3 и 4 сжаты. Полученные результаты проверим геометрически, т. е. рассмотрим геометрический способ решения этой задачи. Для этого построим замкнутый многоугольник сил  Направления сил
Направления сил  найдем после того, как обойдем периметр построенного силового многоугольника
найдем после того, как обойдем периметр построенного силового многоугольника  , причем направление этого обхода определяется направлением известных сил
, причем направление этого обхода определяется направлением известных сил  . Измерив стороны
. Измерив стороны  силового многоугольника выбранной единицей масштаба, найдем модули искомых сил
силового многоугольника выбранной единицей масштаба, найдем модули искомых сил  и
и  .
.
Так как углы между силами  и
и  заданы, то можно найти углы силового многоугольника, а затем вычислить и длины двух неизвестных его сторон, что и рекомендуется выполнить студенту самостоятельно.
заданы, то можно найти углы силового многоугольника, а затем вычислить и длины двух неизвестных его сторон, что и рекомендуется выполнить студенту самостоятельно.
Чтобы определить, будут ли стержни 3 а 4 растянуты или сжаты, перенесем векторы  с силового многоугольника на стержни ЕС и ЕК фермы; тогда силы
с силового многоугольника на стержни ЕС и ЕК фермы; тогда силы  и
и  будут направлены к узлу Е, а потому эти стержни сжаты.
будут направлены к узлу Е, а потому эти стержни сжаты.

Рис. 22.
Примечание. При аналитическом способе решения этой задачи заранее неизвестно, в какую сторону следует направлять реакции стержней. В таких случаях эти реакции можно направлять по соответствующим стержням в ту или другую сторону произвольно. Если в результате решения уравнений равновесия для этих реакций получим положительные значения, то реакции были направлены верно Если же для какой-нибудь из этих неизвестных сил получим отрицательное значение, то выбранное направление реакции нужно изменить на противоположное. В дальнейшем условимся неизвестную реакцию стержня, приложенную к шарниру (к узлу), направлять по самому стержню от этого узла. Если, решая уравнения равновесия, получим для этой реакции положительное значение, то реакция направлена верно и, следовательно, стержень растянут. Если же для искомой реакции получим отрицательное значение, то это укажет на то, что в действительности реакция данного стержня имеет направление, противоположное принятому нами, т. е. она направлена к узлу и, следовательно, данный стержень сжат.
Таким образом, при указанном условии относительно направления реакции стержня, по знаку этой реакции можно определить, будет ли данный стержень растянут или сжат.
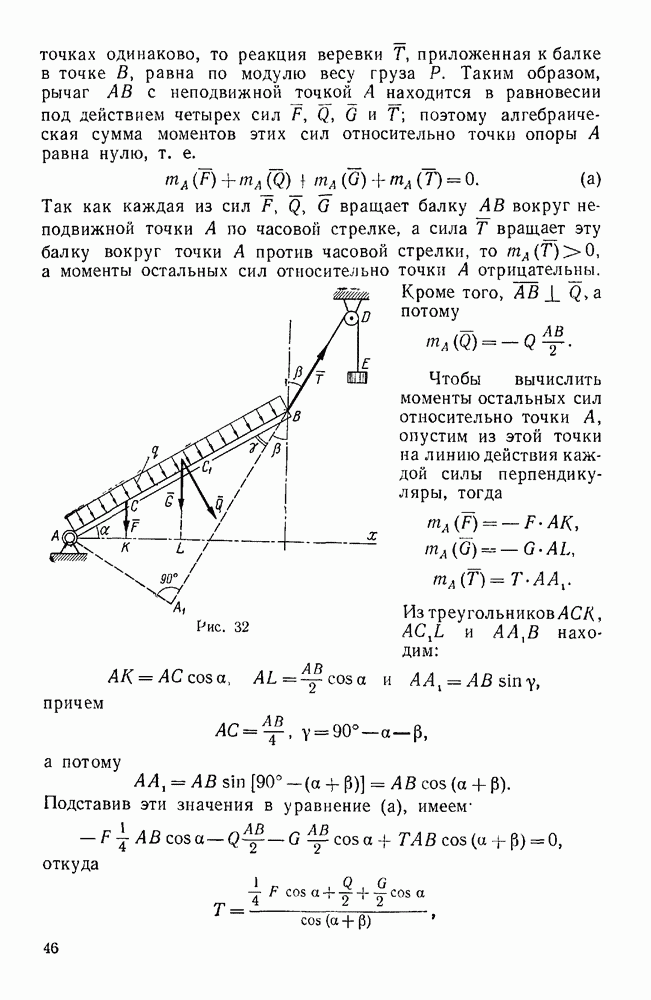
Пример 9. Груз весом  подвешен при помощи каната, перекинутого через небольшой блок А и идущего к лебедке D. Определить усилия в стержнях АС и В А крана.
подвешен при помощи каната, перекинутого через небольшой блок А и идущего к лебедке D. Определить усилия в стержнях АС и В А крана.
Углы, определяющие направления стержней и каната, заданы на рис. 23.
Решение. Рассмотрим равновесие узла А крана, к которому приложены сила  реакции стержней АС и АВ и сила натяжения каната AD. Обозначим реакцию стержня АВ через
реакции стержней АС и АВ и сила натяжения каната AD. Обозначим реакцию стержня АВ через  , реакцию стержня АС через
, реакцию стержня АС через  и силу натяжения каната AD через Т.
и силу натяжения каната AD через Т.
Реакции стержней  и
и  направим вдоль этих стержней от узла А; сила Т направлена, очевидно, вдоль каната от А к D, так как канат растянут. Кроме того,
направим вдоль этих стержней от узла А; сила Т направлена, очевидно, вдоль каната от А к D, так как канат растянут. Кроме того,  , так как при отсутствии трения в блоке натяжение каната, перекинутого через этот блок, во всех точках
, так как при отсутствии трения в блоке натяжение каната, перекинутого через этот блок, во всех точках  .
.
Так как узел А находится в равновесии под действием сил  , то можно составить два уравнения равновесия этой системы сходящихся сил.
, то можно составить два уравнения равновесия этой системы сходящихся сил.

Рис 23.
Выберем оси координат, как указано на рис. 23, найдем проекцию каждой силы на эти оси и составим два уравнения равновесия, приравнивая нулю сумму проекций всех сил на каждую из координатных осей:

Из второго уравнения находим:

Теперь из первого уравнения получаем:

Так как полученное значение силы  отрицательно, то сила
отрицательно, то сила  имеет направление, противоположное направлению, выбранному на рисунке, т. е. она направлена от С к А, и, следовательно, стержень АС сжат.
имеет направление, противоположное направлению, выбранному на рисунке, т. е. она направлена от С к А, и, следовательно, стержень АС сжат.
Задачу можно решить и геометрически, построив замкнутый многоугольник сил  (рис. 24).
(рис. 24).
Направления сил  и
и  найдем после того, как обойдем периметр построенного силового многоугольника, причем направление этого обхода определяется направлением известных сил Р и Т.
найдем после того, как обойдем периметр построенного силового многоугольника, причем направление этого обхода определяется направлением известных сил Р и Т.

Рис. 24.
Измерив стороны  силового многоугольника выбранной единицей масштаба, найдем величину
силового многоугольника выбранной единицей масштаба, найдем величину  . Так как углы между силами
. Так как углы между силами  заданы, то можно найти углы силового многоугольника, а затем вычислить и длины двух неизвестных его сторон. В самом деле, из построения силового многоугольника следует, что
заданы, то можно найти углы силового многоугольника, а затем вычислить и длины двух неизвестных его сторон. В самом деле, из построения силового многоугольника следует, что

а потому

Если соединим точки а и с, то треугольник  будет равнобедренным, так как
будет равнобедренным, так как  , а потому
, а потому

Отсюда следует, что

и

Применяя теперь к треугольнику  теорему синусов, получим:
теорему синусов, получим:

откуда

Чтобы определить, будут ли стержни АВ и АС сжаты или растянуты (рис. 23), перенесем векторы  и
и  с силового многоугольника на стержни АВ и АС, тогда сила
с силового многоугольника на стержни АВ и АС, тогда сила  будет направлена к узлу А, а сила будет направлена от узла А, а потому стержень АС сжат, а стержень АВ растянут.
будет направлена к узлу А, а сила будет направлена от узла А, а потому стержень АС сжат, а стержень АВ растянут.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
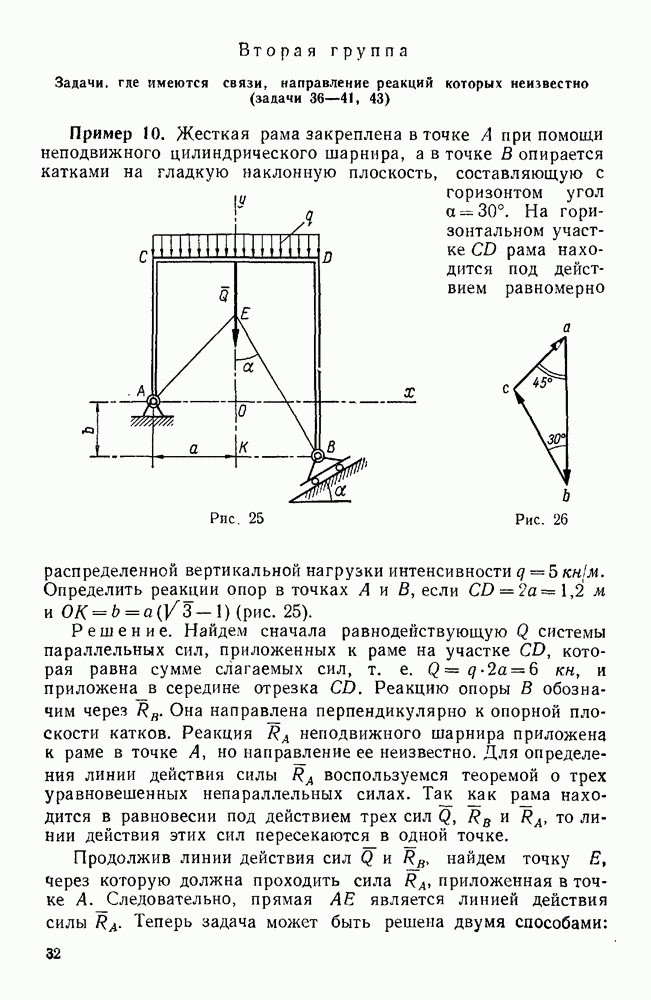
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
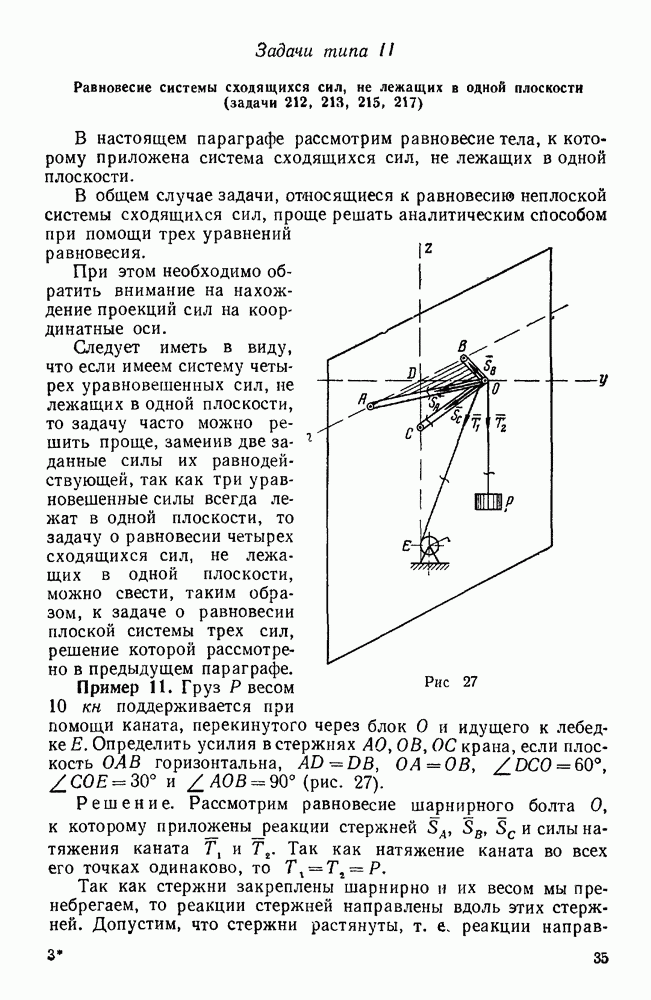
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
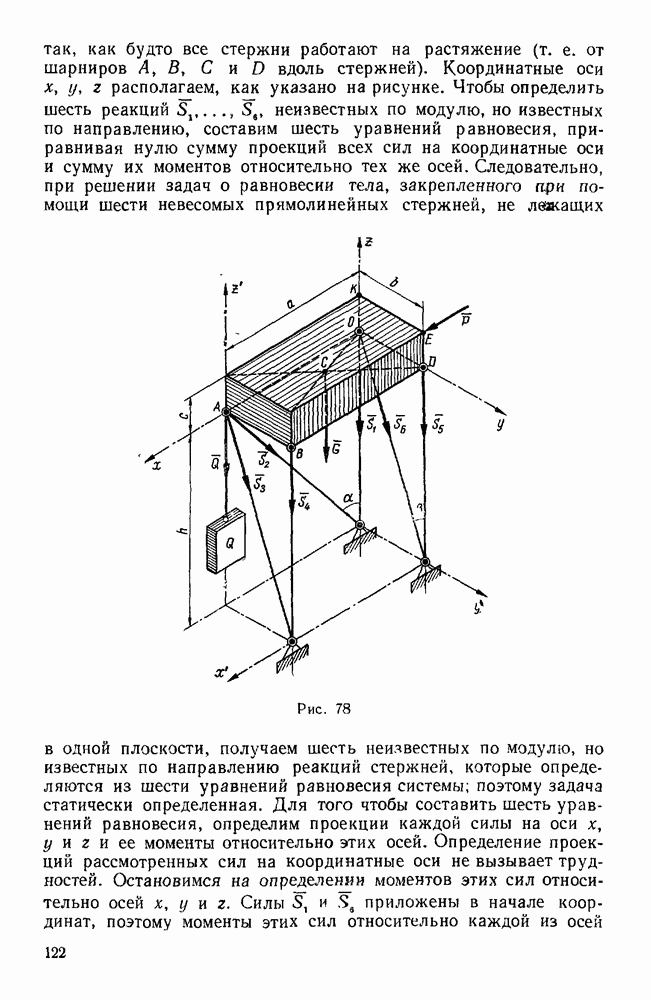
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
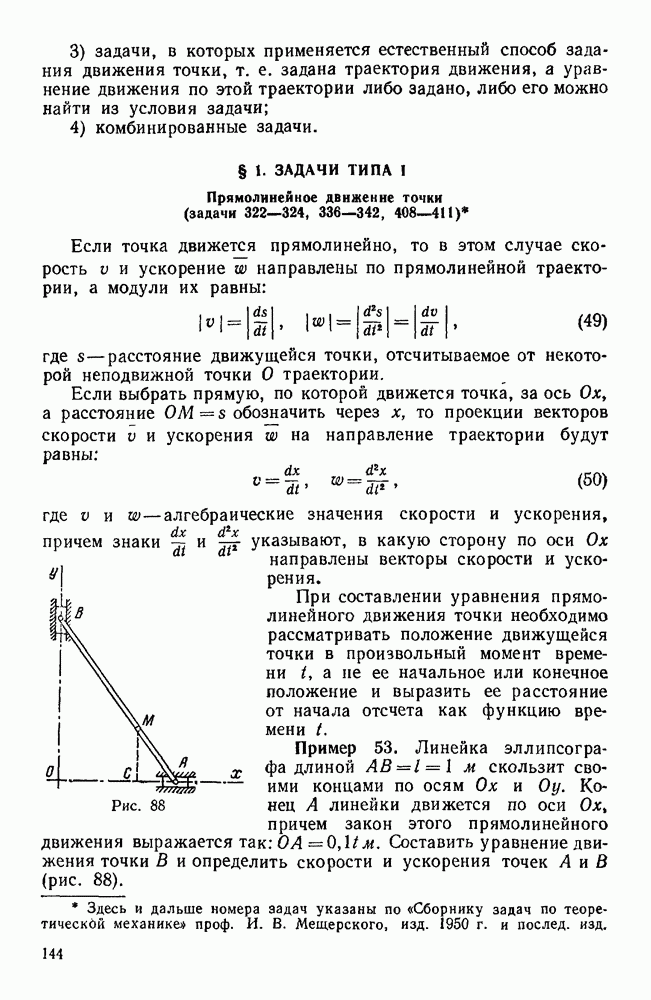
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
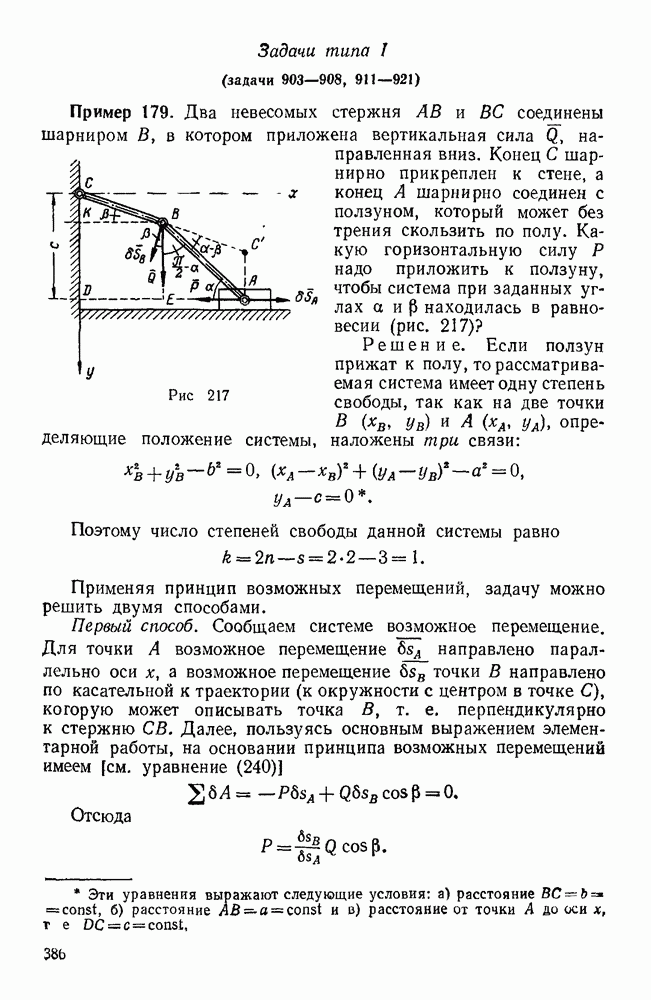
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
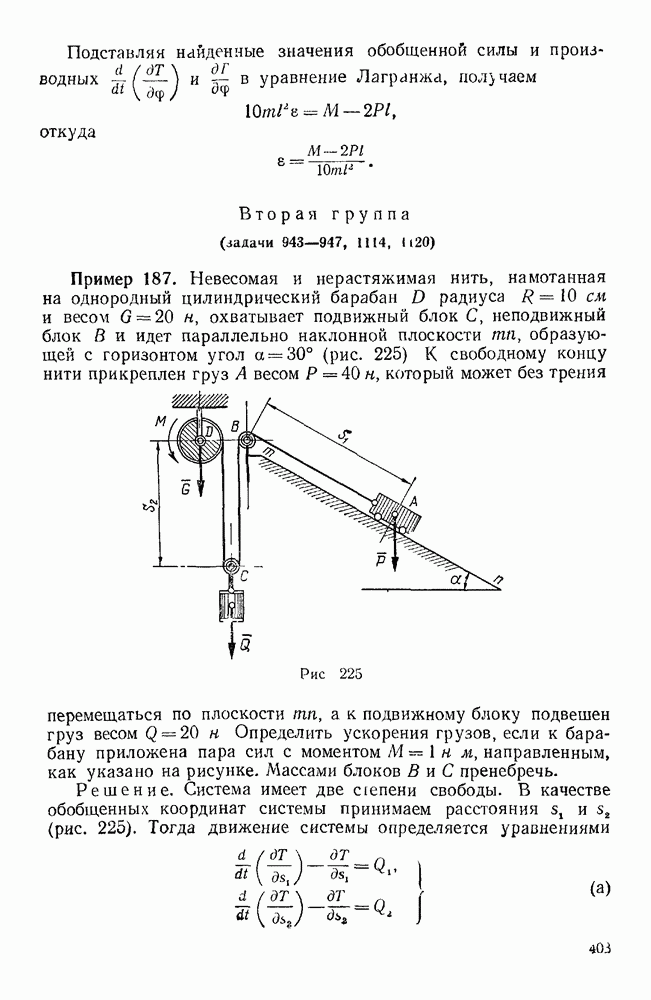
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА