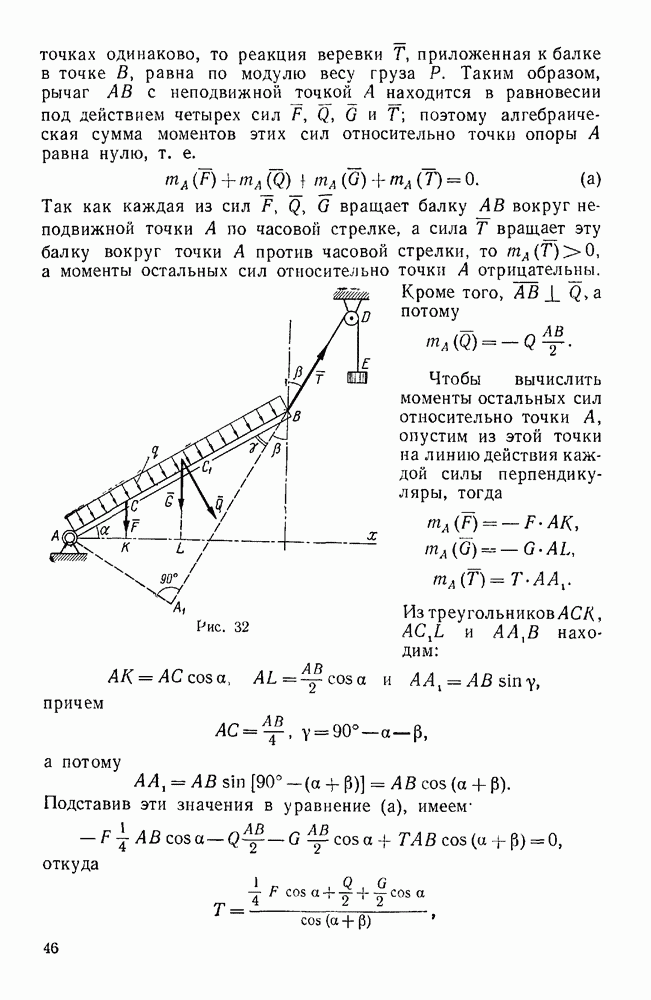
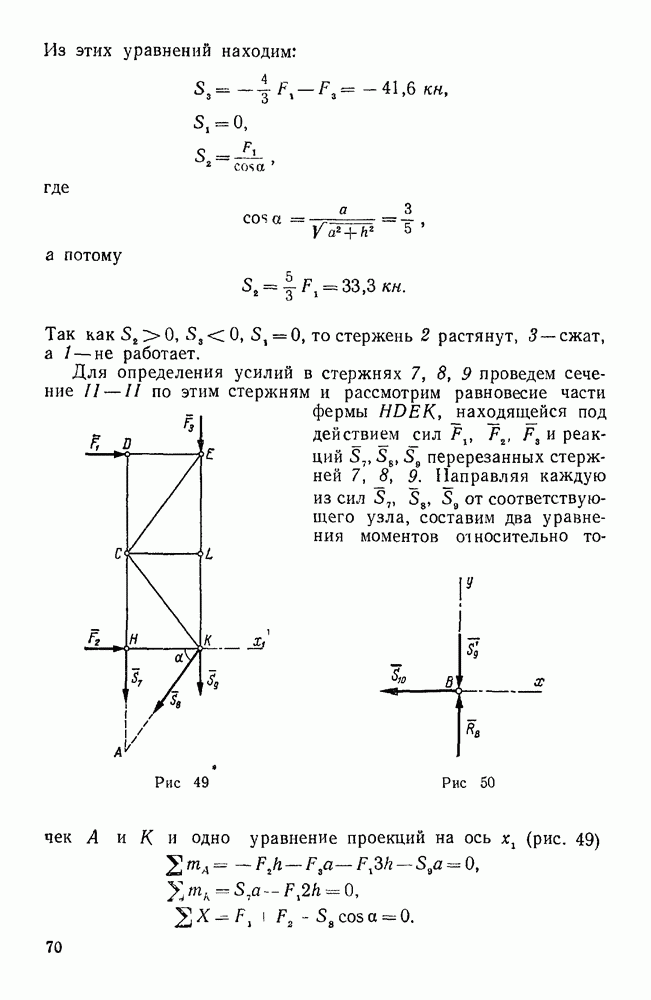
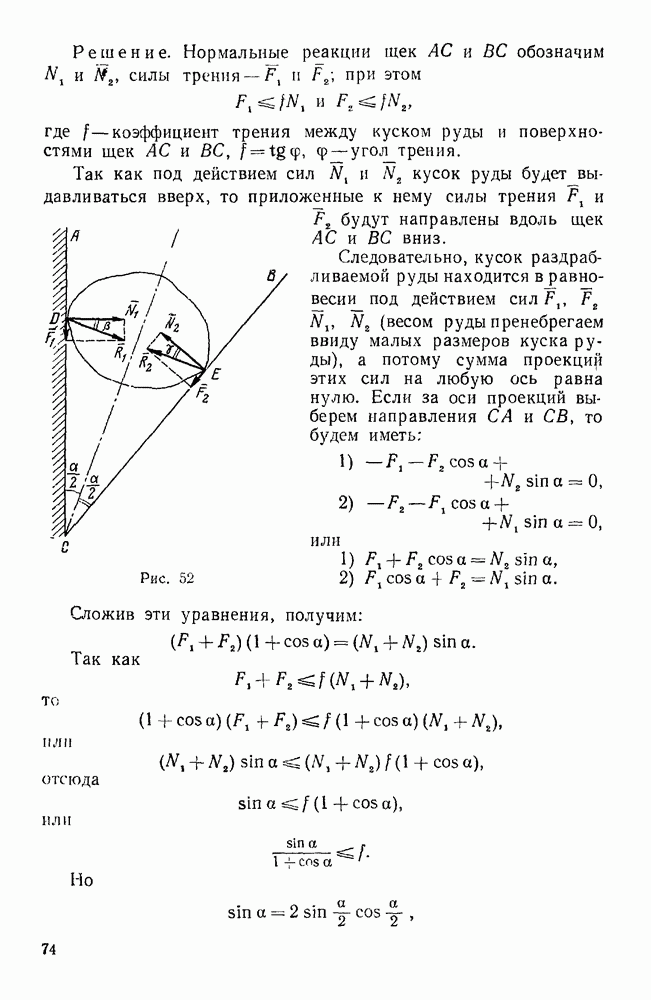
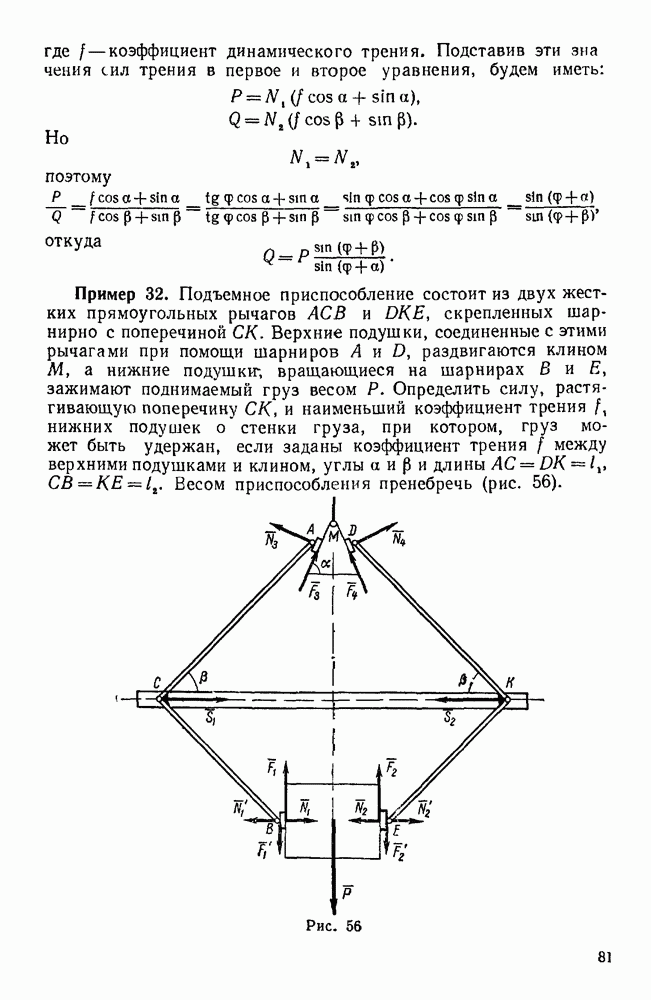
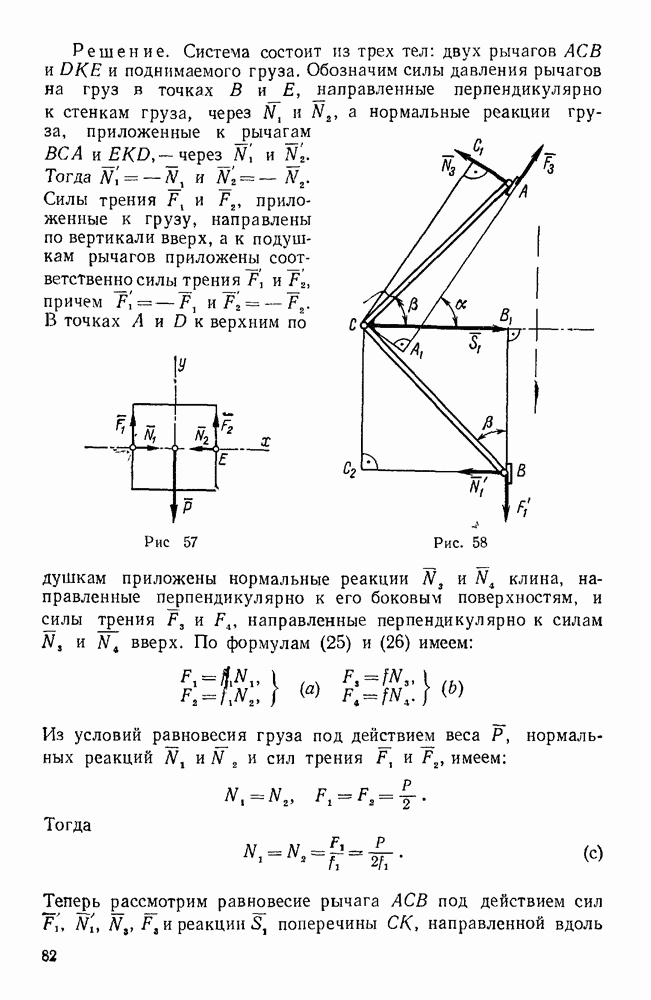
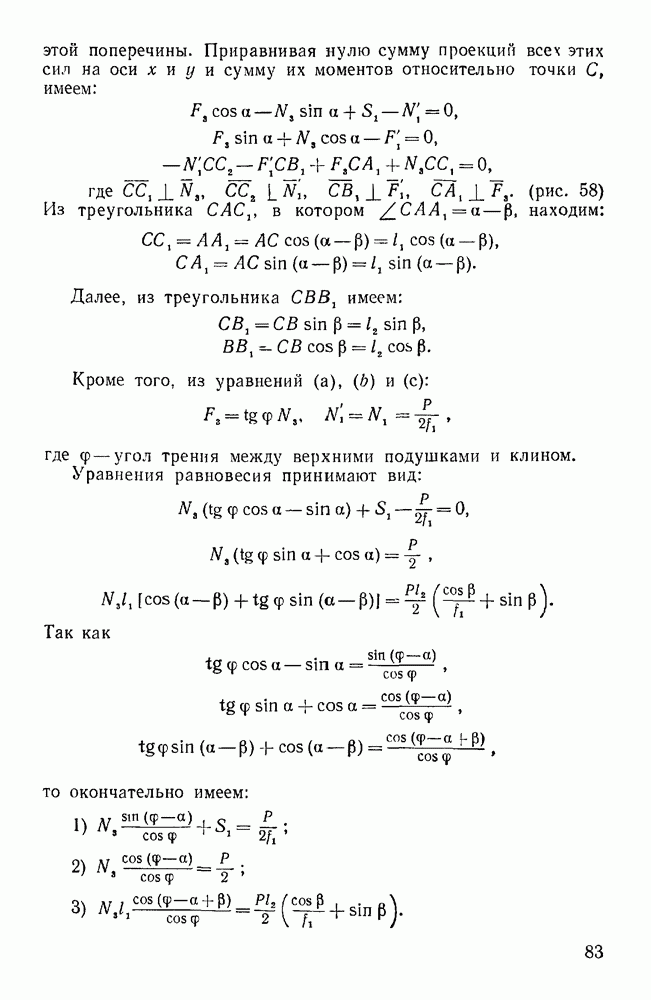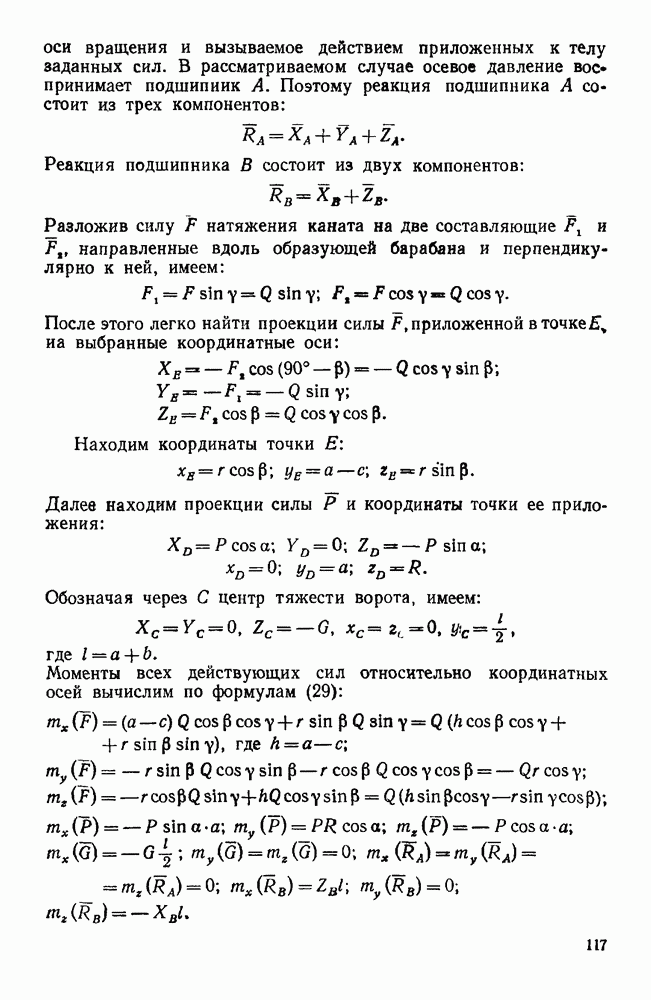| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
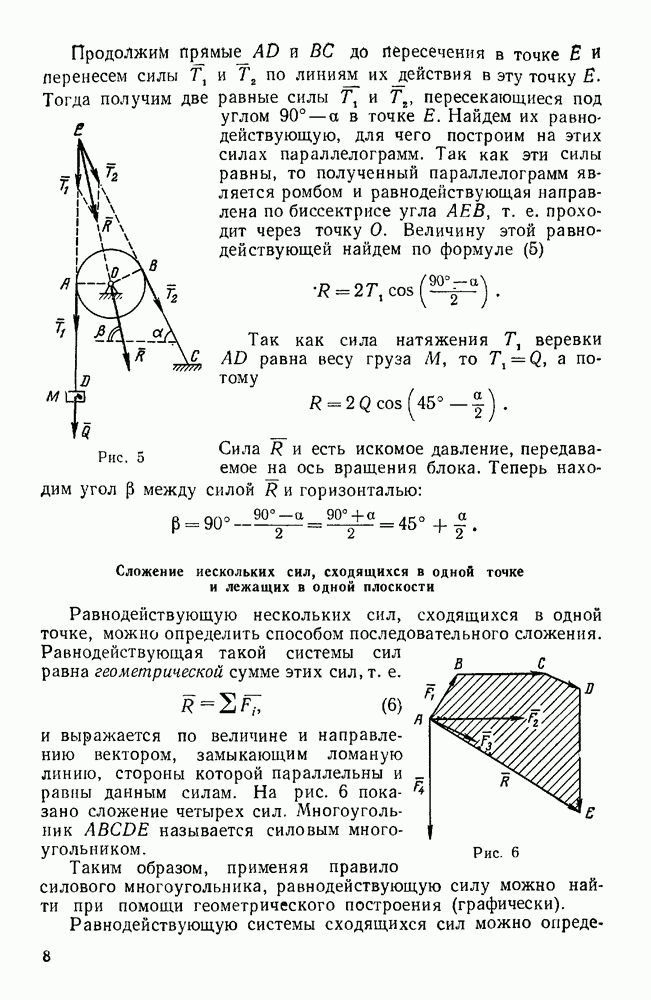
§ 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
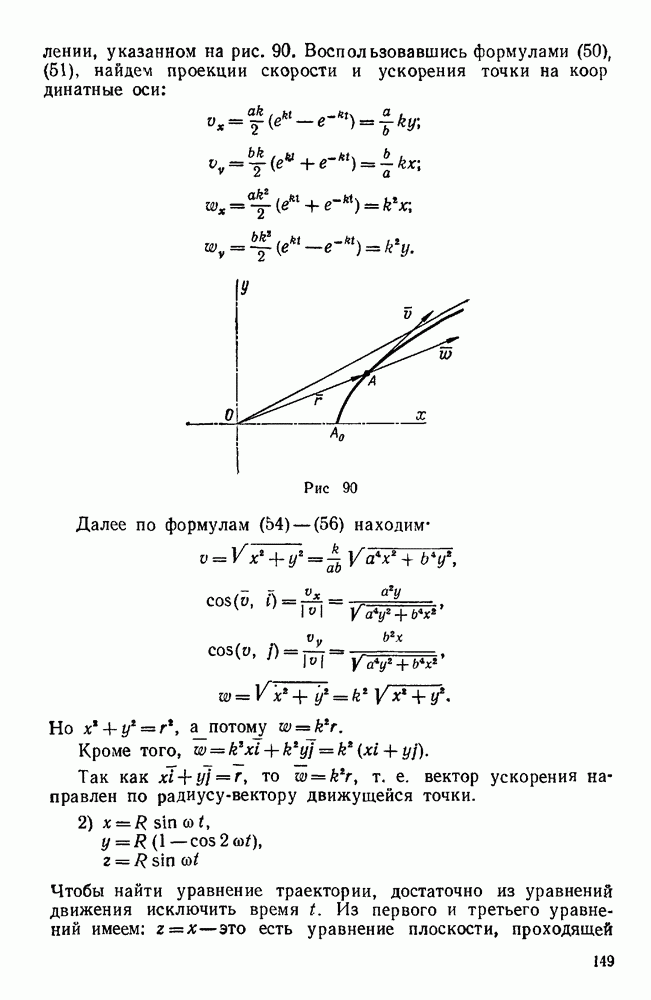
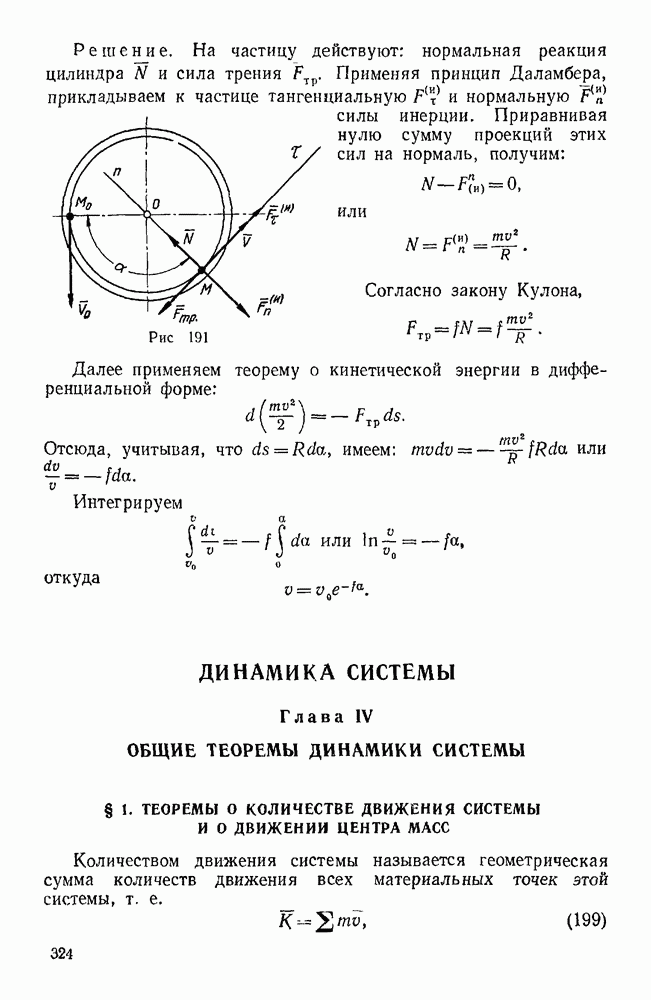
Если относительное и переносное движения тела являются вращательными вокруг пересекающихся осей (рис. 135), то распределение абсолютных скоростей в теле в каждый данный момент такое, как при вращательном движении вокруг мгновенной оси, проходящей через точку пересечения осей составляющих вращений и направленной по диагонали параллелограмма, построенного на угловых скоростях этих вращений. Вектор абсолютной угловой скорости тела равен геометрической сумме векторов его переносной и относительной угловых скоростей:

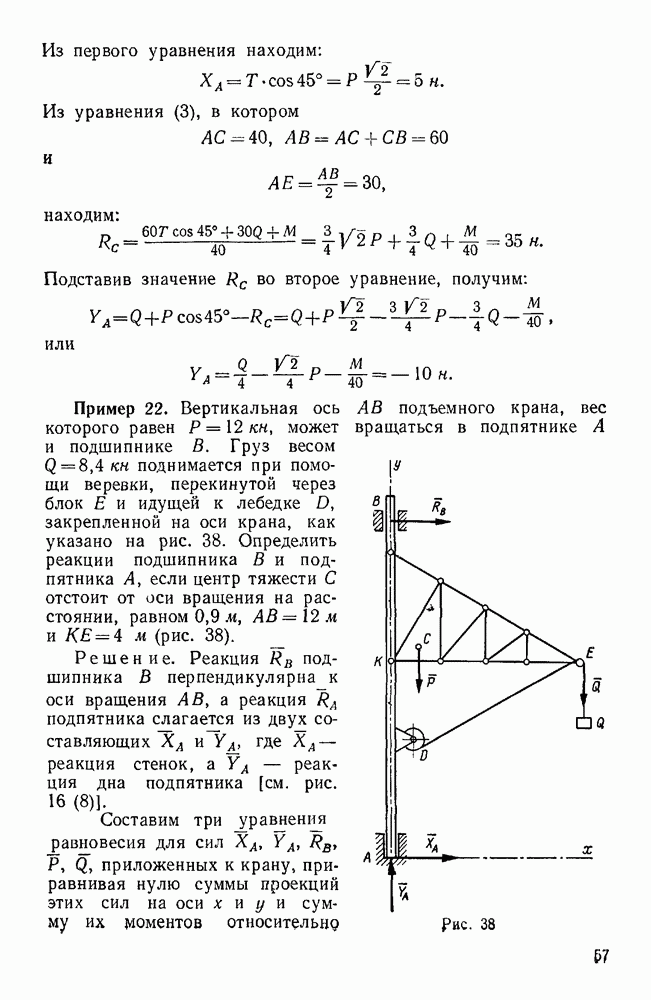
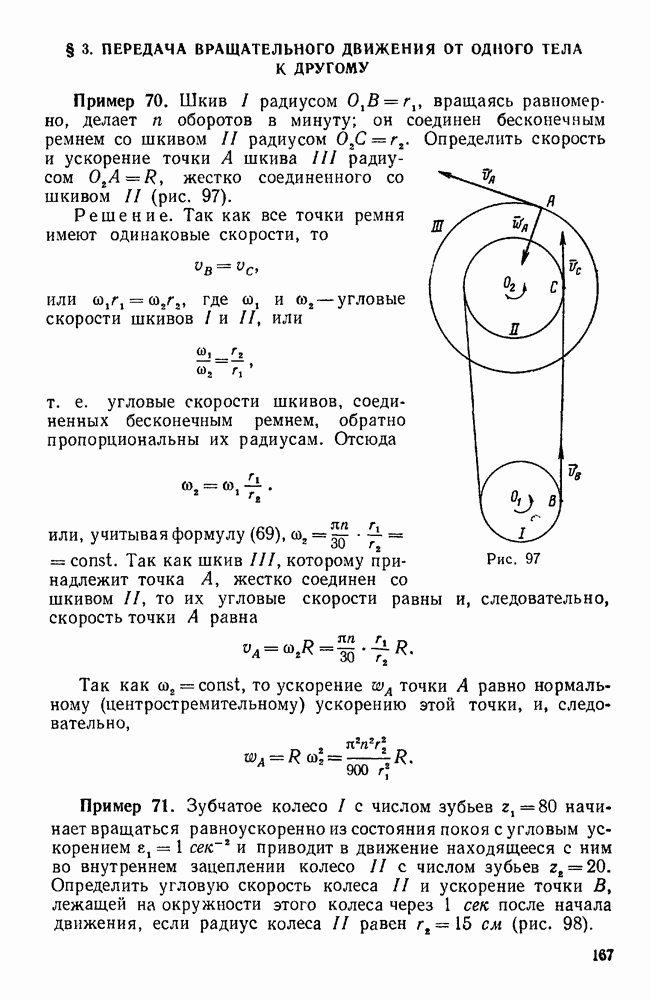
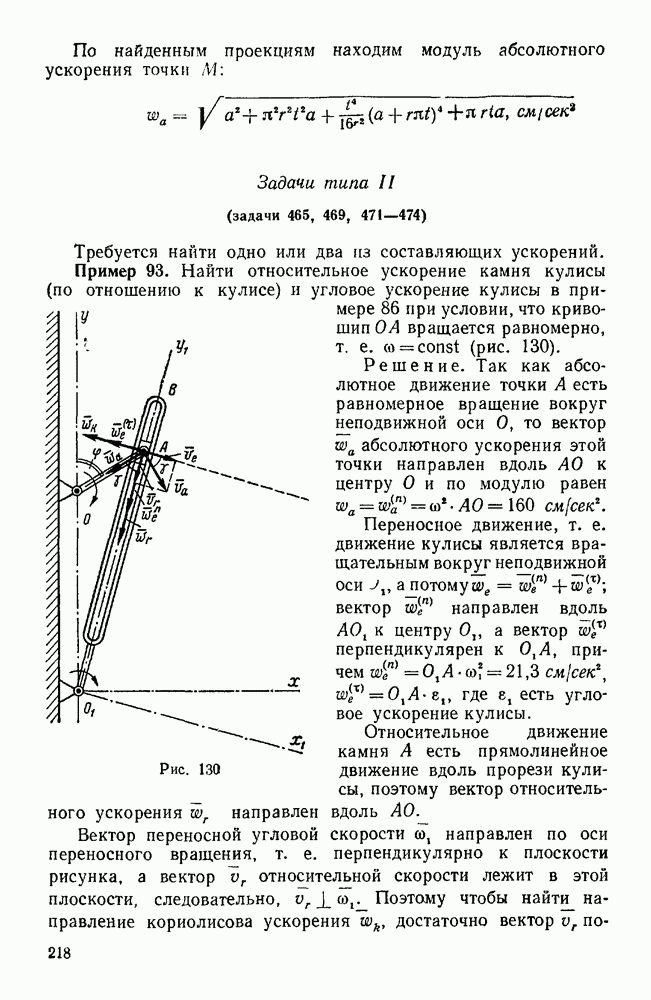
Пример 95. Зная угловую скорость  водила H планетарной конической передачи (рис. 136, а) найти относительную и абсолютную угловые скорости колеса
водила H планетарной конической передачи (рис. 136, а) найти относительную и абсолютную угловые скорости колеса  , находящегося в зацеплении с неподвижным колесом 2.
, находящегося в зацеплении с неподвижным колесом 2.
Даны радиусы и колес, а также углы  и
и  растворов их начальных конусов.
растворов их начальных конусов.

Рис. 135.
Решение. Движение колеса  складывается из вращательного движения водила H вокруг оси
складывается из вращательного движения водила H вокруг оси  с угловой скоростью
с угловой скоростью  (переносное движение) и вращательного движения вокруг оси
(переносное движение) и вращательного движения вокруг оси  по отношению к водилу H с некоторой угловой скоростью
по отношению к водилу H с некоторой угловой скоростью  (относительное движение). При указанном на рис. 136, а круговой стрелкой направлении вращения водила вектор сон переносной угловой скорости колеса 1 направлен по оси
(относительное движение). При указанном на рис. 136, а круговой стрелкой направлении вращения водила вектор сон переносной угловой скорости колеса 1 направлен по оси  вниз. Вектор
вниз. Вектор  его относительной угловой скорости направлен по оси
его относительной угловой скорости направлен по оси  . Мгновенная ось абсолютного движения колеса 1 совпадает с общей образующей ОР начальных конусов колес 1 и 2, так как при работе механизма эти конусы должны катиться один по другому без скольжения, что обеспечивается соответствующей формой зубьев находящихся в зацеплении конических зубчатых колес. Таким образом, вектор
. Мгновенная ось абсолютного движения колеса 1 совпадает с общей образующей ОР начальных конусов колес 1 и 2, так как при работе механизма эти конусы должны катиться один по другому без скольжения, что обеспечивается соответствующей формой зубьев находящихся в зацеплении конических зубчатых колес. Таким образом, вектор  угловой скорости колеса 1 направлен по линии ОР. Применяя формулу (107), имеем:
угловой скорости колеса 1 направлен по линии ОР. Применяя формулу (107), имеем:

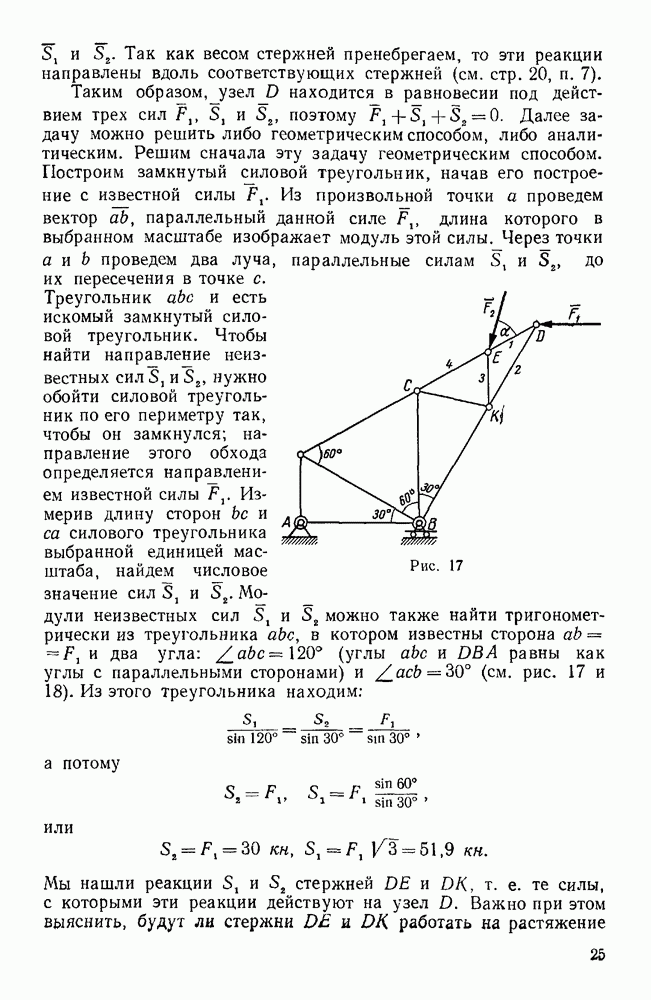
Здесь и в дальнейшем одной чертой внизу подчеркнуты векторы, для которых известны только линии действия, двумя чертами — векторы, известные и по модулю и по направлению.
Для построения параллелограмма угловых скоростей, соответствующего этому векторному равенству, от центра О пересечения осей рассматриваемых вращений откладываем заданный вектор  (рис. 136, а), из конца
(рис. 136, а), из конца  этого вектора проводим прямую, параллельную оси
этого вектора проводим прямую, параллельную оси  до пересечения в точке
до пересечения в точке  с осью ОР абсолютного вращения и дополняем полученный треугольник
с осью ОР абсолютного вращения и дополняем полученный треугольник  до параллелограмма, для чего из точки
до параллелограмма, для чего из точки  проводим прямую, параллельную
проводим прямую, параллельную  , до пересечения в точке
, до пересечения в точке  с осью
с осью  . Векторы
. Векторы  дают соответственно искомую относительную угловую скорость
дают соответственно искомую относительную угловую скорость  и абсолютную угловую скорость со, колеса 1. Вместо построения параллелограмма угловых скоростей можно ограничиться построением треугольника угловых скоростей, который лучше вынести за пределы механизма (рис. 136, б).
и абсолютную угловую скорость со, колеса 1. Вместо построения параллелограмма угловых скоростей можно ограничиться построением треугольника угловых скоростей, который лучше вынести за пределы механизма (рис. 136, б).
Для этого от произвольного центра о откладываем заданный вектор  , а из конца
, а из конца  и начала о этого вектора проводим до взаимного пересечения в точке
и начала о этого вектора проводим до взаимного пересечения в точке  , прямые
, прямые  (т. е. параллельно оси
(т. е. параллельно оси  ) и
) и  (т. е. параллельно оси ОР). Стороны полученного треугольника
(т. е. параллельно оси ОР). Стороны полученного треугольника  , и выражают собой заданную и искомые угловые скорости, т. е.
, и выражают собой заданную и искомые угловые скорости, т. е.  . Из параллелограмма или треугольника угловых скоростей имеем:
. Из параллелограмма или треугольника угловых скоростей имеем:

где  — межосевой угол конической передачи.
— межосевой угол конической передачи.
Отсюда относительная угловая скорость колеса 1 по отношению к водилу H равна  . Абсолютная угловая скорость колеса 1 равна
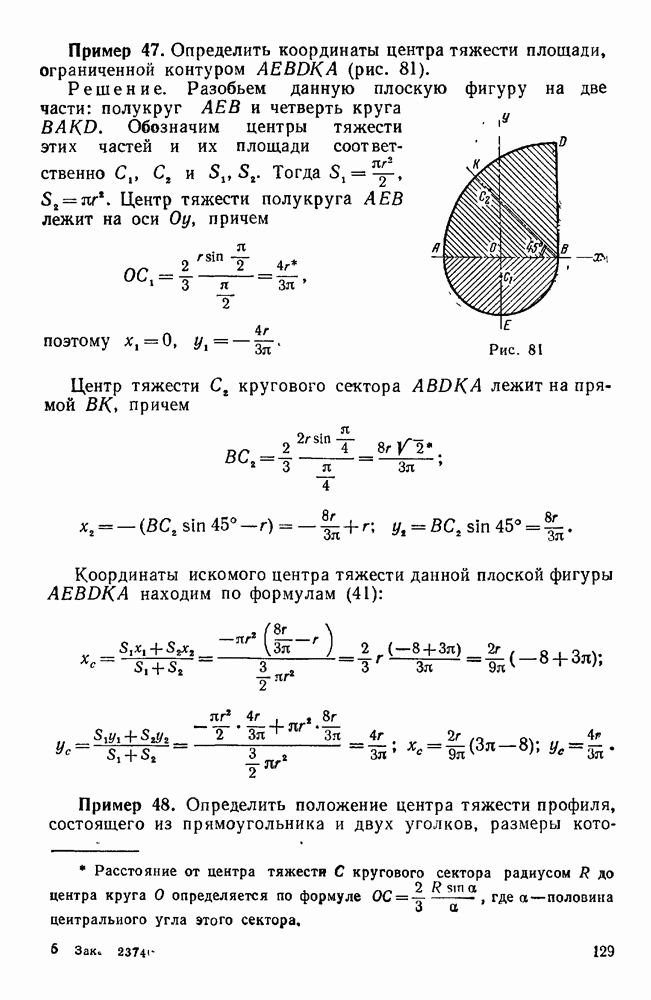
. Абсолютная угловая скорость колеса 1 равна  . Модуль абсолютной угловой скорости можно определить также по теореме косинусов:
. Модуль абсолютной угловой скорости можно определить также по теореме косинусов:

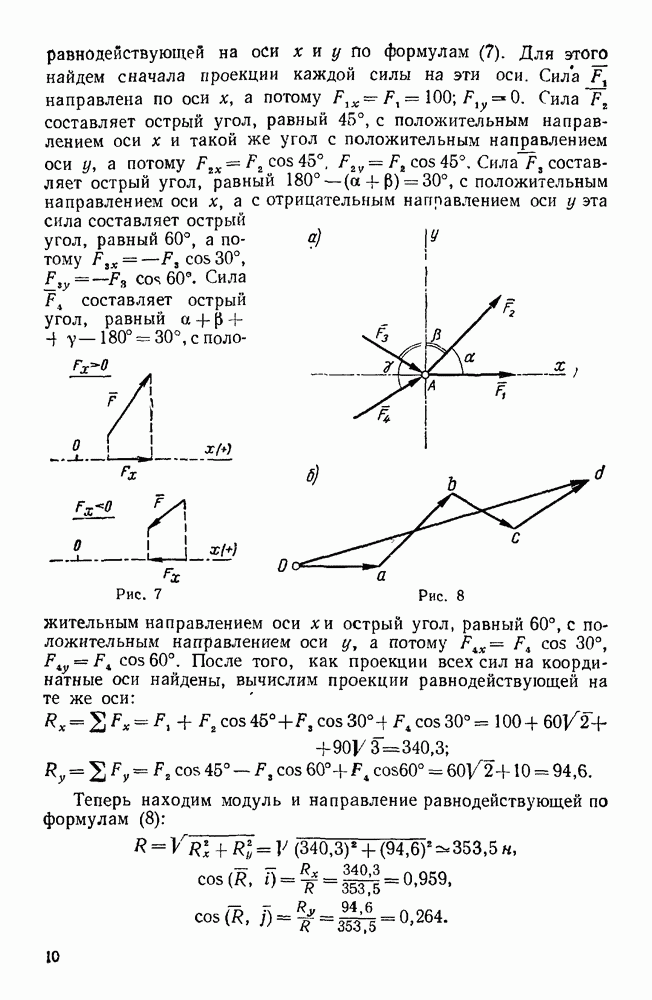
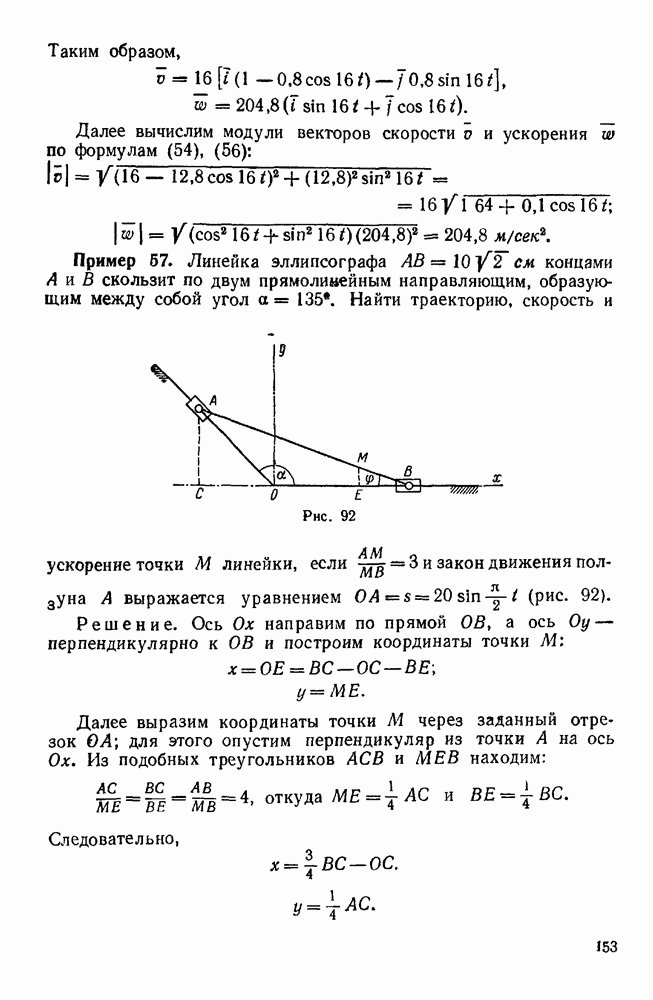
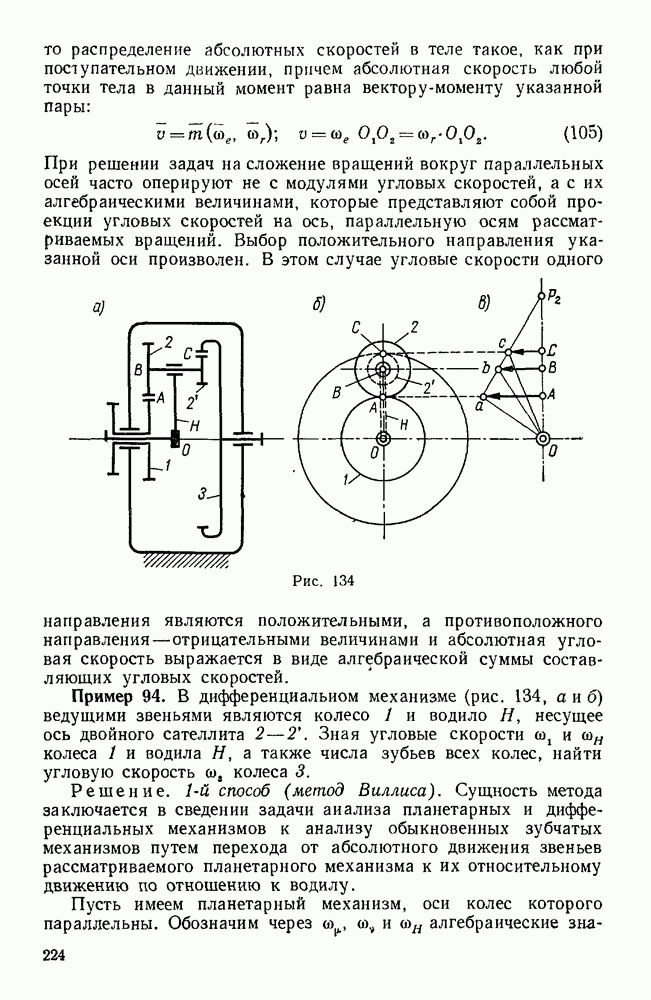
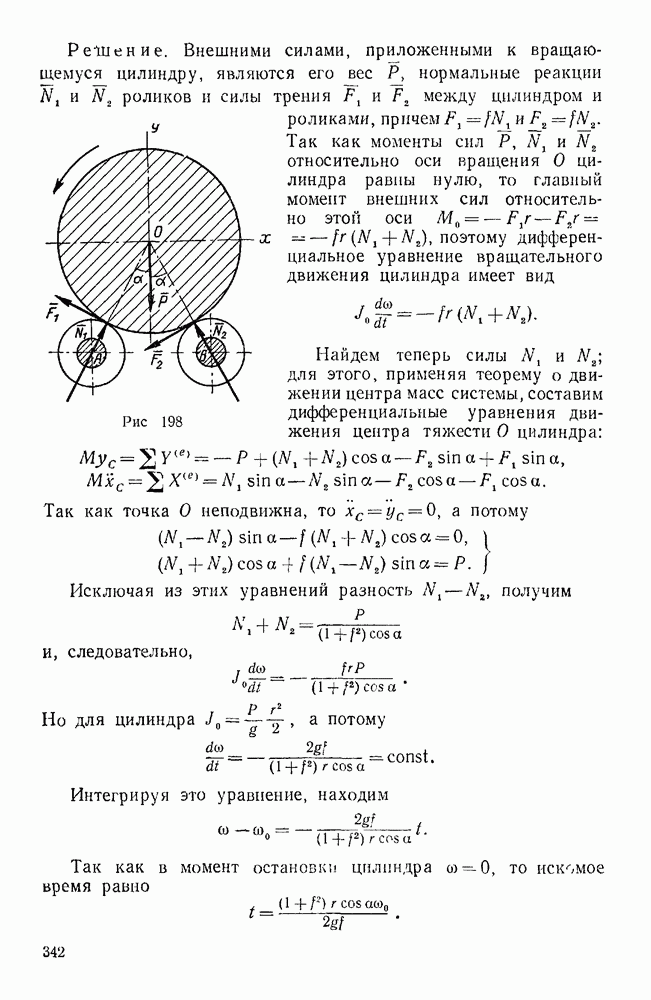
Пример 96. На ведущем валу  планетарной передачи с коническими колесами (рис. 137, а) заклинено колесо 1, находящееся в зацеплении с колесами 2 двойных сателлитов, свободно сидящих на осях водила H. Колесо 2 находится в зацеплении с неподвижным колесом 4, а колесо
планетарной передачи с коническими колесами (рис. 137, а) заклинено колесо 1, находящееся в зацеплении с колесами 2 двойных сателлитов, свободно сидящих на осях водила H. Колесо 2 находится в зацеплении с неподвижным колесом 4, а колесо  - с колесом 3, заклиненным на ведомом валу II. Определить передаточное отношение между валами
- с колесом 3, заклиненным на ведомом валу II. Определить передаточное отношение между валами  .
.
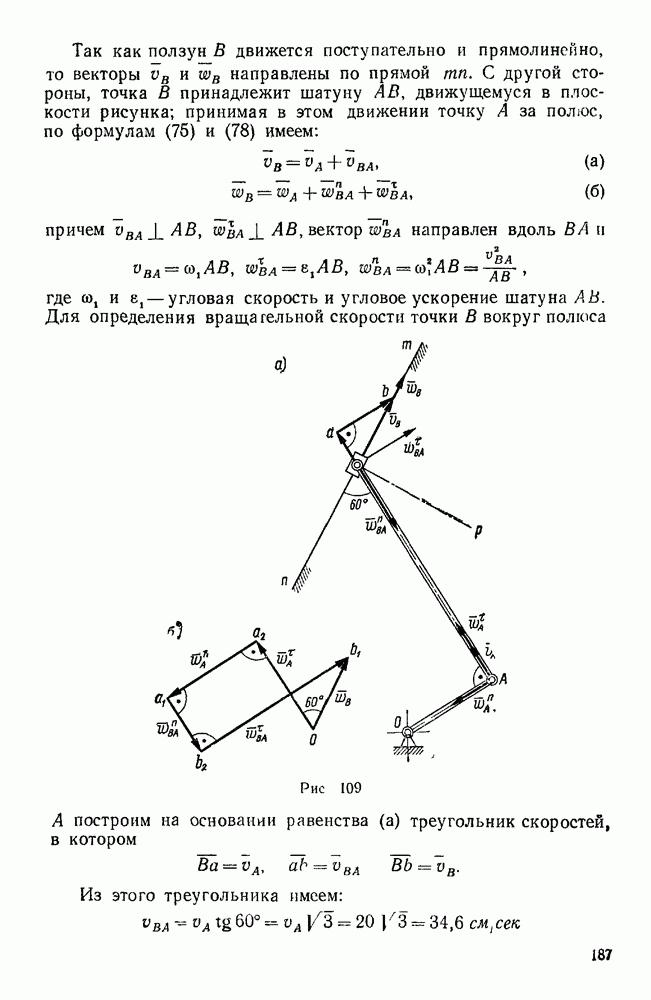
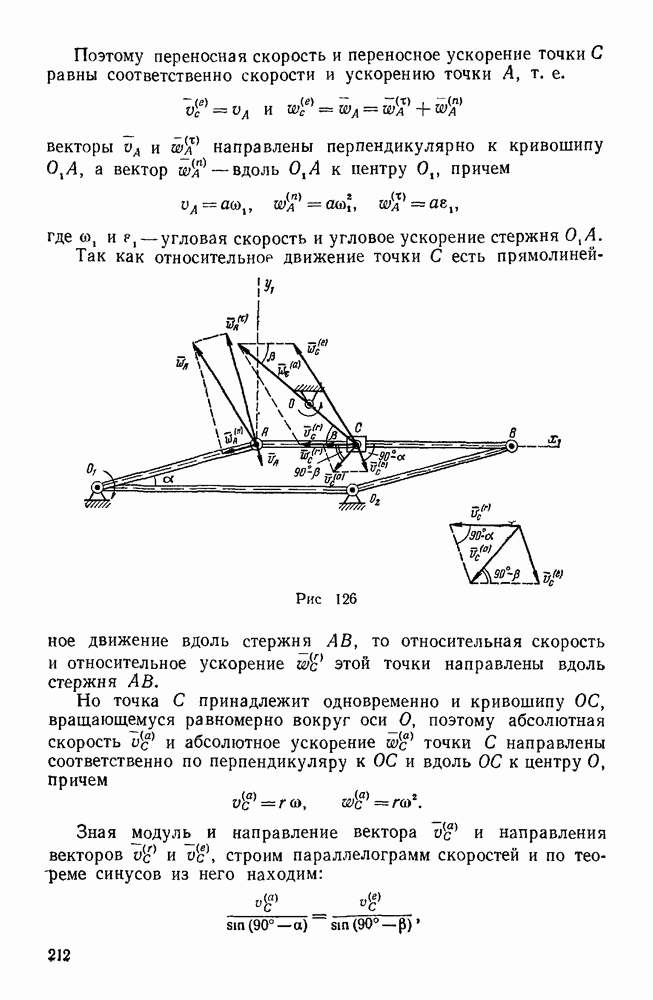
Решение. 1-й способ (метод Виллиса). Обозначим через  радиусы колес 1, 2, 2, 3, 4. Перейдем от абсолютного движения звеньев рассматриваемого механизма к их относительному движению по отношению к водилу H.
радиусы колес 1, 2, 2, 3, 4. Перейдем от абсолютного движения звеньев рассматриваемого механизма к их относительному движению по отношению к водилу H.

Рис. 136.
Для этого сообщим мысленно всей системе вращение вокруг  с угловой скоростью
с угловой скоростью  . Тогда водило, несущее ось сателлитов, остановится и мы получим обыкновенную коническую передачу, колеса которой вращаются вокруг неподвижных осей с угловыми скоростями
. Тогда водило, несущее ось сателлитов, остановится и мы получим обыкновенную коническую передачу, колеса которой вращаются вокруг неподвижных осей с угловыми скоростями  , где 1, 3, 4. Пользуясь методом Виллиса, установим связь между угловыми скоростями колес 1, 3, 4 и водила H.
, где 1, 3, 4. Пользуясь методом Виллиса, установим связь между угловыми скоростями колес 1, 3, 4 и водила H.

Рис. 137.
Так как звенья I, 3, 4 и H имеют общую ось вращения, то угловые скорости этих звеньев являются параллельными векторами и их можно рассматривать как алгебраические величины.
Применяя формулу Виллиса к колесам 1 и 4, имеем:

где  — относительные угловые скорости колес
— относительные угловые скорости колес  и 4 по отношению к водилу H.
и 4 по отношению к водилу H.
Передаточное отношение в данном случае считаем отрицательным, Так как колеса 1 и 4 при неподвижном водиле (при неподвижной оси колеса 2) вращаются в разные стороны (линейные скорости точек А и В этих колес при неподвижной оси колеса 2 имеют противоположные направления). Колесо 2 здесь играет роль паразитного колеса, его радиус не влияет на величину передаточного отношения между колесами 1 и 4. Так как абсолютная угловая скорость четвертого колеса  , то из последнего уравнения находим:
, то из последнего уравнения находим:

Применяя вторично формулу Виллиса, уже теперь к колесам 3 и 4, имеем:

Передаточное отношение в данном случае равно произведению двух передаточных отношений (от колеса 3 к колесу 2 и от колеса 2 к колесу 4), причем это передаточное отношение является величиной положительной, так как колеса 3 и 4 при неподвижной оси колес 2 и 2 вращаются в одну сторону (линейные скорости точек В и С имеют одинаковое направление). Таким образом,

Равенства (а) и (б) выражают абсолютные угловые скорости колес  и 3 через угловую скорость водила. Разделив равенство (а) на (б), получим передаточное отношение между ведущим и ведомым валами рассматриваемой передачи, т. е. передаточное отношение между колесами 1 и 3 при неподвижном колесе 4:
и 3 через угловую скорость водила. Разделив равенство (а) на (б), получим передаточное отношение между ведущим и ведомым валами рассматриваемой передачи, т. е. передаточное отношение между колесами 1 и 3 при неподвижном колесе 4:

В этой формуле отношения радиусов находящихся в зацеплении колес могут быть заменены отношениями чисел их зубьев.
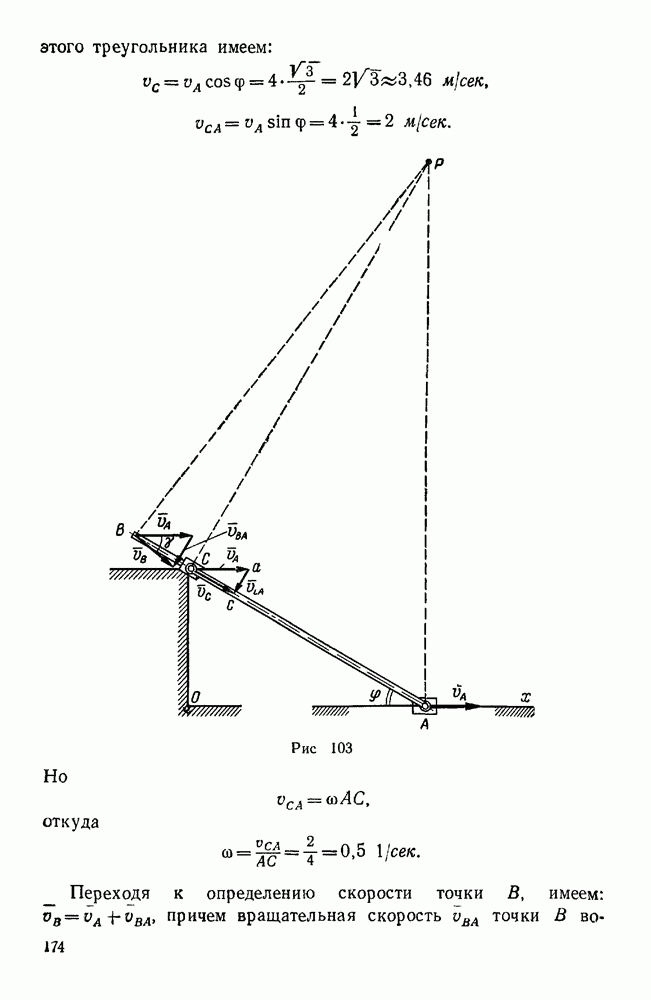
2-й способ (геометрический). Этот способ основан на построении векторных треугольников угловых скоростей. При построении указанных треугольников исходят из векторных уравнений, выражающих зависимость между угловыми скоростями звеньев рассматриваемого механизма.
Принимая движение колеса 2 за переносное движение и применяя формулу (107) к колесу 1 имеем:

где  — абсолютная угловая скорость колеса
— абсолютная угловая скорость колеса  , известная по Модулю и направлению (что показывают две черты снизу);
, известная по Модулю и направлению (что показывают две черты снизу);
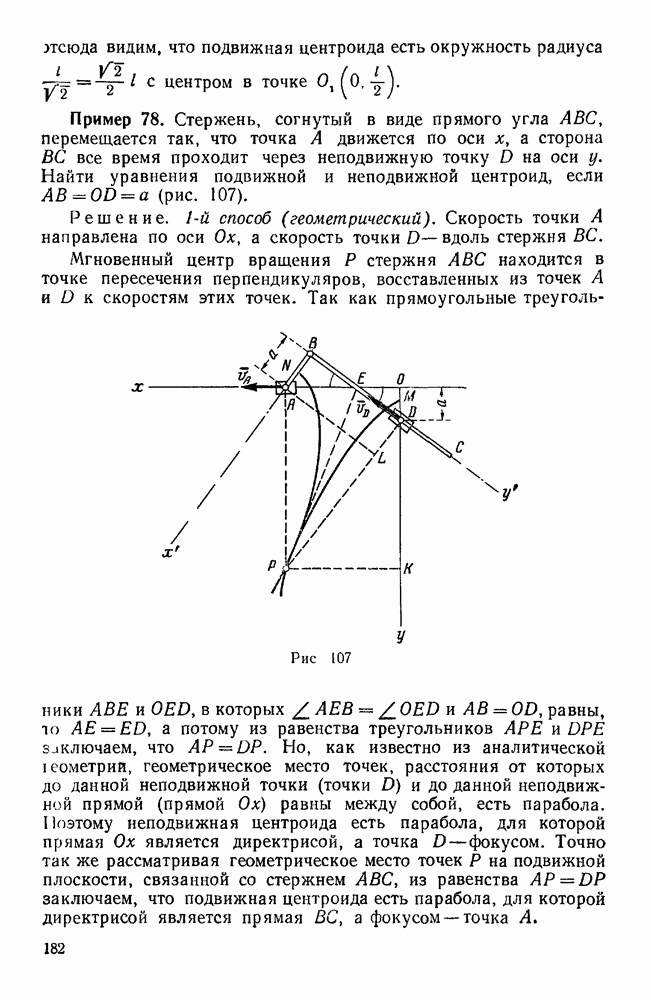
 абсолютная угловая скорость колеса 2, которая по отношению к колесу 1 является переносной угловой скоростью и для которой известна линия действия (что показывает одна черта снизу);
абсолютная угловая скорость колеса 2, которая по отношению к колесу 1 является переносной угловой скоростью и для которой известна линия действия (что показывает одна черта снизу);
 относительная угловая скорость колеса 1 по отношению к колесу 2, для которой линия действия тоже известна (что показывает одна черта снизу). Вектор
относительная угловая скорость колеса 1 по отношению к колесу 2, для которой линия действия тоже известна (что показывает одна черта снизу). Вектор  направлен по мгновенной оси вращения колеса 2, которая совпадает с общей образующей ОБ начальных конусов колеса 2 и неподвижного колеса 4, а вектор
направлен по мгновенной оси вращения колеса 2, которая совпадает с общей образующей ОБ начальных конусов колеса 2 и неподвижного колеса 4, а вектор  — по общей образующей ОА начальных конусов колес 1 и 2 (рис. 137, а).
— по общей образующей ОА начальных конусов колес 1 и 2 (рис. 137, а).
Для построения треугольника угловых скоростей, соответствующего последнему векторному уравнению, от произвольного центра о (рис. 137,б) откладываем заданный вектор  , а из начала о и конца
, а из начала о и конца  этого вектора проводим до взаимного пересечения в точке
этого вектора проводим до взаимного пересечения в точке  прямые
прямые  . Тогда имеем:
. Тогда имеем:

Определив угловую скорость  колеса 2, переходим к определению угловой скорости и, колеса 3. Принимая опять движение колеса 2 за переносное, имеем:
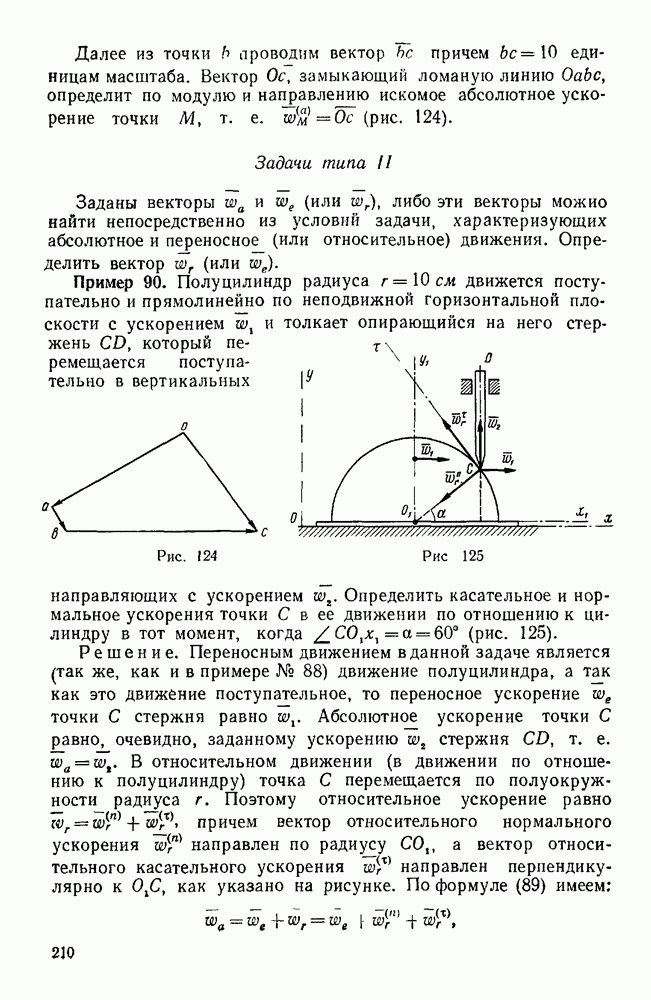
колеса 2, переходим к определению угловой скорости и, колеса 3. Принимая опять движение колеса 2 за переносное, имеем:

Вектор и, направлен по той же оси I—II, что и вектор  , а вектор
, а вектор  общей образующей ОС колес 3 и 2. Для построения треугольника угловых скоростей достаточно из точки
общей образующей ОС колес 3 и 2. Для построения треугольника угловых скоростей достаточно из точки  провести прямую
провести прямую  ОС до пересечения в точке
ОС до пересечения в точке  с прямой
с прямой  что дает:
что дает:

Угловую скорость юн водила и угловую скорость двойного сателлита  по отношению к водилу находим на основании уравнения
по отношению к водилу находим на основании уравнения

Вектор (он направлен по оси I — II, а вектор  оси
оси  .
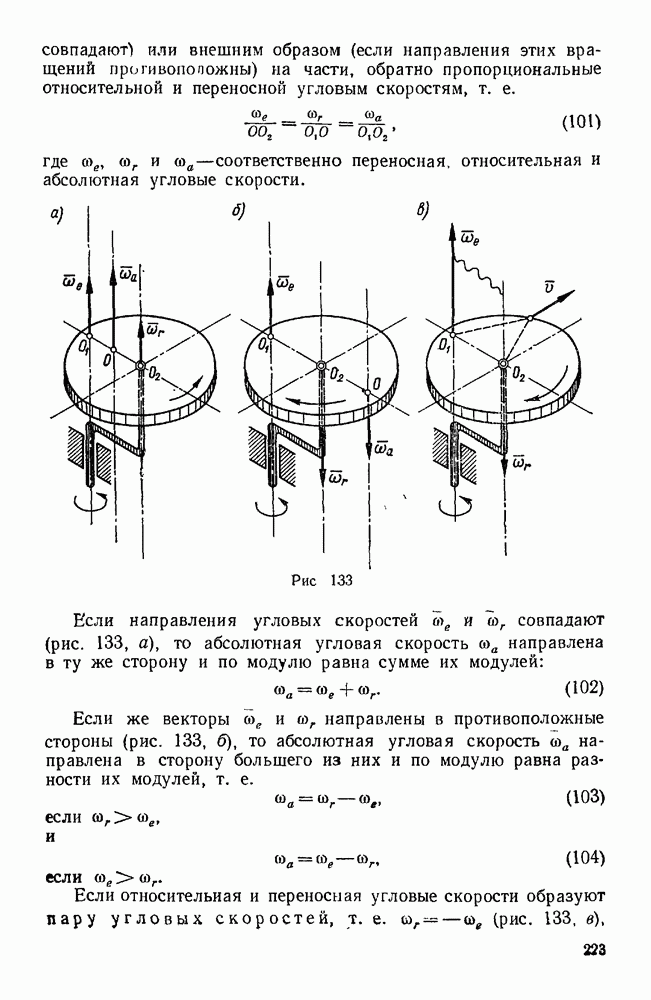
.
Проведя из конца  вектора
вектора  прямую
прямую  до пересечения в точке
до пересечения в точке  с прямой
с прямой  , имеем:
, имеем:

Искомое передаточное отношение определяется так:

Это передаточное отношение можно выразить также через углы растворов начальных конусов конических колес. Обозначив половины указанных углов через  треугольника
треугольника  имеем:
имеем:

Из треугольника  следует:
следует:

Поделив эти равенства, получим

Выражая функции углов  . через радиусы конических колес, этот ответ можно привести к виду, найденному ранее.
. через радиусы конических колес, этот ответ можно привести к виду, найденному ранее.
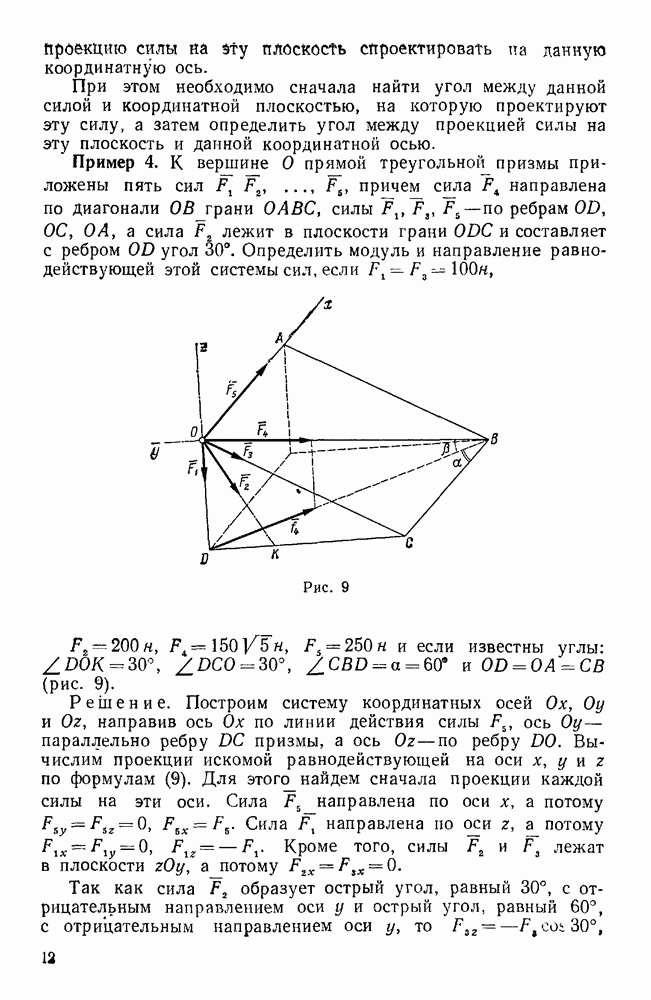
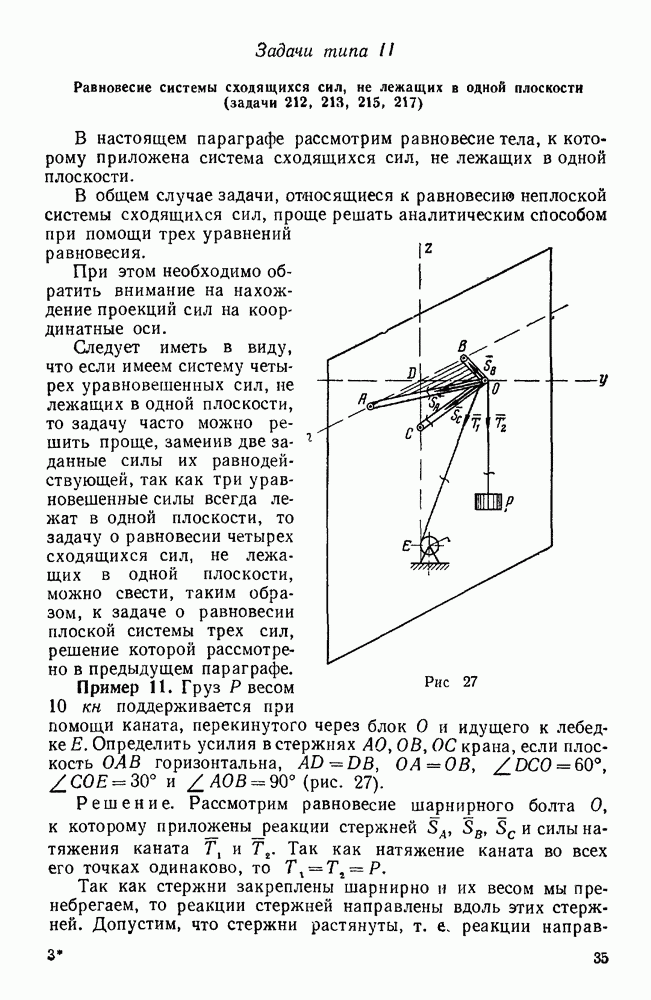
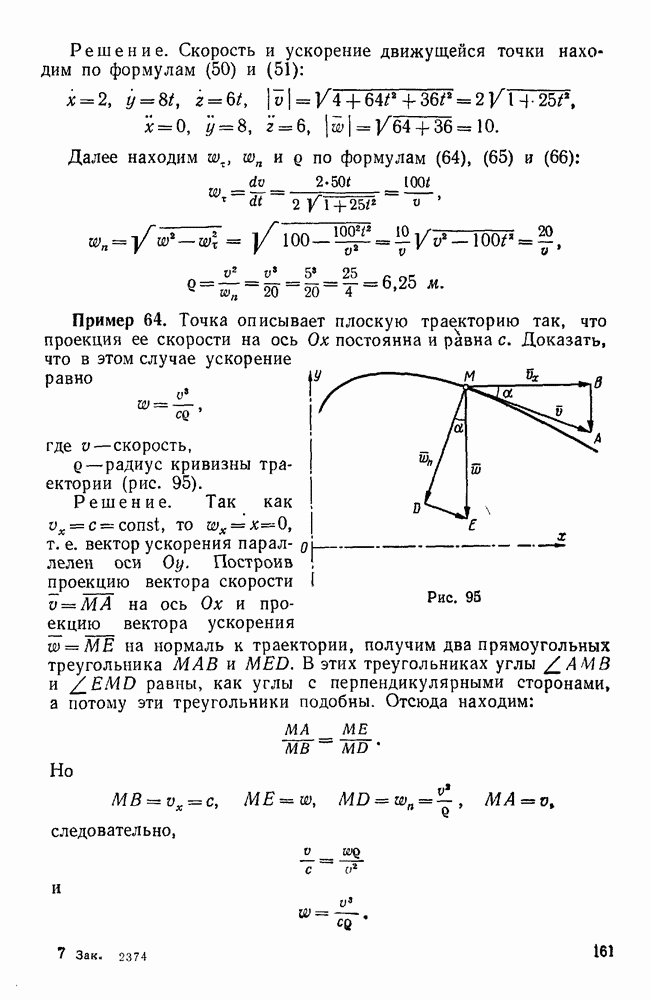
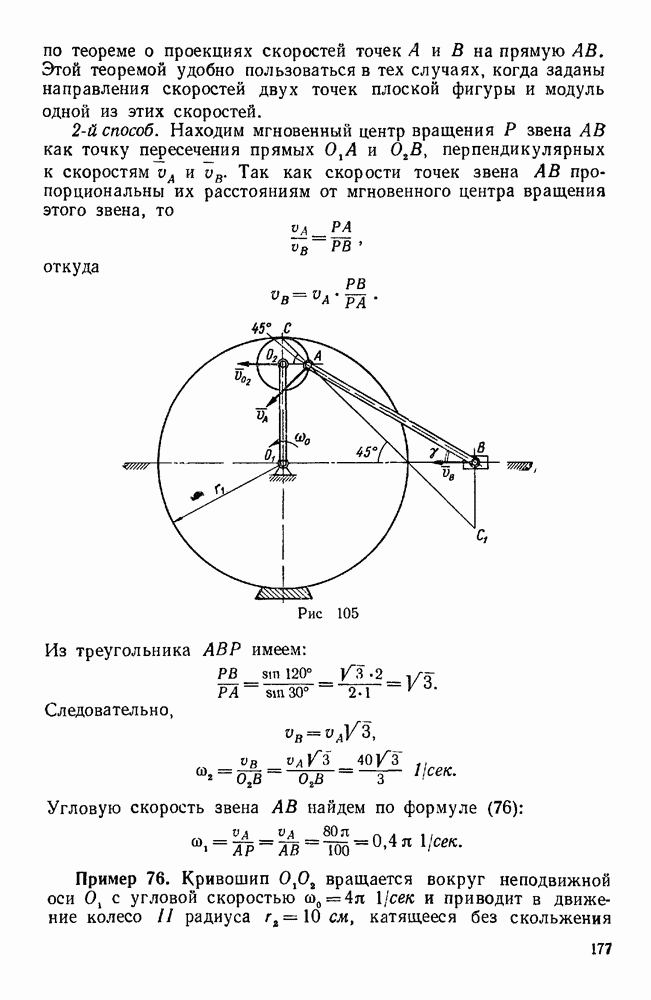
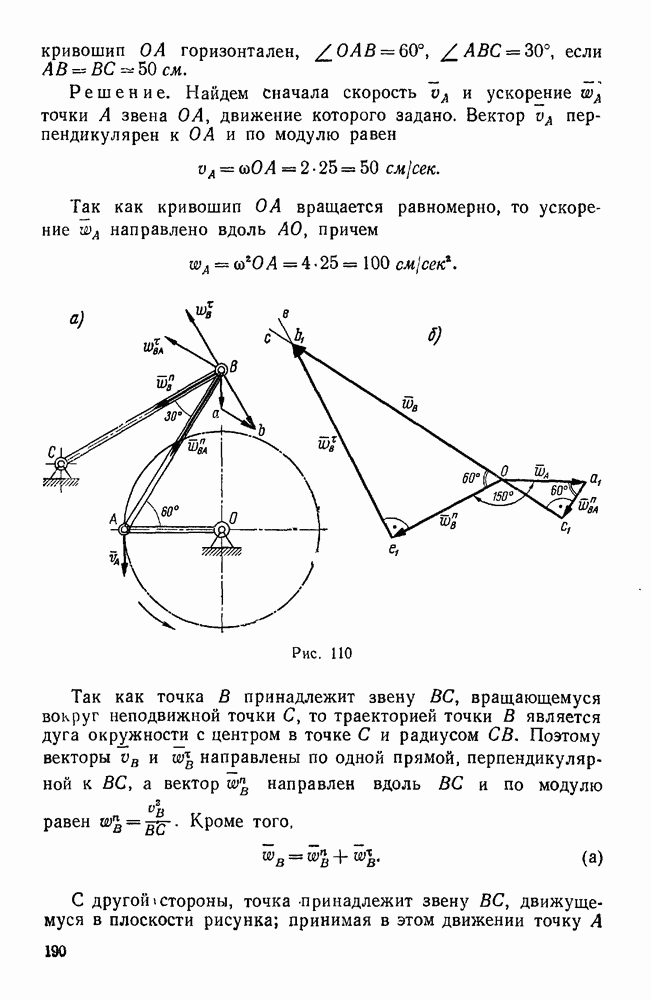
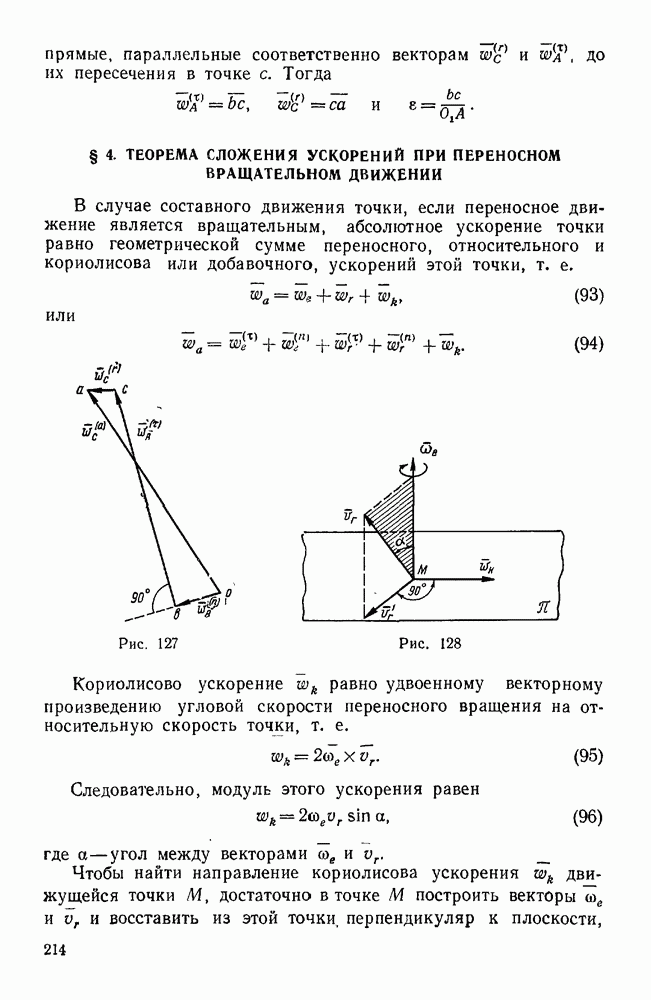
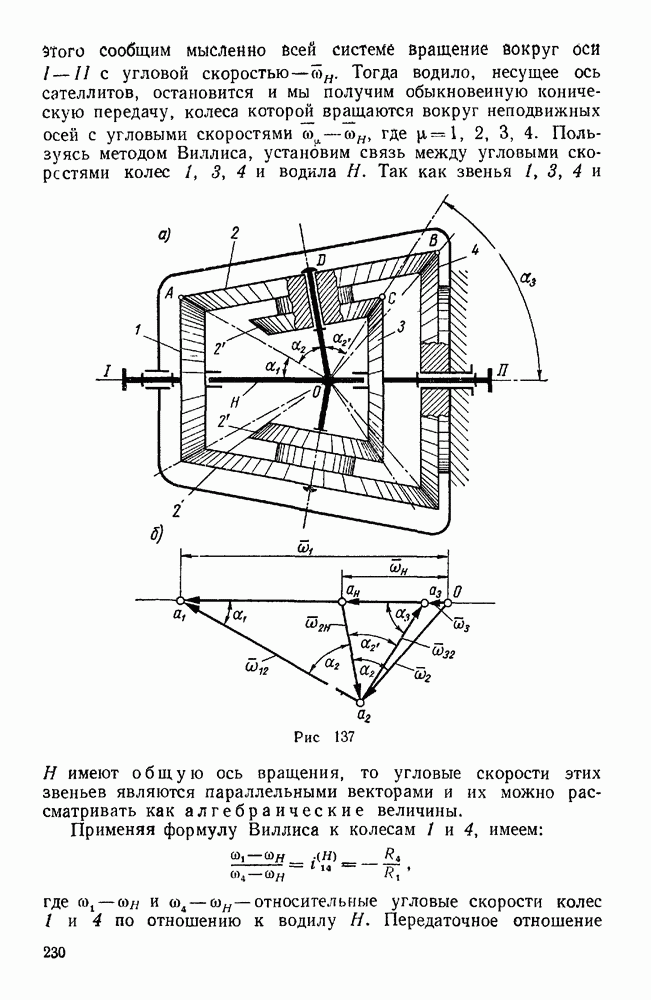
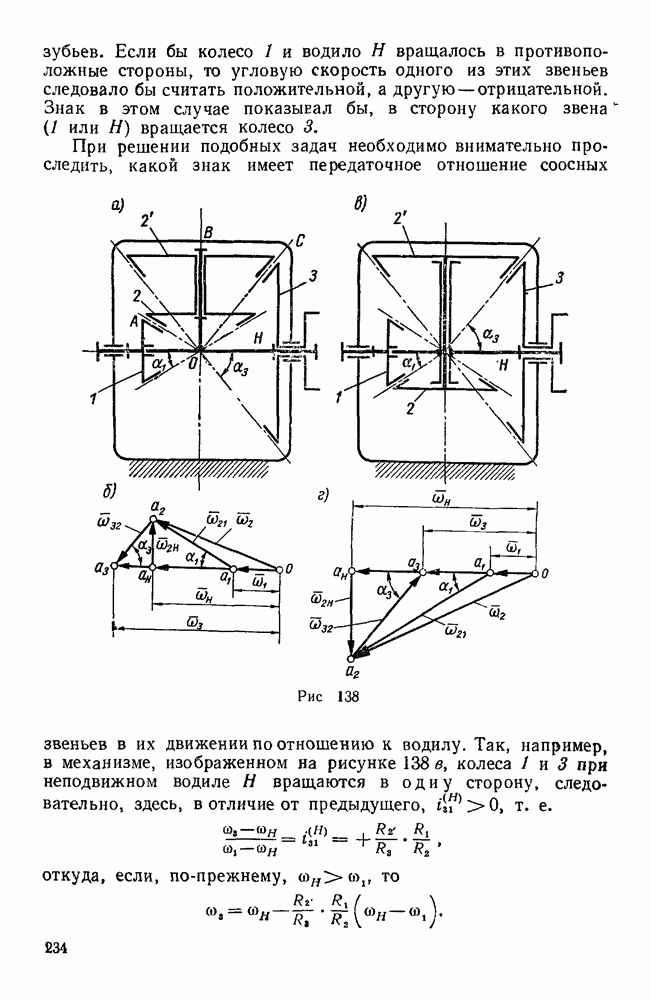
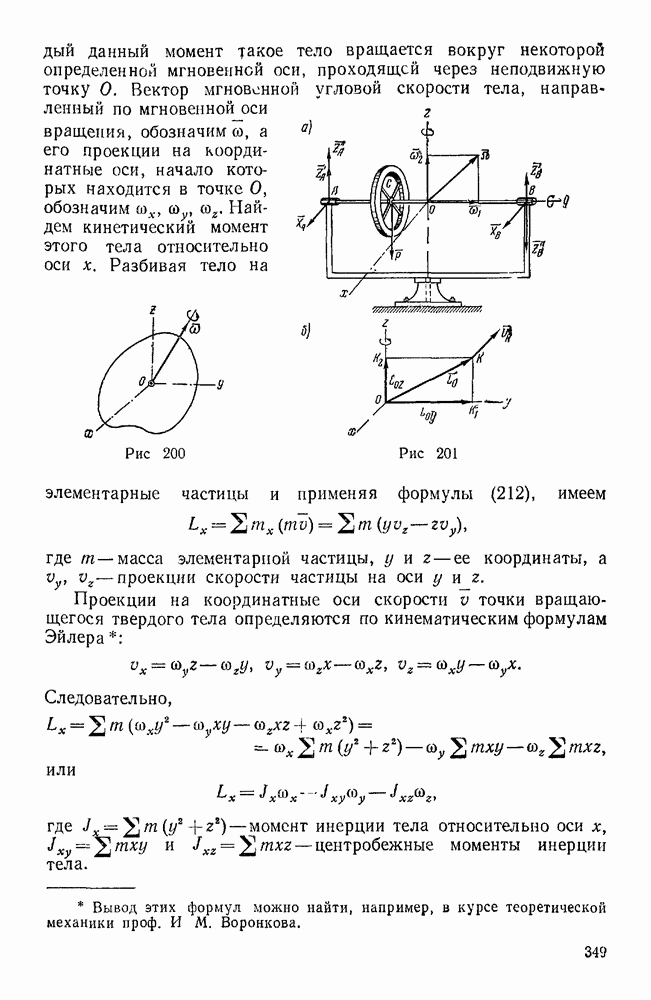
Пример 97. В дифференциальном механизме (рис. 138) ведущими звеньями являются колесо 1 и водило H, несущее ось двойного сателлита  . Зная угловые скорости со, и колеса
. Зная угловые скорости со, и колеса  и водила H, а также радиусы всех колес, найти угловую скорость колеса 3. Известно, что
и водила H, а также радиусы всех колес, найти угловую скорость колеса 3. Известно, что  .
.
Решение.  способ (метод Виллиса). Сообщим мысленно всей системе вращение с угловой скоростью
способ (метод Виллиса). Сообщим мысленно всей системе вращение с угловой скоростью  . Тогда водило H остановится, а к векторам угловых скоростей остальных звеньев механизма прибавится вектор —
. Тогда водило H остановится, а к векторам угловых скоростей остальных звеньев механизма прибавится вектор —  . Рассматривая угловые скорости звеньев 1, H и 3, имеющих общую ось вращения, как алгебраические величины, получаем следующее соотношение между относительными угловыми скоростями колес 1 и 3 по отношению к водилу Я:
. Рассматривая угловые скорости звеньев 1, H и 3, имеющих общую ось вращения, как алгебраические величины, получаем следующее соотношение между относительными угловыми скоростями колес 1 и 3 по отношению к водилу Я:

Передаточное отношение между колесами 3 и 1 в их относительном движении по отношению к водилу Я здесь отрицательно потому, что при неподвижном водиле Я эти колеса вращаются в разные стороны. Отсюда, учитывая, что  имеем:
имеем:

В этой формуле отношения радиусов находящихся в зацеплении колес могут быть заменены отношениями чисел их зубьев.
Если бы колесо 1 и водило H вращалось в противоположные стороны, то угловую скорость одного из этих звеньев следовало бы считать положительной, а другую — отрицательной. Знак в этом случае показывал бы, в сторону какого звена ( или H) вращается колесо 3.
или H) вращается колесо 3.
При решении подобных задач необходимо внимательно проследить, какой знак имеет передаточное отношение соосных звеньев в их движении по отношению к водилу.

Рис. 138.
Так, например, в механизме, изображенном на рисунке 138 в, колеса 1 и 3 при неподвижном водиле H вращаются в одну сторону, следовательно, здесь, в отличие от предыдущего, т. е.

откуда, если, по-прежнему,  , то
, то

2-й способ (геометрический). Решим эту же задачу при В данном случае мгновенная ось абсолютного движения двойного сателлита  заранее неизвестна, поэтому для определения его абсолютной угловой скорости воспользуемся двумя векторными уравнениями, приняв сначала за переносное движение вращение колеса
заранее неизвестна, поэтому для определения его абсолютной угловой скорости воспользуемся двумя векторными уравнениями, приняв сначала за переносное движение вращение колеса  , а затем — вращение водила:
, а затем — вращение водила:

Вектор сом относительной угловой скорости сателлита  по отношению к колесу
по отношению к колесу  направлен по общей образующей ОА начальных конусов этих колес, а вектор
направлен по общей образующей ОА начальных конусов этих колес, а вектор  относительной угловой скорости сателлита
относительной угловой скорости сателлита  по отношению к водилу H — по оси ОВ (рис. 138, а). От произвольного центра
по отношению к водилу H — по оси ОВ (рис. 138, а). От произвольного центра  (рис. 138, б) откладываем заданные векторы
(рис. 138, б) откладываем заданные векторы  , из концов а, и
, из концов а, и  этих векторов проводим до взаимного пересечения в точке
этих векторов проводим до взаимного пересечения в точке  прямые
прямые  и
и  , тогда получим:
, тогда получим:

Определив вектор  , переходим к определению угловой скорости
, переходим к определению угловой скорости  , колеса 3, исходя из равенства:
, колеса 3, исходя из равенства:

Вектор направлен по оси вращения колеса 3, совпадающей с осями вращения звеньев  и H, а вектор
и H, а вектор  общей образующей ОС начальных конусов колес 2 и 3. Проведя из начала о и конца
общей образующей ОС начальных конусов колес 2 и 3. Проведя из начала о и конца  вектора
вектора  прямые
прямые  до их взаимного пересечения в точке
до их взаимного пересечения в точке  , получаем треугольник
, получаем треугольник  угловых скоростей колеса 3, из которого находим:
угловых скоростей колеса 3, из которого находим:

Обозначая половины углов раствора начальных конусов конических колес 1 и 3 соответственно через  и
и  , имеем (рис. 138, а и б):
, имеем (рис. 138, а и б):

откуда окончательно:

Учитывая, что  (см. рис. 138, а), придем к найденному ранее результату. На рис. 438, г показаны треугольники угловых скоростей для механизма, изображенного на рис. 138, в.
(см. рис. 138, а), придем к найденному ранее результату. На рис. 438, г показаны треугольники угловых скоростей для механизма, изображенного на рис. 138, в.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
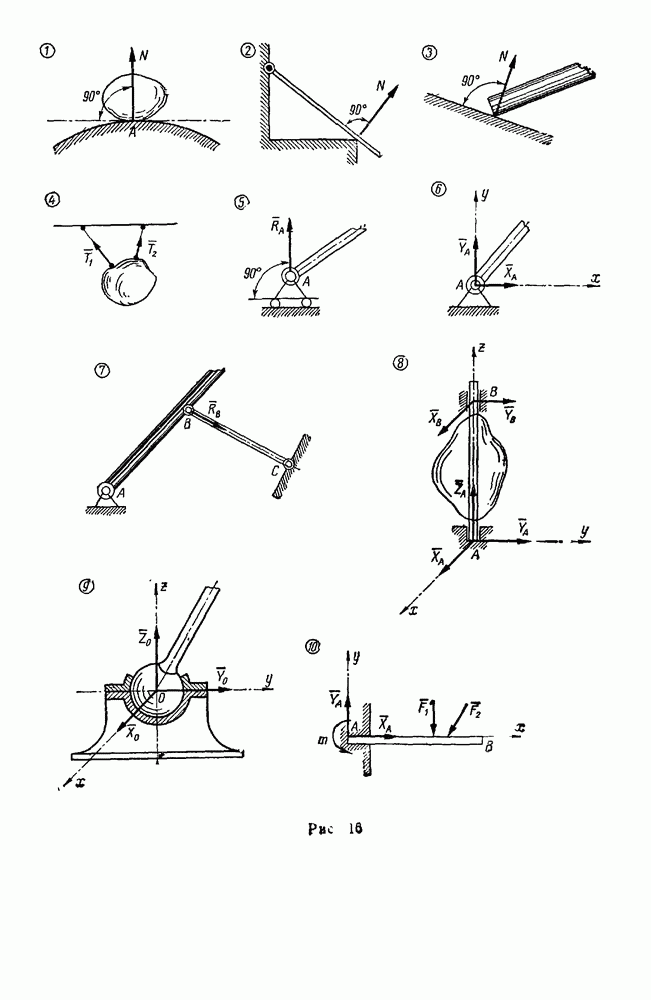
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
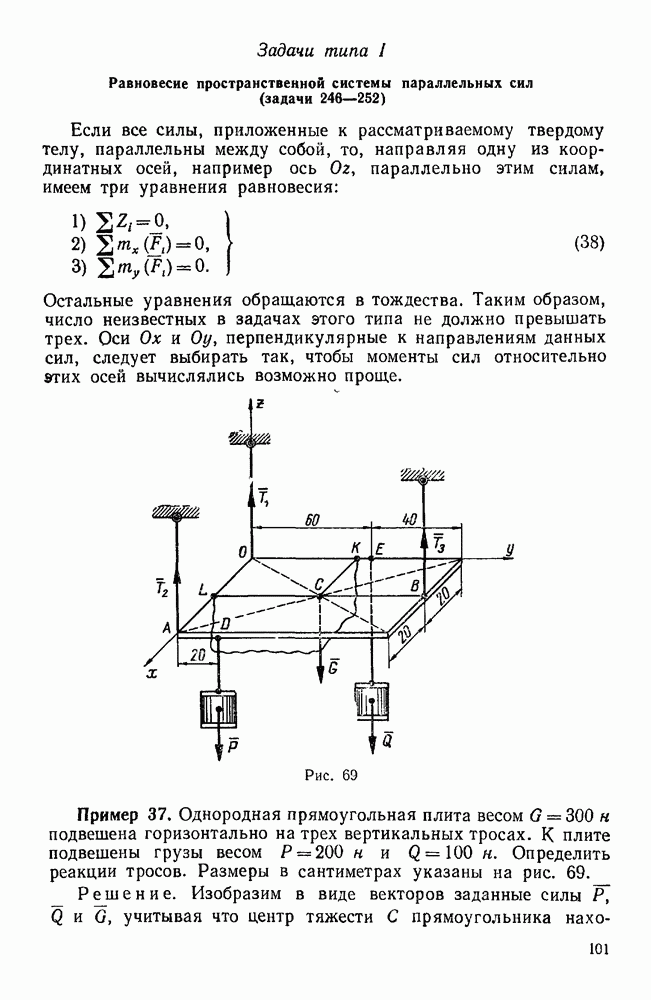
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
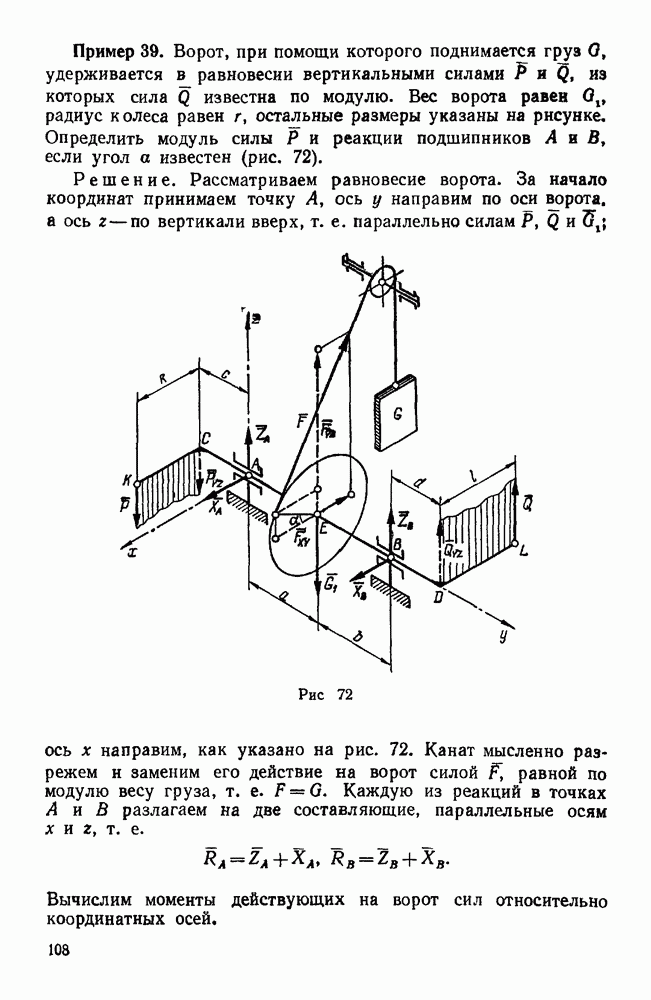
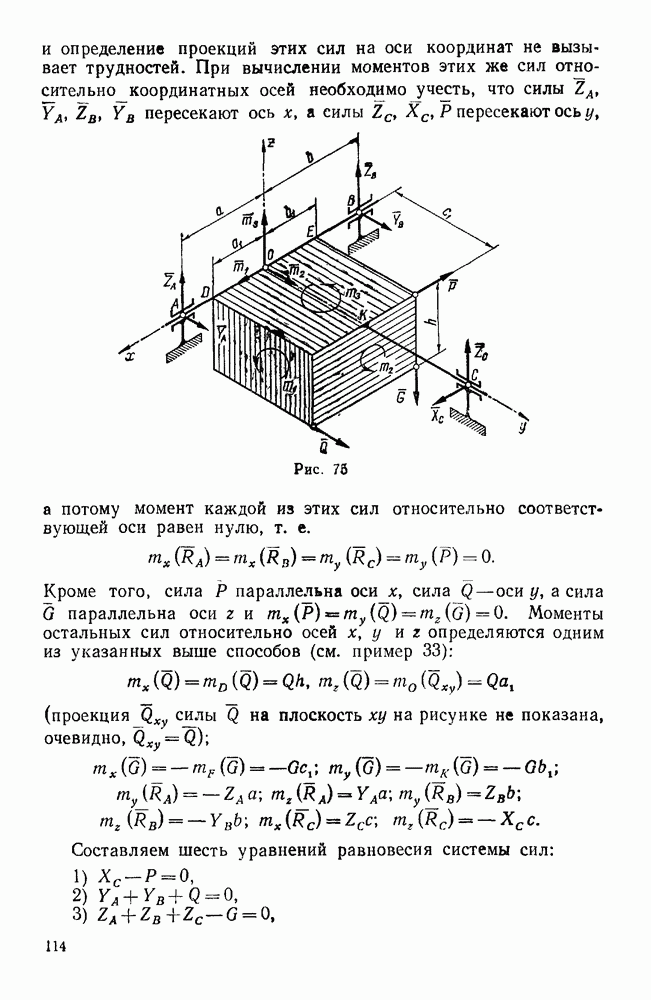
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
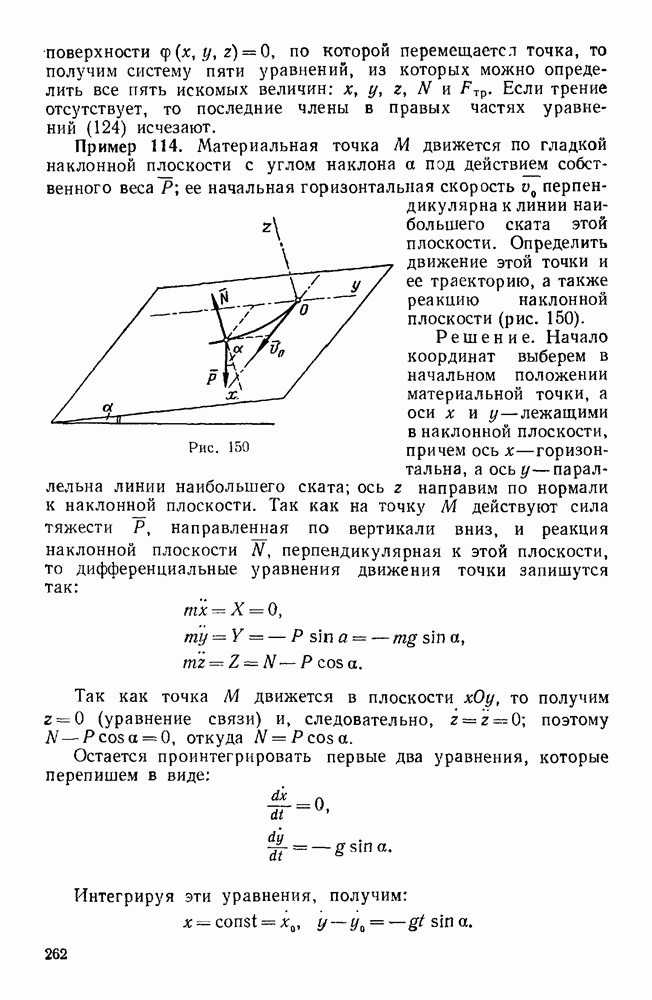
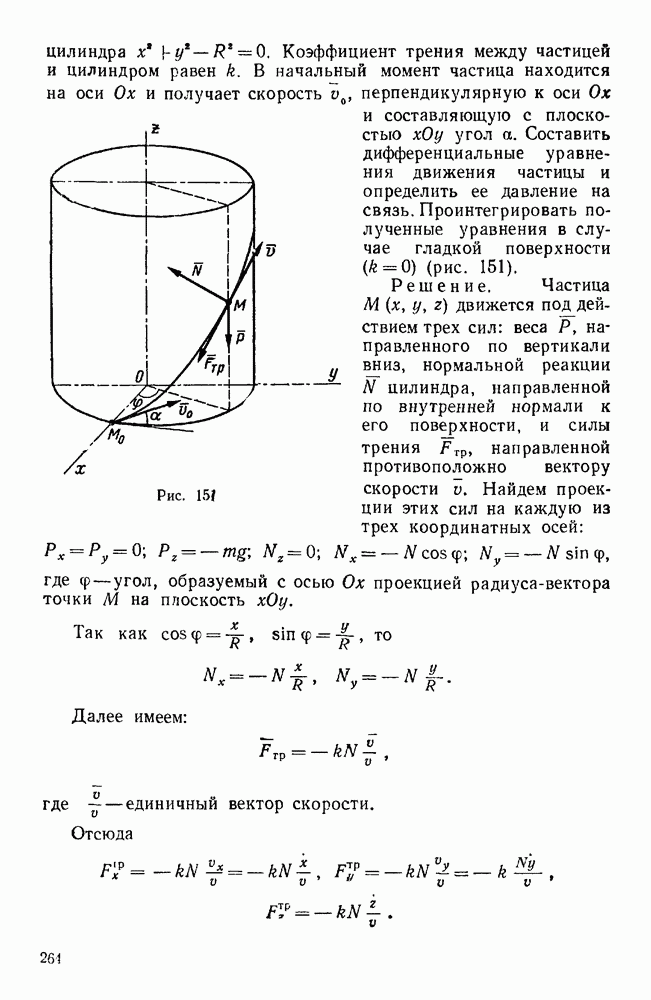
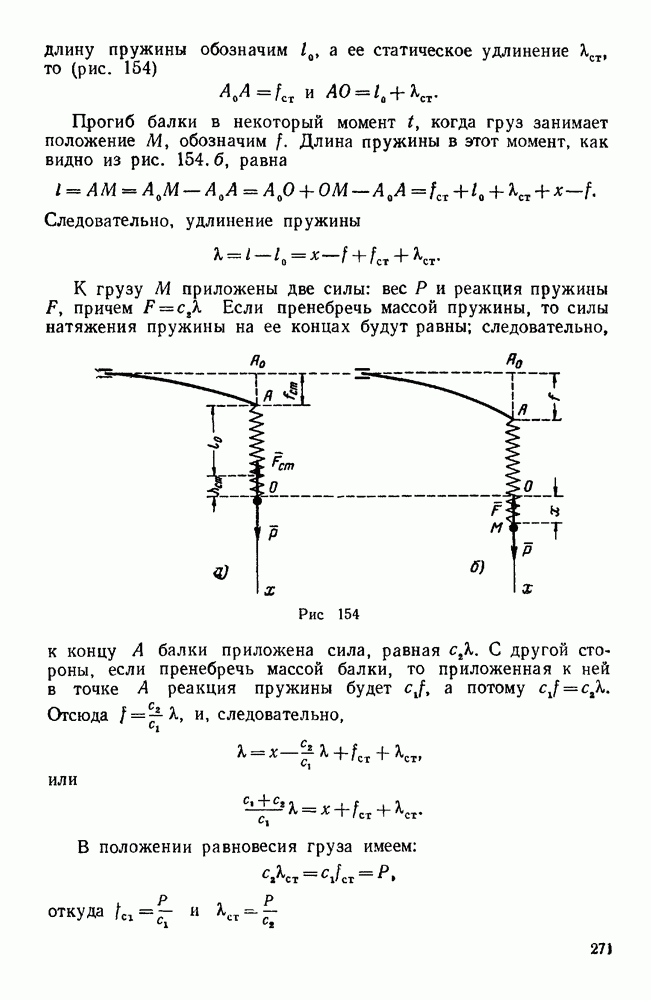
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. РАБОТА И МОЩНОСТЬ
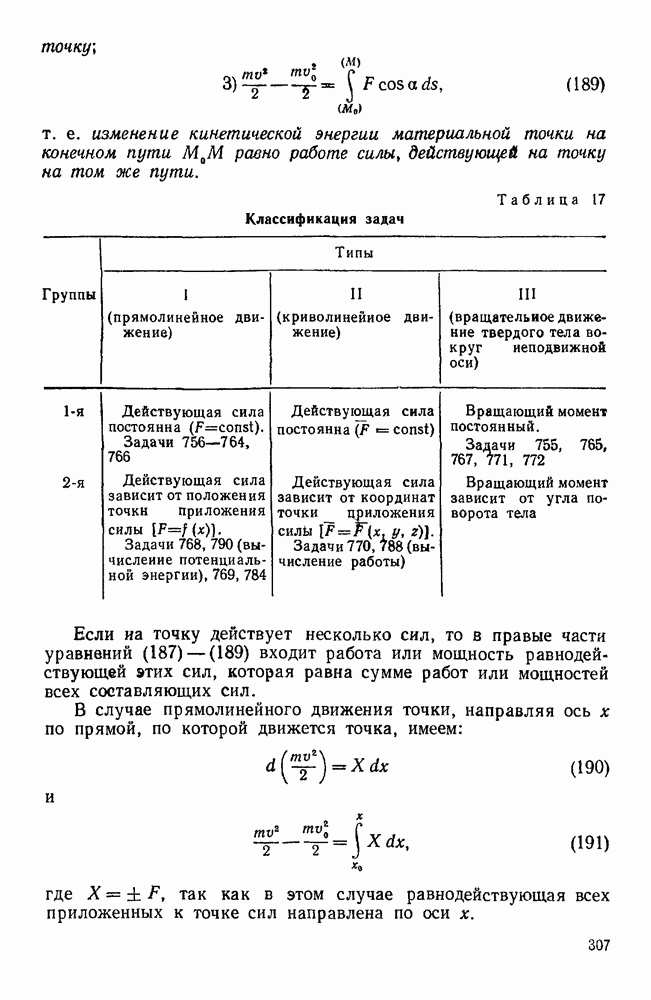
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
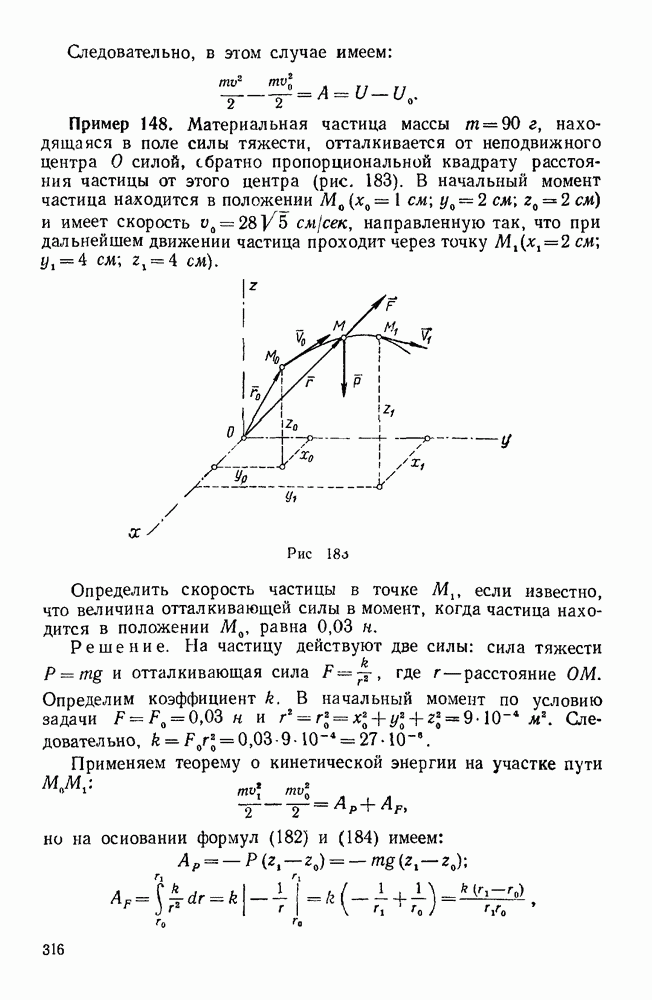
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
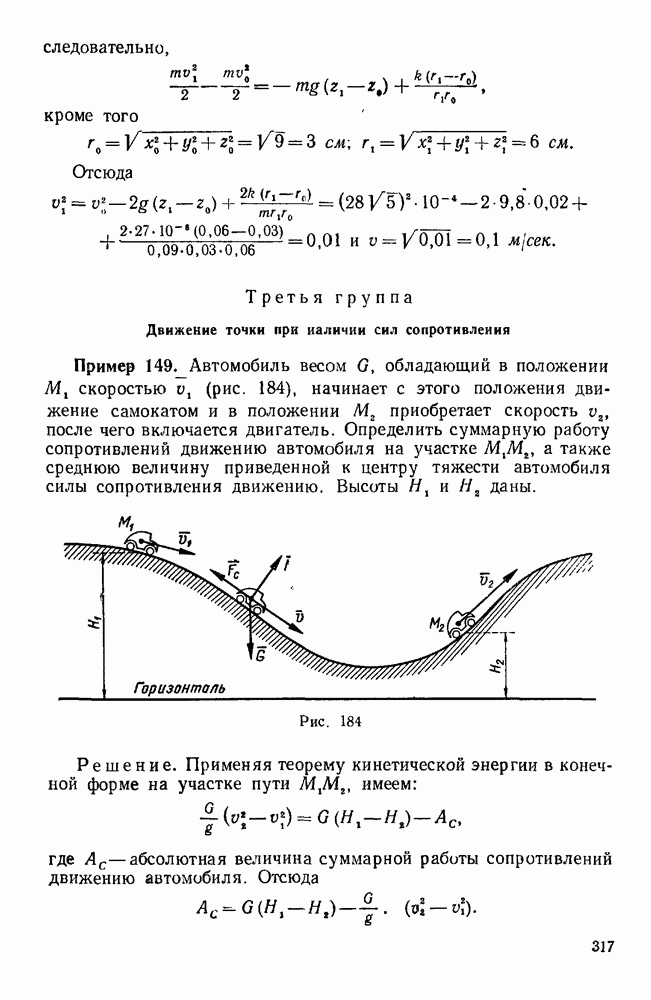
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
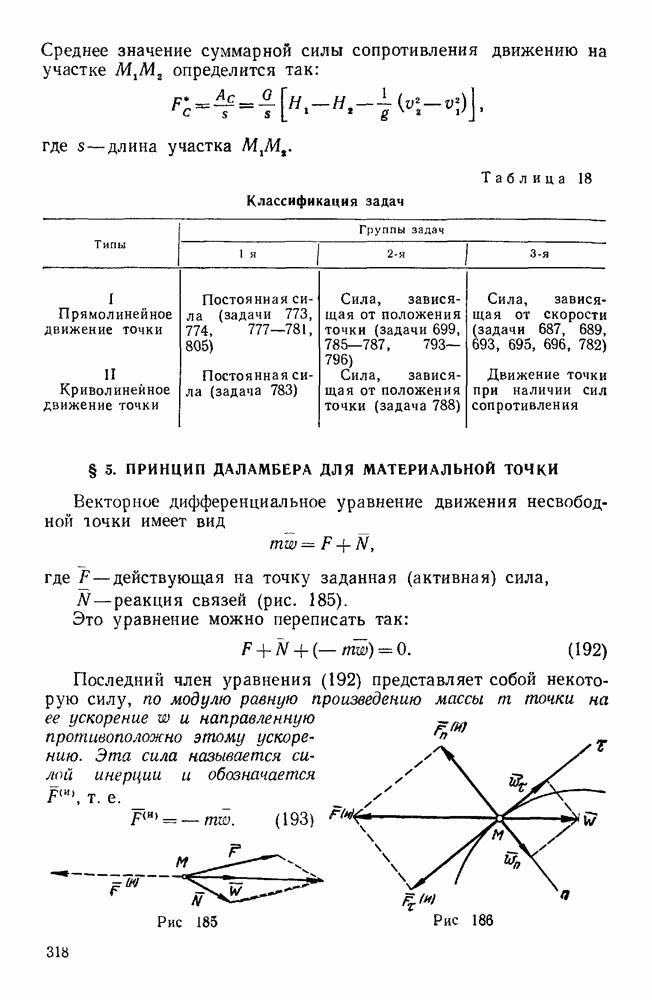
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
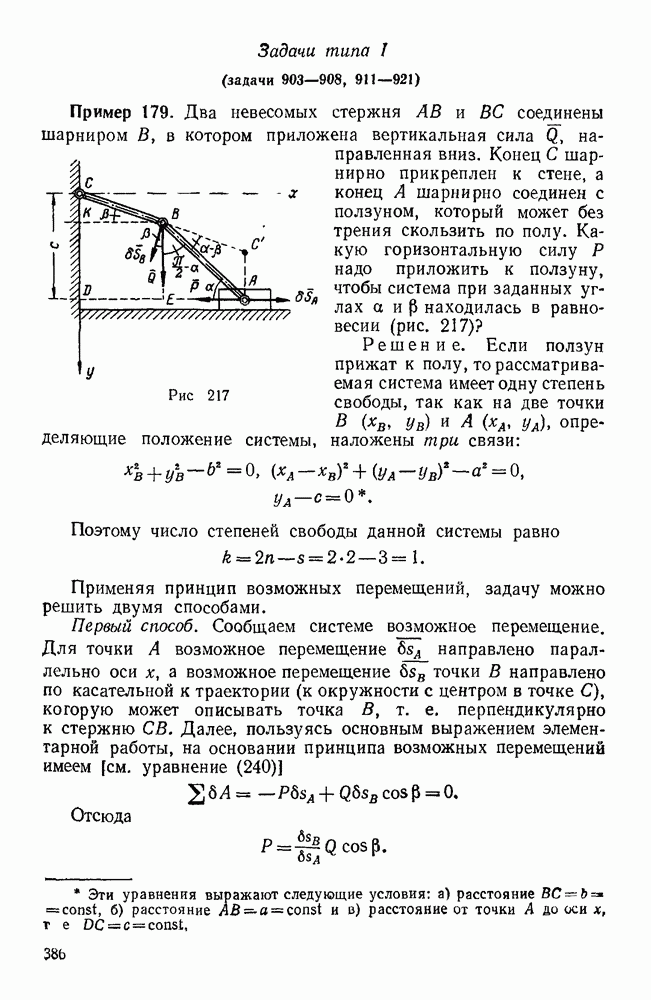
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
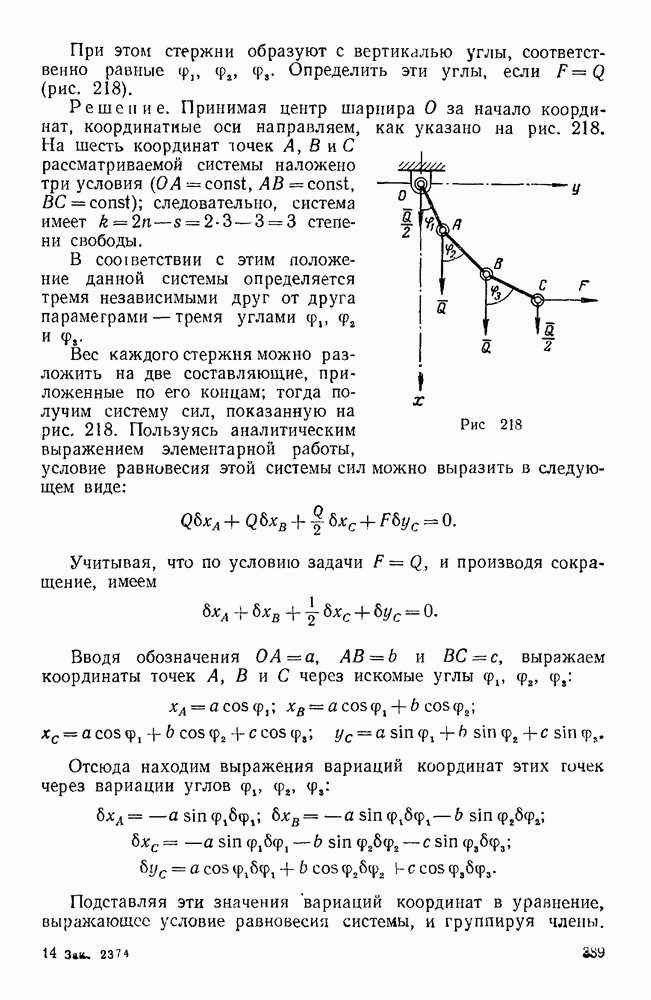
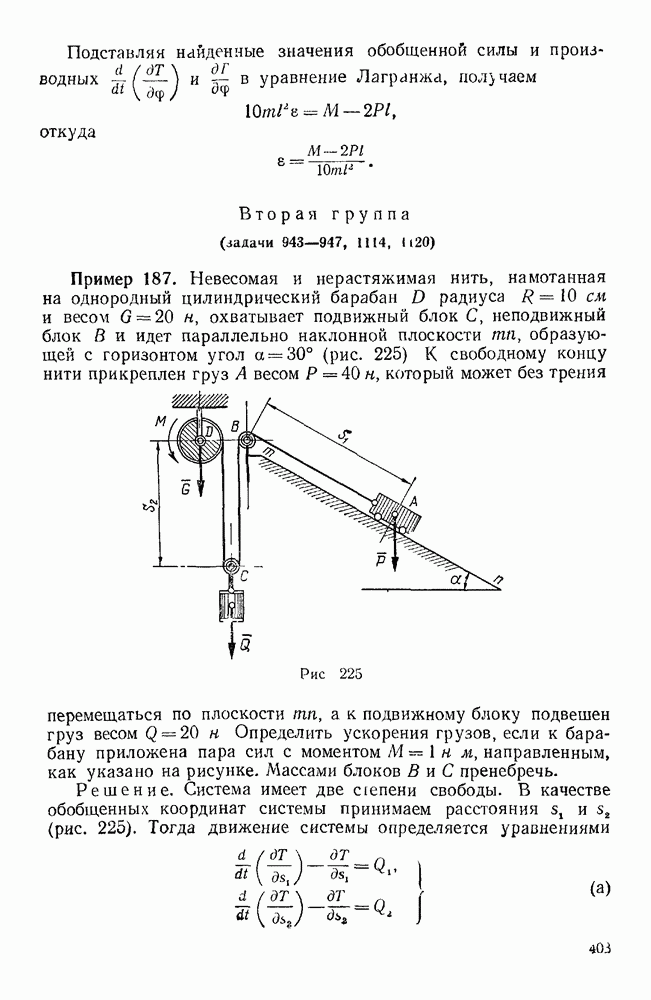
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА