| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
§ 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
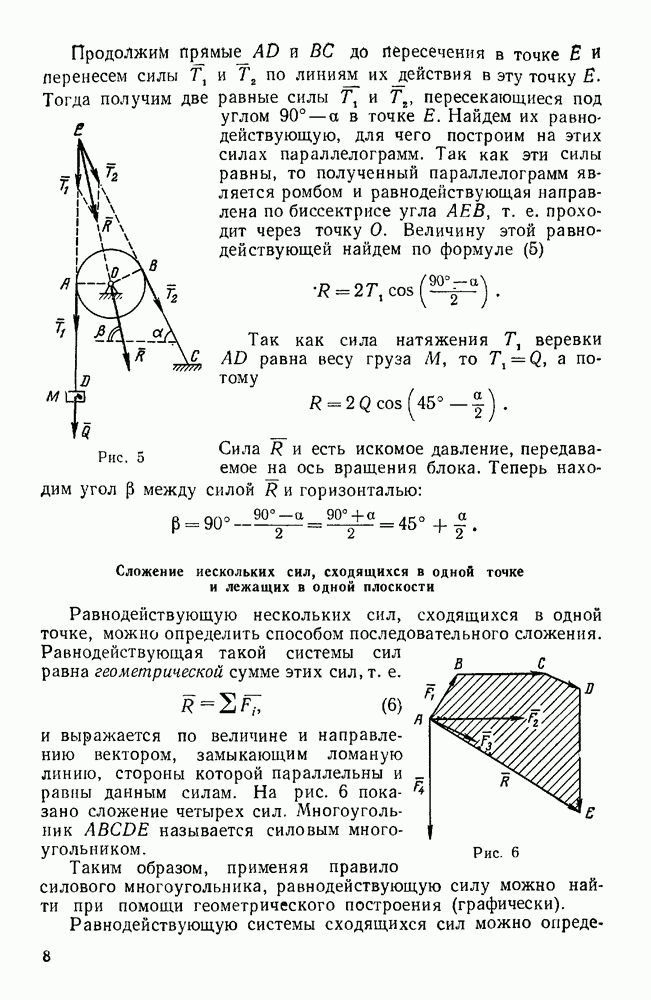
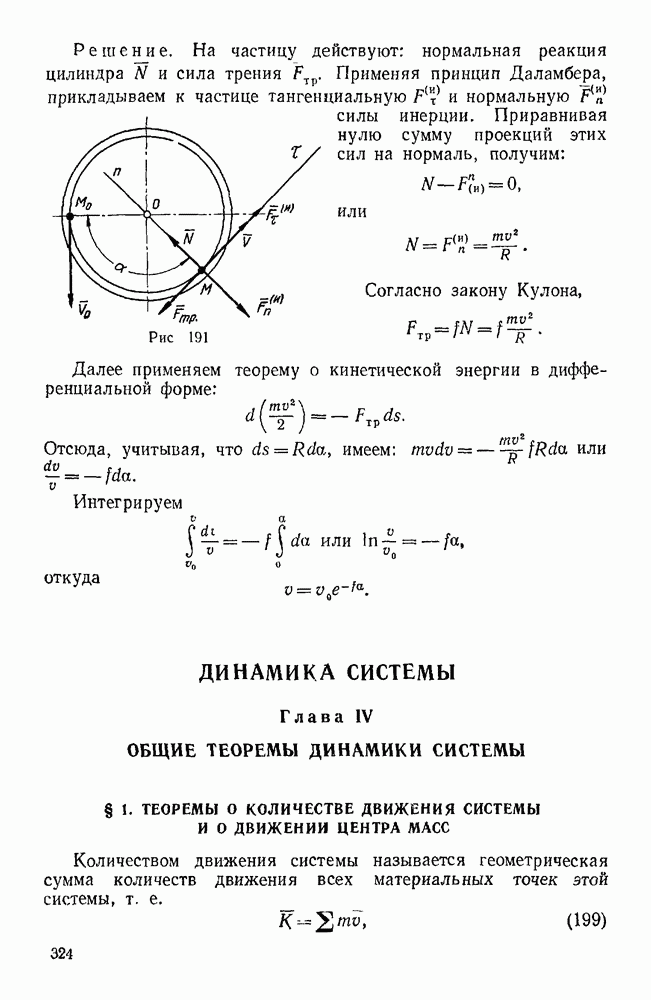
При изучении системы сил в пространстве момент силы  относительно точки О изображается вектором, приложенным в точке О, перпендикулярным к плоскости
относительно точки О изображается вектором, приложенным в точке О, перпендикулярным к плоскости  , в которой лежат сила F и точка О, и направленным так, чтобы наблюдатель, смотрящий с конца этого вектора на плоскость
, в которой лежат сила F и точка О, и направленным так, чтобы наблюдатель, смотрящий с конца этого вектора на плоскость  , видел силу F направленной по отношению к точке О против часовой стрелки.
, видел силу F направленной по отношению к точке О против часовой стрелки.

Рис. 59.
Модуль этого момента равен произведению силы F на длину перпендикуляра d, опущенного из точки О на линию действия этой силы (рис. 59).

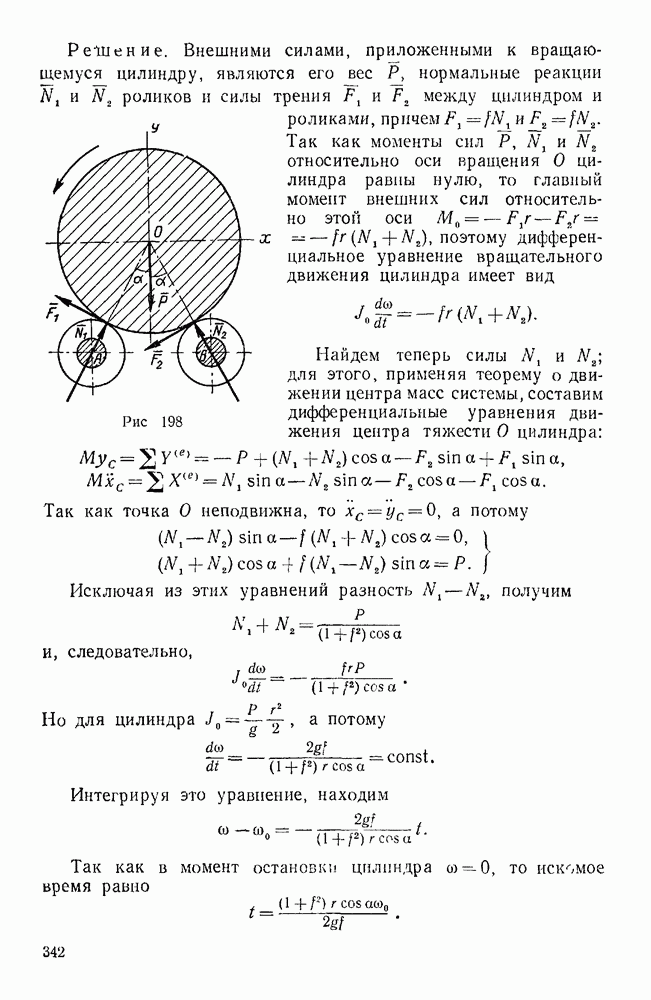
Рис. 60.
Аналогично в виде вектора изображается и момент пары, а именно: вектор - момент пары перпендикулярен к плоскости этой пары и направлен так, что наблюдатель, смотрящий на пару с конца этого вектора, видел направление вращения, вызываемого парой, против часовой стрелки.
Абсолютное значение момента пары равно произведению модуля одной из сил пары на плечо этой пары (рис. 60). Вектор-момент пары равен вектору-моменту одной из сил пары относительно точки приложения второй силы этой пары.
Кроме момента силы относительно точки, при изучении системы сил в - пространстве приходится рассматривать также и момент силы относительно - той или иной оси.
Моментом силы F относительно данной оси называется алгебраическое значение момента проекции этой силы на плоскость, перпендикулярную к этой оси, относительно точки пересечения оси с этой плоскостью.
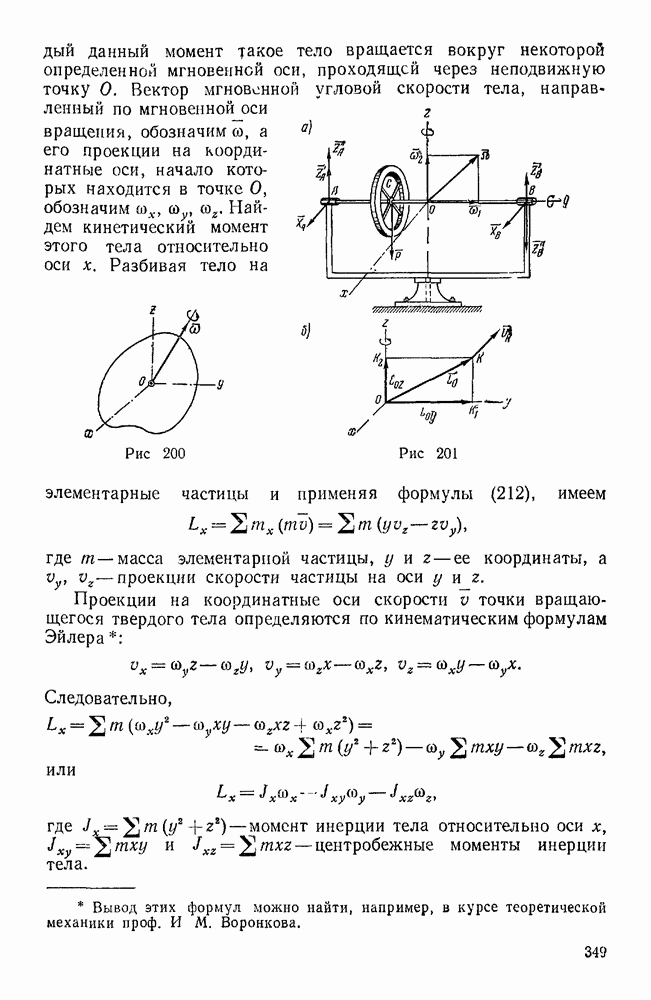
Следовательно, чтобы найти момент силы F относительно оси z, нужно спроектировать силу F на плоскость, перпендикулярную к оси z и проведенную через произвольную точку О, лежащую на этой оси, и затем полученную проекцию  умножить на длину h перпендикуляра, опущенного из точки О на линию действия проекции f. При этом произведение
умножить на длину h перпендикуляра, опущенного из точки О на линию действия проекции f. При этом произведение  берется со знаком плюс или минус (рис. 61).
берется со знаком плюс или минус (рис. 61).
Таким образом, 

Знак момента силы относительно данной оси выбирается следующим образом: если наблюдатель, смотрящий с положительного конца оси, видит проекцию f направленной по отношению к точке О против часовой стрелки, то момент силы F относительно этой оси считается положительным. В противном случае этот момент считается отрицательным. Поэтому на рис. 61 момент силы F относительно оси  положителен.
положителен.

Рис. 61.
Из формулы (28) следует, что момент силы относительно оси  равен нулю, если
равен нулю, если  , или
, или  , т. е. когда сила
, т. е. когда сила  параллельна оси либо когда линия действия этой силы пересекает данную ось.
параллельна оси либо когда линия действия этой силы пересекает данную ось.
Моменты силы F относительно трех координатные осей х, у и z выражаются следующими формулами:

где X, Y, Z — проекции силы F на координатные оси, а х, у, z — координаты точки приложения силы.
Между моментом силы F относительно данной оси и вектором моментом той же силы относительно какой-нибудь точки, лежащей на этой оси, существует следующая зависимость: проекция вектора-момента силы F относительно произвольной точки О на какую-либо ось, проходящую через эту точку, равна моменту силы F относительно этой оси, т. е.

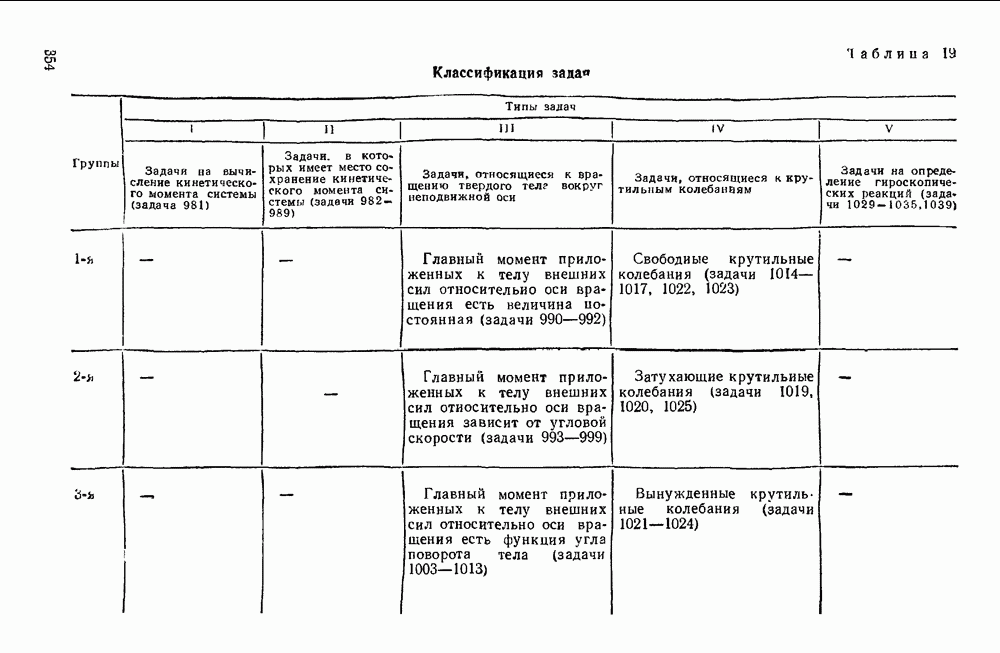
Пример 33. К вершинам С, В и D куба со стороной а приложены равные по модулю силы  и Q, направленные соответственно по стороне BE и по диагоналям DA и DK. Найти моменты каждой из этих сил относительно координатных осей х, у и z (рис. 62).
и Q, направленные соответственно по стороне BE и по диагоналям DA и DK. Найти моменты каждой из этих сил относительно координатных осей х, у и z (рис. 62).

Рис. 62.
Решение. Первый способ (геометрический). При вычислении моментов нескольких сил относительно координатных осей следует сначала выделить те силы, которые пересекают одну из координатных осей или ей параллельны, так как в этих с  момент силы относительно оси равен нулю. Сила Р параллельна оси
момент силы относительно оси равен нулю. Сила Р параллельна оси  , а сила S пересекает ось z, а потому
, а сила S пересекает ось z, а потому  . Далее следует выделить те силы, которые расположены в плоскости, перпендикулярной к одной из координатных осей;
. Далее следует выделить те силы, которые расположены в плоскости, перпендикулярной к одной из координатных осей;
В этом случае момент силы относительно такой оси по абсолютной величине равен моменту силы относительно точки пересечения этой оси с перпендикулярной к ней плоскостью, в которой расположена эта сила.
Сила Q лежит в плоскости  перпендикулярной к оси
перпендикулярной к оси  , причем
, причем  — точка пересечения оси х с этой плоскостью. Так как
— точка пересечения оси х с этой плоскостью. Так как  , то плечо силы Q относительно точки А, равно
, то плечо силы Q относительно точки А, равно  . Следовательно,
. Следовательно,  . Для наблюдателя, смотрящего с положительного конца оси х на плоскость
. Для наблюдателя, смотрящего с положительного конца оси х на плоскость  , сила Q стремится вращать куб вокруг оси х против часовой стрелки, поэтому момент силы Q относительно оси х положителен, и, следовательно,
, сила Q стремится вращать куб вокруг оси х против часовой стрелки, поэтому момент силы Q относительно оси х положителен, и, следовательно,  .
.
Аналогично вычисляются моменты силы Р относительно осей у и z, так как сила Р расположена в плоскости EBCD, перпендикулярной к оси у, и в плоскости  перпендикулярной к оси z:
перпендикулярной к оси z:

Теперь переходим  вычислению моментов силы Q относительно осей у и z и моментов силы S относительно осей х и у.
вычислению моментов силы Q относительно осей у и z и моментов силы S относительно осей х и у.
Чтобы вычислить момент силы Q относительно оси у, следует сначала эту силу спроектировать на координатную плоскость  . Для этого следует из начала D и конца D, силы Q провести прямые, параллельные оси у, до пересечения с плоскостью
. Для этого следует из начала D и конца D, силы Q провести прямые, параллельные оси у, до пересечения с плоскостью  в точках
в точках  . Тогда вектор
. Тогда вектор  является проекцией силы Q на плоскость
является проекцией силы Q на плоскость  . Плечо этой проекции относительно точки О равно
. Плечо этой проекции относительно точки О равно  . Для наблюдателя, смотрящего с положительного конца оси у на плоскость
. Для наблюдателя, смотрящего с положительного конца оси у на плоскость  , сила
, сила  стремится вращать куб вокруг оси у по часовой стрелке, поэтому момент силы Q относительно оси у отрицателен, и, следовательно,
стремится вращать куб вокруг оси у по часовой стрелке, поэтому момент силы Q относительно оси у отрицателен, и, следовательно,

Но

а потому

Для вычисления момента силы Q относительно оси z спроектируем эту силу на плоскость  , для этого из конца
, для этого из конца  силы Q проведем прямую параллельную оси z, до пересечения с плоскостью
силы Q проведем прямую параллельную оси z, до пересечения с плоскостью  в точке d.
в точке d.
Тогда вектор  является проекцией силы Q на плоскость
является проекцией силы Q на плоскость  . Плечо силы
. Плечо силы  относительно точки О равно
относительно точки О равно  . Так как момент силы Q относительно оси z отрицателен, то
. Так как момент силы Q относительно оси z отрицателен, то

Но

а потому

Чтобы вычислить моменты силы  относительно осей х и у, находим проекции этой силы
относительно осей х и у, находим проекции этой силы  на координатные плоскости
на координатные плоскости  . Так как грани куба являются квадратами, то
. Так как грани куба являются квадратами, то  , а потому
, а потому

Далее

из прямоугольного треугольника DAC находим

Следовательно,

Второй способ (аналитический). Под аналитическим способом определения моментов силы относительно координатных осей понимается вычисление этих моментов по формуле (29). При этом нужно предварительно найти (если они не заданы) координаты точки приложения силы и ее проекции на оси координат. Принимая во внимание, что сила  параллельна оси х, сила Q перпендикулярна к этой оси и составляет с осями у и 2 углы 45°, получим:
параллельна оси х, сила Q перпендикулярна к этой оси и составляет с осями у и 2 углы 45°, получим:

Обозначим угол  через
через  . Тогда
. Тогда  . Чтобы вычислить проекции силы S на оси х и у, спроектируем эту силу на плоскость
. Чтобы вычислить проекции силы S на оси х и у, спроектируем эту силу на плоскость  , а затем полученную проекцию
, а затем полученную проекцию  , направленную по прямой DO, спроектируем на оси х и у. Тогда имеем:
, направленную по прямой DO, спроектируем на оси х и у. Тогда имеем:

или  .
.
Из прямоугольного треугольника  находим:
находим:

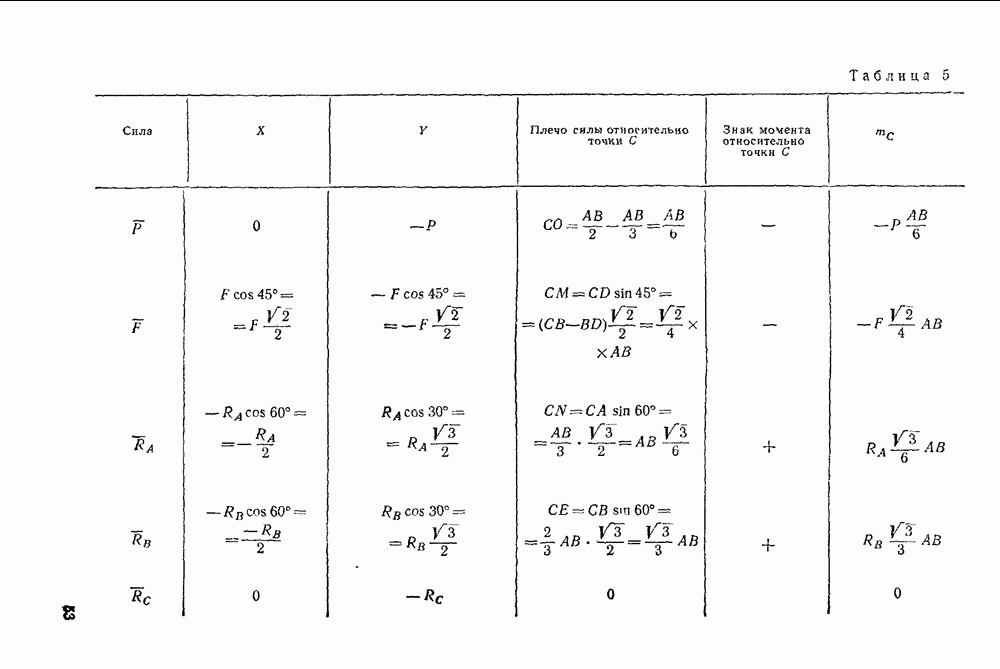
Значения координат точек приложения заданных сил, которые находим непосредственно из чертежа, и значения моментов этих сил, вычисляемые по формулам (29), указаны в табл. 6 и 7.
Таблица 6

Таблица 7

Таким образом, момент силы относительно координатной оси можно вычислить двумя способами:
1) аналитическим способом, пользуясь формулами (29), выражающими искомый момент силы через проекции этой силы на координатные оси и через координаты точки ее приложения;
2) геометрическим способом.
При геометрическом способе определения момента силы относительно координатной оси следует различать три случая:
1) сила лежит в координатной плоскости, перпендикулярной к координатной оси, относительно которой вычисляется момент, тогда момент силы относительно этой оси равен по модулю ее моменту относительно начала координат;
2) через линию действия силы можно провести плоскость, перпендикулярную к одной из координатных осей, тогда момент силы относительно такой оси равен по модулю моменту силы относительно точки пересечения этой плоскости с данной координатной осью;
3) если сила не лежит в плоскости, перпендикулярной к данной координатной оси, то следует эту силу спроектировать на координатную плоскость, перпендикулярную к данной оси, и вычислить момент полученной проекции относительно начала координат.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
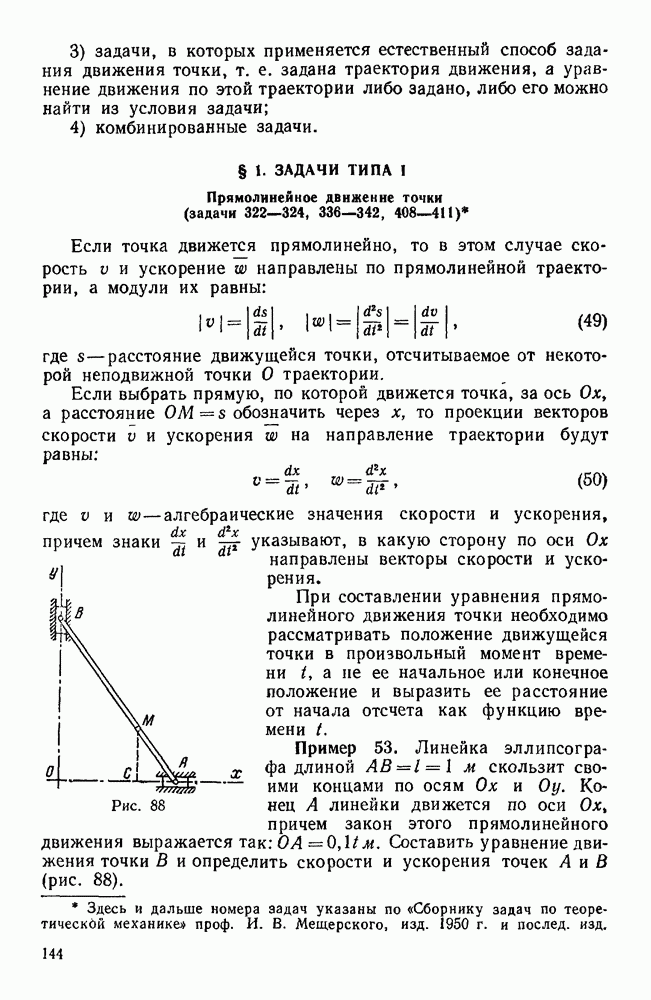
- § 1. ЗАДАЧИ ТИПА I
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
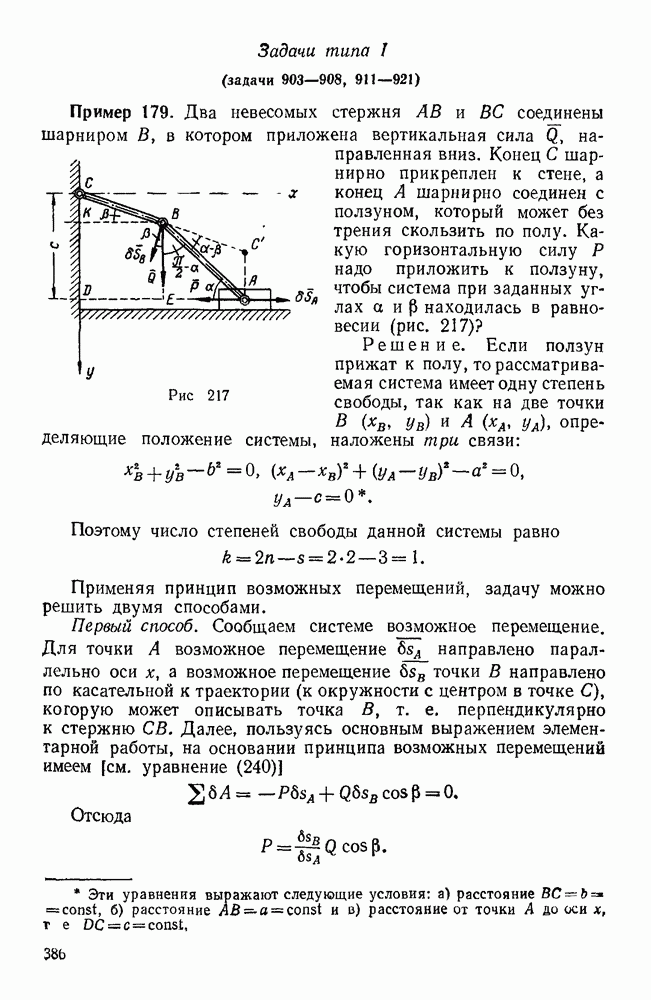
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
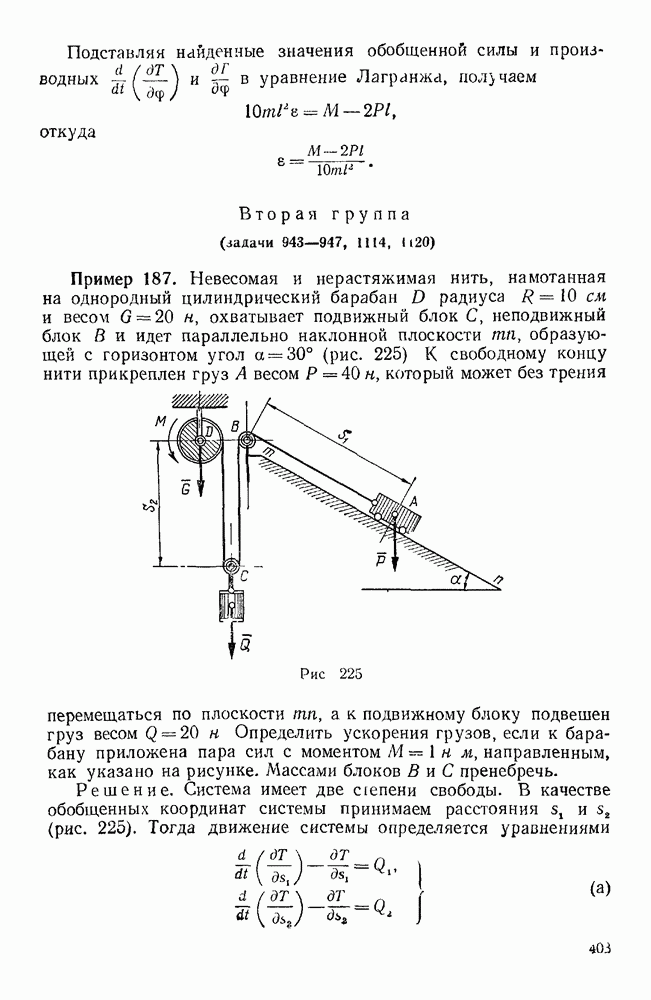
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА