| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Вторая группа
В этом случае сила F, а следовательно, и ее проекции на координатные оси являются известными функциями времени, т. е.

Теорема о количестве движения применяется здесь в конечной форме (147).
Выполняя интегрирование, находим из этих уравнений проекции скорости, а затем и скорость  .
.
Пример 126. На материальную точку массой  кг действует сила, проекции которой на координатные оси равны:
кг действует сила, проекции которой на координатные оси равны:

(сила выражена в н, время t — в сек).
Определить скорость  точки в момент
точки в момент  , если в момент
, если в момент  ее скорость
ее скорость  равна по модулю
равна по модулю  и составляет с координатными осями х, у, z углы, равные соответственно 30°, 60° и 90°.
и составляет с координатными осями х, у, z углы, равные соответственно 30°, 60° и 90°.
Решение. Так как проекции силы на координатные оси являются функциями времени, то теорему о количестве движения можно применить в конечной форме (147). Для этого вычислим сначала проекции на координатные оси импульса действующей силы за промежуток времени от момента  до момента
до момента  :
:

Так как Z отличается от Y только знаком, то  . Далее на основании уравнений (147) получаем:
. Далее на основании уравнений (147) получаем:

Отсюда при  находим проекции искомой скорости:
находим проекции искомой скорости:

Так как

то

Следовательно,

Если углы вектора  с координатными осями обозначим
с координатными осями обозначим  , то
, то

Отсюда  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- РА3ДЕЛ 1. СТАТИКА
- § 1. СЛОЖЕНИЕ СИЛ, СХОДЯЩИХСЯ В ОДНОЙ ТОЧКЕ
- Сложение нескольких сил, сходящихся в одной точке и лежащих в одной плоскости
- Сложение сходящихся сил, не лежащих в одной плоскости
- § 2 РАЗЛОЖЕНИЕ СИЛЫ НА СОСТАВЛЯЮЩИЕ
- § 3. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ
- § 4. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ
- Задачи типа I. Равновесие плоской системы сходящихся сил
- Вторая группа. Задачи, где имеются связи, направление реакций которых неизвестно (задачи 36—41, 43)
- Задачи типа II. Равновесие системы сходящихся сил, не лежащих в одной плоскости (задачи 212, 213, 215, 217)
- Глава II. ПЛОСКАЯ СИСТЕМА СИЛ
- § 1. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 2. РАВНОВЕСИЕ РЫЧАГА
- Первая группа. Равновесие рычага (задачи 81—84, 112, 113)
- Вторая группа. Равновесие тела, которое может опрокидываться (задачи 94—97)
- § 3. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПЛОСКОЙ СИСТЕМЫ СИЛ
- Задачи типа I. Равновесие плоской системы параллельных сил (задачи 89—94)
- Задачи типа II. Равновесие плоской системы сил в общем случае
- Первая группа. Задачи, в которых линии действия реакций всех связей известны (задачи 118—125)
- Вторая группа. Задачи, в которых линия действия реакции одной из связей неизвестна (задачи 129—135)
- § 4. РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ
- Задачи типа I. Тела, входящие в систему, опираются свободно друг на друга (задачи 108, 109, 164, 166—168)
- Задачи типа II. Тела, входящие в систему, соединены между собой гибкой нитью или невесомым стержнем, концы которого прикреплены к этим телам при помощи шарниров (задачи 108, 162, 163)
- Задачи типа III. Тела, входящие в систему, соединены между собой шарнирно (задачи 110—112, 143, 147—154)
- Задачи типа IV. Задачи, относящиеся к определению усилий в стержнях плоской фермы (задачи 197—207)
- Глава III. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ
- Задачи типа I. Первая группа
- Задачи, решаемые при помощи двух уравнений равновесия (задачи 73, 74)
- Вторая группа. Задачи, решаемые при помощи трех уравнений равновесия (задачи 175—182)
- Задачи типа II. Равновесие системы тел при наличии трения (задачи 186 — 188)
- Глава IV. СИСТЕМА СИЛ, РАСПОЛОЖЕННЫХ КАК УГОДНО В ПРОСТРАНСТВЕ
- § 1. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
- § 2. ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ
- § 3. РАВНОВЕСИЕ СИСТЕМЫ СИЛ В ПРОСТРАНСТВЕ
- Задачи типа I. Равновесие пространственной системы параллельных сил (задачи 246—252)
- Задачи типа II. Равновесие сил. образующих систему непараллельных компланарных векторов
- Задачи типа III. Равновесие системы некомпланарных сил, каждая из которых параллельна одной из координатных осей
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 277, 278)
- Вторая группа. Задачи в равновесии тела, имеющего три цилиндрические опоры
- Задачи типа IV. Равновесие системы некомпланарных сил в общем случае
- Первая группа. Задачи о равновесии тела, имеющего неподвижную ось вращения (задачи 270, 271, 273, 274)
- Вторая группа. Задачи о равновесии тела, имеющего одну из опор в виде сферического шарнира (задачи 265, 267, 275)
- Третья группа. Задачи о равновесии тела, закрепленного при помощи шести стержней, соединенных с телом и опорами шарнирно (задачи 268, 269)
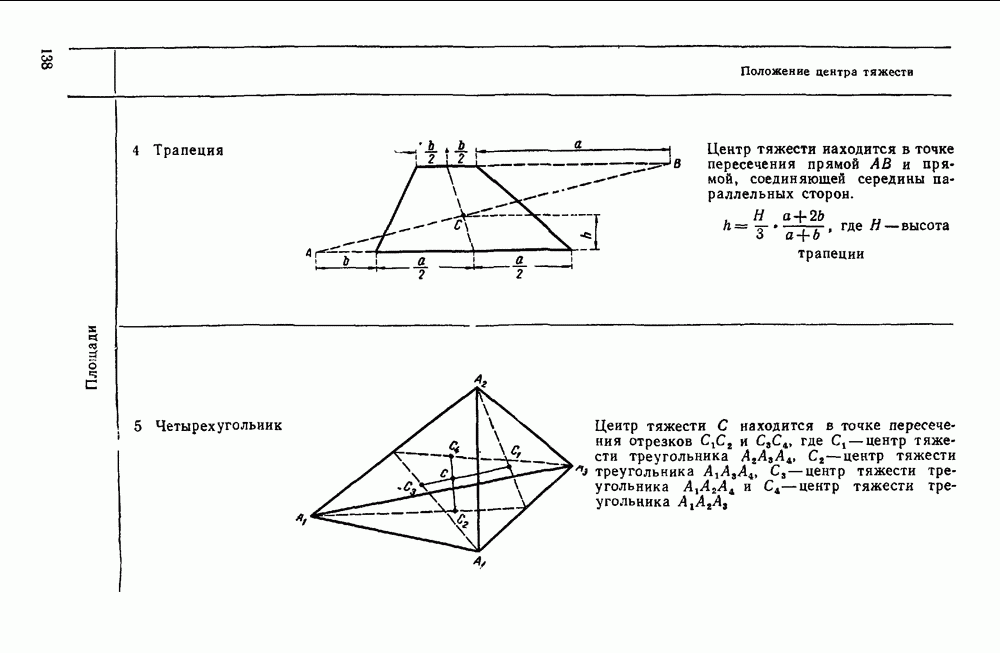
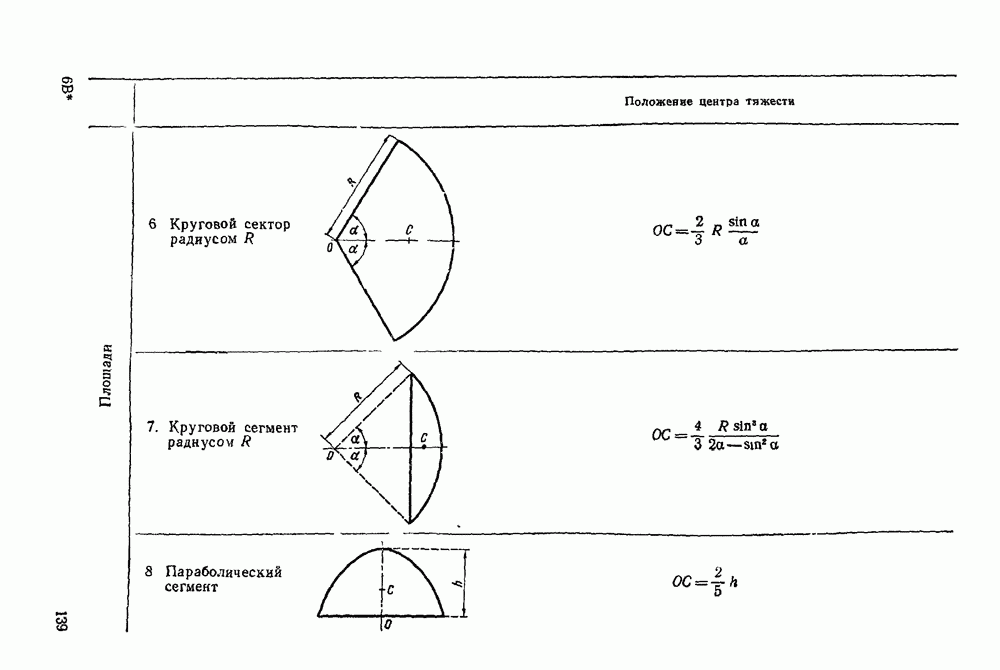
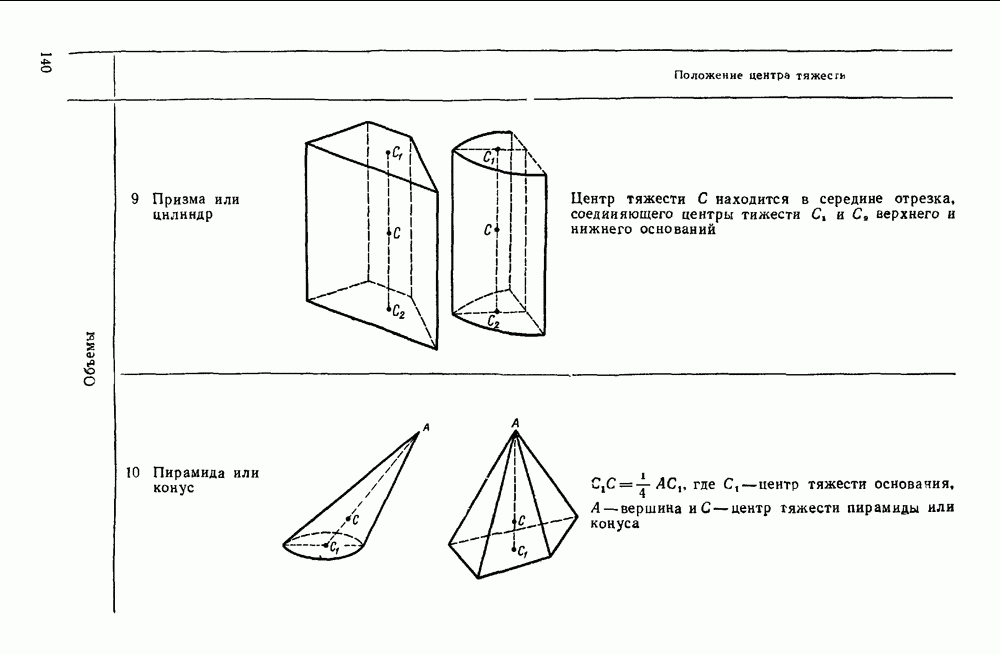
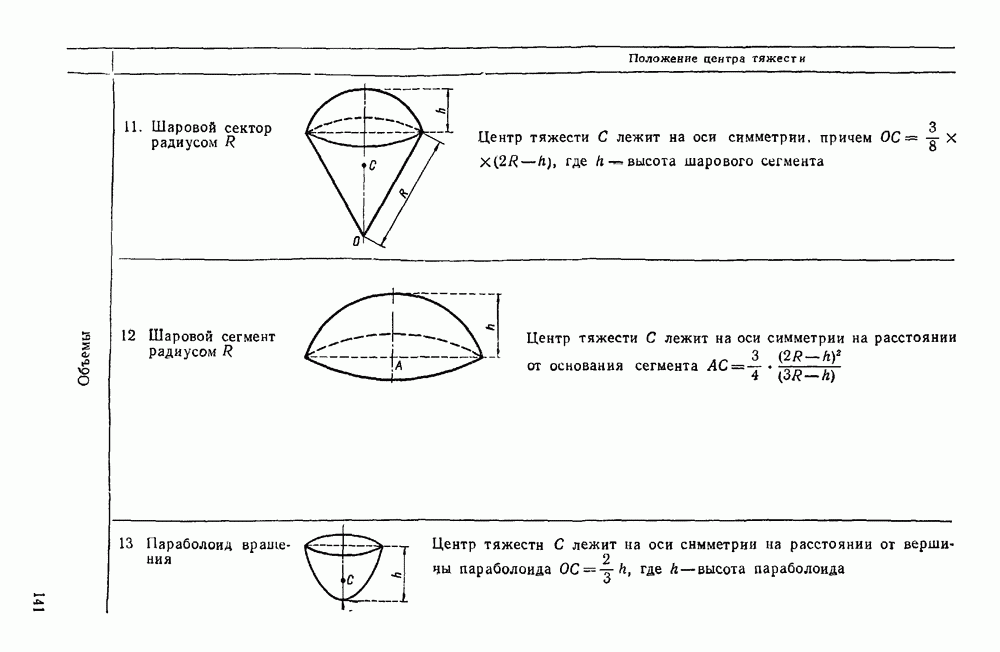
- Глава V. ЦЕНТР ТЯЖЕСТИ
- Четвертая группа
- РАЗДЕЛ II. КИНЕМАТИКА
- Глава I. КИНЕМАТИКА ТОЧКИ
- § 1. ЗАДАЧИ ТИПА I
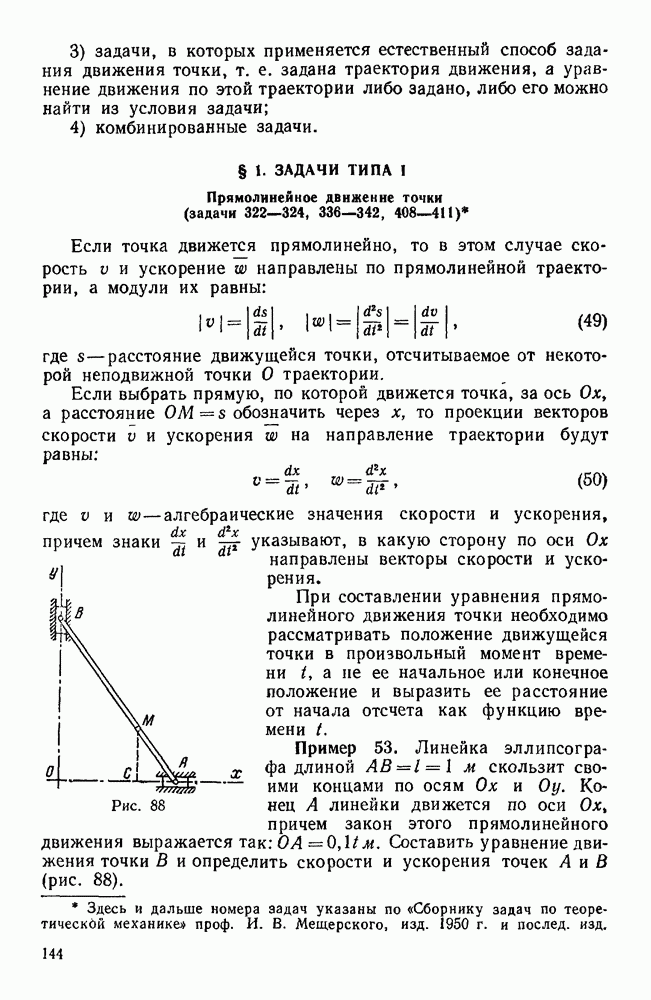
- Прямолинейное движение точки (задачи 322—324, 336-342, 408-411)
- § 2. ЗАДАЧИ ТИПА II
- Вторая группа.
- § 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ ЕСТЕСТВЕННОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава II. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 1. ОПРЕДЕЛЕНИЕ УГЛА ПОВОРОТА, УГЛОВОЙ СКОРОСТИ И УГЛОВОГО УСКОРЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ И УСКОРЕНИЙ ТОЧЕК ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ПЕРЕДАЧА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ОТ ОДНОГО ТЕЛА К ДРУГОМУ
- Глава III. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ
- § 2. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ, ДВИЖУЩЕЙСЯ В СВОЕЙ ПЛОСКОСТИ
- § 3. ЦЕНТРОИДЫ
- § 4. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Глава IV. СОСТАВНОЕ ДВИЖЕНИЕ ТОЧКИ
- § 1. УРАВНЕНИЯ ДВИЖЕНИЯ И ТРАЕКТОРИЯ СОСТАВНОГО ДВИЖЕНИЯ ТОЧКИ
- § 2. ТЕОРЕМА СЛОЖЕНИЯ СКОРОСТЕЙ
- Задачи типа II (задачи 433, 441—443)
- Задачи типа III
- Задачи типа IV
- § 3. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОЕ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I
- Задачи типа II
- Задачи типа III (задачи 445, 446)
- § 4. ТЕОРЕМА СЛОЖЕНИЯ УСКОРЕНИЙ ПРИ ПЕРЕНОСНОМ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
- Задачи типа I (задачи 462—464, 466—468, 470, 476—483, 489, 490)
- Задачи типа II (задачи 465, 469, 471—474)
- Глава V. СОСТАВНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- § 2. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПАРАЛЛЕЛЬНЫХ ОСЕЙ
- § 3. СЛОЖЕНИЕ ВРАЩЕНИЙ ТВЕРДОГО ТЕЛА ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ
- РАЗДЕЛ III. ДИНАМИКА
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- § 3. ВТОРАЯ ОСНОВНАЯ ЗАДАЧА ДИНАМИКИ ТОЧКИ
- Задачи типа I
- Вторая группа
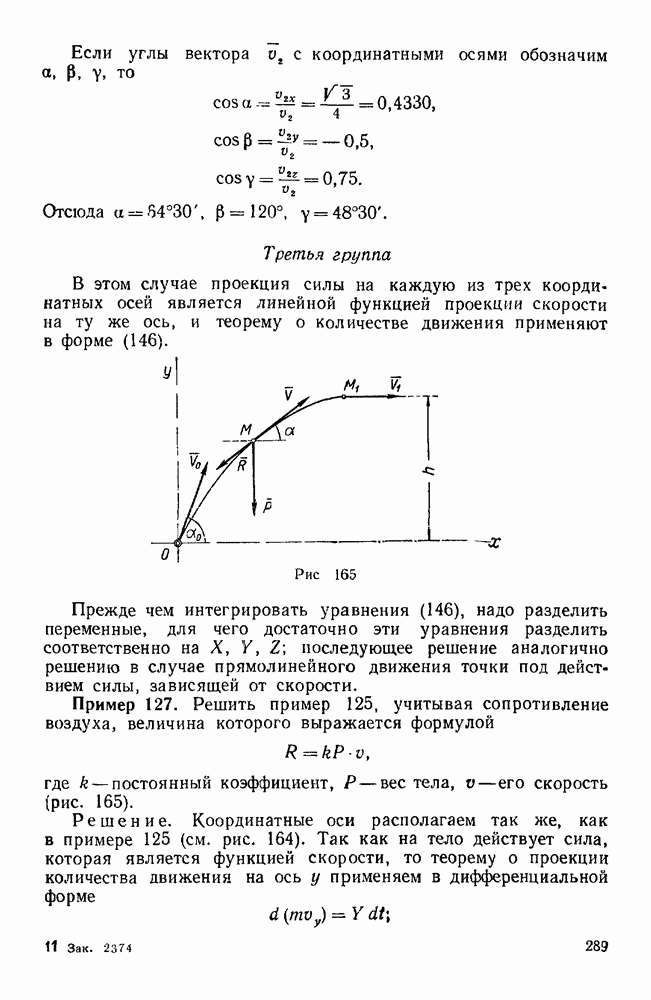
- Третья группа
- Четвертая группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Четвертая группа
- Задачи типа III
- Первая группа
- Глава II. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 2. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 3. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
- Глава III. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ И ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ТЕОРЕМА О КОЛИЧЕСТВЕ ДВИЖЕНИЯ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа III
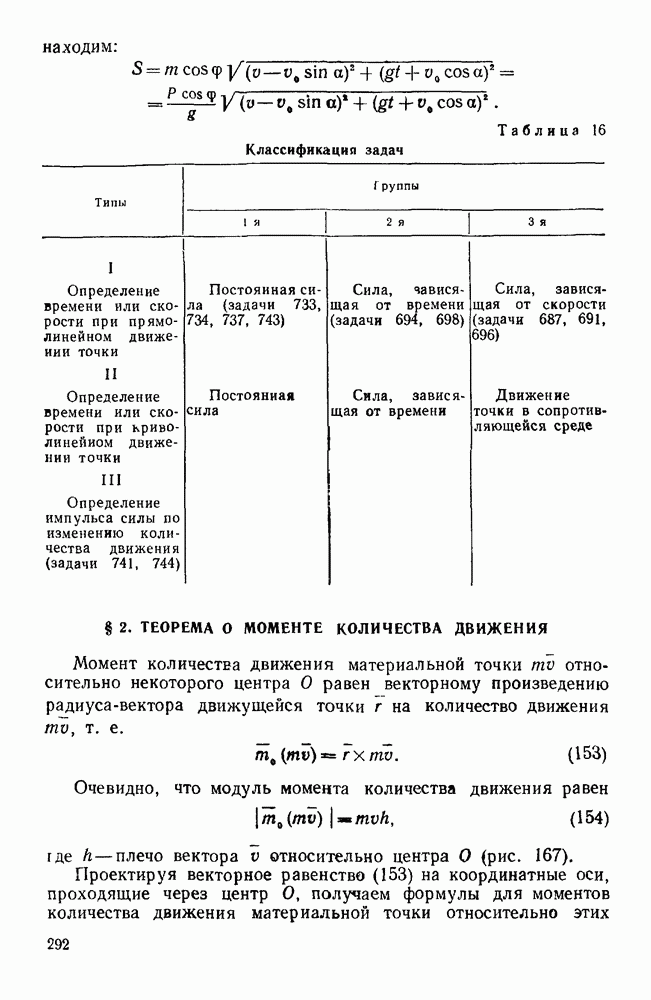
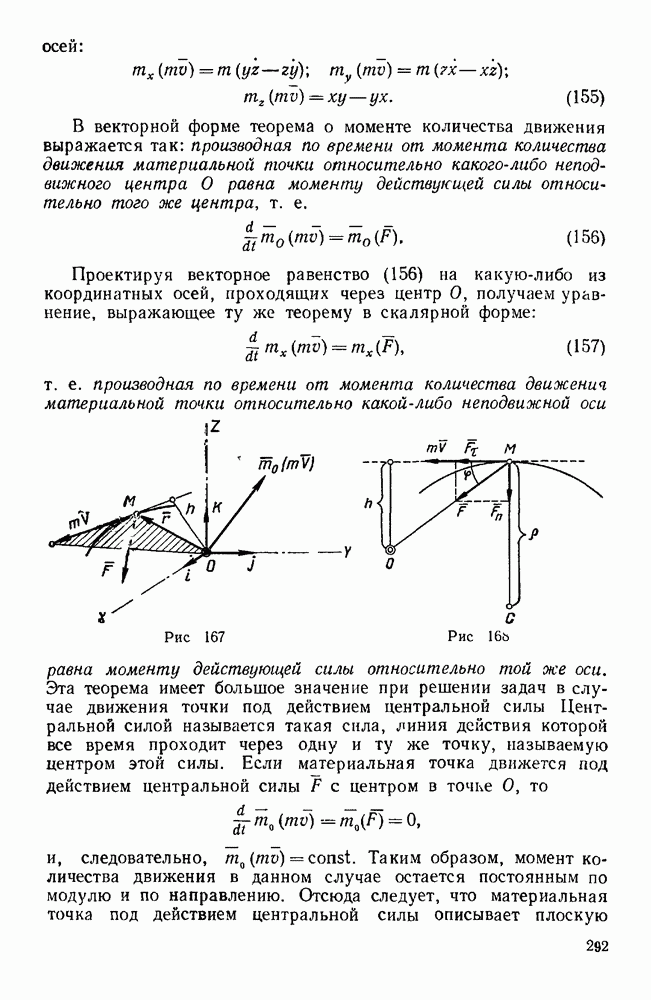
- § 2. ТЕОРЕМА О МОМЕНТЕ КОЛИЧЕСТВА ДВИЖЕНИЯ
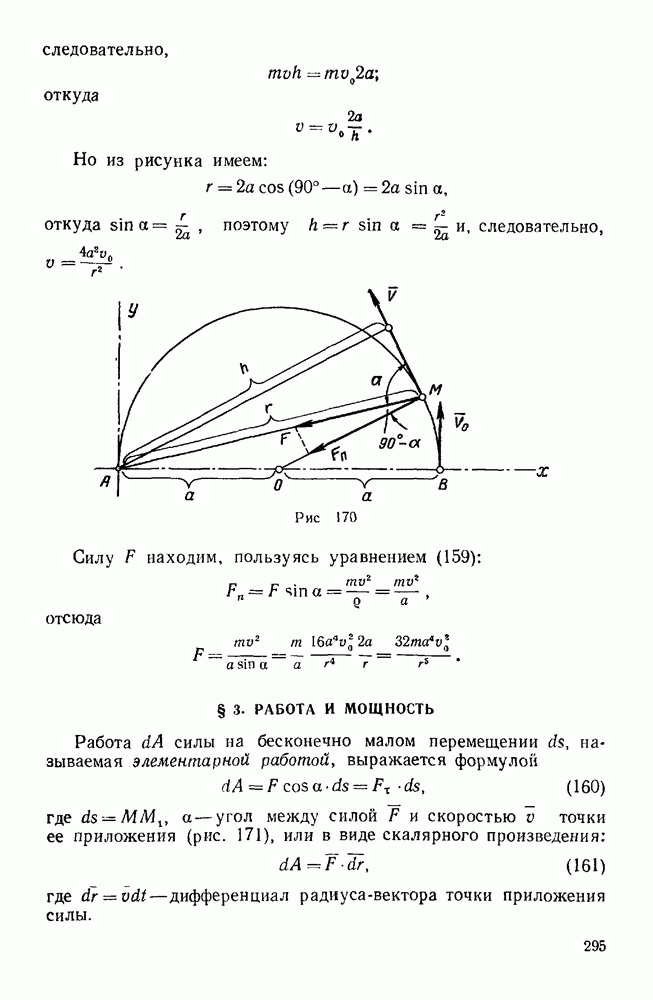
- § 3. РАБОТА И МОЩНОСТЬ
- § 4. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- Третья группа
- § 5. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- Задачи типа I. Прямолинейное движение несвободной материальной точки
- Задачи типа II. Равномерное криволинейное движение несвободной материальной точки
- Задачи типа III. Неравномерное криволинейное движение несвободной материальной точки
- ДИНАМИКА СИСТЕМЫ
- § 1. ТЕОРЕМЫ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ СИСТЕМЫ И О ДВИЖЕНИИ ЦЕНТРА МАСС
- Задачи типа II
- Задачи типа III
- § 2. ТЕОРЕМА О КИНЕТИЧЕСКОМ МОМЕНТЕ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Задачи типа III
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа IV
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа V
- § 3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ
- Задачи типа I
- Задачи типа II
- Вторая группа
- Третья группа
- § 4. КОМБИНИРОВАННЫЕ ЗАДАЧИ
- Глава V. ПРИНЦИП ДАЛАМБЕРА И ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- § 1. ПРИНЦИП ДАЛАМБЕРА ДЛЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- Первая группа
- Вторая группа
- Третья группа
- Задачи типа II
- Первая группа
- Вторая группа
- § 2. ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
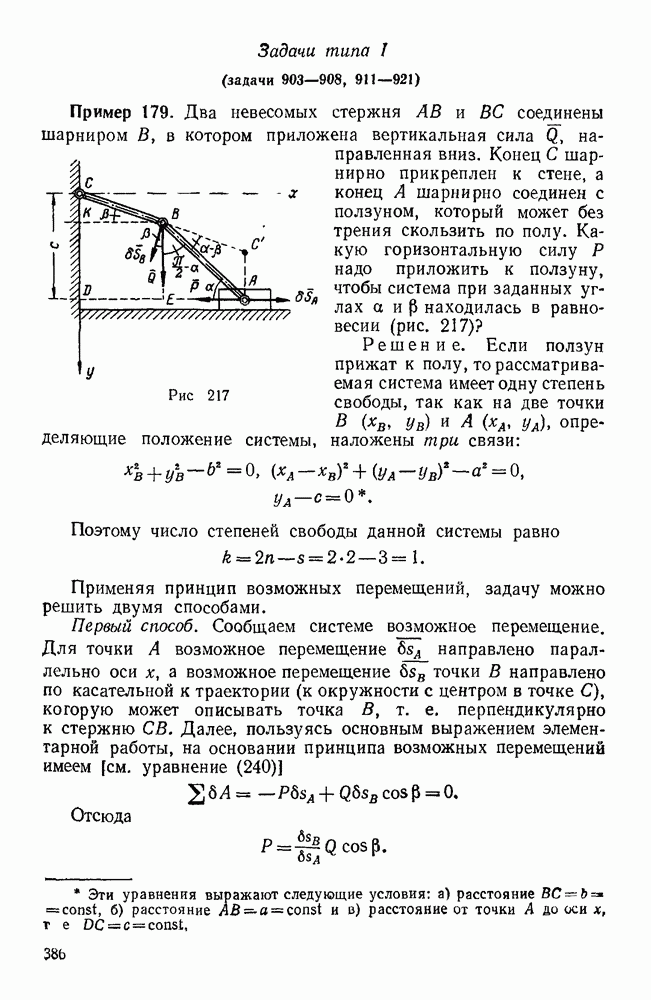
- Задачи типа I (задачи 903—908, 911—921)
- Задачи типа II (задачи 909, 910)
- Задачи типа III (задачи 922—924)
- § 3. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
- Задачи типа II (задачи 930, 943—948)
- § 4. УРАВНЕНИЯ ЛАГРАНЖА И РОДА (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ)
- Задачи типа I
- Вторая группа (задачи 1210, 1213, 1214, 1218, 1221)
- Задачи типа II
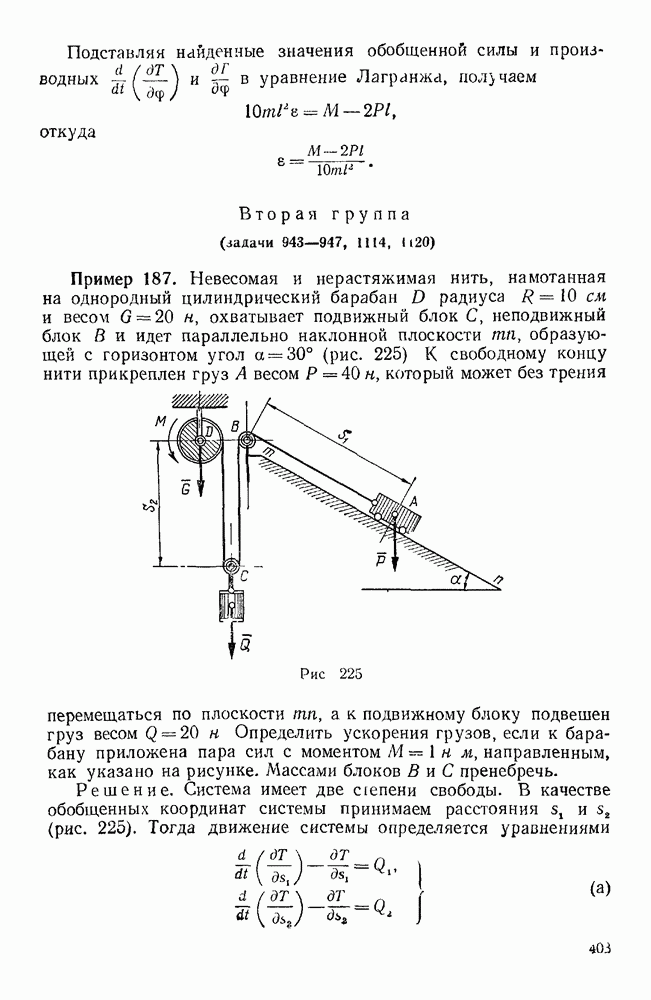
- Вторая группа (задачи 943—947, 1114, 1120)
- Задачи типа III
- Первая группа (задачи 1243—1247)
- Вторая группа (задачи 1219, 1301, 1303, 1304)
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА