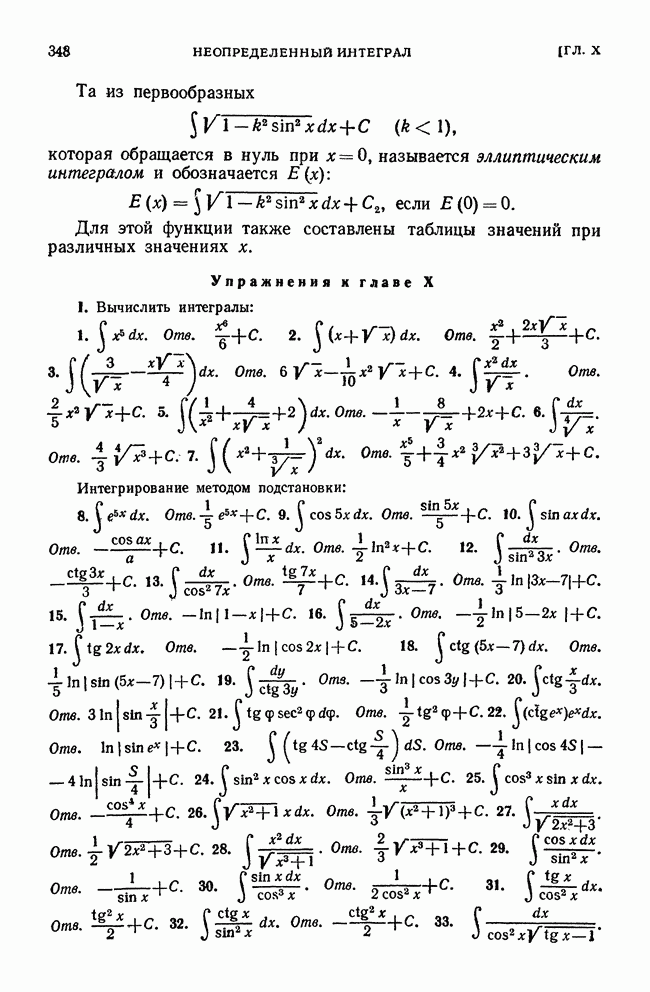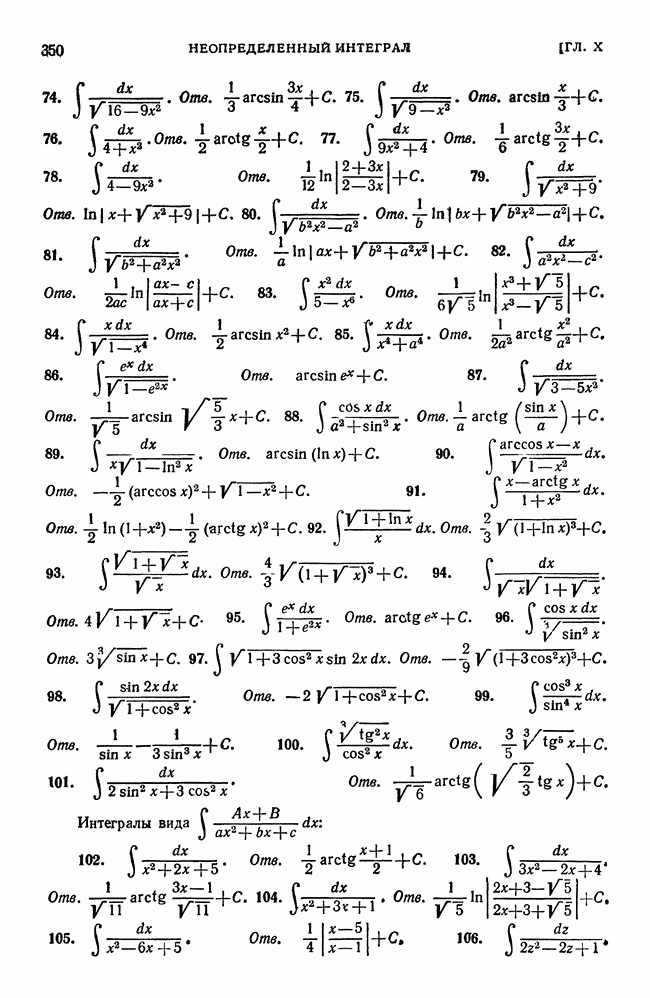| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 17. Максимум и минимум функции нескольких переменных
Определение 1. Мы говорим» что функция  имеет максимум в точке
имеет максимум в точке  (т. е. при
(т. е. при  ), если
), если

для всех точек  достаточно близких к точке
достаточно близких к точке  и отличных от нее.
и отличных от нее.
Определение 2. Совершенно аналогично говорят, что функция  имеет минимум в точке
имеет минимум в точке  если
если

для всех точек  достаточно близких к точке
достаточно близких к точке  и отличных от нее.
и отличных от нее.
Максимум и минимум функции называются экстремумами функции, т. е. говорят, что функция имеет экстремум в данной точке, если эта функция имеет максимум или минимум в данной точке.
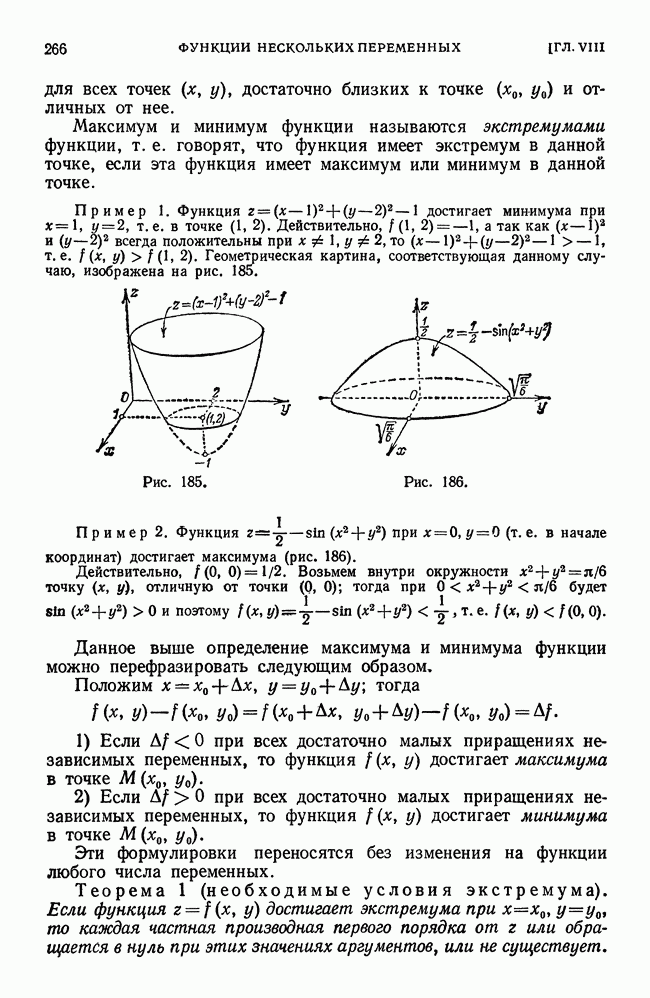
Пример 1. Функция  достигает минимума при
достигает минимума при  , т. е. в точке (1, 2). Действительно,
, т. е. в точке (1, 2). Действительно,  , а так как
, а так как  всегда положительны при
всегда положительны при  то
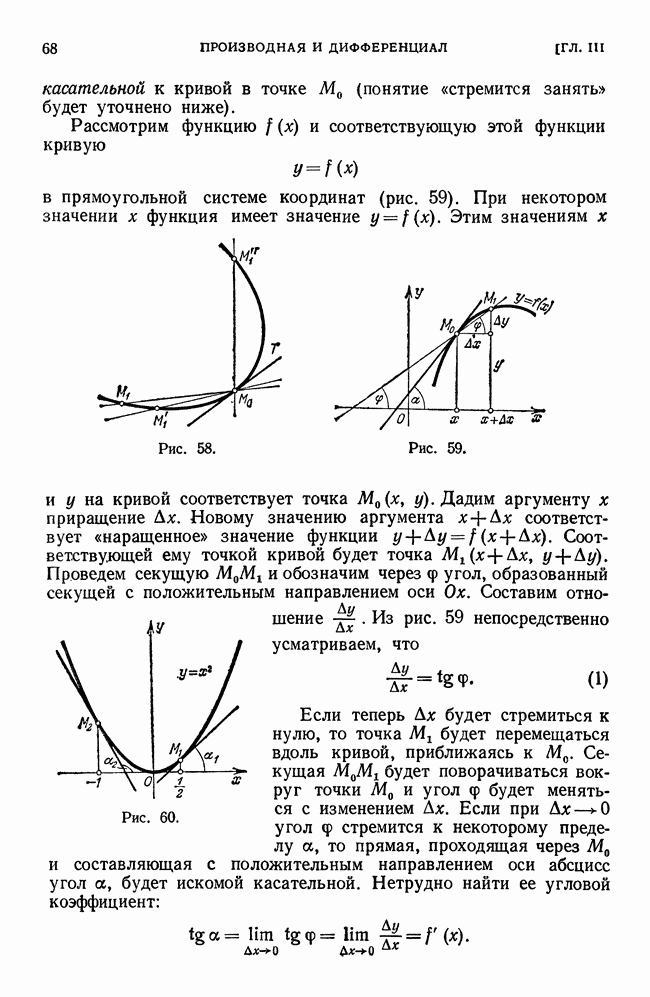
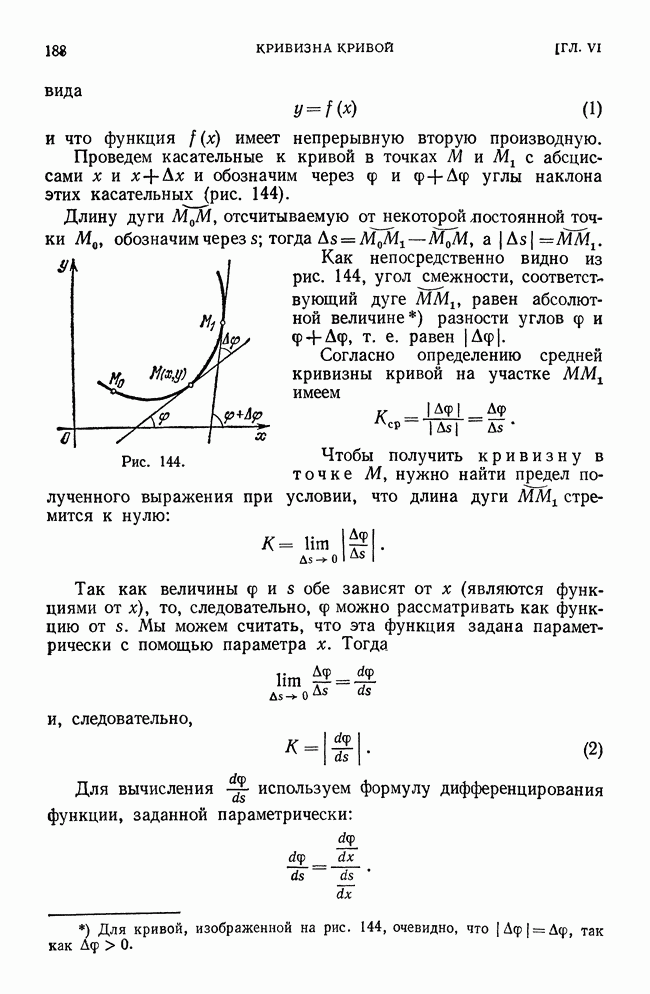
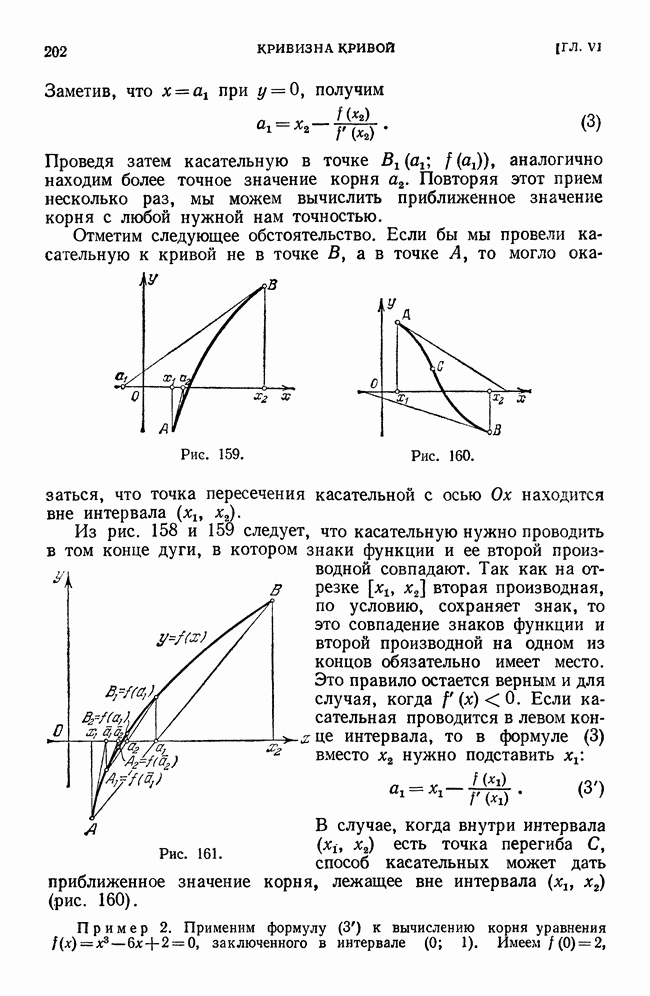
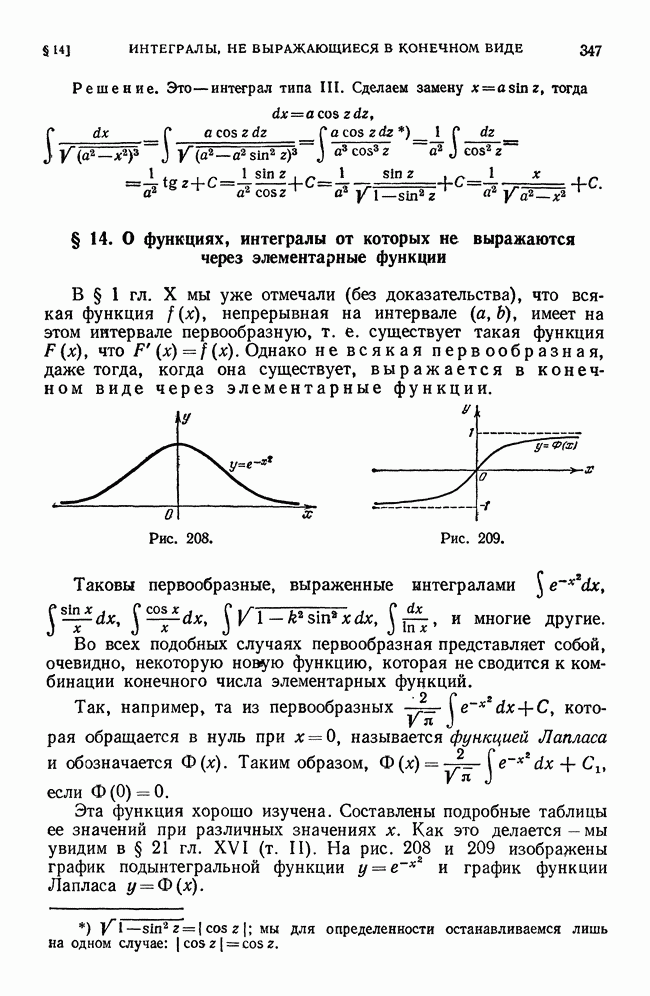
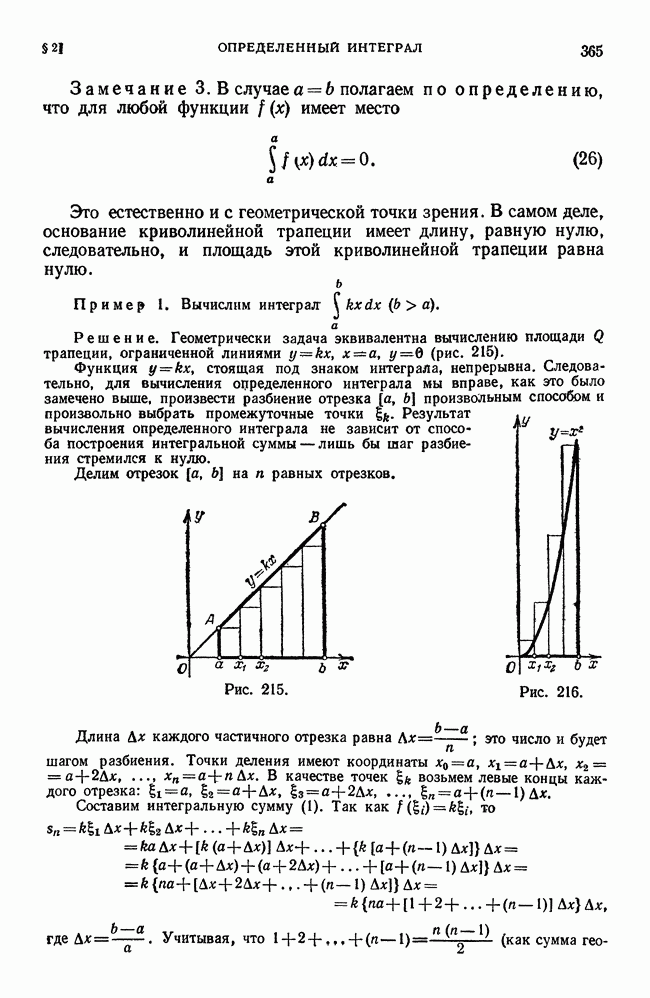
то  Геометрическая картина, соответствующая данному случаю, изображена на рис. 185.
Геометрическая картина, соответствующая данному случаю, изображена на рис. 185.

Рис. 185.

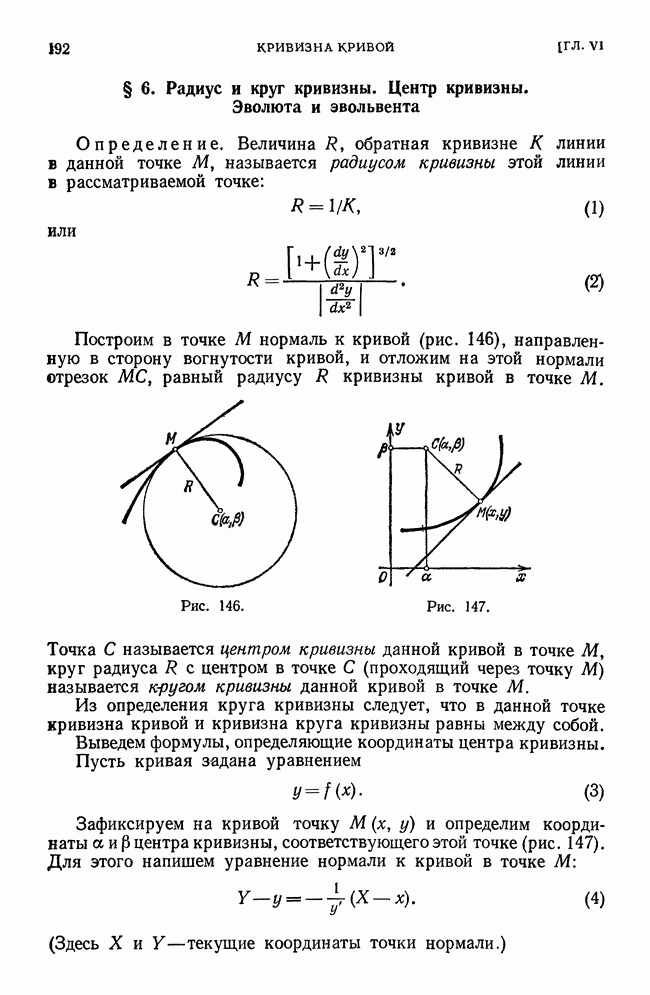
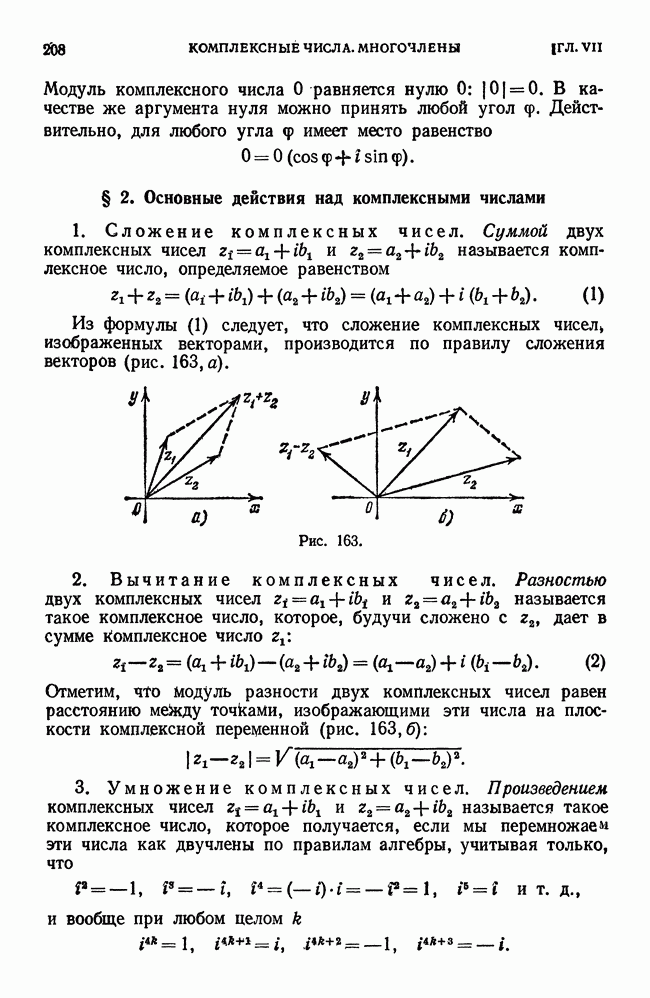
Рис. 186.
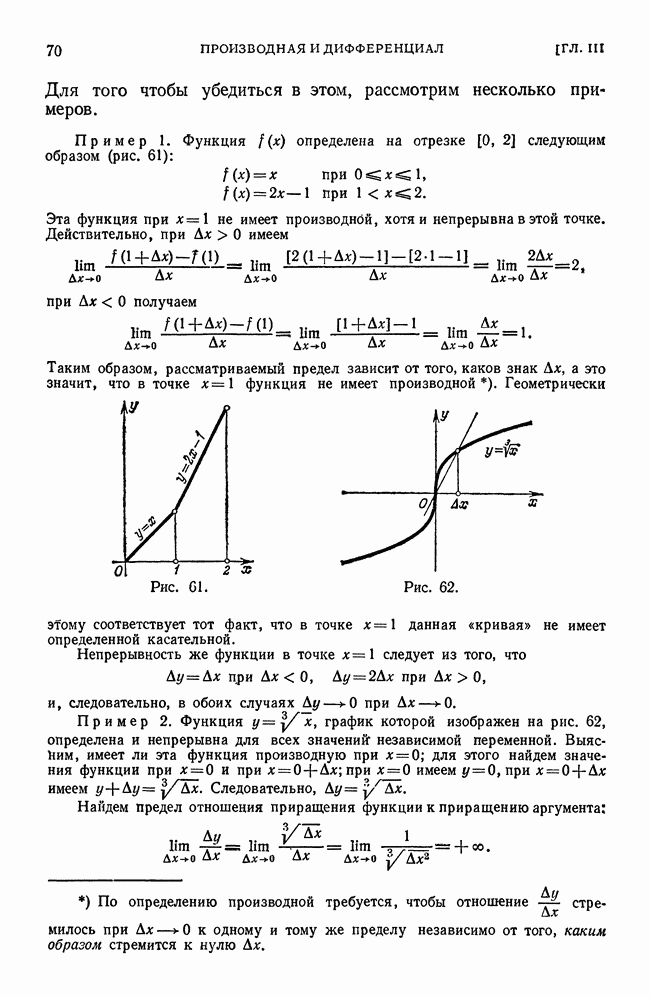
Пример 2. Функция  при
при  (т. е. в начале координат) достигает максимума (рис. 186).
(т. е. в начале координат) достигает максимума (рис. 186).
Действительно,  Возьмем внутри окружности
Возьмем внутри окружности  точку
точку  отличную от точки (0, 0); тогда при
отличную от точки (0, 0); тогда при  будет
будет  и поэтому
и поэтому 
Данное выше определение максимума и минимума функции можно перефразировать следующим образом.
Положим  тогда
тогда

1) Если  при всех достаточно малых приращениях независимых переменных, то функция
при всех достаточно малых приращениях независимых переменных, то функция  достигает максимума в точке
достигает максимума в точке 
2) Если  при всех достаточно малых приращениях независимых переменных, то функция
при всех достаточно малых приращениях независимых переменных, то функция  достигает минимума в точке
достигает минимума в точке 
Эти формулировки переносятся без изменения на функции любого числа переменных.
Теорема 1 (необходимые условия экстремума). Если функция  достигает экстремума при
достигает экстремума при  , то каждая частная производная первого порядка от
, то каждая частная производная первого порядка от  или обращается в нуль при этих значениях аргументов, или не существует.
или обращается в нуль при этих значениях аргументов, или не существует.
Действительно, дадим переменной у определенное значение, именно  . Тогда функция
. Тогда функция  будет функцией одной переменной х. Так как при
будет функцией одной переменной х. Так как при  она имеет экстремум (максимум или минимум), то, следовательно,
она имеет экстремум (максимум или минимум), то, следовательно,  или равно нулю, или не существует. Совершенно аналогично можно доказать, что
или равно нулю, или не существует. Совершенно аналогично можно доказать, что  или равно нулю, или не существует.
или равно нулю, или не существует.
Эта теорема не является достаточной для исследования вопроса об экстремальных значениях функции, но позволяет находить эти значения в тех случаях, в которых мы заранее уверены в существовании максимума или минимума. В противном случае требуется дополнительное исследование.
Так, например, функция  имеет
имеет  производные
производные  , которые обращаются в нуль при
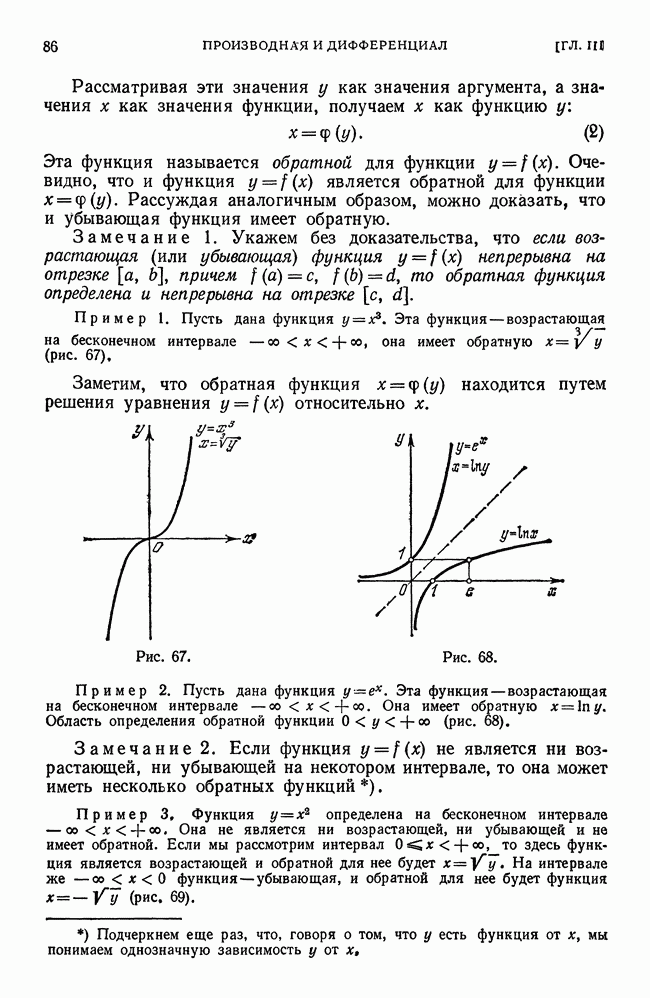
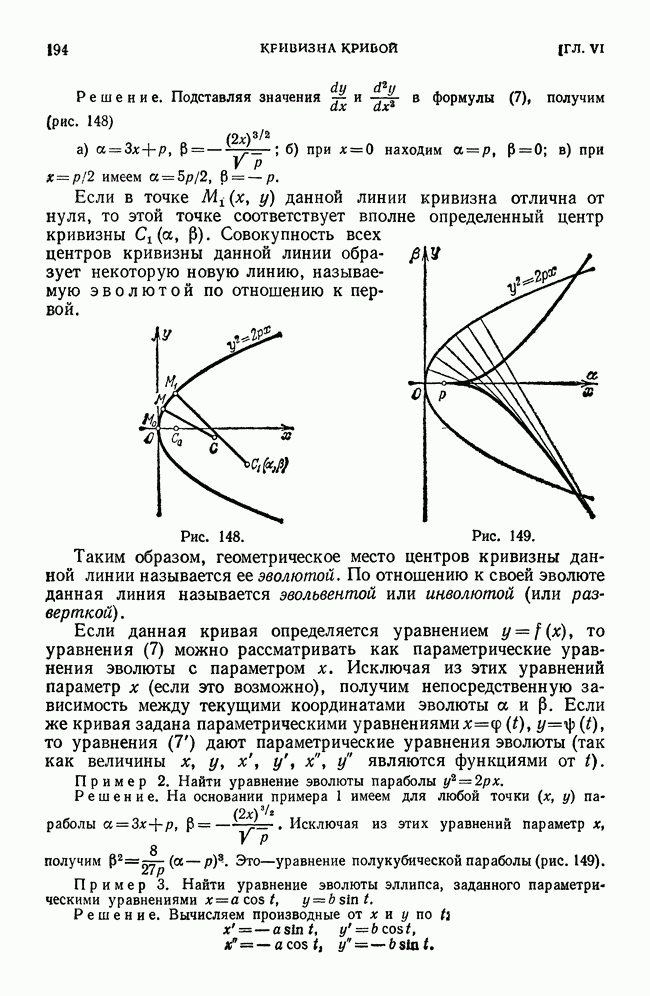
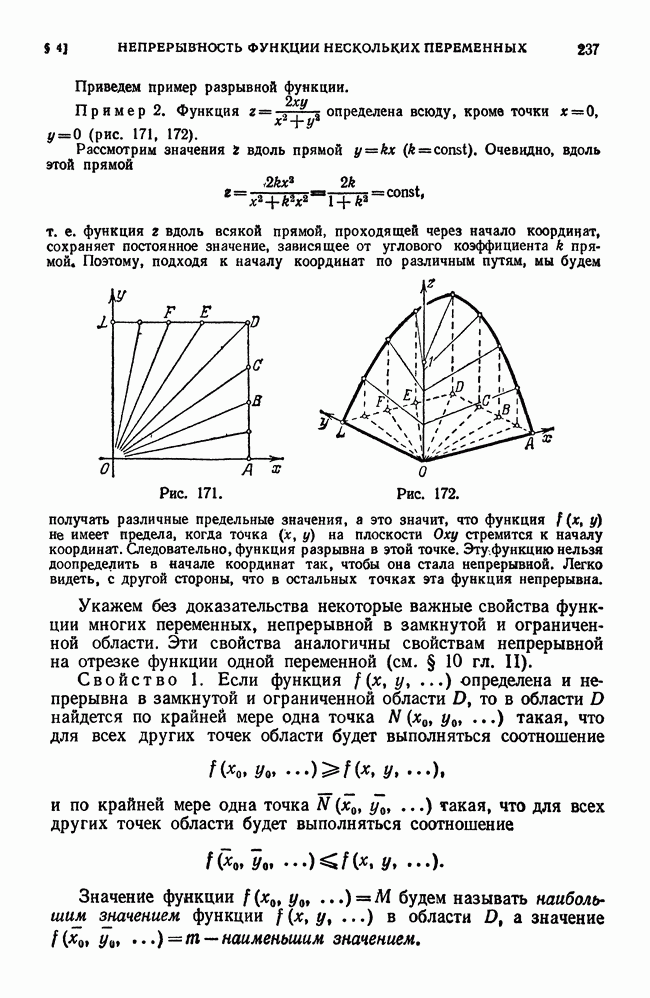
, которые обращаются в нуль при  Но эта функция при указанных значениях не имеет ни максимума, ни минимума. Действительно, эта функция равна нулю в начале координат и принимает в как угодно близких точках от начала координат как положительные, так и отрицательные значения. Следовательно, значение нуль не является ни максимумом, ни минимумом (рис. 187).
Но эта функция при указанных значениях не имеет ни максимума, ни минимума. Действительно, эта функция равна нулю в начале координат и принимает в как угодно близких точках от начала координат как положительные, так и отрицательные значения. Следовательно, значение нуль не является ни максимумом, ни минимумом (рис. 187).

Рис. 187.
Точки, в которых  не существует)
не существует)  не существует), называются критическими точками функции
не существует), называются критическими точками функции  Если функция достигает экстремума в какой-либо точке, то (в силу теоремы 1) это может случиться только в критической точке.
Если функция достигает экстремума в какой-либо точке, то (в силу теоремы 1) это может случиться только в критической точке.
Для исследования функции в критических точках установим достаточные условия экстремума функции двух переменных.
Теорема 2. Пусть в некоторой области, содержащей точку  функция
функция  имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, точка
имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, точка  является критической точкой функции
является критической точкой функции  , т. е.
, т. е.

Тогда при 
1)  имеет максимум, если
имеет максимум, если

2)  имеет минимум, если
имеет минимум, если

3)  не имеет ни максимума, ни минимума, если
не имеет ни максимума, ни минимума, если

4) если  , то экстремум может быть и может не быть (в этом случае требуется дальнейшее исследование).
, то экстремум может быть и может не быть (в этом случае требуется дальнейшее исследование).
Доказательство. Напишем формулу Тейлора второго порядка для функции  (формула (6) § 16). Полагая
(формула (6) § 16). Полагая  , будем иметь
, будем иметь

где  стремится к нулю при
стремится к нулю при  .
.
По условию

Следовательно,

Обозначим теперь значения вторых частных производных в точке  через А, В, С:
через А, В, С:

Обозначим: через  угол между направлением отрезка
угол между направлением отрезка  , где М есть точка
, где М есть точка  , и осью
, и осью  тогда
тогда  . Подставляя эти выражения в формулу для
. Подставляя эти выражения в формулу для  найдем
найдем

Предположим, что  .
.
Разделив и умножив на А выражение, стоящее в квадратных скобках, получим

Рассмотрим теперь четыре возможных случая.
1) Пусть  . Тогда в числителе дроби стоит сумма двух неотрицательных величин. Они одновременно в нуль
. Тогда в числителе дроби стоит сумма двух неотрицательных величин. Они одновременно в нуль
не обращаются, так как первый член обращается в нуль при  второй при
второй при  .
.
Если  то дробь есть отрицательная величина, не обращающаяся в нуль. Обозначим ее через
то дробь есть отрицательная величина, не обращающаяся в нуль. Обозначим ее через  тогда
тогда

где  не зависит от
не зависит от  при
при  . Следовательно, при достаточно малых
. Следовательно, при достаточно малых  будет
будет  или
или  тогда для всех точек
тогда для всех точек  достаточно близких к точке
достаточно близких к точке  имеет место неравенство
имеет место неравенство

а это означает, что в точке  функция
функция  достигает максимума.
достигает максимума.
2) Пусть  Тогда, рассуждая аналогично, получим
Тогда, рассуждая аналогично, получим

или

т. е.  имеет минимум в точке
имеет минимум в точке 
Пусть  . В этом случае функция не имеет ни максимума, ни минимума. Функция возрастает, Когда мы движемся из точки
. В этом случае функция не имеет ни максимума, ни минимума. Функция возрастает, Когда мы движемся из точки  по одним направлениям, и убывает, когда мы движемся по другим направлениям. Действительно, при перемещении вдоль луча
по одним направлениям, и убывает, когда мы движемся по другим направлениям. Действительно, при перемещении вдоль луча  имеем
имеем

при движении вдоль этого луча функция возрастает. Если же перемещаться вдоль луча  , такого, что
, такого, что  , то при
, то при  будет
будет

при движении вдоль этого луча функция убывает.
3) Пусть  . В этом случае функция тоже не имеет ни максимума, ни минимума. Исследование проводится так же, как и в случае 3.
. В этом случае функция тоже не имеет ни максимума, ни минимума. Исследование проводится так же, как и в случае 3.
3) Пусть  Тогда
Тогда  и равенство (2) можно переписать в виде
и равенство (2) можно переписать в виде

При достаточно малых значениях  выражение, стоящее в круглых скобках, сохраняет знак, так как оно близко к
выражение, стоящее в круглых скобках, сохраняет знак, так как оно близко к  а множитель
а множитель
 меняет знак в зависимости от того, будет ли
меняет знак в зависимости от того, будет ли  больше нуля или меньше нуля (после выбора
больше нуля или меньше нуля (после выбора  мы можем
мы можем  взять настолько малым, что
взять настолько малым, что  не будет изменять знак всей квадратной скобки). Следовательно, и в этом случае
не будет изменять знак всей квадратной скобки). Следовательно, и в этом случае  меняет знак при различных
меняет знак при различных  т. е. при различных
т. е. при различных  следовательно, и в этом случае нет ни максимума, ни минимума.
следовательно, и в этом случае нет ни максимума, ни минимума.
Таким образом, каков бы ни был знак А, имеем всегда следующее положение:
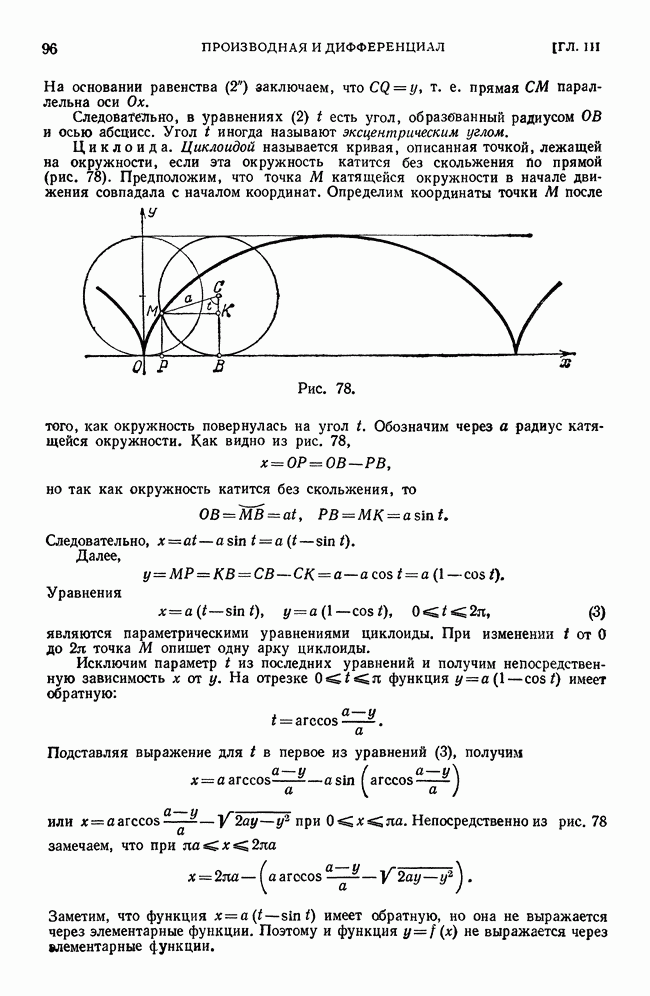
Если  в точке
в точке  то функция не имеет в этой точке ни максимума, ни минимума. В этом случае поверхность, служащая графиком функции, может вблизи этой точки иметь, например, форму седла (см. выше рис. 187). Говорят, что функция имеет в этой точке минимакс.
то функция не имеет в этой точке ни максимума, ни минимума. В этом случае поверхность, служащая графиком функции, может вблизи этой точки иметь, например, форму седла (см. выше рис. 187). Говорят, что функция имеет в этой точке минимакс.
4) Пусть  . В этом случае на основании формул (2) и (3) сделать заключение о знаке
. В этом случае на основании формул (2) и (3) сделать заключение о знаке  нельзя. Так, например, при
нельзя. Так, например, при  будем иметь
будем иметь

при  знак
знак  определяется знаком
определяется знаком  здесь требуется специальное дальнейшее исследование (например, с помощью формулы Тейлора более высокого порядка или каким-либо иным способом). Таким образом, теорема 2 полностью доказана.
здесь требуется специальное дальнейшее исследование (например, с помощью формулы Тейлора более высокого порядка или каким-либо иным способом). Таким образом, теорема 2 полностью доказана.
Пример 3. Исследовать на максимум и минимум функцию

Решение. 1) Находим критические точки:

Решая систему уравнений

получаем

2) Находим производные второго порядка в критической точке (-4/3; 1 /3) и определяем характер критической точки:

Следовательно, в точке (-4/3; 1/3) данная функция имеет - минимум, а именно:

Пример 4. Исследовать на максимум и минимум функцию

Решение. 1). Найдем критические точки, пользуясь необходимыми  ловиями экстремума:
ловиями экстремума:

Отсюда получаем две критические точки:

2) Найдем производные второго порядка:

3) Исследуем характер первой критической точки:

Следовательно; в точке (1; 1) данная функция имеет минимум, именно:

4) Исследуем характер второй критической точки 

Следовательно, во второй критической точке функция не имеет ни максимума, ни минимума (минимакс).
Пример 5. Разложить данное положительное число а на три положительных слагаемых так, чтобы их произведение имело наибольшее значение.
Релгение. Обозначим слагаемые: первое через  второе через
второе через  тогда третье будет
тогда третье будет  Произведение этих слагаемых равно
Произведение этих слагаемых равно  По условии задачи
По условии задачи  Следовательно,
Следовательно,  и у могут принимать значения, принадлежащие области, ограниченной прямыми
и у могут принимать значения, принадлежащие области, ограниченной прямыми 
Найдем частные производные функции и:

Приравнивая производные нулю, получим систему уравнений

Решая эту систему находим критические точки:

Первые три точки лежат на границе области, последняя — внутри. На границе  функция а равна нулю, а внутри области она положительна; следовательно, в точке
функция а равна нулю, а внутри области она положительна; следовательно, в точке  функция и имеет максимум (так как
функция и имеет максимум (так как  единственная экстремальная точка внутри треугольника). Максимальное значение произведения есть
единственная экстремальная точка внутри треугольника). Максимальное значение произведения есть

Проведем исследование характера критических точек, пользуясь достаточными условиями. Найдем частные производные второго порядка функции и:

В точке  имеем
имеем 
Следовательно, в точке  нет ни максимума, ни минимума.
нет ни максимума, ни минимума.
В точке  имеем
имеем  Значит, в точке
Значит, в точке  тоже нет ни максимума, ни минимума. В точке
тоже нет ни максимума, ни минимума. В точке  имеем
имеем  И в точке
И в точке  нет ни максимума, ни минимума. В точке
нет ни максимума, ни минимума. В точке  имеем
имеем  Следовательно, в точке
Следовательно, в точке  имеем максимум.
имеем максимум.
Замечание. Теория максимумов и минимумов функции нескольких переменных является основой для одного метода получения формул для изображения функциональных зависимостей на основании экспериментальных данных. Этот вопрос изложен в § 19.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА I. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ
- § 1. Действительные числа.
- § 2. Абсолютная величина действительного числа
- § 3. Переменные и постоянные величины
- § 4. Область изменения переменной величины
- § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина
- § 6. Функция
- § 7. Способы задания функции
- § 8. Основные элементарные функции. Элементарные функции
- § 9. Алгебраические функции
- § 10. Полярная система координат
- Упражнения к главе I
- ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
- § 1. Предел переменной величины. Бесконечно большая переменная величина
- § 2. Предел функции
- § 3. Функция, стремящаяся к бесконечности. Ограниченные функции
- § 4. Бесконечно малые и их основные свойства
- § 5. Основные теоремы о пределах
- § 6. Предел функции (sin x)/x при x->0
- § 7. Число e
- § 8. Натуральные логарифмы
- § 9. Непрерывность функций
- § 10. Некоторые свойства непрерывных функций
- § 11. Сравнение бесконечно малых
- Упражнения к главе II
- ГЛАВА III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
- § 2. Определение производной
- § 3. Геометрическое значение производной
- § 4. Дифференцируемость функций
- § 5. Производная от функции y = x^n при n целом и положительном
- § 6. Производные от функций y = sinx; y = cosx
- § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного
- § 8. Производная логарифмической функции
- § 9. Производная от сложной функции
- § 10. Производные функций y = tgx, y = ctgx, y = ln|x|
- § 11. Неявная функция и ее дифференцирование
- § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции
- § 13. Обратная функция и ее дифференцирование
- § 14. Обратные тригонометрические функции и их дифференцирование
- § 15. Таблица основных формул дифференцирования
- § 16. Параметрическое задание функции
- § 17. Уравнения некоторых кривых в параметрической форме
- § 18. Производная функции, заданной параметрически
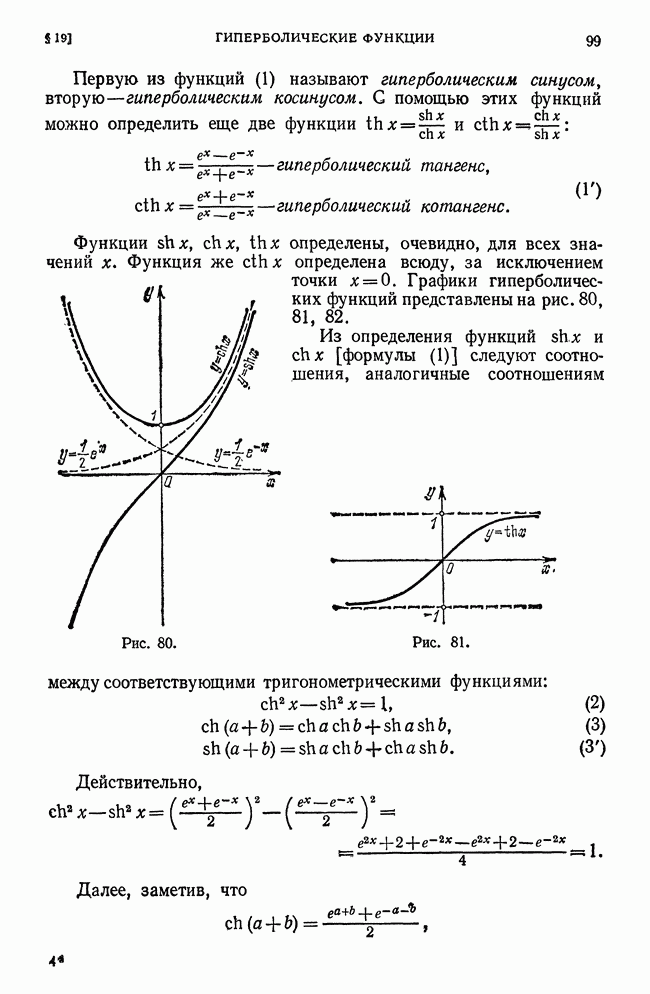
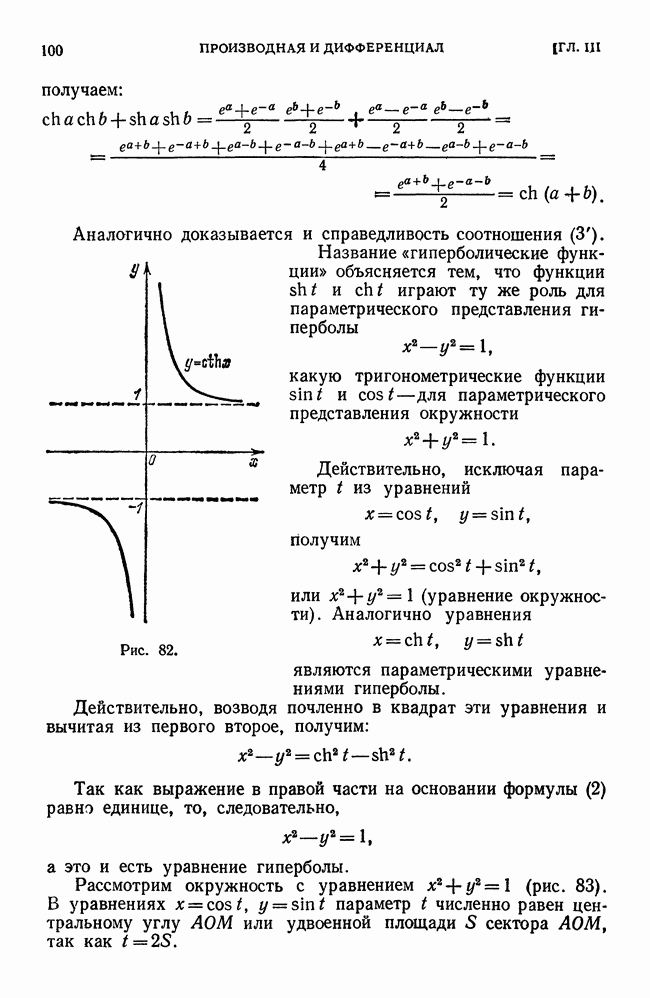
- § 19. Гиперболические функции
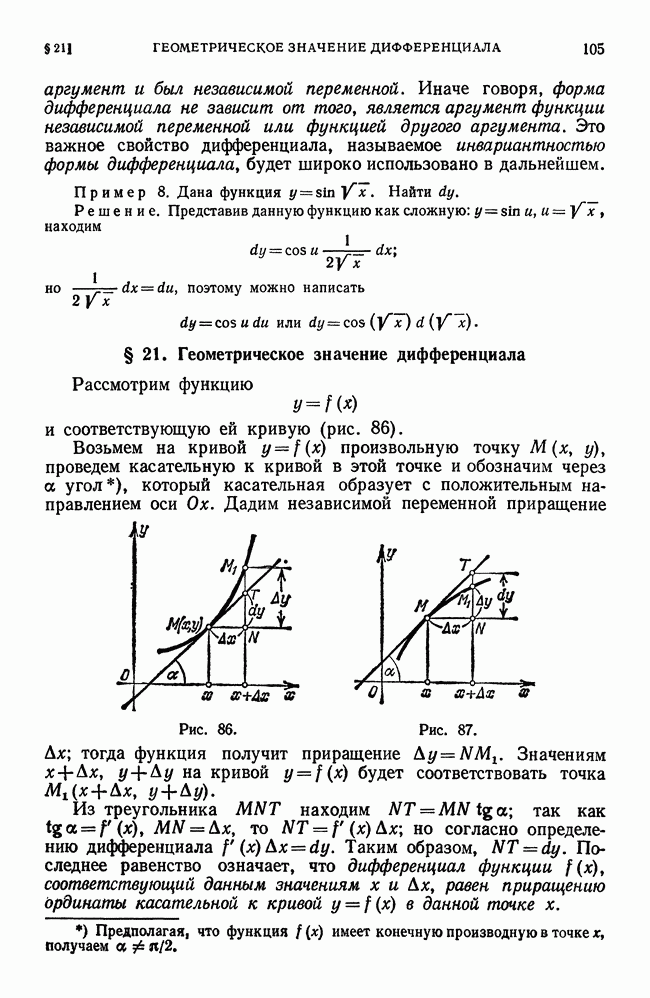
- § 20. Дифференциал
- § 21. Геометрическое значение дифференциала Рассмотрим функцию
- § 22. Производные различных порядков
- § 23. Дифференциалы различных порядков
- § 24. Производные различных порядков от неявных функций и функций, заданных параметрически
- § 25. Механическое значение второй производной
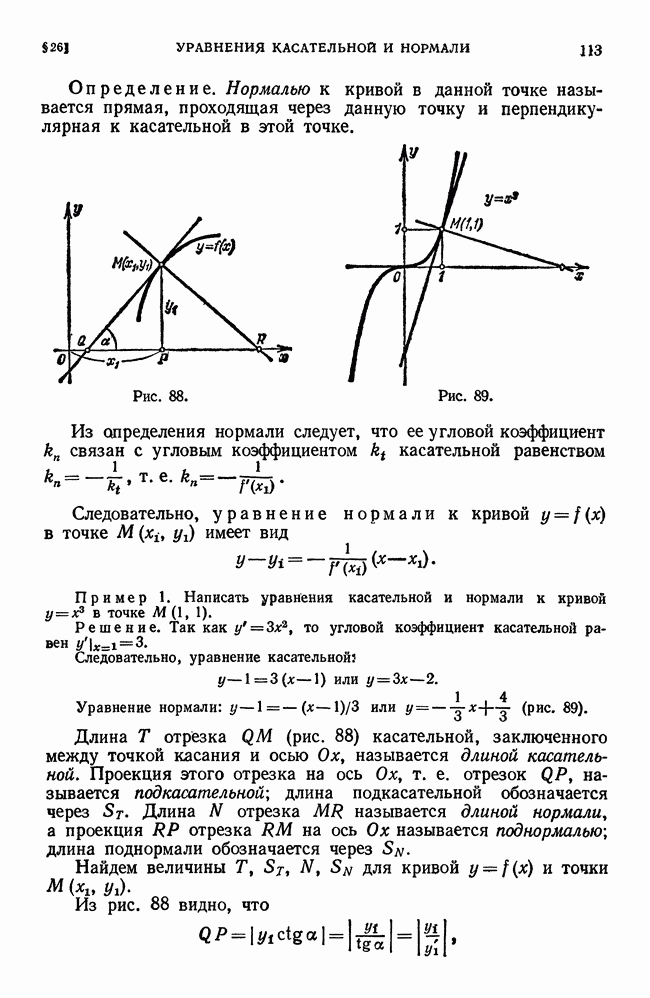
- § 26. Уравнения касательной и нормали. Длины подкасательной и поднормали
- § 27. Геометрическое значение производной радиус-вектора по полярному углу
- Упражнения к главе III
- ГЛАВА IV. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
- § 1. Теорема о корнях производной (теорема Ролля)
- § 2. Теорема о конечных приращениях (теорема Лагранжа)
- § 3. Теорема об отношении приращений двух функций (теорема Коши)
- § 4. Предел отношения двух бесконечно малых величин «раскрытие неопределенностей вида 0/0»)
- § 5. Предел отношения двух бесконечно больших величин «раскрытие неопределенностей вида oo/oo»)
- § 6. Формула Тейлора
- § 7. Разложение по формуле Тейлора функций e^x, sin x, cos x
- Упражнения к главе IV
- ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
- § 2. Возрастание и убывание функции
- § 3. Максимум и минимум функций
- § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной
- § 5. Исследование функции на максимум и минимум с помощью второй производной
- § 6. Наибольшее и наименьшее значения функции на отрезке
- § 7. Применение теории максимума и минимума функций к решению задач
- § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора
- § 9. Выпуклость и вогнутость кривой. Точки перегиба
- § 10. Асимптоты
- § 11. Общий план исследования функций и построения графиков
- § 12. Исследование кривых, заданных параметрически
- Упражнения к главе V
- ГЛАВА VI. КРИВИЗНА КРИВОЙ
- § 1. Длина дуги и ее производная
- § 2. Кривизна
- § 3. Вычисление кривизны
- § 4. Вычисление кривизны линии, заданной параметрически
- § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах
- § 6. Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента
- § 7. Свойства эволюты
- § 8. Приближенное вычисление действительных корней уравнения
- Упражнения к главе VI
- ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ
- § 1. Комплексные числа. Исходные определения
- § 2. Основные действия над комплексными числами
- § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа
- § 4. Показательная функция с комплексным показателем и ее свойства
- § 5. Формула Эйлера. Показательная форма комплексного числа
- § 6. Разложение многочлена на множители
- § 7. О кратных корнях многочлена
- § 8. Разложение многочлена на множители в случае комплексных корней
- § 9. Интерполирование. Интерполяционная формула Лагранжа
- § 10. Интерполяционная формула Ньютона
- § 11. Численное дифференцирование
- § 12. О наилучшем приближении функций многочленами. Теория Чебышева
- Упражнения к главе VII
- ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. Определение функции нескольких переменных
- § 2. Геометрическое изображение функции двух переменных
- § 3. Частное и полное приращение функции
- § 4. Непрерывность функции нескольких переменных
- § 5. Частные производные функции нескольких переменных
- § 6. Геометрическая интерпретация частных производных функции двух переменных
- § 7. Полное приращение и полный дифференциал
- § 8. Применение полного дифференциала в приближенных вычислениях
- § 9. Приложение дифференциала к оценке погрешности при вычислениях
- § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции
- § 11. Производная от функции, заданной неявно
- § 12. Частные производные различных порядков
- § 13. Поверхности уровня
- § 14. Производная по направлению
- § 15. Градиент
- § 16. Формула Тейлора для функции двух переменных
- § 17. Максимум и минимум функции нескольких переменных
- § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы)
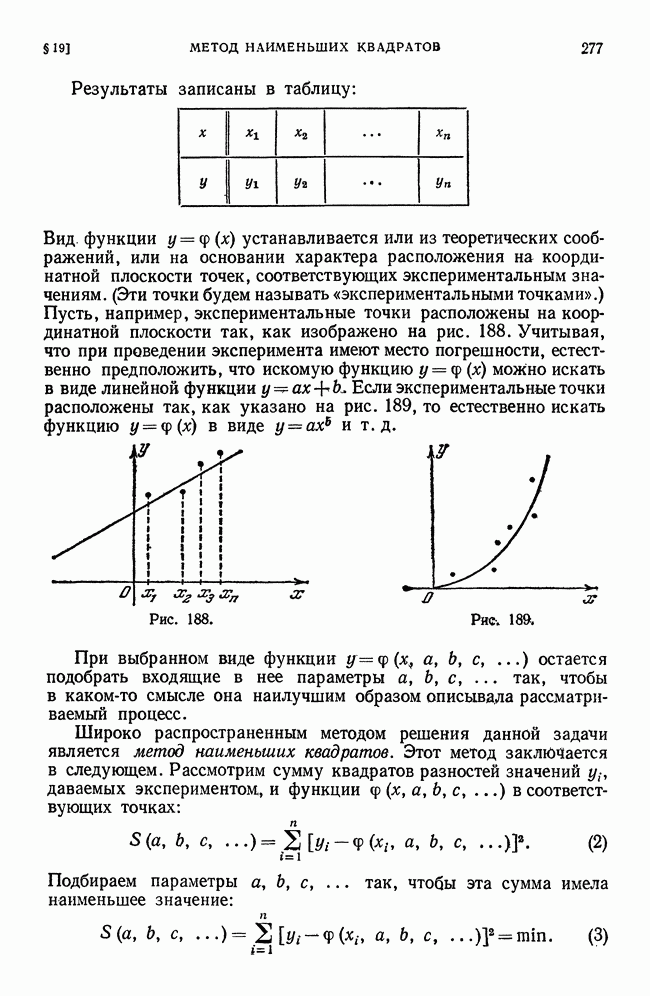
- § 19. Получение функции на основании экспериментальных данных по методу наименьших квадратов
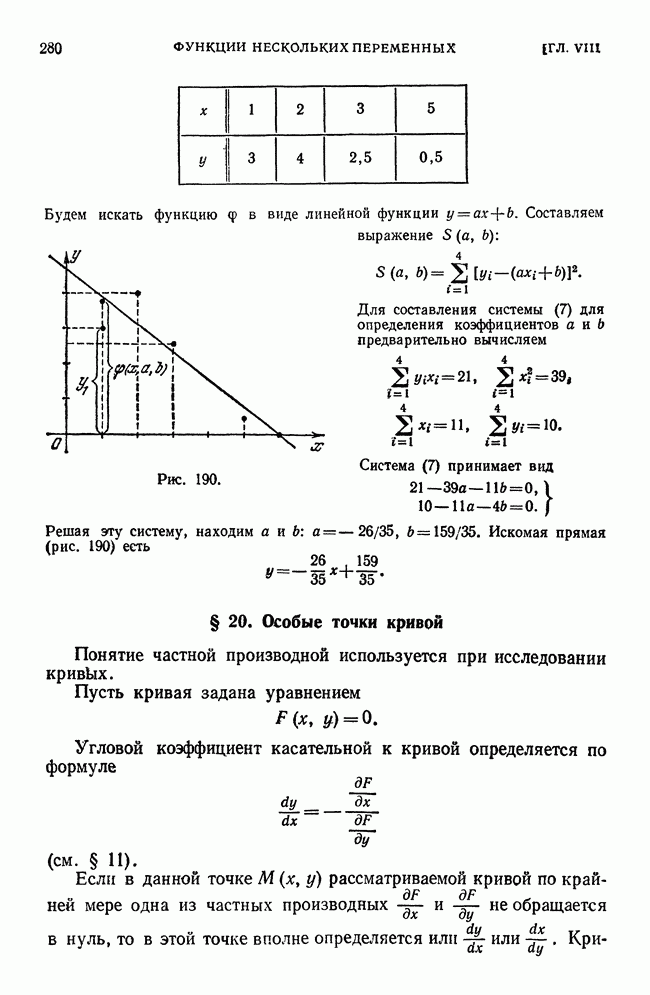
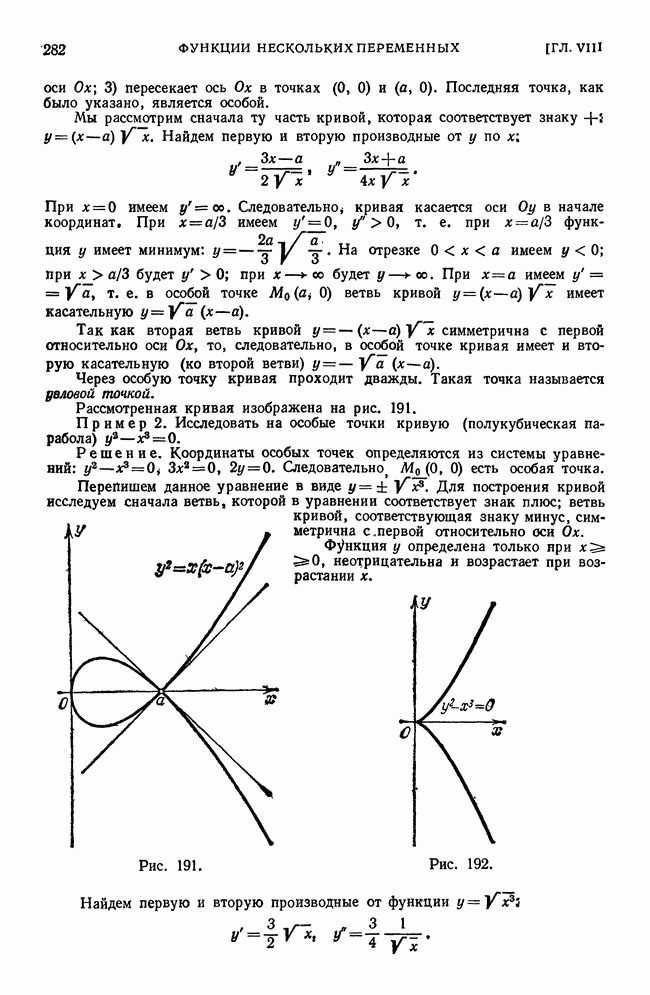
- § 20. Особые точки кривой
- Упражнения к главе VIII
- ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ
- § 1. Уравнения кривой в пространстве
- § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости
- § 3. Правила дифференцирования векторов (векторных функций)
- § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении
- § 5. Соприкасающаяся плоскость. Бинормаль. Кручение.
- § 6. Касательная плоскость и нормаль к поверхности
- Упражнения к главе IX
- ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. Первообразная и неопределенный интеграл
- § 2. Таблица интегралов
- § 3. Некоторые свойства неопределенного интеграла
- § 4. Интегрирование методом замены переменной или способом подстановки
- § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
- § 6. Интегрирование по частям
- § 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- § 8. Разложение рациональной дроби на простейшие
- § 9. Интегрирование рациональных дробей
- § 10. Интегралы от иррациональных функций
- § 11. Интегралы вида …
- § 12. Интегрирование некоторых классов тригонометрических функций
- § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
- § 14. О функциях, интегралы от которых не выражаются через элементарные функции
- Упражнения к главе X
- ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. Постановка задачи. Нижняя и верхняя интегральные суммы
- § 2. Определенный интеграл. Теорема о существовании определенного интеграла
- § 3. Основные свойства определенного интеграла
- § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
- § 5. Замена переменной в определенном интеграле
- § 6. Интегрирование по частям
- § 7. Несобственные интегралы
- § 8. Приближенное вычисление определенных интегралов
- § 9. Формула Чебышева
- § 10. Интегралы, зависящие от параметра. Гамма-функция
- § 11. Интегрирование комплексной функции действительной переменной
- Упражнения кглаве XI
- ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- § 1. Вычисление площадей в прямоугольных координатах
- § 2. Площадь криволинейного сектора в полярных координатах
- § 3. Длина дуги кривой
- § 4. Вычисление объема тела по площадям параллельных сечений
- § 5. Объем тела вращения
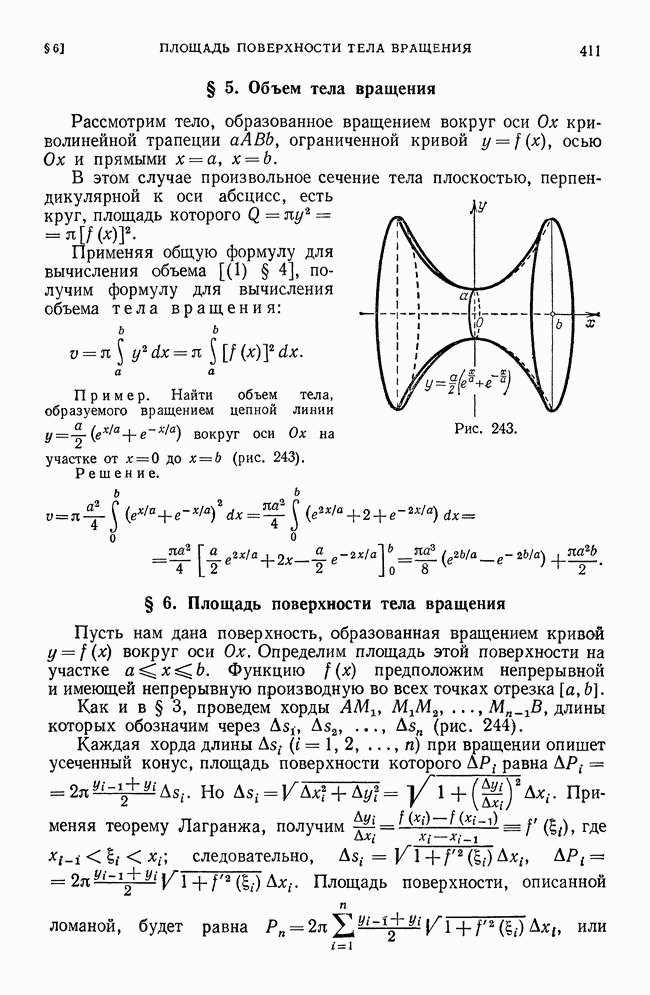
- § 6. Площадь поверхности тела вращения
- § 7. Вычисление работы с помощью определенного интеграла
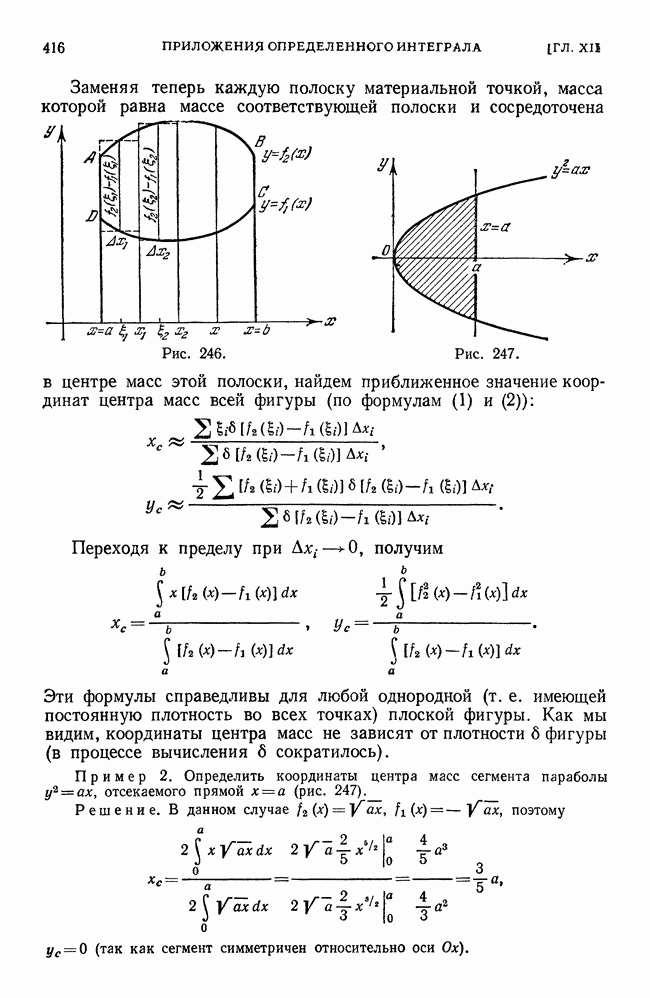
- § 8. Координаты центра масс
- § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла
- Упражнения к главе XII