| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
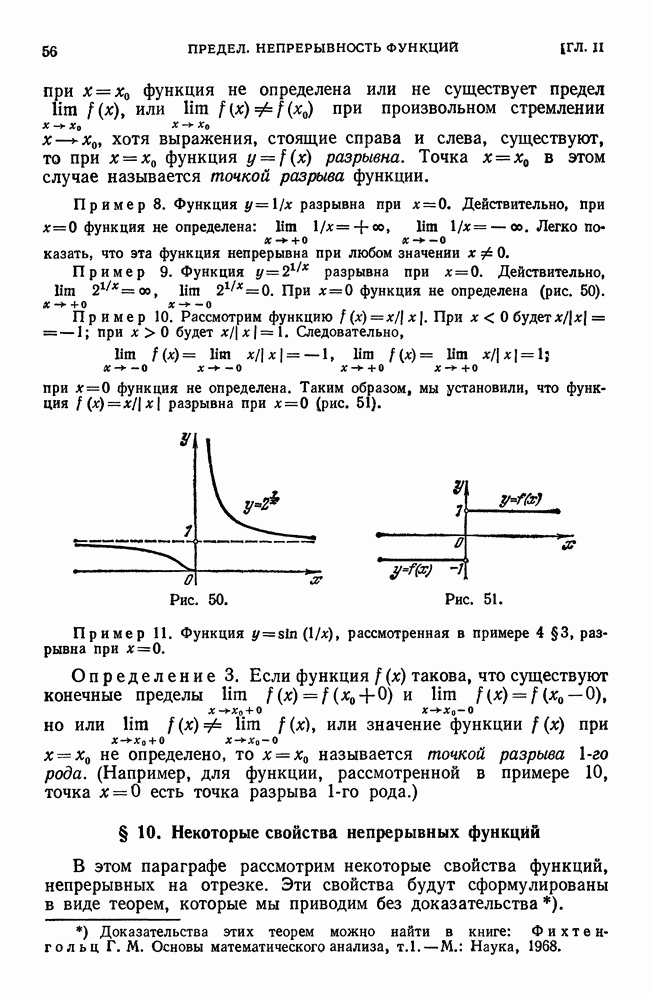
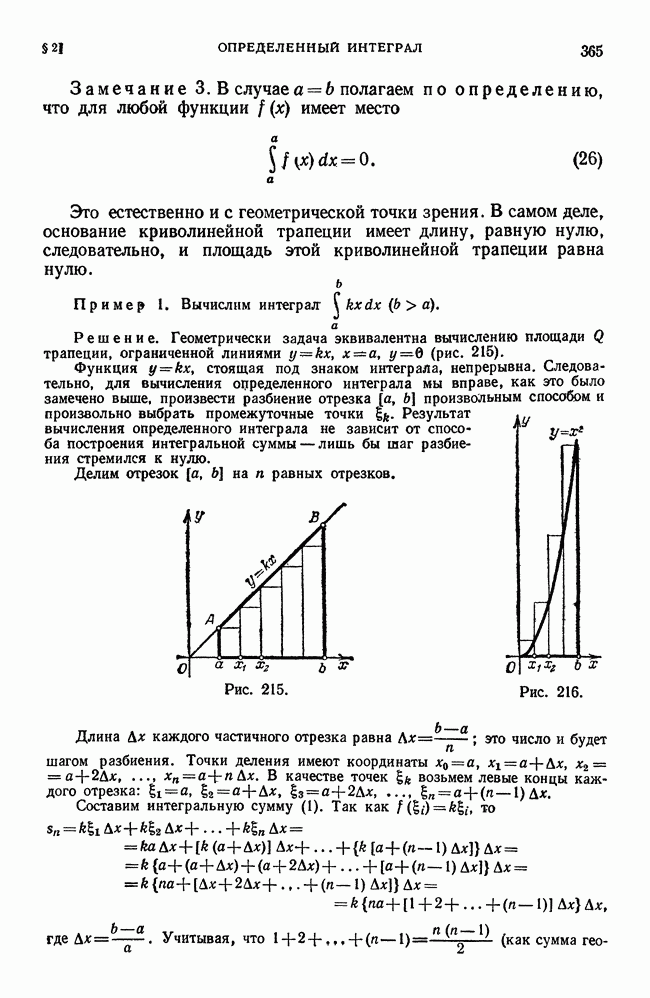
§ 3. Геометрическое значение производной
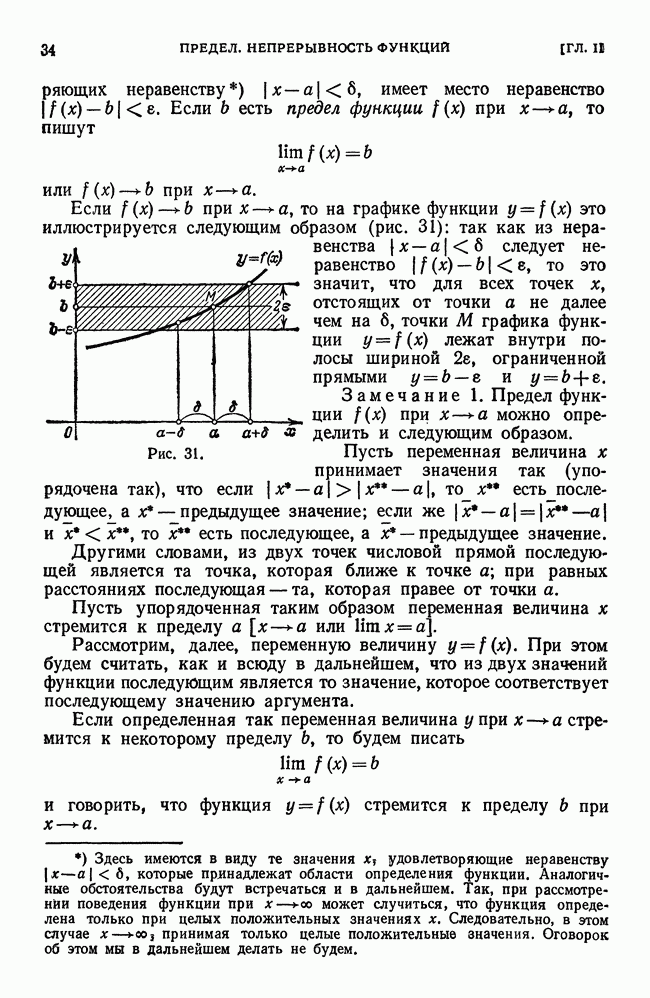
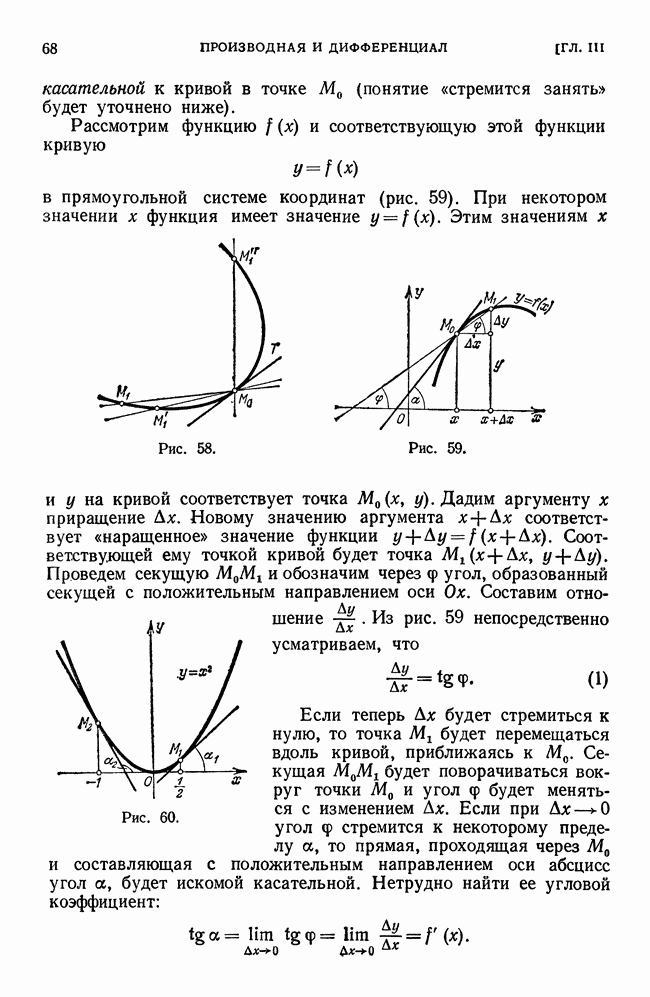
Мы подошли к понятию производной, рассматривая скорость движущегося тела (точки), т. е. исходя из механических представлений. Теперь мы дадим не менее важное геометрическое истолкование производной. Для этого нам прежде всего потребуется определение касательной к кривой в данной точке.
Пусть имеем кривую и на ней фиксированную точку  Возьмем на кривой точку и проведем секущую
Возьмем на кривой точку и проведем секущую  Если точка
Если точка  неограниченно приближается по кривой к точке
неограниченно приближается по кривой к точке  то секущая
то секущая  занимает различные положения
занимает различные положения  и т. д. Если при неограниченном приближении точки
и т. д. Если при неограниченном приближении точки  по кривой к точке
по кривой к точке  с любой стороны секущая стремится занять положение определенной прямой
с любой стороны секущая стремится занять положение определенной прямой  то прямая
то прямая  называется
называется
касательной к кривой в точке  (понятие «стремится занять» будет уточнено ниже).
(понятие «стремится занять» будет уточнено ниже).

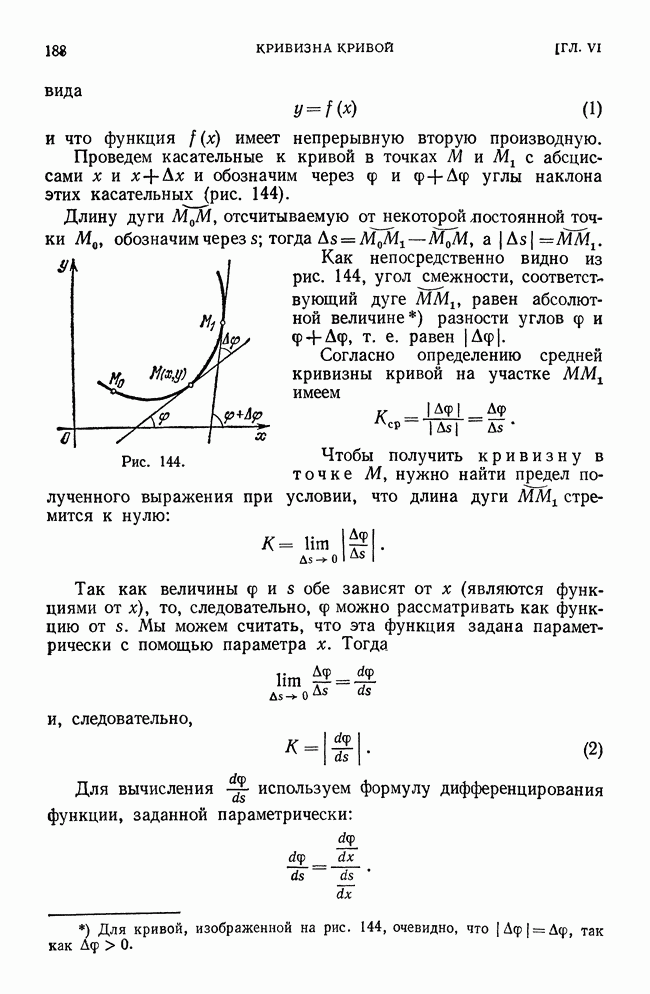
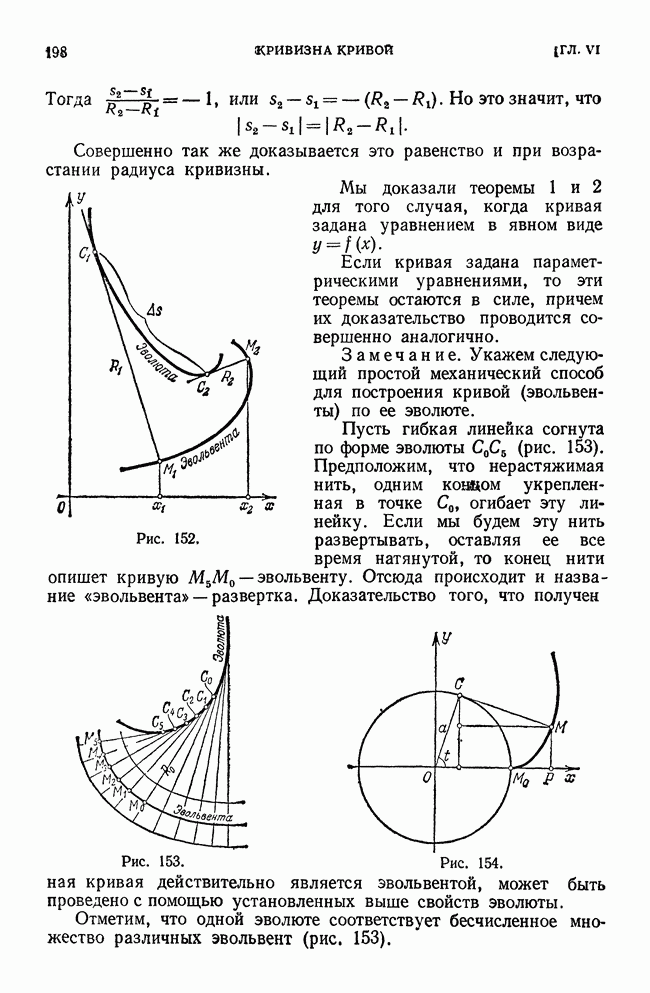
Рис. 58.
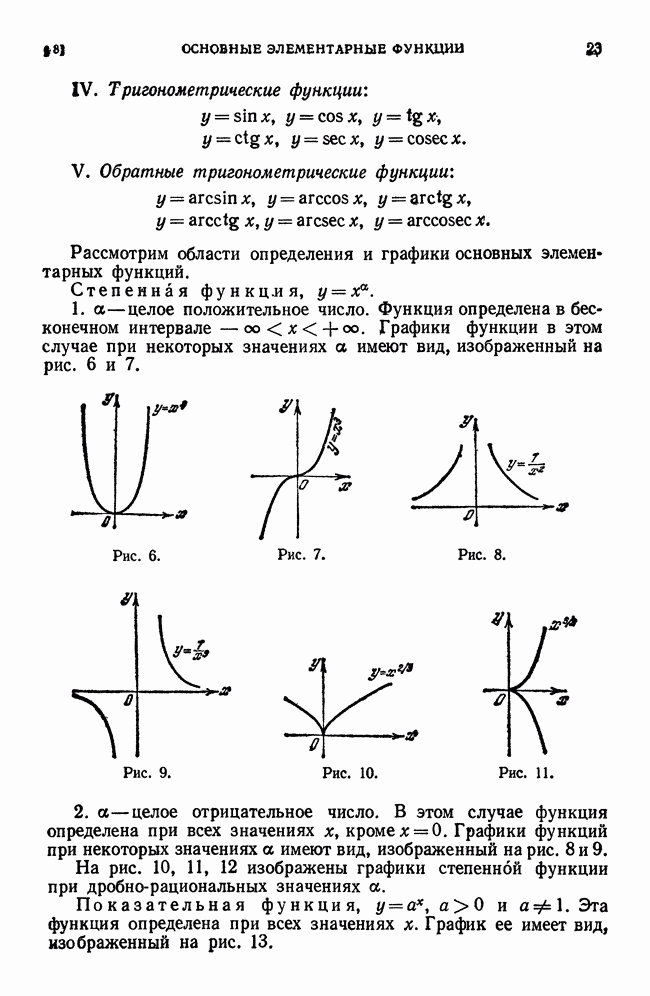
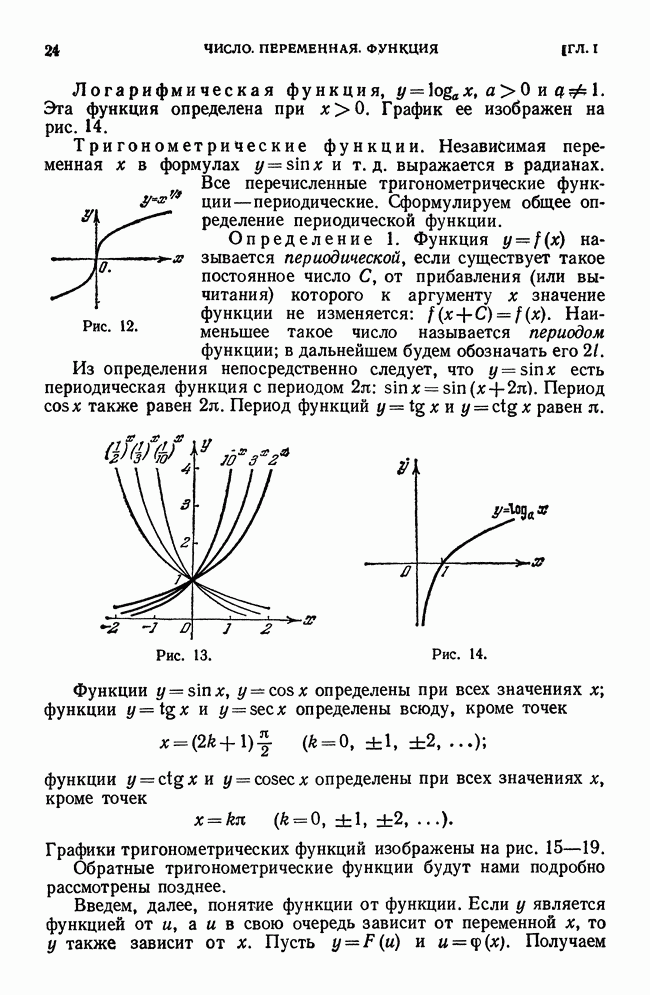
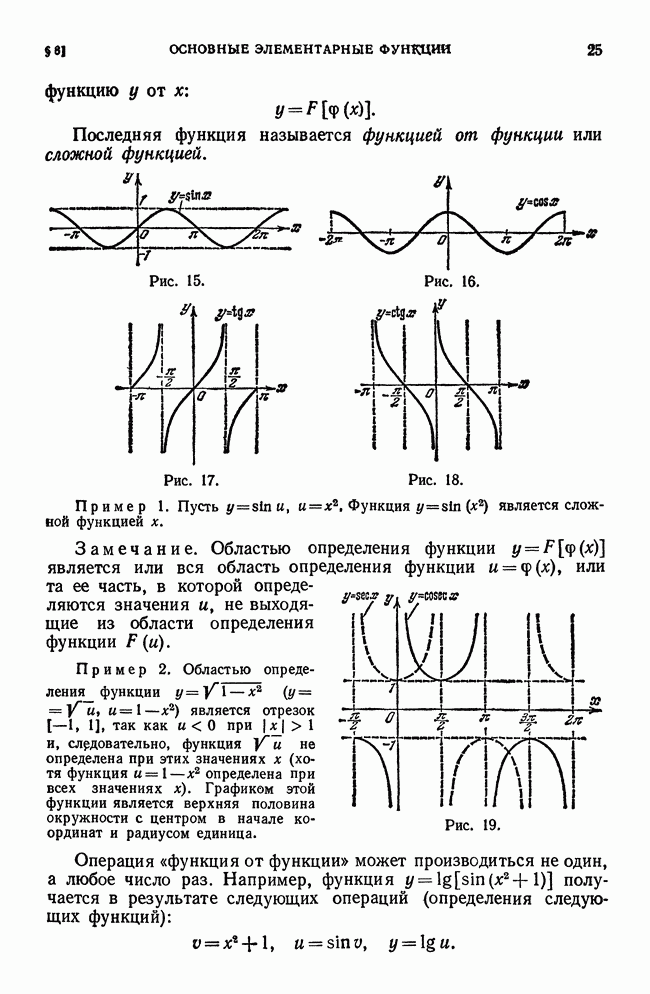
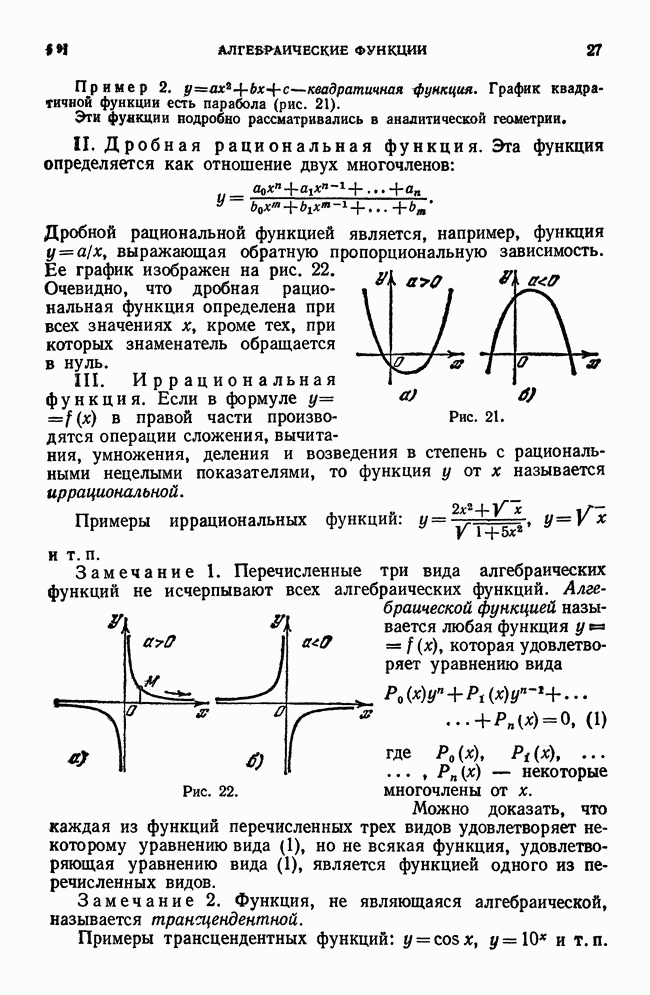
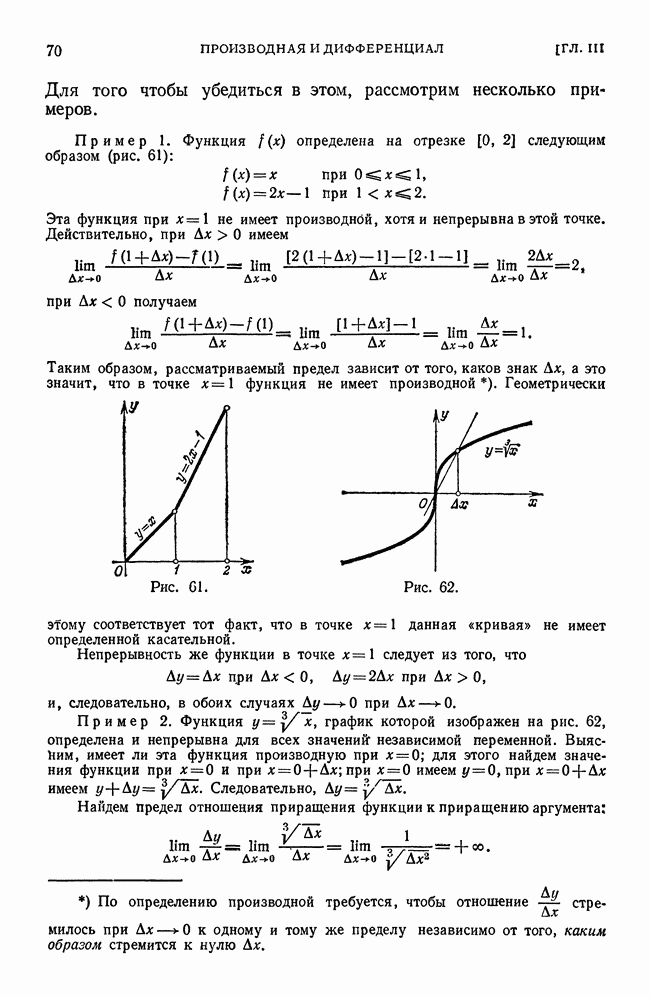
Рассмотрим функцию  и соответствующую этой функции кривую
и соответствующую этой функции кривую

в прямоугольной системе координат (рис. 59).

Рис. 59.
При некотором значении  функция имеет значение y = f(x). Этим значениям х и у на кривой соответствует точка
функция имеет значение y = f(x). Этим значениям х и у на кривой соответствует точка  Дадим аргументу
Дадим аргументу  приращение
приращение  Новому значению аргумента
Новому значению аргумента  соответствует «наращенное» значение функции
соответствует «наращенное» значение функции  . Соответствующей ему точкой кривой будет точка
. Соответствующей ему точкой кривой будет точка  . Проведем секущую и обозначим через
. Проведем секущую и обозначим через  угол, образованный секущей с положительным направлением оси Ох. Составим отношение Из рис. 59 непосредственно усматриваем, что
угол, образованный секущей с положительным направлением оси Ох. Составим отношение Из рис. 59 непосредственно усматриваем, что

Если теперь  будет стремиться к нулю, то точка
будет стремиться к нулю, то точка  будет перемещаться вдоль кривой, приближаясь к
будет перемещаться вдоль кривой, приближаясь к  Секущая
Секущая  будет поворачиваться вокруг точки
будет поворачиваться вокруг точки  и угол
и угол  будет меняться с изменением
будет меняться с изменением  Если при
Если при  угол
угол  стремится к некоторому пределу а, то прямая, проходящая через
стремится к некоторому пределу а, то прямая, проходящая через  и составляющая с положительным направлением оси абсцисс угол а, будет искомой касательной. Нетрудно найти ее угловой коэффициент:
и составляющая с положительным направлением оси абсцисс угол а, будет искомой касательной. Нетрудно найти ее угловой коэффициент:


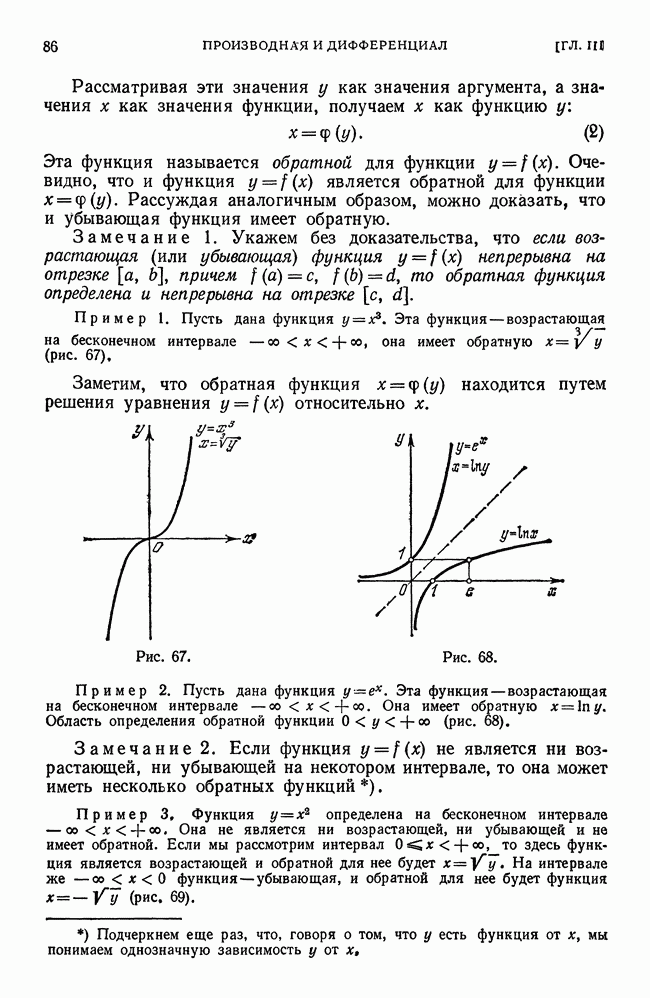
Рис. 60.
Следовательно,

т. e. значение производной  при данном значении аргумента
при данном значении аргумента  равняется тангенсу угла, образованного касательной к графику функции
равняется тангенсу угла, образованного касательной к графику функции  в соответствующей точке
в соответствующей точке  с положительным направлением оси Ох.
с положительным направлением оси Ох.
Пример. Найти тангенсы углов наклона касательной к кривой  в точках
в точках 
Решение. На основании примера 1 § 2 имеем  следовательно,
следовательно,

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА I. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ
- § 1. Действительные числа.
- § 2. Абсолютная величина действительного числа
- § 3. Переменные и постоянные величины
- § 4. Область изменения переменной величины
- § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина
- § 6. Функция
- § 7. Способы задания функции
- § 8. Основные элементарные функции. Элементарные функции
- § 9. Алгебраические функции
- § 10. Полярная система координат
- Упражнения к главе I
- ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
- § 1. Предел переменной величины. Бесконечно большая переменная величина
- § 2. Предел функции
- § 3. Функция, стремящаяся к бесконечности. Ограниченные функции
- § 4. Бесконечно малые и их основные свойства
- § 5. Основные теоремы о пределах
- § 6. Предел функции (sin x)/x при x->0
- § 7. Число e
- § 8. Натуральные логарифмы
- § 9. Непрерывность функций
- § 10. Некоторые свойства непрерывных функций
- § 11. Сравнение бесконечно малых
- Упражнения к главе II
- ГЛАВА III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
- § 2. Определение производной
- § 3. Геометрическое значение производной
- § 4. Дифференцируемость функций
- § 5. Производная от функции y = x^n при n целом и положительном
- § 6. Производные от функций y = sinx; y = cosx
- § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного
- § 8. Производная логарифмической функции
- § 9. Производная от сложной функции
- § 10. Производные функций y = tgx, y = ctgx, y = ln|x|
- § 11. Неявная функция и ее дифференцирование
- § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции
- § 13. Обратная функция и ее дифференцирование
- § 14. Обратные тригонометрические функции и их дифференцирование
- § 15. Таблица основных формул дифференцирования
- § 16. Параметрическое задание функции
- § 17. Уравнения некоторых кривых в параметрической форме
- § 18. Производная функции, заданной параметрически
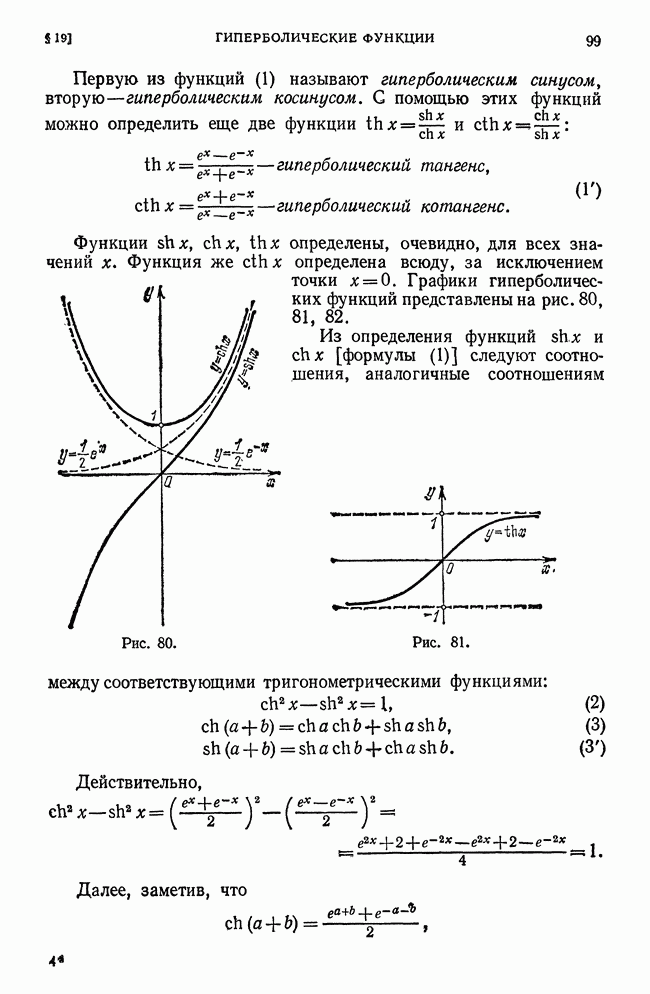
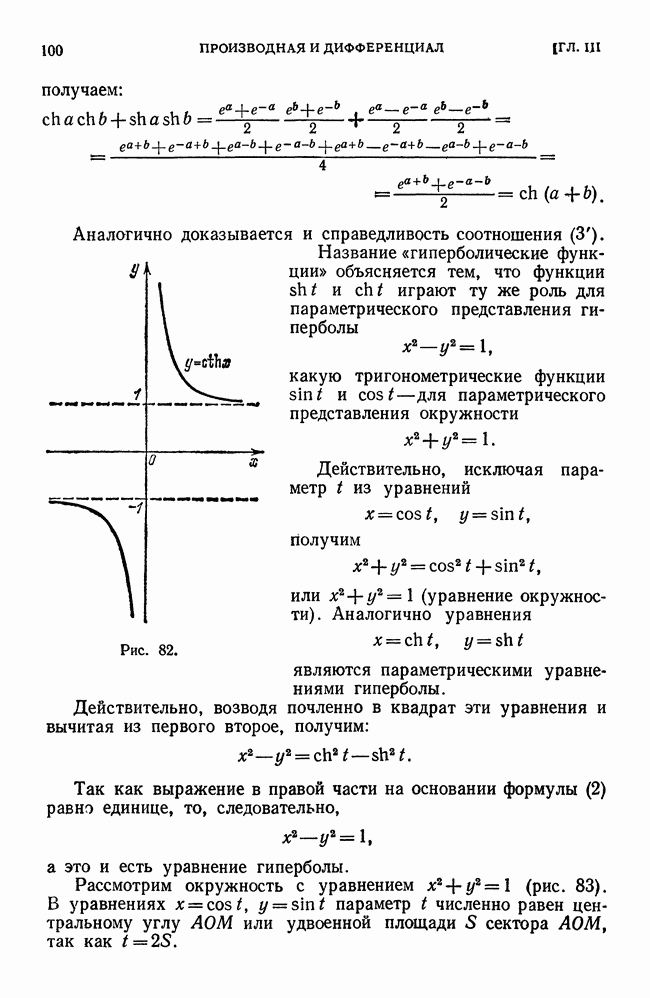
- § 19. Гиперболические функции
- § 20. Дифференциал
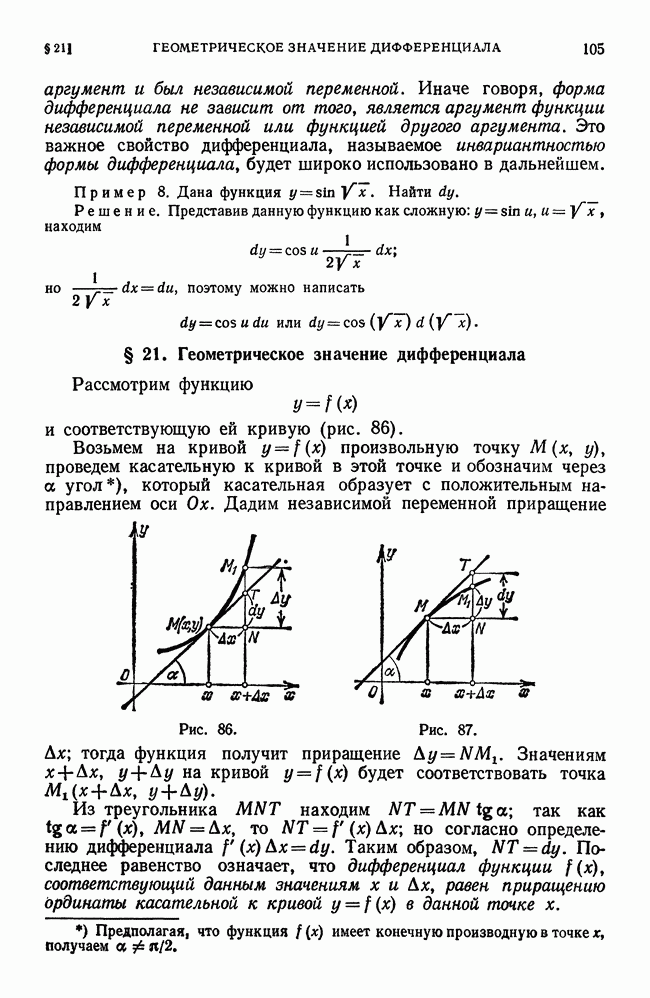
- § 21. Геометрическое значение дифференциала Рассмотрим функцию
- § 22. Производные различных порядков
- § 23. Дифференциалы различных порядков
- § 24. Производные различных порядков от неявных функций и функций, заданных параметрически
- § 25. Механическое значение второй производной
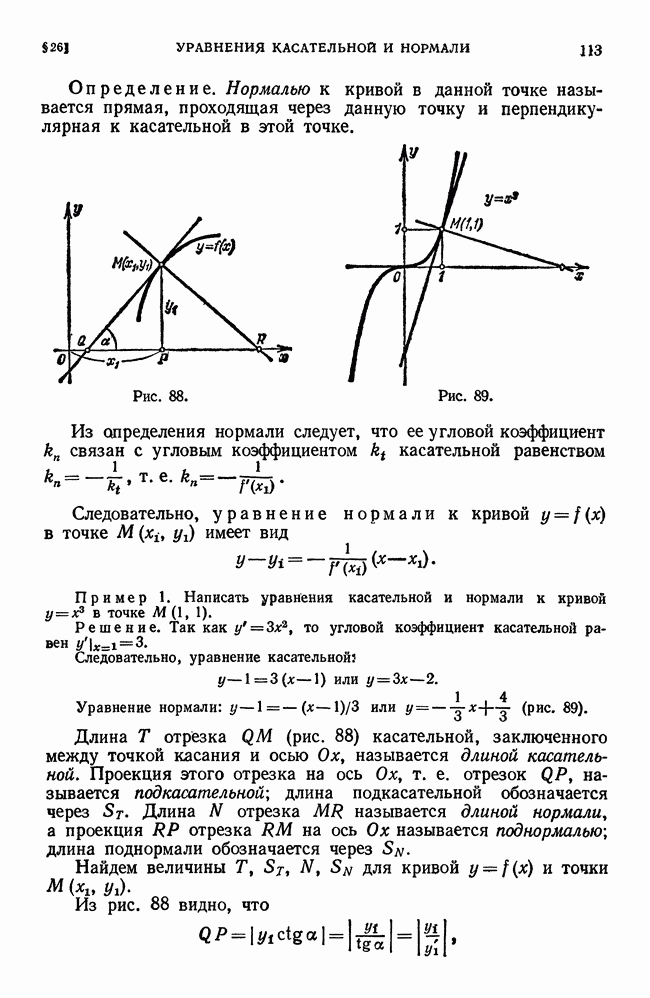
- § 26. Уравнения касательной и нормали. Длины подкасательной и поднормали
- § 27. Геометрическое значение производной радиус-вектора по полярному углу
- Упражнения к главе III
- ГЛАВА IV. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
- § 1. Теорема о корнях производной (теорема Ролля)
- § 2. Теорема о конечных приращениях (теорема Лагранжа)
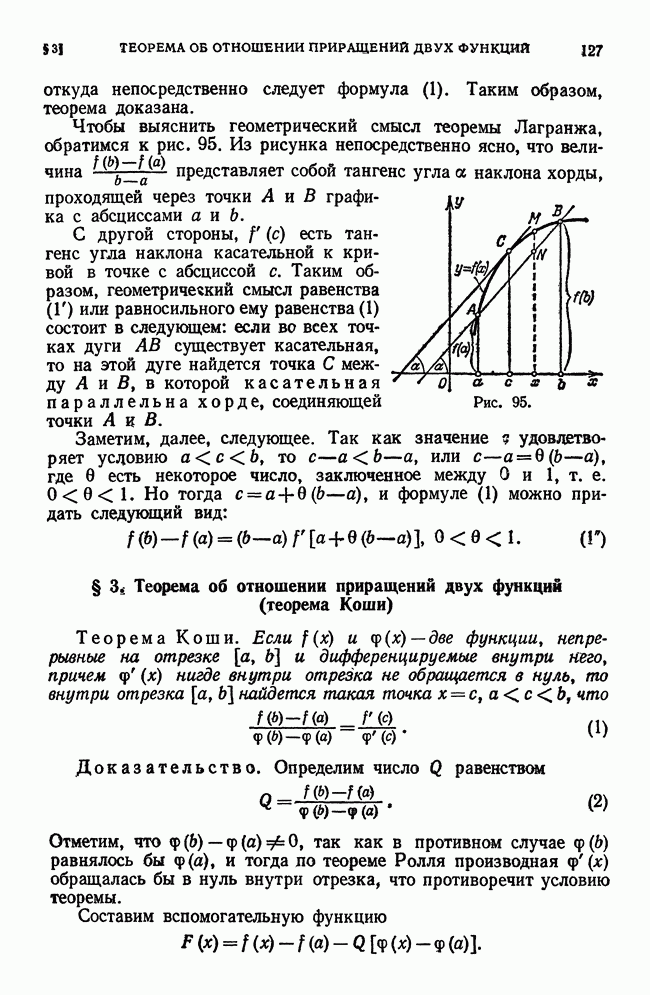
- § 3. Теорема об отношении приращений двух функций (теорема Коши)
- § 4. Предел отношения двух бесконечно малых величин «раскрытие неопределенностей вида 0/0»)
- § 5. Предел отношения двух бесконечно больших величин «раскрытие неопределенностей вида oo/oo»)
- § 6. Формула Тейлора
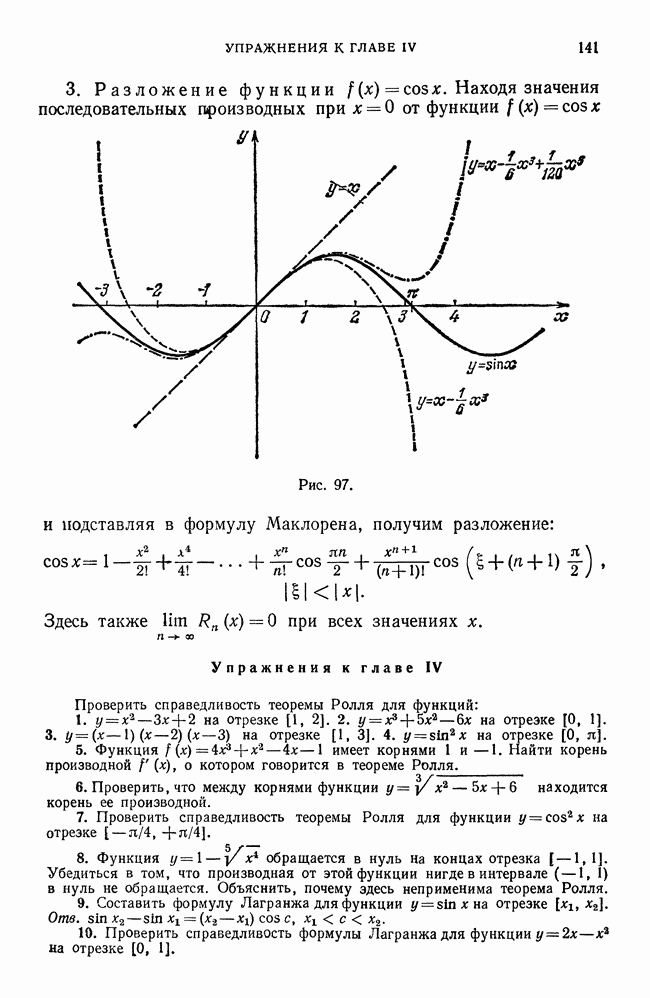
- § 7. Разложение по формуле Тейлора функций e^x, sin x, cos x
- Упражнения к главе IV
- ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
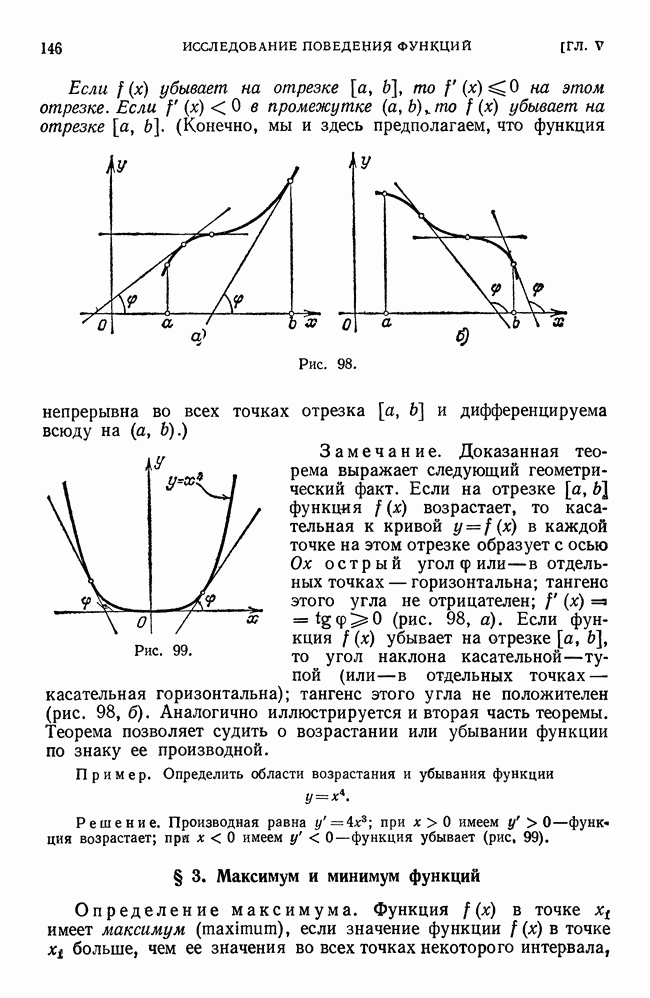
- § 2. Возрастание и убывание функции
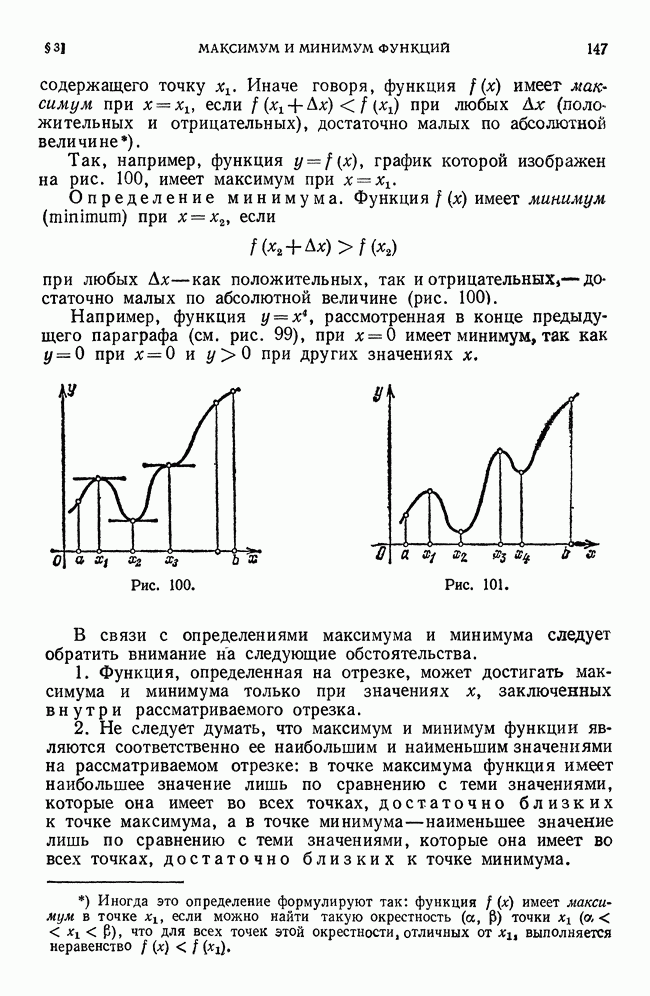
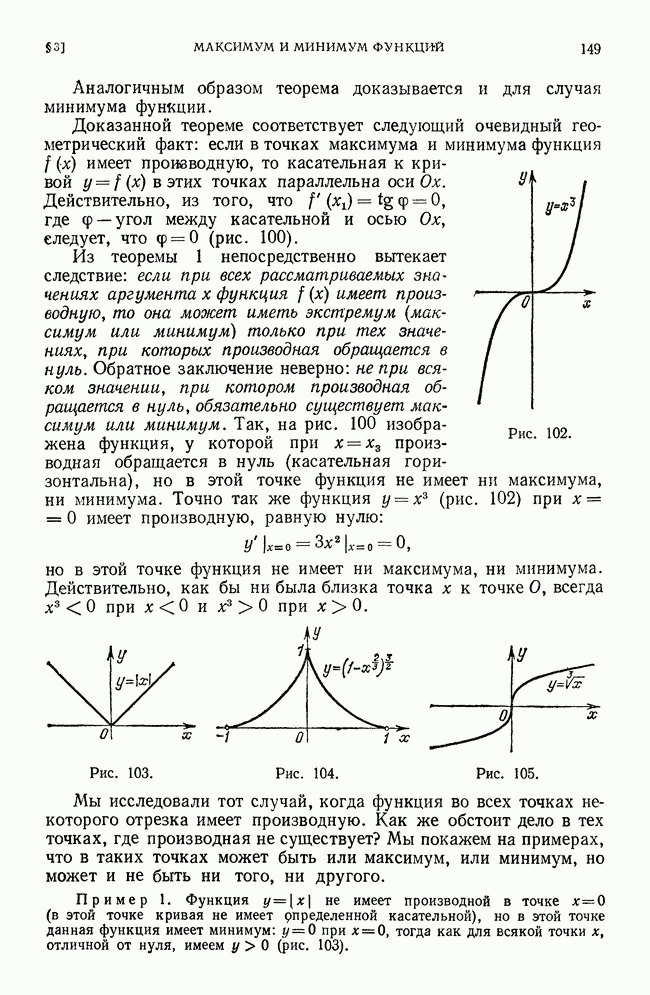
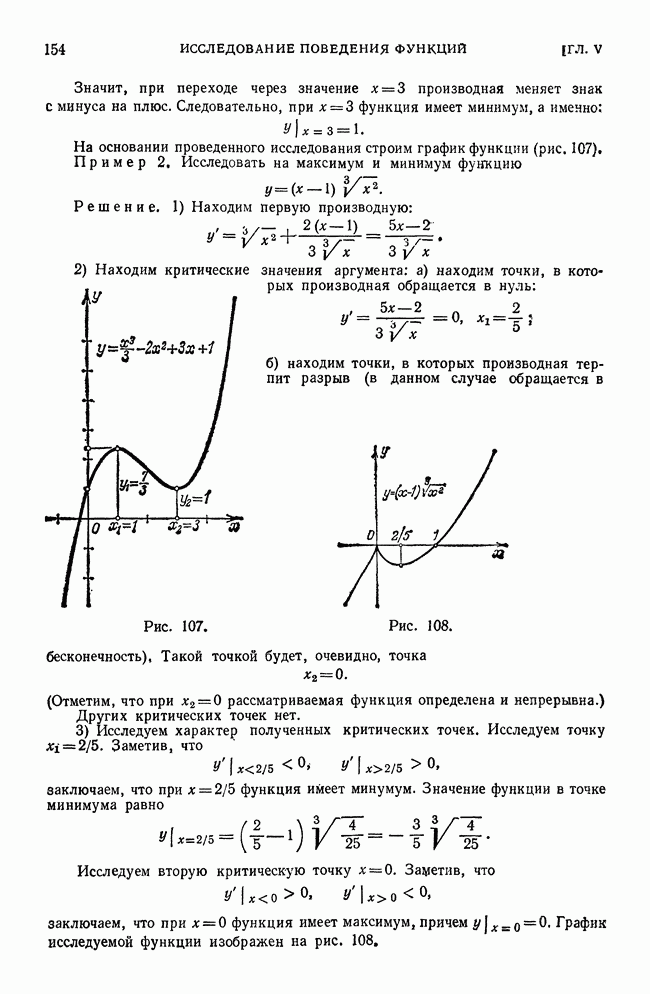
- § 3. Максимум и минимум функций
- § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной
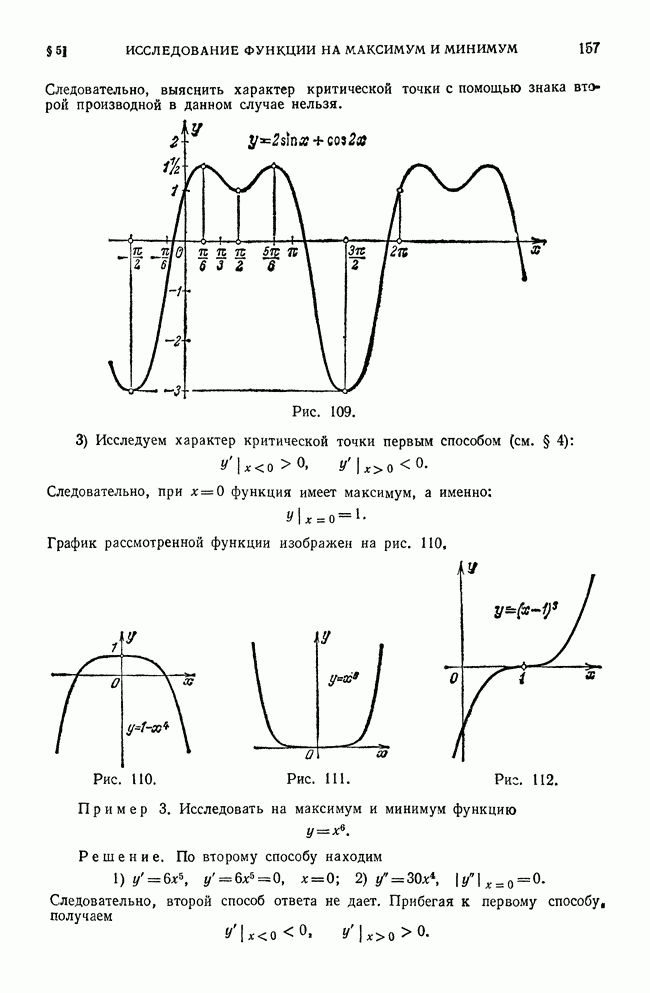
- § 5. Исследование функции на максимум и минимум с помощью второй производной
- § 6. Наибольшее и наименьшее значения функции на отрезке
- § 7. Применение теории максимума и минимума функций к решению задач
- § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора
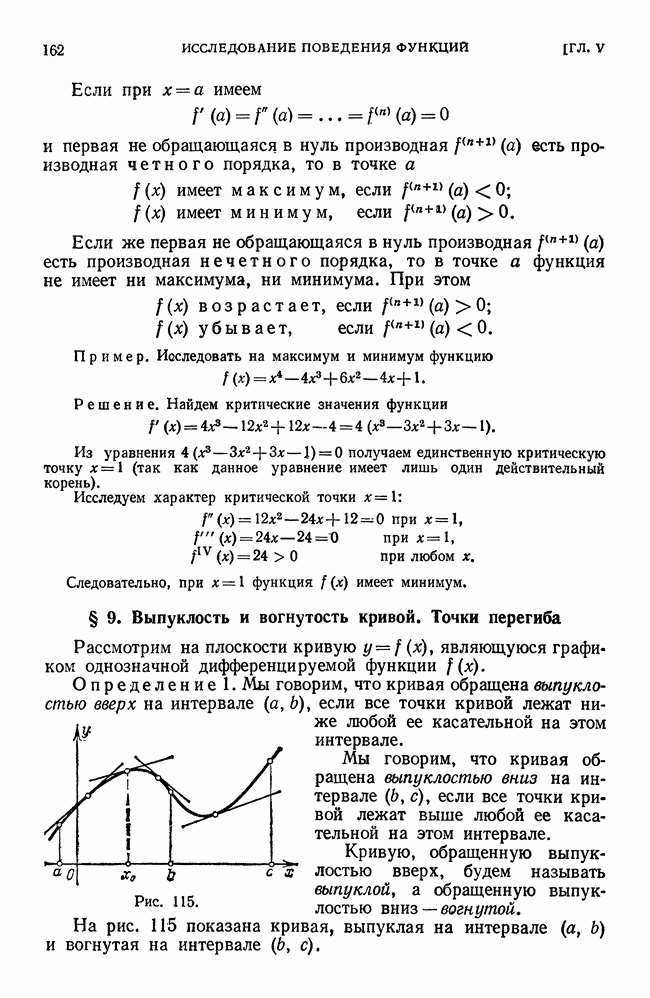
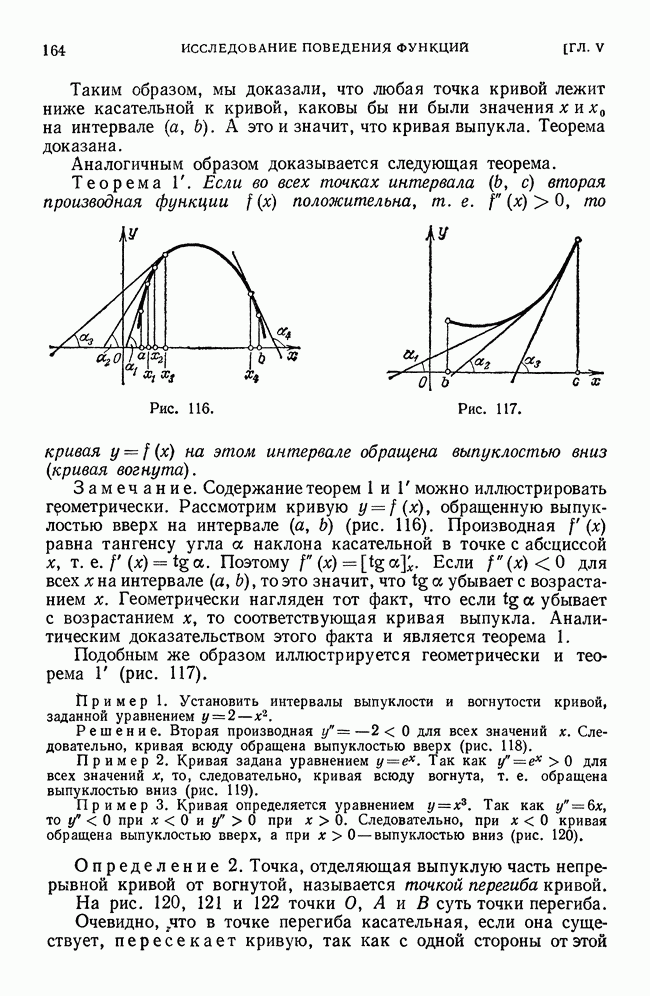
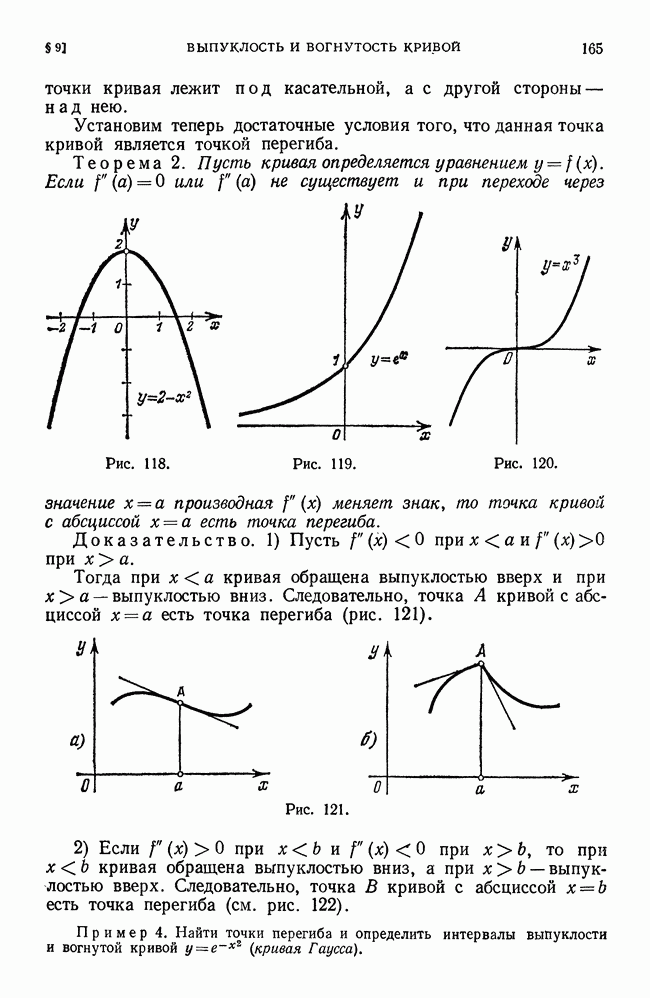
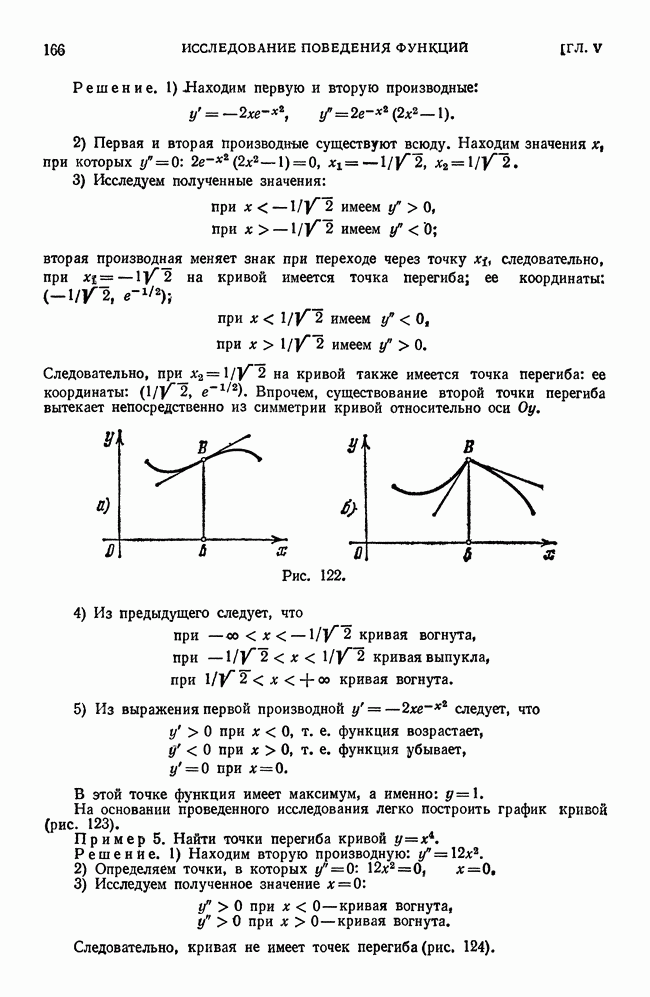
- § 9. Выпуклость и вогнутость кривой. Точки перегиба
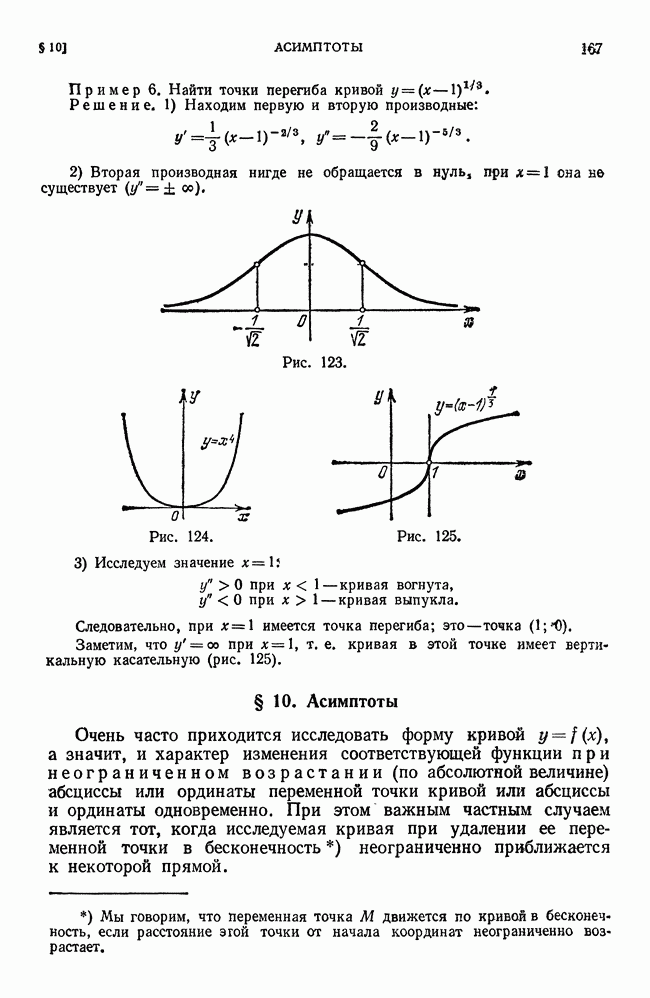
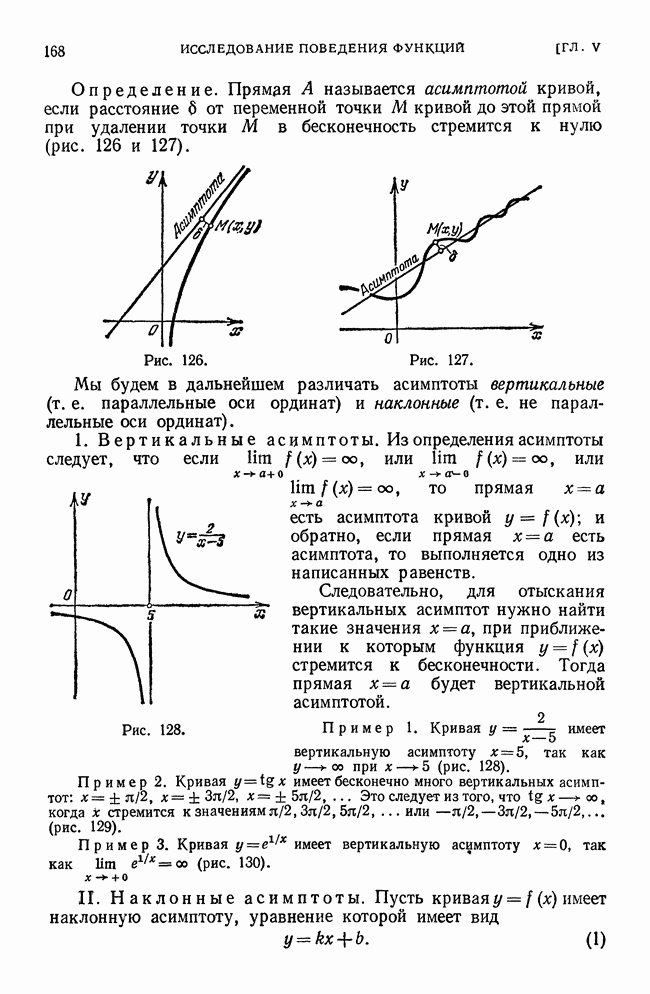
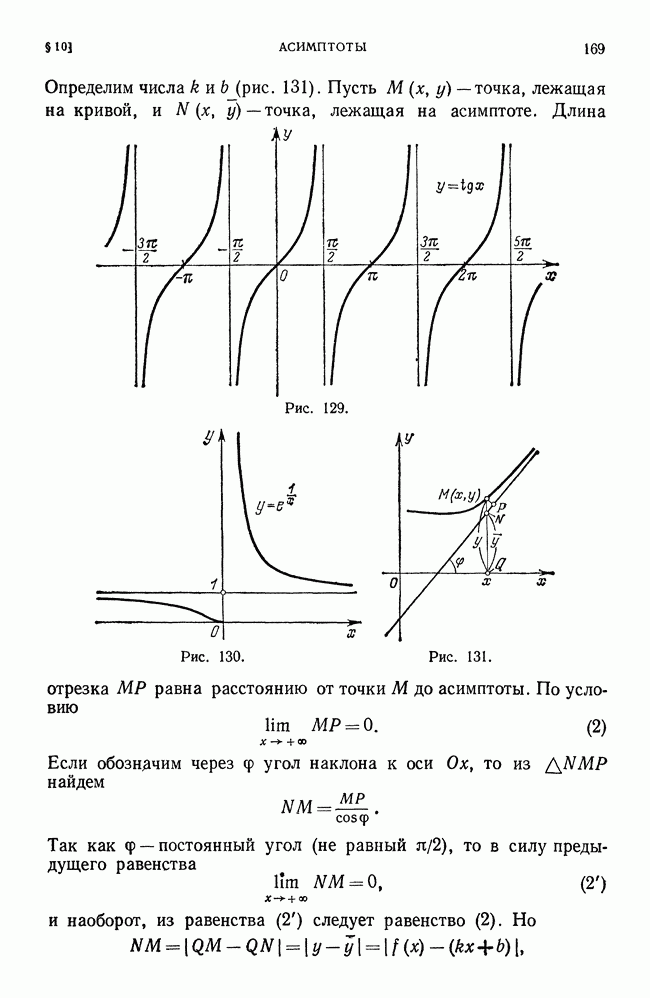
- § 10. Асимптоты
- § 11. Общий план исследования функций и построения графиков
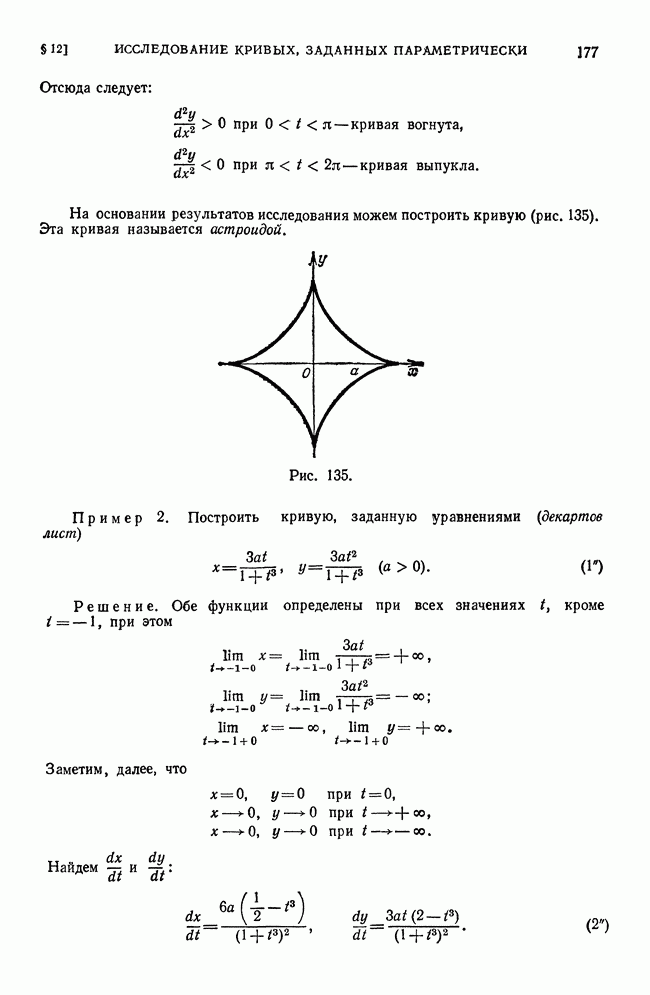
- § 12. Исследование кривых, заданных параметрически
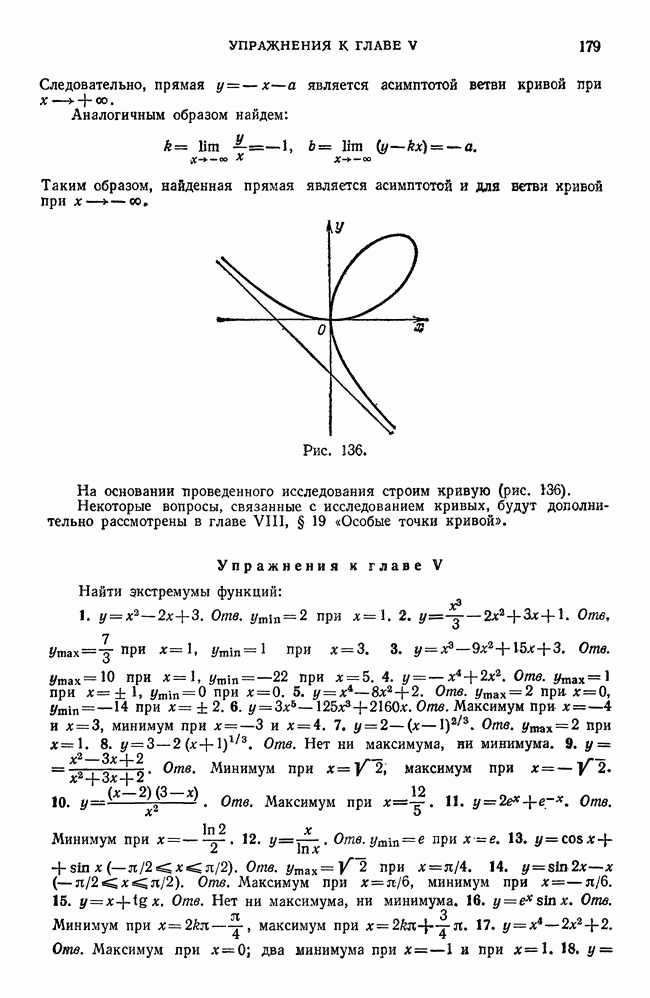
- Упражнения к главе V
- ГЛАВА VI. КРИВИЗНА КРИВОЙ
- § 1. Длина дуги и ее производная
- § 2. Кривизна
- § 3. Вычисление кривизны
- § 4. Вычисление кривизны линии, заданной параметрически
- § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах
- § 6. Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента
- § 7. Свойства эволюты
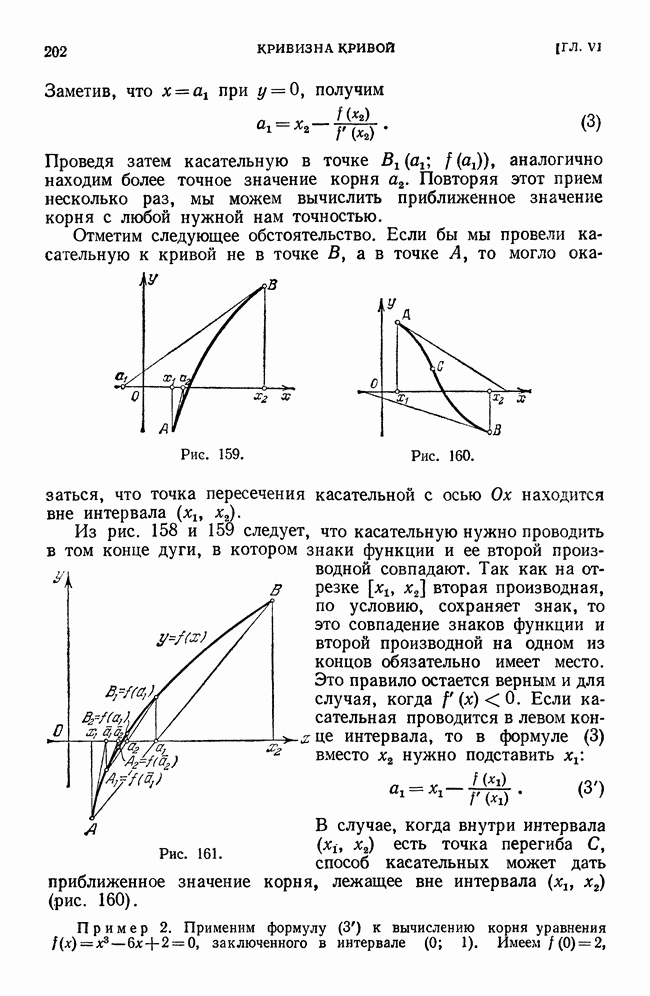
- § 8. Приближенное вычисление действительных корней уравнения
- Упражнения к главе VI
- ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ
- § 1. Комплексные числа. Исходные определения
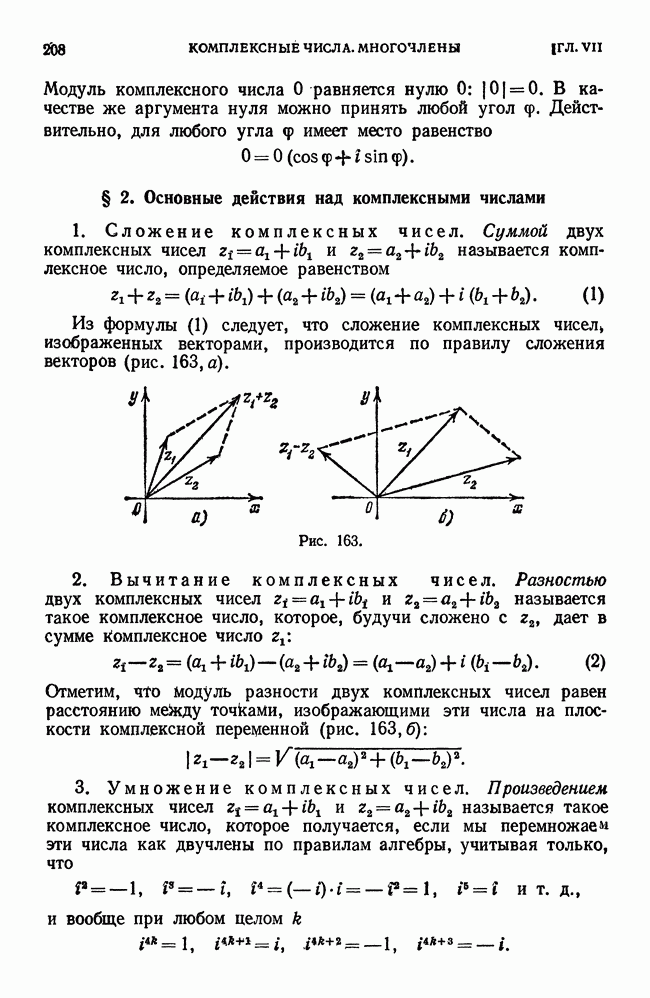
- § 2. Основные действия над комплексными числами
- § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа
- § 4. Показательная функция с комплексным показателем и ее свойства
- § 5. Формула Эйлера. Показательная форма комплексного числа
- § 6. Разложение многочлена на множители
- § 7. О кратных корнях многочлена
- § 8. Разложение многочлена на множители в случае комплексных корней
- § 9. Интерполирование. Интерполяционная формула Лагранжа
- § 10. Интерполяционная формула Ньютона
- § 11. Численное дифференцирование
- § 12. О наилучшем приближении функций многочленами. Теория Чебышева
- Упражнения к главе VII
- ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. Определение функции нескольких переменных
- § 2. Геометрическое изображение функции двух переменных
- § 3. Частное и полное приращение функции
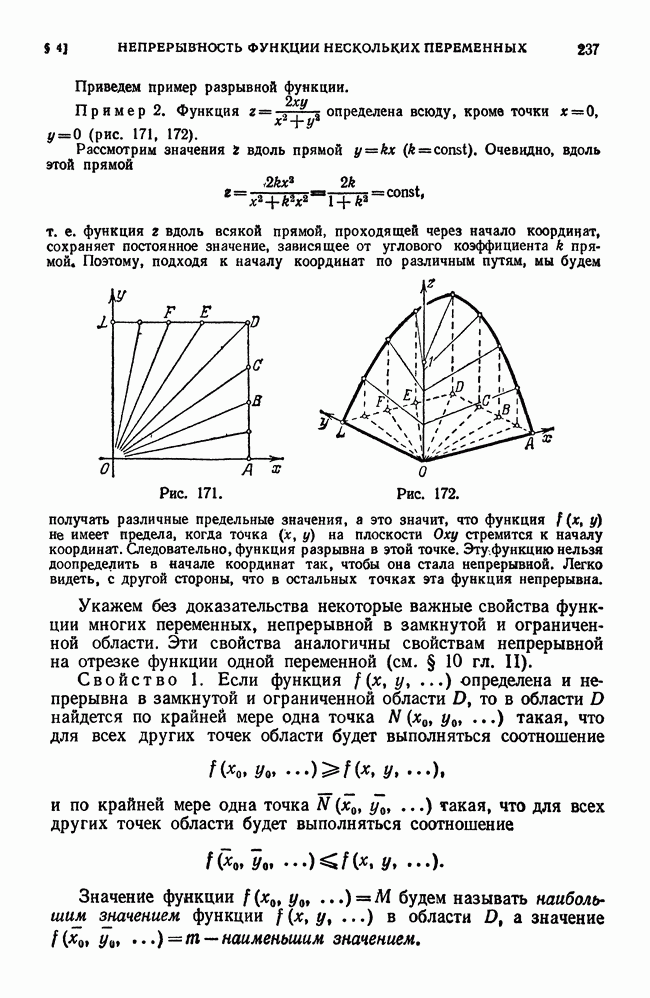
- § 4. Непрерывность функции нескольких переменных
- § 5. Частные производные функции нескольких переменных
- § 6. Геометрическая интерпретация частных производных функции двух переменных
- § 7. Полное приращение и полный дифференциал
- § 8. Применение полного дифференциала в приближенных вычислениях
- § 9. Приложение дифференциала к оценке погрешности при вычислениях
- § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции
- § 11. Производная от функции, заданной неявно
- § 12. Частные производные различных порядков
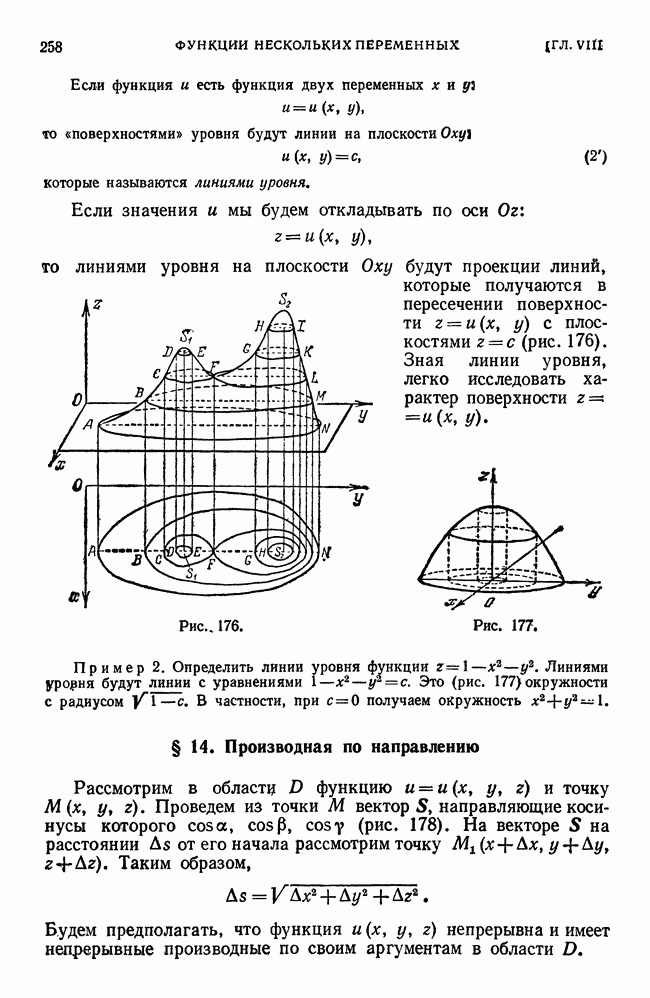
- § 13. Поверхности уровня
- § 14. Производная по направлению
- § 15. Градиент
- § 16. Формула Тейлора для функции двух переменных
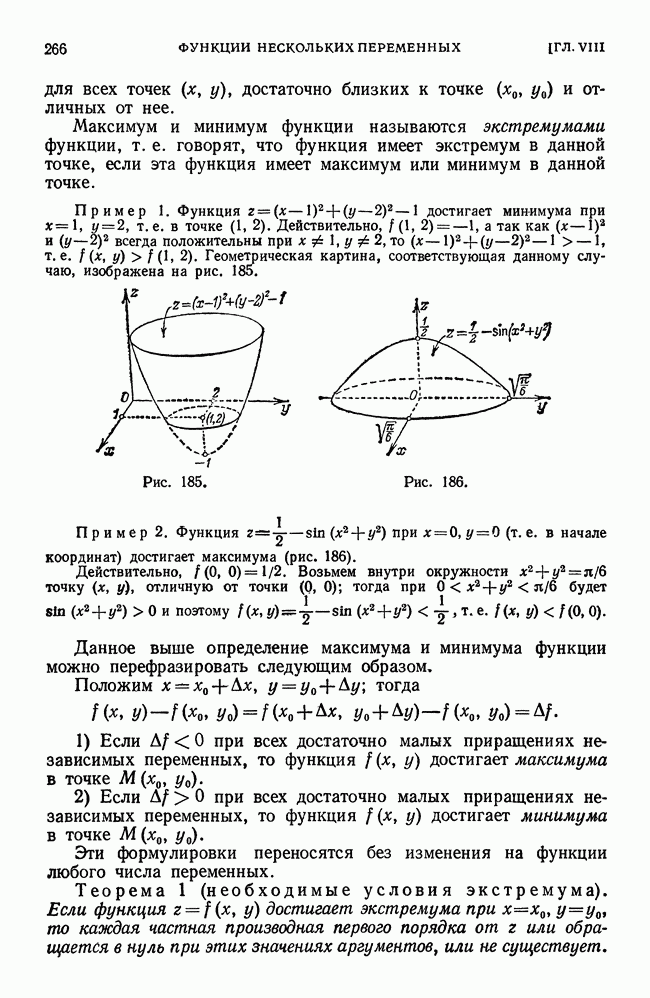
- § 17. Максимум и минимум функции нескольких переменных
- § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы)
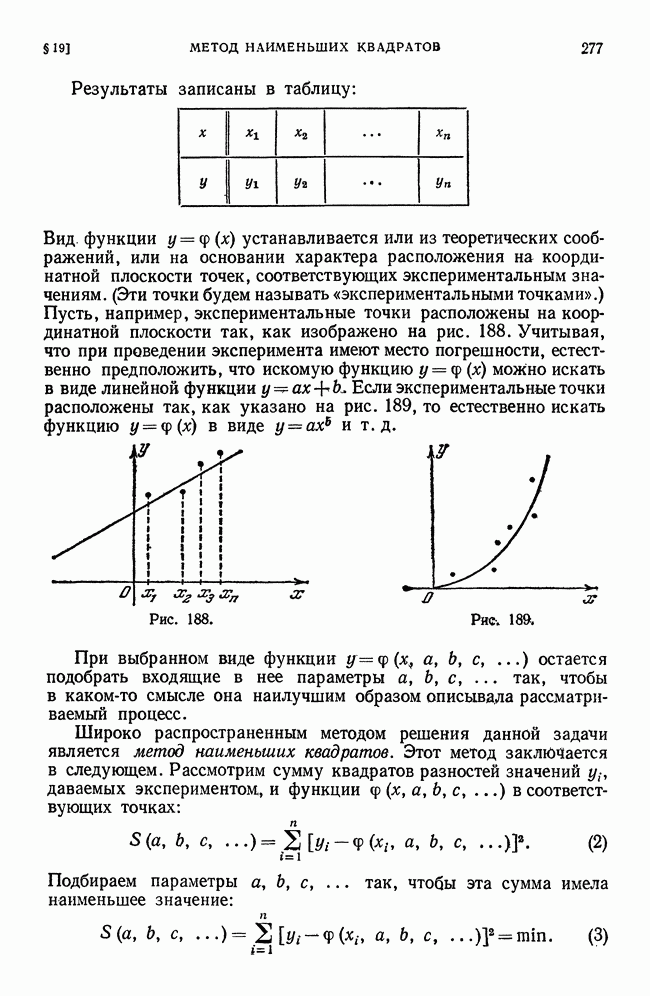
- § 19. Получение функции на основании экспериментальных данных по методу наименьших квадратов
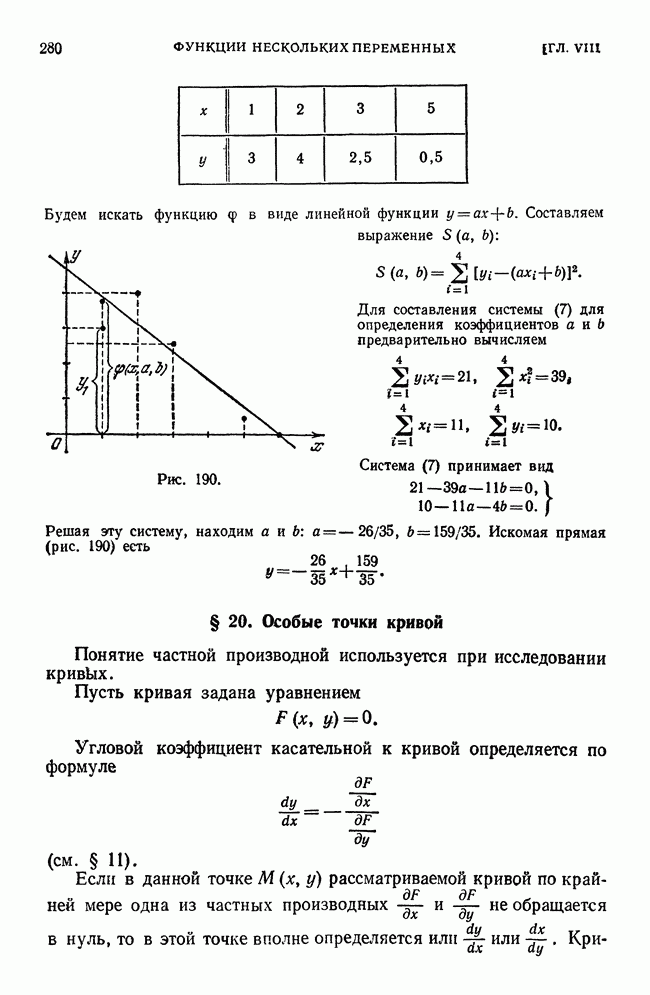
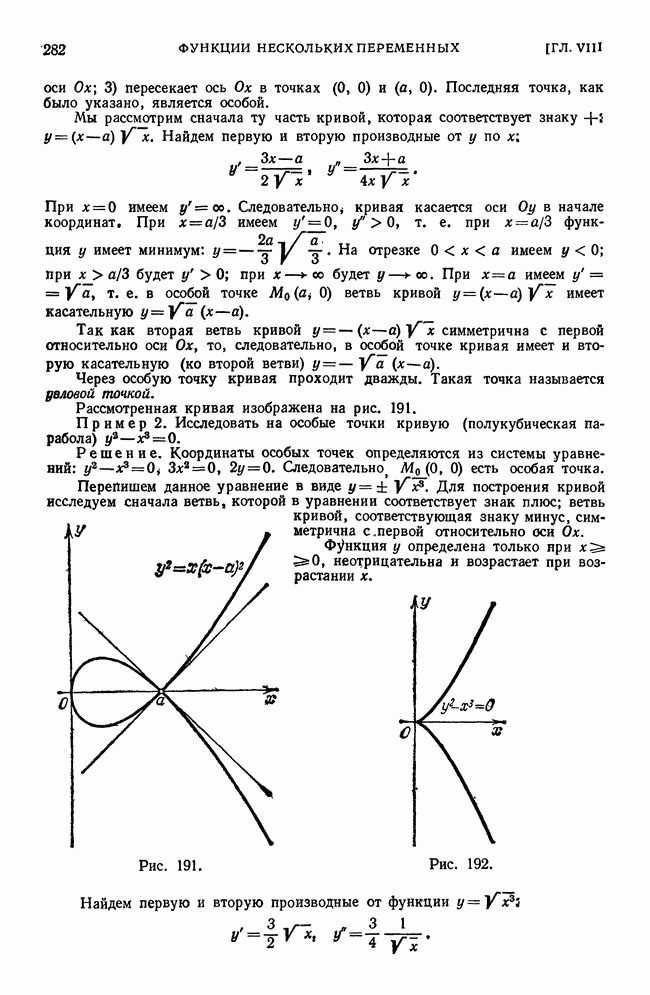
- § 20. Особые точки кривой
- Упражнения к главе VIII
- ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ
- § 1. Уравнения кривой в пространстве
- § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости
- § 3. Правила дифференцирования векторов (векторных функций)
- § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении
- § 5. Соприкасающаяся плоскость. Бинормаль. Кручение.
- § 6. Касательная плоскость и нормаль к поверхности
- Упражнения к главе IX
- ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. Первообразная и неопределенный интеграл
- § 2. Таблица интегралов
- § 3. Некоторые свойства неопределенного интеграла
- § 4. Интегрирование методом замены переменной или способом подстановки
- § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
- § 6. Интегрирование по частям
- § 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- § 8. Разложение рациональной дроби на простейшие
- § 9. Интегрирование рациональных дробей
- § 10. Интегралы от иррациональных функций
- § 11. Интегралы вида …
- § 12. Интегрирование некоторых классов тригонометрических функций
- § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
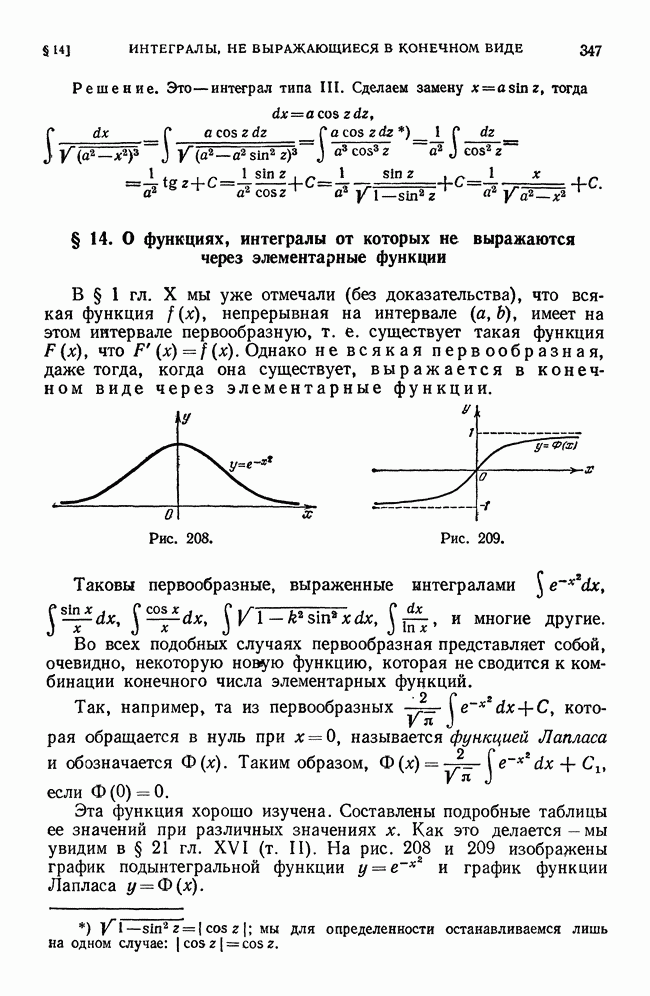
- § 14. О функциях, интегралы от которых не выражаются через элементарные функции
- Упражнения к главе X
- ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. Постановка задачи. Нижняя и верхняя интегральные суммы
- § 2. Определенный интеграл. Теорема о существовании определенного интеграла
- § 3. Основные свойства определенного интеграла
- § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
- § 5. Замена переменной в определенном интеграле
- § 6. Интегрирование по частям
- § 7. Несобственные интегралы
- § 8. Приближенное вычисление определенных интегралов
- § 9. Формула Чебышева
- § 10. Интегралы, зависящие от параметра. Гамма-функция
- § 11. Интегрирование комплексной функции действительной переменной
- Упражнения кглаве XI
- ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- § 1. Вычисление площадей в прямоугольных координатах
- § 2. Площадь криволинейного сектора в полярных координатах
- § 3. Длина дуги кривой
- § 4. Вычисление объема тела по площадям параллельных сечений
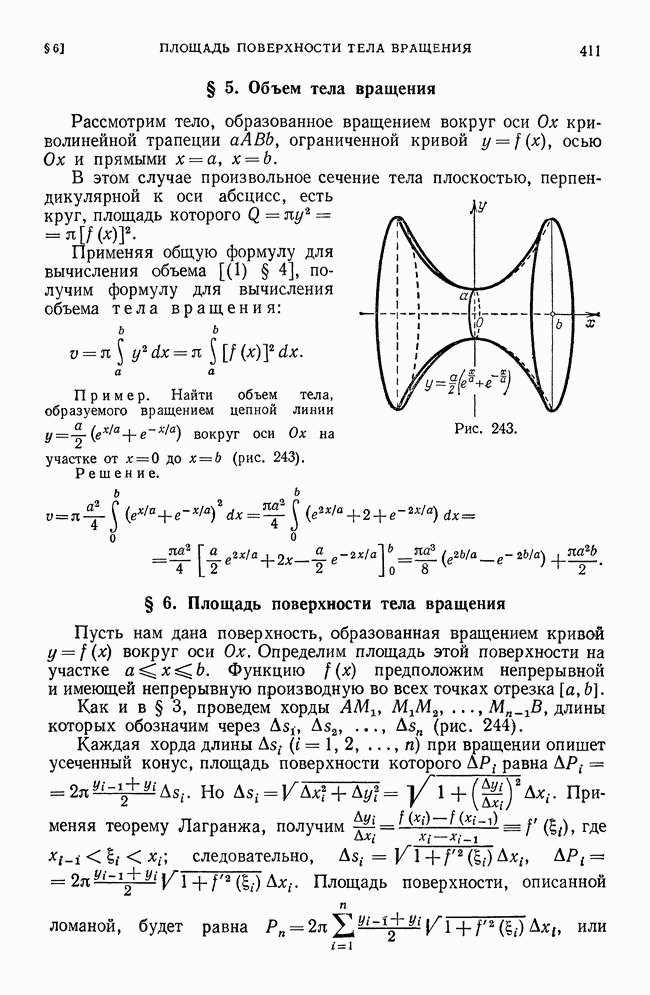
- § 5. Объем тела вращения
- § 6. Площадь поверхности тела вращения
- § 7. Вычисление работы с помощью определенного интеграла
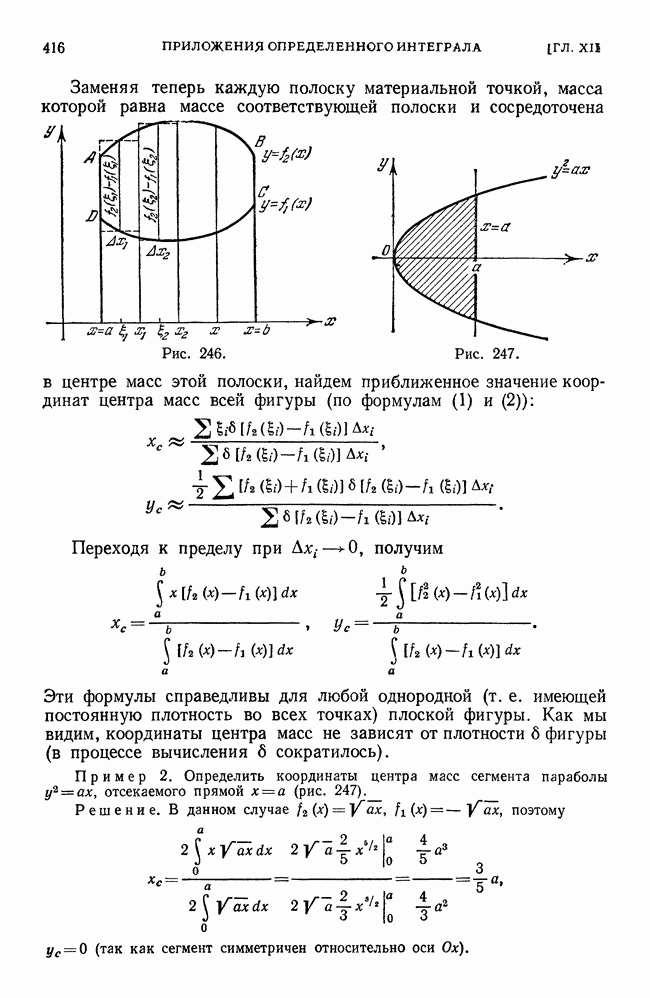
- § 8. Координаты центра масс
- § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла
- Упражнения к главе XII