| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4. Интеграл от формы по многообразию.
Определение 7. Пусть М —  -мерное гладкое ориентированное многообразие, на котором координаты
-мерное гладкое ориентированное многообразие, на котором координаты  и ориентация задаются одной картой
и ориентация задаются одной картой  с областью параметров
с областью параметров  Пусть
Пусть  —
—  -форма на М и а
-форма на М и а  — ее координатное представление в области
— ее координатное представление в области  Тогда
Тогда

где слева стоит определяемый интеграл от формы  по ориентированному многообразию М, а справа — интеграл от функции а
по ориентированному многообразию М, а справа — интеграл от функции а  по области
по области 
Если  — другой состоящий из одной карты атлас М, задающий на М ту же ориентацию, что и атлас
— другой состоящий из одной карты атлас М, задающий на М ту же ориентацию, что и атлас  то якобиан
то якобиан  функции
функции  преобразования координат всюду положителен в области
преобразования координат всюду положителен в области  Форме
Форме  отвечает форма
отвечает форма

По теореме о замене переменных в кратном интеграле имеет место равенство

показывающее независимость левой части соотношения (16) от выбора системы координат на М.
Итак, определение 7 корректно.
Определение 8. Носителем определенной на многообразии М формы  называется замыкание множества тех точек
называется замыкание множества тех точек  где
где 
Носитель формы  обозначается символом
обозначается символом  . В случае
. В случае  -форм, т. е. функций, мы уже с этим понятием встречались. Вне носителя координатное представление формы в любой локальной системе координат является нулевой формой данной степени.
-форм, т. е. функций, мы уже с этим понятием встречались. Вне носителя координатное представление формы в любой локальной системе координат является нулевой формой данной степени.
 Определение 9. Заданная на многообразии М форма
Определение 9. Заданная на многообразии М форма  называется финитной формой, если
называется финитной формой, если  — компакт в М.
— компакт в М.
Определение 10. Пусть  — финитная форма степени
— финитная форма степени  на
на  -мерном гладком многообразии М, ориентированном атласом А. Пусть
-мерном гладком многообразии М, ориентированном атласом А. Пусть  — конечный набор карт атласа А, районы
— конечный набор карт атласа А, районы  действия которых покрывают
действия которых покрывают  — подчиненное этому покрытию разбиение единицы на
— подчиненное этому покрытию разбиение единицы на  Повторяя некоторые карты по нескольку раз, можно считать, что
Повторяя некоторые карты по нескольку раз, можно считать, что  и что
и что  .
.
Интегралом от финитной формы  по ориентированному многообразию М называется величина
по ориентированному многообразию М называется величина

где  - координатное представление формы
- координатное представление формы  в области
в области  изменения координат соответствующей локальной карты.
изменения координат соответствующей локальной карты.
Докажем корректность этого определения.
Пусть  — другой атлас, задающий на М ту же гладкую структуру и ориентацию, что и атлас А, и пусть
— другой атлас, задающий на М ту же гладкую структуру и ориентацию, что и атлас А, и пусть  соответствующее покрытие
соответствующее покрытие  и подчиненное ему разбиение единицы на
и подчиненное ему разбиение единицы на  Введем функции
Введем функции  и положим
и положим 
Заметим, что  муст
муст  Отсюда и из корректности определения 7 интеграла по задаваемому одной картой ориентированному многообразию вытекает, что
Отсюда и из корректности определения 7 интеграла по задаваемому одной картой ориентированному многообразию вытекает, что

Суммируя эти равенства по  от 1 до
от 1 до  и по
и по  от 1 до
от 1 до  с учетом того, что
с учетом того, что  получим интересующее
получим интересующее  нас тождество.
нас тождество.
5. Формула Стокса.
Теорема. Пусть М — ориентированное гладкое  -мерное многообразие и
-мерное многообразие и  — гладкая финитная дифференциальная форма степени
— гладкая финитная дифференциальная форма степени  на нем. Тогда
на нем. Тогда

где ориентация края  многообразия М берется согласованной с ориентацией многообразия М. Если же
многообразия М берется согласованной с ориентацией многообразия М. Если же  то
то 
Без ограничения общности можно считать, что областями изменения координат (параметров) всех локальных карт многообразия М являются либо открытый куб  либо куб
либо куб  с одной (определенной!) присоединяемой к кубу
с одной (определенной!) присоединяемой к кубу  гранью.
гранью.
С помощью разбиения единицы утверждение теоремы сводится к случаю, когда  лежит в районе
лежит в районе  действия одной карты вида
действия одной карты вида  или
или  :
:  . В координатах этой карты форма
. В координатах этой карты форма  имеет вид
имеет вид

где символ  как обычно, означает пропуск соответствующего множителя.
как обычно, означает пропуск соответствующего множителя.
В силу линейности интеграла утверждение достаточно доказать для одного члена

суммы. Дифференциалом такой формы является  -форма
-форма

Для карты вида  оба интеграла в (18) от соответствующих форм (19), (20) равны нулю: первый потому, что
оба интеграла в (18) от соответствующих форм (19), (20) равны нулю: первый потому, что  а второй — по той же причине, если учесть теорему Фубини и соотношение
а второй — по той же причине, если учесть теорему Фубини и соотношение  Этим заодно исчерпывается случай, когда
Этим заодно исчерпывается случай, когда 
Таким образом, остается проверить равенство (18) для карты 
Если  , то и для такой карты оба интеграла равны нулю, что следует из приведенных выше соображений.
, то и для такой карты оба интеграла равны нулю, что следует из приведенных выше соображений.
Если

Итак, при  формула (18) доказана.
формула (18) доказана.
Случай  совпадает с формулой Ньютона — Лейбница, если принять, что концы а, Р ориентированного отрезка
совпадает с формулой Ньютона — Лейбница, если принять, что концы а, Р ориентированного отрезка  отмечаются знаками
отмечаются знаками  а интеграл от
а интеграл от  -формы
-формы  по, такой ориентированной точке полагается равным
по, такой ориентированной точке полагается равным  соответственно.
соответственно. 
По поводу доказанной теоремы сделаем некоторые замечания. Замечание 1. В формулировке теоремы ничего не говорится о гладкости многообразия М и формы со. В таких случаях обычно подразумевают, что каждый из этих объектов имеет гладкость  Из доказательства теоремы видно, однако, что формула (18) верна и для форм класса
Из доказательства теоремы видно, однако, что формула (18) верна и для форм класса  на многообразии М, допускающем формы такой гладкости.
на многообразии М, допускающем формы такой гладкости.
Замечание 2. Из доказательства теоремы, как, впрочем, и из самой формулы (18), видно также, что если  — компакт, лежащий строго внутри М, т. е.
— компакт, лежащий строго внутри М, т. е.  то
то 
Замечание 3. Если М — компактное многообразие, то для любой формы со на М ее носитель  , как замкнутое подмножество компакта М, является компактом. Следовательно, в этом случае любая форма
, как замкнутое подмножество компакта М, является компактом. Следовательно, в этом случае любая форма  на М является финитной и имеет место равенство (18). В частности, если М — компактное многообразие без края, то для любой гладкой формы на М имеет место равенство
на М является финитной и имеет место равенство (18). В частности, если М — компактное многообразие без края, то для любой гладкой формы на М имеет место равенство 
Замечание 4. Для произвольных (не финитных) форм  на многообразии, не являющемся само по себе компактом, формула (18), вообще говоря, не имеет места.
на многообразии, не являющемся само по себе компактом, формула (18), вообще говоря, не имеет места.
Рассмотрим, например, знакомую нам форму  в круговом кольце
в круговом кольце  наделенном стандартными декартовыми координатами. В этом случае М —
наделенном стандартными декартовыми координатами. В этом случае М —
компактное двумерное ориентированное многообразие, край  которого состоит из двух окружностей
которого состоит из двух окружностей  . Поскольку
. Поскольку  , то по формуле (18) находим, что
, то по формуле (18) находим, что

где обе окружности и  пробегаются против часовой стрелки. Мы знаем, что
пробегаются против часовой стрелки. Мы знаем, что

Значит, если вместо М рассмотреть многообразие  то
то  и
и

Задачи и упражнения
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА IX. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ (ОБЩАЯ ТЕОРИЯ)
- 2. Открытые и замкнутые подмножества метрического пространства.
- 3. Подпространство метрического пространства.
- 4. Прямое произведение метрических пространств.
- § 2. Топологическое пространство
- 2. Подпространство топологического пространства.
- 3. Прямое произведение топологических пространств.
- § 3. Компакты
- 2. Метрические компакты.
- § 4. Связные топологические пространства
- § 5. Полные метрические пространства
- 2. Пополнение метрического пространства.
- § 6. Непрерывные отображения топологических пространств
- 2. Непрерывные отображения.
- § 7. Принцип сжимающих отображений
- ГЛАВА X. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ С БОЛЕЕ ОБЩЕЙ ТОЧКИ ЗРЕНИЯ
- 2. Норма в линейном пространстве.
- 3. Скалярное произведение в векторном пространстве.
- § 2. Линейные и полилинейные операторы
- 2. Норма оператора.
- 3. Пространство непрерывных операторов.
- § 3. Дифференциал отображения
- 2. Общие законы дифференцирования.
- 3. Некоторые примеры.
- 4. Частные производные отображения.
- § 4. Теорема о конечном приращении и некоторые примеры ее использования
- 2. Некоторые примеры применения теоремы о конечном приращении.
- § 5. Производные отображения высших порядков
- 2. Производная по вектору и вычисление значений n-го дифференциала.
- 3. Симметричность дифференциалов высшего порядка.
- 4. Некоторые замечания.
- § 3. Формула Тейлора и исследование экстремумов
- 2. Исследование внутренних экстремумов.
- 3. Некоторые примеры.
- § 7. Общая теорема о неявной функции
- ГЛАВА XI. КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. Интеграл Римана на n-мерном промежутке
- 2. Критерий Лебега интегрируемости функции по Риману.
- 3. Критерий Дарбу.
- § 2. Интеграл по множеству
- 2. Интеграл по множеству.
- 3. Мера (объем) допустимого множества.
- § 3. Общие свойства интеграла
- 2. Аддитивность интеграла.
- 3. Оценки интеграла.
- § 4. Сведение кратного интеграла к повторному
- 2. Некоторые следствия.
- § 5. Замена переменных в кратном интеграле
- 2. Измеримые множества и гладкие отображения.
- 3. Одномерный случай.
- 4. Случай простейшего диффеоморфизма в R^n.
- 5. Композиция отображений и формула замены переменных.
- 6. Аддитивность интеграла и завершение доказательства формулы замены переменных в интеграле.
- 7. Некоторые следствия и обобщения формулы замены переменных в кратных интегралах.
- § 6. Несобственные кратные интегралы
- 2. Мажорантный признак сходимости несобственного интеграла.
- 3. Замена переменных в несобственном интеграле.
- ГЛАВА XII. ПОВЕРХНОСТИ И ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В R^n
- § 2. Ориентация поверхности
- § 3. Край поверхности и его ориентация
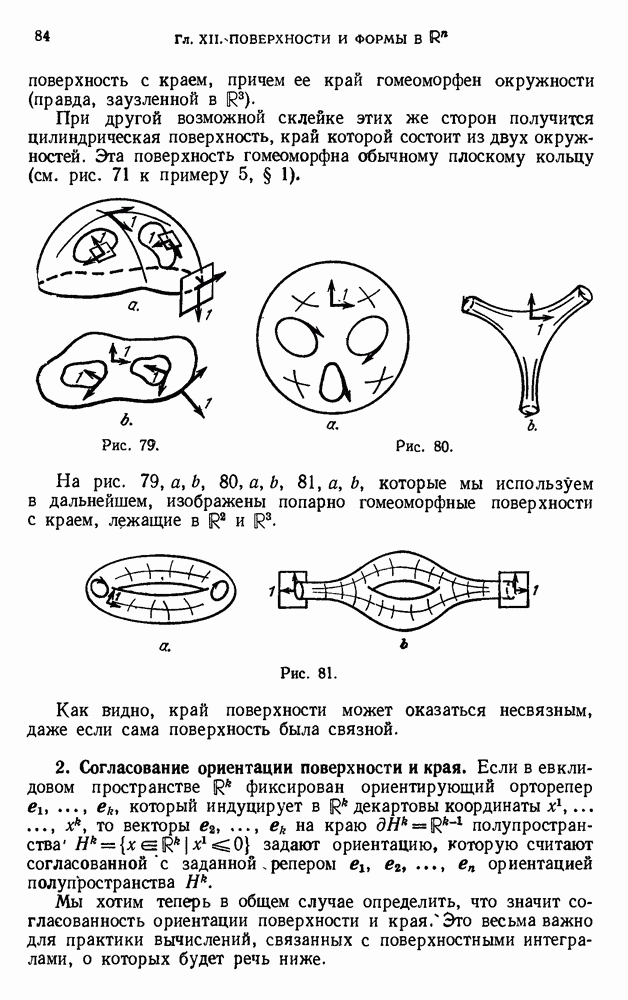
- 2. Согласование ориентации поверхности и края.
- § 4. Площадь поверхности в евклидовом пространстве
- § 5. Начальные сведения о дифференциальных формах
- 2. Координатная запись дифференциальной формы.
- 3. Внешний дифференциал формы.
- 4. Перенос векторов и форм при отображениях.
- 5. Формы на поверхностях.
- ГЛАВА XIII. КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 2. Определение интеграла от формы по ориентированной поверхности.
- § 2. Форма объема, интегралы первого и второго рода
- 2. Площадь поверхности как интеграл от формы.
- 3. Форма объема.
- 4. Выражение формы объема в декартовых координатах.
- 5. Интегралы первого и второго рода.
- § 3. Основные интегральные формулы анализа
- 2. Формула Гаусса — Остроградского.
- 3. Формула Стокса в R^3.
- 4. Общая формула Стокса.
- ГЛАВА XIV. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА И ТЕОРИИ ПОЛЯ
- § 1. Дифференциальные операции векторного анализа
- 2. Векторные поля и формы в R^3.
- 3. Дифференциальные операторы rad, rot, div и V.
- 5. Векторные операции в криволинейных координатах.
- § 2. Интегральные формулы теории поля
- 2. Физическая интерпретация div, rot, grad.
- 3. Некоторые дальнейшие интегральные формулы.
- § 3. Потенциальные поля
- 2. Необходимое условие потенциальности.
- 3. Критерий потенциальности векторного поля.
- 4. Топологическая структура области и потенциал.
- 5. Векторный потенциал. Точные и замкнутые формы.
- § 4. Примеры приложений
- 2. Уравнение неразрывности.
- 3. Основные уравнения динамики сплошной среды.
- 4. Волновое уравнение.
- ГЛАВА XV. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ НА МНОГООБРАЗИЯХ
- 2. Алгебра кососимметрических форм.
- 3. Линейные отображения линейных пространств и сопряженные отображения сопряженных пространств.
- § 2. Многообразие
- 2. Гладкие многообразия и гладкие отображения.
- 3. Ориентация многообразия и его края.
- 4. Разбиение единицы и реализация многообразий в виде поверхностей в R^n.
- § 3. Дифференциальные формы и их интегрирование на многообразиях
- 2. Дифференциальная форма на многообразии.
- 3. Внешний дифференциал.
- 4. Интеграл от формы по многообразию.
- § 4. Замкнутые и точные формы на многообразии
- 2. Гомологии и когомологии.
- ГЛАВА XVI. РАВНОМЕРНАЯ СХОДИМОСТЬ И ОСНОВНЫЕ ОПЕРАЦИИ АНАЛИЗА НАД РЯДАМИ И СЕМЕЙСТВАМИ ФУНКЦИЙ
- § 1. Поточечная и равномерная сходимость
- 2. Постановка основных вопросов.
- 3. Сходимость и равномерная сходимость семейства функций, зависящих от параметра.
- 4. Критерий Коши равномерной сходимости.
- § 2. Равномерная сходимость рядов функций
- 2. Признак Вейерштрасса равномерной сходимости ряда.
- § 3. Функциональные свойства предельной функции
- 2. Условия коммутирования двух предельных переходов.
- 3. Непрерывность и предельный переход.
- 4. Интегрирование и предельный переход.
- 5. Дифференцирование и предельный переход.
- § 4. Компактные и плотные подмножества пространства непрерывных функций
- 2. Метрическое пространство C(K,Y).
- 3. Теорема Стоуна.
- ГЛАВА XVII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 1. Собственные интегралы, зависящие от параметра
- 2. Непрерывность интеграла, зависящего от параметра.
- 3. Дифференцирование интеграла, зависящего от параметра.
- 4. Интегрирование интеграла, зависящего от параметра.
- § 2. Несобственные интегралы, зависящие от параметра
- 2. Предельный переход под знаком несобственного интеграла и непрерывность несобственного интеграла, зависящего от параметра.
- 3. Дифференцирование несобственного интеграла по параметру.
- 4. Интегрирование несобственного интеграла по параметру.
- § 3. Эйлеровы интегралы
- 2. Гамма-функция.
- 3. Связь между функциями В и Г.
- 4. Некоторые примеры.
- § 4. Свертка функций и начальные сведения об обобщенных функциях
- 2. Некоторые общие свойства свертки.
- 3. Дельтаобразные семейства функций и аппроксимационная теорема Вейерштрасса.
- 4. Начальные представления о распределениях
- § 5. Кратные интегралы, зависящие от параметра
- 2. Несобственные кратные интегралы, зависящие от параметра.
- 3. Несобственные интегралы с переменной особенностью.
- 4. Свертка, фундаментальное решение и обобщенные функции в многомерном случае.
- ГЛАВА XVIII. РЯД ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. Основные общие представления, связанные с понятием ряда Фурье
- 2. Коэффициенты Фурье.
- 3. Ряд Фурье.
- 4. Об одном важном источнике ортогональных систем функций в анализе.
- § 2. Тригонометрический ряд Фурье
- 2. Исследование поточечной сходимости тригонометрического ряда Фурье.
- 3. Гладкость функции и скорость убывания коэффициентов Фурье.
- 4. Полнота тригонометрической системы
- § 3. Преобразование Фурье
- 2. Регулярность функции и скорость убывания ее преобразования Фурье.
- 3. Важнейшие аппаратные свойства преобразования Фурье.
- 4. Примеры приложений.
- ГЛАВА XIX. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ
- § 1. Асимптотическая формула и асимптотический ряд
- 2. Общие сведения об асимптотических рядах.
- 3. Степенные асимптотические ряды.
- § 2. Асимптотика интегралов (метод Лапласа)
- 2. Принцип локализации для интеграла Лапласа.
- 3. Канонические интегралы и их асимптотика.
- 4. Главный член асимптотики интеграла Лапласа.
- 5. Асимптотические разложения интегралов Лапласа.
- ЛИТЕРАТУРА
- УКАЗАТЕЛЬ ОСНОВНЫХ ОБОЗНАЧЕНИЙ