| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Исследование поточечной сходимости тригонометрического ряда Фурье.
а. Лемма Римана.
Одним из принципиальных наблюдений, связанных с характером поточечной сходимости тригонометрического ряда Фурье, является следующая
Лемма 1 (Римана). Если локально интегрируемая функция  абсолютно интегрируема (хотя бы в несобственном смысле) на промежутке
абсолютно интегрируема (хотя бы в несобственном смысле) на промежутке  то
то

Фиксировав произвольно  выберем сначала отрезок
выберем сначала отрезок  так, чтобы при любом
так, чтобы при любом  было
было

Ввиду оценок

и абсолютной интегрируемости  указанный отрезок
указанный отрезок  конечно, существует.
конечно, существует.
Поскольку  (точнее
(точнее  то найдется такая нижняя интегральная сумма Дарбу
то найдется такая нижняя интегральная сумма Дарбу  где
где

Вводя теперь кусочно постоянную на  функцию
функцию  если
если  получаем, таким образом, что
получаем, таким образом, что  на
на  и
и

Но

Сопоставляя соотношения  получаем то, что и утверждалось.
получаем то, что и утверждалось. 
Замечание 1. Отделяя в (15) действительную и мнимую части, получаем, что

при  Если бы в последних интегралах функция f была комплекснозначна, то, отделяя уже в них действительную и мнимою части, мы получили бы, что соотношения
Если бы в последних интегралах функция f была комплекснозначна, то, отделяя уже в них действительную и мнимою части, мы получили бы, что соотношения  а значит,
а значит,
и соотношение (15), на самом-то деле, конечно, справедливы и для комплекснозначных функций 
Замечание 2. Если известно, что  , то в силу неравенства Бесселя (8) можно сразу заключить, что
, то в силу неравенства Бесселя (8) можно сразу заключить, что

при  Этим дискретным вариантов леммы Римана в принципе уже можно было бы обойтись в тех начальных исследованиях классических рядов Фурье, которые будут здесь проведены.
Этим дискретным вариантов леммы Римана в принципе уже можно было бы обойтись в тех начальных исследованиях классических рядов Фурье, которые будут здесь проведены.
b. Интегральное представление частичной суммы ряда Фурье.
Вернемся теперь к частичной сумме (9) ряда Фурье (6) и, подставив в ее комплексную запись (9) выражения (13) коэффициентов Фурье, проделаем следующие преобразования:

Но

поэтому

и

c. Ядро Дирихле.
Введенная соотношением (20) и преобразованная затем к виду (21) функция  называется ядром Дирихле или, точнее,
называется ядром Дирихле или, точнее,  ядром Дирихле
ядром Дирихле
Укажем используемые в дальнейшем свойства ядра Дирихле. Лемма 2 (о свойствах ядер Дирихле). Функция  обладает следующими свойствами:
обладает следующими свойствами:
 -периодическая и четная на
-периодическая и четная на 
 для любого
для любого 
с) для любого 

Периодичность и четность  очевидно, явно присутствуют в самом определении (6) функции
очевидно, явно присутствуют в самом определении (6) функции  Из этого же соотношения получаем
Из этого же соотношения получаем

поскольку при  интегралы равны нулю.
интегралы равны нулю.
Если теперь  то, используя представление (21) функции
то, используя представление (21) функции  и полагая
и полагая  при
при  , по лемме Римана получаем с).
, по лемме Римана получаем с).
d. Принцип локализации.
Теорема 2 (принцип локализации). Пусть  — вещественно или комплектозначные локально интегрируемые на промежутке
— вещественно или комплектозначные локально интегрируемые на промежутке  и абсолютно интегрируемые на нем (хотя бы в несобственном смысле) функции.
и абсолютно интегрируемые на нем (хотя бы в несобственном смысле) функции.
Если функции  совпадают в сколь угодно малой окрестности
совпадают в сколь угодно малой окрестности  точки
точки  то их ряды Фурье
то их ряды Фурье

сходятся или расходятся в точке  одновременно, а в случае сходимости их суммы в
одновременно, а в случае сходимости их суммы в  совпадают.
совпадают.
Фуркции  продолжим с периодом
продолжим с периодом  на всю числовую ось. Пренебрегая не существенными для последующих вычислений значениями продолженных функций в изолированных точках вида
на всю числовую ось. Пренебрегая не существенными для последующих вычислений значениями продолженных функций в изолированных точках вида  , где
, где  можно считать что
можно считать что  - периодические функции на
- периодические функции на  абсолютно интегрируемые (быть может, в несобственном смысле) на любом конечном отрезке прямой
абсолютно интегрируемые (быть может, в несобственном смысле) на любом конечном отрезке прямой 
Пользуясь  -периодичностью ядра Дирихле и тем, что интеграл от периодической на
-периодичностью ядра Дирихле и тем, что интеграл от периодической на  функции по отрезку, длина которого равна периоду функции, не зависит от расположения отрезка на
функции по отрезку, длина которого равна периоду функции, не зависит от расположения отрезка на  цосле замены
цосле замены  из (22) получаем симметричное прежнему представление
из (22) получаем симметричное прежнему представление

интегральной суммы ряда Фурье.
Пусть теперь  Тогда
Тогда

Здесь при получении последнего интеграла мы воспользовались выражением (21) ядра Дирихле и заменой  свели интеграл по промежутку
свели интеграл по промежутку  к интегралу по промежутку
к интегралу по промежутку 
Теперь, учитывая ограниченность  при
при  , ссылаясь на лемму Римана, можно заключить, что, каково бы ни было
, ссылаясь на лемму Римана, можно заключить, что, каково бы ни было 

Значит, поведение  при
при  полностью определяется значениями периодической функции
полностью определяется значениями периодической функции  в сколь угодно малой
в сколь угодно малой  -окрестнссти точки х. Это и есть принцип локализации, из которого немедленно вытекает другая его форма, высказанная в теореме 2.
-окрестнссти точки х. Это и есть принцип локализации, из которого немедленно вытекает другая его форма, высказанная в теореме 2.
Замесание 3. Как видно из доказательства (и это существенно!), если  тбчка
тбчка  была концом отрезка
была концом отрезка  то для локального совпадения в окрестности точки
то для локального совпадения в окрестности точки  продолженных на
продолженных на  функций
функций  необходимо (и достаточно), чтобы заданные лишь на отрезке
необходимо (и достаточно), чтобы заданные лишь на отрезке  исходные функции
исходные функции  совпадали в окрестности обоих концов этого отрезка.
совпадали в окрестности обоих концов этого отрезка.
e. Достаточные условия сходимости ряда Фурье в точке.
Определение  Говорят, что функция
Говорят, что функция  . заданная в проколотой окрестности точки
. заданная в проколотой окрестности точки  удовлетворяет в точке х условиям Цини, если
удовлетворяет в точке х условиям Цини, если
a) в точке х существуют оба односторонних предела

b) оба интеграла

сходятся абсолютно.
Пример 2. Если  непрерывная в
непрерывная в  функция, удовлетворяющая в точке х условию Гёльдера
функция, удовлетворяющая в точке х условию Гёльдера

то, поскольку тогда справедлива оценка

функция  удовлетворяет в точке х условиям Дини.
удовлетворяет в точке х условиям Дини.
Ясно также, что если определенная в проколотой окрестности и  точки х непрерывная функция
точки х непрерывная функция  имеет односторонние пределы
имеет односторонние пределы  и удовлетворяет односторонним условиям Гёльдера
и удовлетворяет односторонним условиям Гёльдера

где  — положительная постоянная, то функция
— положительная постоянная, то функция  по той же причине, что и выше, будет удовлетворять условиям Дини.
по той же причине, что и выше, будет удовлетворять условиям Дини.
Определение 3. Вещественно- или комплекснозначную функцию  будем называть кусочно непрерывной на отрезке
будем называть кусочно непрерывной на отрезке  если существует такой конечный набор точек
если существует такой конечный набор точек  этого отрезка, что функция
этого отрезка, что функция  определена, непрерывна на каждом интервале
определена, непрерывна на каждом интервале  и имеет односторонние пределы при подходе, к его концам.
и имеет односторонние пределы при подходе, к его концам.
Определение 4. Функцию, имеющую на данном отрезке кусочно непрерывную производную, будем называть кусочно непрерывно дифференцируемой функцией на этом отрезке.
Пример 3. Если функция кусочно непрерывно дифференцируема на отрезке то она удовлетворяет условиям Гёльдера С показателем  в любой точке этого отрезка (это вытекает из теоремы Лагранжа о конечном приращении). Значит, в силу примера 1 такая функция удовлетворяет условиям Дини в любой точке рассматриваемого отрезка. В концах отрезка, разумеется, проверке подлежит только соответствующая односторонняя пара условий Дини.
в любой точке этого отрезка (это вытекает из теоремы Лагранжа о конечном приращении). Значит, в силу примера 1 такая функция удовлетворяет условиям Дини в любой точке рассматриваемого отрезка. В концах отрезка, разумеется, проверке подлежит только соответствующая односторонняя пара условий Дини.
Пример 4. Функция  удовлетворяет условиям Дини в любой точке
удовлетворяет условиям Дини в любой точке  в том числе и в нуле.
в том числе и в нуле.
Теорема 3 (достаточные условия сходимости ряда Фурье в точке). Пусть  -периодическая функцияи абсолютно интегрируемая на отрезке
-периодическая функцияи абсолютно интегрируемая на отрезке  Если функция
Если функция  удовлетворяет 8 точке
удовлетворяет 8 точке  условиям Дини, то ее ряд Фурье сходится в точке х, причем
условиям Дини, то ее ряд Фурье сходится в точке х, причем

Используя свойства ядра Дирихле приведем сначала следующие простые преобразования интеграла (22):

Поскольку  при
при  благодаря условиям Дини на основании леммы Римана можно теперь утверждать, что при
благодаря условиям Дини на основании леммы Римана можно теперь утверждать, что при  последний интеграл стремится к нулю.
последний интеграл стремится к нулю.
Замечание 4. Формула (24) показывает, что ряд Фурье, сходясь к полусумме односторонних пределов функции  в точке х, совсем не реагирует на само значение
в точке х, совсем не реагирует на само значение  функции в точке х. Ничего удивительного в этом не должно быть, если вспомнить, что коэффициенты Фурье, а значит, и сам ряд Фурье не изменятся от изменения значений функции в индивидуальной точке. Пример 5. В примере 8 из § 1 мы нашли ряд Фурье
функции в точке х. Ничего удивительного в этом не должно быть, если вспомнить, что коэффициенты Фурье, а значит, и сам ряд Фурье не изменятся от изменения значений функции в индивидуальной точке. Пример 5. В примере 8 из § 1 мы нашли ряд Фурье

функции  на промежутке
на промежутке  . Продолжая функцию
. Продолжая функцию  периодично с интервала
периодично с интервала  на всю числовую ось, можно считать, что ряд (25) является рядом Фурье этой продолженной функции Тогда на основании теоремы 3 получаем, что
на всю числовую ось, можно считать, что ряд (25) является рядом Фурье этой продолженной функции Тогда на основании теоремы 3 получаем, что

В частности, при  следует, что
следует, что

Пример 6. Пусть  . Рассмотрим
. Рассмотрим  -периодическую функцию
-периодическую функцию  задаваемую на отрезке
задаваемую на отрезке  формулой
формулой 
По формулам (4), (5) найдем ее коэффициенты Фурье:

По теореме 3 в любой точке  имеет место равенство
имеет место равенство

При  отсюда получаем, что
отсюда получаем, что

Если  , то
, то  поэтому стоящий в правой части равенства (26) ряд сходится равномерно по а на любом отрезке
поэтому стоящий в правой части равенства (26) ряд сходится равномерно по а на любом отрезке  Значит, законно его почленное интегрирование, т. е.
Значит, законно его почленное интегрирование, т. е.

и

что

и окончательно

Мы доказали, таким образом, соотношение (27), на которое в свое время ссылались при выводе формулы дополнения для функции  Эйлера.
Эйлера.
f. Теорема Фейера.
Рассмотрим теперь последовательность функций

являющихся средним арифметическим соответствующих частичных сумм  тригонометрического ряда Фурье (6) периодической функции
тригонометрического ряда Фурье (6) периодической функции 
Используя интегральное представление (22) частичной суммы ряда Фурье, в результате простых преобразований получаем

где

Функция  называется ядром Фейера, точнее
называется ядром Фейера, точнее  ядром Фейера.
ядром Фейера.
Лемма 3 (о свойствах ядер Фейера). Последовательность функций

является  -образной на
-образной на 
Поскольку

то неотрицательность  очевидна.
очевидна.
Далее,

Наконец, при любом 

при 
Теорема 4 (Фейера). Пусть  -
-  -периодическая абсолютно интегрируемая на отрезке
-периодическая абсолютно интегрируемая на отрезке  функция. Тогда:
функция. Тогда:
a) если на множестве  функция
функция  равномерно непрерывна, то
равномерно непрерывна, то

b) если  , то
, то

c) если  непрерывна в точке
непрерывна в точке  то
то

Утверждения  являются специальными случаями утверждения а).
являются специальными случаями утверждения а).
Само же утверждение а) является частным случаем общего утверждения 5 из § 4 гл. XVII о сходимости свертки, поскольку

Следствие 1 (теорема Вейерштрасса об аппроксимации тригонометрическими многочленами). Если функция  непрерывна на отрезке
непрерывна на отрезке  , то эта функция может быть сколь угодно точно равномерно на отрезке
, то эта функция может быть сколь угодно точно равномерно на отрезке  аппроксимирована тригонометрическими многочленами.
аппроксимирована тригонометрическими многочленами.
Продолжая  периодически, получим непрерывную периодическую на
периодически, получим непрерывную периодическую на  функцию, к которой по теореме Фейера равномерно сходятся тригонометрические многочлены
функцию, к которой по теореме Фейера равномерно сходятся тригонометрические многочлены 
Следствие 2. Если функция  непрерывна в точке х, то ее ряд Фурье либо вовсе расходится в этой точке, - либо сходится к
непрерывна в точке х, то ее ряд Фурье либо вовсе расходится в этой точке, - либо сходится к 
Формально в проверке нуждается только случай сходимости.
Если последоватёльность  при
при  имеет предел, то тот же предел имеет и последовательность
имеет предел, то тот же предел имеет и последовательность 
Но по теореме Фейера  при
при  значит, и
значит, и  при
при  если вообще предел
если вообще предел  при
при  существует.
существует.
Замечание 5. Отметим, что ряд Фурье непрерывной функции и в самом деле может в некоторых точках расходиться.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА IX. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ (ОБЩАЯ ТЕОРИЯ)
- 2. Открытые и замкнутые подмножества метрического пространства.
- 3. Подпространство метрического пространства.
- 4. Прямое произведение метрических пространств.
- § 2. Топологическое пространство
- 2. Подпространство топологического пространства.
- 3. Прямое произведение топологических пространств.
- § 3. Компакты
- 2. Метрические компакты.
- § 4. Связные топологические пространства
- § 5. Полные метрические пространства
- 2. Пополнение метрического пространства.
- § 6. Непрерывные отображения топологических пространств
- 2. Непрерывные отображения.
- § 7. Принцип сжимающих отображений
- ГЛАВА X. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ С БОЛЕЕ ОБЩЕЙ ТОЧКИ ЗРЕНИЯ
- 2. Норма в линейном пространстве.
- 3. Скалярное произведение в векторном пространстве.
- § 2. Линейные и полилинейные операторы
- 2. Норма оператора.
- 3. Пространство непрерывных операторов.
- § 3. Дифференциал отображения
- 2. Общие законы дифференцирования.
- 3. Некоторые примеры.
- 4. Частные производные отображения.
- § 4. Теорема о конечном приращении и некоторые примеры ее использования
- 2. Некоторые примеры применения теоремы о конечном приращении.
- § 5. Производные отображения высших порядков
- 2. Производная по вектору и вычисление значений n-го дифференциала.
- 3. Симметричность дифференциалов высшего порядка.
- 4. Некоторые замечания.
- § 3. Формула Тейлора и исследование экстремумов
- 2. Исследование внутренних экстремумов.
- 3. Некоторые примеры.
- § 7. Общая теорема о неявной функции
- ГЛАВА XI. КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. Интеграл Римана на n-мерном промежутке
- 2. Критерий Лебега интегрируемости функции по Риману.
- 3. Критерий Дарбу.
- § 2. Интеграл по множеству
- 2. Интеграл по множеству.
- 3. Мера (объем) допустимого множества.
- § 3. Общие свойства интеграла
- 2. Аддитивность интеграла.
- 3. Оценки интеграла.
- § 4. Сведение кратного интеграла к повторному
- 2. Некоторые следствия.
- § 5. Замена переменных в кратном интеграле
- 2. Измеримые множества и гладкие отображения.
- 3. Одномерный случай.
- 4. Случай простейшего диффеоморфизма в R^n.
- 5. Композиция отображений и формула замены переменных.
- 6. Аддитивность интеграла и завершение доказательства формулы замены переменных в интеграле.
- 7. Некоторые следствия и обобщения формулы замены переменных в кратных интегралах.
- § 6. Несобственные кратные интегралы
- 2. Мажорантный признак сходимости несобственного интеграла.
- 3. Замена переменных в несобственном интеграле.
- ГЛАВА XII. ПОВЕРХНОСТИ И ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В R^n
- § 2. Ориентация поверхности
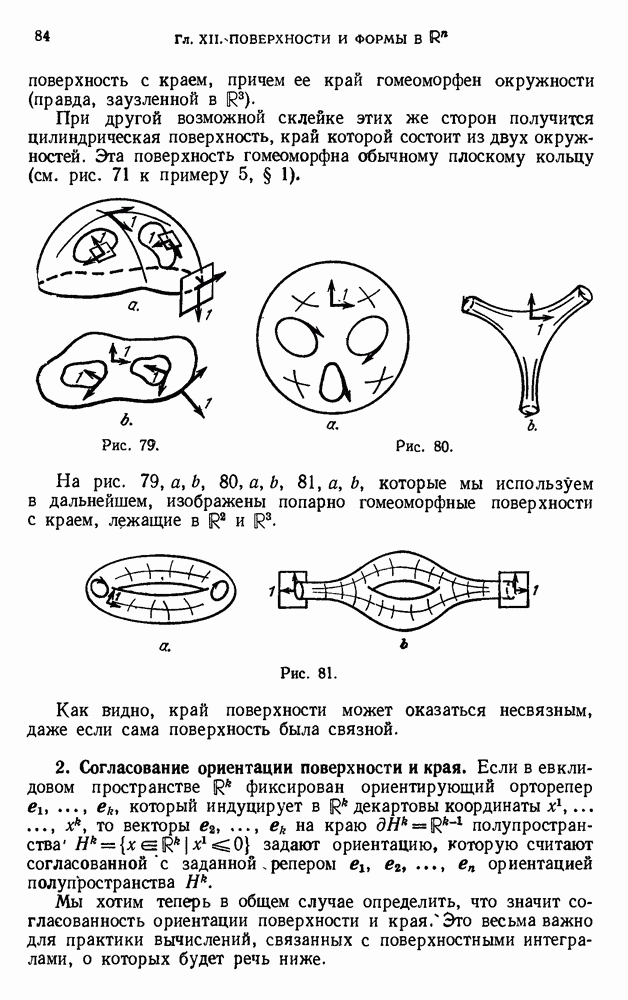
- § 3. Край поверхности и его ориентация
- 2. Согласование ориентации поверхности и края.
- § 4. Площадь поверхности в евклидовом пространстве
- § 5. Начальные сведения о дифференциальных формах
- 2. Координатная запись дифференциальной формы.
- 3. Внешний дифференциал формы.
- 4. Перенос векторов и форм при отображениях.
- 5. Формы на поверхностях.
- ГЛАВА XIII. КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 2. Определение интеграла от формы по ориентированной поверхности.
- § 2. Форма объема, интегралы первого и второго рода
- 2. Площадь поверхности как интеграл от формы.
- 3. Форма объема.
- 4. Выражение формы объема в декартовых координатах.
- 5. Интегралы первого и второго рода.
- § 3. Основные интегральные формулы анализа
- 2. Формула Гаусса — Остроградского.
- 3. Формула Стокса в R^3.
- 4. Общая формула Стокса.
- ГЛАВА XIV. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА И ТЕОРИИ ПОЛЯ
- § 1. Дифференциальные операции векторного анализа
- 2. Векторные поля и формы в R^3.
- 3. Дифференциальные операторы rad, rot, div и V.
- 5. Векторные операции в криволинейных координатах.
- § 2. Интегральные формулы теории поля
- 2. Физическая интерпретация div, rot, grad.
- 3. Некоторые дальнейшие интегральные формулы.
- § 3. Потенциальные поля
- 2. Необходимое условие потенциальности.
- 3. Критерий потенциальности векторного поля.
- 4. Топологическая структура области и потенциал.
- 5. Векторный потенциал. Точные и замкнутые формы.
- § 4. Примеры приложений
- 2. Уравнение неразрывности.
- 3. Основные уравнения динамики сплошной среды.
- 4. Волновое уравнение.
- ГЛАВА XV. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ НА МНОГООБРАЗИЯХ
- 2. Алгебра кососимметрических форм.
- 3. Линейные отображения линейных пространств и сопряженные отображения сопряженных пространств.
- § 2. Многообразие
- 2. Гладкие многообразия и гладкие отображения.
- 3. Ориентация многообразия и его края.
- 4. Разбиение единицы и реализация многообразий в виде поверхностей в R^n.
- § 3. Дифференциальные формы и их интегрирование на многообразиях
- 2. Дифференциальная форма на многообразии.
- 3. Внешний дифференциал.
- 4. Интеграл от формы по многообразию.
- § 4. Замкнутые и точные формы на многообразии
- 2. Гомологии и когомологии.
- ГЛАВА XVI. РАВНОМЕРНАЯ СХОДИМОСТЬ И ОСНОВНЫЕ ОПЕРАЦИИ АНАЛИЗА НАД РЯДАМИ И СЕМЕЙСТВАМИ ФУНКЦИЙ
- § 1. Поточечная и равномерная сходимость
- 2. Постановка основных вопросов.
- 3. Сходимость и равномерная сходимость семейства функций, зависящих от параметра.
- 4. Критерий Коши равномерной сходимости.
- § 2. Равномерная сходимость рядов функций
- 2. Признак Вейерштрасса равномерной сходимости ряда.
- § 3. Функциональные свойства предельной функции
- 2. Условия коммутирования двух предельных переходов.
- 3. Непрерывность и предельный переход.
- 4. Интегрирование и предельный переход.
- 5. Дифференцирование и предельный переход.
- § 4. Компактные и плотные подмножества пространства непрерывных функций
- 2. Метрическое пространство C(K,Y).
- 3. Теорема Стоуна.
- ГЛАВА XVII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 1. Собственные интегралы, зависящие от параметра
- 2. Непрерывность интеграла, зависящего от параметра.
- 3. Дифференцирование интеграла, зависящего от параметра.
- 4. Интегрирование интеграла, зависящего от параметра.
- § 2. Несобственные интегралы, зависящие от параметра
- 2. Предельный переход под знаком несобственного интеграла и непрерывность несобственного интеграла, зависящего от параметра.
- 3. Дифференцирование несобственного интеграла по параметру.
- 4. Интегрирование несобственного интеграла по параметру.
- § 3. Эйлеровы интегралы
- 2. Гамма-функция.
- 3. Связь между функциями В и Г.
- 4. Некоторые примеры.
- § 4. Свертка функций и начальные сведения об обобщенных функциях
- 2. Некоторые общие свойства свертки.
- 3. Дельтаобразные семейства функций и аппроксимационная теорема Вейерштрасса.
- 4. Начальные представления о распределениях
- § 5. Кратные интегралы, зависящие от параметра
- 2. Несобственные кратные интегралы, зависящие от параметра.
- 3. Несобственные интегралы с переменной особенностью.
- 4. Свертка, фундаментальное решение и обобщенные функции в многомерном случае.
- ГЛАВА XVIII. РЯД ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. Основные общие представления, связанные с понятием ряда Фурье
- 2. Коэффициенты Фурье.
- 3. Ряд Фурье.
- 4. Об одном важном источнике ортогональных систем функций в анализе.
- § 2. Тригонометрический ряд Фурье
- 2. Исследование поточечной сходимости тригонометрического ряда Фурье.
- 3. Гладкость функции и скорость убывания коэффициентов Фурье.
- 4. Полнота тригонометрической системы
- § 3. Преобразование Фурье
- 2. Регулярность функции и скорость убывания ее преобразования Фурье.
- 3. Важнейшие аппаратные свойства преобразования Фурье.
- 4. Примеры приложений.
- ГЛАВА XIX. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ
- § 1. Асимптотическая формула и асимптотический ряд
- 2. Общие сведения об асимптотических рядах.
- 3. Степенные асимптотические ряды.
- § 2. Асимптотика интегралов (метод Лапласа)
- 2. Принцип локализации для интеграла Лапласа.
- 3. Канонические интегралы и их асимптотика.
- 4. Главный член асимптотики интеграла Лапласа.
- 5. Асимптотические разложения интегралов Лапласа.
- ЛИТЕРАТУРА
- УКАЗАТЕЛЬ ОСНОВНЫХ ОБОЗНАЧЕНИЙ