| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Критерий Лебега интегрируемости функции по Риману.
Изучая интеграл Римана в одномерном случае, мы уже познакомили читателя (без доказательств) с критерием Лебега существования интеграла. Здесь мы напомним некоторые понятия и докажем этот критерий.
а. Множество меры нуль в R^n.
Определение 9. Говорят, что множество  имеет (
имеет ( -мерную) меру нуль или является множеством меры нуль (в смысле Лебега), если для любого
-мерную) меру нуль или является множеством меры нуль (в смысле Лебега), если для любого  существует покрытие множества Е не более чем счетной системой
существует покрытие множества Е не более чем счетной системой  -мерных промежутков, сумма
-мерных промежутков, сумма  объемов которых не превышает
объемов которых не превышает  .
.
Лемма 2. а) Точка и конечное число точек суть множества меры нуль.
 Объединение конечного или счетного числа множеств меры нуль есть множество меры нуль.
Объединение конечного или счетного числа множеств меры нуль есть множество меры нуль.
c) Подмножество множества меры нуль само есть множество меры нупь.
d) Невырожденный промежуток  не является множеством меры нуль.
не является множеством меры нуль.
Доказательство леммы 2 ничем не отличается от доказательства ее одномерного варианта, рассмотренного в  § 1, гл. VI, поэтому мы на нем не останавливаемся.
§ 1, гл. VI, поэтому мы на нем не останавливаемся.
Пример 1. Множество рациональных точек в  (точек, все координаты которых рациональны) счетно и потому является множеством меры нуль.
(точек, все координаты которых рациональны) счетно и потому является множеством меры нуль.
Пример 2. Пусть  — непрерывная вещественнозначная функция, определенная на
— непрерывная вещественнозначная функция, определенная на  -мерном промежутке
-мерном промежутке  Покажем, что ее график в
Покажем, что ее график в  есть множество
есть множество  -мерной меры нуль.
-мерной меры нуль.
Поскольку функция  равномерно непрерывна на I, то по
равномерно непрерывна на I, то по  найдем
найдем  так, чтобы для любых точек
так, чтобы для любых точек  при условии
при условии  иметь
иметь  Если теперь взять разбиение Р промежутка I с параметром
Если теперь взять разбиение Р промежутка I с параметром  то на каждом промежутке
то на каждом промежутке  такого разбиения колебание функции
такого разбиения колебание функции  будет меньше е. Значит, если
будет меньше е. Значит, если  — произвольная фиксированная точка промежутка
— произвольная фиксированная точка промежутка  то
то  -мерный промежуток
-мерный промежуток  очевидно, содержит всю часть графика функции
очевидно, содержит всю часть графика функции  которая лежит над промежутком
которая лежит над промежутком  а объединение
а объединение  промежутков
промежутков  покрывает весь график функции
покрывает весь график функции  над I. Но
над I. Но  (здесь
(здесь  — объем
— объем  — объем
— объем  Таким образом, уменьшая
Таким образом, уменьшая  действительно можно общий объем покрытия сделать сколь угодно близким к нулю.
действительно можно общий объем покрытия сделать сколь угодно близким к нулю.
Замечание 1. Сопоставляя утверждение  леммы 2 с примером 2, можно заключить, что вообще график непрерывной функции
леммы 2 с примером 2, можно заключить, что вообще график непрерывной функции  или непрерывной функции
или непрерывной функции  где
где  является множеством
является множеством  -мерной меры нуль в
-мерной меры нуль в 
Лемма 3. а) Класс множеств меры нуль не изменится от того, понимать ли в определении 9 покрытие множества Е системой промежутков  в обычном смысле, т. е. считая
в обычном смысле, т. е. считая  или в более жестком смысле, требуя, чтобы каждая точка множества была внутренней точкой по крайней мере одного из промежутков покрытия.
или в более жестком смысле, требуя, чтобы каждая точка множества была внутренней точкой по крайней мере одного из промежутков покрытия.
 Компакт
Компакт  является множеством меры нуль в том и только в том случае, если для любого
является множеством меры нуль в том и только в том случае, если для любого  существует конечное покрытие
существует конечное покрытие  промежутками, сумма объемов которых меньше
промежутками, сумма объемов которых меньше  .
.
а) Если  — покрытие множества Е, т. е.
— покрытие множества Е, т. е.  причем
причем  то, взяв вместо каждого промежутка
то, взяв вместо каждого промежутка  гомотеточный ему относительно его центра промежуток
гомотеточный ему относительно его центра промежуток  получим систему промежутков
получим систему промежутков  такую, что
такую, что  где — общий для всех промежутков коэффициент гомотетии. Если
где — общий для всех промежутков коэффициент гомотетии. Если  то, очевидно, система
то, очевидно, система  будет покрывать множество Е так, что любая точка Е является внутренней точкой по крайней мере одного из промежутков покрытия.
будет покрывать множество Е так, что любая точка Е является внутренней точкой по крайней мере одного из промежутков покрытия.
 Это следует из а) и возможности извлечь конечное покрытие из любого открытого покрытия компакта
Это следует из а) и возможности извлечь конечное покрытие из любого открытого покрытия компакта  . (В качестве такого покрытия может выступать система
. (В качестве такого покрытия может выступать система  открытых промежутков, получаемая из рассмотренной в а) системы
открытых промежутков, получаемая из рассмотренной в а) системы 
b. Одно обобщение теоремы Кантора.
Напомним, что колебанием функции  на множестве Е мы назвали величину со
на множестве Е мы назвали величину со  а колебанием функции в точке
а колебанием функции в точке  — величину
— величину  где
где  -окрестность точки х в множестве Е.
-окрестность точки х в множестве Е.
Лемма 4. Если в каждой точке компакта  для функции
для функции  имеет место соотношение
имеет место соотношение  то для любого
то для любого  найдется
найдется  такое, что для любой точки будет выполнено неравенство
такое, что для любой точки будет выполнено неравенство  .
.
При  это утверждение превращается в теорему Кантора о равномерной непрерывности функции непрерывной на компакте. Доказательство леммы 4 буквально повторяет схему доказательства теоремы Кантора
это утверждение превращается в теорему Кантора о равномерной непрерывности функции непрерывной на компакте. Доказательство леммы 4 буквально повторяет схему доказательства теоремы Кантора  § 2, гл. VI), поэтому мы на нем не задерживаемся.
§ 2, гл. VI), поэтому мы на нем не задерживаемся.
c. Критерий Лебега.
Как и прежде, будем говорить, что некоторое свойство имеет место почти во всех точках множества М или выполнено почти всюду на М, если подмножество М, где это свойство может нарушаться, имеет меру нуль.
Теорема 1 (критерий Лебега),  ограничена на
ограничена на  непрерывна почти всюду на
непрерывна почти всюду на 
Необходимость. Если  то по утверждению 1 функция
то по утверждению 1 функция  ограничена на I. Пусть
ограничена на I. Пусть  на I.
на I.
Проверим, что  непрерывна почти во всех точках
непрерывна почти во всех точках  Для этого покажем, что если множество Е точек разрыва функции не есть множество меры нуль, то
Для этого покажем, что если множество Е точек разрыва функции не есть множество меры нуль, то 
Действительно, представив Е в виде  где
где  на основании леммы 2 заключаем, что если Е не имеет меру нуль, то найдется номер
на основании леммы 2 заключаем, что если Е не имеет меру нуль, то найдется номер  такой, что множество
такой, что множество  тоже не есть множество меры нуль. Пусть Р — произвольное разбиение промежутка I на промежутки
тоже не есть множество меры нуль. Пусть Р — произвольное разбиение промежутка I на промежутки  Разделим промежутки разбиения Р на две группы А и В, где
Разделим промежутки разбиения Р на две группы А и В, где

Система промежутков А образует покрытие множества  . В самом деле, каждая точка
. В самом деле, каждая точка  лежит либо внутри некоторого промежутка
лежит либо внутри некоторого промежутка  и тогда, очевидно,
и тогда, очевидно,  , либо на границе некоторых промежутков разбиения Р. В последнем случае хотя бы на одном из этих промежутков колебание функции должно быть (в силу неравенства треугольника) не менее чем и он войдет в систему А.
, либо на границе некоторых промежутков разбиения Р. В последнем случае хотя бы на одном из этих промежутков колебание функции должно быть (в силу неравенства треугольника) не менее чем и он войдет в систему А.
Покажем теперь, что, выбирая различным образом набор  отмеченных точек в промежутках разбиения Р, мы можем заметно менять величину интегральной суммы.
отмеченных точек в промежутках разбиения Р, мы можем заметно менять величину интегральной суммы.
Именно, выберем наборы точек  , так, чтобы в промежутках системы В отмеченные точки обоих наборов совпадали, а в промежутках
, так, чтобы в промежутках системы В отмеченные точки обоих наборов совпадали, а в промежутках  системы А точки выберем так, что Тогда
системы А точки выберем так, что Тогда 
Существование такой постоянной с вытекает из того, что промежутки системы А образуют покрытие множества  которое по предположению не есть множество меры нуль.
которое по предположению не есть множество меры нуль.
Поскольку Р было произвольным разбиением промежутка I, на основании критерия Коши заключаем, что интегральные суммы  не могут иметь предел при
не могут иметь предел при  т. е.
т. е.
Достаточность. Пусть  — произвольное положительное число, а
— произвольное положительное число, а  По условию Ее есть множество меры нуль.
По условию Ее есть множество меры нуль.
Кроме того,  , очевидно, замкнуто в
, очевидно, замкнуто в  поэтому Ее — компакт.
поэтому Ее — компакт.
По лемме 3 существует такая конечная система  промежутков в
промежутков в  что
что  Положим
Положим  а через
а через  обозначим объединение промежутков, полученных из промежутков
обозначим объединение промежутков, полученных из промежутков  гомотетией с центром в центре
гомотетией с центром в центре  и коэффициентом 2 и 3 соответственно. Ясно, что
и коэффициентом 2 и 3 соответственно. Ясно, что  лежит
лежит
строго внутри  и что расстояние
и что расстояние  между границами множеств
между границами множеств  положительно.
положительно.
Отметим, что сумма объемов любой конечной системы промежутков, которые лежат в  и попарно не имеют общих внутренних точек, не больше чем
и попарно не имеют общих внутренних точек, не больше чем  где
где  -размерность пространства
-размерность пространства  Это следует из определения множества
Это следует из определения множества  и свойств меры промежутка (лемма 1).
и свойств меры промежутка (лемма 1).
Отметим также, что любое подмножество промежутка  диаметр которого меньше
диаметр которого меньше  либо содержится в множестве
либо содержится в множестве  либо лежит в компакте
либо лежит в компакте  где
где  — граница
— граница  (и, следовательно,
(и, следовательно,  — совокупность внутренних точек множества
— совокупность внутренних точек множества 
По построению  поэтому в любой точке
поэтому в любой точке  должно быть
должно быть  . По лемме 4 найдется число
. По лемме 4 найдется число  такое, что для любой пары точек
такое, что для любой пары точек  удаленных друг от друга не больше чем на
удаленных друг от друга не больше чем на  имеет место неравенство
имеет место неравенство  .
.
Сделанные построения позволяют теперь следующим образом провести доказательство достаточности условии интегрируемости. Берем любые два разбиения  промежутка 1 с параметрами
промежутка 1 с параметрами  меньшими, чем
меньшими, чем  Пусть Р — разбиение, полученное пересечением промежутков разбиений
Пусть Р — разбиение, полученное пересечением промежутков разбиений  т. е. в естественных обозначениях
т. е. в естественных обозначениях  Сравним интегральные суммы
Сравним интегральные суммы  Учитывая, что
Учитывая, что  можно записать:
можно записать:

Здесь в первую сумму  вошли те промежутки
вошли те промежутки  разбиения Р, которые лежат в промежутках
разбиения Р, которые лежат в промежутках  разбиения Р, содержащихся в множестве
разбиения Р, содержащихся в множестве  а остальные промежутки разбиения Р отнесены к сумме
а остальные промежутки разбиения Р отнесены к сумме  т. е. все они обязательно содержатся в
т. е. все они обязательно содержатся в  (ведь
(ведь  ).
).
Поскольку  на
на  заменяя в первой сумме
заменяя в первой сумме  величиной
величиной  заключаем, что первая сумма не превосходит
заключаем, что первая сумма не превосходит  .
.
Учитывая, что во второй сумме  заключаем, что
заключаем, что  и, следовательно, вторая сумма не превосходит
и, следовательно, вторая сумма не превосходит 
Таким образом,  откуда (ввиду равноправности Р и
откуда (ввиду равноправности Р и  используя неравенство треугольника, получаем, что
используя неравенство треугольника, получаем, что

для любых разбиений  с достаточно малыми параметрами.
с достаточно малыми параметрами.
В силу критерия Коши теперь заключаем, что 
Замечание 2. Поскольку критерий Коши существования предела функций имеет силу в любом полном метрическом пространстве, то критерий Лебега, как видно из доказательства, справедлив для функций со значениями в любом полном линейном нормированном пространстве.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА IX. НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ (ОБЩАЯ ТЕОРИЯ)
- 2. Открытые и замкнутые подмножества метрического пространства.
- 3. Подпространство метрического пространства.
- 4. Прямое произведение метрических пространств.
- § 2. Топологическое пространство
- 2. Подпространство топологического пространства.
- 3. Прямое произведение топологических пространств.
- § 3. Компакты
- 2. Метрические компакты.
- § 4. Связные топологические пространства
- § 5. Полные метрические пространства
- 2. Пополнение метрического пространства.
- § 6. Непрерывные отображения топологических пространств
- 2. Непрерывные отображения.
- § 7. Принцип сжимающих отображений
- ГЛАВА X. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ С БОЛЕЕ ОБЩЕЙ ТОЧКИ ЗРЕНИЯ
- 2. Норма в линейном пространстве.
- 3. Скалярное произведение в векторном пространстве.
- § 2. Линейные и полилинейные операторы
- 2. Норма оператора.
- 3. Пространство непрерывных операторов.
- § 3. Дифференциал отображения
- 2. Общие законы дифференцирования.
- 3. Некоторые примеры.
- 4. Частные производные отображения.
- § 4. Теорема о конечном приращении и некоторые примеры ее использования
- 2. Некоторые примеры применения теоремы о конечном приращении.
- § 5. Производные отображения высших порядков
- 2. Производная по вектору и вычисление значений n-го дифференциала.
- 3. Симметричность дифференциалов высшего порядка.
- 4. Некоторые замечания.
- § 3. Формула Тейлора и исследование экстремумов
- 2. Исследование внутренних экстремумов.
- 3. Некоторые примеры.
- § 7. Общая теорема о неявной функции
- ГЛАВА XI. КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. Интеграл Римана на n-мерном промежутке
- 2. Критерий Лебега интегрируемости функции по Риману.
- 3. Критерий Дарбу.
- § 2. Интеграл по множеству
- 2. Интеграл по множеству.
- 3. Мера (объем) допустимого множества.
- § 3. Общие свойства интеграла
- 2. Аддитивность интеграла.
- 3. Оценки интеграла.
- § 4. Сведение кратного интеграла к повторному
- 2. Некоторые следствия.
- § 5. Замена переменных в кратном интеграле
- 2. Измеримые множества и гладкие отображения.
- 3. Одномерный случай.
- 4. Случай простейшего диффеоморфизма в R^n.
- 5. Композиция отображений и формула замены переменных.
- 6. Аддитивность интеграла и завершение доказательства формулы замены переменных в интеграле.
- 7. Некоторые следствия и обобщения формулы замены переменных в кратных интегралах.
- § 6. Несобственные кратные интегралы
- 2. Мажорантный признак сходимости несобственного интеграла.
- 3. Замена переменных в несобственном интеграле.
- ГЛАВА XII. ПОВЕРХНОСТИ И ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В R^n
- § 2. Ориентация поверхности
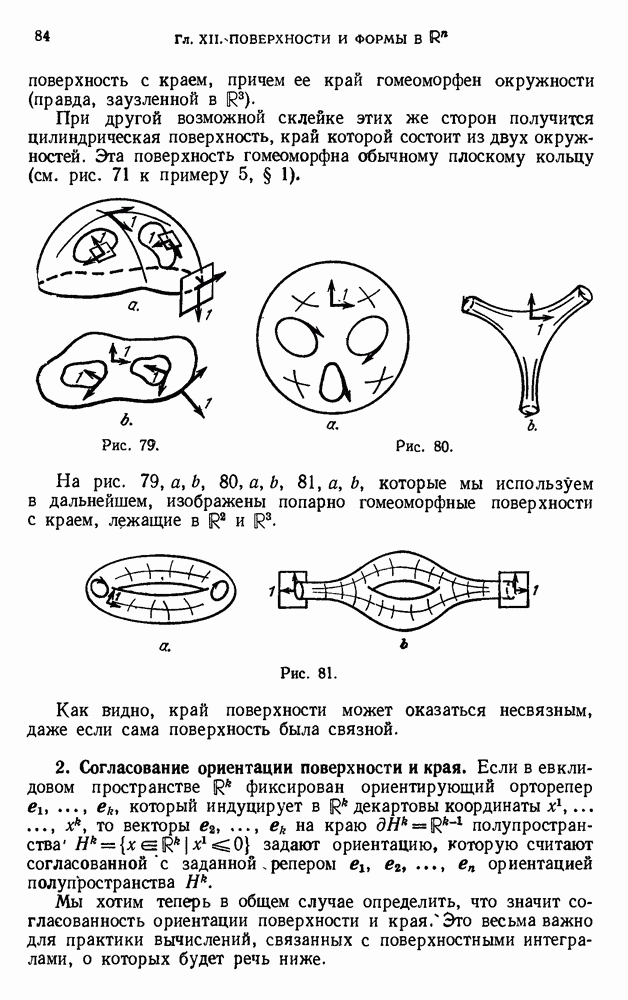
- § 3. Край поверхности и его ориентация
- 2. Согласование ориентации поверхности и края.
- § 4. Площадь поверхности в евклидовом пространстве
- § 5. Начальные сведения о дифференциальных формах
- 2. Координатная запись дифференциальной формы.
- 3. Внешний дифференциал формы.
- 4. Перенос векторов и форм при отображениях.
- 5. Формы на поверхностях.
- ГЛАВА XIII. КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- 2. Определение интеграла от формы по ориентированной поверхности.
- § 2. Форма объема, интегралы первого и второго рода
- 2. Площадь поверхности как интеграл от формы.
- 3. Форма объема.
- 4. Выражение формы объема в декартовых координатах.
- 5. Интегралы первого и второго рода.
- § 3. Основные интегральные формулы анализа
- 2. Формула Гаусса — Остроградского.
- 3. Формула Стокса в R^3.
- 4. Общая формула Стокса.
- ГЛАВА XIV. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА И ТЕОРИИ ПОЛЯ
- § 1. Дифференциальные операции векторного анализа
- 2. Векторные поля и формы в R^3.
- 3. Дифференциальные операторы rad, rot, div и V.
- 5. Векторные операции в криволинейных координатах.
- § 2. Интегральные формулы теории поля
- 2. Физическая интерпретация div, rot, grad.
- 3. Некоторые дальнейшие интегральные формулы.
- § 3. Потенциальные поля
- 2. Необходимое условие потенциальности.
- 3. Критерий потенциальности векторного поля.
- 4. Топологическая структура области и потенциал.
- 5. Векторный потенциал. Точные и замкнутые формы.
- § 4. Примеры приложений
- 2. Уравнение неразрывности.
- 3. Основные уравнения динамики сплошной среды.
- 4. Волновое уравнение.
- ГЛАВА XV. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ НА МНОГООБРАЗИЯХ
- 2. Алгебра кососимметрических форм.
- 3. Линейные отображения линейных пространств и сопряженные отображения сопряженных пространств.
- § 2. Многообразие
- 2. Гладкие многообразия и гладкие отображения.
- 3. Ориентация многообразия и его края.
- 4. Разбиение единицы и реализация многообразий в виде поверхностей в R^n.
- § 3. Дифференциальные формы и их интегрирование на многообразиях
- 2. Дифференциальная форма на многообразии.
- 3. Внешний дифференциал.
- 4. Интеграл от формы по многообразию.
- § 4. Замкнутые и точные формы на многообразии
- 2. Гомологии и когомологии.
- ГЛАВА XVI. РАВНОМЕРНАЯ СХОДИМОСТЬ И ОСНОВНЫЕ ОПЕРАЦИИ АНАЛИЗА НАД РЯДАМИ И СЕМЕЙСТВАМИ ФУНКЦИЙ
- § 1. Поточечная и равномерная сходимость
- 2. Постановка основных вопросов.
- 3. Сходимость и равномерная сходимость семейства функций, зависящих от параметра.
- 4. Критерий Коши равномерной сходимости.
- § 2. Равномерная сходимость рядов функций
- 2. Признак Вейерштрасса равномерной сходимости ряда.
- § 3. Функциональные свойства предельной функции
- 2. Условия коммутирования двух предельных переходов.
- 3. Непрерывность и предельный переход.
- 4. Интегрирование и предельный переход.
- 5. Дифференцирование и предельный переход.
- § 4. Компактные и плотные подмножества пространства непрерывных функций
- 2. Метрическое пространство C(K,Y).
- 3. Теорема Стоуна.
- ГЛАВА XVII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- § 1. Собственные интегралы, зависящие от параметра
- 2. Непрерывность интеграла, зависящего от параметра.
- 3. Дифференцирование интеграла, зависящего от параметра.
- 4. Интегрирование интеграла, зависящего от параметра.
- § 2. Несобственные интегралы, зависящие от параметра
- 2. Предельный переход под знаком несобственного интеграла и непрерывность несобственного интеграла, зависящего от параметра.
- 3. Дифференцирование несобственного интеграла по параметру.
- 4. Интегрирование несобственного интеграла по параметру.
- § 3. Эйлеровы интегралы
- 2. Гамма-функция.
- 3. Связь между функциями В и Г.
- 4. Некоторые примеры.
- § 4. Свертка функций и начальные сведения об обобщенных функциях
- 2. Некоторые общие свойства свертки.
- 3. Дельтаобразные семейства функций и аппроксимационная теорема Вейерштрасса.
- 4. Начальные представления о распределениях
- § 5. Кратные интегралы, зависящие от параметра
- 2. Несобственные кратные интегралы, зависящие от параметра.
- 3. Несобственные интегралы с переменной особенностью.
- 4. Свертка, фундаментальное решение и обобщенные функции в многомерном случае.
- ГЛАВА XVIII. РЯД ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. Основные общие представления, связанные с понятием ряда Фурье
- 2. Коэффициенты Фурье.
- 3. Ряд Фурье.
- 4. Об одном важном источнике ортогональных систем функций в анализе.
- § 2. Тригонометрический ряд Фурье
- 2. Исследование поточечной сходимости тригонометрического ряда Фурье.
- 3. Гладкость функции и скорость убывания коэффициентов Фурье.
- 4. Полнота тригонометрической системы
- § 3. Преобразование Фурье
- 2. Регулярность функции и скорость убывания ее преобразования Фурье.
- 3. Важнейшие аппаратные свойства преобразования Фурье.
- 4. Примеры приложений.
- ГЛАВА XIX. АСИМПТОТИЧЕСКИЕ РАЗЛОЖЕНИЯ
- § 1. Асимптотическая формула и асимптотический ряд
- 2. Общие сведения об асимптотических рядах.
- 3. Степенные асимптотические ряды.
- § 2. Асимптотика интегралов (метод Лапласа)
- 2. Принцип локализации для интеграла Лапласа.
- 3. Канонические интегралы и их асимптотика.
- 4. Главный член асимптотики интеграла Лапласа.
- 5. Асимптотические разложения интегралов Лапласа.
- ЛИТЕРАТУРА
- УКАЗАТЕЛЬ ОСНОВНЫХ ОБОЗНАЧЕНИЙ