| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
Целью настоящей главы является рассмотрение свойств и методов решения начально-краевых задач для уравнения колебаний

Это уравнение мы будем рассматривать как с постоянными, так и с переменными коэффициентами, в ограниченной области и в неограниченном пространстве. Причем рассмотрение будет одновременно проводиться для случая как одной, так и многих пространственных переменных.
Мы начнем с рассмотрения обоснования постановки начально-краевой задачи для уравнения колебаний в ограниченной области.
§ 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
Пусть задана ограниченная область  с кусочно-гладкой границей
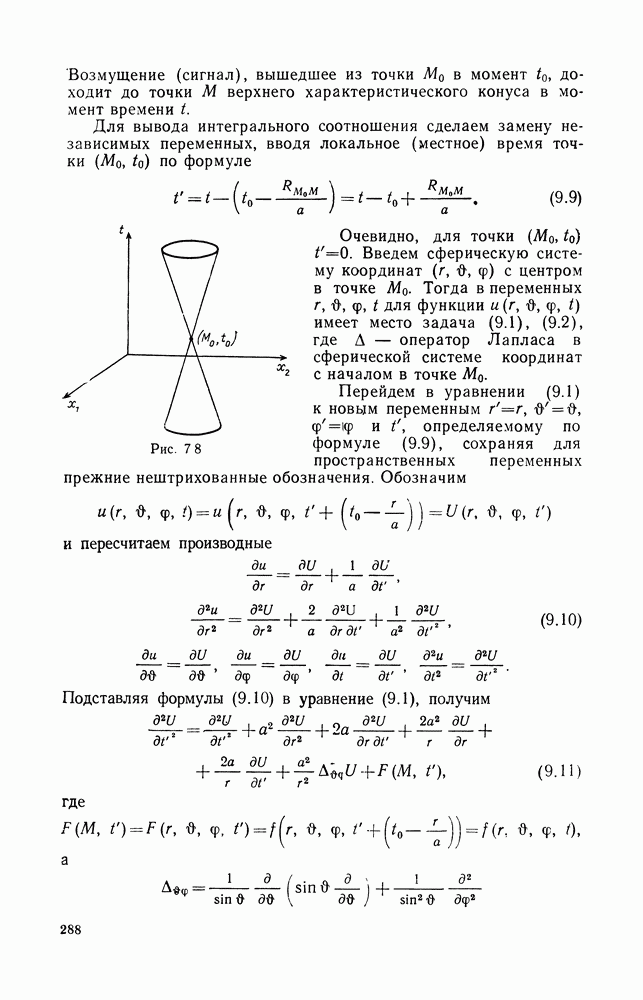
с кусочно-гладкой границей  допускающей применение формул Грина. Начально-краевая задача для уравнения колебаний
допускающей применение формул Грина. Начально-краевая задача для уравнения колебаний  области
области  заключается в определении в цилиндре
заключается в определении в цилиндре  функции
функции  удовлетворяющей уравнению колебаний, начальным и граничному условиям:
удовлетворяющей уравнению колебаний, начальным и граничному условиям:

где 
Определение классического решения задачи (1.1) — (1.3) было дано в гл. III. Напомним его.
Определение. Классическим решением начально-краевой задачи (1.1) — (1.3) называется функция  непрерывная вместе с первыми производными в замкнутом цилиндре
непрерывная вместе с первыми производными в замкнутом цилиндре  имеющая непрерывные производные второго порядка в открытом цилиндре
имеющая непрерывные производные второго порядка в открытом цилиндре  удовлетворяющая в
удовлетворяющая в  уравнению (1.1), начальным условиям (1.2) и граничному условию (1.3).
уравнению (1.1), начальным условиям (1.2) и граничному условию (1.3).
Если граничное условие (1.3) есть условие Дирихле  то непрерывность первых производных по
то непрерывность первых производных по  в замкнутой области
в замкнутой области  не требуется.
не требуется.
Заметим, что для существования классического решения необходимо (но недостаточно) выполнение условия согласования начального и граничного условий следующего вида:

Будем предполагать, что  и
и  причем а
причем а 
В силу линейности начально-краевой задачи (1.1) — (1.3) можно провести ее редукцию и представить решение  в виде суммы решений трех задач (см. гл. III):
в виде суммы решений трех задач (см. гл. III):

 -решение начально-краевой задачи для однородного уравнения колебаний с неоднородными начальными и однородными граничными условиями,
-решение начально-краевой задачи для однородного уравнения колебаний с неоднородными начальными и однородными граничными условиями,  -решение начально-краевой задачи для неоднородного уравнения колебаний с однородными начальными и граничными условиями,
-решение начально-краевой задачи для неоднородного уравнения колебаний с однородными начальными и граничными условиями,  решение начально-краевой задачи для однородного уравнения колебаний с однородными начальными и неоднородными граничными условиями. Причем с помощью методов, изложенных в гл. III, третья задача может быть сведена к первым двум. Поэтому в этой главе мы сосредоточим внимание на построении и изучении решений первых двух задач.
решение начально-краевой задачи для однородного уравнения колебаний с однородными начальными и неоднородными граничными условиями. Причем с помощью методов, изложенных в гл. III, третья задача может быть сведена к первым двум. Поэтому в этой главе мы сосредоточим внимание на построении и изучении решений первых двух задач.
§ 2. ТЕОРЕМА ЕДИНСТВЕННОСТИ
Докажем следующую теорему.
Теорема 7.1. Задача (1.1) — (1.3) может иметь только одно классическое решение.
Доказательство. Предположим, что задача (1.1) — (1.3) имеет два классических решения:  Рассмотрим их разность:
Рассмотрим их разность:

В силу линейности задачи (1.1) — (1.3) функция  является классическим решением следующей однородной начальнокраевой задачи:
является классическим решением следующей однородной начальнокраевой задачи:


где 
Используя функцию  построим интеграл
построим интеграл

Функция  неотрицательна:
неотрицательна:  и в силу начальных условий (2.2)
и в силу начальных условий (2.2)

Покажем, что интеграл  не изменяется во времени. Для этого вычислим его производную (дифференцирование по
не изменяется во времени. Для этого вычислим его производную (дифференцирование по  под знаком интеграла в (2.4) возможно)
под знаком интеграла в (2.4) возможно)

Согласно первой формуле Грина (см. (2.2), § 2 гл. III)

Подставляя (2.7) в (2.6) и учитывая уравнение (2.1), получаем

Для первой краевой задачи  и для второй краевой задачи
и для второй краевой задачи  в силу (2.3) из (2.8) находим
в силу (2.3) из (2.8) находим  Следовательно,
Следовательно,  Согласно
Согласно  Поэтому
Поэтому  при всех 0. Для третьей краевой задачи
при всех 0. Для третьей краевой задачи  согласно (2.3) и (2.8) получаем
согласно (2.3) и (2.8) получаем

Отсюда

Следовательно,

Из (2.5) и (2.2) следует, что  Поэтому при всех
Поэтому при всех 

Так как  отсюда вытекает, что
отсюда вытекает, что  при всех
при всех 
Итак, для всех трех краевых задач  Учитывая выражение (2.4) для
Учитывая выражение (2.4) для  получаем
получаем

Следовательно,  В силу
В силу  т. е.
т. е.  Таким образом, задача (2.1) — (2.3) имеет только тривиальное решение, а решение задачи (1.1) — (1.3) единственно.
Таким образом, задача (2.1) — (2.3) имеет только тривиальное решение, а решение задачи (1.1) — (1.3) единственно.
Замечания.
1) Доказательство теоремы единственности не зависит от размерности пространственной области 
2) Используемый при доказательстве теоремы 7.1 интеграл  имеет физический смысл полной (кинетической и потенциальной) энергии колебаний системы. Второе слагаемое в левой части формулы (2.9) в случае граничных условий третьего рода имеет физический смысл энергии упругого закрепления.
имеет физический смысл полной (кинетической и потенциальной) энергии колебаний системы. Второе слагаемое в левой части формулы (2.9) в случае граничных условий третьего рода имеет физический смысл энергии упругого закрепления.
§ 3. УСТОЙЧИВОСТЬ РЕШЕНИЯ
С помощью интеграла энергии  введенного в предыдущем параграфе, можно доказать устойчивость в пространстве
введенного в предыдущем параграфе, можно доказать устойчивость в пространстве  классического решения начально-краевой задачи (1.1) — (1.3) по правой части уравнения и начальным условиям. Напомним, что, как было показано в гл. III при рассмотрении общей схемы метода разделения переменных, задача с неоднородными граничными условиями всегда может быть сведена к задаче с однородными граничными условиями.
классического решения начально-краевой задачи (1.1) — (1.3) по правой части уравнения и начальным условиям. Напомним, что, как было показано в гл. III при рассмотрении общей схемы метода разделения переменных, задача с неоднородными граничными условиями всегда может быть сведена к задаче с однородными граничными условиями.
Мы проведем доказательство теоремы устойчивости для одномерной начально-краевой задачи на отрезке:

 постоянный коэффициент. Напомним, что, когда задача (3.1), (3.2) является математической моделью задачи о продольных колебаниях упругого стержня,
постоянный коэффициент. Напомним, что, когда задача (3.1), (3.2) является математической моделью задачи о продольных колебаниях упругого стержня,  где
где  линейная плотность стержня,
линейная плотность стержня,  коэффициент упругости.
коэффициент упругости.
Теорема 7.2. Решение задачи (3.1) — (3.3) устойчиво в пространстве  по правой части и начальным данным.
по правой части и начальным данным.
Доказательство. Составим функцию (интеграл энергии)

Для интеграла (3.4) выполнены условия дифференцируемости по параметру. Продифференцировав по параметру  получим
получим

где штрих означает производную по 
Второй интеграл в правой части формулы (3.5) проинтегрируем по частям, учитывая, что в силу граничных условий (3.3) подстановки обратятся в нуль. В результате, учитывая уравнение (3.1), будем иметь

и, используя неравенство Коши-Буняковского, получим

где норма в пространстве  определяется следующим образом:
определяется следующим образом:

С другой стороны, из формулы (3.4) вытекает, что

Из неравенств (3.6) и (3.7) следует неравенство

интегрируя которое по  получим
получим

Формулы (3.7) и (3.9) дают

Продифференцируем по  квадрат нормы функции
квадрат нормы функции 

и применим неравенство Коши-Буняковского

Отсюда в силу неравенства (3.10) получим неравенство

которое после интегрирования от 0 до  примет вид
примет вид

Двойной интеграл при  легко оценивается:
легко оценивается:

Учтем теперь, что

и поэтому

Окончательно при  из неравенств (3.11) и (3.13) получаем
из неравенств (3.11) и (3.13) получаем

Последнее неравенство означает устойчивость решения задачи  по правой части и начальным функциям: для любого
по правой части и начальным функциям: для любого  найдутся такие положительные постоянные
найдутся такие положительные постоянные  что если выполняются неравенства
что если выполняются неравенства  то
то  при
при 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
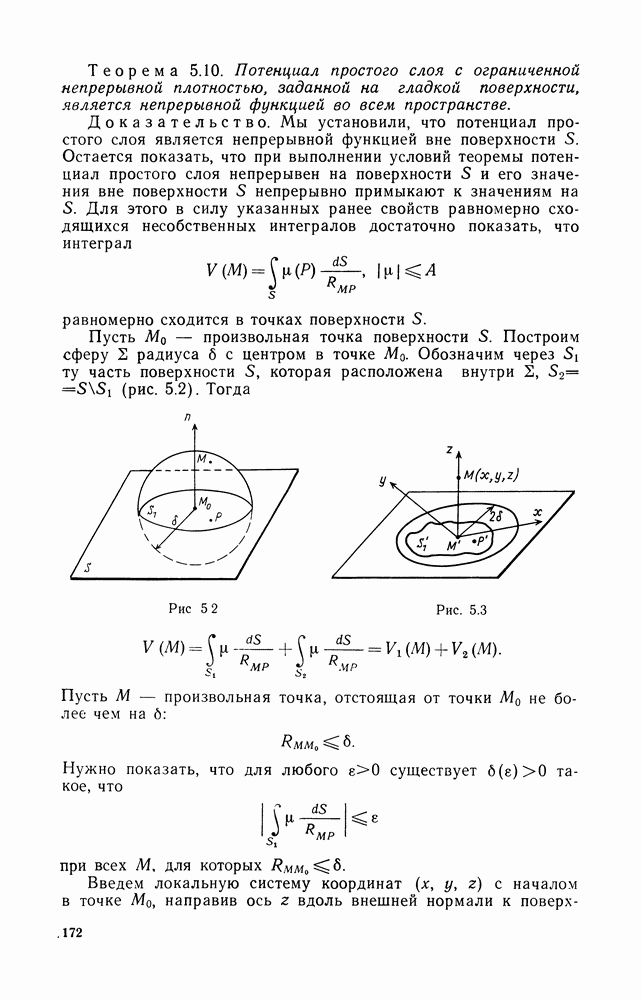
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
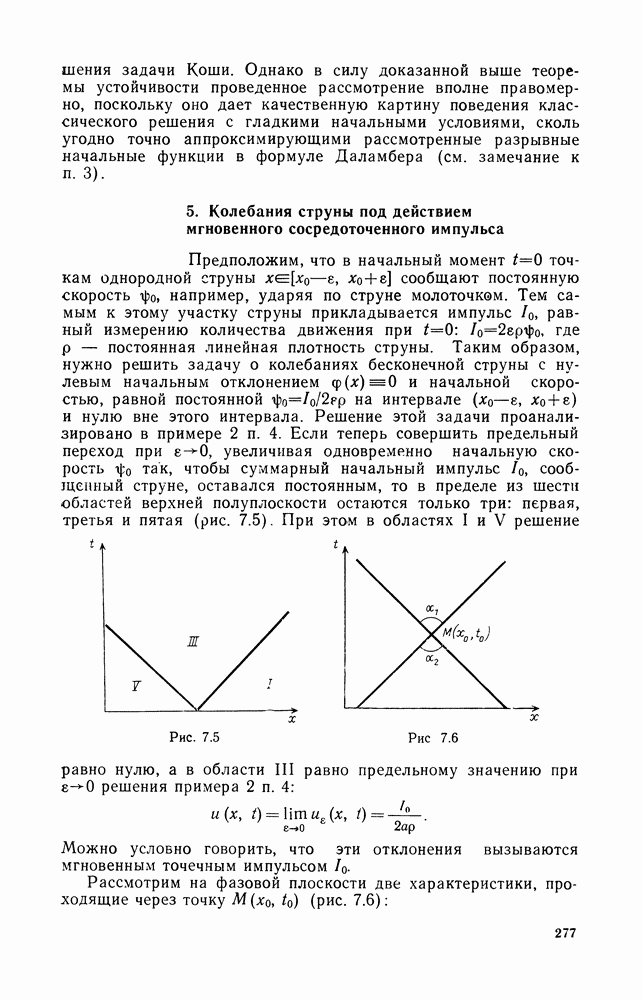
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
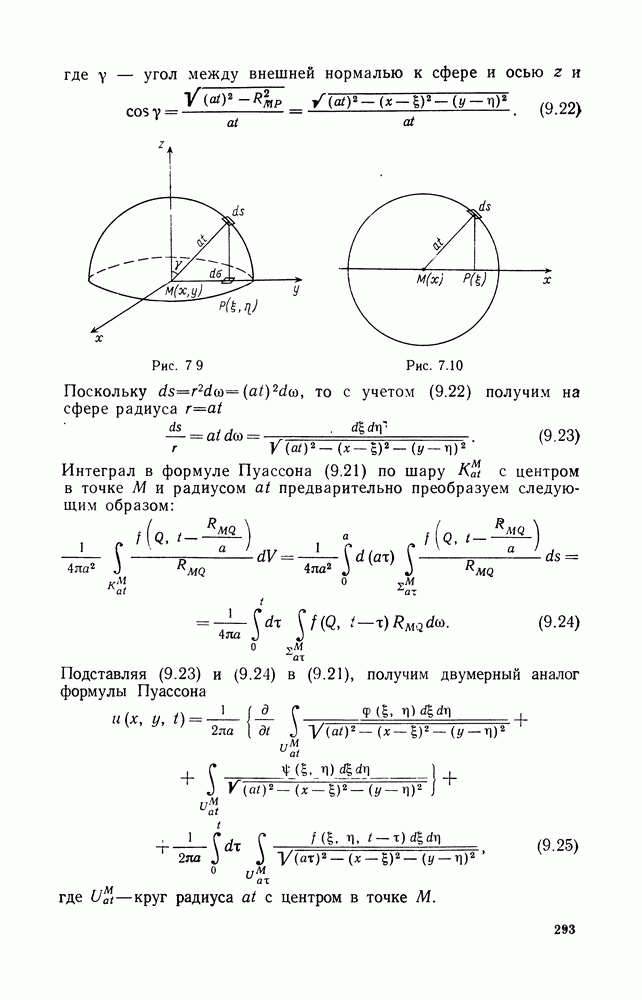
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
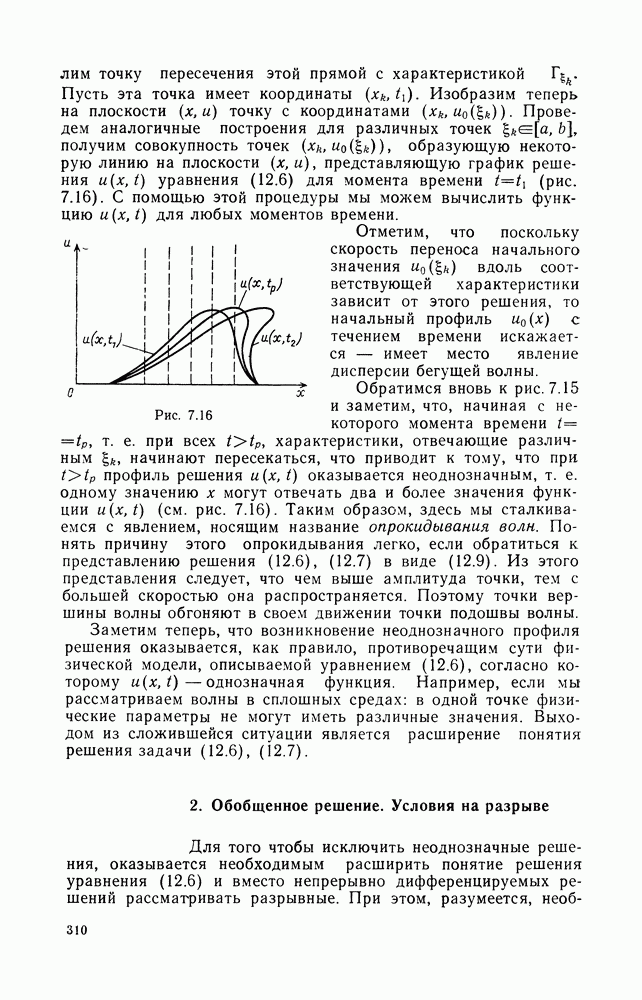
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
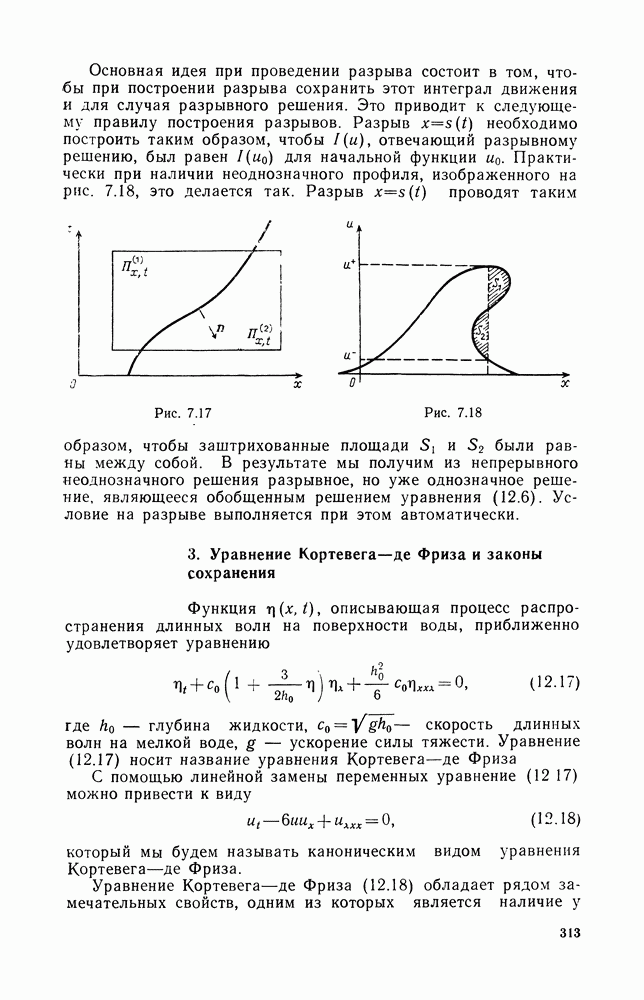
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ