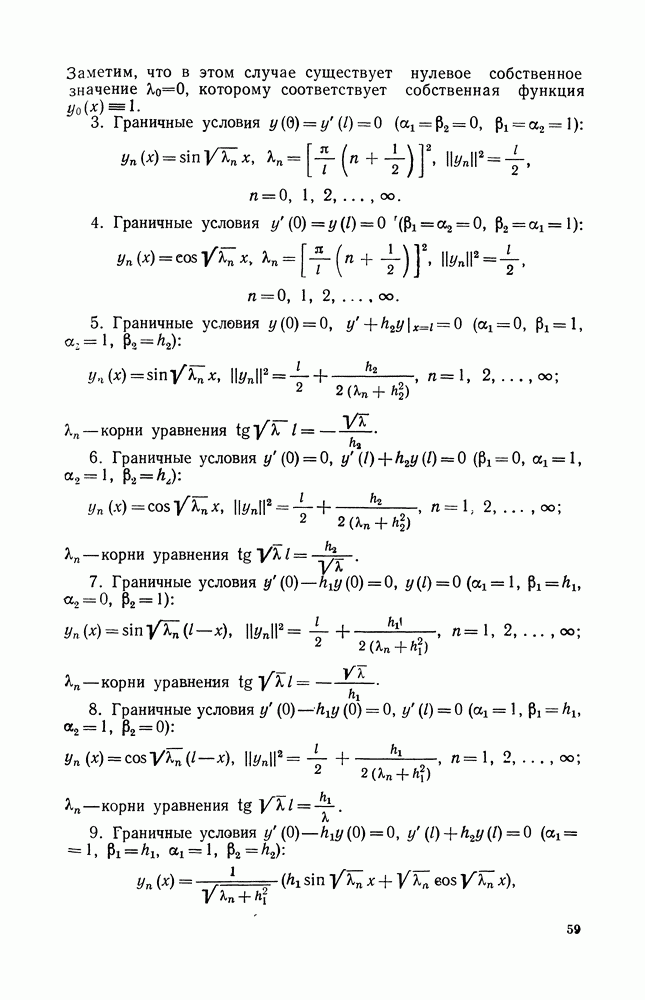| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
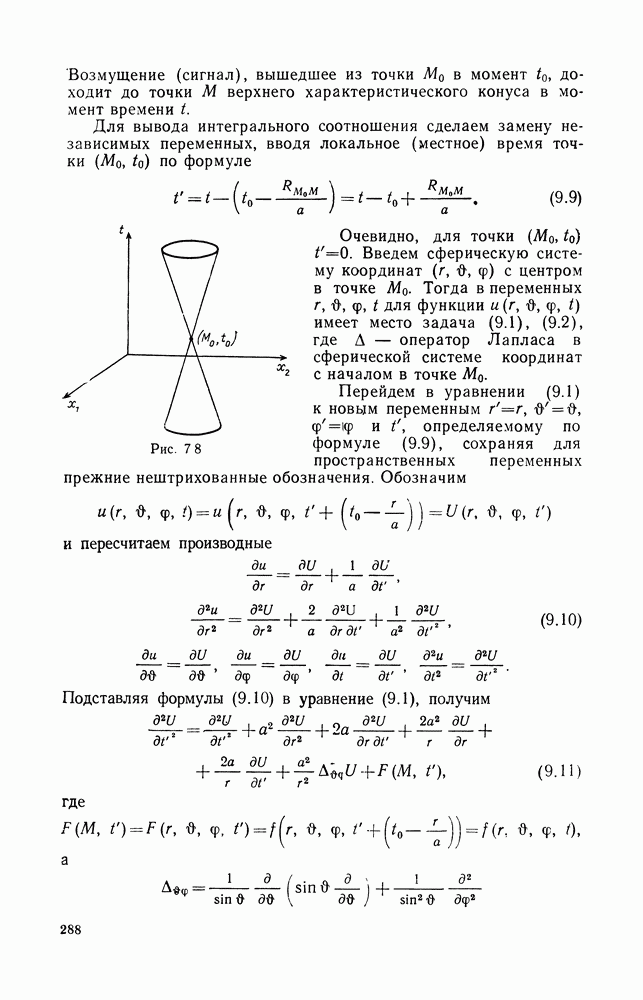
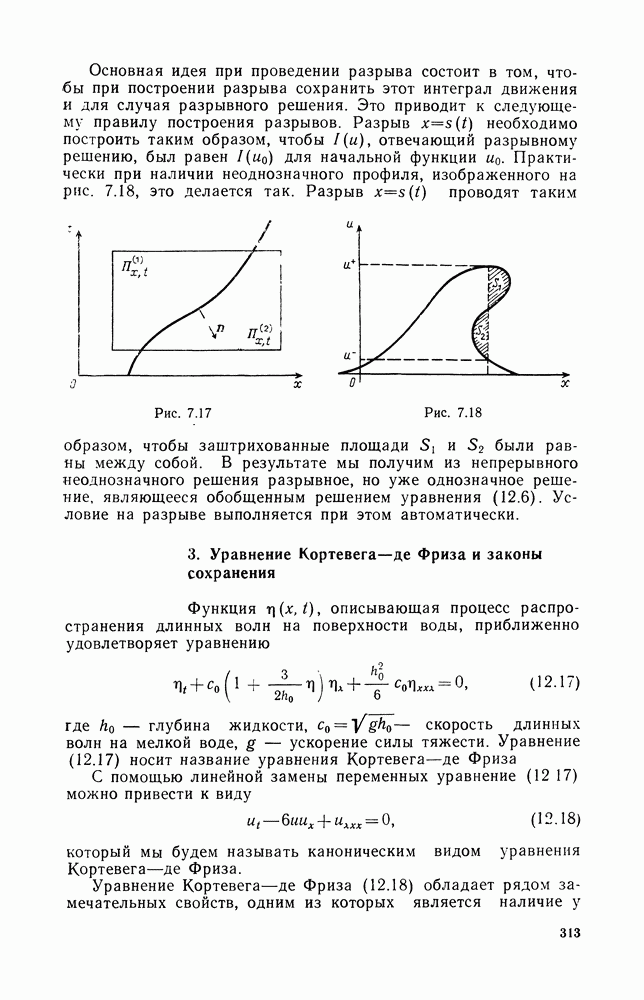
§ 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ ... В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
При изучении уравнения  в неограниченной области ситуация более сложная. Решения (2.3), (2.4), полученные в § 2, на бесконечности убывают одинаково. Требования равномерного стремления к нулю на бесконечности явно недостаточно для выделения единственного решения. Нужны более тонкие условия. В этом параграфе будут сформулированы сначала физические условия, а затем и математические условия на бесконечности, и доказана соответствующая теорема единственности.
в неограниченной области ситуация более сложная. Решения (2.3), (2.4), полученные в § 2, на бесконечности убывают одинаково. Требования равномерного стремления к нулю на бесконечности явно недостаточно для выделения единственного решения. Нужны более тонкие условия. В этом параграфе будут сформулированы сначала физические условия, а затем и математические условия на бесконечности, и доказана соответствующая теорема единственности.
1. Условия излучения
Рассмотрим в неограниченном пространстве уравнение

где  локальная функция. В § 2 было установлено, что решение уравнения (6.1) можно рассматривать как амплитуду установившихся гармонических колебаний (волн), создаваемых локальным источником с амплитудой
локальная функция. В § 2 было установлено, что решение уравнения (6.1) можно рассматривать как амплитуду установившихся гармонических колебаний (волн), создаваемых локальным источником с амплитудой  Поскольку функция
Поскольку функция  локальна, то источники волн расположены в конечной области пространства, и от этих источников на бесконечность уходят волны, которые вдали от источников ведут себя как уходящие сферические волны. Поэтому физическим условием, выделяющим единственное решение уравнения
локальна, то источники волн расположены в конечной области пространства, и от этих источников на бесконечность уходят волны, которые вдали от источников ведут себя как уходящие сферические волны. Поэтому физическим условием, выделяющим единственное решение уравнения  является следующее требование: найти решение, соответствующее уходящим на бесконечность волнам. Теперь нужно
является следующее требование: найти решение, соответствующее уходящим на бесконечность волнам. Теперь нужно
оформить это требование математически, т. е. сформулировать такие математические условия, которые бы выделяли единственное решение уравнения (6.1) (соответствующее уходящим на бесконечность волнам).
Чтобы сформулировать эти условия, снова рассмотрим уравнение колебаний

В одномерном случае оно имеет вид

и допускает решение в виде плоских волн:

распространяющейся в положительном направлении оси х, и

распространяющейся в отрицательном направлении оси х. Легко проверить, что каждая из них удовлетворяет «своему» соотношению:

и не удовлетворяет «чужому». Если рассматривать установившиеся гармонические волны с временной зависимостью 

то эти соотношения принимают вид

для волны, распространяющейся в положительном направлении оси 

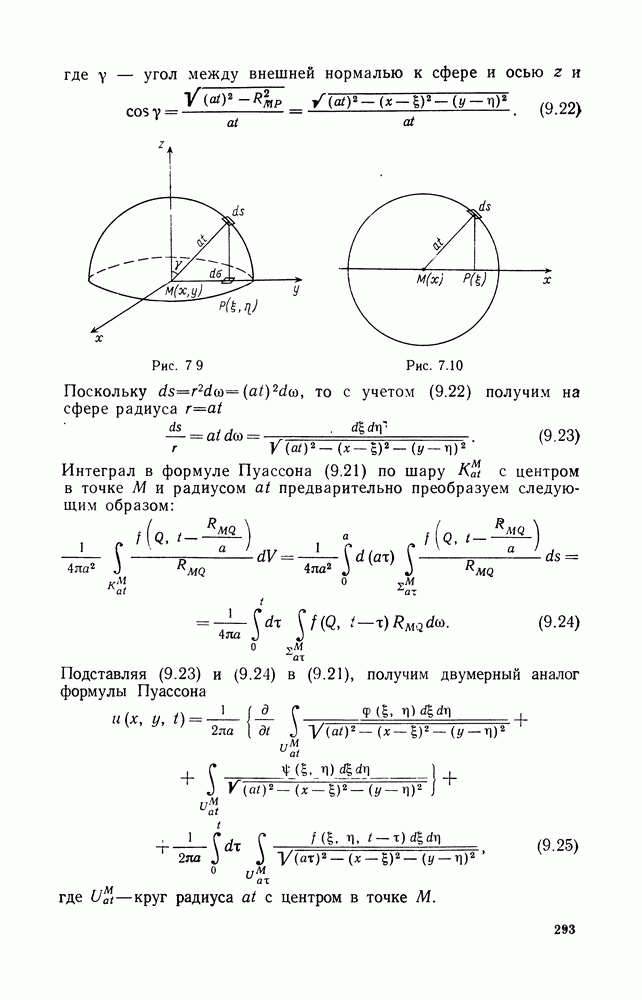
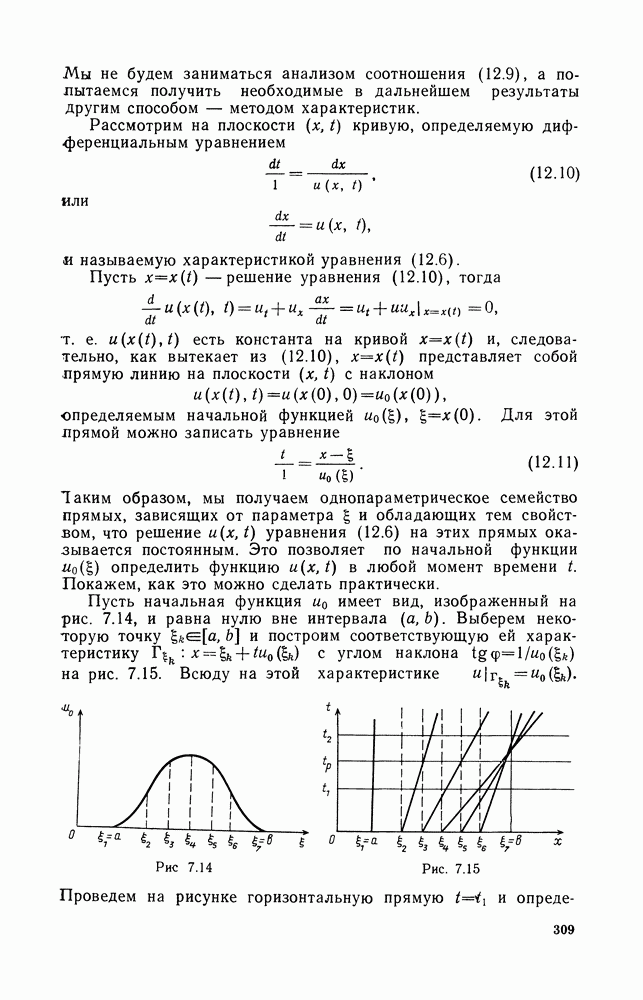
для волны, распространяющейся в отрицательном направлении оси х.
В этих формулах для нас существенным является то, что знак в этих условиях выделяет волну определенного направления.
Отметим, что при выбранной временной зависимости в виде комплекснозначной функции амплитуда установившихся колебаний также, вообще говоря, оказывается комплекснозначной функцией. В этом случае для нее часто применяется термин «комплексная амплитуда».
Рассмотрим теперь сферические волны, т. е. сферически-симметричные решения уравнения колебаний в пространстве:

Это уравнение можно переписать в виде

Следовательно, для функции  получается одномерное уравнение колебаний, общее решение которого имеет вид
получается одномерное уравнение колебаний, общее решение которого имеет вид

Итак, сферические волны в пространстве имеют вид

Первая из них —  представляет волну, уходящую на бесконечность (уходящая сферическая волна), вторая —
представляет волну, уходящую на бесконечность (уходящая сферическая волна), вторая —  — волну, приходящую из бесконечности.
— волну, приходящую из бесконечности.
По аналогии с одномерным случаем рассмотрим дифференциальные выражения

Для волны 

Функции  естественно считать ограниченными. Поэтому
естественно считать ограниченными. Поэтому

Аналогично

Опять рассмотрим установившиеся гармонические волны с временной зависимостью 

Тогда получаем соотношения для расходящихся волн:

и для сходящихся волн:

Опять видно, что условия, которым удовлетворяют сходящиеся и расходящиеся сферические волны, различны.
Поскольку физически ясно, что волна, созданная источниками, расположенными в конечной области, вдали от источников подобна уходящей сферической волне, то естественно предположить, что математическими условиями, выделяющими уходящие (расходящиеся) волны, будут условия

Условия (6.2) называются условиями излучения, или условиями Зоммерфельда. Первое из условий (6.2) означает, что  при
при  ведет себя как сферическая волна, второе — что эта волна, уходящая на бесконечность. Далее мы покажем, что условия излучения (6.2) действительно выделяют единственное решение уравнения (6.1).
ведет себя как сферическая волна, второе — что эта волна, уходящая на бесконечность. Далее мы покажем, что условия излучения (6.2) действительно выделяют единственное решение уравнения (6.1).
Сначала покажем, что условия (6.2) из фундаментальных решений (2.3), (2.4) выделяют только одно.
Введем сферическую систему координат. Пусть точка  имеет координаты
имеет координаты  точка
точка  Тогда
Тогда

где  Следовательно, при
Следовательно, при  и фиксированном значении
и фиксированном значении 

Поэтому 

независимо от положения точки  находящейся на конечном расстоянии
находящейся на конечном расстоянии  от начала координат.
от начала координат.
Следовательно, решение  при фиксированном положении точкй
при фиксированном положении точкй  -оо удовлетворяет условиям излучения (6.2). Легко проверить, что два других решения (2.3), (2.4) условиям (6.2) не удовлетворяют. Таким образом, условия (6.2) выделяют единственное решение из (2.3), (2.4).
-оо удовлетворяет условиям излучения (6.2). Легко проверить, что два других решения (2.3), (2.4) условиям (6.2) не удовлетворяют. Таким образом, условия (6.2) выделяют единственное решение из (2.3), (2.4).
Теорема 8.7. Уравнение  где
где  локальная функция, в неограниченном пространстве не может иметь более одного решения, удовлетворяющего на бесконечности условиям излучения
локальная функция, в неограниченном пространстве не может иметь более одного решения, удовлетворяющего на бесконечности условиям излучения

Доказательство. Пусть существуют два решения  поставленной задачи. Функция
поставленной задачи. Функция  является решением однородного уравнения
является решением однородного уравнения  удовлетворяющим условиям излучения на бесконечности.
удовлетворяющим условиям излучения на бесконечности.
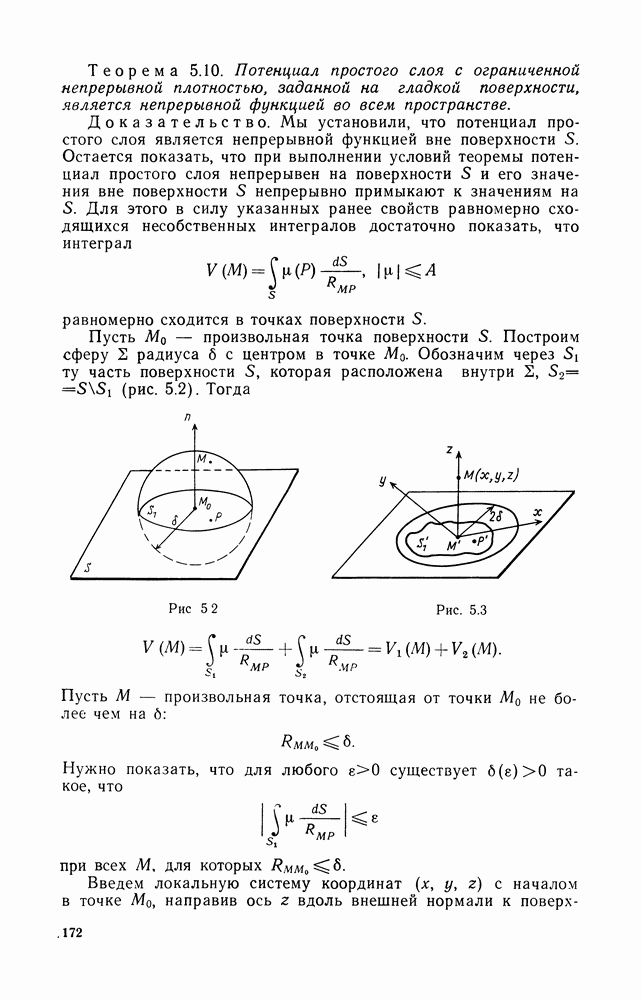
Пусть  сфера радиуса
сфера радиуса  с центром в начале координат. Внутри шара, ограниченного сферой
с центром в начале координат. Внутри шара, ограниченного сферой  справедлива третья формула Грина
справедлива третья формула Грина

Заметим, что взята третья формула Грина с тем фундаментальным решением, которое удовлетворяет условиям излучения на бесконечности. Оценим подынтегральную функцию в (6.3) при  Используя условия на бесконечности, получим
Используя условия на бесконечности, получим

Эта оценка показывает, что при  интеграл по
интеграл по  в (6.3) стремится к нулю. Следовательно,
в (6.3) стремится к нулю. Следовательно,  т. е.
т. е. 
Заметим, что условие  при
при  является следствием второго условия
является следствием второго условия  доказательстве этого факта мы не останавливаемся. Это условие нами сохранено для упрощения доказательства теоремы единственности.
доказательстве этого факта мы не останавливаемся. Это условие нами сохранено для упрощения доказательства теоремы единственности.
Рассуждениями, аналогичными тем, которые использовались при доказательстве этой теоремы, можно показать, что
для функций, удовлетворяющих условиям излучения на бесконечности, справедливы формулы Грина во внешней неограниченной области.
Как мы установили, фундаментальное решение

удовлетворяет условиям излучения. Поэтому тем же условиям на бесконечности будет удовлетворять и объемный потенциал

построенный на его основе. Отсюда сразу следует, что при соответствующих ограничениях на  функция
функция

является единственным решением уравнения  удовлетворяющим условиям излучения на бесконечности.
удовлетворяющим условиям излучения на бесконечности.
С помощью установленной формулы Грина для уравнения Гельмгольца во внешней неограниченной области могут быть доказаны и теоремы единственности решений внешних краевых задач для этого уравнения, удовлетворяющих условиям излучения на бесконечности. Однако эти доказательства требуют привлечения дополнительных аналитических свойств решений однородного уравнения Гельмгольца и ряда вспомогательных рассмотрений, которые здесь приводить не будем.
Сделаем еще одно важное замечание об условиях излучения. Условие

согласовано с выбранной временной зависимостью  и выделяет уходящую волну только при этой временной зависимости. Если временная зависимость выбрана в виде
и выделяет уходящую волну только при этой временной зависимости. Если временная зависимость выбрана в виде  то условие, выделяющее уходящую волну, имеет вид
то условие, выделяющее уходящую волну, имеет вид

Это означает, что если временная гармоническая зависимость известна заранее, то в соответствии с ней выбираются условия на бесконечности.
Если временная зависимость заранее не известна, то на бесконечности можно поставить как условие (6.4), так и условие (6.5). И то и другое условия будут выделять единственное
решение уравнения  но эти решения будут различны. А при физической интерпретации решения следует учитывать нужную временную зависимость, которая соответствует расходящимся волнам.
но эти решения будут различны. А при физической интерпретации решения следует учитывать нужную временную зависимость, которая соответствует расходящимся волнам.
В двумерном случае условия излучения имеют вид

при временной зависимости  или
или

при временной зависимости  Первое условие в (6.6) и (6.7) также является следствием второго. Доказательство теорем единственности проводится аналогично.
Первое условие в (6.6) и (6.7) также является следствием второго. Доказательство теорем единственности проводится аналогично.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
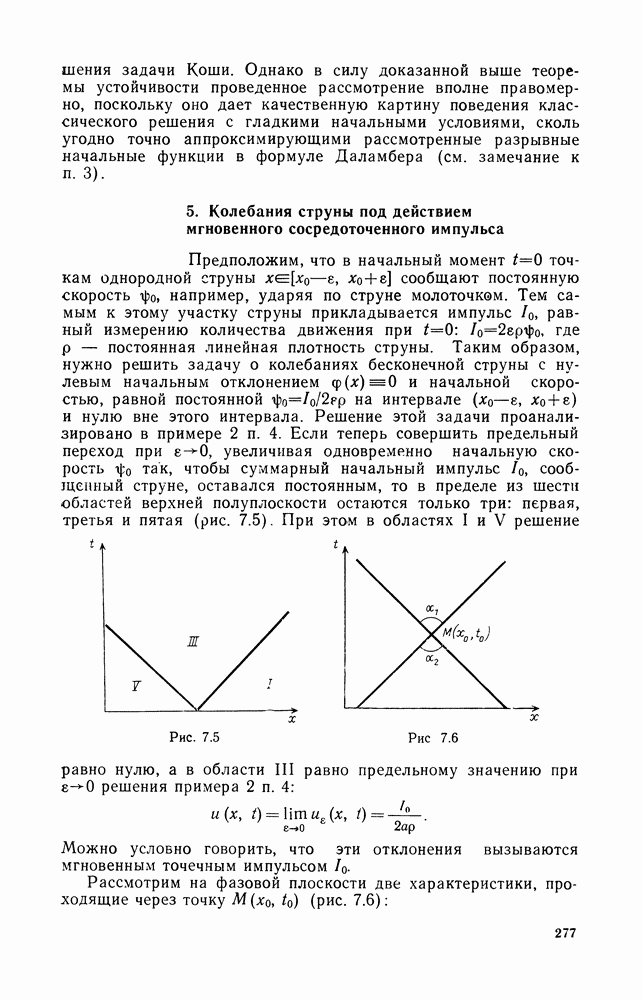
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
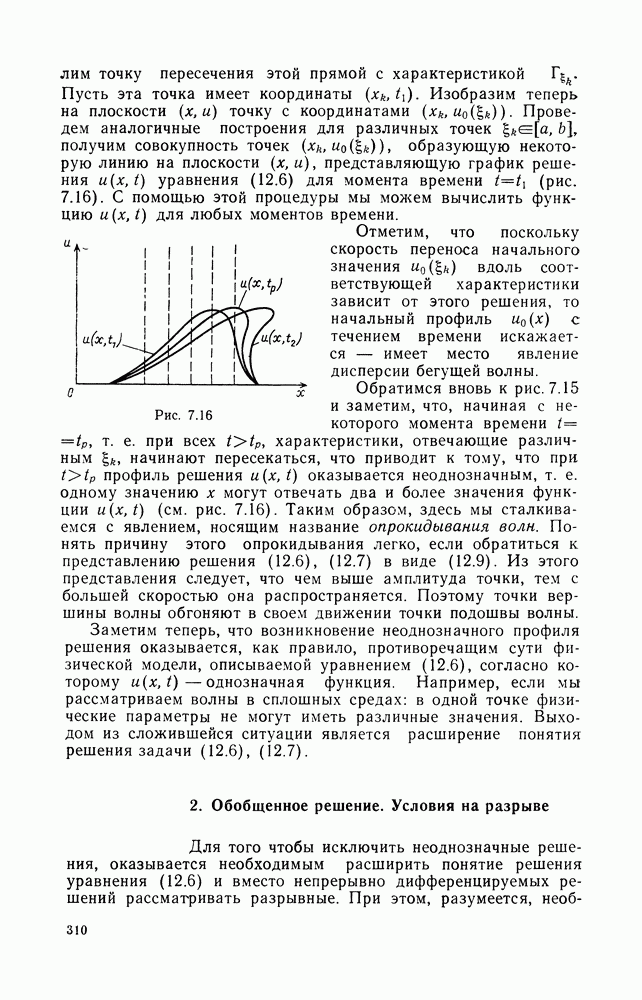
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ