| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
До сих пор мы рассматривали процессы, математической моделью которых является начально-краевая задача для линейного уравнения параболического типа с линейными дополнительными условиями. Простейшим примером является одномерное уравнение теплопроводности (7.7). В этом параграфе мы кратко остановимся на математических моделях
физических процессов, описываемых одномерным квазилинейным уравнением теплопроводности, содержащим источник объемного выделения тепла:

где  некоторые постоянные. Функция
некоторые постоянные. Функция  обозначает температуру сплошной среды в каждой ее точке в момент времени
обозначает температуру сплошной среды в каждой ее точке в момент времени  Первый член в правой части уравнения (13.1) описывает механизм нелинейной теплопроводности, причем коэффициент теплопроводности
Первый член в правой части уравнения (13.1) описывает механизм нелинейной теплопроводности, причем коэффициент теплопроводности  зависит от температуры по нелинейному закону. Второй член в правой части уравнения (13.1) описывает процесс энерговыделения. Фактически — это мощность источника тепла. Этот член описывает процесс горения сплошной среды. Интенсивность горения зависит от температуры по нелинейному закону, причем безразмерный показатель
зависит от температуры по нелинейному закону. Второй член в правой части уравнения (13.1) описывает процесс энерговыделения. Фактически — это мощность источника тепла. Этот член описывает процесс горения сплошной среды. Интенсивность горения зависит от температуры по нелинейному закону, причем безразмерный показатель  больше единицы (сверхинтенсивное горение).
больше единицы (сверхинтенсивное горение).
Уравнение (13.1) мы будем рассматривать на бесконечной прямой  Для полной формулировки задачи инициирования процесса горения необходимо задать начальное тепловое возмущение. В результате приходим к следующей задаче Коши:
Для полной формулировки задачи инициирования процесса горения необходимо задать начальное тепловое возмущение. В результате приходим к следующей задаче Коши:

Отметим, что для корректной постановки задачи (13.2), (13.3) функция  должна отвечать некоторым дополнительным требованиям. Задание с помощью функции
должна отвечать некоторым дополнительным требованиям. Задание с помощью функции  распределенной в пространстве специальным образом начальной тепловой энергии приводит к горению среды, причем ввиду нелинейности уравнения (13.2) интенсивность горения, а также теплоперенос в различных участках прямой протекают различным образом. С течением времени в среде возникают меняющиеся в пространстве и во времени распределения температуры, называемые обычно тепловыми структурами.
распределенной в пространстве специальным образом начальной тепловой энергии приводит к горению среды, причем ввиду нелинейности уравнения (13.2) интенсивность горения, а также теплоперенос в различных участках прямой протекают различным образом. С течением времени в среде возникают меняющиеся в пространстве и во времени распределения температуры, называемые обычно тепловыми структурами.
Физический процесс, описываемый уравнением, заключается в конкуренции двух нелинейных процессов. С одной стороны, наличие нелинейной теплопроводности приводит к выравниванию тепловых неоднородностей, к созданию стационарного распределения температуры. С другой стороны, в процессе горения происходит выделение тепловой энергии, что может приводить к росту температуры. Причем чем выше температура, тем выше интенсивность тепловыделения. Но в то же время с ростом температуры увеличивается и коэффициент теплопроводности.
Одним из главных результатов конкуренции нелинейных процессов теплопередачи и тепловыделения является эффект локализации процесса горения, который в данном конкретном случае выступает как проявление процесса самоорганизации
нелинейной диссипативной среды. Он может приводить к возникновению в среде целого набора различных структур, не взаимодействующих друг с другом.
С помощью преобразования переменных

запишем уравнение (13.2) в безразмерном виде (черточки над  опускаем):
опускаем):

Свойства решений уравнения (13.4) существенно различаются в случаях 
Рассмотрим частный случай уравнения (13.4), когда в среде горения нет и тепло распространяется за счет теплопроводности:

Уравнение (13.5) имеет частные решения специального вида, так называемые точные автомодельные решения, выражающиеся через функцию  одного аргумента, который в свою очередь является определенной комбинацией независимых переменных
одного аргумента, который в свою очередь является определенной комбинацией независимых переменных  Чтобы получить такое решение уравнения (13.5), будем искать
Чтобы получить такое решение уравнения (13.5), будем искать  в виде
в виде

где

Непосредственной подстановкой легко убедиться, что функция  данного вида удовлетворяет уравнению (13.5), если функция
данного вида удовлетворяет уравнению (13.5), если функция  является решением обыкновенного дифференциального уравнения
является решением обыкновенного дифференциального уравнения

где  в свою очередь, — решение обыкновенного дифференциального уравнения
в свою очередь, — решение обыкновенного дифференциального уравнения

Одно из полученных таким путем частных автомодельных решений уравнения (13.5) — решение Зельдовича-Компанейца-Баренблатта - имеет следующий вид:

где  физический смысл постоянной
физический смысл постоянной  будет ясен из дальнейшего.
будет ясен из дальнейшего.
Функция  для различных моментов времени изображена на рис. 6.2. За счет механизма нелинейной теплопроводности происходит быстрое растекание локального начального возмущения с максимальной температурой в точке
для различных моментов времени изображена на рис. 6.2. За счет механизма нелинейной теплопроводности происходит быстрое растекание локального начального возмущения с максимальной температурой в точке 

Рис. 6.2
В начальный момент времени  температура в точке
температура в точке  бесконечно велика, но в остальных точках бесконечной прямой она равна нулю:
бесконечно велика, но в остальных точках бесконечной прямой она равна нулю:  при
при  В точке
В точке  с течением времени температура уменьшается по закону
с течением времени температура уменьшается по закону  м в пределе при
м в пределе при  происходит выравнивание температуры по всей бесконечной прямой
происходит выравнивание температуры по всей бесконечной прямой  Решение (13.6) называется решением типа мгновенного точечного источника, поскольку функция
Решение (13.6) называется решением типа мгновенного точечного источника, поскольку функция  физически означает температуру точки х бесконечной прямой
физически означает температуру точки х бесконечной прямой  в момент времени
в момент времени  если возбуждение осуществлялось мгновенным точечным источником мощности
если возбуждение осуществлялось мгновенным точечным источником мощности  действовавшим в точке
действовавшим в точке  в момент времени
в момент времени  Таким образом, функция
Таким образом, функция  является аналогом фундаментального решения уравнения теплопроводности, введенного в § 7. Однако решение (13.6) существенно отличается от фундаментального решения (7.16). Функция
является аналогом фундаментального решения уравнения теплопроводности, введенного в § 7. Однако решение (13.6) существенно отличается от фундаментального решения (7.16). Функция  в каждый момент времени
в каждый момент времени  является финитной, т. е. решение строго положительно на конечном интервале
является финитной, т. е. решение строго положительно на конечном интервале  Тем самым уравнение (13.5) описывает тепловые волны — тепловые процессы с конечной скоростью распространения возмущений. При этом есть координата правого фронта тепловой волны, а
Тем самым уравнение (13.5) описывает тепловые волны — тепловые процессы с конечной скоростью распространения возмущений. При этом есть координата правого фронта тепловой волны, а  координата левого фронта. Это принципиальное отличие механизма нелинейной теплопроводности, описываемого уравнением (13,5), от линейного механизма передачи тепла, описываемого уравнением (7.7). Отметим, что это свойство имеет место и при наличии в среде источников тепла вида
координата левого фронта. Это принципиальное отличие механизма нелинейной теплопроводности, описываемого уравнением (13,5), от линейного механизма передачи тепла, описываемого уравнением (7.7). Отметим, что это свойство имеет место и при наличии в среде источников тепла вида 
Пусть теперь в среде имеется источник тепловой энергии, соответствующий 

Если искать автомодельное решение (13.7) в виде

то для функции  получим обыкновенное дифференциальное уравнение
получим обыкновенное дифференциальное уравнение

откуда соответствующее автомодельное решение уравнения (13.7) получим в виде

где  время существования решения,
время существования решения,  длина носителя решения в любой момент времени. В отличие от решения Зельдовича-Компанейца-Баренблатта уравнения (13.5) решение (13.8) уравнения (13.7) локализовано в области
длина носителя решения в любой момент времени. В отличие от решения Зельдовича-Компанейца-Баренблатта уравнения (13.5) решение (13.8) уравнения (13.7) локализовано в области  вне которой температура остается равной нулю. Тепловые фронты структуры (13.8) неподвижны в течение всего времени ее существования:
вне которой температура остается равной нулю. Тепловые фронты структуры (13.8) неподвижны в течение всего времени ее существования:  координата правого фронта тепловой волны,
координата правого фронта тепловой волны,  координата левого фронта. При этом во всех точках интервала
координата левого фронта. При этом во всех точках интервала  температура неограниченно возрастает по мере приближения
температура неограниченно возрастает по мере приближения  к моменту
к моменту  В центре структуры
В центре структуры  температура растет по закону
температура растет по закону

Такие тепловые структуры называются режимами с обострением, а соответствующие решения уравнения (13.7) или более общего уравнения (13.2) называются неограниченными решениями.
Тепловая структура (13.8) называется локализованным  -режимом с обострением и представляет собой стоячую температурную волну.
-режимом с обострением и представляет собой стоячую температурную волну.
Рассмотрим теперь уравнение (13.2) при 

Фиксируем время существования  тепловой структуры и рассмотрим выражение
тепловой структуры и рассмотрим выражение

где  неизвестная функция. Подставив (13.10) в уравнение (13.9), получим, что На
неизвестная функция. Подставив (13.10) в уравнение (13.9), получим, что На  является решением нелинейного
является решением нелинейного
ного параболического уравнения (13.9), если функция  решение обыкновенного дифференциального уравнения
решение обыкновенного дифференциального уравнения

Это решение представляет собой функцию, строго положительную на интервале  и равную нулю вне его. Конкретный вид функции
и равную нулю вне его. Конкретный вид функции  и величину
и величину  определяющую положение фронтов соответствующей тепловой структуры, можно найти численно.
определяющую положение фронтов соответствующей тепловой структуры, можно найти численно.
Из формулы (13.10) вытекают следующие свойства изучаемой тепловой структуры. Во-первых, эта структура развивается в режиме с обострением. Значение максимальной температуры в центре  структуры неограниченно возрастает по закону
структуры неограниченно возрастает по закону

Во-вторых, в любой момент времени тепловая структура имеет конечные фронты в точках  которые определяются из равенства
которые определяются из равенства  Следовательно, правый и левый фронты движутся по законам
Следовательно, правый и левый фронты движутся по законам

В-третьих, из последней формулы следует, что фронты тепловой структуры движутся со все увеличивающейся скоростью, в пределе, в момент обострения  тепловая структура охватывает всю прямую
тепловая структура охватывает всю прямую  нагревая ее всюду до бесконечной температуры.
нагревая ее всюду до бесконечной температуры.
Такой процесс горения, описываемый уравнением (13.9), называется  -режимом.
-режимом.
И наконец, рассмотрим уравнение (13.2) при 

В этом уравнении мощность источника энерговыделения  при больших температурах выше, чем в
при больших температурах выше, чем в  -режиме
-режиме  и тем более
и тем более  -режиме
-режиме  Поэтому возникающие тепловые структуры должны быть локализованными, причем локализация должна проявляться более сильно, чем в
Поэтому возникающие тепловые структуры должны быть локализованными, причем локализация должна проявляться более сильно, чем в  -режиме горения с обострением.
-режиме горения с обострением.
Уравнение  допускает решение следующего вида:
допускает решение следующего вида:

где  время обострения решения. Подставив (13.12) в уравнение (13.11), получим уравнение для функции
время обострения решения. Подставив (13.12) в уравнение (13.11), получим уравнение для функции 

В отличие от случая  -режима функция
-режима функция  строго положительна всюду, причем при больших значениях
строго положительна всюду, причем при больших значениях  она имеет следующую асимптотику:
она имеет следующую асимптотику:

где  постоянная, которую можно найти численно.
постоянная, которую можно найти численно.
Из формулы (13.12) следует, что в отличие от  -режима решение (13.12) не может описывать локализацию процесса горения в строгом смысле. Локализация понимается в эффективном смысле. Решение растет со временем во всех точках, но неограниченный рост температуры в режиме с обострением имеет место только в одной точке
-режима решение (13.12) не может описывать локализацию процесса горения в строгом смысле. Локализация понимается в эффективном смысле. Решение растет со временем во всех точках, но неограниченный рост температуры в режиме с обострением имеет место только в одной точке  Развитие тепловой структуры приводит к тому, что температура прямой
Развитие тепловой структуры приводит к тому, что температура прямой  остается ограниченной во всех точках, за исключением точки
остается ограниченной во всех точках, за исключением точки  Температура ограничена сверху некоторым предельным распределением которое получается из (13.12) после предельного перехода
Температура ограничена сверху некоторым предельным распределением которое получается из (13.12) после предельного перехода 

Процесс горения, описываемый уравнением (13.11), называется  -режимом. В энергетическом смысле этот режим определяет еще более сильную локализацию тепла, чем в случае
-режимом. В энергетическом смысле этот режим определяет еще более сильную локализацию тепла, чем в случае  -режима. В
-режима. В  -режиме температура неограниченно растет на интервале длины
-режиме температура неограниченно растет на интервале длины  а в случае
а в случае  -режима — только в одной точке, и выделившаяся на развитой стадии горения тепловая энергия практически вся локализуется во все сужающейся со временем окрестности точки максимума температуры.
-режима — только в одной точке, и выделившаяся на развитой стадии горения тепловая энергия практически вся локализуется во все сужающейся со временем окрестности точки максимума температуры.
Итак, при различных показателях интенсивности горения развивающиеся в режиме обострения тепловые структуры принимают формы  и
и  -режимов, обладающие разными свойствами. Исследование нелинейных математических моделей эволюции диссипативных процессов в сплошных средах позволяет сделать вывод, что на развитой стадии более сложных существенно нестационарных процессов, как правило, обнаруживаются черты, свойственные одному из этих режимов.
-режимов, обладающие разными свойствами. Исследование нелинейных математических моделей эволюции диссипативных процессов в сплошных средах позволяет сделать вывод, что на развитой стадии более сложных существенно нестационарных процессов, как правило, обнаруживаются черты, свойственные одному из этих режимов.
Если задача допускает неограниченное решение, то она называется глобально (по времени) неразрешимой. Исследования пространственно-временной структуры неограниченных решений вблизи момента обострения связаны с широким использованием в практике физических экспериментов разнообразных эффектов, порождаемых сверхбыстрыми процессами, например эффекта самофокусировки световых пучков в нелинейных средах, коллапса ленгмюровских волн в плазме и др. Большое значение имеет исследование особых режимов сжатия в задачах, связанных с лазерным термоядерным синтезом.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
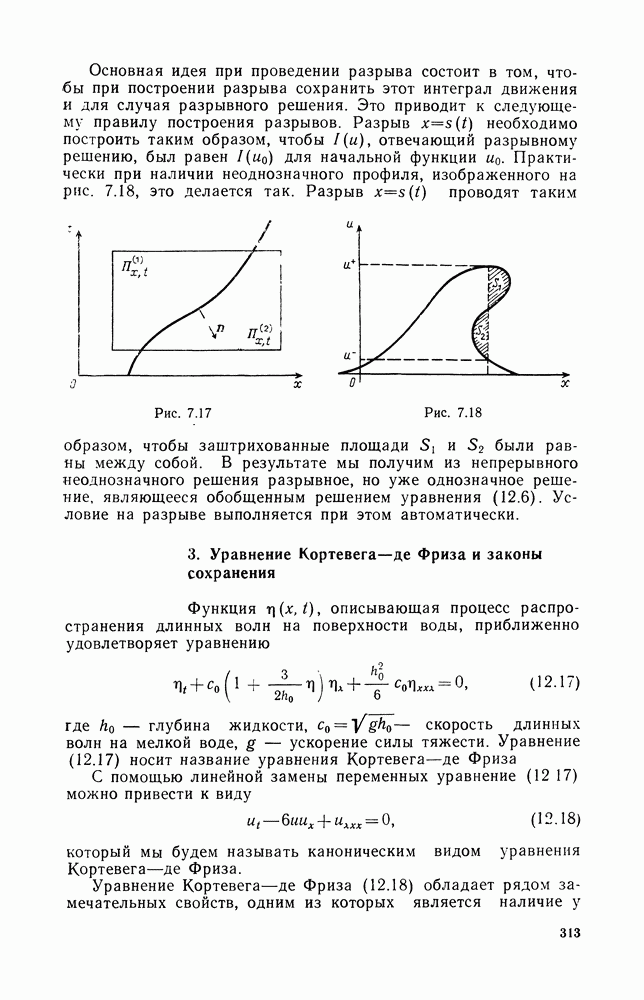
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ