| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
Рассмотрение следующей группы физических задач, характеризующих процессы переноса в среде тепла или вещества, начнем с вывода так называемого уравнения теплопроводности, описывающего процесс изменения теплового состояния тела. Построим математическую модель изменения под действием заданных физических условий температуры точек тела, занимающего объем  ограниченный поверхностью
ограниченный поверхностью 
Выделим в области  малый объем
малый объем  с границей
с границей  Обозначим через
Обозначим через  температуру тела
температуру тела  в точке
в точке  в момент времени
в момент времени  плотность тела,
плотность тела,  - удельную теплоемкость,
- удельную теплоемкость,  - коэффициент теплопроводности,
- коэффициент теплопроводности,  объемную плотность источников (стоков) тепла.
объемную плотность источников (стоков) тепла.
В дальнейшем нам понадобятся следующие экспериментально установленные физические закономерности.
Закон Фурье. Если температура тела распределена неравномерно, то в нем возникают тепловые потоки, направленные от более нагретых участков тела к менее нагретым.
Количество тепла  протекающее через площадку
протекающее через площадку  за промежуток времени
за промежуток времени  равно
равно

где  производная по нормали к площадке
производная по нормали к площадке 
Закон Ньютона. Количество тепла  протекающего в единицу времени через площадку а поверхности тела в окружающую среду, равно
протекающего в единицу времени через площадку а поверхности тела в окружающую среду, равно

где  температура окружающей среды, и — температура поверхности тела,
температура окружающей среды, и — температура поверхности тела,  коэффициент теплообмена.
коэффициент теплообмена.
Используем для вывода уравнения теплопроводности метод баланса. Запишем уравнение теплового баланса для выделенного малого объема 
Пусть за промежуток времени  температура объема
температура объема  изменилась на
изменилась на  При этом, как обычно, считаем объем столь малым, что в его пределах температуру можно считать постоянной. Количество тепла
При этом, как обычно, считаем объем столь малым, что в его пределах температуру можно считать постоянной. Количество тепла  которое нужно сообщить объему
которое нужно сообщить объему  в течение промежутка времени
в течение промежутка времени  для повышения его температуры на
для повышения его температуры на  равно
равно

Между объемом  и остальной частью тела
и остальной частью тела  через поверхность
через поверхность  происходит теплообмен, который согласно закону Фурье определяется формулой (2.1). Количество тепла
происходит теплообмен, который согласно закону Фурье определяется формулой (2.1). Количество тепла  участвующее в этом теплообмене, равно
участвующее в этом теплообмене, равно

где  производная по нормали к поверхности
производная по нормали к поверхности  внешней по отношению к области
внешней по отношению к области 
Предположим, что функции  являются достаточно гладкими, и преобразуем поверхностный интеграл в правой части формулы (2.4) к объемному с помощью теоремы Остроградского-Гаусса. В результате получим
являются достаточно гладкими, и преобразуем поверхностный интеграл в правой части формулы (2.4) к объемному с помощью теоремы Остроградского-Гаусса. В результате получим

Внутри объема  за промежуток времени
за промежуток времени  может выделяться или поглощаться некоторое количество тепла, например за счет прохождения тока, вследствие различных химических реакций и т. д. Это количество тепла
может выделяться или поглощаться некоторое количество тепла, например за счет прохождения тока, вследствие различных химических реакций и т. д. Это количество тепла  выражается с помощью введенной плотности источников (стоков) тепла следующим образом:
выражается с помощью введенной плотности источников (стоков) тепла следующим образом:

Уравнение теплового баланса имеет вид

Подставляя (2.3), (2.5), (2.6) в формулу (2.7), получим интегральное уравнение теплового баланса, справедливое для любого достаточно малого элемента  рассматриваемого тела
рассматриваемого тела 

Чтобы из интегрального соотношения (2.8) получить дифференциальное уравнение, потребуем, чтобы функция  была дважды непрерывно дифференцируема по координатам и один раз непрерывно дифференцируема по времени, функция
была дважды непрерывно дифференцируема по координатам и один раз непрерывно дифференцируема по времени, функция  непрерывно дифференцируема, а функции
непрерывно дифференцируема, а функции  непрерывны. Тогда, применяя к выражению (2.8) формулу конечных приращений и теорему о среднем и переходя к пределу при
непрерывны. Тогда, применяя к выражению (2.8) формулу конечных приращений и теорему о среднем и переходя к пределу при  и
и  стягивающемся в точку
стягивающемся в точку  получим
получим

Для постановки начально-краевой задачи к уравнению (2 9) необходимо добавить дополнительные условия. Это начальное условие, определяющее температуру тела  в начальный момент времени
в начальный момент времени  Отметим, что в случае уравнения теплопроводности, в котором старшей производной по времени является производная первого порядка, достаточно одного начального условия. В этом отношении уравнение теплопроводности отличается от уравнения колебаний, рассмотренного в § 1, для которого необходима постановка двух начальных условий. Более подробно эти вопросы будут рассмотрены в дальнейшем. Граничное условие задает тепловой режим на поверхности
Отметим, что в случае уравнения теплопроводности, в котором старшей производной по времени является производная первого порядка, достаточно одного начального условия. В этом отношении уравнение теплопроводности отличается от уравнения колебаний, рассмотренного в § 1, для которого необходима постановка двух начальных условий. Более подробно эти вопросы будут рассмотрены в дальнейшем. Граничное условие задает тепловой режим на поверхности  тела
тела  Если граница
Если граница  поддерживается при заданной
поддерживается при заданной
температуре  имеем граничное условие первого рода, или граничное условие Дирихле:
имеем граничное условие первого рода, или граничное условие Дирихле:

Если на поверхности  задан тепловой поток
задан тепловой поток  имеем граничное условие второго рода, или граничное условие Неймана:
имеем граничное условие второго рода, или граничное условие Неймана:

где  производная по нормали к поверхности
производная по нормали к поверхности  Это условие обычно записывается следующим образом:
Это условие обычно записывается следующим образом:

где  заданная функция.
заданная функция.
Наконец, если на поверхности  происходит теплообмен с внешней средой заданной температуры, то, применяя закон Ньютона (2.2), после несложных преобразований получаем граничное условие третьего рода
происходит теплообмен с внешней средой заданной температуры, то, применяя закон Ньютона (2.2), после несложных преобразований получаем граничное условие третьего рода

где  и
и  -заданные функции,
-заданные функции, 
Таким образом, начально-краевая задача для уравнения теплопроводности ставится следующим образом:

где  заданные функции. При этом, если
заданные функции. При этом, если  , имеем граничное условие (2.10), если
, имеем граничное условие (2.10), если  граничное условие (2.11), а если
граничное условие (2.11), а если  граничное условие (2.12).
граничное условие (2.12).
Для уравнения теплопроводности, как и для уравнения колебаний, могут возникать и более сложные граничные условия, чем условия (2.10) - (2.12). В дальнейшем мы ограничимся рассмотрением только граничных условий первого, второго и третьего рода.
Заметим, что к уравнению теплопроводности приводит не только рассмотрение процессов распространения тепла, но и процессов диффузии, процессов переноса вещества и др. Например, уравнение диффузии имеет вид

где  концентрация газа в точке
концентрация газа в точке  в момент времени
в момент времени  , с - коэффициент пористости, равный отношению объема пор к полному объему,
, с - коэффициент пористости, равный отношению объема пор к полному объему,  коэффициент диффузии,
коэффициент диффузии,  плотность источников (стоков) вещества. Уравнения теплопроводности (2.9) и диффузии (2.14) отличаются только обозначением коэффициентов.
плотность источников (стоков) вещества. Уравнения теплопроводности (2.9) и диффузии (2.14) отличаются только обозначением коэффициентов.
В ряде случаев и процессы распространения электромагнитных волн могут описываться уравнениями типа уравнения теплопроводности.
В заключение параграфа заметим, что если уравнение теплопроводности рассматривается в неограниченном пространстве или в области внешней относительно замкнутой поверхности, то для однозначного описания процесса нужно ставить определенные условия на бесконечности. Конкретный вид этих условий будет рассмотрен в гл. VI.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
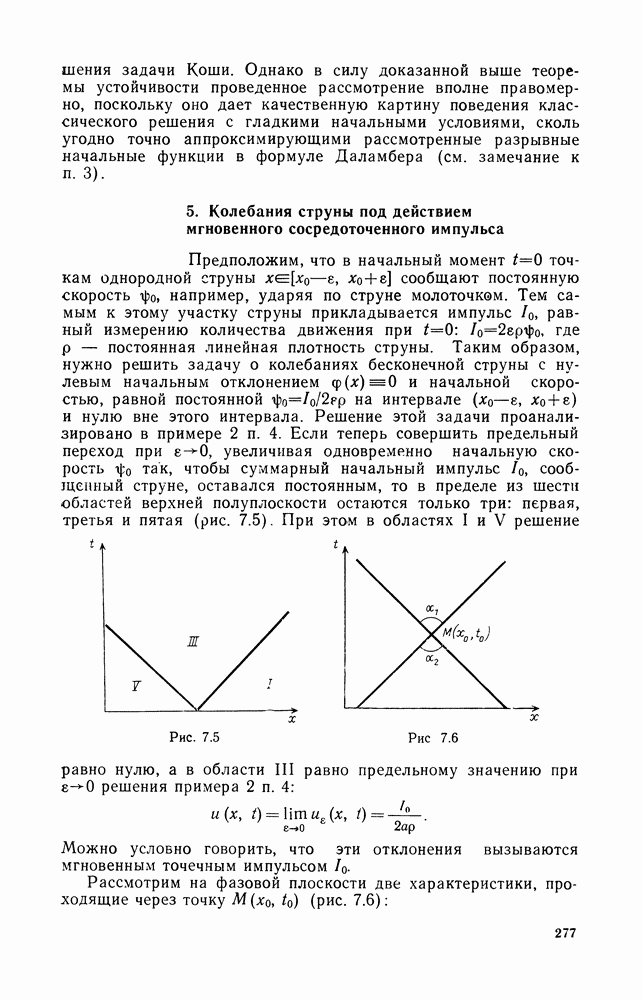
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
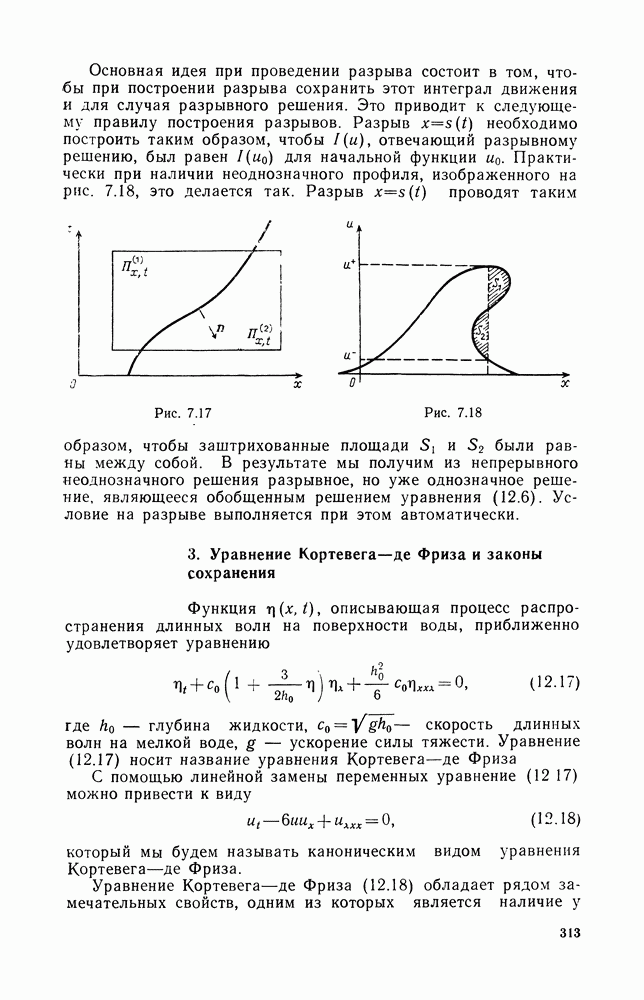
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ