| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Случай многих пространственных переменных
1) Малые поперечные колебания мембраны.
В качестве первого примера рассмотрим уравнение, описывающее малые поперечные колебания мембраны.
Мембраной называется натянутая плоская пленка, не сопротивляющаяся изгибу или сдвигу, но оказывающая сопротивление растяжению. Например, мембраной в некоторых случаях можно считать плоскую пластину, толщина которой мала по сравнению с двумя другими измерениями.
Уравнение, описывающее малые поперечные колебания мембраны, можно вывести методом, аналогичным тому, которым было получено уравнение (1.18), описывающее малые поперечные колебания струны. Обозначим через  величину поперечного смещения точки
величину поперечного смещения точки  мембраны в момент времени
мембраны в момент времени  Если рассматривать малые поперечные колебания мембраны, при которых смещение происходит перпендикулярно плоскости мембраны
Если рассматривать малые поперечные колебания мембраны, при которых смещение происходит перпендикулярно плоскости мембраны  и при которых квадратами величин их и
и при которых квадратами величин их и  можно пренебречь, то уравнение малых поперечных колебаний мембраны будет иметь вид
можно пренебречь, то уравнение малых поперечных колебаний мембраны будет иметь вид

где  поверхностная плотность мембраны,
поверхностная плотность мембраны,  натяжение,
натяжение,  плотность импульса внешней поперечной силы, действующей на мембрану в точке
плотность импульса внешней поперечной силы, действующей на мембрану в точке  в момент времени
в момент времени 
Пусть в положении равновесия мембрана занимает область  плоскости
плоскости  ограниченную контуром
ограниченную контуром 
Как и в одномерном случае, для однозначного определения процесса колебаний мембраны необходимо задание начальных и граничных условий. Например, если граница  мембраны движется заданным образом в поперечном направлении, то граничное условие имеет следующий вид (граничное условие первого рода, или условие Дирихле):
мембраны движется заданным образом в поперечном направлении, то граничное условие имеет следующий вид (граничное условие первого рода, или условие Дирихле):

где  заданная функция. В частности, при
заданная функция. В частности, при  получается условие закрепленной границы мембраны. Если к границе приложена заданная поперечная сила, то приходим к граничному условию второго рода, или условию Неймана
получается условие закрепленной границы мембраны. Если к границе приложена заданная поперечная сила, то приходим к граничному условию второго рода, или условию Неймана

где - означает производную по нормали к контуру 1, лежащей в плоскости  В частности, при
В частности, при  имеем условие свободной границы.
имеем условие свободной границы.
Если же граница  мембраны закреплена упруго и при этом движется по заданному закону в поперечном направлении, то граничным условием является граничное условие третьего рода, связывающее значение функции поперечного смещения
мембраны закреплена упруго и при этом движется по заданному закону в поперечном направлении, то граничным условием является граничное условие третьего рода, связывающее значение функции поперечного смещения  и ее нормальной производной:
и ее нормальной производной:

где  заданные на контуре
заданные на контуре  функции
функции
Разумеется, в зависимости от реальных физических задач граничные условия могут быть и более сложного вида, в частности нелинейные и содержащие производные высших порядков, но мы в дальнейшем ограничимся условиями Дирихле, Неймана и третьего рода.
Таким образом, начально-краевая задача, описывающая процесс малых поперечных колебаний мембраны, ставится следующим образом:

2) Уравнения малых акустических колебаний в сплошной среде. Во многих задачах газодинамики можно не учитывать молекулярную структуру газа и рассматривать газ как сплошную среду. Иными словами, говоря о бесконечно малых элементах объема, подразумевают, что объем мал по сравнению с характерным размером системы, но содержит очень большое число молекул. Аналогично, когда говорят о движении частицы газа, то имеют в виду не движение отдельной молекулы газа, а смещение элемента объема, содержащего много молекул, но рассматриваемого в газодинамике как точка.
Пусть газ движется со скоростью  проекции которой на оси координат обозначим
проекции которой на оси координат обозначим  Заметим, что
Заметим, что  есть скорость газа в данной точке
есть скорость газа в данной точке  пространства в момент времени
пространства в момент времени  т. е. относится к определенным точкам пространства, а не к определенным частицам газа, перемещающимся в пространстве.
т. е. относится к определенным точкам пространства, а не к определенным частицам газа, перемещающимся в пространстве.
Введем также плотность газа  давление
давление  и плотность внешних действующих сил
и плотность внешних действующих сил  рассчитанных на единицу массы.
рассчитанных на единицу массы.
При таком способе описания говорят, что задача рассматривается в координатах Эйлера.
Получим прежде всего уравнение движения газа. Обозначим через  некоторый объем газа, ограниченный поверхностью
некоторый объем газа, ограниченный поверхностью  Равнодействующая сил давления, приложенных к поверхности
Равнодействующая сил давления, приложенных к поверхности  равна
равна

где  единичный вектор внешней нормали и поверхности
единичный вектор внешней нормали и поверхности 
Для преобразования этого интеграла воспользуемся формулами Остроградского

Поскольку  где
где  единичные векторы ортонормированного базиса, умножая первую формулу на
единичные векторы ортонормированного базиса, умножая первую формулу на  вторую на
вторую на  третью на к и складывая, получим
третью на к и складывая, получим

С учетом последней формулы уравнение движения для объема газа  в интегральной форме имеет следующий вид:
в интегральной форме имеет следующий вид:

Вычисляя ускорение  некоторой частицы газа, нужно учесть перемещение самой этой частицы. Траектории отдельных частиц газа определяются уравнениями
некоторой частицы газа, нужно учесть перемещение самой этой частицы. Траектории отдельных частиц газа определяются уравнениями

откуда

где оператор  определяется следующим образом:
определяется следующим образом:

Предполагая, что все функции, входящие в формулу (1.20), являются достаточно гладкими, применяя формулу среднего
значения и переходя к пределу, стягивая объем  в точку, получим, учитывая (1.21), уравнение движения газа в форме Эйлера
в точку, получим, учитывая (1.21), уравнение движения газа в форме Эйлера

Выведем теперь уравнение непрерывности, выражающее закон сохранения вещества. Пусть в выделенном объеме  отсутствуют источники и стоки газа. Тогда изменение в единицу времени количества газа, заключенного внутри объема
отсутствуют источники и стоки газа. Тогда изменение в единицу времени количества газа, заключенного внутри объема  равно потоку газа через границу:
равно потоку газа через границу:

Преобразуя правую часть последней формулы по формуле Остроградского

будем иметь

Применяя формулу среднего значения и переходя к пределу, получим уравнение непрерывности

К полученному уравнению движения газа и уравнению непрерывности необходимо добавить термодинамическое уравнение состояния, которое мы запишем в общем виде:

где С — заданная функция.
В результате получается система пяти скалярных уравнений относительно пяти неизвестных функций 

Система уравнений (1.22) — (1.24) представляет замкнутую систему уравнений газодинамики.
Колебательные движения в газе с малыми амплитудами называются звуковыми волнами. В каждой точке звуковой волны происходят поперечные сжатия и разрежения газа.
В силу малости колебаний в звуковой волне скорость  в ней мала, так что в уравнении (1.22) можно пренебречь членами второго порядка вида
в ней мала, так что в уравнении (1.22) можно пренебречь членами второго порядка вида  и т. д. По той же причине относительные изменения плотности и давления газа также малы.
и т. д. По той же причине относительные изменения плотности и давления газа также малы.
Положим  где
где  и
и  - равновесные значения давления и плотности газа,
- равновесные значения давления и плотности газа,  их изменения в звуковой волне, причем
их изменения в звуковой волне, причем  Величина
Величина  называется звуковым давлением.
называется звуковым давлением.
Пренебрегая в системе (1.22) — (1.24) членами второго порядка, получим линеаризованную систему уравнений. Функцию  разложим в ряд по степеням
разложим в ряд по степеням  и учтем члены первого порядка. В результате получим
и учтем члены первого порядка. В результате получим

и, поскольку 

Таким образом, замкнутая система малых акустических колебаний в сплошной среде имеет вид

Получим теперь уравнение относительно функции  Продифференцируем уравнение (1.26) по t:
Продифференцируем уравнение (1.26) по t:

— 0 и подействуем оператором  на уравнение (1.25):
на уравнение (1.25):

Наконец, в линейном приближении из (1.27) получим

Обозначим  Тогда из трех последних уравнений получим уравнение второго порядка относительно функции
Тогда из трех последних уравнений получим уравнение второго порядка относительно функции 

Уравнение (1.28) является уравнением колебаний в трехмерном случае. Оно часто называется уравнением акустики.
В случае адиабатического процесса уравнение газового состояния имеет вид

где постоянная у — показатель адиабаты  — теплоемкость при постоянном давлении;
— теплоемкость при постоянном давлении;  теплоемкость при постоянном объеме. В линейном приближении будем иметь
теплоемкость при постоянном объеме. В линейном приближении будем иметь

откуда

Сравнивая (1.29) с (1.27), получим

3) Уравнения Максвелла. В качестве третьего примера рассмотрим систехму уравнений Максвелла в однородной и изотропной среде. В системе СИ уравнения Максвелла имеют вид

где  плотность тока проводимости,
плотность тока проводимости,  плотность тока сторонних сил,
плотность тока сторонних сил,  плотность объемных зарядов. К уравнениям (1.30) — (1.33) добавим материальные уравнения
плотность объемных зарядов. К уравнениям (1.30) — (1.33) добавим материальные уравнения

где  абсолютная диэлектрическая проницаемость,
абсолютная диэлектрическая проницаемость,  относительная диэлектрическая проницаемость,
относительная диэлектрическая проницаемость,  электрическая постоянная, — абсолютная магнитная проницаемость,
электрическая постоянная, — абсолютная магнитная проницаемость,  относительная магнитная проницаемость,
относительная магнитная проницаемость,  магнитная постоянная.
магнитная постоянная.
Плотность тока проводимости  связана с вектором
связана с вектором  уравнением, выражающим закон Ома в дифференциальной форме:
уравнением, выражающим закон Ома в дифференциальной форме:

где  проводимость среды.
проводимость среды.
Поскольку среда по предположению однородна и изотропна, то величины  о являются постоянными скалярными величинами.
о являются постоянными скалярными величинами.
Подействуем на обе части уравнения (1.30) оператором  В результате получим (с учетом
В результате получим (с учетом 

С другой стороны, по известной формуле векторного анализа к) имеем

Из формул (1.31), (1.34), (1.36) и (1.37) получим уравнение

Аналогичное уравнение получается для вектора 
Уравнение (1.38) называется векторным волновым уравнением. Как будет следовать из дальнейшего рассмотрения, первая производная по времени определяет затухание колебаний — диссипативные потери энергии.
Для компонент вектора магнитного поля  из (1.38) получим скалярные волновые уравнения, которые в декартовых координатах можно записать в виде
из (1.38) получим скалярные волновые уравнения, которые в декартовых координатах можно записать в виде

где  — оператор Лапласа, и — любая из декартовых компонент вектора
— оператор Лапласа, и — любая из декартовых компонент вектора 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
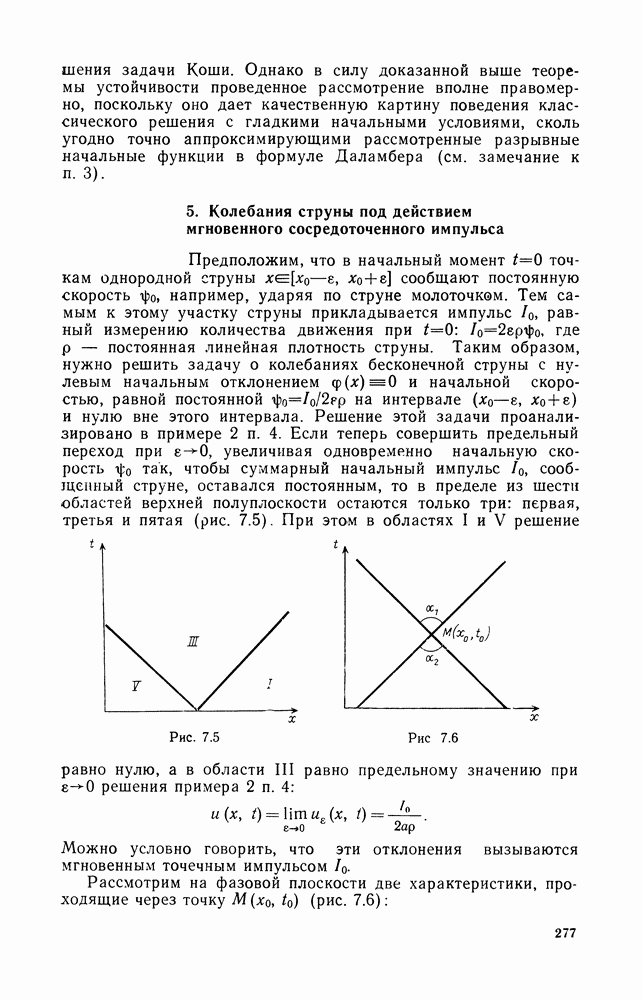
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ