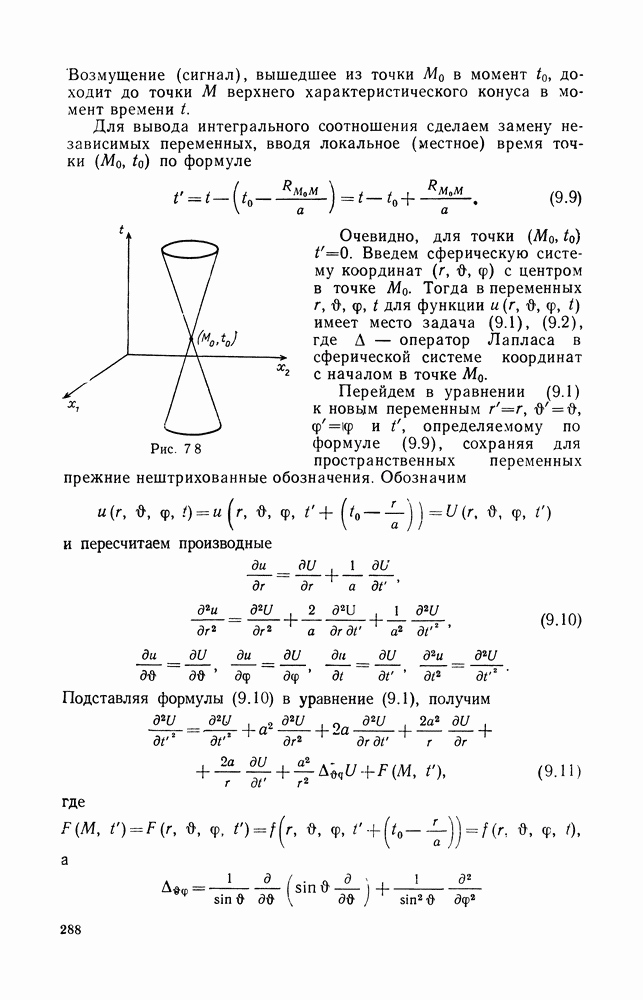
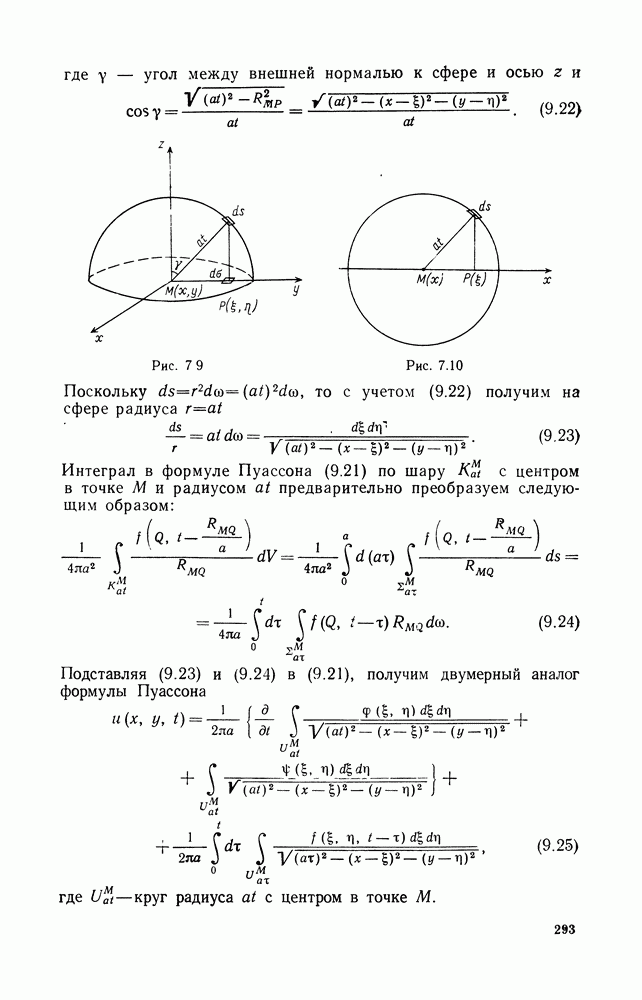
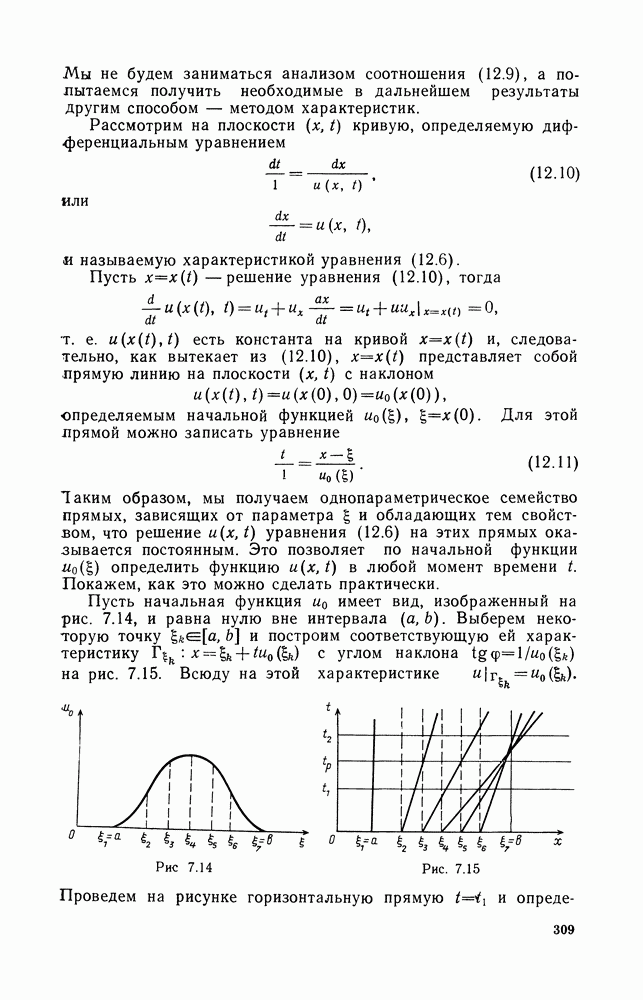
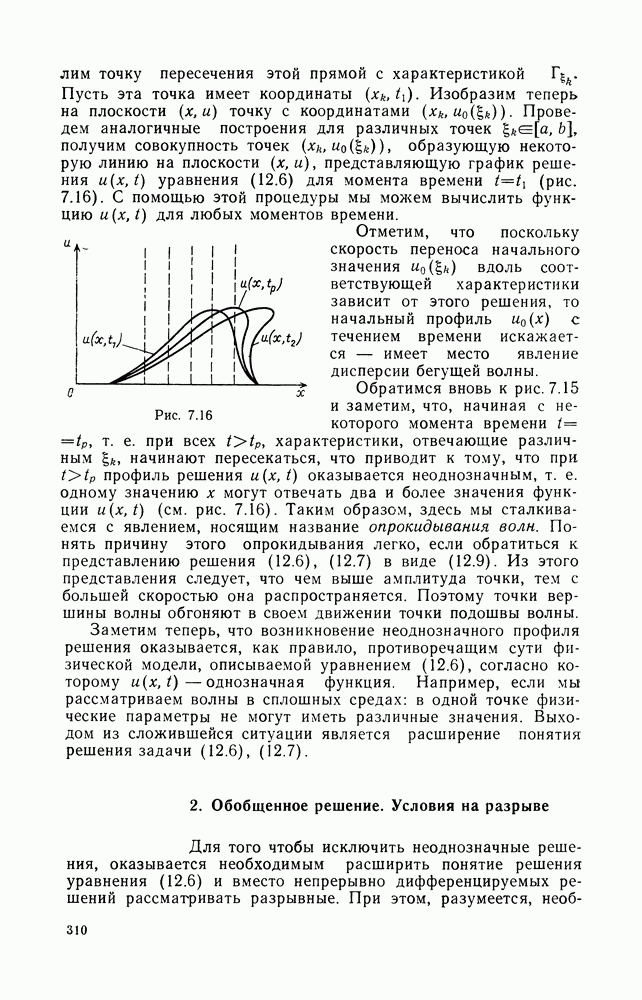
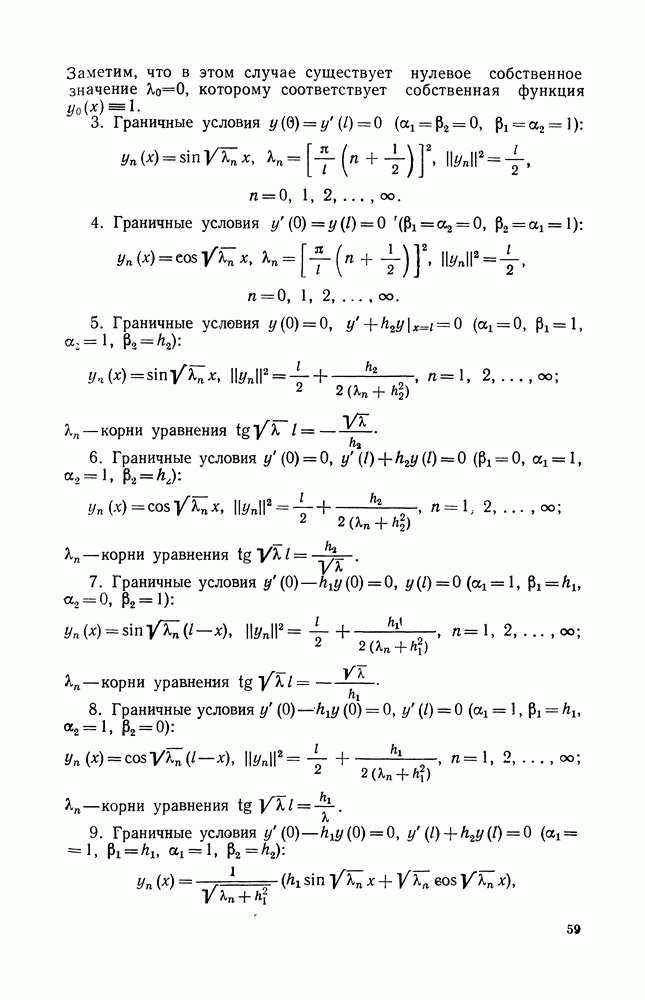| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Существование классического решения уравнения теплопроводности на отрезке
Рассмотрим задачу для уравнения теплопроводности с постоянными коэффициентами на отрезке при однородных условиях Дирихле:


где коэффициент  коэффициент теплопроводности, с — удельная теплоемкость,
коэффициент теплопроводности, с — удельная теплоемкость,  плотность. Коэффициент
плотность. Коэффициент  часто называют коэффициентом температуропроводности.
часто называют коэффициентом температуропроводности.
Формальное построение решения этой задачи методом Фурье было проведено в гл. III. Оно имеет вид

где

Покажем, что при определенных условиях на функцию  ряд (4.13) с коэффициентами, вычисляемыми по формуле (4.14), представляет собой классическое решение задачи
ряд (4.13) с коэффициентами, вычисляемыми по формуле (4.14), представляет собой классическое решение задачи 
Напомним, что необходимым условием существования классического решения задачи (4.10) — (4.12) является условие согласования начального (4.11) и граничных (4.12) условий: 
Предварительно сформулируем полезное вспомогательное положение — обобщенный принцип суперпозиции.
Лемма 6.1 (обобщенный принцип суперпозиции). Пусть  частные решения линейного однородного дифференциального уравнения обыкновенного или в частных производных
частные решения линейного однородного дифференциального уравнения обыкновенного или в частных производных  и пусть все дифференциальные операции над функцией
и пусть все дифференциальные операции над функцией  входящие в это уравнение, можно проводить путем почленного дифференцирования ряда. Тогда функция
входящие в это уравнение, можно проводить путем почленного дифференцирования ряда. Тогда функция  также удовлетворяет уравнению
также удовлетворяет уравнению 
Доказательство. При выполнении сформулированных в лемме условий получаем

В качестве достаточного условия для возможности почленного дифференцирования ряда будем пользоваться равномерной сходимостью ряда  получаемого в результате дифференцирования.
получаемого в результате дифференцирования.
Напомним также известное свойство рядов Фурье.
Если периодическая с периодом 21 функция  имеет на отрезке
имеет на отрезке  непрерывных производных, а
непрерывных производных, а  производная ее на этом отрезке кусочно-непрерывна, то сходится числовой ряд
производная ее на этом отрезке кусочно-непрерывна, то сходится числовой ряд

где  коэффициенты Фурье в разложении функции
коэффициенты Фурье в разложении функции  по тригонометрической системе
по тригонометрической системе 
Если функция  задана на отрезке
задана на отрезке  и разлагается в ряд Фурье только по
и разлагается в ряд Фурье только по  то сформулированные требования должны выполняться для функции
то сформулированные требования должны выполняться для функции  являющейся нечетным продолжением функции
являющейся нечетным продолжением функции  В частности, для непрерывности и периодичности с периодом 21 функции
В частности, для непрерывности и периодичности с периодом 21 функции  необходимо, чтобы
необходимо, чтобы  Непрерывность первой производной в точках
Непрерывность первой производной в точках  при нечетном продолжении получается автоматически.
при нечетном продолжении получается автоматически.
Теорема 6.7. Пусть функция  непрерывна на отрезке
непрерывна на отрезке  имеет на нем кусочно-непрерывную производную и удовлетворяет условиям
имеет на нем кусочно-непрерывную производную и удовлетворяет условиям  Тогда существует классическое решение задачи (4.10) — (4.12), представимое рядом (4.13) с коэффициентами (4.14).
Тогда существует классическое решение задачи (4.10) — (4.12), представимое рядом (4.13) с коэффициентами (4.14).
Доказательство. Ряд (4.13) с коэффициентами (4.14) удовлетворяет однородным граничным условиям (4.12), поскольку им удовлетворяют все собственные функции  и при
и при  переходит в тригонометрический ряд Фурье на отрезке
переходит в тригонометрический ряд Фурье на отрезке  для функции
для функции  удовлетворяющей условию разложимости в ряд Фурье:
удовлетворяющей условию разложимости в ряд Фурье:

Остается доказать, что ряд (4.13) сходится в области  и функция
и функция  представимая этим рядом, непрерывна в области
представимая этим рядом, непрерывна в области  обладает непрерывными производными, входящими в уравнение (4.10), и удовлетворяет однородному уравнению (4.10) в области
обладает непрерывными производными, входящими в уравнение (4.10), и удовлетворяет однородному уравнению (4.10) в области  Так как каждый член ряда (4.13) является частным решением однородного уравнения (4.10), то в силу обобщенного принципа суперпозиции достаточно показать, что в области
Так как каждый член ряда (4.13) является частным решением однородного уравнения (4.10), то в силу обобщенного принципа суперпозиции достаточно показать, что в области  существуют производные функции
существуют производные функции  входящие в уравнение (4.10), и их можно вычислять путем почленного дифференцирования ряда (4.13).
входящие в уравнение (4.10), и их можно вычислять путем почленного дифференцирования ряда (4.13).
Покажем прежде всего, что функция  представимая рядом (4.13), непрерывна в области й. Из формулы (4.15) следует, что мажорантным для ряда (4.13) будет ряд из модулей коэффициентов Фурье функции
представимая рядом (4.13), непрерывна в области й. Из формулы (4.15) следует, что мажорантным для ряда (4.13) будет ряд из модулей коэффициентов Фурье функции 

который сходится в силу условий, наложенных на функцию  и сформулированных выше свойств рядов Фурье. Тем самым ряд (4.13) сходится равномерно к функции
и сформулированных выше свойств рядов Фурье. Тем самым ряд (4.13) сходится равномерно к функции  в области
в области  и функция
и функция  непрерывна в
непрерывна в 
Следовательно, при  функция
функция  удовлетворяет начальному условию (4.11), а при
удовлетворяет начальному условию (4.11), а при  функция
функция  удовлетворяет однородным граничным условиям (4.12).
удовлетворяет однородным граничным условиям (4.12).
Покажем теперь, что при  где
где  любое число, сходятся равномерно ряды из производных
любое число, сходятся равномерно ряды из производных

где

— общий член ряда (4.13).
Поскольку функция  непрерывна на отрезке
непрерывна на отрезке  то она ограничена на нем
то она ограничена на нем

где  некоторая постоянная и
некоторая постоянная и

Поэтому при  получаем
получаем

и


Из формул (4.17), (4.18) вытекает, что для доказательства равномерной сходимости рядов (4.16) нужно доказать сходимость мажорантных рядов вида

где  Для первого мажорантного ряда к
Для первого мажорантного ряда к  для второго.
для второго.
Сходимость ряда вида (4.19) следует из признака сходимости Даламбера, так как

Поскольку при  мажорантные ряды для рядов (4.16) сходятся, то сами ряды сходятся равномерно и ряд (4.13) можно дифференцировать почленно дважды по х и один раз по
мажорантные ряды для рядов (4.16) сходятся, то сами ряды сходятся равномерно и ряд (4.13) можно дифференцировать почленно дважды по х и один раз по  при
при  или, ввиду произвольности
или, ввиду произвольности  в области
в области 
В силу обобщенного принципа суперпозиции функция  представимая рядом (4.13), удовлетворяет уравнению (4.10).
представимая рядом (4.13), удовлетворяет уравнению (4.10).
Итак, мы доказали, что при условиях теоремы функция  представимая формулой (4.13) с коэффициентами (4.14), является классическим решением начально-краевой задачи
представимая формулой (4.13) с коэффициентами (4.14), является классическим решением начально-краевой задачи 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
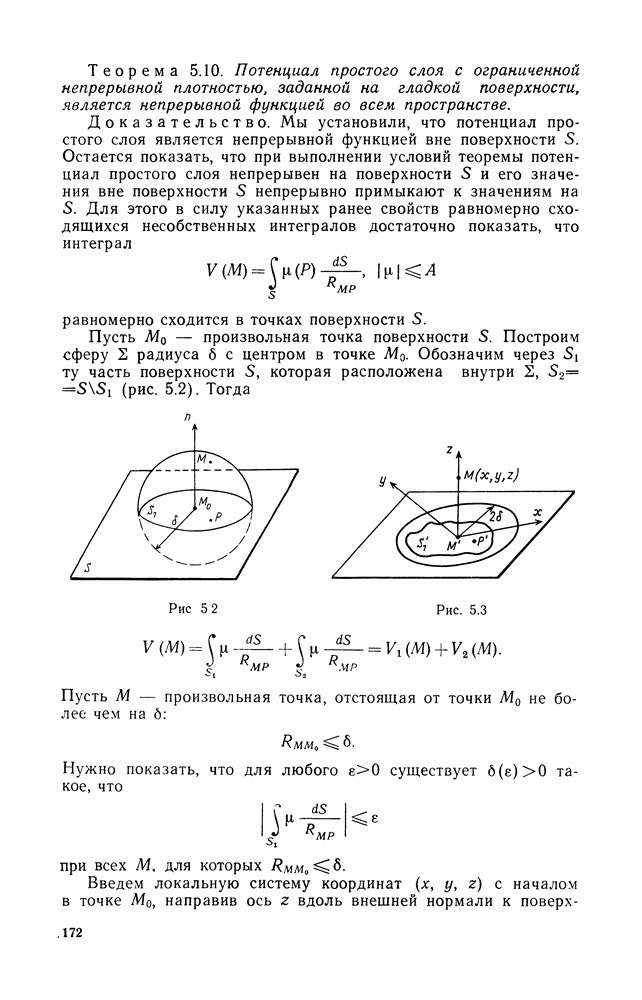
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
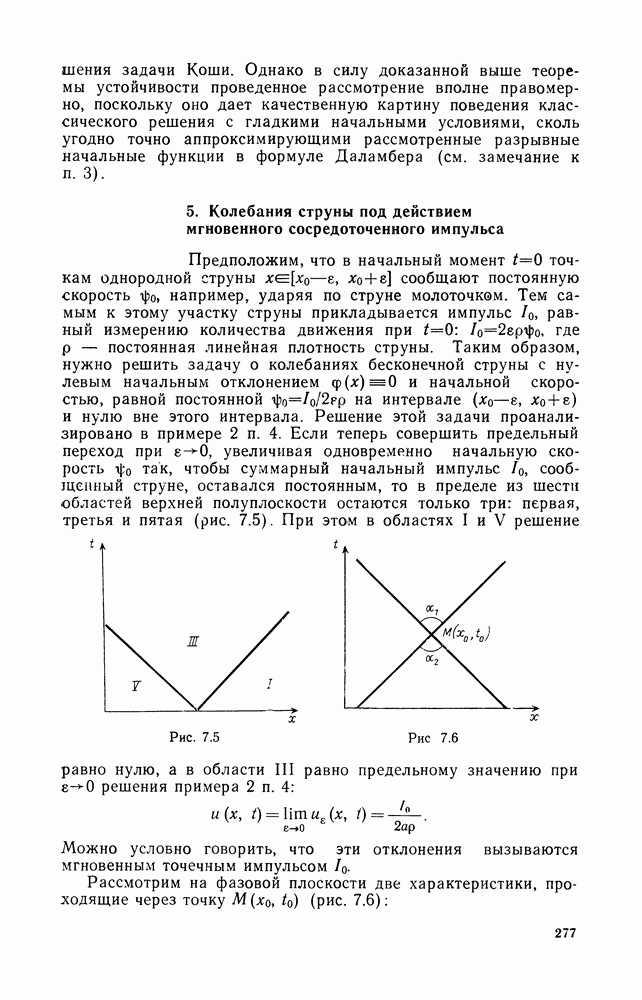
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
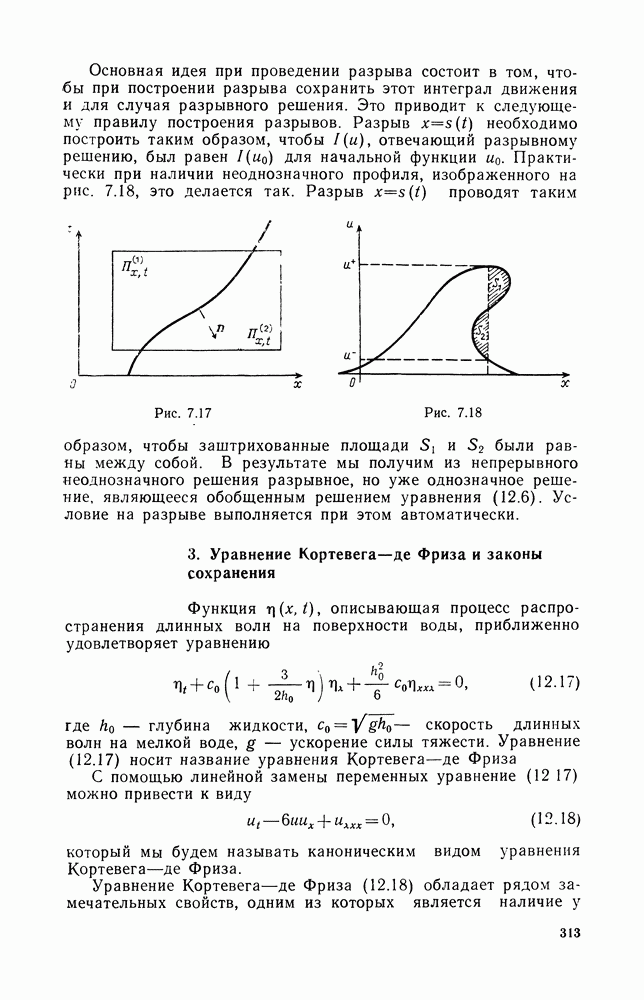
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ