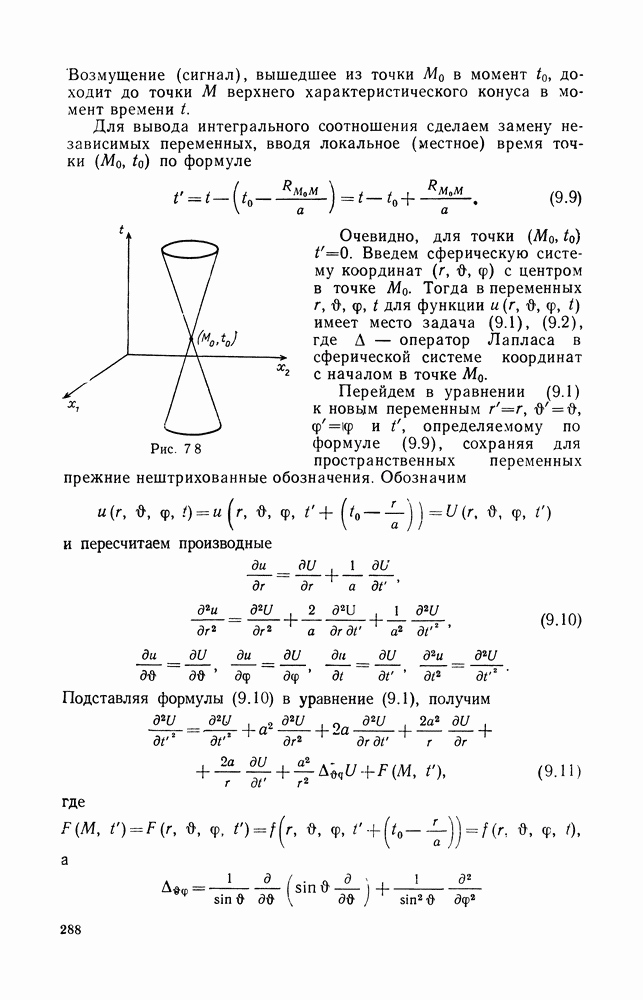
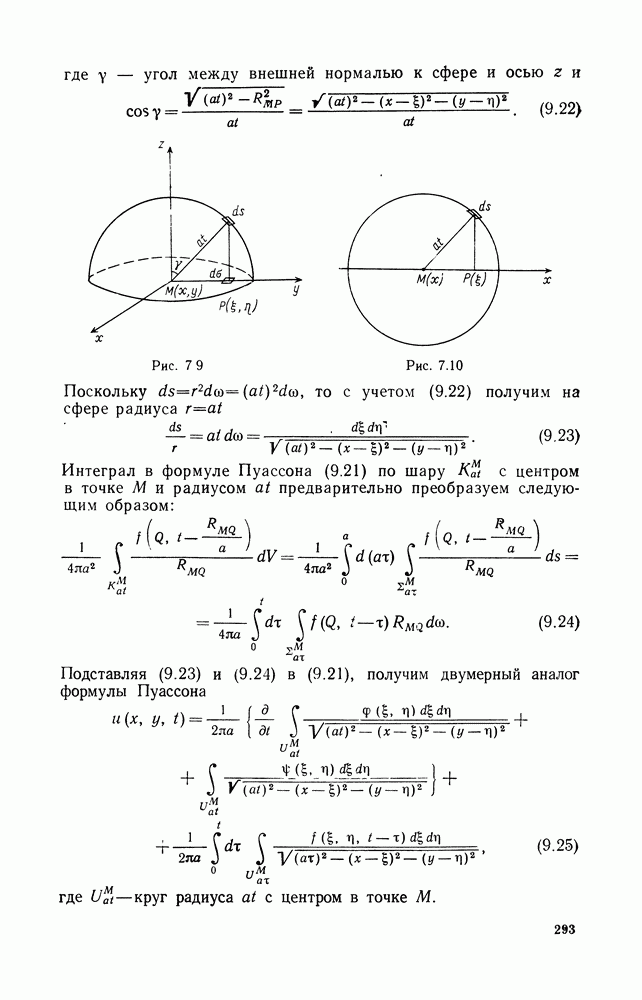
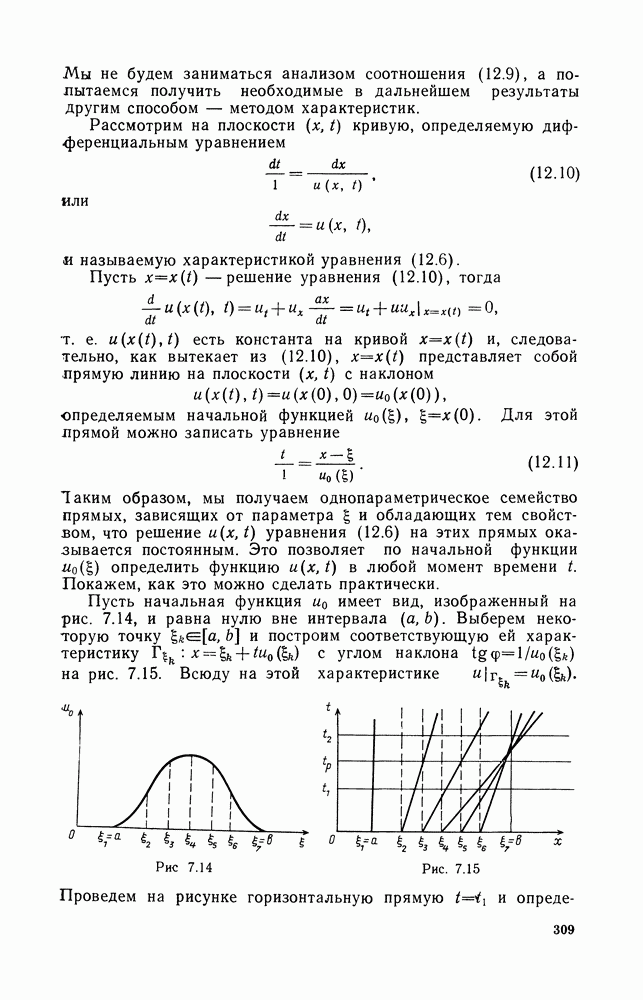
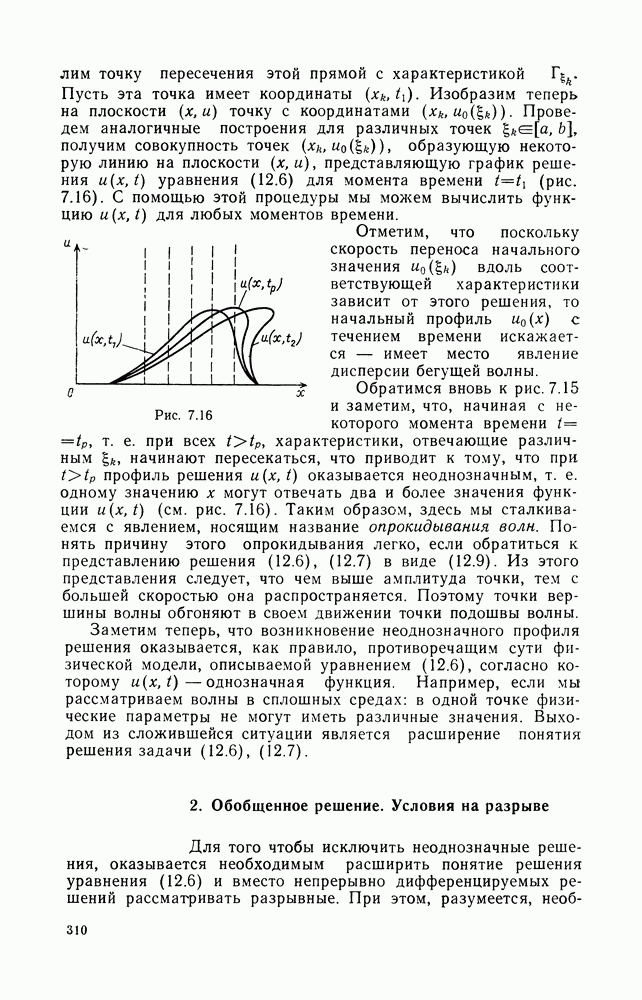
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Основные свойства классических ортогональных полиномов
1) Классические ортогональные полиномы по определению ортогональны на отрезке  с весом
с весом 

2) Теорема о нулях.
Теорема 4.1. Классический ортогональный полином  имеет
имеет  простых нулей строго внутри отрезка
простых нулей строго внутри отрезка 
Доказательство. Пусть  произвольное фиксированное целое положительное число. В силу ортогональности полиномов
произвольное фиксированное целое положительное число. В силу ортогональности полиномов  имеем
имеем

Следовательно, полином  меняет знак на интервале
меняет знак на интервале  в некотором числе
в некотором числе  различных точек
различных точек  при
при  Тогда полином
Тогда полином  имеет вид
имеет вид

где  не меняет знака на
не меняет знака на  Для доказательства теоремы достаточно показать, что
Для доказательства теоремы достаточно показать, что  Предположим противное: пусть
Предположим противное: пусть  Так как система классических ортогональных полиномов
Так как система классических ортогональных полиномов  содержит полиномы всех степеней, то для полинома
содержит полиномы всех степеней, то для полинома  справедливо разложение
справедливо разложение

где  Так как
Так как  имеем
имеем

С другой стороны,

так как функция  не меняет знак на интервале
не меняет знак на интервале  Сравнивая последние две формулы, получаем противоречие.
Сравнивая последние две формулы, получаем противоречие.
Следовательно,  а поскольку полином
а поскольку полином  степени не может иметь более
степени не может иметь более  нулей, то
нулей, то  Отсюда вытекает, что все корни простые. Теорема доказана.
Отсюда вытекает, что все корни простые. Теорема доказана.
Замечание. В силу основной теоремы высшей алгебры любой полином  степени
степени  на комплексной плоскости
на комплексной плоскости  имеет ровно
имеет ровно  нулей (с учетом их кратности). Из доказанной теоремы следует, что все нули классического ортогонального полинома
нулей (с учетом их кратности). Из доказанной теоремы следует, что все нули классического ортогонального полинома  сосредоточены строго внутри отрезка
сосредоточены строго внутри отрезка  действительной оси комплексной плоскости
действительной оси комплексной плоскости 
Так как между двумя нулями дифференцируемой функции  по теореме Ролля имеется хотя бы один нуль ее производной
по теореме Ролля имеется хотя бы один нуль ее производной  то из этого свойства и доказанной теоремы получаем
то из этого свойства и доказанной теоремы получаем
Следствие. Все нули производных классического ортогонального полинома  простые и расположены строго внутри отрезка
простые и расположены строго внутри отрезка 
3) Покажем, что производные  также являются классическими ортогональными полиномами, заданными на отрезке
также являются классическими ортогональными полиномами, заданными на отрезке  и ортогональными с новым весом
и ортогональными с новым весом 
При  имеем
имеем

Действительно,  есть полином степени
есть полином степени  и может быть представлен в виде
и может быть представлен в виде

откуда следует (3.6). Воспользуемся уравнением Пирсона (3.1) для  и вычислим интеграл по частям. Учитывая, что в силу условия (3.2) подстановки обратятся в нуль, получим
и вычислим интеграл по частям. Учитывая, что в силу условия (3.2) подстановки обратятся в нуль, получим

Так как  полином степени не выше
полином степени не выше  аналогично формуле (3.6) получаем, что второй интеграл в формуле (3.7) равен нулю. Поэтому
аналогично формуле (3.6) получаем, что второй интеграл в формуле (3.7) равен нулю. Поэтому

Следовательно, при  полином
полином  степени
степени  ортогонален ко всем полиномам меньшей степени
ортогонален ко всем полиномам меньшей степени  с весом
с весом 

Осталось показать, что весовая функция  удовлетворяет уравнению Пирсона (3.1). Имеем
удовлетворяет уравнению Пирсона (3.1). Имеем

где  — линейная функция. Очевидно, что произведение
— линейная функция. Очевидно, что произведение  обращается в нуль в точках а и
обращается в нуль в точках а и 
Замечание. Методом математической индукции легко показать, что  производные классических ортогональных полиномов
производные классических ортогональных полиномов  образуют на отрезке
образуют на отрезке  систему классических ортогональных полиномов ортогональных с весом
систему классических ортогональных полиномов ортогональных с весом  (очевидно,
(очевидно, 
4) Получим дифференциальное уравнение для классических ортогональных полиномов.
Запишем формулу (3.8) в виде 

Интегрируя по частям, получим

откуда, используя уравнение Пирсона (3.1), находим

при всех  Обозначим
Обозначим

Полином  степени
степени  разложим по системе классических ортогональных полиномов:
разложим по системе классических ортогональных полиномов:

Учитывая (3.9), получим

откуда  при
при  следовательно,
следовательно,  Обозначив
Обозначив  будем иметь
будем иметь

Уравнение (3.10) можно записать в самосопряженной форме. Для этого умножим (3.10) на  используя уравнение Пирсона (3.1), приведем его к виду
используя уравнение Пирсона (3.1), приведем его к виду

5) В случае конечного отрезка  в силу поведения функции
в силу поведения функции  при
при  или
или  граничные точки отрезка
граничные точки отрезка  являются особыми точками уравнения (3.11). Тем самым классические ортогональные полиномы являются собственными функциями краевой задачи Штурма-Лиувилля для уравнения (3.11) на отрезке
являются особыми точками уравнения (3.11). Тем самым классические ортогональные полиномы являются собственными функциями краевой задачи Штурма-Лиувилля для уравнения (3.11) на отрезке  с условиями ограниченности в граничных точках:
с условиями ограниченности в граничных точках:

При постановке задачи Штурма-Лиувилля граничные условия выделяют одно из двух линейно независимых решений линейного дифференциального уравнения второго порядка.
В силу леммы 4.1 в случае, когда граничные точки являются особыми точками уравнения, условия ограниченности достаточны для выделения единственного решения.
Поскольку в силу теоремы Вейерштрасса ортогональные полиномы образуют на конечном отрезке полную и замкнутую систему, для них имеет место теорема разложимости Стеклова и они исчерпывают все собственные функции краевой задачи (3.12). В самом деле, если предположить, что при некотором значении параметра Я, отличного от  существует
существует
собственная функция  задачи (3.12), не являющаяся классическим ортогональным полиномом, то в силу общих свойств собственных функций непрерывная функция
задачи (3.12), не являющаяся классическим ортогональным полиномом, то в силу общих свойств собственных функций непрерывная функция  должна быть ортогональна ко всем функциям системы классических ортогональных полиномов
должна быть ортогональна ко всем функциям системы классических ортогональных полиномов  и в силу замкнутости этой системы тождественно равна нулю.
и в силу замкнутости этой системы тождественно равна нулю.
Постановку краевой задачи Штурма-Лиувилля в случае бесконечного или полубесконечного интервала мы рассмотрим позже на примере конкретных классических ортогональных полиномов.
Найдем выражение для собственных значений задачи (3.12). Выпишем коэффициент при  в уравнении (3.10). Поскольку
в уравнении (3.10). Поскольку

то, подставляя эти выражения в (3.10), получим коэффициент при  в виде
в виде

где

Отсюда, приравнивая коэффициент при  в уравнении (3.10) нулю, получим
в уравнении (3.10) нулю, получим

6) Уравнение (3.11) можно записать в виде

где  Так как производные
Так как производные  порядка
порядка  классических ортогональных полиномов снова являются классическими ортогональными полиномами, то, повторяя рассуждения п. 4), получим для них уравнение
классических ортогональных полиномов снова являются классическими ортогональными полиномами, то, повторяя рассуждения п. 4), получим для них уравнение

где

7) Получим явное представление для классических ортогональных полиномов. В силу уравнения (3.14)

и, в частности, рекуррентно применяя последнюю формулу, находим

где

Так как  то, полагая в формуле
то, полагая в формуле  получим
получим

или, обозначая 

Формула (3.16) называется обобщенной формулой Родрига. Коэффициенты  в формуле (3.16) определяются из условия нормировки, поскольку классические ортогональные полиномы как решения однородного уравнения определяются с точностью до множителя.
в формуле (3.16) определяются из условия нормировки, поскольку классические ортогональные полиномы как решения однородного уравнения определяются с точностью до множителя.
8) Формула Родрига позволяет получить значение квадрата нормы классических ортогональных полиномов. Учитывая, что  где
где  полином степени
полином степени  получим
получим

Отсюда, используя формулу Родрига (3.16), будем иметь

Интегрируя  раз по частям и учитывая, что в силу условия (3.2) подстановки обратятся в нуль, получим формулу для квадрата нормы классических ортогональных полиномов
раз по частям и учитывая, что в силу условия (3.2) подстановки обратятся в нуль, получим формулу для квадрата нормы классических ортогональных полиномов

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
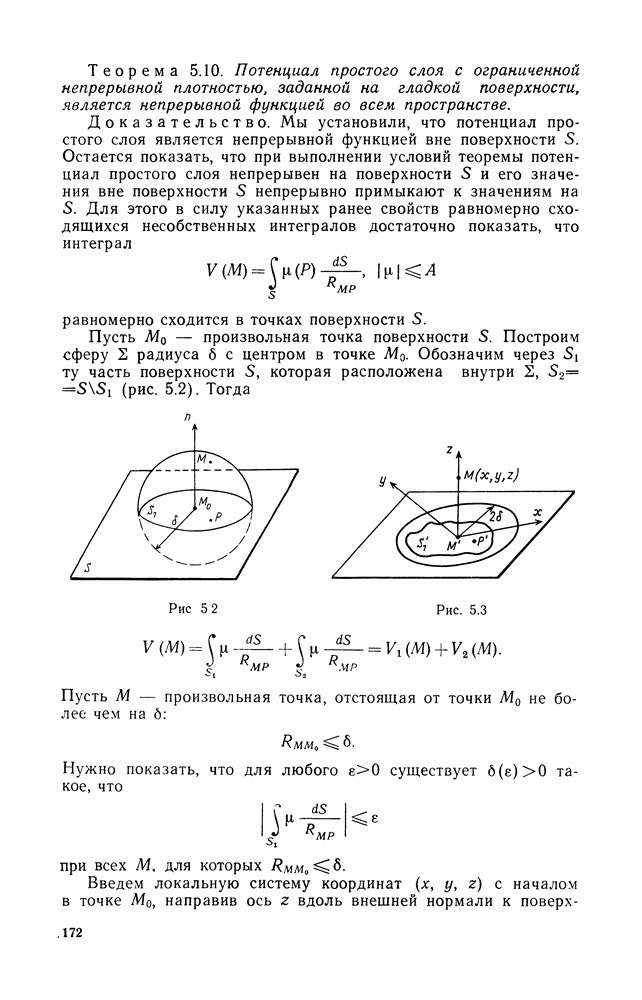
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
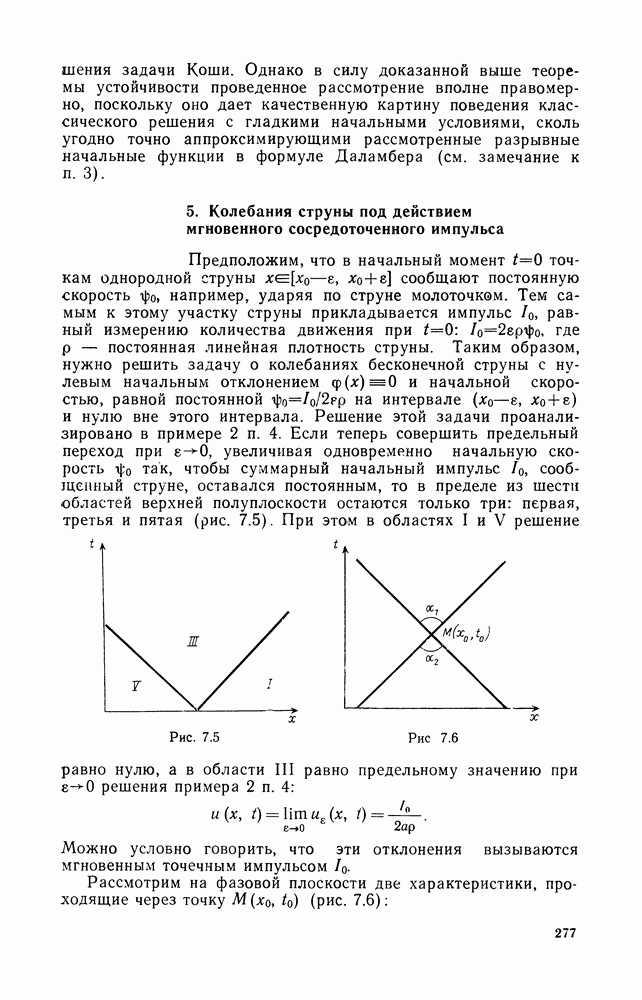
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
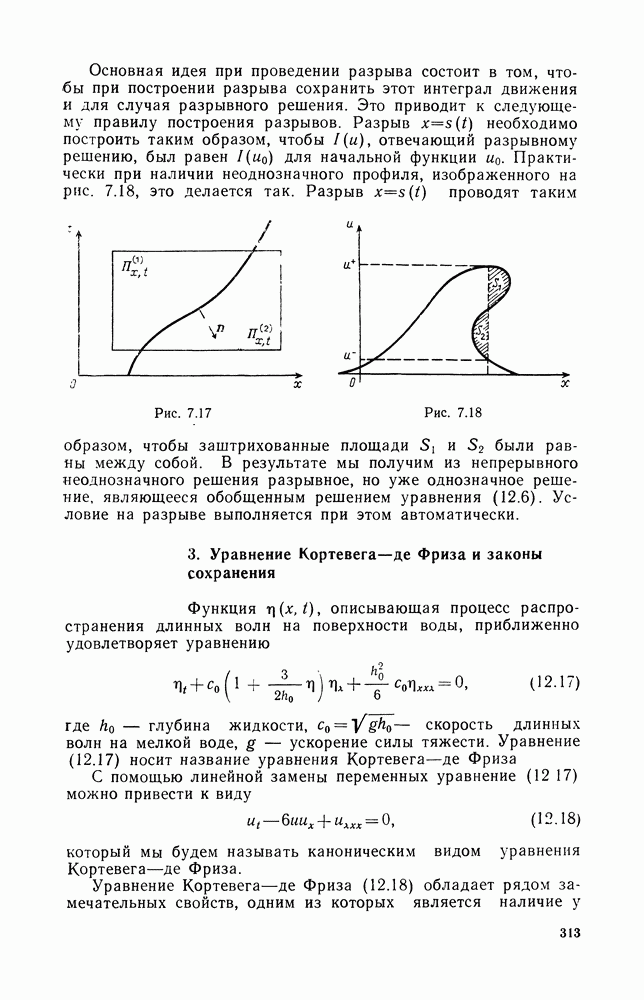
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ