§ 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ

1. Простейшие уравнения и метод характеристик

Рассматривая простейшие уравнения колебаний с постоянным коэффициентом а на бесконечной прямой:

мы установили, что его общее решение представляется в виде суперпозиции прямой и обратной бегущих волн:

где произвольные дважды непрерывно дифференцируемые функции своих аргументов. Как легко проверить, прямая и обратная волны удовлетворяют следующим уравнениям в частных производных первого порядка:

и

Уравнения (12.3) и (12.4) часто называются уравнениями переноса, поскольку их решения (функции переносят соответственно начальный профиль или вдоль оси х с постоянной скоростью а в прямом или обратном направлении. Легко показать, что если решение уравнения переноса является дважды непрерывно дифференцируемой функцией своего аргумента, то оно удовлетворяет и уравнению колебаний. При этом не происходит искажения профиля волны во времени, т. е. отсутствует эффект дисперсии волны, что связано с постоянством скорости распространения, в свою очередь определяющимся постоянством параметров среды. Однако во многих физических задачах приходится учитывать изменение свойств среды под действием распространяющихся в ней волн. Это приводит к зависимости скорости распространения от решения, что связано с необходимостью рассматривать квазилинейное уравнение переноса вида

В этом параграфе мы рассмотрим свойства решения простейшего квазилинейного уравнения переноса вида

Поставим для него задачу Коши, задав начальное условие

По аналогии с линейным уравнением переноса с постоянным коэффициентом будем искать решение уравнения (12.6) в виде

и попытаемся найти функцию такую, чтобы удовлетворялись как уравнение (12.6), так и начальное условие (12.7). Вычисляя частные производные их и получим

Подстановка этих выражений в уравнение (12.6) дает

или

Так как решение уравнения (12.6), то данное соотношение удовлетворяется при любой дифференцируемой функции Отсюда следует, что решение исходной задачи Коши (12.6), (12.7) определяется из неявного уравнения

Мы не будем заниматься анализом соотношения (12.9), а полытаемся получить необходимые в дальнейшем результаты другим способом — методом характеристик.

Рассмотрим на плоскости кривую, определяемую дифференциальным уравнением

или

и называемую характеристикой уравнения (12.6).

Пусть — решение уравнения (12.10), тогда

т. e. есть константа на кривой следовательно, как вытекает из (12.10), представляет собой прямую линию на плоскости с наклоном

определяемым начальной функцией Для этой лрямой можно записать уравнение

Таким образом, мы получаем однопараметрическое семейство прямых, зависящих от параметра и обладающих тем свойством, что решение уравнения (12.6) на этих прямых оказывается постоянным. Это позволяет по начальной функции определить функцию в любой момент времени Покажем, как это можно сделать практически.

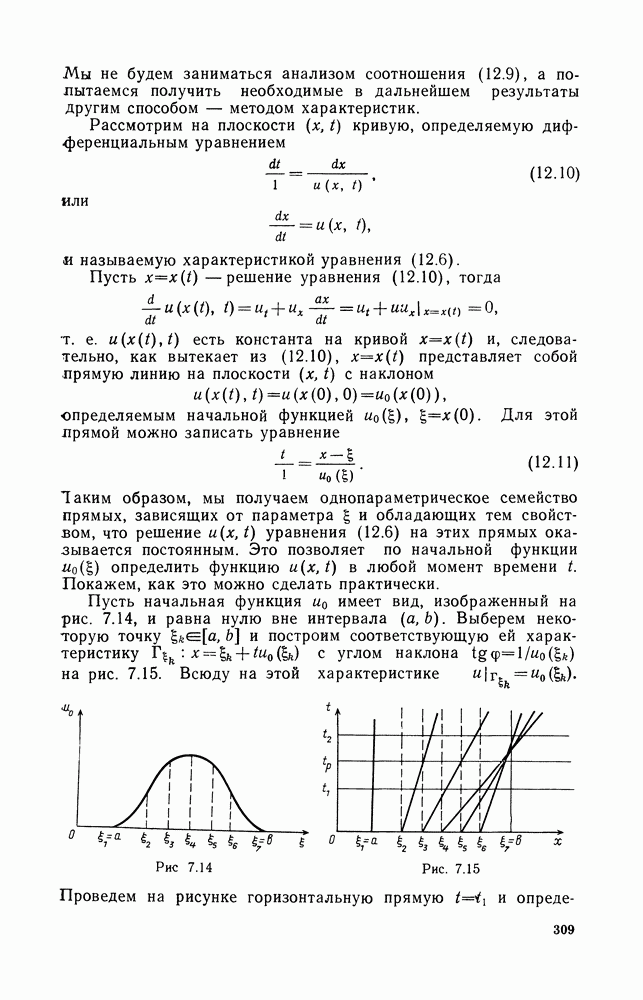
Пусть начальная функция имеет вид, изображенный на рис. 7.14, и равна нулю вне интервала Выберем некоторую точку и построим соответствующую ей характеристику с углом наклона на рис. 7.15. Всюду на этой характеристике

Рис. 7.14

Рис. 7.15

Проведем на рисунке горизонтальную прямую и

определим точку пересечения этой прямой с характеристикой Пусть эта точка имеет координаты Изобразим теперь на плоскости точку с координатами Проведем аналогичные построения для различных точек получим совокупность точек у образующую некоторую линию на плоскости представляющую график решения уравнения (12.6) для момента времени С помощью этой процедуры мы можем вычислить функцию для любых моментов времени.

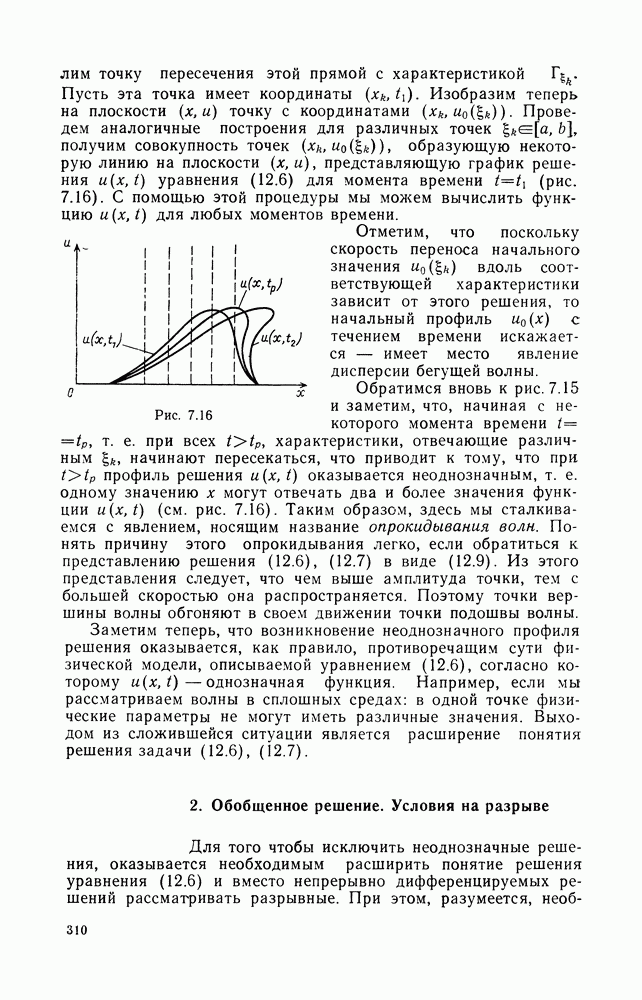
Рис. 7.16

Отметим, что поскольку скорость переноса начального значения вдоль соответствующей характеристики зависит от этого решения, то начальный профиль с течением времени искажается — имеет место явление дисперсии бегущей волны.

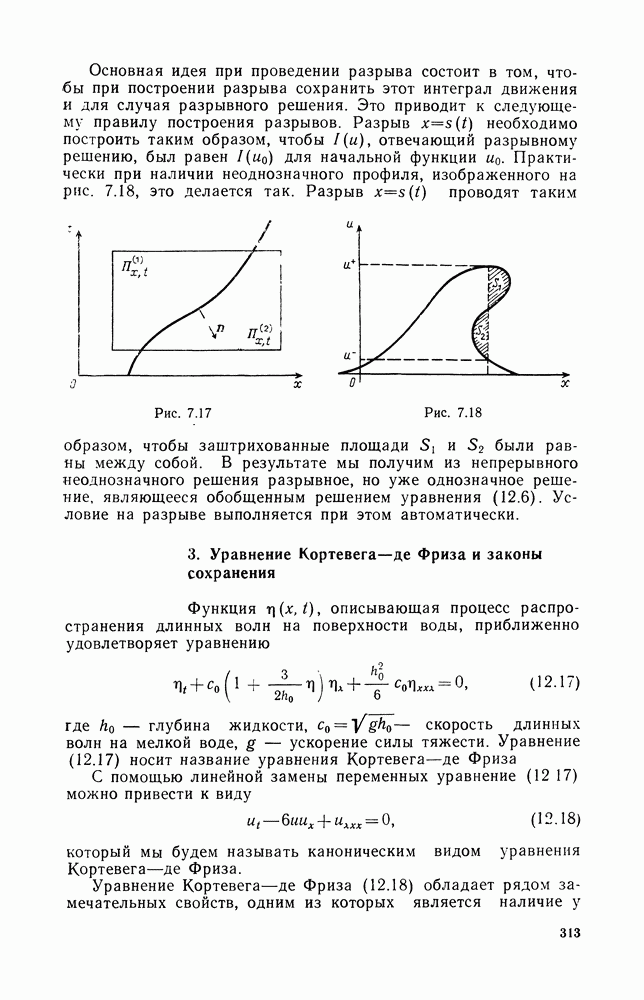
Обратимся вновь к рис. 7.15 и заметим, что, начиная с некоторого момента времени т. е. при всех характеристики, отвечающие различным начинают пересекаться, что приводит к тому, что при профиль решения оказывается неоднозначным, т. е. одному значению х могут отвечать два и более значения функции (см. рис. 7.16). Таким образом, здесь мы сталкиваемся с явлением, носящим название опрокидывания волн. Понять причину этого опрокидывания легко, если обратиться к представлению решения (12.6), (12.7) в виде (12.9). Из этого представления следует, что чем выше амплитуда точки, тем с большей скоростью она распространяется. Поэтому точки вершины волны обгоняют в своем движении точки подошвы волны.

Заметим теперь, что возникновение неоднозначного профиля решения оказывается, как правило, противоречащим сути физической модели, описываемой уравнением (12.6), согласно которому однозначная функция. Например, если мы рассматриваем волны в сплошных средах: в одной точке физические параметры не могут иметь различные значения. Выходом из сложившейся ситуации является расширение понятия решения задачи (12.6), (12.7).