| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5. Колебания струны под действием мгновенного сосредоточенного импульса
Предположим, что в начальный момент  точкам однородной струны
точкам однородной струны  сообщают постоянную скорость
сообщают постоянную скорость  например, ударяя по струне молоточком. Тем самым к этому участку струны прикладывается импульс
например, ударяя по струне молоточком. Тем самым к этому участку струны прикладывается импульс  равный измерению количества движения при
равный измерению количества движения при  где
где  постоянная линейная плотность струны. Таким образом, нужно решить задачу о колебаниях бесконечной струны с нулевым начальным отклонением
постоянная линейная плотность струны. Таким образом, нужно решить задачу о колебаниях бесконечной струны с нулевым начальным отклонением  и начальной скоростью, равной постоянной
и начальной скоростью, равной постоянной  на интервале
на интервале  и нулю вне этого интервала. Решение этой задачи проанализировано в примере
и нулю вне этого интервала. Решение этой задачи проанализировано в примере  Если теперь совершить предельный переход при
Если теперь совершить предельный переход при  увеличивая одновременно начальную скорость
увеличивая одновременно начальную скорость  так, чтобы суммарный начальный импульс
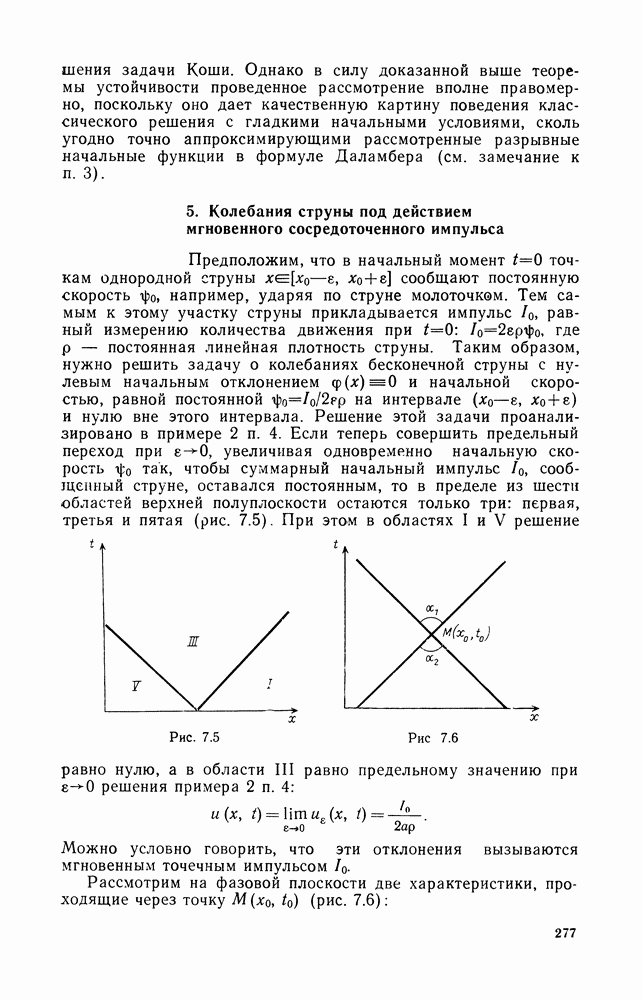
так, чтобы суммарный начальный импульс  сообщенный струне, оставался постоянным, то в пределе из шести областей верхней полуплоскости остаются только три: первая, третья и пятая (рис. 7.5).
сообщенный струне, оставался постоянным, то в пределе из шести областей верхней полуплоскости остаются только три: первая, третья и пятая (рис. 7.5).

Рис. 7.5

Рис. 7.6
При этом в областях  решение равно нулю, а в области III равно предельному значению при
решение равно нулю, а в области III равно предельному значению при  решения примера 2 п. 4:
решения примера 2 п. 4:

Можно условно говорить, что эти отклонения вызываются мгновенным точечным импульсом 
Рассмотрим на фазовой плоскости две характеристики, проходящие через точку  (рис. 7.6):
(рис. 7.6):

Эти характеристики определяют два угла  называемых соответственно верхним и нижним характеристическими углами точки
называемых соответственно верхним и нижним характеристическими углами точки  Действие мгновенного точечного импульса
Действие мгновенного точечного импульса  в точке
в точке  вызывает отклонение, равное
вызывает отклонение, равное  внутри верхнего характеристического угла точки
внутри верхнего характеристического угла точки  и нулю вне его.
и нулю вне его.
Эту функцию  естественно называть функцией мгновенного сосредоточенного импульса, приложенного к точке струны в момент времени
естественно называть функцией мгновенного сосредоточенного импульса, приложенного к точке струны в момент времени 
С другой стороны, из этих рассуждений следует, что отклонение в произвольной точке х струны в момент времени  вызываемое мгновенным импульсом 10 в точке
вызываемое мгновенным импульсом 10 в точке  в момент времени
в момент времени  зависит от того, находится ли точка фазовой плоскости
зависит от того, находится ли точка фазовой плоскости  внутри верхнего характеристического угла точки
внутри верхнего характеристического угла точки  или нет. Если точка
или нет. Если точка  расположена внутри верхнего характеристического угла точки
расположена внутри верхнего характеристического угла точки  то
то  если нет, то
если нет, то 
Предположим теперь, что в момент времени  струне сообщается распределенный импульс с плотностью распределения
струне сообщается распределенный импульс с плотностью распределения  Отклонение, вызываемое таким импульсом, на основании принципа суперпозиции равно при
Отклонение, вызываемое таким импульсом, на основании принципа суперпозиции равно при 

Если внешняя сила, распределенная непрерывно в пространстве и во времени, начинает действовать в момент времени  причем начальные смещения и скорости точек струны нулевые, то в силу принципа суперпозиции отклонение равно
причем начальные смещения и скорости точек струны нулевые, то в силу принципа суперпозиции отклонение равно

Отметим, что из формулы (7.19) следует, что отклонение точек струны под действием распределенной с плотностью  силы определяется лишь значениями функции
силы определяется лишь значениями функции  внутри нижнего характеристического угла точки
внутри нижнего характеристического угла точки  на фазовой плоскости и не зависит от распределения этой силы вне данного характеристического угла. В этом проявляется эффект конечной скорости распространения внешних воздействий на точки струны.
на фазовой плоскости и не зависит от распределения этой силы вне данного характеристического угла. В этом проявляется эффект конечной скорости распространения внешних воздействий на точки струны.
Формула (7.19) получена на физическом уровне строгости. Получим теперь строго математически более общую формулу, из которой будет следовать формула (7.19).
Напомним известные из курса математического анализа формулы Грина, которые сформулируем в удобном для нас виде. Пусть функция  непрерывно дифференцируема в области
непрерывно дифференцируема в области  и непрерывна в области
и непрерывна в области  где
где  двумерная область с границей
двумерная область с границей  в плоскости
в плоскости  Тогда имеют место следующие формулы:
Тогда имеют место следующие формулы:

где контур  проходится в положительном направлении (чтобы область
проходится в положительном направлении (чтобы область  находилась слева от направления движения).
находилась слева от направления движения).
Предположим, что классическое решение задачи (7.1), (7.2) для неоднородного уравнения колебаний с неоднородными начальными условиями существует.
Возьмем на фазовой плоскости точку  и построим характеристический треугольник
и построим характеристический треугольник  (рис. 7.7). Проинтегрируем уравнение (7.1) колебаний по этому треугольнику, предварительно умножив его на 1/2а. В результате получим
(рис. 7.7). Проинтегрируем уравнение (7.1) колебаний по этому треугольнику, предварительно умножив его на 1/2а. В результате получим


Рис. 7.7
Применим к интегралам в левой части формулы Грина (7.20):

Поскольку на отрезке  а на отрезках характеристик
а на отрезках характеристик  и
и  имеют место соотношения
имеют место соотношения  из формул (7.22) имеем
из формул (7.22) имеем


Из (7.21) и (7.23) следует формула

Учитывая, что точки  имеют соответственно координаты
имеют соответственно координаты  , и используя начальные условия (7.2), окончательно получаем формулу для решения задачи
, и используя начальные условия (7.2), окончательно получаем формулу для решения задачи

Заметим, что формула (7.24) представляет решение задачи (7.1), (7.2) в виде суммы решения двух задач. Если положить в  то формула (7.24) дает решение задачи для однородного уравнения колебаний и неоднородных начальных условий и совпадает с полученной в п. 2 § 7 формулой Даламбера (7.10). При
то формула (7.24) дает решение задачи для однородного уравнения колебаний и неоднородных начальных условий и совпадает с полученной в п. 2 § 7 формулой Даламбера (7.10). При  формула (7.24) представляет решение задачи для неоднородного уравнения колебаний с однородными начальными условиями. В этом случае она совпадает с формулой (7.19), полученной из физических соображений.
формула (7.24) представляет решение задачи для неоднородного уравнения колебаний с однородными начальными условиями. В этом случае она совпадает с формулой (7.19), полученной из физических соображений.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
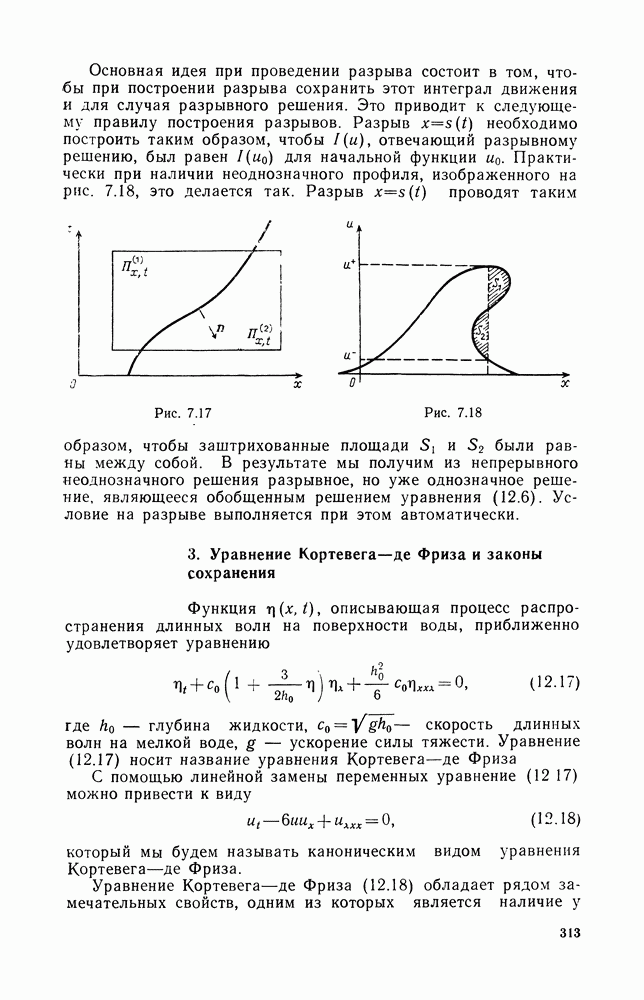
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ