| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
В гл. V были подробно рассмотрены свойства гармонических функций, т. е. решений уравнения Лапласа. Сейчас будем исследовать свойства решений уравнения  где с — некоторая постоянная.
где с — некоторая постоянная.
1. Фундаментальные решения уравнения Гельмгольца
При изучении свойств гармонических функций важную роль играло фундаментальное решение уравнения Лапласа. Построим фундаментальное решение уравнения 
Рассмотрим сначала трехмерный случай. Будем действовать по той же схеме, что и при построении фундаментального решения уравнения Лапласа. Пусть  некоторая фиксированная точка. Введем сферическую систему координат
некоторая фиксированная точка. Введем сферическую систему координат  с
с
центром в точке  Найдем решение уравнения
Найдем решение уравнения  зависящее только от
зависящее только от  (радиально-симметричное решение). Расписывая оператор Лапласа в сферической системе координат и учитывая, что и зависит только от
(радиально-симметричное решение). Расписывая оператор Лапласа в сферической системе координат и учитывая, что и зависит только от  получим
получим

Поскольку

то, сделав замену

уравнение (2.1) запишем в виде

Рассмотрим отдельно случаи  Пусть
Пусть  -действительно,
-действительно,  Уравнение (2.2) принимает вид
Уравнение (2.2) принимает вид

Решение его можно записать в виде

или, используя вещественные линейно независимые решения, в виде

При  действительно,
действительно,  решение уравнения (2.2) имеет вид
решение уравнения (2.2) имеет вид

Таким образом, найдены следующие радиально-симметричные относительно точки  решения уравнения
решения уравнения 

Отметим, что все эти решения при  имеют одинаковую особенность, совпадающую с особенностью фундаментального решения уравнения Лапласа.
имеют одинаковую особенность, совпадающую с особенностью фундаментального решения уравнения Лапласа.
Рассмотрим поведение этих решений при  В случае
В случае  одно решение
одно решение  экспоненциально убывает
экспоненциально убывает
на бесконечности, второе  неограниченно возрастает на бесконечности и физического смысла не имеет. Фундаментальным решением при
неограниченно возрастает на бесконечности и физического смысла не имеет. Фундаментальным решением при  называется решение
называется решение

При  ситуация более сложная, поскольку оба решения
ситуация более сложная, поскольку оба решения

а также действительное решение

при  убывают по одному и тому же закону. Еще одно действительное решение
убывают по одному и тому же закону. Еще одно действительное решение  мы не рассматриваем, так как оно ограничено во всем пространстве.
мы не рассматриваем, так как оно ограничено во всем пространстве.
При изучении уравнения  в ограниченной области решения (2.3), (2.4) эквивалентны и каждое из них является фундаментальным решением этого уравнения.
в ограниченной области решения (2.3), (2.4) эквивалентны и каждое из них является фундаментальным решением этого уравнения.
Рассмотрим физическую интерпретацию этих решений в неограниченном пространстве и выясним, чем они отличаются друг от друга. Ранее мы установили (гл. VII), что волновое уравнение

описывает распространение волн в однородном пространстве (а — скорость распространения волн). Если рассматривать установившиеся гармонические волны, зависящие от времени по закону

то для амплитуды волны  получаем интересующее нас уравнение
получаем интересующее нас уравнение

Таким образом, сферически-симметричные относительно точки  решения уравнения (2.5), построенные на основе (2.3) — (2.4), имеют вид
решения уравнения (2.5), построенные на основе (2.3) — (2.4), имеют вид

Решение  представляет собой сферическую волну, расходящуюся от точки М (волну, уходящую на бесконечность); решение
представляет собой сферическую волну, расходящуюся от точки М (волну, уходящую на бесконечность); решение  представляет собой волну, сходящуюся к точке М (приходящую из бесконечности); решение
представляет собой волну, сходящуюся к точке М (приходящую из бесконечности); решение  стоячая волна с особенностью в точке
стоячая волна с особенностью в точке  (содержащая волну, приходящую из бесконечности). Если мы считаем, что все источники волн расположены в конечной области пространства, то два последних решения, содержащие приходящие из бесконечности волны, не имеют физического смысла. Решением, имеющим физический смысл, является решение
(содержащая волну, приходящую из бесконечности). Если мы считаем, что все источники волн расположены в конечной области пространства, то два последних решения, содержащие приходящие из бесконечности волны, не имеют физического смысла. Решением, имеющим физический смысл, является решение

Решения  представляют собой амплитуды распространяющихся сферических волн. Они называются фундаментальными решениями уравнения Гельмгольца в неограниченной области. Для выделения одного из них следует на бесконечности поставить дополнительное условие, которое будет рассмотрено позже.
представляют собой амплитуды распространяющихся сферических волн. Они называются фундаментальными решениями уравнения Гельмгольца в неограниченной области. Для выделения одного из них следует на бесконечности поставить дополнительное условие, которое будет рассмотрено позже.
Еще раз подчеркнем, что в ограниченной области решения (2.3), (2.4) эквивалентны.
Рассмотрим теперь плоский случай. Введем полярную систему координат  с началом в точке
с началом в точке  Решение и, зависящее только от
Решение и, зависящее только от  удовлетворяет уравнению
удовлетворяет уравнению

или

При  это уравнение Бесселя нулевого порядка. Следовательно, его общее решение имеет вид
это уравнение Бесселя нулевого порядка. Следовательно, его общее решение имеет вид

или

При  есть уравнение для функций Бесселя чисто мнимого аргумента нулевого порядка, и его общее решение можно записать в виде
есть уравнение для функций Бесселя чисто мнимого аргумента нулевого порядка, и его общее решение можно записать в виде

При  фундаментальным решением уравнения
фундаментальным решением уравнения  называется функция
называется функция

экспоненциально убывающая на бесконечности и при  имеющая особенность вида
имеющая особенность вида

При  ситуация аналогична трехмерному случаю. В ограниченной области решения
ситуация аналогична трехмерному случаю. В ограниченной области решения

эквивалентны и являются фундаментальными решениями уравнения Гельмгольца  Напомним, что эти функции при
Напомним, что эти функции при  имеют логарифмическую особенность, поскольку
имеют логарифмическую особенность, поскольку

В неограниченной области фундаментальным решением уравнения Гельмгольца  при
при  является одна из функций
является одна из функций  в зависимости от того, какое дополнительное условие поставлено на бесконечность. Напомним также поведение этих функций на бесконечности:
в зависимости от того, какое дополнительное условие поставлено на бесконечность. Напомним также поведение этих функций на бесконечности:

Отметим, что все фундаментальные решения уравнения  на плоскости имеют такую же логарифмическую особенность, как и фундаментальное решение уравнения Лапласа на плоскости.
на плоскости имеют такую же логарифмическую особенность, как и фундаментальное решение уравнения Лапласа на плоскости.
2. Формулы Грина
В гл. III получены первая и вторая формулы Грина для общего эллиптического самосопряженного оператора. Естественно, что они справедливы и для оператора  При выводе третьей формулы Грина использовалось фундаментальное решение уравнения Лапласа. Мы только что установили, что особенности фундаментальных решений уравнения Лапласа и уравнения Гельмгольца совпадают. Поэтому для вывода третьей формулы Грина для оператора
При выводе третьей формулы Грина использовалось фундаментальное решение уравнения Лапласа. Мы только что установили, что особенности фундаментальных решений уравнения Лапласа и уравнения Гельмгольца совпадают. Поэтому для вывода третьей формулы Грина для оператора  нужно повторить все те же рассуждения, которые проведены в § 1 гл.
нужно повторить все те же рассуждения, которые проведены в § 1 гл.  Мы этого делать не будем, а приведем в качестве примера окончательную формулу для случая
Мы этого делать не будем, а приведем в качестве примера окончательную формулу для случая  Она имеет вид
Она имеет вид


В формуле (2.7), как и прежде,  -дважды непрерывно дифференцируемая в
-дважды непрерывно дифференцируемая в  функция, непрерывная вместе с первыми производными в
функция, непрерывная вместе с первыми производными в  поверхность Ляпунова,
поверхность Ляпунова,  внешняя нормаль к
внешняя нормаль к  (внешняя по отношению к области
(внешняя по отношению к области  В формуле (2.7) можно использовать и другое фундаментальное решение. Аналогичная формула имеет место и при
В формуле (2.7) можно использовать и другое фундаментальное решение. Аналогичная формула имеет место и при 
Из (2.7) сразу получается интегральное представление решения уравнения 

в любой внутренней точке области 
Отсюда, так же как и для гармонических функций, получаем, что любое решение уравнения Гельмгольца в любой внутренней точке области  имеет производные всех порядков.
имеет производные всех порядков.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
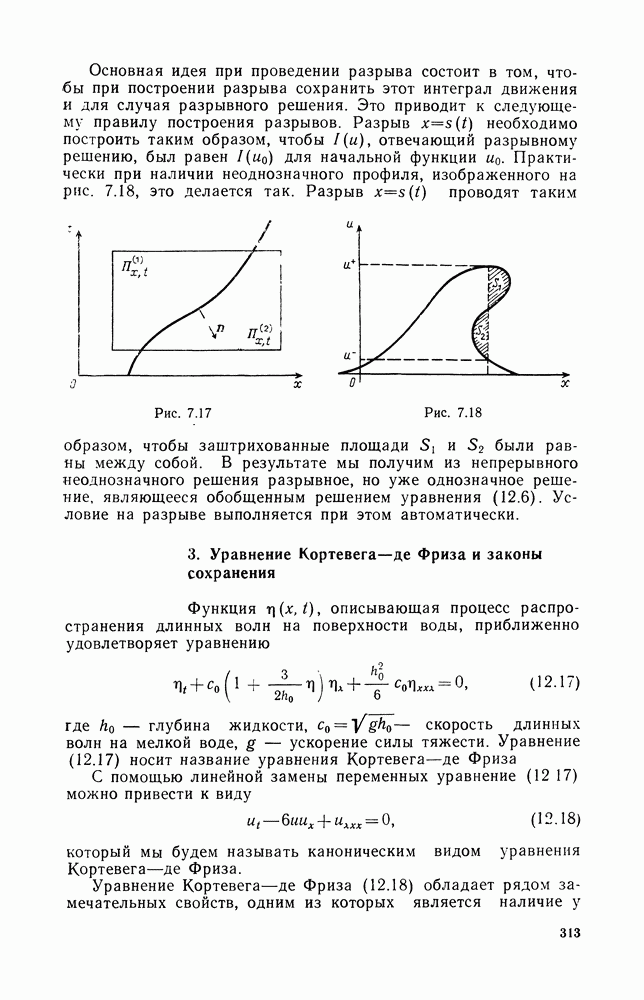
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ