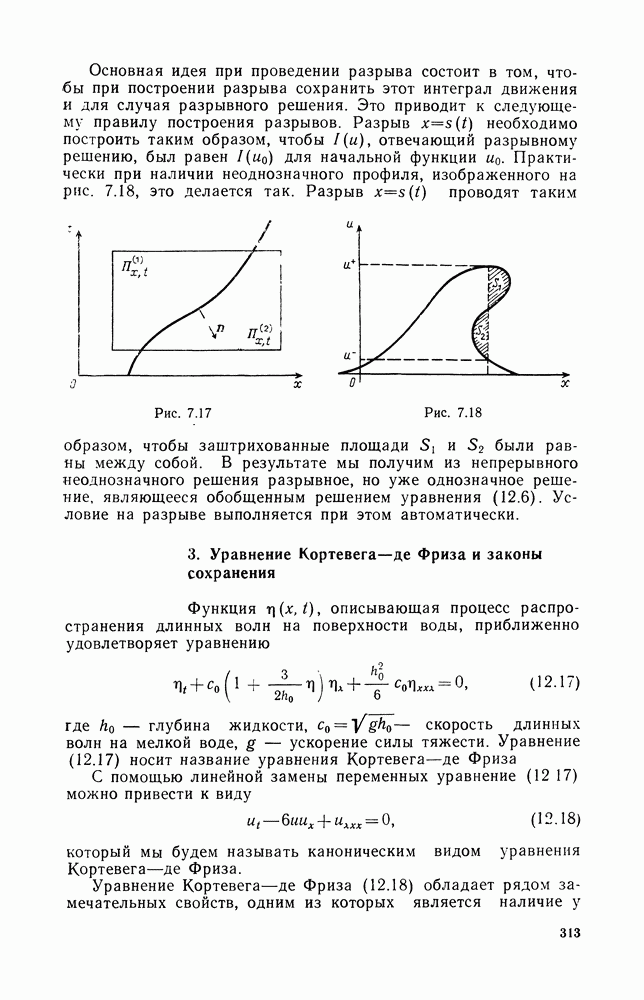
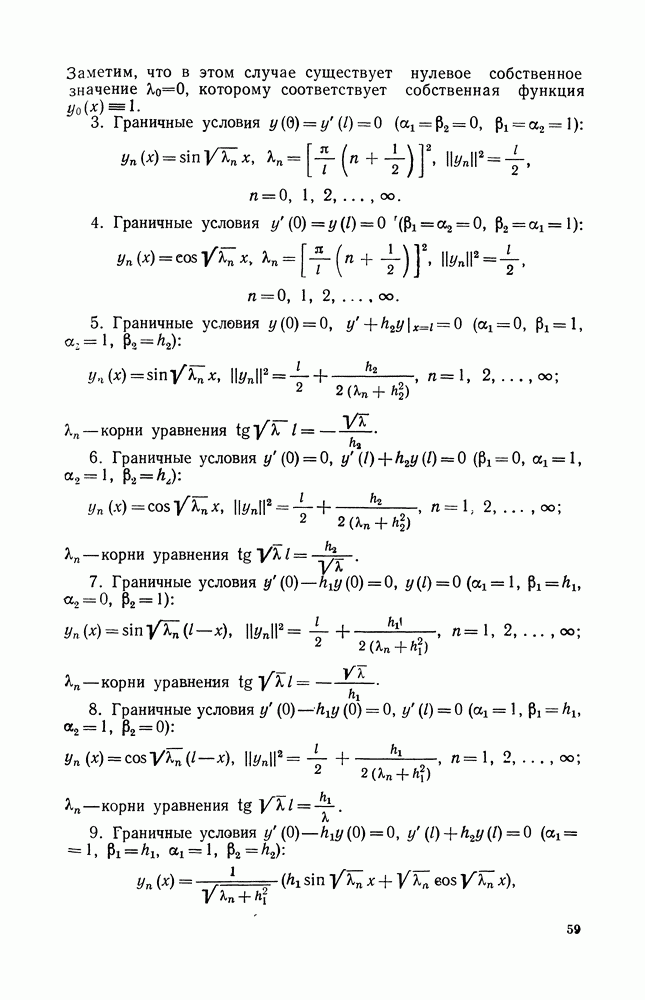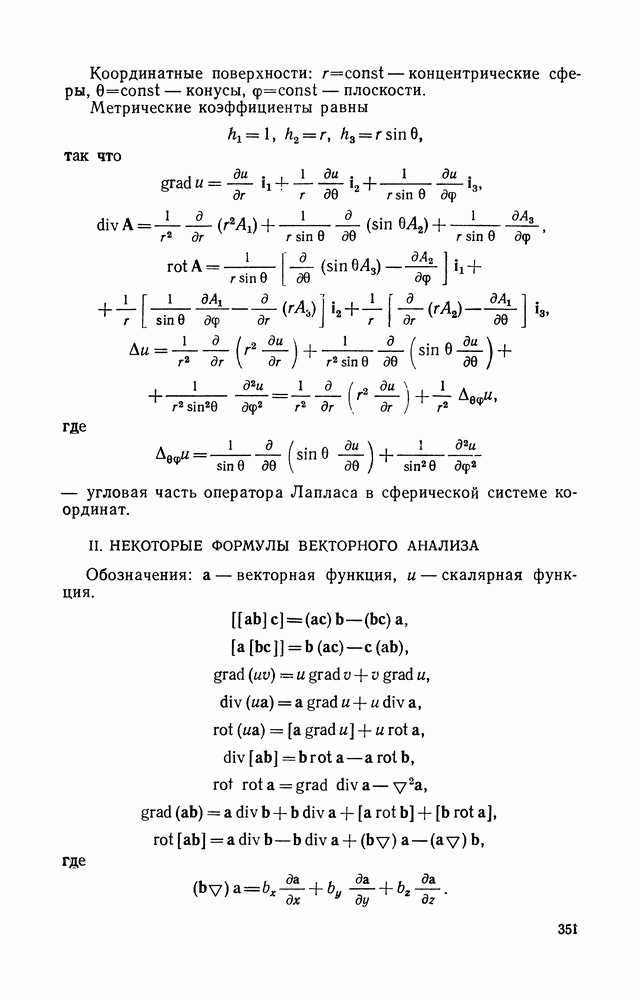| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4. Схема метода обратной задачи
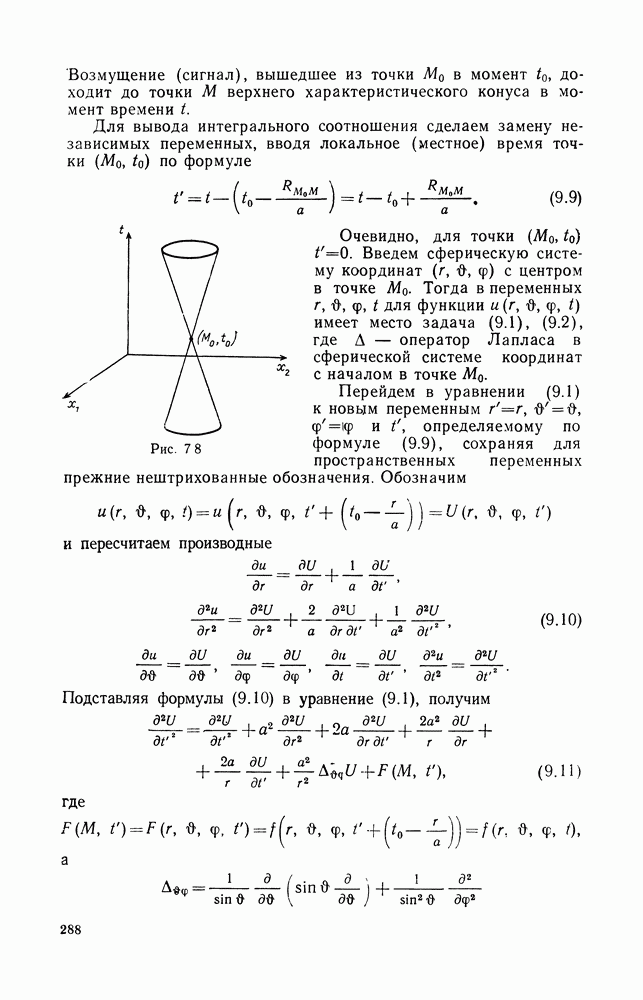
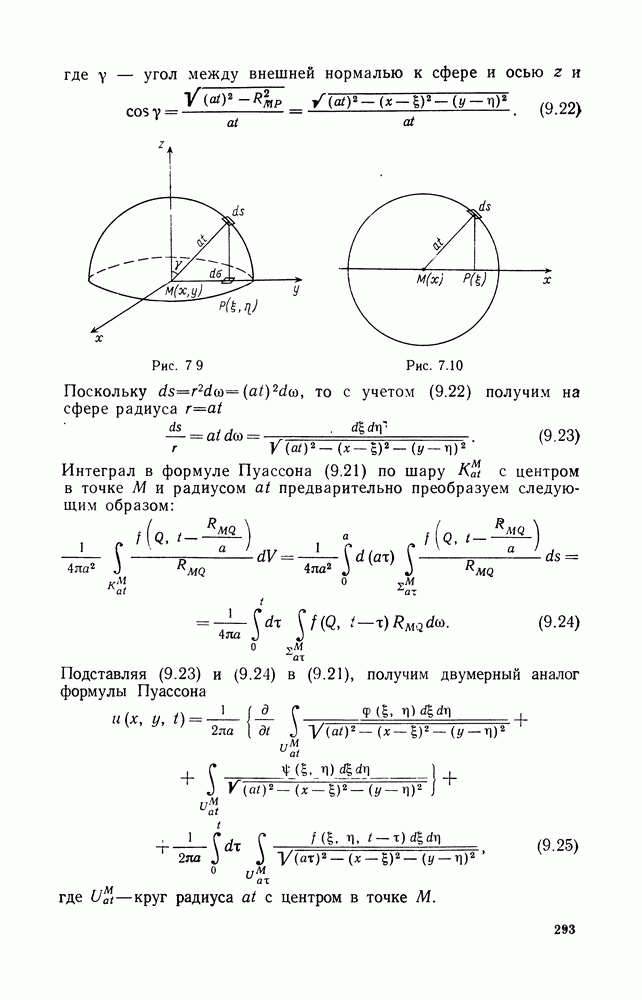
1) Прямая и обратная задачи рассеяния
Одним из методов интегрирования уравнения Кортевега — де Фриза является метод обратной задачи. В этом методе для интегрирования нелинейного уравнения необходимо последовательно решить две линейные задачи. При этом оказалось, что с уравнением (12.17) тесно связано дифференциальное уравнение

которое в физической литературе часто называется стационарным уравнением Шредингера с потенциалом  Функция
Функция  зависит от
зависит от  как от параметра,
как от параметра,  в (12.19) — числовой параметр.
в (12.19) — числовой параметр.
Приведем некоторые необходимые сведения об уравнении (12.19).
Определение. Функцию  будем называть быстроубывающей, если
будем называть быстроубывающей, если

Ниже будем предполагать, что потенциал  является быстроубывающим.
является быстроубывающим.
Для уравнения (12.19) рассмотрим две задачи. Первая из них состоит в нахождении таких значений  при которых уравнение (12.19) имеет нетривиальные решения
при которых уравнение (12.19) имеет нетривиальные решения 
Вторая — в нахождении при  ограниченных решений уравнения (12.19) с заданным характером асимптотического поведения при
ограниченных решений уравнения (12.19) с заданным характером асимптотического поведения при 

Здесь  и функции
и функции  подлежат определению. С физической точки зрения рассмотренные задачи можно трактовать следующим образом. Первую задачу — как задачу о нахождении собственных значений (квантовомеханических уровней энергии) так называемых связанных состояний, определяемых нормируемыми на единицу в
подлежат определению. С физической точки зрения рассмотренные задачи можно трактовать следующим образом. Первую задачу — как задачу о нахождении собственных значений (квантовомеханических уровней энергии) так называемых связанных состояний, определяемых нормируемыми на единицу в  волновыми функциями
волновыми функциями  Вторую — как задачу рассеяния плоской волны единичной амплитуды на потенциале
Вторую — как задачу рассеяния плоской волны единичной амплитуды на потенциале  Коэффициенты
Коэффициенты  трактуются при этом как коэффициенты отражения и прохождения соответственно, причем
трактуются при этом как коэффициенты отражения и прохождения соответственно, причем

Первая задача для (12.19) может иметь решение лишь при  при этом эти решения имеют при
при этом эти решения имеют при  асимптотику следующего вида:
асимптотику следующего вида:

где  собственное значение. Таким образом, для нормированных на единицу в
собственное значение. Таким образом, для нормированных на единицу в  собственных функций
собственных функций  отвечающих собственным значениям
отвечающих собственным значениям  величины
величины  определяются из равенства
определяются из равенства

Предположим теперь, что обе задачи для уравнения (12.19) решены и определены совокупности  Эти совокупности принято называть данными рассеяния. Отыскание их для заданного потенциала
Эти совокупности принято называть данными рассеяния. Отыскание их для заданного потенциала  составляет прямую задачу рассеяния.
составляет прямую задачу рассеяния.
Пусть нам известны данные рассеяния для некоторого потенциала  Поставим теперь задачу об отыскании по заданным данным рассеяния соответствующего потенциала. Эта задача носит название обратной задачи рассеяния.
Поставим теперь задачу об отыскании по заданным данным рассеяния соответствующего потенциала. Эта задача носит название обратной задачи рассеяния.
Оказывается, что данных рассеяния вполне достаточно для однозначного определения потенциала. Конструктивно процедура его нахождения выглядит следующим образом.
По данным рассеяния строится функция

называемая ядром уравнения Гельфанда-Левитана, а затем ищется решение  следующего линейного интегрального уравнения:
следующего линейного интегрального уравнения:

Решив уравнение Гельфанда-Левитана (12.24), по формуле

определяем функцию  которая и является искомым потенциалом и тем самым решением обратной задачи рассеяния.
которая и является искомым потенциалом и тем самым решением обратной задачи рассеяния.
2) Схема метода
Рассмотрим задачу Коши для уравнения (12.17):

Решение задачи Коши (12.26) назовем быстроубывающим, если функция  и все ее производные по до третьего порядка включительно являются быстроубывающими функциями.
и все ее производные по до третьего порядка включительно являются быстроубывающими функциями.
Возможность использования обратной задачи рассеяния для построения быстроубывающих решений (12.26) основана на следующих теоремах.
Теорема 7.7. Если потенциал  в (12.19) является быстроубывающим решением уравнения Кортевега—де Фриза, то собственные значения
в (12.19) является быстроубывающим решением уравнения Кортевега—де Фриза, то собственные значения  не зависят от времени
не зависят от времени 
Теорема 7.8. Если потенциал  в (12.19) является быстроубывающим решением уравнения Кортевега—де Фриза, то данные рассеяния
в (12.19) является быстроубывающим решением уравнения Кортевега—де Фриза, то данные рассеяния  зависят от времени следующим образом:
зависят от времени следующим образом:

Пусть  быстроубывающее решение задачи (12.26), отвечающее быстроубывающей функции
быстроубывающее решение задачи (12.26), отвечающее быстроубывающей функции  Тогда данные рассеяния для этой функции
Тогда данные рассеяния для этой функции  рассматриваемой как потенциал в (12.19), связаны с данными рассеяния для потенциала
рассматриваемой как потенциал в (12.19), связаны с данными рассеяния для потенциала  формулами (12.27). Следовательно, зная данные рассеяния для
формулами (12.27). Следовательно, зная данные рассеяния для  можно по формулам (12.27) найти данные рассеяния для
можно по формулам (12.27) найти данные рассеяния для  и затем, построив и решив уравнения Гельфанда-Левитана, определить функцию
и затем, построив и решив уравнения Гельфанда-Левитана, определить функцию 
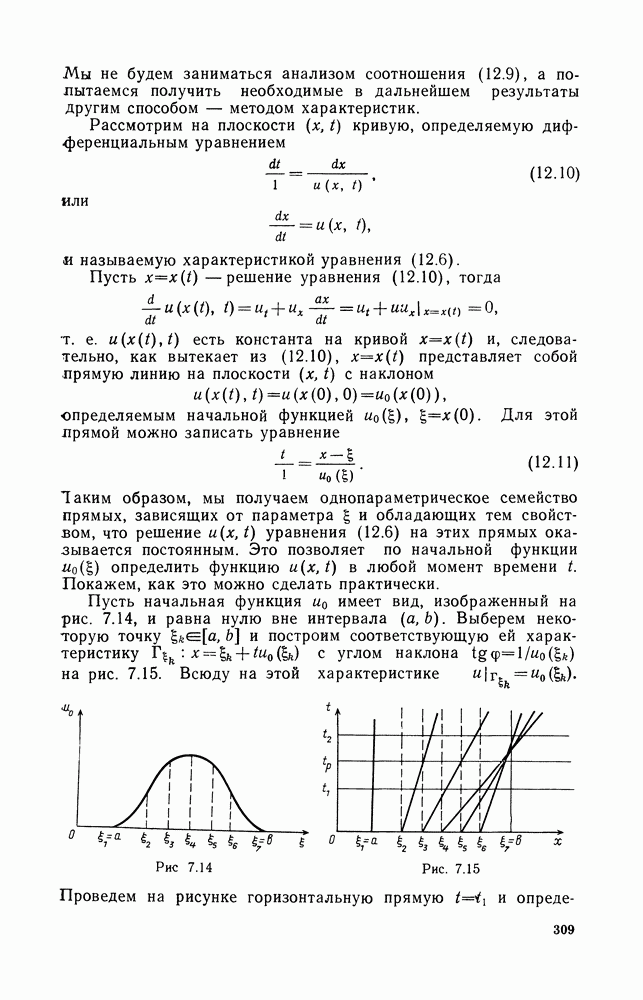
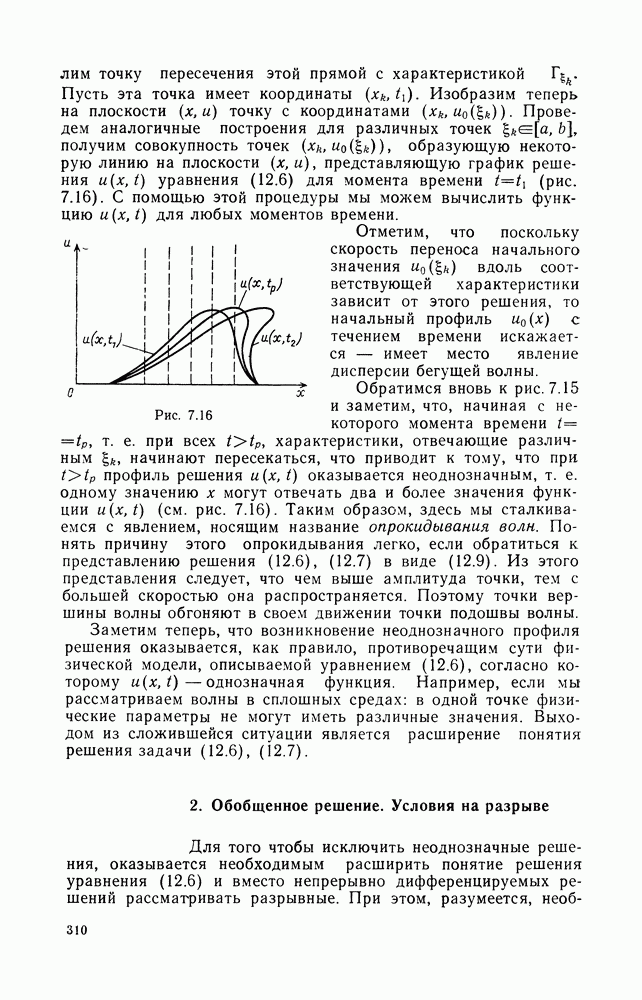
Таким образом, мы приходим к следующей схеме отыскания быстроубывающих решений (12.26).
Рассматривая уравнение

определяем данные рассеяния  начального условия
начального условия  Затем по формулам (12.27) определяем
Затем по формулам (12.27) определяем  и с помощью этих функций строим ядро уравнения Гельфанда-Левитана
и с помощью этих функций строим ядро уравнения Гельфанда-Левитана

Решив далее уравнение Гельфанда-Левитана (12.24) с ядром (12.28), по формуле (12.25) определяем решение  задачи Коши (12.26) для уравнения Кортевега - де Фриза.
задачи Коши (12.26) для уравнения Кортевега - де Фриза.
Итак, интегрирование уравнения Кортевега — де Фриза с начальным условием  в классе быстроубывающих функций сводится к последовательному решению двух линейных задач: прямой задачи рассеяния для потенциала
в классе быстроубывающих функций сводится к последовательному решению двух линейных задач: прямой задачи рассеяния для потенциала  уравнения Гельфанда-Левитана (12.24) с ядром (12.28).
уравнения Гельфанда-Левитана (12.24) с ядром (12.28).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
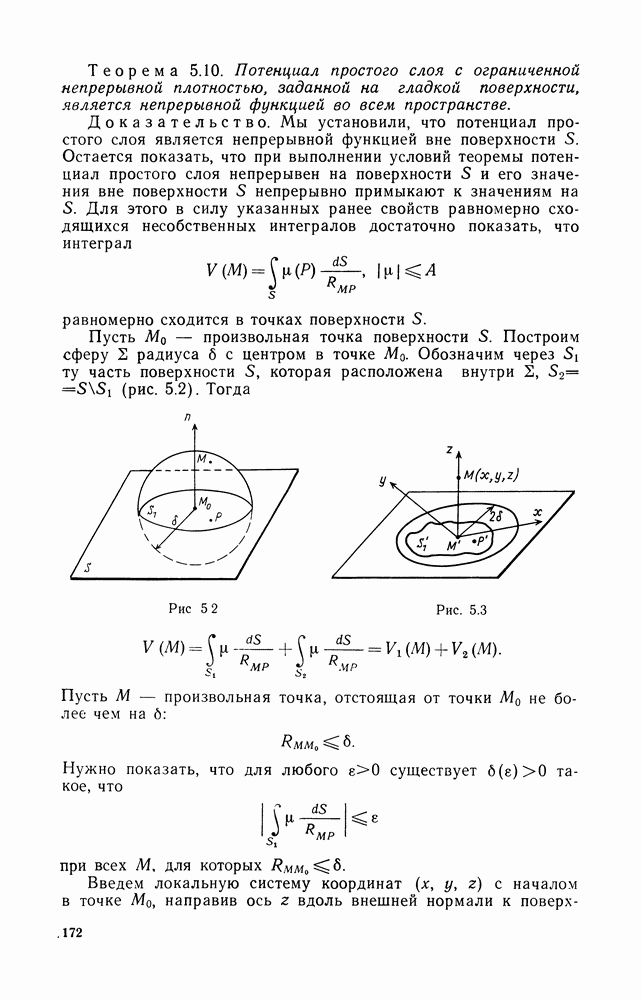
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
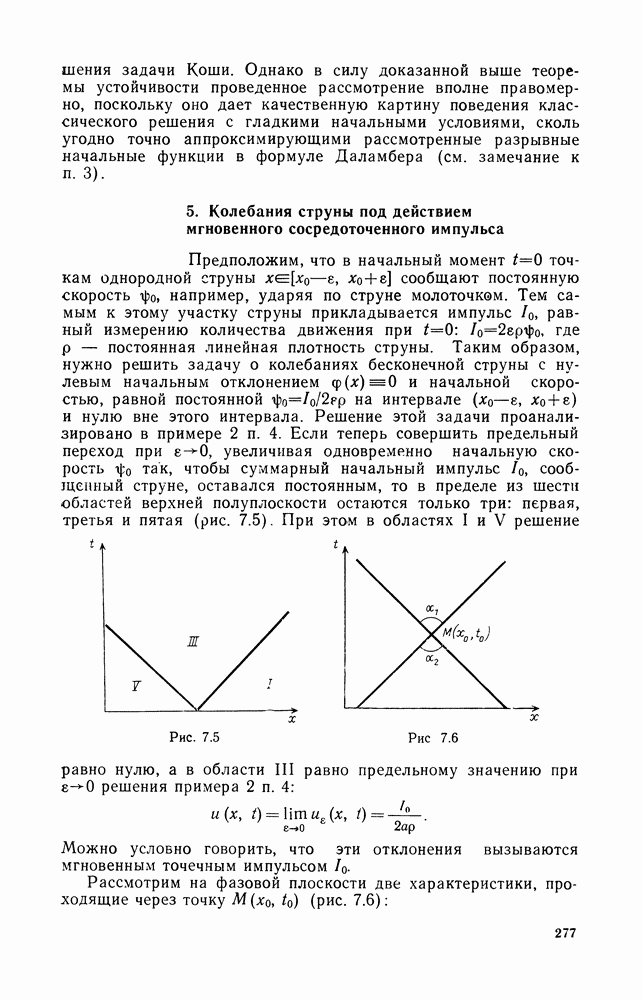
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ