| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Физическая интерпретация решения
Функция  определяемая формулой (7.10), представляет процесс распространения начального отклонения и начальной скорости. Если фиксировать некоторый момент времени
определяемая формулой (7.10), представляет процесс распространения начального отклонения и начальной скорости. Если фиксировать некоторый момент времени  то функция
то функция  дает профиль струны в момент времени
дает профиль струны в момент времени  Зафиксировав точку
Зафиксировав точку  мы получим функцию
мы получим функцию  которая описывает процесс движения точки
которая описывает процесс движения точки  Предположим теперь, что некоторый наблюдатель, находившийся в точке
Предположим теперь, что некоторый наблюдатель, находившийся в точке  в момент времени
в момент времени  движется со скоростью а в положительном направлении оси х. Введем систему координат
движется со скоростью а в положительном направлении оси х. Введем систему координат  связанную с наблюдателем. Для этого положим
связанную с наблюдателем. Для этого положим

В системе координат  функция
функция  определяется формулой
определяется формулой  т. е. наблюдатель все время видит тот же профиль, что и в начальный момент. Следовательно, функция
т. е. наблюдатель все время видит тот же профиль, что и в начальный момент. Следовательно, функция  представляет собой неизменный профиль
представляет собой неизменный профиль  который перемещается вправо (в положительном направлении оси
который перемещается вправо (в положительном направлении оси  со скоростью а. Иными словами, функция
со скоростью а. Иными словами, функция  представляет собой бегущую волну, распространяющуюся в положительном направлении оси
представляет собой бегущую волну, распространяющуюся в положительном направлении оси  скоростью а. Для краткости мы будем называть ее правой бегущей волной. Аналогично функция
скоростью а. Для краткости мы будем называть ее правой бегущей волной. Аналогично функция  представляет собой бегущую волну, распространяющуюся со скоростью а в отрицательном направлении оси х, т. е. левую бегущую волну.
представляет собой бегущую волну, распространяющуюся со скоростью а в отрицательном направлении оси х, т. е. левую бегущую волну.
Таким образом, общее решение (7.6) задачи Коши для бесконечной струны (7.3), (7.4) есть суперпозиция двух бегущих волн: правой волны

и левой волны

где функция  имеет вид
имеет вид

а  — некоторая постоянная.
— некоторая постоянная.
Для выяснения характера решения (7.6) задачи К (7.3), (7.4) удобно пользоваться плоскостью состояния  или фазовой плоскостью. Как было отмечено в
или фазовой плоскостью. Как было отмечено в  где
где  некоторые постоянные, являются характеристиками уравнения (7 3). Функция
некоторые постоянные, являются характеристиками уравнения (7 3). Функция  вдоль характеристики
вдоль характеристики  сохраняет постоянное значение
сохраняет постоянное значение  функция
функция  постоянна вдоль характеристики
постоянна вдоль характеристики  и равна
и равна 
Пусть функция  отлична от нуля в интервале
отлична от нуля в интервале  и равна нулю вне этого интервала. Проведем на фазовой плоскости через точки
и равна нулю вне этого интервала. Проведем на фазовой плоскости через точки  соответственно характеристики
соответственно характеристики  Эти характеристики разбивают верхнюю полуплоскость
Эти характеристики разбивают верхнюю полуплоскость  фазовой плоскости на три области (рис. 7.1). Функция
фазовой плоскости на три области (рис. 7.1). Функция

отлична от нуля только в области II, где выполняются неравенства 
В областях I и III выполняются соответственно неравенства  и функция
и функция  равна нулю. Характеристика
равна нулю. Характеристика  представляет собой передний фронт правой бегущей волны
представляет собой передний фронт правой бегущей волны  а характеристика
а характеристика  ее задний фронт. Аналогичным образом можно дать интерпретацию левой бегущей волны на фазовой плоскости
ее задний фронт. Аналогичным образом можно дать интерпретацию левой бегущей волны на фазовой плоскости 
Выберем на фазовой плоскости некоторую фиксированную точку  и проведем через нее характеристики
и проведем через нее характеристики  Эти характеристики пересекут ось х соответственно в точках
Эти характеристики пересекут ось х соответственно в точках  (рис. 7.2). Значение функции (7.6) в точке
(рис. 7.2). Значение функции (7.6) в точке  равно
равно


Рис. 7.1

Рис. 7.2
Таким образом, значение функции  в точке
в точке  определяется значениями функций
определяется значениями функций  в точках
в точках  соответственно, являющихся вершинами треугольника
соответственно, являющихся вершинами треугольника  образованного отрезками двух характеристик и отрезком оси х (см. рис. 7.2). Этот треугольник называется характеристическим треугольником точки
образованного отрезками двух характеристик и отрезком оси х (см. рис. 7.2). Этот треугольник называется характеристическим треугольником точки  формулы Даламбера (7.10) видно, что отклонение
формулы Даламбера (7.10) видно, что отклонение  точки
точки  струны в момент времени
струны в момент времени  зависит только от значений начального отклонения в вершинах
зависит только от значений начального отклонения в вершинах  характеристического треугольника
характеристического треугольника  и от значений начальной скорости на стороне
и от значений начальной скорости на стороне  Поэтому формулу (7.10) удобно переписать так:
Поэтому формулу (7.10) удобно переписать так:

Начальные данные  заданные вне отрезка
заданные вне отрезка  не оказывают влияния на значения функции
не оказывают влияния на значения функции  в точке
в точке  Физически это связано с конечной скоростью распространения возмущения вдоль колеблющейся струны.
Физически это связано с конечной скоростью распространения возмущения вдоль колеблющейся струны.
Рассмотрим два примера.
Пример 1. Пусть начальные скорости равны нулю:  а начальное отклонение струны является локальным, т. е. отличным от нуля на отрезке
а начальное отклонение струны является локальным, т. е. отличным от нуля на отрезке  и равным нулю вне этого отрезка. Пусть, например, функция
и равным нулю вне этого отрезка. Пусть, например, функция  имеет следующий вид:
имеет следующий вид:

Обратимся снова к фазовой плоскости. Проведем через точки  правые и левые характеристики. Эти характеристики разобьют верхнюю полуплоскость фазовой плоскости на шесть областей (рис. 7.3). Рассмотрим, чему будет равно отклонение
правые и левые характеристики. Эти характеристики разобьют верхнюю полуплоскость фазовой плоскости на шесть областей (рис. 7.3). Рассмотрим, чему будет равно отклонение  струны в каждой из этих областей.
струны в каждой из этих областей.

Рис. 7.3

Рис. 7.4
Так как начальная скорость равна нулю  из формулы Даламбера (7.10) следует, что отклонение струны в каждой из областей есть сумма левой и правой бегущих волн:
из формулы Даламбера (7.10) следует, что отклонение струны в каждой из областей есть сумма левой и правой бегущих волн:

Из формулы (7.14) следует, что в областях I, III и V отклонение равно нулю.
В самом деле, если взять в любой из этих областей точку  и построить для нее характеристический треугольник, то вершины при основании этого треугольника на оси
и построить для нее характеристический треугольник, то вершины при основании этого треугольника на оси  лежат вне отрезка
лежат вне отрезка  на котором функция начальных условий отлична от нуля. Из аналогичных построений вытекает, что в области II будет существовать только правая
на котором функция начальных условий отлична от нуля. Из аналогичных построений вытекает, что в области II будет существовать только правая
волна и  а в области IV — левая волна
а в области IV — левая волна  Если, наконец, построить характеристический треугольник для любой точки
Если, наконец, построить характеристический треугольник для любой точки  области VI, то обе вершины при основании этого треугольника будут находиться в пределах отрезка
области VI, то обе вершины при основании этого треугольника будут находиться в пределах отрезка  Следовательно, в области VI отклонение будет представлять собой сумму правой и левой волн (7.15).
Следовательно, в области VI отклонение будет представлять собой сумму правой и левой волн (7.15).
Итак, в различных областях отклонения будут иметь следующий вид:

т. e. в этой области суперпозиция правой и левой бегущих волн дает стоячую волну.
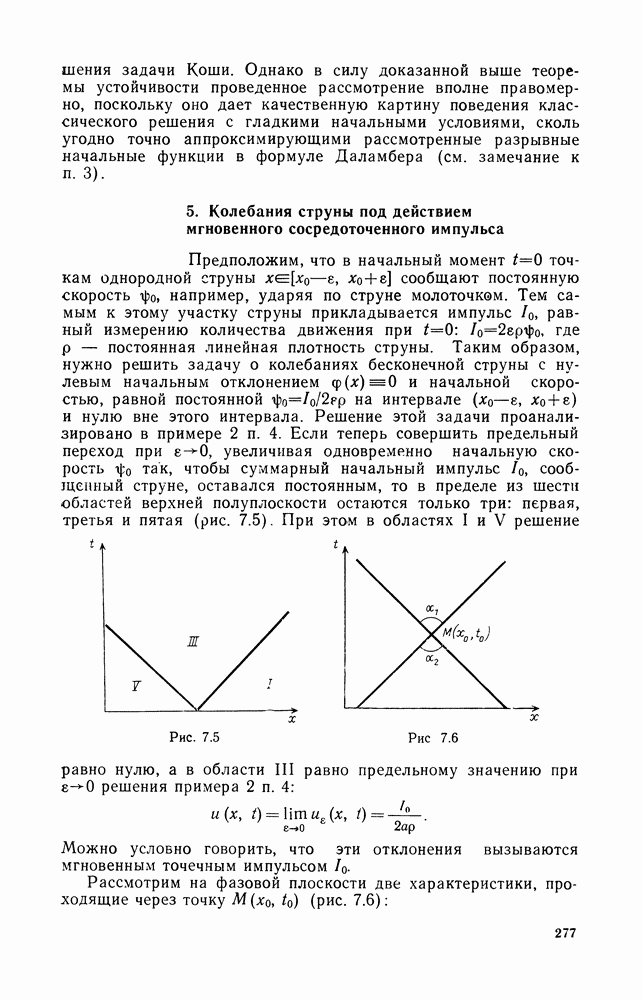
Пример 2. В качестве второго примера рассмотрим случай, когда начальное отклонение тождественно равно нулю  а начальная скорость отлична от нуля и равна постоянной
а начальная скорость отлична от нуля и равна постоянной  только в
только в  -окрестности точки
-окрестности точки 

В этом случае из формулы Даламбера (7.10) следует, что возмущение струны можно записать следующим образом:

Снова рассмотрим фазовую плоскость  и проведем через точки
и проведем через точки  характеристики, которые разобьют верхнюю полуплоскость на шесть областей (рис. 7.4).
характеристики, которые разобьют верхнюю полуплоскость на шесть областей (рис. 7.4).
В области I выполнены неравенства  Поэтому согласно формуле (7.16) подынтегральная функция в интеграле (7.17) равна нулю и
Поэтому согласно формуле (7.16) подынтегральная функция в интеграле (7.17) равна нулю и 
В области II выполнены неравенства  и согласно формулам (7.16) и (7.17) будем иметь
и согласно формулам (7.16) и (7.17) будем иметь

 правую бегущую волну, профиль которой при фиксированном
правую бегущую волну, профиль которой при фиксированном  линейно изменяется от
линейно изменяется от  до 0 при
до 0 при 
В области III выполнены неравенства  откуда
откуда

Тем самым в области III смещение точек струны не зависит ни от  ни от
ни от 
В области IV имеем неравенства  и
и

т. е. в области IV существует левая бегущая волна.
В области V выполнены неравенства  поэтому согласно (7.16) подынтегральная функция в интеграле (7.17) равна нулю и
поэтому согласно (7.16) подынтегральная функция в интеграле (7.17) равна нулю и 
Наконец, в области VI имеем неравенства  откуда
откуда

Таким образом, смещение всех точек х струны, попавших в эту область, линейно растет во времени, достигая в точке  в момент времени
в момент времени  (точка
(точка  фазовой плоскости принадлежит областям II, III, IV и VI одновременно) значения
фазовой плоскости принадлежит областям II, III, IV и VI одновременно) значения  т. е. значения постоянного смещения точек струны в области III фазовой плоскости. Отметим, что эффект постоянного смещения точек струны в области III фазовой плоскости при локальном возбуждении начальной скоростью очевиден, поскольку пределы интегрирования в формуле (7.18) не зависят ни от
т. е. значения постоянного смещения точек струны в области III фазовой плоскости. Отметим, что эффект постоянного смещения точек струны в области III фазовой плоскости при локальном возбуждении начальной скоростью очевиден, поскольку пределы интегрирования в формуле (7.18) не зависят ни от  ни от
ни от 
Если начальная скорость удовлетворяет условию  то эффекта последействия нет, в противном случае точки струны получают постоянное смещение, расплывающееся по струне в обе стороны со скоростью а вдоль характеристик
то эффекта последействия нет, в противном случае точки струны получают постоянное смещение, расплывающееся по струне в обе стороны со скоростью а вдоль характеристик 
Замечание. В рассмотренных примерах начальные данные не удовлетворяют условиям гладкости, которые были сформулированы в теореме существования классического
решения задачи Коши. Однако в силу доказанной выше теоремы устойчивости проведенное рассмотрение вполне правомерно, поскольку оно дает качественную картину поведения классического решения с гладкими начальными условиями, сколь угодно точно аппроксимирующими рассмотренные разрывные начальные функции в формуле Даламбера (см. замечание к п. 3).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
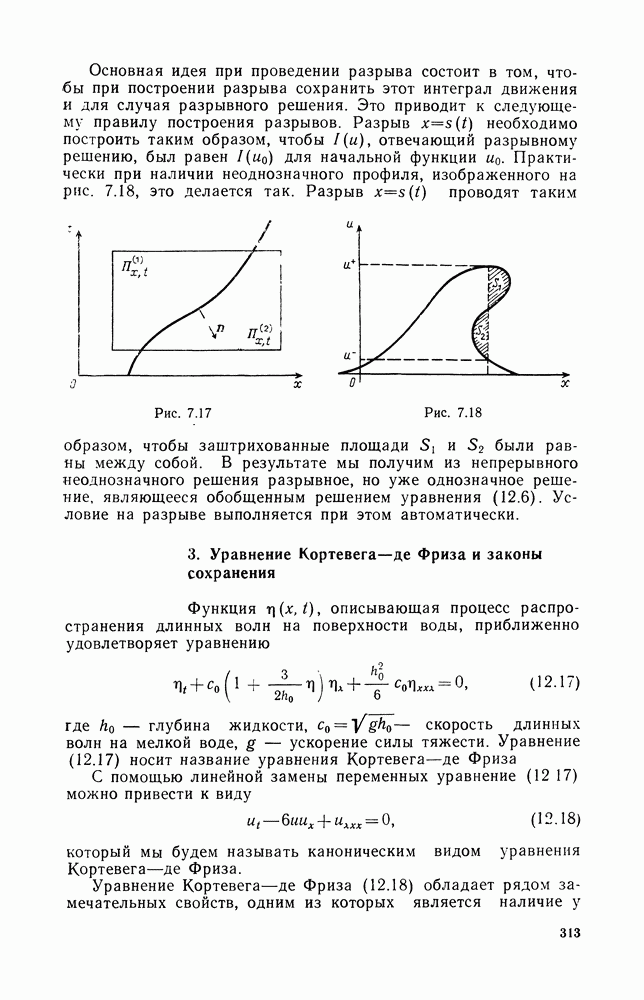
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ