| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
В предыдущих главах рассмотрены некоторые физические задачи, приводящие к уравнениям в частных производных второго порядка, и приведена классификация уравнений. Уравнения каждого типа (гиперболического, параболического и эллиптического) обладают рядом специфических свойств, и для них разработаны свои методы решения и исследования. Но существуют и общие методы, применимые для уравнений всех типов. Один из таких методов — метод разделения переменных, или метод Фурье, — будет изложен в настоящей главе. Это один из самых старых и распространенных методов аналитического решения уравнений. Метод Фурье будет рассмотрен на примере уравнения более общего, чем те, которые рассмотрены ранее. Это уравнение будем записывать в виде

где

 функции переменной
функции переменной  в области
в области  ограниченной замкнутой поверхностью
ограниченной замкнутой поверхностью  непрерывные функции переменной
непрерывные функции переменной  Уравнение рассматривается в области
Уравнение рассматривается в области 
Заметим, что при  это уравнение гиперболического типа, при
это уравнение гиперболического типа, при  параболического, при
параболического, при  эллиптического. В случае
эллиптического. В случае  область
область  отождествляется с областью
отождествляется с областью 
§ 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
При решении дифференциальных уравнений можно ставить различные цели. Можно искать общее решение уравнения или искать некоторое частное решение, удовлетворяющее некоторым дополнительным условиям. В нашем курсе мы
исходим из того, что каждое изучаемое уравнение в рамках определенной математической модели описывает некоторый реальный физический процесс или явление, состояние которого однозначно определено. Поэтому основное внимание будет уделено исследованию полной математической модели явления, т. е. решению дифференциального уравнения со всеми дополнительными условиями, однозначно определяющими это явление. Сразу возникает вопрос: сколько дополнительных условий должно быть и какие это условия? Дополнительные условия всегда вытекают из физической постановки конкретной задачи и определяются ее природой. Однако очевидно, что с математической точки зрения они должны удовлетворять следующим требованиям:
1) дополнительные условия должны выделять единственное решение (т. е. этих условий должно быть не слишком мало);
2) решение, удовлетворяющее всем дополнительным условиям, должно существовать (т. е. условий должно быть не слиш-, ком много, так чтобы задача не оказалась переопределенной). Кроме того, желательно, чтобы дополнительные условия были таковы, что решение мало изменяется при малых изменениях дополнительных условий. В этом случае говорят, что решение устойчиво по отношению к этим условиям (при этом, конечно, нужно определить, как понимается малость изменения дополнительных условий и решения). Этому требованию удается удовлетворить не всегда, так как дополнительные условия вытекают из физической постановки задачи.
Если задано дифференциальное уравнение со всеми дополнительными условиями, будем говорить, что поставлена начально-краевая задача (или краевая задача — для уравнения эллиптического типа). Задача называется корректно поставленной, если:
1) решение существует;
2) решение единственно;
3) решение устойчиво по отношению ко всем дополнительным условиям. В том случае, когда эти требования нарушаются, задача называется некорректно поставленной.
До середины нашего века, главным образом под влиянием высказываний французского математика Ж. С. Адамара, считалось, что некорректно поставленные задачи математической физики не могут служить математическими моделями реальных физических процессов и не заслуживают изучения математиков. Однако последующие исследования и в первую очередь основополагающие работы русского математика академика А. Н. Тихонова показали, что для весьма широкого класса ес-стественнонаучных проблем некорректно поставленные задачи являются адекватными математическими моделями. Это потребовало разработки новых эффективных математических подходов к их изучению, что позволило создать устойчивые алгоритмы решения определенного класса некорректно поставленных
задач. Для частного случая некорректно поставленных задач, сводящихся к интегральным уравнениям первого рода, эти методы изложены, например, в учебнике А. Б. Васильевой и Н. А. Тихонова.
Дополнительные условия, как уже отмечалось, вытекают из физического содержания изучаемого процесса. Как следует из конкретных примеров, рассмотренных в гл. I, если уравнение содержит производные по времени  , т. е. процесс развивается во времени, следует фиксировать некоторое начальное состояние процесса. При этом, очевидно, нужно задать в начальный момент времени (для определенности будем считать при
, т. е. процесс развивается во времени, следует фиксировать некоторое начальное состояние процесса. При этом, очевидно, нужно задать в начальный момент времени (для определенности будем считать при  значение неизвестной функции
значение неизвестной функции  и ее производных до
и ее производных до  порядка:
порядка:

Условия (1.1) называются начальными условиями.
Физически очевидно, что, в том случае, когда процесс развивается в ограниченной области пространства, для однозначного определения этого процесса следует задать условие на границе области. Конкретный вид этого условия зависит от физической задачи. Как было показано в гл. I на конкретных примерах, наиболее типичными являются условия вида

Условие (1.2) называется краевым, или граничным, условием. При  оно называется первым краевым условием, или условием Дирихле, при
оно называется первым краевым условием, или условием Дирихле, при  вторым краевым условием, или условием Неймана, а в общем случае — третьим краевым условием. Таким образом, полная постановка начальнокраевой задачи имеет вид
вторым краевым условием, или условием Неймана, а в общем случае — третьим краевым условием. Таким образом, полная постановка начальнокраевой задачи имеет вид

Естественно, что для эллиптического уравнения  описывающего стационарный процесс, начальные условия не нужны.
описывающего стационарный процесс, начальные условия не нужны.
Прежде чем переходить к исследованию задачи (1.3) — (1.5) и построению ее решения, следует точно определить, что является решением этой задачи.
Определение. Классическим решением задачи (1.3)
(1.5) называется функция  определенная и непрерывная вместе со всеми производными, входящими в уравнение (1.3, в области
определенная и непрерывная вместе со всеми производными, входящими в уравнение (1.3, в области  удовлетворяющая уравнению (1.3) в этой области, непрерывная вместе с первыми производными по
удовлетворяющая уравнению (1.3) в этой области, непрерывная вместе с первыми производными по  производными по
производными по  при
при  и удовлетворяющая граничному (1.4) и начальным (1.5) условиям.
и удовлетворяющая граничному (1.4) и начальным (1.5) условиям.
В случае граничного условия Дирихле  непрерывности первых производных по
непрерывности первых производных по  в замкнутой области
в замкнутой области  не требуется.
не требуется.
При таком определении классического решения сразу появляются некоторые необходимые условия его существования.
В частности, функции  должны быть непрерывны в соответствующих областях. Появляются также условия согласования граничного и начальных условий. При невыполнении этих условий классического решения не существует. В этом случае можно видоизменить понятие решения и ввести понятие решения в некотором обобщенном смысле.
должны быть непрерывны в соответствующих областях. Появляются также условия согласования граничного и начальных условий. При невыполнении этих условий классического решения не существует. В этом случае можно видоизменить понятие решения и ввести понятие решения в некотором обобщенном смысле.
Полная начально-краевая задача (1.3) — (1.5) в силу ее линейности может быть сведена к трем более простым. Эта процедура называется редукцией общей задачи.
Пусть функции  являются классическими решениями следующих задач:
являются классическими решениями следующих задач:

Тогда непосредственной проверкой можно убедиться, что функция 

является решением общей задачи (1.3) — (1.5).
В дальнейшем будет рассмотрена отдельно каждая из задач (1.6) — (1.8).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
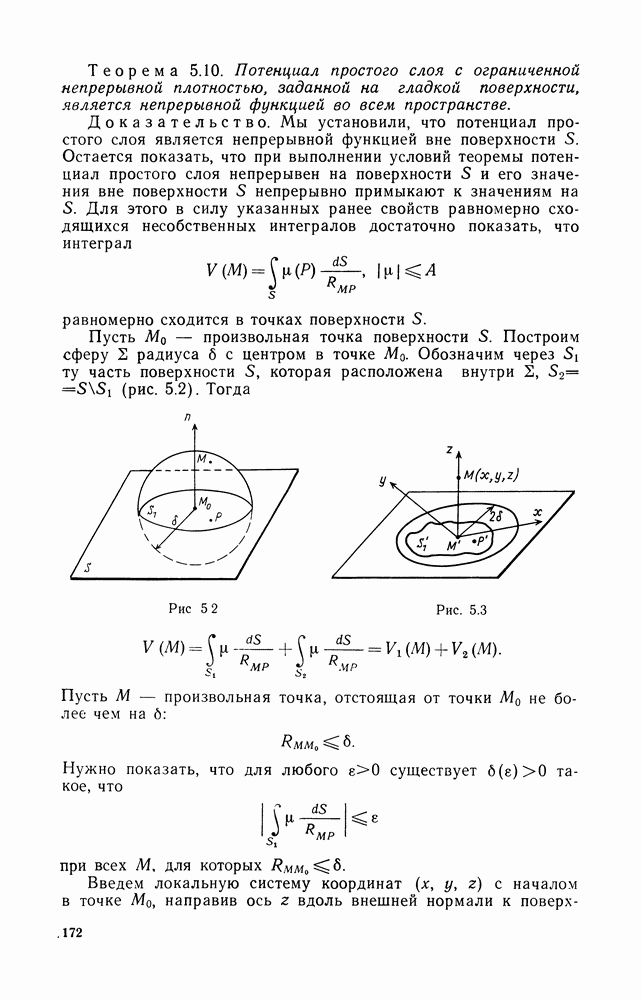
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
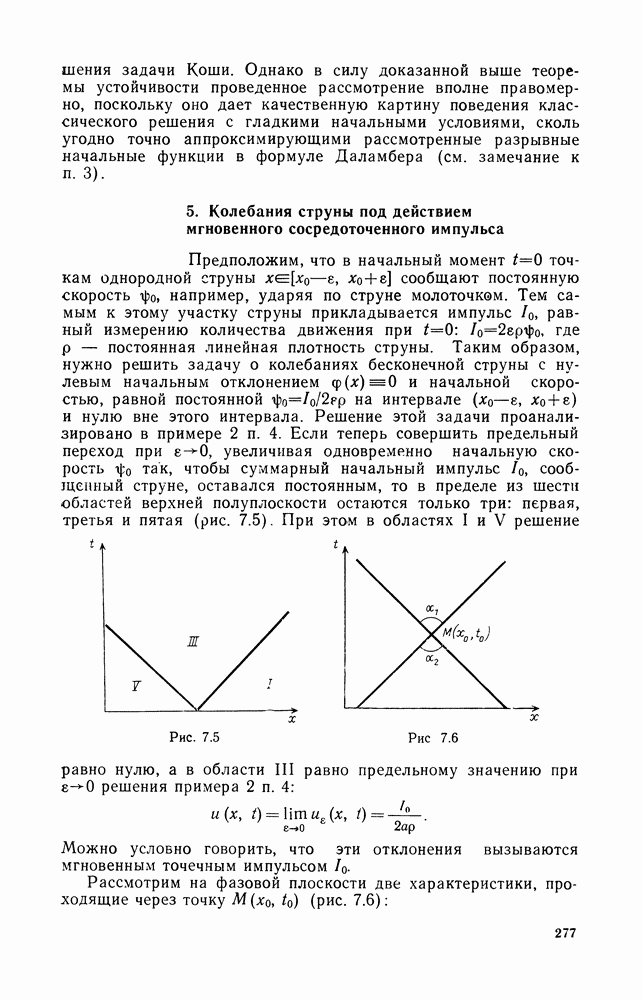
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
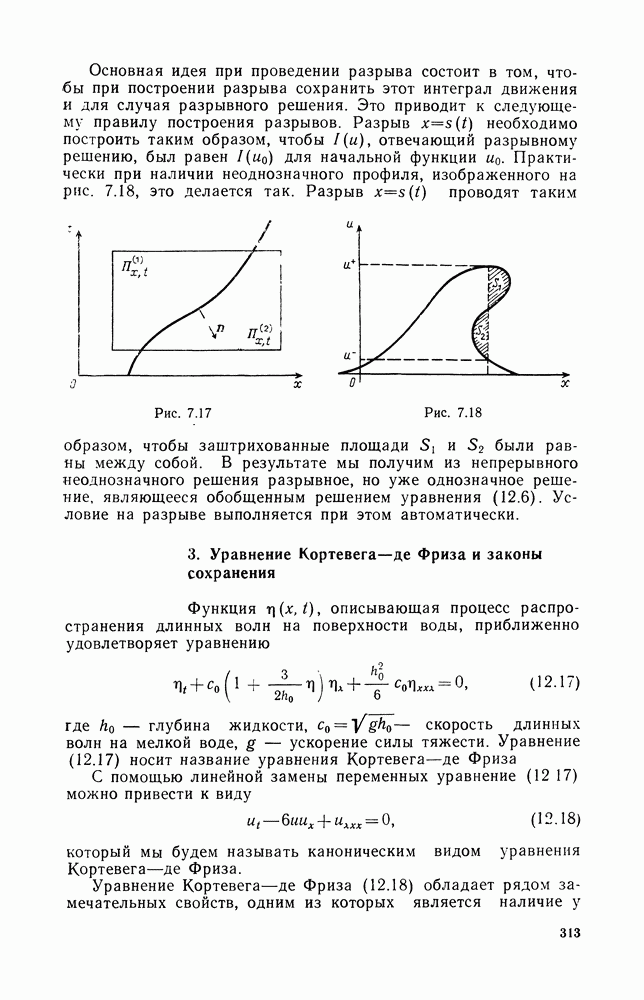
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ