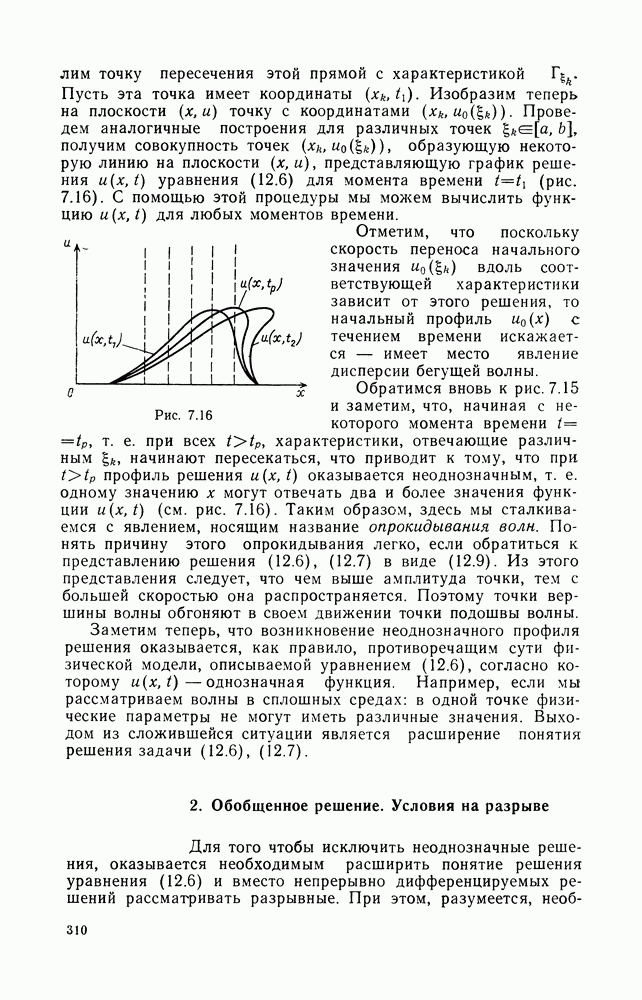
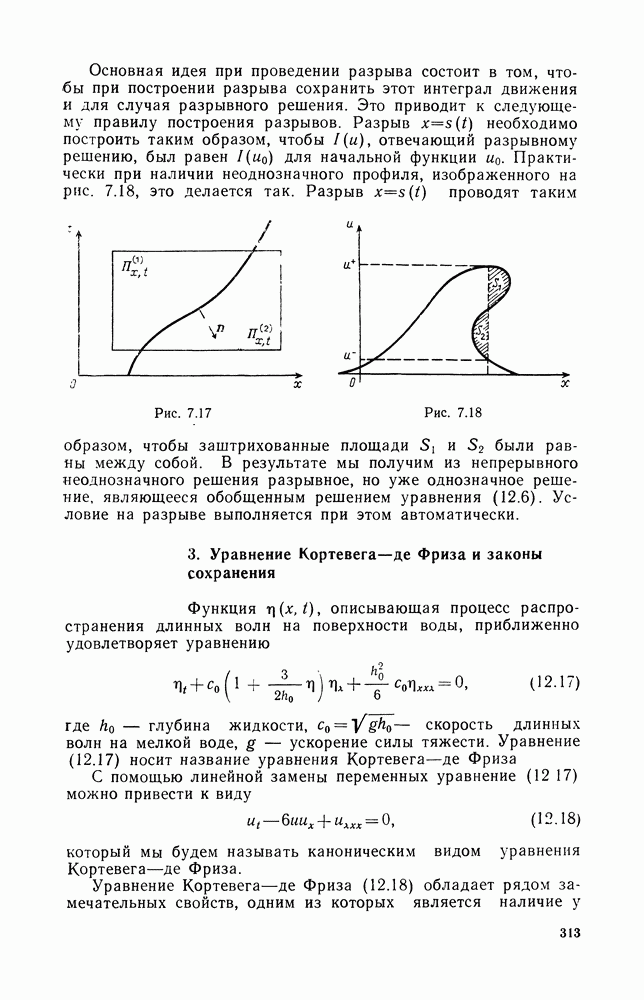
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Основные свойства гармонических функций
Используем формулы Грина для вывода основных свойств гармонических функций.
1. Если и — гармоническая в области  функция, то
функция, то

где  любая гладкая замкнутая поверхность, целиком лежащая в области
любая гладкая замкнутая поверхность, целиком лежащая в области 
Действительно, полагая  и применяя первую формулу Грина к функции и и
и применяя первую формулу Грина к функции и и  в области, ограниченной поверхностью
в области, ограниченной поверхностью  сразу получим (1.12). Формула (1.12) иногда называется формулой Гаусса для гармонических функций. Ее можно интерпретировать как отсутствие источников внутри
сразу получим (1.12). Формула (1.12) иногда называется формулой Гаусса для гармонических функций. Ее можно интерпретировать как отсутствие источников внутри 
Если

что можно интерпретировать как выражение для потока через границу области при наличии источников внутри области.
2. Теорема о среднем. Теорема 5.1. Пусть  гармоническая в области
гармоническая в области  функция. Тогда
функция. Тогда

где  — сфера радиуса а с центром в точке
— сфера радиуса а с центром в точке  целиком лежащая в области
целиком лежащая в области 
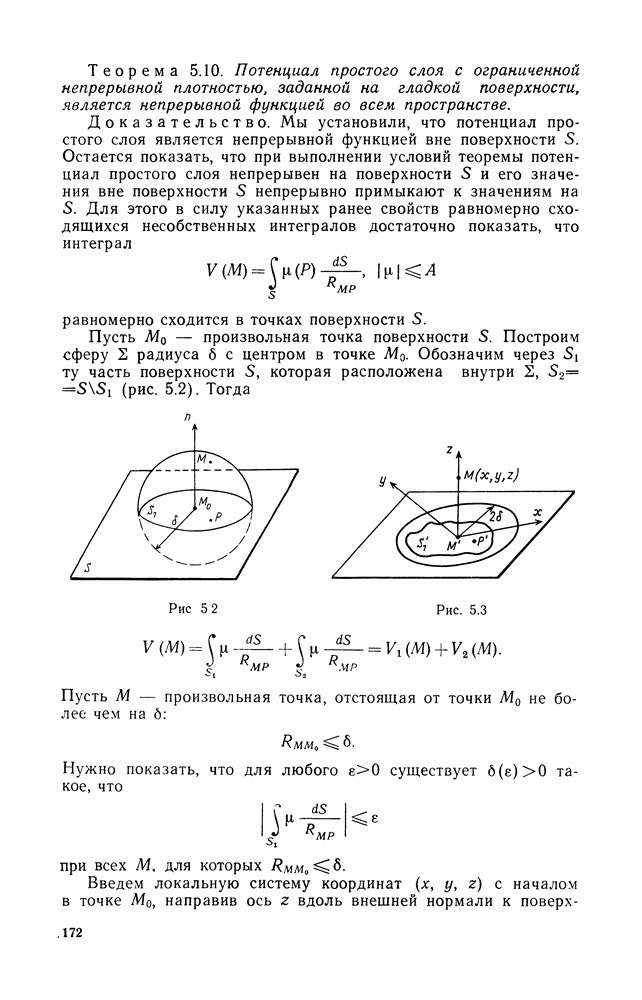
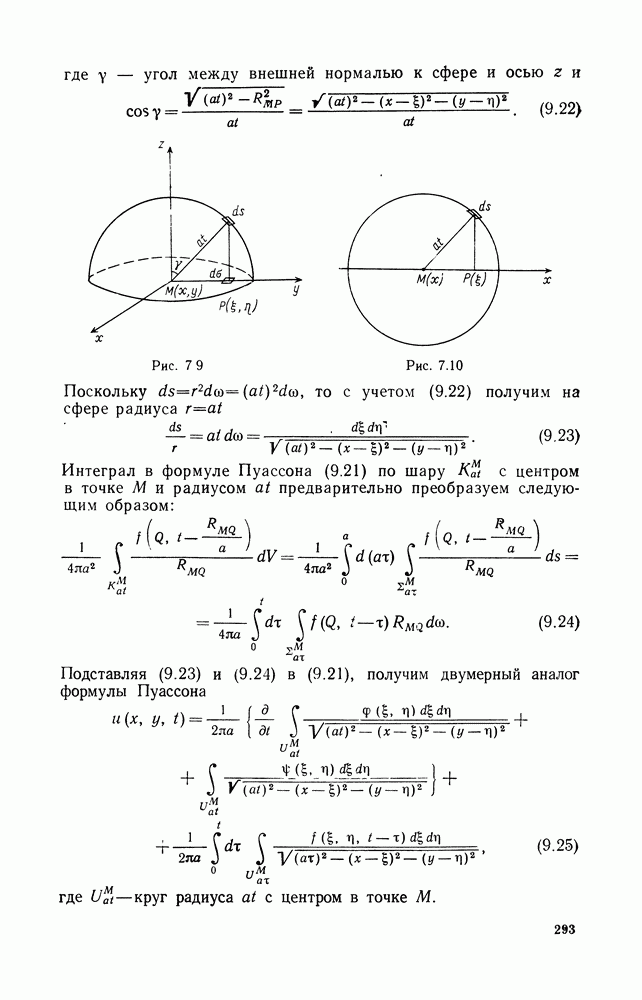
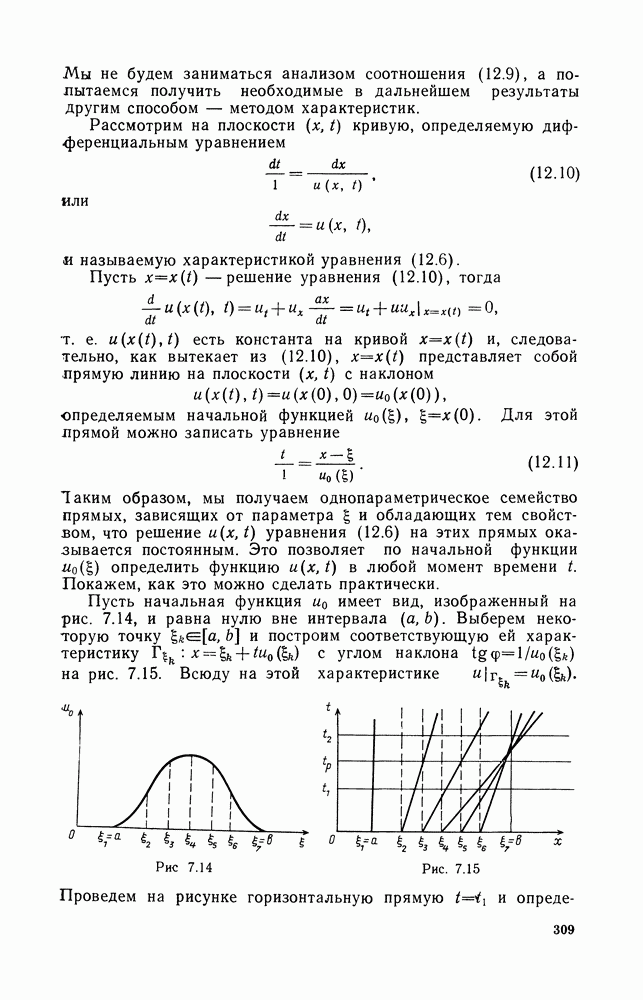
Доказательство. Применим формулу (1.8) к шару с центром в точке  и поверхностью
и поверхностью 

Поскольку

то, принимая во внимание формулу (1.12), получим

Эта теорема утверждает, что значение гармонической функции в точке  равно среднему значению этой функции на любой сфере
равно среднему значению этой функции на любой сфере  с центром в
с центром в  если сфера
если сфера  не выходит из области гармоничности функции
не выходит из области гармоничности функции  .
.
Заметим, что для гармонической функции, непрерывной в замкнутой области  формула среднего значения справедлива и тогда, когда сфера касается границы области
формула среднего значения справедлива и тогда, когда сфера касается границы области 
Действительно, пусть сфера  радиуса
радиуса  касается поверхности
касается поверхности  Формула среднего значения справедлива для любой сферы
Формула среднего значения справедлива для любой сферы  меньшего радиуса
меньшего радиуса 

Переходя в этой формуле к пределу при  и учитывая непрерывность и в замкнутой области
и учитывая непрерывность и в замкнутой области  получим
получим

Для случая двух переменных имеет место аналогичная теорема о среднем значении:

где  окружность радиуса а с центром в
окружность радиуса а с центром в  лежащая в области гармоничности функции
лежащая в области гармоничности функции 
3. Гармоническая в области  функция имеет внутри
функция имеет внутри  производные всех порядков.
производные всех порядков.
Это утверждение непосредственно следует из третьей формулы Грина (1.8), так как при  поверхностные интегралы являются собственными и их можно дифференцировать по координатам точки
поверхностные интегралы являются собственными и их можно дифференцировать по координатам точки  любое число раз.
любое число раз.
Заметим, что из этой же формулы (1.8) следует, что гармоническая функция во всех внутренних точках области аналитична, т. е. разлагается в сходящийся степенной ряд в окрестности любой внутренней точки  При этом радиус сходимости соответствующего ряда не меньше, чем расстояние точки
При этом радиус сходимости соответствующего ряда не меньше, чем расстояние точки  до границы
до границы  области
области 
4. Принцип максимума. Теорема 5.2. Гармоническая в области  функция
функция  непрерывная в замкнутой области
непрерывная в замкнутой области  достигает своих максимальных и минимальных значений на границе
достигает своих максимальных и минимальных значений на границе  области
области 
Доказательство. Так как функция  непрерывна в замкнутой области
непрерывна в замкнутой области  то она достигает своего максимального значения в этой замкнутой области. Докажем, что это максимальное значение достигается функцией
то она достигает своего максимального значения в этой замкнутой области. Докажем, что это максимальное значение достигается функцией  на поверхности
на поверхности  Предположим противное. Пусть функция
Предположим противное. Пусть функция  достигает своего максимального значения в некоторой внутренней точке
достигает своего максимального значения в некоторой внутренней точке  области
области 

 любая точка области
любая точка области  Окружим точку
Окружим точку  сферой
сферой  радиуса
радиуса  целиком лежащей в области
целиком лежащей в области  и применим теорему о среднем:
и применим теорему о среднем:

Написанная цепочка соотношений верна только в случае, если

Действительно, так как крайние элементы цепочки равны, то

Если теперь предположить, что хотя бы в одной точке  сферы
сферы 

то это неравенство, в силу непрерывности  будет иметь
будет иметь
место и в некоторой окрестности точки  на сфере
на сфере  откуда
откуда 

что приводит к противоречию. Следовательно, всюду на сфере

Поскольку  произвольно, то его можно выбрать так, чтобы сфера 2° касалась поверхности
произвольно, то его можно выбрать так, чтобы сфера 2° касалась поверхности  Точку касания обозначим
Точку касания обозначим  В точке
В точке  и достигается максимальное значение
и достигается максимальное значение 
Применяя проведенные рассуждения к гармонической функции  докажем достижение на поверхности
докажем достижение на поверхности  минимального значения.
минимального значения.
Замечание. Формулировку принципа максимума можно усилить. Покажем, что если непрерывная в замкнутой области  гармоническая функция
гармоническая функция  достигает своего максимального значения в некоторой внутренней точке
достигает своего максимального значения в некоторой внутренней точке  области
области  то она равна постоянной. Из проведенных рассуждений следует, что функция
то она равна постоянной. Из проведенных рассуждений следует, что функция  равна
равна  не только на сфере
не только на сфере  , но и, в силу произвольности
, но и, в силу произвольности  всюду внутри шара
всюду внутри шара  ограниченного этой сферой.
ограниченного этой сферой.
Возьмем произвольную точку  области
области  Соединим точки
Соединим точки  и
и  кривой С, целиком лежащей в области
кривой С, целиком лежащей в области  Обозначим наименьшее расстояние точек С от поверхности
Обозначим наименьшее расстояние точек С от поверхности  через
через  а длину кривой С — через
а длину кривой С — через  Пусть точка
Пусть точка  является последней точкой пересечения кривой С и сферы
является последней точкой пересечения кривой С и сферы  . Поскольку
. Поскольку  то, повторяя проведенные рассуждения, получим, что всюду внутри шара
то, повторяя проведенные рассуждения, получим, что всюду внутри шара  радиуса
радиуса  с центром в
с центром в  функция и постоянна и равна
функция и постоянна и равна  Взяв на кривой С точку
Взяв на кривой С точку  являющуюся последней точкой пересечения кривой С и сферы
являющуюся последней точкой пересечения кривой С и сферы  и продолжая данный процесс, в результате конечного числа шагов, которое не более
и продолжая данный процесс, в результате конечного числа шагов, которое не более  получим, что внутри шара, которому принадлежит точка
получим, что внутри шара, которому принадлежит точка  функция и постоянна и равна
функция и постоянна и равна  В силу произвольности точки
В силу произвольности точки  и непрерывности функции и в замкнутой области
и непрерывности функции и в замкнутой области  заключаем, что
заключаем, что  всюду в замкнутой области
всюду в замкнутой области  Таким образом, из всех гармонических функций, непрерывных в
Таким образом, из всех гармонических функций, непрерывных в  только постоянная может достигать своего максимального значения во внутренних точках области.
только постоянная может достигать своего максимального значения во внутренних точках области.
Аналогичное утверждение можно доказать и относительно минимального значения.
Таким образом, формулировку принципа максимума можно усилить и сформулировать его так: гармоническая в области  функция, отличная от постоянной, непрерывная в замкнутой области
функция, отличная от постоянной, непрерывная в замкнутой области  достигает своих максимальных и минимальных значений только на границе
достигает своих максимальных и минимальных значений только на границе  области
области 
Доказанное свойство гармонических функций чрезвычайно важно, и мы неоднократно будем его использовать.
Укажем одно следствие из принципа максимума: если две гармонические в  функции
функции  непрерывны в замкнутой области
непрерывны в замкнутой области  и
и

то всюду внутри области и  Доказательство этого утверждения, носящего название принципа сравнения, очевидно.
Доказательство этого утверждения, носящего название принципа сравнения, очевидно.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
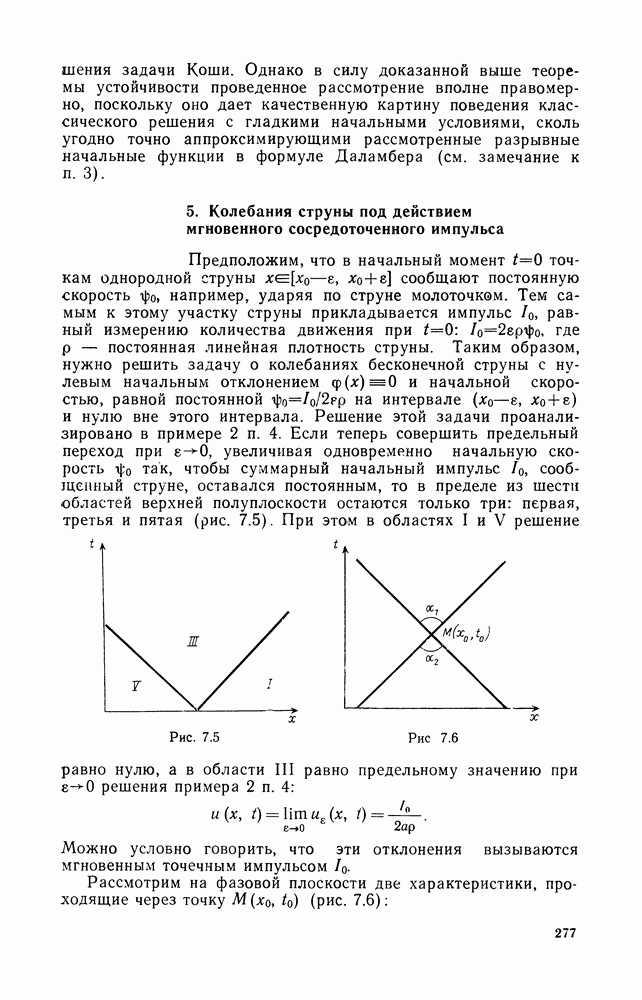
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ