| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
При исследовании реальных физических процессов и явлений методами математического моделирования одним из важных этапов является формулировка математической модели, т. е. четкая постановка математической задачи, достаточно адекватной исследуемому кругу физических явлений
Весьма широкий класс математических моделей, описывающих физические явления, представляют собой дифференциальные уравнения в частных производных.
В этой главе рассматриваются наиболее типичные физические задачи, математическими моделями которых служат начально-краевые задачи для дифференциальных уравнений в частных производных второго порядка.
§ 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
1. Малые продольные колебания упругого стержня
Рассмотрим упругий стержень длины  расположенный в состоянии равновесия вдоль оси х от точки
расположенный в состоянии равновесия вдоль оси х от точки  до точки
до точки 
Будем рассматривать малые продольные колебания стержня, при которых напряжения, возникающие в процессе колебаний, подчиняются закону Гука. Тогда стержень можно рассматривать как абсолютно упругий.
Поскольку рассматриваются продольные колебания упругого стержня, то все точки одного сечения испытывают одно и то же смещение. Обозначим через  продольное смещение в момент времени
продольное смещение в момент времени  сечения стержня, характеризующегося абсциссой х в состоянии равновесия. Выбранная нами геометрическая переменная х называется переменной Лагранжа. В переменных Лагранжа каждая физическая точка стержня в течение всего рассматриваемого процесса характеризуется одной и той же геометрической координатой х. Физическая точка, занимавшая в начальный момент в состоянии равновесия
сечения стержня, характеризующегося абсциссой х в состоянии равновесия. Выбранная нами геометрическая переменная х называется переменной Лагранжа. В переменных Лагранжа каждая физическая точка стержня в течение всего рассматриваемого процесса характеризуется одной и той же геометрической координатой х. Физическая точка, занимавшая в начальный момент в состоянии равновесия
положение х, в любой последующий момент времени будет находиться в точке с координатой 
Обозначим через  линейную плотность стержня,
линейную плотность стержня,  коэффициент упругости материала стержня,
коэффициент упругости материала стержня,  плотность импульса продольной внешней силы, приложенной к стержню.
плотность импульса продольной внешней силы, приложенной к стержню.
Поскольку рассматриваются малые колебания, то согласно закону Гука сила, вызывающая упругую деформацию бесконечно малого элемента  стержня, равна
стержня, равна

где  — относительное удлинение элемента:
— относительное удлинение элемента:

Поскольку в формуле (1.1)

и сила упругого натяжения в сечении х равна

Для вывода дифференциального уравнения, описывающего малые продольные колебания стержне воспользуемся вариационным принципом.
Вариационный принцип. Если материальная система, находящаяся в поле внешних сил, характеризуется для любого момента времени  кинетической энергией
кинетической энергией  и потенциальной энергией
и потенциальной энергией  то переход ее из состояния в момент времени
то переход ее из состояния в момент времени  в новое состояние в момент времени
в новое состояние в момент времени  происходит так, что функционал
происходит так, что функционал

имеет экстремальное значение.
Так как рассматривается случай малых колебаний, при подсчете кинетической и потенциальной энергии членами высшего порядка малости можно пренебречь.
Кинетическая энергия  малого участка стержня
малого участка стержня  равна (считаем, что в пределах участка
равна (считаем, что в пределах участка  все параметры сохраняют постоянное значение)
все параметры сохраняют постоянное значение)

Следовательно, кинетическая энергия всего стержня равна

Потенциальная энергия системы «стержень в поле внешних сил»  складывается из потенциальной энергии упругой деформации
складывается из потенциальной энергии упругой деформации  и из работы А внешней силы:
и из работы А внешней силы:

Работа  внешней силы, затраченная на перемещение малого элемента
внешней силы, затраченная на перемещение малого элемента  из состояния равновесия в состояние
из состояния равновесия в состояние  равна
равна

Полная работа А внешней силы записывается следующим образом:

Подсчитаем энергию упругой деформации. Выделим малый участок стержня длиной  считая, что в пределах данного участка коэффициент упругости является постоянным
считая, что в пределах данного участка коэффициент упругости является постоянным  На участок
На участок  со стороны соседнего элемента действует сила упругого напряжения
со стороны соседнего элемента действует сила упругого напряжения  равная
равная  где
где  относительное удлинение элемента
относительное удлинение элемента  При перемещении элемента
При перемещении элемента  на расстояние
на расстояние  будет совершена работа
будет совершена работа

С перемещением на расстояние  связано изменение относительного удлинения
связано изменение относительного удлинения  на величину Де, причем
на величину Де, причем

Следовательно,  и
и

Проинтегрировав последнее равенство от 0 до  получаем выражение для энергии упругой деформации, которой обладает выделенный элемент:
получаем выражение для энергии упругой деформации, которой обладает выделенный элемент:

Рассмотрим теперь неоднородный стержень с коэффициен том упругости  и применим формулу (1.3) для бесконечно малого элемента
и применим формулу (1.3) для бесконечно малого элемента  учитывая, что
учитывая, что 

Проинтегрировав последнее равенство по х от 0 до I, получим

Составим функционал (1.2): и 

Выпишем для функционала (1.5) уравнение Эйлера-Остроградского, являющееся необходимым условием экстремума функционала

где

Вычисляя производные, входящие в формулу (1.6), получим уравнение Эйлера-Остроградского для функционала (1.5), описывающее малые продольные колебания упругого стержня:

Выражение в левой части уравнения (1.7) описывает силы инерции, первое слагаемое в правой части — упругое взаимодействие и второй член в правой части — действие внешней силы.
Если стержень однородный и его линейная плотность и коэффициент упругости постоянны:  то уравнение (1.7) обычно записывается в следующем виде:
то уравнение (1.7) обычно записывается в следующем виде:

где

Уравнения (1.7) и (1.8) представляют собой простейшие примеры уравнений колебаний.
При математическом описании физического явления необходимо прежде всего грамотно поставить задачу, т. е. сформулировать условия, достаточные для однозначного определения процесса.
Дифференциальные уравнения с обыкновенными и тем более частными производными имеют бесконечное множество решений. Для однозначной характеристики процесса кроме
уравнения нужно задать еще некоторые дополнительные условия. Задавая дополнительные условия, нужно помнить, что эти условия должны обеспечивать единственность и существование решения, т. е. задача не должна быть недоопределенной или переопределенной.
Как известно в случае обыкновенных дифференциальных уравнений эти условия определяются постановкой конкретной физической задачи и могут иметь различную форму, в зависимости от которой приходят к задаче Коши или к краевой задаче. В случае дифференциальных уравнений в частных производных в качестве дополнительных тоже используются начальные и граничные условия.
Начальные условия. Начальные условия определяют состояние системы в  некоторый выделенный момент времени, который считается «начальным». Например, в качестве начального момента времени можно взять
некоторый выделенный момент времени, который считается «начальным». Например, в качестве начального момента времени можно взять  В случае уравнения (1.7), описывающего малые продольные колебания стержня, нужно в начальный момент
В случае уравнения (1.7), описывающего малые продольные колебания стержня, нужно в начальный момент  задать положение каждой точки стержня и ее скорость:
задать положение каждой точки стержня и ее скорость:

где  и
и  -некоторые заданные функции. Если функция
-некоторые заданные функции. Если функция  отлична от нуля, это означает, что в начальный момент времени стержень не находился в положении равновесия. Если функция
отлична от нуля, это означает, что в начальный момент времени стержень не находился в положении равновесия. Если функция  отлична от нуля, это означает, что в начальный момент каждой точке стержня была сообщена мгновенная начальная скорость, например двигавшийся стержень мгновенно остановился.
отлична от нуля, это означает, что в начальный момент каждой точке стержня была сообщена мгновенная начальная скорость, например двигавшийся стержень мгновенно остановился.
Граничные условия. Мы будем рассматривать линейные граничные условия. Будем считать, что стержень имеет длину  и занимает вдоль оси х отрезок от 0 до
и занимает вдоль оси х отрезок от 0 до  Для определенности будем рассматривать левый конец стержня
Для определенности будем рассматривать левый конец стержня  . С физической точки зрения ясно, что левый конец стержня может находиться в различных условиях. Например, он может быть жестко закреплен (стержень заделан в стену) или же двигаться по определенному закону (стержень жестко прикреплен к плите, совершающей заданное движение). Математически это условие записывается следующим образом:
. С физической точки зрения ясно, что левый конец стержня может находиться в различных условиях. Например, он может быть жестко закреплен (стержень заделан в стену) или же двигаться по определенному закону (стержень жестко прикреплен к плите, совершающей заданное движение). Математически это условие записывается следующим образом:

где  некоторая постоянная,
некоторая постоянная,  -заданная функция Условие (1.9) называется граничным условием первого рода, или условием Дирихле. В частности, если функция
-заданная функция Условие (1.9) называется граничным условием первого рода, или условием Дирихле. В частности, если функция  тождественно равна нулю, что соответствует жестко закрепленному левому концу стержня, то граничное условие (1.9) называется однородным граничным условием первого рода, или
тождественно равна нулю, что соответствует жестко закрепленному левому концу стержня, то граничное условие (1.9) называется однородным граничным условием первого рода, или
однородным условием Дирихле. Если же функция  отличается от нуля, то условие (1.9) называется неоднородным граничным условием первого рода, или неоднородным условием Дирихле.
отличается от нуля, то условие (1.9) называется неоднородным граничным условием первого рода, или неоднородным условием Дирихле.
Если задан закон изменения силы  приложенной к левому концу
приложенной к левому концу  стержня и действующей в продольном направлении, то, используя закон Гука, граничный режим на этом конце можно записать следующим образом (напомним, что
стержня и действующей в продольном направлении, то, используя закон Гука, граничный режим на этом конце можно записать следующим образом (напомним, что  коэффициент упругости стержня):
коэффициент упругости стержня):

или

где  заданная функция.
заданная функция.  к (0)
к (0)
Условие (1.10) называется граничным условием второго рода, или условием Неймана. Если  то условие (1.10) называется однородным граничным условием второго рода, или однородным условием Неймана. Физически это условие означает, что левый конец стержня свободен: к нему не приложена внешняя сила, и он не закреплен.
то условие (1.10) называется однородным граничным условием второго рода, или однородным условием Неймана. Физически это условие означает, что левый конец стержня свободен: к нему не приложена внешняя сила, и он не закреплен.
Пусть, наконец, левый конец стержня закреплен упруго, например с помощью пружины, коэффициент жесткости которой равен а. Сила упругости, стремящаяся вернуть левый конец стержня в положение равновесия, согласно закону Гука пропорциональна смещению  Граничный режим можно записать следующим образом:
Граничный режим можно записать следующим образом:

или

где  Условие (1.11) называется однородным граничным условием третьего рода.
Условие (1.11) называется однородным граничным условием третьего рода.
Возможно задание при  линейной комбинации упругого закрепления и смещения. Например, стержень с помощью пружины может быть прикреплен к плите, которая перемещается по некоторому закону, определяемому функцией
линейной комбинации упругого закрепления и смещения. Например, стержень с помощью пружины может быть прикреплен к плите, которая перемещается по некоторому закону, определяемому функцией  параллельно стержню. В этом случае получается граничное условие следующего вида:
параллельно стержню. В этом случае получается граничное условие следующего вида:

или

где  - заданная функция. Условие (1.12) называется неоднородным граничным условием третьего рода.
- заданная функция. Условие (1.12) называется неоднородным граничным условием третьего рода.
Разумеется, физическая постановка задачи может приводить и к более сложным граничным условиям, в частности
нелинейным. Такие условия возникают, например, при упругом закреплении, не подчиняющемся закону Гука. Если натяжение на левом конце стержня является нелинейной функцией смещения и  то граничное условие примет вид
то граничное условие примет вид

где  определяет упругую силу, приложенную к левому концу стержня и действующую в продольном направлении.
определяет упругую силу, приложенную к левому концу стержня и действующую в продольном направлении.
В граничное условие могут входить производные функции по  Например, если к концу пружины прикреплена пластинка, плоскость которой перпендикулярна оси пружины, и конец пружины испытывает сопротивление среды, пропорциональное скорости его движения, то граничное условие записывается в виде
Например, если к концу пружины прикреплена пластинка, плоскость которой перпендикулярна оси пружины, и конец пружины испытывает сопротивление среды, пропорциональное скорости его движения, то граничное условие записывается в виде

где а — коэффициент сопротивления среды.
Аналогичные граничные условия становятся на правом конце стержня. При этом возможны комбинации различных граничных условий на правом и левом концах стержня.
Граничные условия могут включать и производные порядков выше первого. Пусть, например, упругий стержень длины
I расположен вертикально и его верхний конец закреплен неподвижно (заделан в потолок). К нижнему концу стержня прикреплен массивный абсолютно жесткий (т. е. недеформируемый) груз  Груз находится на площадке и не растягивает и не сжимает стержень. В начальный момент времени
Груз находится на площадке и не растягивает и не сжимает стержень. В начальный момент времени  площадку убирают. Предположим, что масса стержня
площадку убирают. Предположим, что масса стержня  много меньше массы груза
много меньше массы груза  и действием силы тяжести на стержень можно пренебречь. Направим ось вдоль стержня, так что его верхний конец будет иметь абсциссу
и действием силы тяжести на стержень можно пренебречь. Направим ось вдоль стержня, так что его верхний конец будет иметь абсциссу  Тогда на верхнем конце стержня
Тогда на верхнем конце стержня  граничным условием будет однородное условие Дирихле
граничным условием будет однородное условие Дирихле

а граничное условие на нижнем конце стержня  имеет вид
имеет вид

где  площадь поперечного сечения стержня.
площадь поперечного сечения стержня.
В дальнейшем мы будем говорить о трех основных типах граничных условий первого, второго и третьего рода. Рассмотрим, например, нагруженный стержень с приложенной к нему внешней силой, всем точкам которого в начальный момент времени  задаются некоторые смещение и некоторая скорость. Пусть левый конец стержня упруго прикреплен к движущейся точке закрепления, а правый конец движется по заданному
задаются некоторые смещение и некоторая скорость. Пусть левый конец стержня упруго прикреплен к движущейся точке закрепления, а правый конец движется по заданному
закону. Сформулируем математическую задачу, описывающую процесс движения такого стержня:

где  заданные функции,
заданные функции,  постоянные коэффициенты.
постоянные коэффициенты.
Задача (1.13) называется начально-краевой задачей.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ОСНОВНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ И ПОСТАНОВКА НАЧАЛЬНО-КРАЕВЫХ ЗАДАЧ
- § 1. ФИЗИЧЕСКИЕ ЗАДАЧИ, СВЯЗАННЫЕ С ВОЛНОВЫМИ ПРОЦЕССАМИ
- 2. Малые поперечные колебания упругой струны
- 3. Случай многих пространственных переменных
- § 2. ПРОЦЕССЫ ТЕПЛОМАССОПЕРЕНОСА
- § 3. СТАЦИОНАРНЫЕ ПРОЦЕССЫ
- 1. Стационарное распределение тепла
- 2. Задачи электростатики
- 3. Установившиеся колебания
- 4. Установившиеся электромагнитные колебания
- 5. Постановка краевых задач
- § 4. ОБЩИЕ ЗАМЕЧАНИЯ
- Глава II. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
- § 1. КЛАССИФИКАЦИЯ УРАВНЕНИЙ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. ПРИВЕДЕНИЕ УРАВНЕНИЯ С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ К КАНОНИЧЕСКОМУ ВИДУ
- § 3. КЛАССИФИКАЦИЯ УРАВНЕНИЙ В СЛУЧАЕ МНОГИХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
- Глава III. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- § 2. ПЕРВАЯ И ВТОРАЯ ФОРМУЛЫ ГРИНА
- § 3. ПОЛНЫЕ И ЗАМКНУТЫЕ СИСТЕМЫ ФУНКЦИЙ
- § 4. ОБЩАЯ СХЕМА МЕТОДА РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ
- § 5. МЕТОД РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ ДЛЯ НЕОДНОРОДНОГО УРАВНЕНИЯ
- § 6. НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- § 7. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ДЛЯ ЭЛЛИПТИЧЕСКОГО УРАВНЕНИЯ
- § 8. ПРОСТЕЙШИЕ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ
- Глава IV. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 1. УРАВНЕНИЕ СПЕЦИАЛЬНЫХ ФУНКЦИЙ И СВОЙСТВА ЕГО РЕШЕНИЙ
- § 2. ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ
- 2. Свойства гамма-функции
- 3. Степенной ряд для функций Бесселя
- 4. Рекуррентные формулы
- 5. Функции Бесселя полуцелого порядка
- 6. Интегральное представление функций Бесселя
- 7. Функции Ханкеля. Интегральное представление
- 8. Связь функций Ханкеля и Бесселя. Функция Неймана
- 9. Линейная независимость цилиндрических функций
- 10. Асимптотика цилиндрических функций
- 11. Цилиндрические функции чисто мнимого аргумента. Функции Инфельда и Макдональда
- § 3. КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
- 2. Основные свойства классических ортогональных полиномов
- 3. Производящая функция классических ортогональных полиномов
- 4. Полиномы Якоби
- 5. Полиномы Лежандра
- 6. Полиномы Лагерра
- 7. Полиномы Эрмита
- § 4. ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
- 2. Краевая задача для присоединенных функций Лежандра
- 3. Полнота и замкнутость системы присоединенных функций Лежандра
- § 5. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 6. ШАРОВЫЕ ФУНКЦИИ
- § 7. СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА ЛАПЛАСА ДЛЯ КАНОНИЧЕСКИХ ОБЛАСТЕЙ
- 2. Собственные функции цилиндра
- 3. Собственные функции шара
- Глава V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Основные свойства гармонических функций
- § 2. ВНУТРЕННИЕ КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА
- 2. Внутренние вторая и третья краевые задачи
- § 3. ВНЕШНИЕ КРАЕВЫЕ ЗАДАЧИ
- 2. Единственность решения внешних задач в трехмерном случае
- 3. Единственность решения внешних задач для уравнения Лапласа на плоскости
- § 4. ФУНКЦИЯ ГРИНА ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства функции Грина задачи Дирихле
- 3. Функция Грина внутренней третьей краевой задачи
- 4. Функция Грина внутренней задачи Неймана
- 5. Функции Грина внешних краевых задач
- 6. Примеры построения функций Грина
- 7. Функция Грина задачи Дирихле на плоскости
- § 5. РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В КРУГЕ И ПРЯМОУГОЛЬНИКЕ
- 2. Краевая задача для уравнения Лапласа в прямоугольнике
- § 6. ОСНОВЫ ТЕОРИИ ПОТЕНЦИАЛА
- 2. Несобственные интегралы, зависящие от параметра
- 3. Поверхностные потенциалы
- 4. Непрерывность потенциала простого слоя
- 5. Поверхности Ляпунова
- 6. Существование и непрерывность прямых значений потенциала двойного слоя на поверхности
- 7. Разрыв потенциала двойного слоя
- 8. Разрыв нормальной производной потенциала простого слоя
- § 7. МЕТОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ
- 2. Интегральное уравнение для внутренней задачи Дирихле
- 3. Интегральное уравнение для внешней задачи Неймана
- 4. Интегральное уравнение для внутренней задачи Неймана и внешней задачи Дирихле
- Глава VI. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. ПОСТАНОВКА НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ
- § 2. ПРИНЦИП МАКСИМУМА
- § 3. ТЕОРЕМЫ ЕДИНСТВЕННОСТИ И УСТОЙЧИВОСТИ
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В СЛУЧАЕ ОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Существование классического решения уравнения теплопроводности на отрезке
- § 5. ФУНКЦИЯ ГРИНА
- § 6. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ И НЕОДНОРОДНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- 2. Неоднородное граничное условие
- § 7. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Теорема единственности
- 3. Фундаментальное решение. Интеграл Пуассона
- 4. Свойства фундаментального решения
- § 8. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- 2. Пример
- § 9. НЕОДНОРОДНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ НА БЕСКОНЕЧНОЙ ПРЯМОЙ
- § 10. НАЧАЛЬНАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПРОСТРАНСТВЕ
- § 11. РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ НА ПОЛУПРЯМОЙ
- 2. Однородные граничные условия
- 3. Краевой режим
- 4. Неоднородное граничное условие второго рода
- § 12. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
- § 13. УРАВНЕНИЕ НЕЛИНЕЙНОЙ ТЕПЛОПРОВОДНОСТИ И ГОРЕНИЯ
- Глава VII. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 4. СУЩЕСТВОВАНИЕ РЕШЕНИЯ УРАВНЕНИЯ КОЛЕБАНИЙ В ОГРАНИЧЕННОЙ ОБЛАСТИ
- § 5. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОГРАНИЧЕННОЙ СТРУНЫ
- § 6. ФОРМУЛА ГРИНА ДЛЯ УРАВНЕНИЯ КОЛЕБАНИЙ
- § 7. УРАВНЕНИЕ КОЛЕБАНИЙ НА НЕОГРАНИЧЕННОЙ ПРЯМОЙ
- 2. Формула Даламбера
- 3. Существование, единственность и устойчивость решения задачи Коши
- 4. Физическая интерпретация решения
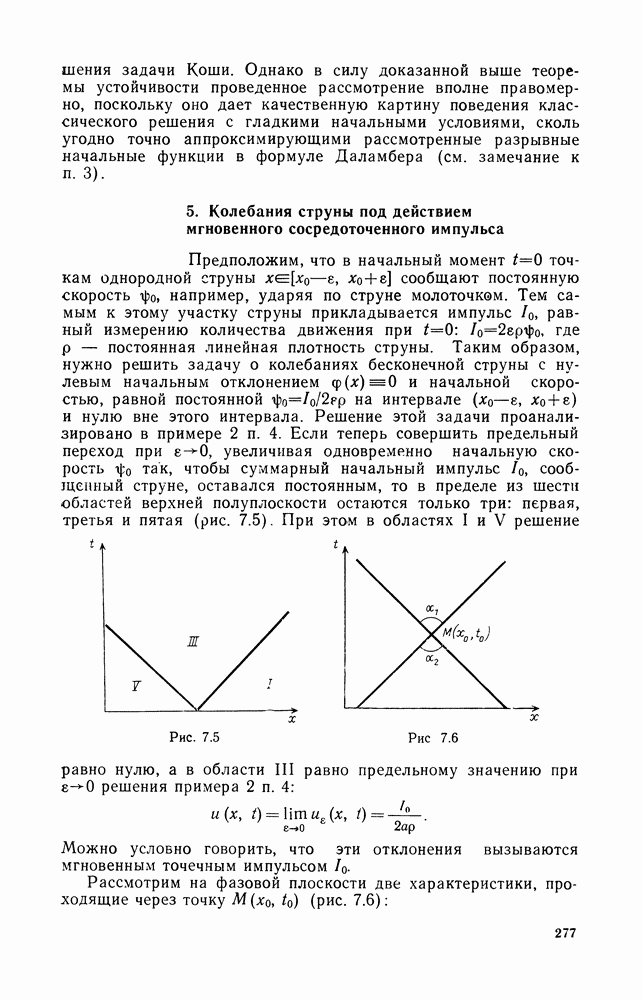
- 5. Колебания струны под действием мгновенного сосредоточенного импульса
- 6. Существование и единственность решения
- § 8. ЗАДАЧИ ДЛЯ ПОЛУОГРАНИЧЕННОЙ ПРЯМОЙ
- § 9. КОЛЕБАНИЯ В НЕОГРАНИЧЕННОМ ПРОСТРАНСТВЕ
- 2. Формула Кирхгофа
- 3. Формула Пуассона
- 4. Метод спуска
- 5. Локальные начальные условия
- 6. Установившиеся колебания
- § 10. ЗАДАЧА С ДАННЫМИ НА ХАРАКТЕРИСТИКАХ (ЗАДАЧА ГУРСА)
- § 11. ОБЩАЯ ЗАДАЧА КОШИ. ФУНКЦИЯ РИМАНА
- § 12. НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
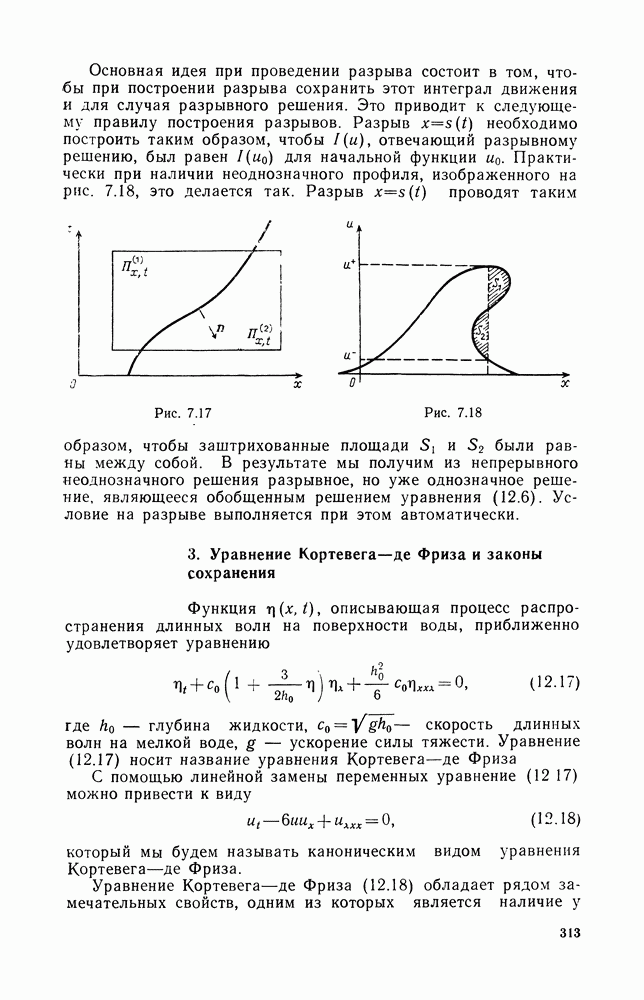
- 2. Обобщенное решение. Условия на разрыве
- 3. Уравнение Кортевега — де Фриза и законы сохранения
- 4. Схема метода обратной задачи
- 5. Солитонные решения
- Глава VIII. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА. КРАЕВЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 1. ЗАДАЧА ШТУРМА—ЛИУВИЛЛЯ ДЛЯ ОПЕРАТОРА ЛАПЛАСА
- 2. Свойства собственных значений и собственных функций
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- 3. Потенциалы уравнения Гельмгольца
- 4. Принцип максимума для уравнения …
- § 3. ВНУТРЕННИЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 4. ФУНКЦИЯ ГРИНА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЯ ГЕЛЬМГОЛЬЦА
- § 5. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- § 6. ЗАДАЧА ДЛЯ УРАВНЕНИЯ … В НЕОГРАНИЧЕННОЙ ОБЛАСТИ
- 2. Принцип предельного поглощения
- ЛИТЕРАТУРА
- ДОПОЛНЕНИЕ